|
|
[ Fearless
Engineers ] [ Seitenende ] |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
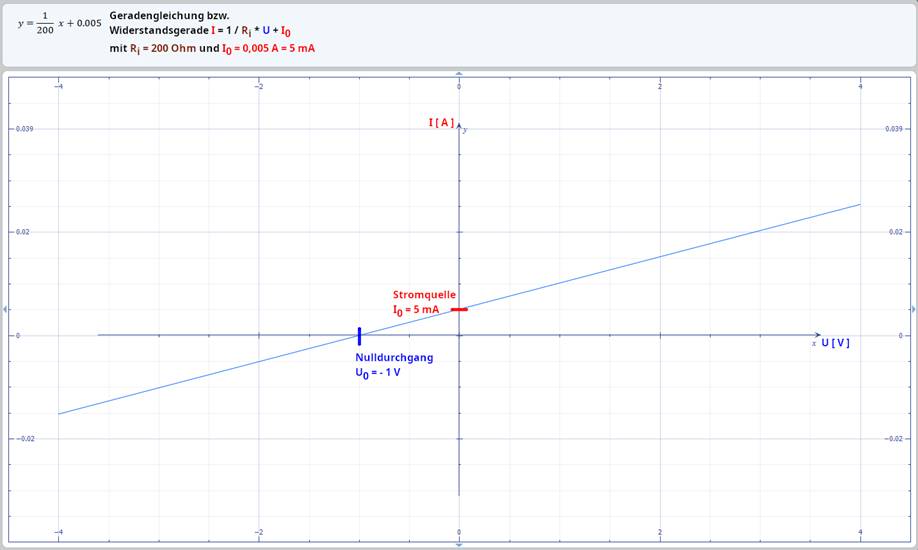
Fearless Engineers – Rätselhafter Strom IR = f(UR) Einfache
Schaltung mit einem ohmschen Widerstand Eine einfache elektrische Schaltung besteht
aus einem ohmschen Widerstand R unbekannter Größe, sodass dessen
Widerstandswert nicht bekannt ist. Zu dem ohmschen Widerstand R gibt es aber eine
Wertetabelle mit IR = f(UR), sprich „IR ist
eine Funktion von UR“ als sogenannte lineare Widerstandsgerade im
Sinne einer Kennlinie:
Leider ist das Aufgabenblatt mit der obenstehenden
Wertetabelle durch versehentliches Verschütten von etwas Wasser aus der
Trinkflasche teilweise unleserlich geworden, sodass sich nur noch zwei
Stromstärkewerte IR erkennen und ablesen lassen. Aufgabe a)
Zeichne den Graphen der Funktion IR = f(UR)
zur obenstehenden Wertetabelle mit dem Maßstab 1 V " 2 cm b)
Welche Stromstärke I0 lässt sich am
Schnittpunkt der Widerstandsgeraden mit der Stromachse (= Senkrechte)
ablesen? c)
Interpretiere den Wert der Stromstärke I0 >
0 am Schnittpunkt mit der Spannung U0 = 0. d)
Wende die mathematische Geradengleichung auf die
elektrotechnische Widerstandsgerade an! e)
Berechne den Konstantstrom I0 an der Stelle I0
= f(U0) mit U0 = 0 V (siehe Wertetabelle). f)
Wird bei der elektrischen Schaltung mit dem linearen, d.h.
rein ohmschen Widerstand die Stromstärke durch den Widerstand durch eine
Spannungs- oder Stromquelle aufgebracht? g)
Wie groß muss die Klemmenspannung Ukl einer
linearen Spannungsquelle sein, damit durch den Innenwiderstand Ri
ein Strom IRi der Stromstärke IRi = 20 mA fließt? Lösung zur Aufgabe a) Zeichne den Graphen der Funktion IR
= f(UR) zur obenstehenden Wertetabelle mit dem Maßstab 1 V " 2 cm In der Mathematik, aber auch in der
Elektrotechnik, gibt zu jeder rechnerischen, formelmäßigen Lösung oder Lösung
mittels der Geradengleichung y = m a + b bzw. der Widerstandsgeraden
I = 1/R * U * I0 eine grafische, d.h.
zeichnerische Lösung. So auch im vorliegenden Fall, wo ausgehend von
der Wertetabelle zunächst die
zeichnerische, d.h. grafische Lösung in Form der Widerstandsgeraden vorgenommen werden soll, um dann später auf
die mathematische bzw. elektrotechnische Lösung mittels der entsprechenden Funktionsgleichung I = f(U) = 1/R * U * I0 zu gehen. Wenn man als geübter und erfahrener
Elektrotechniker die bruchstückhafte Wertetabelle
aus dem Schlaf heraus lesen und interpretieren kann, weil man bei den beiden
Messwerten bzw. Messpunkten P2
= ( U2 / I2 ) = ( U1V / I10 mA )
= ( 1V / 10 mA) und P1 = (
U1 / I1 ) = ( U-2V / I-5 mA )
= ( -2 V / -5 mA ) mit P2
> P1 sofort ·
die Zwei-Punkte-Form,
·
die Geradengleichung
und ·
die Widerstandsgerade I = 1/R * U * I0 vor dem geistigen
Auge sieht, wozu dann auch ·
der mathematische Differenzenquotient
m = ∆y / ∆x für die Steigung der Geradengleichung
mit ·
der elektrotechnische, rezibroke Differenzenquotient 1/R = ∆I / ∆U und ·
der differentielle
Widerstand R = ∆U / ∆I " r = dU / dI gehören, dann sei es einem vergönnt, dass man sich
anstelle der händischen, zeichnerischen Lösung eines entsprechenden
Werkzeuges in Form einer Software bedient. Und zwar des Programms „Microsoft
Mathematics“ von Microsoft, das es kostenlos für das
Windows-Betriebssystem zum Herunterladen
gibt:
Lösung
zur Aufgabe b) Welche Stromstärke I0 lässt sich am
Schnittpunkt der Widerstandsgeraden mit der Stromachse (= Senkrechte)
ablesen? Am Schnittpunkt
der Widerstandsgeraden mit der Stromachse (= Senkrechte) lässt sich die Stromstärke I0 = 5 mA
ablesen! - Lösung
zur Aufgabe c) Interpretiere den Wert der Stromstärke I0
> 0 am Schnittpunkt mit der Spannung U0 = 0. Die Stromstärke I0 = 5 mA > 0
am Schnittpunkt mit der Spannung U0 = 0 V
deutet darauf hin, dass die einfache Widerstandsschaltung mittels einer linearen (Konstant-) Stromquelle I0 mit Strom versorgt
wird! Deswegen auch die Parallelverschiebung der Widerstandsgeraden aus dem Koordinatenursprung
heraus! Wegen der Parallelverschiebung der Widerstandsgeraden aus dem Koordinatenursprung
heraus, d.h. wegen des Vorhandenseins der linearen (Konstant-) Stromquelle I0, muss dann auch
zwingend mit der (linearen) Gleichung für die Widerstandsgeraden gerechnet werden: I = 1/R * U + I0. Und zwar mit Ri = 200 W und I0 = 5 mA (siehe Schnittpunkt bei U = 0 V ). - Lösung
zur Aufgabe d) Wende die (mathematische) Geradengleichung auf
die (elektrotechnische) Widerstandsgerade an! Mathematisch lässt sich die obenstehende
Widerstandsgerade für einen linearen, d.h. rein ohmschen Widerstand mittels
der Geradengleichung wie folgt berechnen: y = m x
+ b " mathematische
Geradengleichung m = Steigung
der Geraden mit m = ∆y / ∆x b = Parallelverschiebung
der Geraden aus dem Koordinatenursprung heraus Elektrotechnisch lässt sich die obenstehende
Widerstandsgerade für einen linearen, d.h. rein ohmschen Widerstand, wie
folgt berechnen: I = 1/R * U + I0 " elektrotechnische
Geradengleichung 1/R = Steigung der
Widerstandsgeraden mit 1/R = ∆IR / ∆UR = ( 10 mA – (-5 mA ) )
/ ( 1 V – (-2 V) ) = ( 10 mA + 5 mA ) / (
1 V + 2 V ) = 15 mA / 3 V = 5 mA / V = 5 mW-1 R = ∆UR / ∆IR = 1 / ( 5 mW-1 ) = 1 / ( 5 * 10-3 W-1 ) = 1 * 103
W / 5 = 1000 / 5 W = 200 W I0 = Konstantstrom,
d.h. Parallelverschiebung der Widerstandsgeraden
aus dem Koordinatenursprung heraus = Schnittpunkt
der Widerstandsgeraden mit der Senkrechten, d.h. der Stromachse I = f(U) =
IR - 1/R * UR = 10 mA – 1/200 W * 1 V = 0,010 A – 1 / ( 200 = 10 mA - 5 mA = 5 mA Lösung zur Aufgabe e) Berechne
den Konstantstrom I0 an der Stelle I0 = f(U0)
mit U0 = 0 V (siehe Wertetabelle).
In die allgemeine Form
der elektrotechnischen
Geradengleichung IR = 1/R * UR + I0 eines linearen, d.h. ohmschen
Widerstandes R lassen sich nun
beliebige Spannungs- und Strom-Werte, insbesondere auch die aus der Wertetabelle, einsetzen. Dabei interessiert uns
gemäß der Fragestellung der (Ergebnis-)
Wert I0V an der Stelle U0V = 0 V: I0V =
1/R * U0V + I0 " Messpunkt M0V = ( U0V / I0V ) = (
0 V / 5 mA ) " Konstantstrom I0 bei U0
= 0 V = 1 / ( 200 W ) * ( 0 V ) + 5 mA = 0,005 A/ = 0,005 A * ( -0 ) + 5 mA = 0 mA + 5 mA
= 5 mA þ
Lösung
zur Aufgabe f) Wird bei der
elektrischen Schaltung mit dem linearen, d.h. rein ohmschen Widerstand R die Stromstärke IR durch den Widerstand
durch eine Spannungs- oder Stromquelle aufgebracht? Messpunkt M1V: I = 1/R * U + I0 I1V = 1/R * U1V + I0
" Messpunkt M1V = ( U1V / I1V ) = (
1 V / 10 mA ) = 1 / ( 200 W ) * 1 V + 5 mA = 0,005 A/ = 0,005 A + 5 mA = 5 mA + 5 mA = 10 mA þ Messpunkt
M-2V: I = 1/R * U + I0 I-2V = 1/R * U-2V + I0
" Messpunkt M-2V = ( U-2V / I-2V ) =
( -2 V / -5 mA ) = 1 / ( 200 W ) * ( -2 V ) + 5 mA = 0,005 A/ = 0,005 A * ( -2 ) + 5 mA = -10 mA + 5
mA = -5 mA þ Messpunkt M0V: I = 1/R * U + I0 I0V =
1/R * U0V + I0 " Messpunkt M0V = ( U0V / I0V ) = (
0 V / 5 mA ) " Konstantstrom I0 bei U0
= 0 V = 1 / ( 200 W ) * ( 0 V ) + 5 mA = 0,005 A/ =
0,005 A * ( -0 ) + 5 mA = 0 mA + 5 mA = 5 mA
þ Um die obenstehende Frage, ob es sich bei der
Stromversorgung der einfachen Widerstandsschaltung um eine Spannungs- oder Stromquelle handelt, beantworten zu können, muss man wissen, dass es
sich beim Strom I0 um den Konstantstrom einer Konstantstromquelle I0 handelt, die die
Schaltung mit dem linearen, ohmschen Widerstand R = 200 W mit Strom versorgt. Dabei verhält es sich
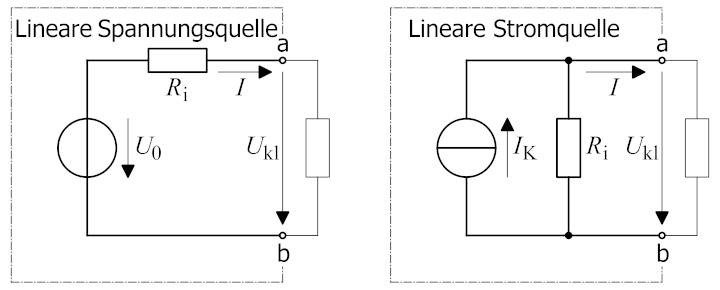
so, dass sich eine lineare Stromquelle
I0
jederzeit in eine lineare Spannungsquelle
U0
umrechnen lässt:
(Wikipedia: Von Saure,
CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=12632634
) Da sich beide
Schaltungen elektrisch äquivalent zueinander verhalten, lässt sich der Kurzschlussstrom IKurz am besten links bei
der linearen Spannungsquelle
U0
mittels Maschenumlauf
wie folgt berechnen: URi + Ukl – U0 = 0 " Ukl = U0 - URi = 0 (!) " Im Kurzschlussfall ist die Klemmenspannung Ukl = 0 V U0 = URi = I0 * Ri = 5 mA * 200 W
= 1000 mV = 1 V Zusammen mit der Klemmenspannung Ukl = 0 V folgt für den Kurzschlussstrom IKurz: IKurz = I0
" IKurz darf nicht dem Konstantstrom
IK
der linearen Stromquelle
I0
verwechselt werden! I0 = U0 / Ri = 1 V / 200 W = 1 Während die lineare Spannungsquelle U0 durchaus
kurzgeschlossen werden darf ( " Kurzschlussspannung Ukl = 0 ), ohne dass die
treibende Spannungsquelle
U0
Schaden nimmt und durchbrennt, weil der maximale Kurzschlussstrom IKurz durch den in Reihe geschalteten Innenwiderstand Ri begrenzt wird,
verhält es sich bei der linearen Stromquelle anders. Bei der linearen Stromquelle gibt es nämlich keinen in Reihe geschalteten Widerstand, der
den maximalen Kurzschlussstrom
IKurz
begrenzen würde! Was aber ist das
Charakteristische einer linearen Stromquelle? Das Charakteristische
einer linearen Stromquelle ist, dass sich die
Größe der Klemmenspannung
Ukl
stets nach dem angeschlossenen Lastwiderstand
Rab
an den Anschlussklemmen a und b richtet! Ist beispielsweise der
Lastwiderstand Rab unendlich groß
(Rab " ¥), dann ist auch die Klemmenspannung Ukl unendlich groß
(Uab " ¥), sodass die lineare Stromquelle wegen der unendlich großen,
parallel anliegenden Klemmenspannung
Ukl
und eines eventuellen Spannungsüberschlages in Form eines Lichtbogens
durchschmort! Des Weiteren würde die
unendlich große, parallel anliegende Klemmenspannung Ukl einen unendlich großen Strom IRi (IRi " ¥) durch den Innenwiderstand Ri der linearen Stromquelle jagen, sodass diese unverzüglich den
Hitzetod stirbt! Lösung
zur Aufgabe g) Wie groß muss die
Quellenspannung U0 einer linearen Spannungsquelle sein, damit
durch den Innenwiderstand Ri ein Strom IRi der
Stromstärke IRi = 20 mA fließt? U0 = I0 * Ri = 5 mA * 200 W = 1000 mA * V/A = 1 Wegen
der Reihenschaltung von U0 und URi fließt der Strom I0 auch durch Ri, sodass gilt: IRi = I0 . Wenn man also die Stromstärke I0 von I0 = 5 mA auf 4 * I0 = IRi = 4 * 5 mA = 20 mA vergrößert, dann
vergrößert sich wegen Ri = 200 W = konstant auch zwangsläufig die
Spannung U0 zu U0’ wie folgt: U0’ = 4 * I0 * Ri = 4 * 5 mA * 200 W = 20
mA * 200 V/A = 0,020 Diese Berechnung ist deswegen falsch,
weil man das Ohmsche Gesetz
auf die Widerstandsgerade anwendet, die wegen des Konstantstroms I0
= 5 mA aus dem Koordinatenursprung heraus parallel
verschoben ist! Wir
kommen also nicht umhin mit der linearen Geradengleichung
bzw. der Funktion für die Widerstandsgerade
rechnen zu müssen. „Linear“ deshalb, weil es sich bei der Geradengleichung um eine Gleichung
bzw. Funktion ersten Grades
handelt: I = 1/R * U + I0 I3V = 1/Ri * U3V + I0 " Maschenumlauf mit
der linearen Spannungsquelle
U0: " siehe weiter oben! URi + Ukl + ( - U0 ) = 0 " Ukl = U3V U3V = URi
- U0 = IRi * Ri - U0 = 20
mA * 200 W - 1 V =
4000 mV - 1 V = 4 V - 1 V = 3 V = 1 / ( 200 W ) *
3 V + 5 mA = 1 / ( 200 = 0,015 A+ 5 mA = 15 mA + 5
mA = 20 mA Gemäß der Berechnung
lässt sich nun die bisherige Wertetabelle wie folgt ergänzen:
Wie man sieht, lässt sich die Wertetabelle
jederzeit erweitern. Allerdings mehr theoretisch, weil wir nicht wissen,
welche maximale Stromstärke sich mittels der linearen Stromquelle einstellen
bzw. realisieren lässt. Dazu muss man wissen, dass es lineare Stromquellen nicht einfach so zu kaufen gibt wie
herkömmliche Batterien
(= Spannungsquellen) in Form von 1,5 Volt Rundzellen vom Typ „AA“ (= „Mignon“),
Typ „AAA“ (= „Micro“)
oder 9 Volt Blockbatterien, da Stromquellen meistens nur in Labornetzgeräten
und deren Elektronik verbaut sind! Immer dann, wenn sich bei einem (Labor-) Netzgerät die abgegebene Stromstärke, z.B. im Bereich von [ 0, …, 2 ]
A,
mittels eines Reglers (= Potentiometer)
einstellen lässt,
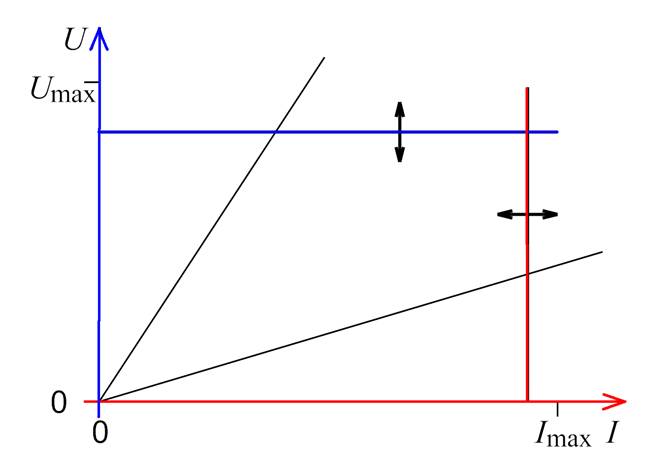
(Programmierbare
Labornetzteile mit zwei Ausgängen | Quelle: Wikipedia) hat man es im Inneren
bei der Elektronik mit einer einstellbaren Konstantstromquelle
zu tun:
(Kennlinie eines
Labornetzgerätes mit einstellbarer Spannungs- und Strombegrenzung; |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
[ Fearless
Engineers ] [ Seitenanfang
] |
|