|
|
[ Easy
Elektro Start ] [ Seitenende ] [
Programmieren 1 ] [ Versuch 2 ] |
|
||||
|
|
Easy Elektro Start - Versuch 1 Spannung,
Strom und Widerstand Wir bauen gleich unsere erste
Versuchsanordnung zum Versuch 1 auf (siehe im
Handbuch, Seite 8-9). Dazu benötigen wir nachfolgende Bauteile (im
Uhrzeigersinn von links nach rechts): ·
1 Stück Batteriefach Nr. 19, ·
3 Stück Leitleisten Nr. 2, ·
1 Stück Leitleiste
Nr. 9, ·
1 Stück Leitleiste
Nr. 3, ·
1 Stück Glühlämpchen Nr. 18, ·
1 Stück Leitleisten Nr. 3, ·
1 Stück Leitleiste
Nr. 7. ·
1 Stück Leitleisten Nr. 3. Wir bauen die Schaltung
zum Versuch 1 ganz professionell von
links nach rechts im Uhrzeigersinn
auf und verwenden dazu die Bauteile entsprechend der Reihenfolge in der
obenstehenden Bauteileliste. So wie wir in der westlichen Welt wie z.B. in
Nord- und Südamerika und Europa von links nach rechts lesen und schreiben,
lesen und bauen wir die nachfolgende Schaltung von links nach rechts im Uhrzeigersinn auf: (Zum Vergrößern bitte
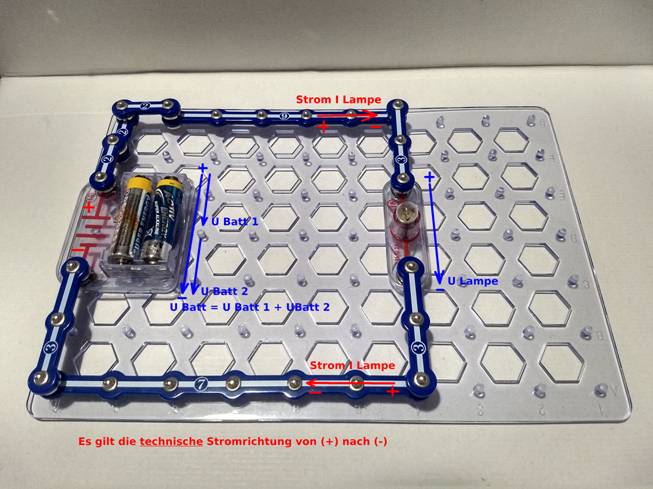
auf das Bild klicken!) Demzufolge befindet sich ganz links das Batteriefach Nr. 19 mit zwei 1,5 Volt Batterien vom „Mignon AA“ als
Energielieferant,
der Physiker, Elektriker und Elektroniker sagt dazu Spannungsquelle.
Im vorliegenden Fall setzt sich unsere Spannungsquelle aus zwei in Serie, d.h. hintereinander
in Reihe geschalteten 1,5 Volt Batterien
zusammen, sodass dass sich die beiden einzelnen Batterie-Spannungen UBatt_1 und UBatt_2 wie folgt addieren:
Ugesamt = UKlemmen
= UBatt_1 + UBatt_2 = 1,5 V + 1,5 V = 3,0 V. Dabei steht der Buchstabe „U“ für den Formelbuchstaben U der elektrischen Spannung
U und der Buchstabe „V“ für die Größe der Spannung U,
die man in Volt [V] misst. Demzufolge gehört zur elektrischen Spannung U der Formelbuchstabe
„U“ und die Maßeinheit Volt [V].
Wenn man Maßeinheiten für sich allein schreibt, dann setzt man diese in eckige
Klammern [V], damit keine
Verwechselung mit Formelbuchstaben wie z.B. „V“ für das Volumen von geschlossenen
Körpern entsteht! Die elektrische Spannung U als treibende Kraft
lässt sich also in Volt [V] messen! Dass die elektrische Spannung U
wirklich die treibende Kraft ist, physikalisch und anschaulich gesprochen, lässt
sich auch beim Versuch 1 beobachten! Du kannst nämlich eine der beiden 1,5 Volt Batterien vom „Mignon AA“
durch eine schwächere, d.h. bereits energiemäßig „verbrauchte“ Batterie im Batteriefach Nr. 19 (links im obenstehenden Bild) ersetzen. Welche von den zwei in Serie, d.h. hintereinander
in Reihe geschalteten 1,5 Volt Batterien
du gegen eine schwächere auswechselst spielt dabei keine Rolle, weil
diese ja hintereinander geschaltet sind: Ugesamt = UKlemmen = UBatt_1 + UBatt_2 = 1,5 V + 1,1 V = 2,6 V L
→ die Glühlampe Nr. 18 leuchtet nicht mehr so hell! = UKlemmen = UBatt_1 + UBatt_2 = 1,1 V + 1,5 V = 2,6 V
L Aber woher weiß ich denn, welche treibende
Kraft in Form der elektrischen Spannung
UGlühlampe die Glühlampe Nr. 18 braucht, um richtig
hell zu leuchten? Ganz einfach: anhand der Nenn-Betriebsdaten, die auf der Schraubfassung der Glühlampe aufgedruckt bzw. eingestempelt sind. Man
kann aber auch ganz einfach anhand des Aufdrucks auf der Halterung
der Glühlampe Nr. 18 nachschauen wie die
Nenn-Betriebsdaten bezüglich der Spannung
U und des Stroms I
lauten, nämlich 3,2 V / 0,2
A,
die übrigens auch auf Seite 4 des Handbuchs im Abschnitt „Elektrische Bauteile“ erwähnt werden! So, jetzt müssen wir wieder etwas Neues
hinzulernen, nämlich dass es bei der Glühlampe Nr. 18 einen elektrischen Nenn-Betriebsstrom von ILampe = 0,2 A gibt. Dabei steht der Buchstabe „I“ für den Formelbuchstaben I als elektrischer Strom I, der wiederum in Ampere [A] für die elektrische Stromstärke
gemessen wird. Dabei entsprechen ILampe = 0,2 A = 200 mA, sprich = 200 Milliampère = 200 * 1/1000
Ampère
= 200 * 0,001 A = 200 * 1 mA = 200 mA. Die Glühlampe Nr. 18 leuchtet also nur dann ganz hell, wenn
die Nenn-Betriebsdaten von UNenn = 3,2 V und INenn
= 0,2 A erreicht werden! In der Praxis mit den beiden 1,5 Volt Batterien vom Typ „Mignon AA“ (IEC
= LR6) in dem Batteriefach
Nr. 19
werden genau diese aber nicht erreicht, weil selbst die fabrikneuen
Batterien zusammen nur
auf eine maximale Spannung von UBatt, ges = 2 * UBatt
= 2 * 1,5 V = 3,0 V kommen! Demzufolge
braucht man also keine Angst zu haben, dass die Glühlampe Nr. 18 selbst bei fabrikneuen
Batterien durchbrennen könnte! Damit aber die Glühlampe Nr. 18 in der Praxis einigermaßen hell leuchtet,
bedarf es noch einer weiteren Bedingung! Nämlich der, dass die beiden 1,5 Volt Batterien vom Typ „Mignon AA“ (IEC
= LR6) im Batteriefach
Nr. 19
genügend Energie W, engl. „work“,
d.h. elektrische Arbeit Wel = Pel * tDauer zur Verfügung
stellen! Was aber bedeutet der Formelbuchstabe „Pel“ in der Formel Arbeit Wel = Pel * tDauer? Der Formelbuchstabe
„P“ steht für engl.
„power“, d.h. Leistung. Und
der Formelbuchstabe „t“ steht für engl. „time“, d.h. Zeit t
im Sinne der Zeitdauer tDauer als Maß für die
verstrichene bzw. aufgewandte Zeit. Diesbezüglich berechnet sich die elektrische Leistung Pel der Glühlampe
Nr. 18
wie folgt: Pel, Lampe = UNenn * INenn = 3,2 V
* 0,2 A = 0,64 VA = 0,64 W
= 0,64 * 1 000 mW = 640 mW (= Milliwatt = 1/1000
Watt) Mit einer Leistungsaufnahme
von Pel, Lampe = 0,64 W ist unsere Glühlampe Nr. 18 wegen der geringen Lichtausbeute und der hohen Wärmeabstrahlung nicht nur ein Energieverschwender, sondern auch eher
ein kleiner Heizofen, wenn man diese mit
einer modernen, hoch effizienten Licht emittierenden Leuchtdiode
(LED), engl. „Light Emitting Diode“, vergleicht. Wer also umwelt- und energiebewusst durch’s
Leben geht, der verwendet Akkus,
umgangssprachlich auch „wieder aufladbare Batterien“ genannt, die es u.a.
auch als 1,2 V
NiMH-Akkus vom Typ „Mignon AA“ gibt. Interessant ist dabei aber nicht nur die etwas
verringerte Akku-Spannung von UAkku
= 1,2 V, sondern auch die
Angabe der im Akku gespeicherten Ladungsträgermenge
QAkku = 2 500 mAh (siehe oben rechts
auf der Verpackung): (Zum Vergrößern bitte
auf das Bild klicken!) Wenn man wissen will, nach welcher Formel sich die Ladungsträgermenge QAkku = 2 500 mAh berechnet, dann muss
man sich nur die Maßeinheit [ Milliamperestunden] = [ mAh ] = [ 1/1000 Ah ] = 1/1000 [ Ah ] = 1/1000 [ 1 A * 1 h ] näher anschauen, um
zu wissen, dass sich diese gemäß der ·
Formel QAkku = IAkku * tEndlade, d.h. aus dem Produkt
von Entladestrom IAkku und Entladezeit tEntkade zusammensetzt. Dabei steht der Formelbuchstabe „Q“ für den lateinischen Ausdruck „Quantum“, d.h. (Ladungsträger-) Menge.
Und bei den Ladungsträgern handelt es sich dabei
um frei bewegliche Elektronen und deren
gehäufte Ansammlung im Sinne eines Ladungsträgerüberschusses am Minuspol
des Akkus sowie eines Ladungsträgermangels am Pluspol des Akkus.
Ferner muss man wissen, dass sich im Inneren des Akkus zwischen den Elektroden,
d.h. im Elektrolyten
zwischen dem Minuspol „-“ und dem Pluspol „+“
keine Elektronen, sondern
vielmehr negativ geladene Ionen (= Anionen) und positiv
geladene Ionen (= Kationen) befinden. Als Ionen
bezeichnet man Atome oder Moleküle denen auf
der äußeren Elektronenschale
mindestens ein Elektron (= negativ
geladenes Elementarteilchen) fehlt, sodass das Atom insgesamt positiv aufgeladen ist. Als Ionen
bezeichnet man aber auch Atome oder Moleküle, die auf der äußeren Elektronenschale
mindestens ein Elektron zu viel haben, sodass das Atom insgesamt negativ aufgeladen ist. Was aber bedeutet jetzt die im Akku gespeicherte Ladungsträgermenge QAkku = 2 500 mAh für die Glühlampe Nr. 18 hinsichtlich der Leuchtdauer (= Entladezeit tEndlade des Akkus)? QAkku = IAkku * tEndlade → tEndlade = QAkku / IAkku = QAkku / IGlühlampe = 2 500 mAh / 0,2 A = 2,5 Wie man sieht, lässt sich die Glühlampe Nr. 18 mit einem 1,2 V NiMH-Akku vom Typ „Mignon AA“ maximal bis zu 12,5 Stunden lang betreiben. Wie aber sieht es aus, wenn wir statt einer
insgesamt zwei in Serie, d.h. hintereinander in Reihe geschaltete 1,2 V NiMH-Akkus vom Typ „Mignon AA“ verwenden, so wie es im Batteriefach Nr. 19 vorgesehen ist? Verdoppelt sich dann
die in beiden Batterien
gespeicherte Ladungsmenge Qges, sodass sich auch die
Leuchtdauer der Glühlampe Nr. 18 verdoppelt? Jetzt wird es etwas komplizierter, da nun die
(Gesamt-) Spannung der beiden in Reihe geschaltete 1,2 V NiMH-Akkus ins Spiel kommt,
obwohl ja die gespeicherte Ladungsträgermenge
QAkku = IAkku * tEndlade gerade nicht
von der Akkuspannung abhängt: Elektrische Kapazität
C eines Akkus: C = Q / U → U = Q / C = Uges
= UAkku1 + UAkku2
→ Reihenschaltung zweier Akkus! = QAkku1 / CAkku1 + QAkku2 / CAkku2 → Mit CAkku1 = CAkku2
und deswegen auch UAkku1 =
UAkku2 folgt: Uges = UAkku1 + UAkku2 = QAkku1 / CAkku1 + QAkku2
/ CAkku2
= ( QAkku1 + QAkku2 ) / CAkku1 = 2 * QAkku1 /
CAkku1 Wenn man sich nicht ganz sicher ist, ob man
die Formel richtig umgestellt hat, und ob man demzufolge auch richtig
rechnet, der kann die sogenannten Dimensionsprobe
machen: [
V ] = [ Ah ] / [ F ] = [ As ] / [ s / Ω ] = [ A Die Maßeinheit
[F] steht für „Farad” zu Ehren des
englischen Naturforschers und Experimentalphysikers Michael
Faraday. Die Maßeinheit
[Ω] = [ V/A ] steht für „Ohm” zu Ehren des
deutschen Physikers Georg Simon Ohm. Wie man sieht, bestätigt die Dimensionsprobe, dass wir bis jetzt
richtig gerechnet haben, sodass folgt: Uges = UAkku1 + UAkku2 = QAkku1 / CAkku1 + QAkku2
/ CAkku2 = ( QAkku1 + QAkku2 ) / CAkku1 = 2 * QAkku1 / CAkku1 → CAkku1 = QAkku1 / UAkku1 = IAkku1 * tAkku1 / UAkku1 Wie man ferner sieht, verdoppelt
sich die Ladungsträgermenge QAkku = QAkku1 = QAkku2 in beiden in Reihe geschalteten 1,2 V NiMH-Akkus! Und zwar unabhängig
vom Strom IAkku = IAkku1
= IAkku2!
= 2 * Außerdem
verdoppelt sich wegen der Reihenschaltung
auch die Teilspannung UAkku1 = UAkku2 zur (Gesamt-) Spannung Uges = 2 * UAkku1 = 2 * UAkku2, während sich die Stromstärke
I = ½ IAkku1 = ½ IAkku2 halbiert! Uges = 2 * QAkku1 / CAkku1 = 2 * IAkku1 * tAkku1 / ( QAkku1 / UAkku1 ) → 2 * IAkku1 * tAkku1 = Uges * ( QAkku1 / UAkku1 ) → tAkku1 = Uges * ( QAkku1 / UAkku1 ) / 2 * IAkku1 = ½ * Uges * ( QAkku1 / UAkku1 ) / IAkku1 = = 2 500
mAh / 0,2
A = 2,5
Bei der obenstehenden Dimensionsprobe [ V ] = [ Ah
] / [ F
] = [ As ] / [ s / Ω ] = [ A tauchte u.a. erstmals die Maßeinheit [Ω] = [ V/A ] auf, die für „Ohm” steht und zwar zu
Ehren des deutschen Physikers Georg Simon Ohm.
Dabei zeigt sich zwecks Umrechnung der Maßeinheit [Ω] im elektrischen Stromkreis, dass
diese dem Quotienten (=
Verhältnis zweier Größen im Sinne eines Bruchs)
von Spannung U, gemessen in Volt [V] und dem Strom I,
gemessen in Ampere [A] oder Milliampere [mA] (= 1/1000 A = 0,001 A = 1 mA) entspricht: Maßeinheit
[Ω] = [ V/A ] → Formel R = U / I → Ohmsches Gesetz!
Das
Ohmsche Gesetz besagt, dass sich die treibende Spannung U ins Verhältnis zum Strom I bzw. zur Stromstärke I setzen lässt und das Verhältnis (= Quotient) bei
sogenannten Ohmschen
Verbrauchern, d.h. elektrischen Widerständen
R stets konstant,
d.h. unverändert bleibt, selbst wenn sich die treibenden Spannung U verdoppelt: R = U / I
→ für die Glühlampe Nr. 18 folgt dann RLampe = ULampe / ILampe = UBatterie1 / ILampe = 1,5 V / 0,1 A = 15 V/A = 15 Ω Wenn die Glühlampe Nr. 18 an nur einer Spannungsquelle UBatterie1 =
1,5 V betrieben wird,
dann „verbraucht“ sie gemäß dem Ohmschen Gesetz nur halb so viel Strom ILampe = 0,1 A! = Ugesamt / ILampe = (
UBatterie1 + UBatterie2 ) / ILampe
→ UBatterie1 = UBatterie2 = ( UBatterie1 + UBatterie1 ) / ILampe = 2 * UBatterie1 / ILampe = 2
* 1,5 V / 0,2 A = 3,0 V / 0,2 A = 15
Ω Werfen
wir in diesem Zusammenhang einen Blick in das „radio“-Praktiker-Buch
„Die elektrischen Grundlagen der Radiotechnik“ von Kurt Leucht,
Franzis-Verlag, 7. Auflage, Mai 1964: (Zum Vergrößern bitte
auf das Bild klicken!) Wie wir inzwischen wissen (siehe oben), ist
das Ohmsche Gesetz ein konstanter
Quotient R, der das Teilungsverhältnis von Zähler und
Nenner bzw. von Spannung und Strom angibt: R = U / I = konstant! Dabei ist die Spannung U beim Quotienten R die unabhängige Variable, während der Strom I die abhängige Variable ist. Mit anderen
Worten: Wenn sich die Spannung U ändert, dann
reagiert der Strom I auf die
Spannungsänderung ∆U indem er sich
ebenfalls im Verhältnis ändert: ∆U → ∆I → Quotient ∆U / ∆I = R = konstant! Demzufolge führt eine Verdoppelung der Spannung
U zwangsläufig zu einer Verdoppelung des Stroms I
bei gleichzeitig konstantem, d.h. unverändertem Widerstand R! Da das Ohmsche Gesetz mathematisch nicht schwer und auch elektrotechnisch gut
zu verstehen ist, bietet es sich an, dass wir es programmieren! [ weiterlesen
] Nachdem wir das Ohmsche Gesetz „programmiert“ haben, geht es nachfolgend darum, das „Sketch“-Programm
„sketch_prog_03_07.ino“ innerhalb der „Arduino“-Entwicklungsumgebung
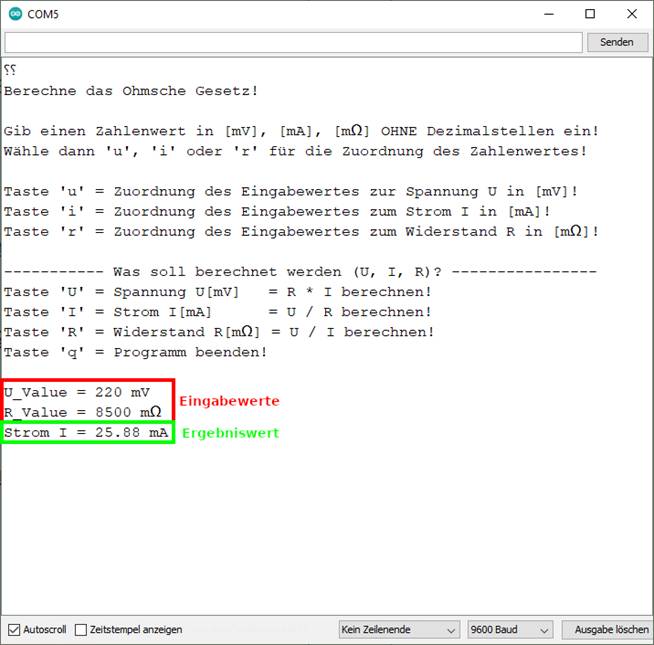
auszuprobieren und anzuwenden. Und zwar indem wir die nachfolgenden Aufgaben lösen: Aufgabe 10: Wie groß ist die Stromstärke in einem
Widerstand von 8,5 kΩ, wenn er an eine Spannung von 220 V (Steckdose)
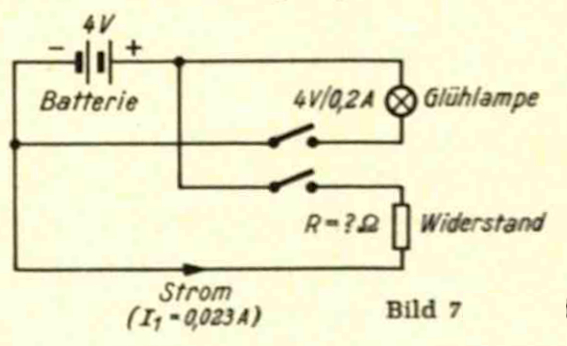
angeschlossen wird? Aufgabe 11: Wie groß ist in vorstehendem Schaltbild
(Bild 7) der Widerstand R, und welchen Widerstand hat das leuchtende
Glühlämpchen, wenn es die Aufschrift 4 V, 0,2 A trägt? Aufgabe 12: Ein Meßinstrument hat einen Widerstand von
96 000 Ω. Wie groß sind die Stromstärken bei a) 50 V. b) 220 V und c)
300 V? Aufgabe 13: Ein 70 m langer Nickelindraht (ρ = 0,4)
liegt an einer Spannung von 220 V. Es fließt ein Strom von 1,8 A. Wie groß
ist der Drahtdurchmesser? Aufgabe
10 Wie groß ist die Stromstärke in einem
Widerstand von 8,5 kΩ, wenn er an eine Spannung von 220 V (Steckdose)
angeschlossen wird? Ohmsches
Gesetz R = U / I umstellen nach I = U / R = 220 V /
8,5 kΩ = 220 V / ( 8,5 * 103 V/A ) = 220 V / 8,5 * 10-3
A = 25,88 mA ≈ 25,9 mA Aufbereiten
für das Berechnungsprogramm
liefert: = 220000 mV / ( 8500 Ω ) = = 220000 mV / 8500000 mΩ = 0,02588 A = 25,88 mA ≈ 25,9
mA Jetzt zeigt sich, dass das „Sketch“-Berechnungsprogramm wider Erwarten nicht
mit so großen Werten im Millivolt- und Milliohm-Bereich umgehen kann, weil
die Größe der Integerwerte im Programm
speichermäßig begrenzt ist. Wenn man aber Zähler und Nenner
ganz einfach durch 1000 kürzt, dann
folgt: = 220000 mV / ( 8500 Ω ) = 220 Voilà, geht doch: (Bild
vergrößern: auf Bild klicken! Webverzeichnis
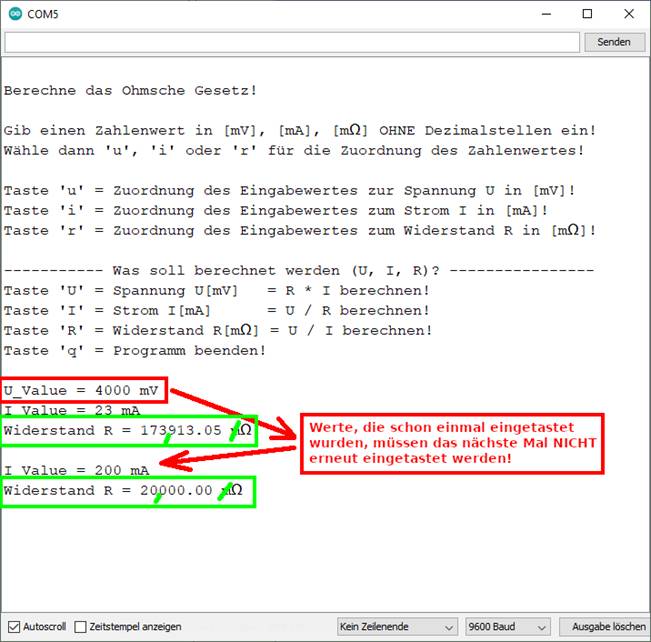
| sketch_prog_03_07.ino) Aufgabe
11 (Zum Vergrößern bitte auf
das Bild klicken!) Wie groß ist in vorstehendem Schaltbild (Bild
7) der Widerstand R, und welchen Widerstand hat das leuchtende Glühlämpchen,
wenn es die Aufschrift 4 V, 0,2 A trägt? Ohmsches
Gesetz R = U / I RWiderstand = U / I = 4 V
/ 0,023 A = 4000 RGlühlampe = U / I = 4 V / 0,2 A = 4000 mV
/ 200 mA = 20000.00 mΩ = 20000 mΩ = 20,0 Ω (Bild
vergrößern: auf Bild klicken! Webverzeichnis
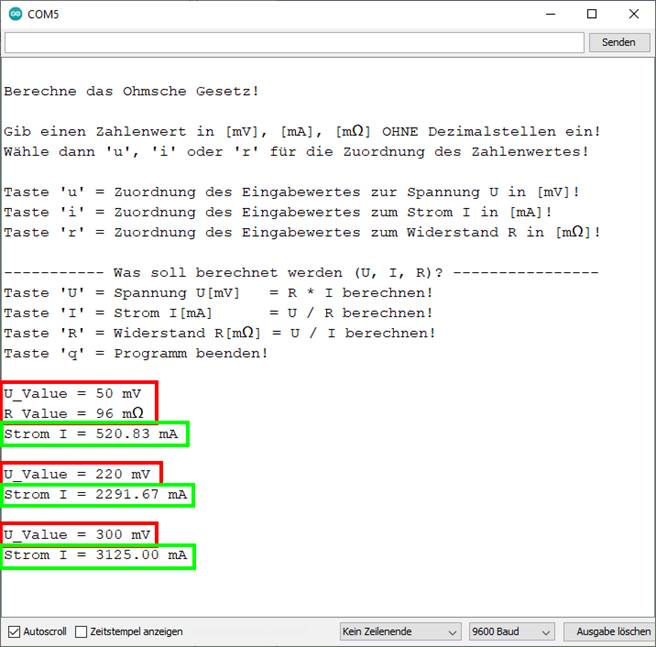
| sketch_prog_03_07.ino) Aufgabe
12 Ein Meßinstrument hat einen Widerstand von 96
000 Ω. Wie groß sind die Stromstärken bei a) 50 V. b)
220 V und c) 300 V? Ohmsches
Gesetz R = U / I a)
I = U / R = 50 V / 96000 Ω = 50 V / 96 KΩ = 50 V /
96 Ω * 10-3 = 50 = 520.83 mA ≈ 521 mA = 0,521 A b)
= 220 V / 96000 Ω = 220 V / 96 KΩ = 220 V /
96 Ω * 10-3 = 220 = 2291,67 mA
≈ 2,29 A c)
= 300 V / 96000 Ω = 300 V / 96 KΩ = 300 V /
96 Ω * 10-3 = 300 = 3125,00 mA
≈ 3,1 A (Bild
vergrößern: auf Bild klicken! Webverzeichnis
| sketch_prog_03_07.ino) Aufgabe
13 Ein 70 m langer Nickelindraht (ρ = 0,4)
liegt an einer Spannung von 220 V. Es fließt ein Strom von 1,8 A. Wie groß
ist der Drahtdurchmesser? Ohmsches
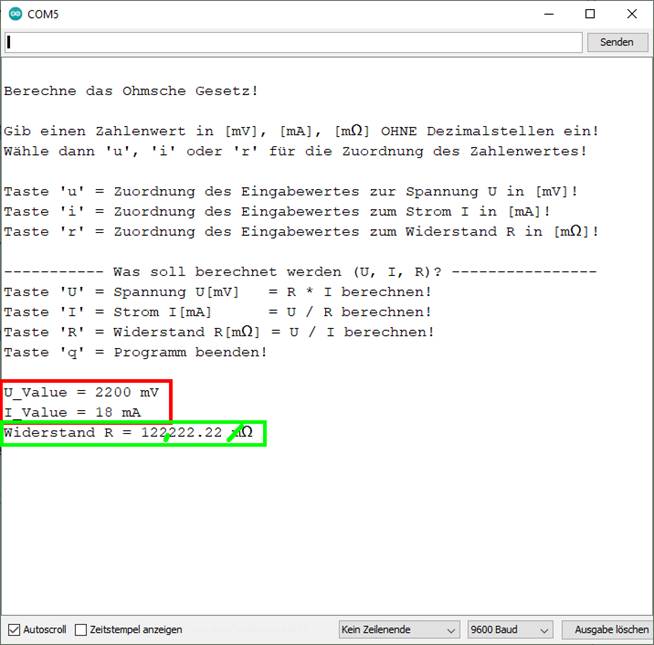
Gesetz R = U / I RNikelin = U / I = 220 V
/ 1,8 A = 2200 =
122,2 Ω ≈ 122 Ω (Bild
vergrößern: auf Bild klicken! Webverzeichnis
| sketch_prog_03_07.ino) Nachdem wir den Widerstand des Nickelindrahtes kennen, lässt sich der Drahtdurchmesser d mittels des spezifischen
Widerstandes wie folgt berechnen: Rspezifisch = ρ * lDraht / ADraht → mit der Drahtlänge lDraht = 70 m und dem Drahtquerschnittsfläche
ADraht ADraht = ρ * lDraht / Rspezifisch = 0,4 dDraht = √ (
4 * 0,2295 m2 / 3,14 ) = √ (
0,2923671295812885 m2 ) = 0,541 m ≈ 0,54
cm þ
Wenden wir uns nun wieder der Schaltung von Versuch 1 zu (siehe Handbuch
„Easy Elektro Start“, Seite 8-9), die aus dem Batteriefach 19 mit zwei in Reihe geschalteten 1,5 Volt Batterien vom „Mignon AA“ sowie
der Glühlampe 18 besteht: (Zum Vergrößern bitte
auf das Bild klicken!) Die obenstehende Schaltung von Versuch 1
besteht aus einem geschlossenen Stromkreis , da nur
in einem geschlossenen Stromkreis elektrischer Strom IBatt = IBatt 1 = IBatt 2 = ILampe fließen kann. Demzufolge müsste die Glühlampe 18 in der obenstehenden Schaltung
eigentlich leuchten! Tut sie aber offensichtlich nicht oder vielleicht doch? Wenn die treibende Spannung
UBatt = ULampe des Batteriefachs 19 zu gering ist,
weil die beiden 1,5 Volt
Batterien
bereits zu sehr entladen sind, dann leuchtet die Glühlampe 18 nicht mehr, obwohl aber immer noch Strom IBatt = ILampe, wenn auch mit geringerer
Stromstärke,
durch die Schaltung fließt! In der Praxis hat sich gezeigt, dass Glühlampen bei einer Betriebsspannung von UBatt = ULampe ≤ 1,0 V nicht mehr
leuchten! Wenn wir unsere „Arduino“-Berechnungsprogramm zum Ohmschen Gesetz aufrufen, dann können
wir die geringe Stromstärke ILampe ganz einfach
berechnen. Dazu muss man aber wissen, dass der elektrische Widerstand RLampe der Heizwendel der Glühlampe innerhalb
eines bestimmten Spannungsbereichs von z.B. [ 1,5 V, …, 3,2 V ] konstant, d.h.
nahezu unverändert bleibt, auch wenn die Glühlampe dabei nicht mehr so hell leuchtet wie bei der Nennspannung der
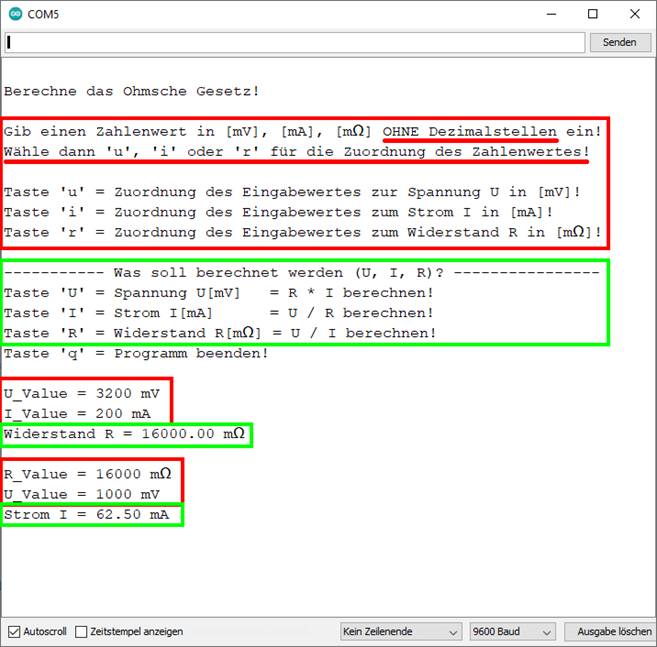
Lampe von ULampe = UNenn = 3,2 V. Gemäß der Nenn-Betriebsdaten 3,2 V 0,2 A der Glühlampe 18 berechnen wir zunächst den (Glühlampen-)
Widerstand RLampe = 16 Ω und dann die Stromstärke ILampe = 62,5 mA = 0,0625 A: (Bild
vergrößern: auf Bild klicken! Webverzeichnis
| sketch_prog_03_07.ino) Ob die Stromstärke
ILampe = 62,5 mA = 0,0625 A der Glühlampe 18 tatsächlich so groß oder klein ist wie
berechnet, wissen wir nicht so genau, da wir noch nicht wirklich wissen,
ob der (Glühlampen-) Widerstand RLampe = 16 Ω bei einer Lampenspannung von ULampe = 1000 mV = 1,0 V tatsächlich noch konstant ist, d.h. sich linear (=
gleichförmig, konstante Steigung) verhält.
Um das zu wissen bzw. herauszufinden, müssten
wir eine sogenannte Wertetabelle mit ILampe
= f(ULampe) aufstellen. Und um eine Wertetabelle aufstellen zu können, bräuchten wir eine veränderliche,
d.h. einstellbare Spannungsquelle z.B. in Form eines regelbaren,
elektronischen Labornetzteils.
Prinzipiell könnte man sich mit dem „Arduino UNO“ auch eine einstellbare Spannungsquelle programmieren.
Und zwar in Verbindung mit einem analogen oder digitalen Ausgang. Da es beim programmierbaren digitalen Ausgang im Prinzip nur zwei Schaltzustände, nämlich „1“ = EIN und „0“ = AUS gibt, müsste man die sogenannte PWM (=
Pulsweitenmodulation) verwenden, um über das unterschiedliche Tastverhältnis von „1“ = EIN und „0“ = AUS verschiedene, einstellbare Mittelwerte der zur Verfügung
gestellten Ausgangsleistung zu
bewerkstelligen. Dabei verhält es sich leider so, dass der „Arduino UNO“ nur kleine Ausgangsströme von bis zu 20 mA
zur Verfügung stellt, die natürlich nicht ausreichen, um die Glühlampe 18 hell leuchten zu lassen. Dazu bräuchte
man nämlich einen Ausgangsstrom von bis zu 200 mA (siehe weiter oben)! - Wenden wir uns aber wieder der Frage zu, ob,
wie und woran man erkennen kann, ob unsere obenstehende Schaltung gemäß dem Versuch 1 „unter Strom steht“
oder eben nicht. Und zwar auch dann, wenn die Glühlampe 18 wider Erwarten nicht hell leuchtet bzw. den
Anschein erweckt, als sei sie „durchgebrannt“. Dass man die hell leuchtende Glühlampe 18 als sprichwörtlich sichtbaren Indikator für den elektrischen Stromfluss
der Stromstärke ILampe = 62,5 mA = 0,0625 A einsetzen kann,
wissen wir ja bereits. Wir wissen aber inzwischen auch, dass die
obenstehende Schaltung gemäß Versuch 1 „unter Strom steht“, wenn die Glühlampe 18 wider Erwarten nicht hell
leuchtet, weil die Lampenspannung mit
ULampe = 1000 mV = 1,0 V zu gering ist!
Was wir also bräuchten, wäre ein Indikator,
ein Sensor, der wesentlich empfindlicher als die Glühlampe 18 ist und demzufolge auch schon bei kleinen Spannungen signalisiert, dass ein kleiner Strom durch die Glühlampe 18 fließt. Gemäß dem Ohmschen Gesetz verhält es sich nämlich so, dass bei einer kleinen
Spannung ein kleiner Strom fließt und bei einer großen ein großen
Spannung ein großer Strom fließt! Vorausgesetzt natürlich, dass der Widerstand RLampe = 16 Ω unverändert gleich
groß, d.h. konstant bleibt, was es aber noch zu beweisen gilt ( → Wertetabelle): ILampe = ULampe / RLampe = 3,2 V / 16 Ω = 0,2 A = 200 mA = ULampe / RLampe = 1,0 V / 16 Ω = 0,0625 A = 62,5 mA Dieser kleine, spannungsempfindliche Sensor ist der Analogeingang „Pin A0“ des „Arduino UNO“, der Spannungen UPin A0 aus dem Bereich [ 0 V, …, +5V ] einlesen und mit seinem Analog-/Digitalwandler
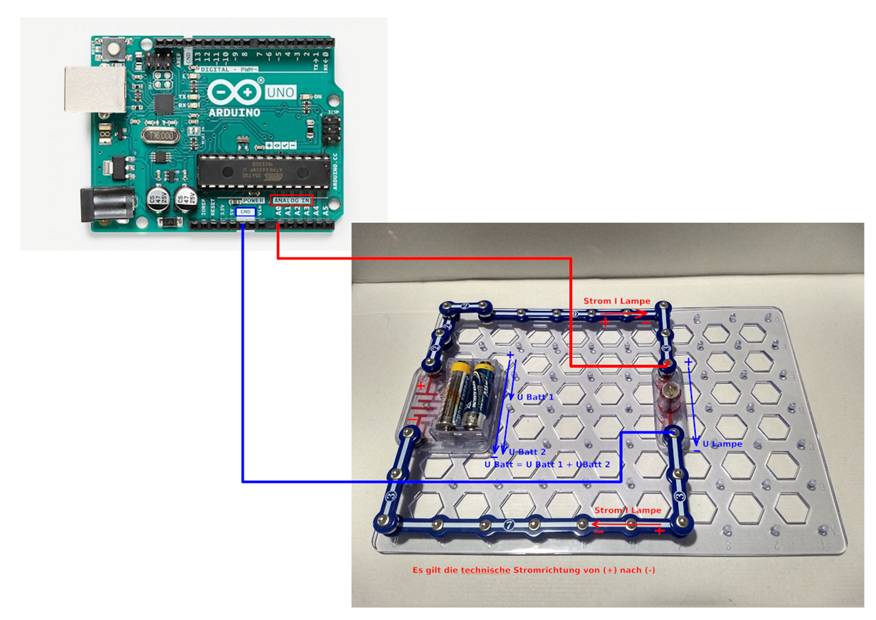
in einen ganzzahligen „integer“-Wert umwandeln kann. Dabei muss der Analogeingang „Pin A0“ zusammen mit dem Masseanschluss, engl. „ground“ (GND), wie im nachfolgenden Bild zu sehen, noch verkabelt
werden: (Zum Vergrößern bitte
auf das Bild klicken!) Was jetzt noch fehlt ist die entsprechende
Software, d.h. das Programm
mit dem sich der Analogeingang „Pin A0“ abfragen, einlesen und die gemessenen Spannungswerte im Arduino-Konsolefenster anzeigen lassen: (Bild
vergrößern: auf Bild klicken! Webverzeichnis
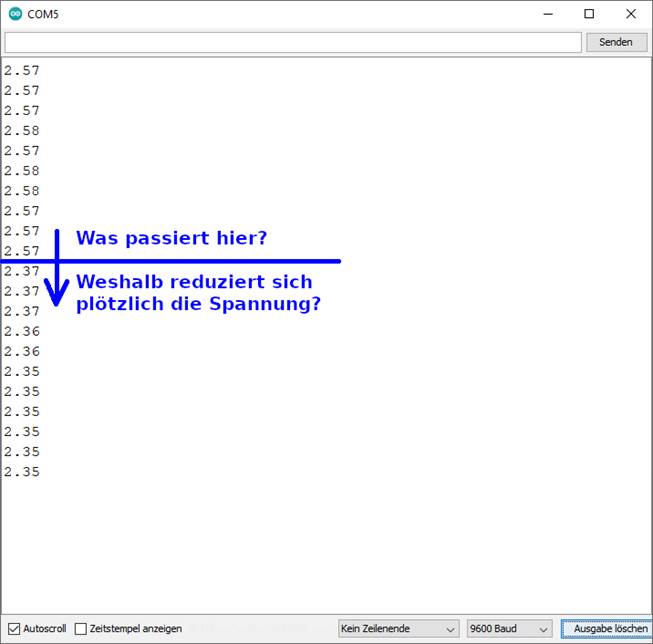
| sketch_prog_03_08.ino) Wie man im obenstehenden Screenshot sieht, reduziert
sich die Spannung UPin A0 am Analogeingang „Pin A0“ plötzlich von UPin A0 = 2,57 V auf nur noch UPin A0 = 2,37 V! Fragt sich nur weshalb? Was ist plötzlich
passiert? Wie kommt es zu dem Spannungssprung von ∆UPin A0 = 0,20 V mit ULampe 2 = ULampe 1 - ∆UPin A0 = 2,57 V - 0,20 V = 2,37 V ? Um das Rätsel lösen zu können, brauchen wir
noch eine weitere Information! Aber welche? Fassen wir kurz zusammen, was wir bereits
alles kennen und wissen: 1. Damit in einem Stromkreis ein elektrischer Strom der Stromstärke
ILampe = 0,2 A fließen kann, bedarf
es einer treibenden Kraft nämlich der elektrischen Spannung mit z.B. der Spannung UBatt = ULampe = 2,37 V, die sich aus den
beiden in Reihe geschalteten 1,5 Volt
Batterien
im Batteriefach 19 speist. 2. Mittels
der Nenn-Betriebsdaten von 3,2 V / 0,2 A der Glühlampe 18 kennen wir den Widerstand RLampe = 16 Ω und mittels des Ohmschen Gesetzes lässt auch die Stromstärke ILampe = ULampe / RLampe = 2,37 V / 16 Ω = 0,148 A = 148 mA durch
die Glühlampe 18 berechnen!
Aber eben noch nicht messen, d.h. durch eine Strommessung
bestätigen! Fassen wir kurz zusammen, was wir noch nicht
kennen und wissen: 1.
Obwohl wir jetzt über Werkzeuge,
d.h. Programme für den „Arduino UNO“ verfügen, das Ohmsche Gesetz vor- und rückwärts berechnen und auch den Spannungsabfall parallel zur Glühlampe 18 messen können, weiß der „Arduino UNO“ nicht, ob durch die Glühlampe tatsächlich auch ein Strom der Stromstärke ILampe = 148 mA fließt, weil er
diesen noch nicht messen kann! Und zwei Augen hat der „Arduino UNO“ auch nicht, um nachzusehen, ob die Glühlampe 18 tatsächlich leuchtet. 2.
Aber bereits mit dem Versuch
9 „Zwei in Reih und Glied“ (siehe Anleitung „Easy
Elektro Start“, Seite 19) werden wir in Verbindung mit dem „Arduino UNO“ über einen zweiten „Sensor“ verfügen mit dem sich dann
der Strom und die Stromstärke ILampe mit dem A/D-Wandler messen lassen! Du darfst
aber schon jetzt spekulieren, um welchen „Sensor“
bzw. Indikator es sich dabei
handelt! So, jetzt geht’s weiter zur Programmierung. Schließlich muss das Spannungs-Messprogramm „sketch_prog_03_08.ino“ noch in das
bisherige Programm „sketch_prog_03_07.ino“
zur „Berechnung“ des Ohmschen Gesetzes,
d.h. von Spannung, Strom und Widerstand, integriert werden! [ weiterlesen ]
|
|
||||
|
|
[ Easy Elektro Start ] [ Seitenanfang ] [ Programmieren 1 ] [ Versuch 2 ] |
|