|
|
[ Easy
Elektro Start ] [ Seitenende ] [
zurück ] |
|
|
|
Easy Elektro Start – Programmieren 1 Spannung,
Strom und Widerstand programmieren Wenn man einen Laien (= Person ohne formale
Fachausbildung) fragt, was elektrischer Strom ist und wie dieser zustande
kommt, dann kann es sein, dass dieser antwortet: „Keine Ahnung, bei uns kommt
der Strom aus der Steckdose!“. Menschen die aber die über gute Schulbildung
oder Allgemeinbildung verfügen, werden sagen, dass der Strom im Kraftwerk
mittels Generatoren (= Umkehrung eines Motors; ein Generator wird mechanisch
angetrieben und erzeugt dabei in Verbindung mit einem zeitlich veränderlichen
Magnetfeld in mehreren Magnetspulen elektrische Energie in Form von
Gleichspannung oder Wechselspannung) erzeugt, über zwei Leitungen für den
Stromhin- und Rückfluss zum Konsumenten und Verbraucher von elektrischer
Energie übertragen wird und beim Endanwender je nach Erfordernis in Licht,
Wärme, Kälte oder Drehbewegung (= Waschmaschine, Spülmaschine, Haartrockner,
Bohrmaschine) umgewandelt wird. Damit der elektrische Strom
unterwegs, d.h. beim Transport vom E-Werk zum Haushalt, nicht „verloren
geht“, braucht man nicht nur Leitungen, sondern müssen diese auch
entsprechend geeignet sein, um den Strom ohne größere Energieverluste
übertragen zu können. Diesbezüglich spricht man auch von elektrischer Leitfähigkeit
einer Leitung oder von einem möglichst geringen elektrischen
(Leitungs-) Widerstand.
>>
Ein elektrischer Leiter ist ein Medium, das
eine hohe Dichte frei beweglicher Ladungsträger und daher
eine gute elektrische
Leitfähigkeit sowie einen möglichst geringen elektrischen
Widerstand besitzt, wodurch dieses zum Transport geladener
Teilchen geeignet ist;[1][2] diesen
Transport nennt man elektrischen
Strom.[3]
Der gleichbedeutende, aber altertümliche Begriff für einen elektrischen
Leiter, Konduktor, bezeichnet im engeren Sinne einen aus Metall
gefertigten Ladungssammler in Form einer Dose oder Kugel an elektrostatischen
Geräten. Zu elektrisch leitenden
Verbindungsdrähten für die Stromversorgung siehe Elektrische Leitung. Siehe auch: Elektrische
Leitfähigkeit
<< (Quelle: Wikipedia) In elektrischen, insbesondere elektronischen
Geräten der Unterhaltungselektronik (= Rundfunkempfänger,
Flachbild-Fernsehgeräten, Computer, Notebooks, Netbooks, Tablet-PCs,
Smartphones usw.) werden elektrische Widerstände verbaut, die je nach
Gerätegröße sehr klein sind und als SMD-Bauteil
nur zwei bis drei Millimeter groß sind. Früher wurden in alten (Röhren-) Rundfunkgeräten
ab den 1920er Jahren noch gewickelte Drahtwiderstände
verbaut, die später ab den 1950er Jahren von den sogenannten Schichtwiderständen
in Transistorradios abgelöst
wurden. Im Physikunterricht der Realschule bzw. des
Gymnasiums wurde das Ohmsche
Gesetz z.B. mittels mehrer, teils unterschiedlich langer Konstantandrähte nebst
unterschiedlichen Widerstandwerten hergeleitet. Im Zeitalter der Vierten industriellen
Revolution bzw. der Industrie
4.0 müsste man den elektrischen Widerstand R aber auch als ein Bauelement
definieren, das es erlaubt, das Verhalten von Spannung U und Strom I zu
beeinflussen und zwar mittels der ·
mathematischen Geradengleichung y
= f(x) = ax +b → bzw. der ·
elektrischen Widerstandsgeraden
I = f(U) = 1/R * U + I0 mit I0 = Konstantstrom Bevor wir uns aber daran machen und den
ohmschen Widerstand mittels einer veränderlichen Konstantstromquelle
I0 und einer veränderlichen Spannungsquelle ∆U mit ∆I = f(∆U) = 1/R * ∆U + I0
programmieren, befassen wir uns zunächst mit der „Programmierung“ des
Ohmschen Gesetzes, d.h. mit der Programmierung eines Programms zur Berechnung
des elektrischen Widerstandes R = U / I. Zu diesem Zweck nehmen wir das
bisherige „Sketch“-Programm „sketch_prog_01_16.ino“ mit dem wir die
Entfernung zwischen Blitz und Donner berechnet haben und passen dieses
Schritt für Schritt an. Dabei geht es zunächst darum, dass wir dem
Anwender mitteilen, worum es geht, d.h. was das neue Programm macht und wie
es sich bedienen lässt. Nämlich gemäß dem Ohmschen Gesetz den Widerstandswert R = ? Ω zu berechnen. Dazu braucht man natürlich noch die Spannung U
im Zähler des Quotienten R = U / I und den Strom I
im Nenner des Quotienten. Da es
diesbezüglich egal ist, ob man als Erstes den Zähler in Form der Spannung U
eingibt oder den Nenner in Form des Stroms
I spielt seitens des Quotienten R = U / I keine Rolle. Bei der Eingabe der Werte müssen wir aber
später noch darauf achten, dass der Stroms
I nicht zu null
wird, da es das Verbot
der Division durch Null (siehe auch hier!)
zu beachten gilt bzw. diesen speziellen Fall I = 0 später im Programm
noch abfragen, abfangen und extra behandeln müssen! Der Zähler des Quotienten
R = U / I in Form der Spannung U kann sehr wohl zu
null werden! Und zwar nicht nur mathematisch, sondern auch elektrotechnisch!
Denn wenn keine treibende Kraft in Form der Spannung U > 0 V an der Glühlampe als Verbraucher anliegt,
dann fließt auch kein Strom I ! Sollte man meinen, denn es gibt eine Ausnahme!
Und zwar die Konstantstromquelle,
die unabhängig von der Spannung
U stets einen konstanten
Strom I0 von z.B. I0
= 10 mA
liefert: I = f(U) = 1/R * U + I0 → Für U = U0 = 0 V folgt für die
Gleichung: I
= I = f(U) = f(U0 = 0) = 1/R * U0
+ I0 = 1/R * 0 V + I0 → I = f(U = 0) = 1/R * 0 V + 10 mA
= 10 mA für U0 = 0 V ! Da man sich eine Konstantstromquelle nicht als Batterie oder Akku
kaufen kann, sondern diese vielmehr selbst mittels Transistoren oder eines Operationsverstärkers
(OPV) bauen muss, werden wir diese erst ziemlich zum Schluss unserer
Experimentalversuche kennenlernen. - Bei der Eingabe der Daten, d.h. in Form von elektrischen
Werten folgen wir dem Ohmschen Gesetz in Form des Quotienten R = U / I und ordnen den ersten
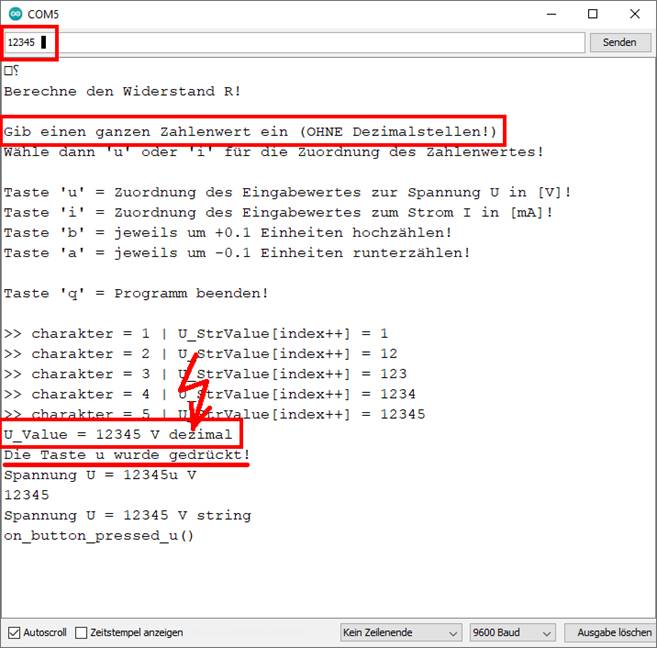
eingetasteten Zahlenwert „123.45“
(ohne Anführungszeichen!) der Spannung
U zu (siehe „Sketch“-Programm
„sketch_prog_03_01.ino“): (Bild
vergrößern: auf Bild klicken! Webverzeichnis
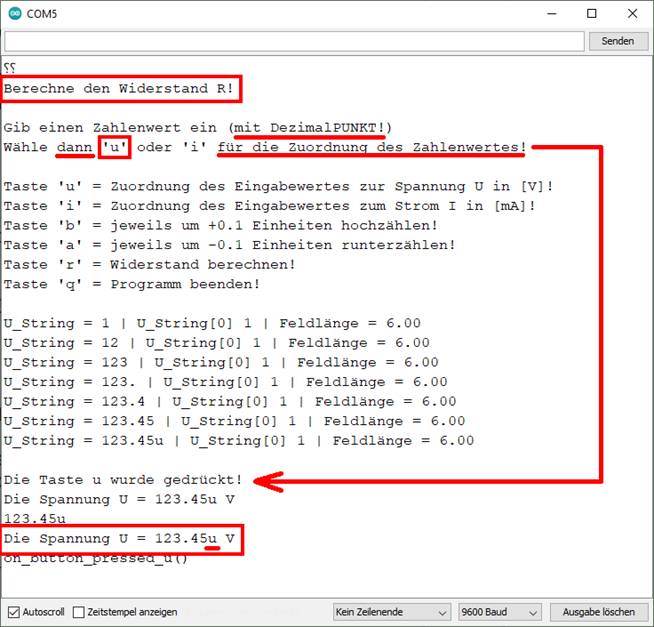
| sketch_prog_03_01.ino) Wie man im obenstehenden Screenshot des
Konsolefensters der Arduino-Entwicklungsumgebung sieht, werden die
eingetasteten Werte, d.h. der Zahlenwert
„123.45“ also auch das Betätigen der Auswahltaste „u“ charakterweise, d.h. zeichenweise nacheinander
eingelesen und wider Erwarten nicht einheitlich als ein Ganzes
bzw. als eine Zeichenkette. Das Eigentümliche dabei ist noch, dass die
Feldlänge der Variablen „U_String_max“ dabei immer konstant
6 Zeichen beträgt: (Bild
vergrößern: auf Bild klicken! Webverzeichnis
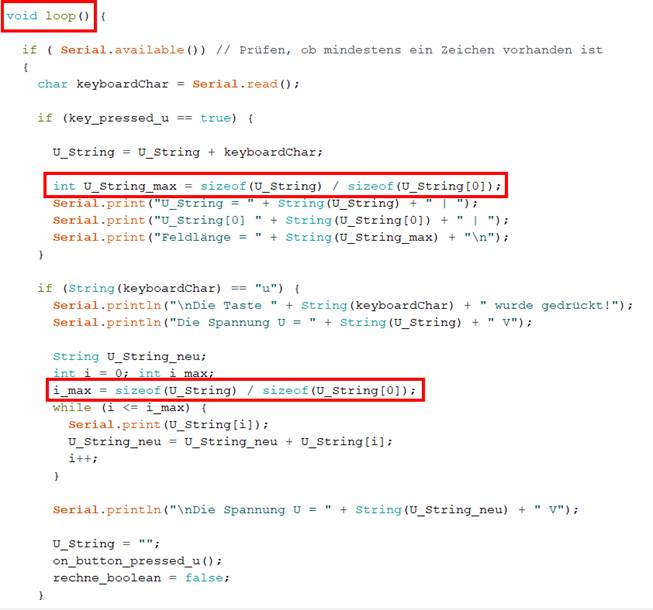
| sketch_prog_03_01.ino) Wie man im obenstehenden Screenshot in den roten Kästen sieht, kommen wir mit
den Statements ·
< int U_String_max = sizeof(U_String) / sizeof(U_String[0]); > ·
< i_max = sizeof(U_String) / sizeof(U_String[0]); > nicht weiter, weil diese nur dazu geeignet sind,
die Größe von Arrays zu berechnen, aber
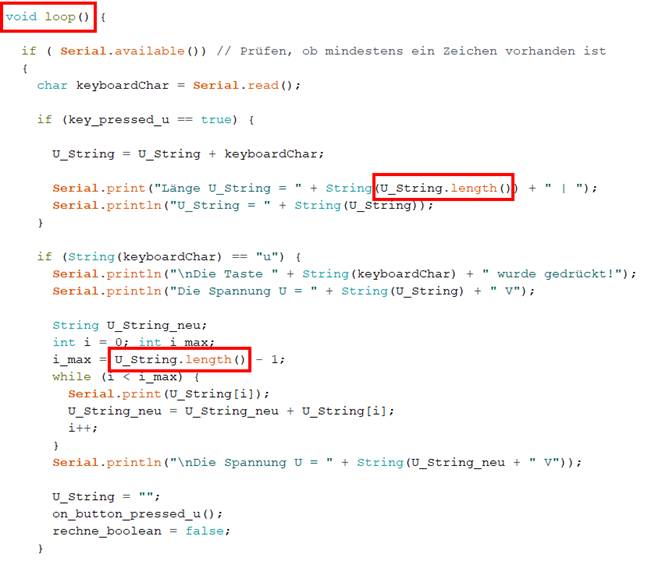
eben nicht die Länge eines Textstrings. Aber schon mit dem nächsten
„String“-Befehl Stringvariable.length() lässt sich die Länge
eines Textstrings
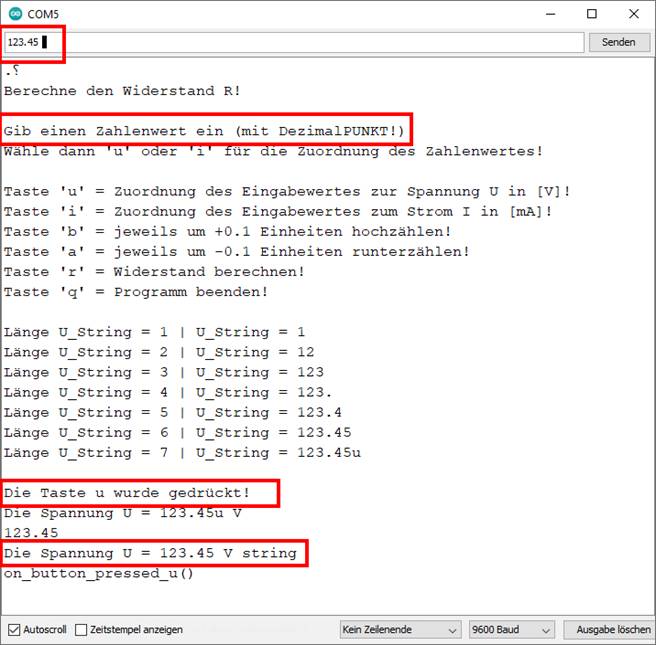
problemlos ermitteln: (Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_03_02.ino) Schauen wir uns noch zu
obenstehenden Programm die Anzeige im Konsolefenster
der Arduino-Entwicklungsumgebung
an: (Zum
Vergrößern bitte auf das Bild klicken!) Beim „Sketch“-Programm
„sketch_prog_03_03.ino“
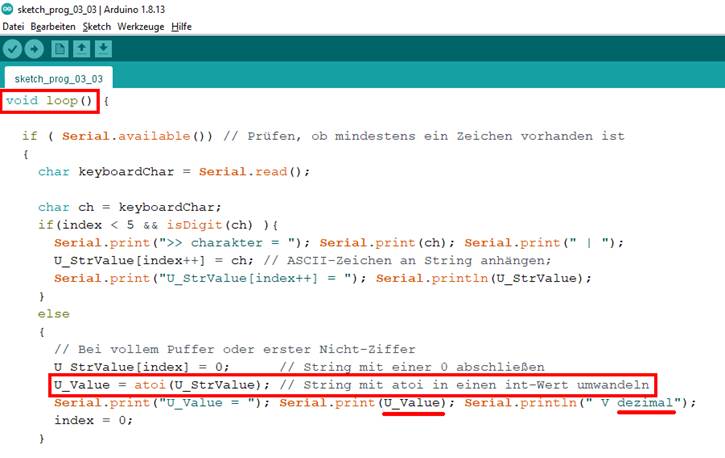
geht es nachfolgend darum, dass wir die Anzeige des Textstrings „Die Spannung U = 123.45 V string“ bzw.
die Ziffernanzeige „123.45“ in den Dezimalwert „123.45“ umwandeln. Da uns aber zu diesem Zweck
im Moment nur das ·
Statement < U_Value = atoi(U_StrValue); > mit der Abkürzung engl. “atoi” (=
„ASCII to
Integer“), d.h. ASCII-Zeichen
von der Konsoleeingabe in ganzzahligen
Wert
umwandeln, zur Verfügung steht, verzichten wir zunächst noch auf die
Eingabe des Dezimalpunktes: (Zum
Vergrößern bitte auf das Bild klicken!) Der Grund dafür, weshalb
der „Arduino
UNO“ noch nicht die Dezimalrechnung in
der engl. „ALU“
(= „Arithmetic Logic Unit“), d.h. Recheneinheit, beherrscht, dürfte der sein,
dass es sich bei diesem dem Ursprung nach und von der Entwicklungsgeschichte
her um einen Mikrocontroller
handelt, um den herum man dann noch ein kleines Betriebssystem nebst
„Sketch“-Programmierung gebaut hat. Bei dem englischen „micro:bit“-Rechner von
der BBC war es anfangs ähnlich, beherrschte dieser auch noch nicht die Dezimalrechnung,
während der deutsche „Calliope mini“ diese von Anfang an
beherrschte, weil er als deutscher Nachkömmling sozusagen bereits über ein
neueres, leistungsfähigeres Betriebssystem verfügte. Der Knackpunkt beim „Arduino UNO“
ist dabei der, dass sich der über die Tastatur und die serielle
Schnittstelle
eingelesene Textstring nicht einfach so per Befehl in einen ganzzahligen
„Integer“-Wert oder einen „float“-Fließkommazahlenwert
umwandeln lässt, weil die Eingaben mittels Tastatur eben nicht
erwartungsgemäß in einer „String“-Variablen,
sondern vielmehr in einem Zeichenarray vom Typ „char“, d.h. „Character“ (= Zeichen, Ziffern) erfolgt
und die einzelnen Zeichen im „Character“-Array nicht ASCII
kodiert sind: (Bild
vergrößern: auf Bild klicken! Webverzeichnis
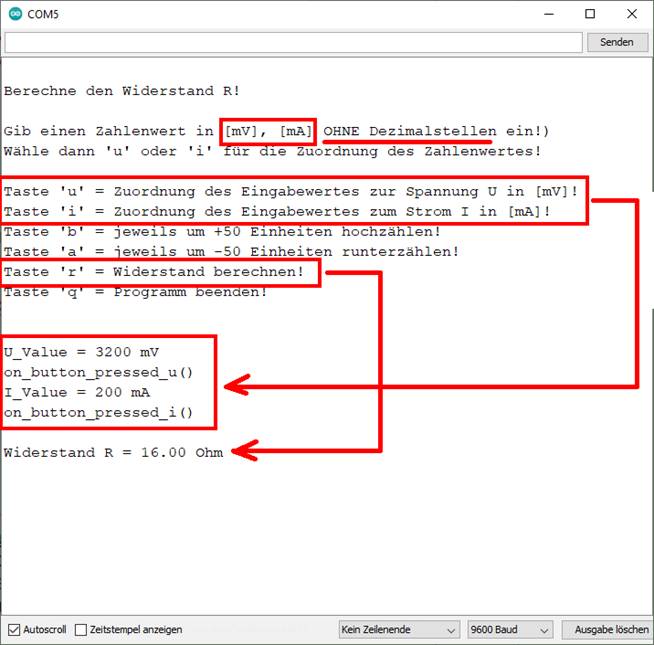
| sketch_prog_03_03.ino) Mit dem „Sketch“-Programm „sketch_prog_03_04.ino“
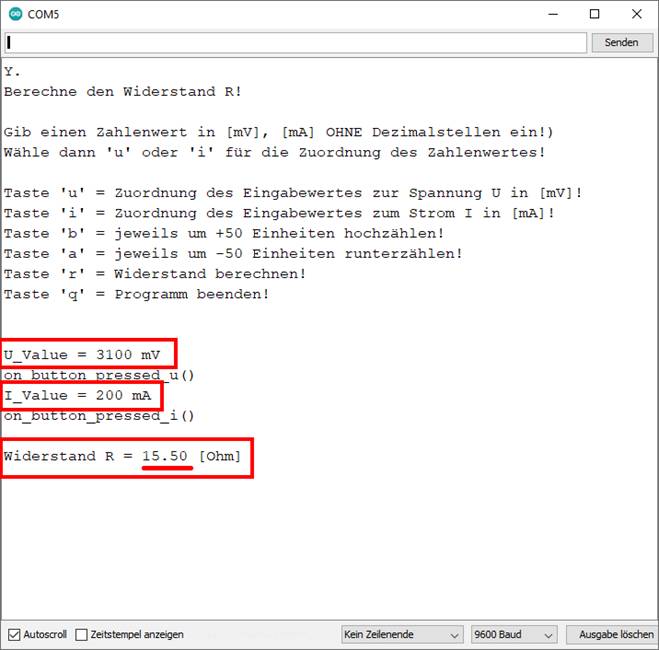
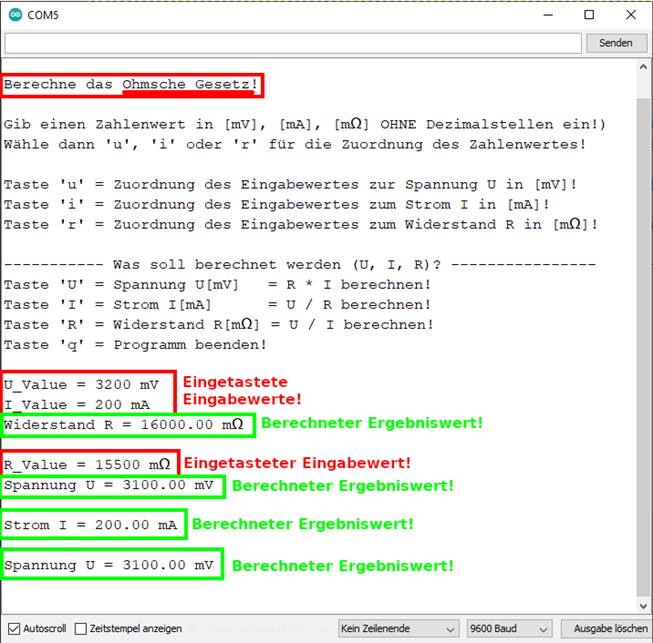
sind wir nun erstmals in der Lage, den ohmschen Widerstand R der Glühlampe Nr. 18 anhand der beiden Nenn-Betriebswerte
von Spannung U = 3,2 V = 3200 mV und Strom I = 0,2 A = 200 mA vom Programm berechnen
zu lassen. Zwar können wir jetzt mit
unserem Programm das eingelesene „Character“-Array „keyboardChar“
vom PC-Keyboard mittels des Statements ·
<
char keyboardChar = Serial.read();
> einlesen und mittels des Statements ·
< Input_Value = atoi(Input_StrValue); > in einen ganzzahligen
„Integer”-Wert umwandeln,
allerdings nicht mit Dezimalzahlen,
sodass demzufolge die Eingabewerte für Spannung
U = 3200 mV und Strom I = 200 mA ausschließlich
in ganzzahligen Werten,
hier also Millivolt [mV] und Milliampere [mA],
eingetastet werden müssen. Und zwar auch ohne Maßeinheit! Da der ohmsche Widerstand R
der Glühlampe Nr. 18
gemäß der Formel R = U / I berechnet werden soll, kürzen sich die Milliwerte
bei den Maßeinheiten im Zähler und
Nenner weg, sodass man den Widerstand R in
der Maßeinheit [Ω]
berechnet bekommt: (Zum
Vergrößern bitte auf das Bild klicken!) Da das Ohmsche Gesetz
mit R = U / I
den Quotienten von U / I
bildet, muss man je nach eingetasteten Werten für Spannung U und Strom I
mit einem krummen Wert, d.h. Dezimalwert für den Widerstand R
als Ergebnis rechnen, der aber wegen der Variablen
„U_Value“
und „I_Value“
vom Typ „int“ (=
integer, ganzzahlig) nicht als Dezimalwert gerechnet werden
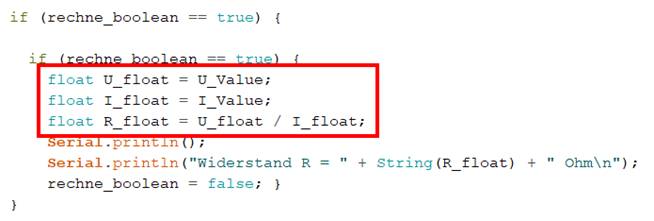
kann, sodass das Ergebnis U = 3100 mV, I = 200 mA = 15 Ω einfach ganzzahlig abgeschnitten wird! Wenn man aber die „Integer“-Werte vor
dem Berechnen in einen Fließkommawert, engl. „float“, umrechnet,
(Bild
vergrößern: auf Bild klicken! Webverzeichnis
| sketch_prog_03_04.ino) dann bekommt man als Ergebniswert ebenfalls einen Dezimalwert
ausgewiesen: (Bild
vergrößern: auf Bild klicken! Webverzeichnis
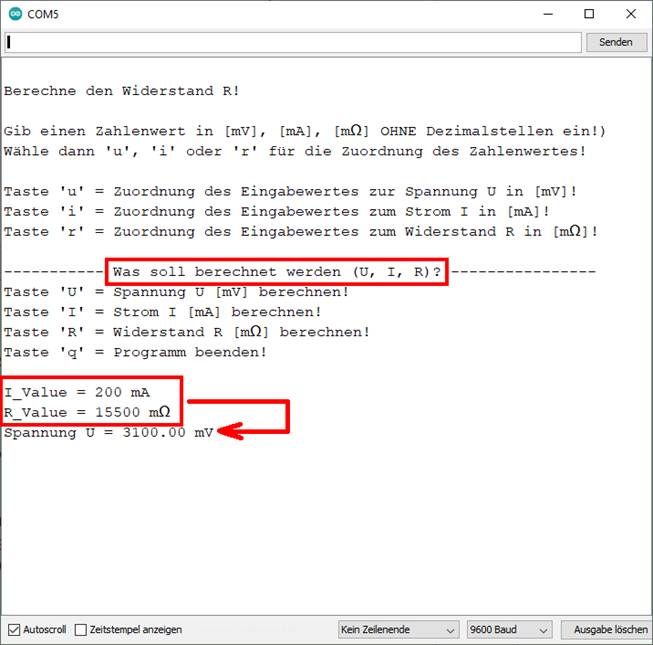
| sketch_prog_03_04.ino) Wir erweitern das bisherige
Programm und zwar in der Weise, dass sich nun auch der Strom I [mA] und der Widerstand R [mΩ]
berechnen lassen. Die Eingabe aller zu berechnenden Werte in Milli (= 1/1000 = 0,001) ist
anfangs etwas gewöhnungsbedürftig, aber nicht dauerhaft stressig, weil man
sich schnell daran gewöhnt. Letztlich muss man nämlich
z.B. bei der Eingabe des Spannungswertes von 3,1 Volt nur das Komma um
drei Stellen
nach rechts verschieben: 3,1 V = 31000 mV. Wenn ich aber z.B. die Spannung U in [mV]
berechnen will, dann muss ich schon das Ohmsche
Gesetz R = U / I kennen! Denn nur wenn ich das Ohmsche Gesetz R = U / I kenne und die Formel gedanklich nach U = R * I umstellen
kann, dann weiß ich, dass ich zur Berechnung der Spannung U in [mV] die beiden Werte von Widerstand R und Strom I
benötige: (Bild
vergrößern: auf Bild klicken! Webverzeichnis
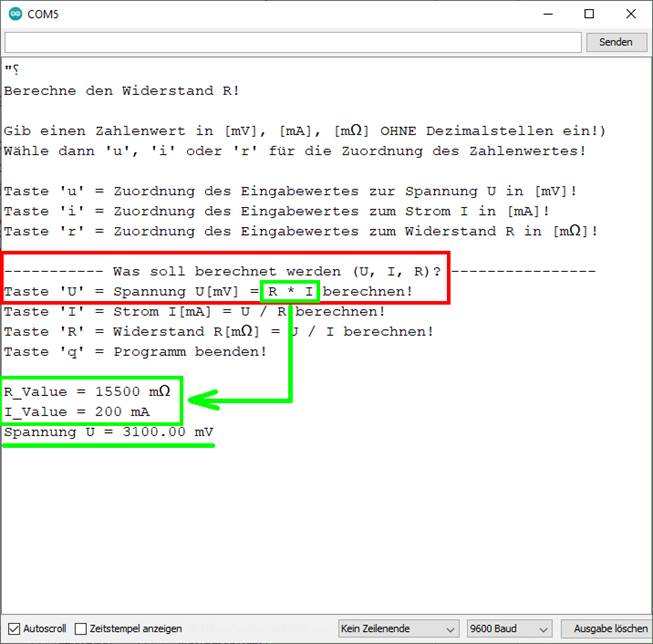
| sketch_prog_03_05.ino) Dem Umstand, dass man zur
Berechnung z.B. der Spannung U in
[mV]
bereits das Ohmsche Gesetz R = U / I verinnerlicht
haben muss, d.h. formelmäßig in- und auswendig kennen muss, lässt sich begegnen, indem man für den
Anfänger die jeweils anzuwendende Formel in das Menü,
d.h. die Bedienerführung, wie folgt einbaut (siehe grüne Kästen): (Bild
vergrößern: auf Bild klicken! Webverzeichnis
| sketch_prog_03_06.ino) Bisher verhielt es sich bei
dem obenstehenden „Sketch“-Programm
„sketch_prog_03_06.ino“
so, dass man gemäß dem Ohmschen Gesetz alle Werte wie z.B. Spannung U = I * R → Strom
I = U / R → oder Widerstand
R = U / I
der Reihe nach oder quer Beet, d.h. in beliebiger Reihenfolge,
berechnen konnte. Allerdings musste man dazu jedes
Mal die zugehörigen Werte erneut eintasten, auch wenn man diese schon
einmal bei der Berechnung eines anderen Wertes eingetastet hatte.
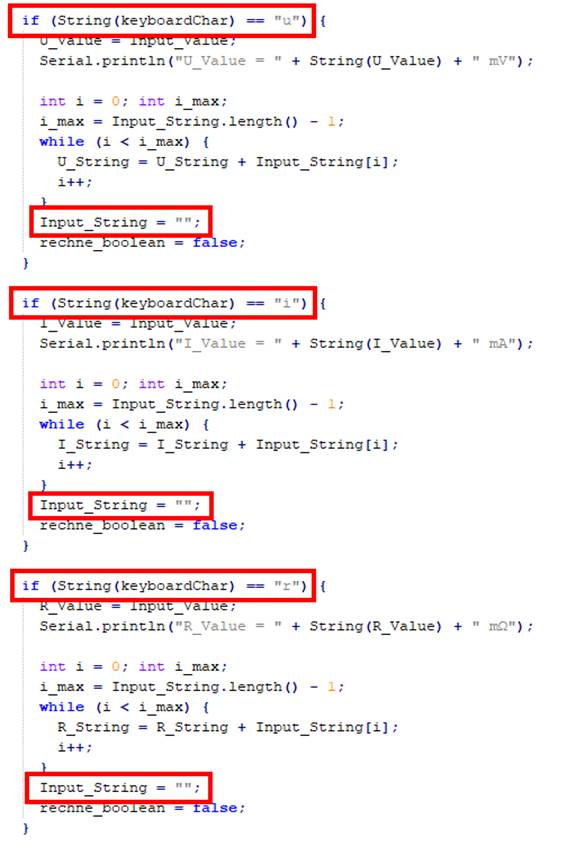
Der Grund dafür ist das ·
Statement
< Input_String = ""; > in jeder Berechnung, das am Ende der Berechnung die Variable „Input_String“ mittels der Zuordnung "" löscht: (Bild
vergrößern: auf Bild klicken! Webverzeichnis
| sketch_prog_03_06.ino) Wenn man das ·
Statement
< Input_String = ""; > aus allen Berechnungen löscht, d.h. einfach aus
dem Quellkode entfernt,
dann lassen sich einmal eingetastete Werte beliebig oft weiter
verwenden, ohne dass diese erneut eingetastet werden müssen (siehe „Sketch“-Programm „sketch_prog_03_07.ino“): (Bild
vergrößern: auf Bild klicken! Webverzeichnis
| sketch_prog_03_07.ino) Den Sourcecode
zum obenstehenden Screenshot des „Arduino“-Konsolefensters
kann man sich direkt im Browser
anzeigen lassen oder durch Mausklick der rechten Maustaste
und <Link
speichern unter …> herunterladen! - Nachdem das Programm
ziemlich ausgereift ist, geht es nachfolgend darum, dieses auszuprobieren und
anzuwenden, indem wir ein paar Aufgaben zum Ohmschen Gesetz, d.h. zur Berechnung des Widerstandes R
usw. rechnen. Kehren wir deshalb wieder an dieser Stelle zurück zum Ohmschen Gesetz
beim Versuch 1 „Spannung, Strom und
Widerstand“. [ weiterlesen ]
Der
Mensch mit seinen sechs Sinnen
wie Sehen, Hören, Riechen, Schmecken und Taste/Fühlen, ist zwar seitens der
Natur recht gut ausgestattet, verfügt aber leider über kein Sinnesorgan für die
Wahrnehmung des elektrischen Stroms. Aber das ist vielleicht auch gut so.
Angesichts der vielen Elektro- und Elektronikgeräte der Unterhaltungsindustrie
im Haushalt würden wir uns bei dem vielen Elektrosmog
wahrscheinlich gar nicht wohlfühlen, wenn der Mensch über einen mehr oder
weniger empfindlichen Sensor bzw. Sinnesorgan für elektrische Spannungen, Ströme
oder die elektrische Energie verfügen. Und, was der Mensch nicht
hat, das schafft er sich. Nämlich einen Sensor für elektrische Spannungen und
Ströme wie z.B. in Form einer Glühlampe,
die nicht nur Licht und Helligkeit verbreitet, sondern auch Wärme als Abfallprodukt wegen der
geringen Lichtausbeute und des schlechten Wirkungsgrades. Aber mit dem „Arduino UNO“ und
das gilt auch für den „Calliope mini“ und den „micro:bit“ kann man sich einen
viel besseren Sensor für elektrische
Spannungen programmieren
als dies jemals mit einer Glühlampe
möglich wäre. Den Sensor für elektrische Spannungen nennt man umgangssprachlich
Voltmeter oder besser Spannungsmessgerät.
Aber unser Spannungsmessgerät in
Form des „Arduino UNO“ ist so klein, dass man es nicht sieht,
weil es im integrierten A/D-Wandler
steckt. Dabei steht „A/D“ für die
englisch/deutsche Abkürzung „Analog/Digital“. Und, da wir unsere Glühlampe 18 mit
elektrischer Energie aus den beiden in Reihe
geschalteten 1,5 Volt Batterien vom Typ „Mignon AA“ des Batteriefachs 19 beziehen, handelt es sich bei der Spannungsversorgung
aus den Batterien um eine Gleichspannung! Genau genommen handelt es
sich dabei um eine analoge Gleichspannung.
Aber da man in der Digitaltechnik
nicht von einer digitalen Gleichspannung
spricht, sondern einfach nur von Digitalsignalen im
Sinne von (Gleich-) Strom „EIN = 1 = Strom fließt“ oder
Strom „AUS = 0 = kein Stromfluss“ spricht, gibt es praktisch
keine Unterscheidung zwischen einer analogen oder digitalen Gleichspannung. Die
Gleichspannung ist, außer bei der Digitaltechnik, immer analog. Wie aber erklärt sich der
Unterschied zwischen analog und digital? „Bei uns kommt der (Wechsel-) Strom)
aus der Steckdose und er fließt so lange bis der Strom ausfällt!“ lautet ja
der dumme Spruch der Atomstrombefürworter bzw. Energieverschwender. Das ist
dann so als würde man sagen bei uns kommen die Himbeeren im Winter aus der
Kühltheke vom REWE Supermarkt. Aber wenn der Strom, in
Wirklichkeit sind es natürlich Spannung und Strom in Form der elektrischen Energie,
fortwährend, sozusagen ununterbrochen vorhanden ist, dann wäre er ewiglich,
d.h. von Raum und Zeit unabhängig! Und
von der Zeit unabhängig sind
Spannung
und Strom aus
der Energieversorgung unseres Batteriefachs 19 tatsächlich,
wenn man mal davon absieht, dass die Batterien
nach etlichen Stunden der Nutzung irgendwann entladen sind. Ob und wann wir also unsere
Glühlampe 18 einschalten
und leuchten lassen spielt zeitlich keine Rolle. Wir können
morgens um sieben Uhr die Glühlampe einschalten oder abends, wenn es dunkel
wird. Der elektrische Strom (umgangssprachlich) steht zeitlich unabhängig
quasi unbefristet immer zur Verfügung. Demzufolge ist die Gleichspannung unserer Batterien UBatt = UBatt_1 + UBatt_2 eben
keine Funktion der Zeit t → U= ≠ f(t) = R * I
mit I=
≠ f(t) =
konstant, auch im Sinne von zeitlich unabhängig! Es macht also einen
Unterschied, ob eine elektrische Spannung zeitlich unabhängig ist mit U= ≠ f(t) wie z.B. unsere Gleichspannung
U= aus dem Batteriefach 19 oder
zeitlich abhängig ist mit U~ = f(t) wie
z.B. die Wechselspannung U~ aus
der Wandsteckdose mit U~ = 230 V~ (Achtung
Hochspannung, lebensgefährlich!). Da die Wechselspannung mit einer Frequenz von f = 50 Hz, d.h. 50 Schwingungen pro
Sekunde, zeitlich wellenförmig verläuft, spricht man auch von
einem sogenannten Sinus mit U~
= f(t) = ȗ * sin (ω t) = USpitze *
sin (ω t)
= USpitze * sin (2π / T * t) mit ω = 2π f = 2π / T und T für die Periodendauer Für t = 0 folgt: U~
= f(t) = f(t=0) = f(0) = ȗ * sin (ω t) = ȗ *
sin (ω 0) = ȗ * sin 0 = ȗ * 1 = ȗ → Gleichspannung
wegen t = 0 ! Charakteristisch für eine Wechselspannung ist
noch, dass diese wegen der 50 Schwingungen/Sekunde, gemessen in Hertz [Hz],
ständig die Richtung des Stromflusses und damit auch die der Polarität
ändert! Der Wechsel der Polarität geschieht aber so schnell, dass das
menschliche Auge wegen seiner Trägheit diesen nicht wahrnimmt. Wäre dem nicht
so, bekämen wir bei der heimischen Beleuchtung mittels Glühlampen ständig
Kopfschmerzen! - Da der analoge Spannungseingang vom
(+) Pin A0 zum
Pin GND gegen
Masse „┴“ geführt ist, lässt
sich mit dem A/D-Wandler nur eine Gleichspannung abtasten
und digitalisieren,
d.h. in Bitwerte im Bereich [0, …, 1023] umwandeln, sodass
sich insgesamt 1024 Messwerte
einschließlich der Null ergeben. Wenn wir in diesem Zusammenhang
davon ausgehen, dass der A/D-Wandler
analoge Eingangsspannungen bis 3,3 Volt abtasten, einlesen und in einen
entsprechenden Bitwert umrechnen kann, dann folgt für die spannungsmäßige
Auflösung: 3,3 V → 1023 Bit 1,0 V → x Bit x = 1023 Bit /
3,3 Probe: 310 Bit/Volt * 3,3 V = 1023 Bit Bei dem gemessenen Spannungsabfall ULampe = 2,37 V an der Glühlampe 18 mit
den Nenn-Betriebsdaten 3,2 V / 0,2 A
müsste also der Bitwert 735 im Konsolefenster der Arduino-Entwicklungsumgebung
angezeigt werden: 3,3 V → 1023 Bit 2,37 V → x Bit x = 1023 Bit /
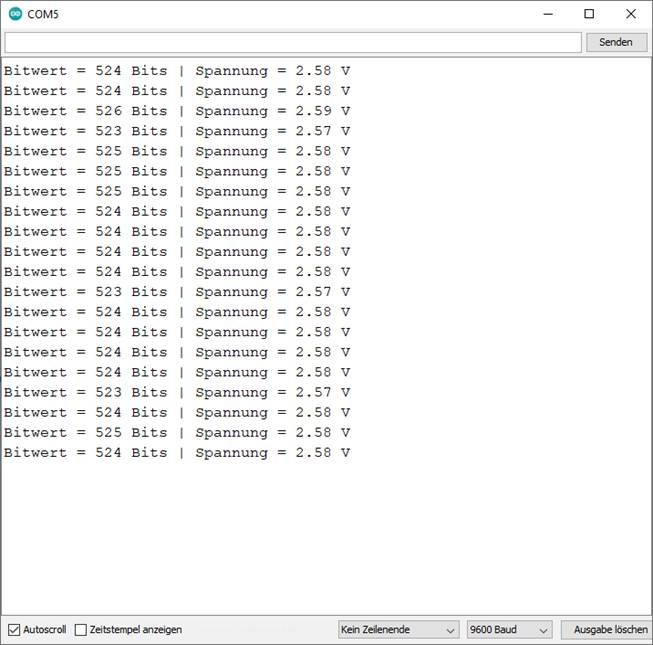
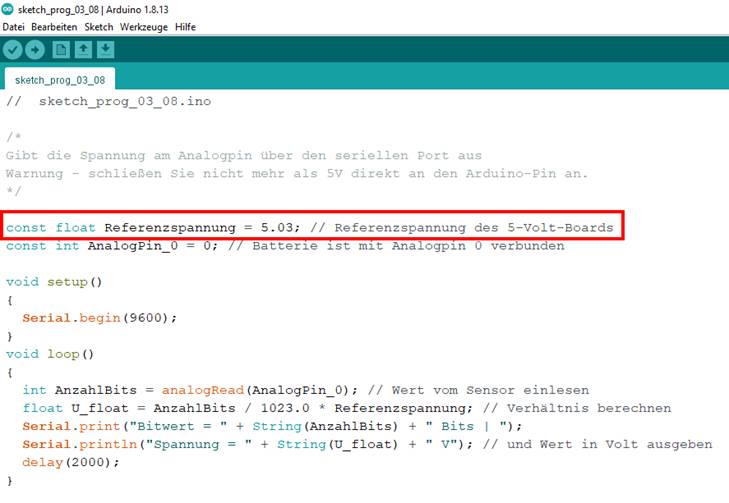
3,3 Was aber bedeutet es, wenn
uns das Messprogramm „sketch_prog_03_08.ino“
eine Spannung UA/D = 2,58 V mit
524 Bit anzeigt (siehe Bild unten)?
(Bild
vergrößern: auf Bild klicken! Webverzeichnis
| sketch_prog_03_08.ino) 524 Bit → 2,58
V 1023 Bit → x V x = 2,58 V / 524 Bit * 1023 Bit = 5,037 V ≈ 5 V Jetzt wissen wir, dass sich
mit dem A/D-Wandler des „Arduino UNO“ eingangsseitig
Gleichspannungen
bis +5V digitalisieren
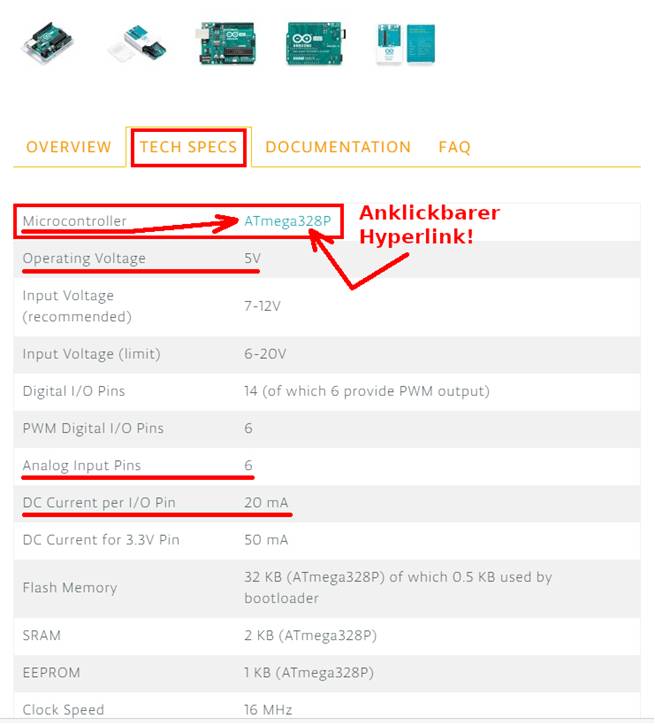
lassen! Auf der Webseite https://store.arduino.cc/arduino-uno-rev3#
von Arduino kann man sich über die
technische Spezifikation des „Arduino UNO“ und den integrierten Mikrocontroller „ATmega328P“
informieren: (Zum
Vergrößern bitte auf das Bild klicken!) Wie man im obenstehenden
Screenshot sieht, arbeitet der „ATmega“-Mikrocontroller, der
u.a. die sechs A/D-Wandler
mit den Pins „A0“
bis „A5“ beherbergt,
mit einer Betriebsspannung von +5 V. Das
deutet darauf hin, dass die A/D-Wandler
ebenfalls (Eingangs-) Spannungen
bis +5 V verarbeiten
können. Wenn man im obenstehenden
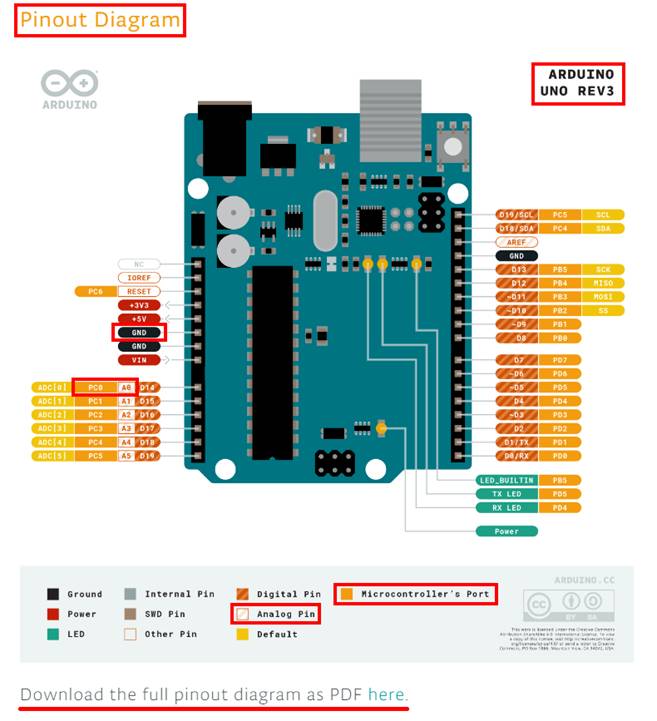
Screenshot auf die Rubrik „Documentation“ klickt,
dann kann man sich das „Pinout“-Diagramm
wie folgt anzeigen lassen und als PDF-Datei
herunterladen: (Zum
Vergrößern bitte auf das Bild klicken!) Werfen wir abschließend
noch einen Blick auf den Sourcecode: (Bild
vergrößern: auf Bild klicken! Webverzeichnis
| sketch_prog_03_08.ino) |
|
|
|
[ Easy Elektro Start ] [ Seitenanfang ] [ zurück ] |
|