[ Easy Elektro Start ] [ Seitenende ] [ zurück ]

Easy Elektro Start – Programmieren 12

Ein Strom für zwei Lampen

Dass die beiden 1,5 Volt Batterien vom Typ „Mignon AA“ im Batteriefach 19 hintereinander, d.h. in Serie geschaltet sind, wissen wir seit dem Versuch 1 „Kreisverkehr“ bei dem es um den geschlossenen Stromkreis geht.

Und, dass sich zwei Glühlampen 18 auch in Serie zusammenschalten lassen, wissen wir seit dem Versuch 9 „Zwei in Reih und Glied“ ebenfalls.

Hier beim Versuch 12 „Ein Strom für zwei Lampen“ könnte man zunächst meinen, dass sich ein gemeinsamer Strom auf zwei Glühlampen 18 aufteilt, der die zwei Lampen gemeinsam mit elektrischer Energie versorgt.

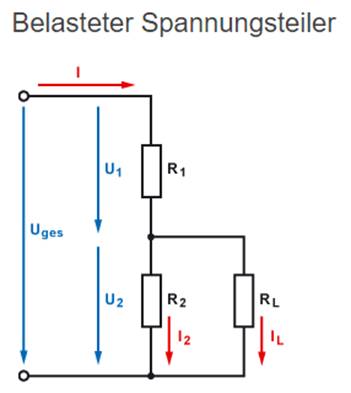
Wäre dem so, dann müsste es sich bei der Schaltung um eine Parallelschaltung zweier Glühlampen 18 handeln, was aber nicht der Fall ist, da diese in Serie, d.h. in einer Reihenschaltung geschaltet sind bei der sich die gemeinsame Spannung auf die beiden Glühlampen 18 aufteilt, weshalb man auch von einem Spannungsteiler spricht. Genau genommen handelt es sich bei diesem sogar um einen unbelasteten Spannungsteiler.

Im Gegensatz dazu handelt es sich beim belasteten Spannungsteiler um eine Kombination einer Reihen- mit anschließender Parallelschaltung nebst Stromteilung.

Doch jetzt geht es um den einfachen Fall eines unbelasteten Spannungsteilers, bei dem die beiden Glühlampen 18 hintereinander in Serie geschaltet sind, sodass sich die Versorgungsspannung in Form der Batteriespannung

U_Batt = U_{Batt 1} + U_{Batt 2} = U_{Batt 1} + U_{Batt 1} mit U_{Batt 2} = U_{Batt 1} →

= 2 * U_{Batt 1} = 2 * 1,5 V = 3 V

auf die beiden in Serie geschalteten Glühlampen 18 aufteilt:

(Zum Vergrößern bitte auf das Bild klicken!)

Erinnern wir uns im Zusammenhang mit der Reihenschaltung der beiden in Serie geschalteten Glühlampen 18 an deren sogenannten Nenn-Betriebsdaten von U_Lampe = 3,2 V und I_Lampe = 0,2 A so fällt auf, dass die beiden im obenstehenden Bild zu sehenden 1,5 Volt Batterien vom Typ „Mignon AA“ im Batteriefach 19 nur eine Versorgungsspannung von max. U_Batt = 3,0 V aufzubringen vermögen, sodass die beiden Glühlampen 18 nur mit der hälftigen Batteriespannung versorgt werden und in Folge dessen nur halb so hell leuchten:

U_Batt = U_Mess + U_{Lampe 1} + U_{Lampe 2} ≈ U_{Lampe 1} + U_{Lampe 2} = U_{Lampe 1} + U_{Lampe 1} = 2 * U_{Lampe 1} mit U_{Lampe 2} = U_{Lampe 1}

= 2 * U_{Lampe 1} →

U_{Lampe 1} = ½ * U_Batt = ½ * 3,0 V = 1,5 V →

I_{Lampe 1} = U_{Lampe 1} / R_{Lampe 1}

= U_{Lampe 1} / ( U_Nenn / I_Nenn ) = ( U_{Lampe 1} / U_Nenn ) * I_Nenn = 1,5 V / 3,2 V * 0,2 A = 0,09375 A = 93,75 mA

Da die beiden im obenstehenden Bild zu sehenden 1,5 Volt Batterien vom „Mignon AA“ im Batteriefach 19 inzwischen energiemäßig ziemlich aufgebraucht sind und die Batteriespannung bei jedem weiteren Gebrauch und jeder weiteren Belastung durch die beiden in Reihe geschaltete Glühlampen 18 „in die Knie geht“, d.h. absinkt, lassen sich mit diesen keine exakte Messungen mehr nebst Auswertung und Berechnung durchführen! Aber das ist kein Problem, da wir die interne Stromversorgung des „Arduino UNO“ anzapfen können!

Demzufolge machen wir uns die interne Spannungsversorgung des „Arduino UNO“ am Pin „+5V“ entsprechend zu Nutze, zumal uns an diesem Stromstärken von bis zu 400 mA ^*) zur Verfügung stehen:

U_{Lampe 1} / U_{Pin +5V} = R_{Lampe 1} / R_ges = R_{Lampe 1} / 2 * R_{Lampe 1} = ½ →

U_{Lampe 1} = ½ * U_{Pin +5V} = ½ * 5,0 V = 2,5 V

I_{Lampe 1} = U_{Lampe 1} / R_Nenn = 2,5 V / 16 Ω = 2,5 V / 16 V/A = 0,15625 A = 156,25 mA

^*) In diesem Zusammenhang muss man aber wissen, dass die maximale Stromstärke von bis zu 400 mA am Pin „+5V“ des „Arduino UNO“ nur dann zur Verfügung steht, wenn wir diesen mittels des USB-Verbindungskabels am USB-Anschluss eines Desktop-PCs oder Notebooks mit Energie versorgen (siehe kleiner grüner Kasten):

(Zum Vergrößern bitte auf das Bild klicken!)

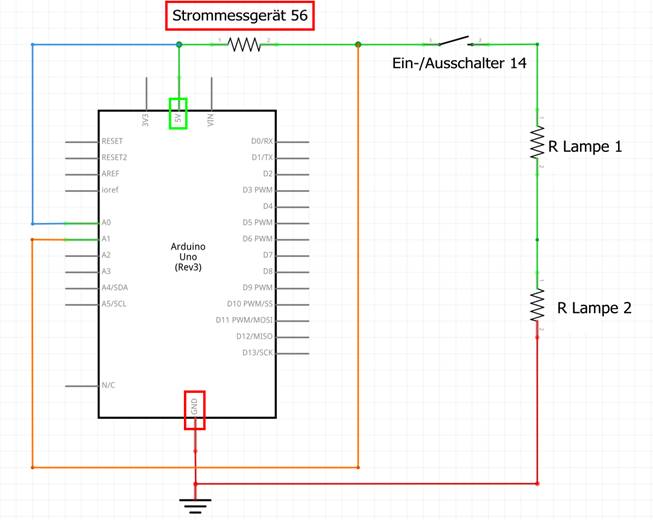
Von unserem „Arduino UNO“ wissen wir, dass dieser hardwaremäßig über sechs analoge Eingänge und zwar in Form der engl. Ports „Pin A0“, …, „Pin A5“ verfügt, sodass sich mittels des integrierten A/D-Wandlers entsprechende Eingangsspannungen U_{Pin_A0} > 0 V und U_{Pin_A0} <= 5,0 V vom Anschluss „Pin A0“ gegen Masse „Pin GND“ („┴“) messen und als Bitwerte im Bereich [ 0, …, 1023 ] anzeigen lassen.

Wie man in der obenstehenden Schaltung sieht, verwenden wir die beiden Ports „Pin A0“ und „Pin A1“, um mit deren integrierte A/D-Wandler eingangsseitig die beiden analogen Spannungen U_{Pin A0} und U_{Pin A1} gegen Masse „Pin GND“ („┴“) zu messen. Und zwar deshalb gegen Masse „Pin GND“ („┴“), weil sich bei integrierten Schaltungen wie z.B. Mikroprozessoren, Mikrocontrollern, ICs, Operationsverstärkern usw. ein- oder ausgangsseitige Spannungen immer auf die Geräte interne Masse „┴“ beziehen.

Der Grund dafür ist der, dass in integrierten Schaltungen abertausende Halbleiter in Form von Dioden, Transistoren, Transistorschaltungen usw. verbaut sind, die alle auf die eine oder andere Weise miteinander verbunden sind, Spannungen, Ströme und Signale verarbeiten, dies aber nur können, wenn sich alle Einzelschaltungen auf ein und dasselbe Massepotential „┴“ beziehen.

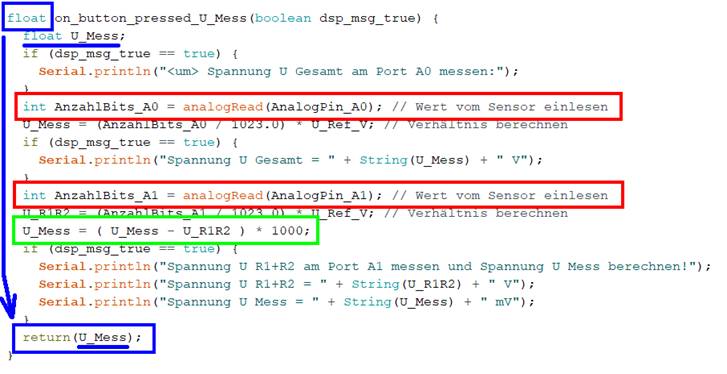
Dies ist dann auch der Grund dafür, weshalb sich der Spannungsabfall U_Mess am Strommessgerät 56 wider Erwarten nicht direkt zwischen den Anschlussklemmen des Messgerätes messen lässt, sondern eben nur indirekt über den gemeinsamen Masseanschluss „Pin GND“ („┴“).

Demzufolge müssen wir die beiden Spannungen U_{Pin A0} und U_{Pin A1} gegen Masse „┴“ einzeln messen und aus den beiden Werten die Spannungsdifferenz(!) mit

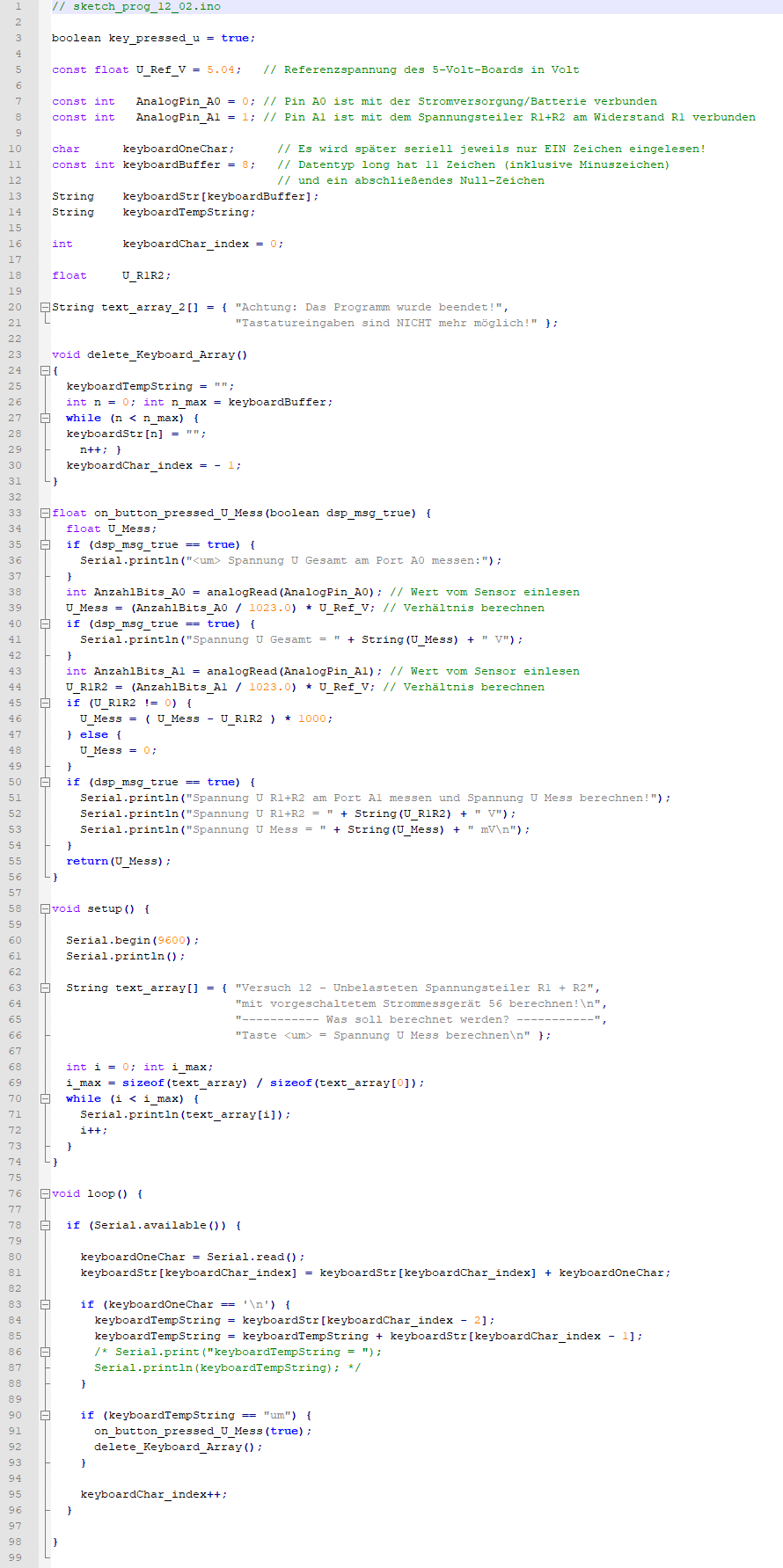
U_Mess = U_{Pin A0} - U_{Pin A1} → und U_{Pin A0} > U_{Pin A1} bilden (siehe grüner Kasten):

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_01.ino)

Wenn man sich den obenstehenden Sourcecode des „Sketch“-Programms „sketch_prog_12_01.ino“ anschaut, dann fällt sofort auf, dass es sich bei der Funktion „on_button_pressed_U_Mess()“ nicht mehr um eine vom Typ „void“, d.h. leer, nichts im Sinne davon, dass bei „void“ keine Werte an andere Variablen, Funktionen oder Programme zurückgegeben werden.

Im vorliegenden Fall wird also der Wert der berechneten Variable „U_Mess“ vom Typ „float“ (= Dezimalzahl, Fließkommazahl mit zwei Nachkommastellen) an das aufrufende

· Statement < on_button_pressed_U_Mess(true); >

im Programmblock „void loop() { … }“ zurückgegeben, obwohl dort der Wert der Variablen „U_Mess“ im Moment noch gar nicht gebraucht oder weiter berechnet wird (siehe blauer Kasten):

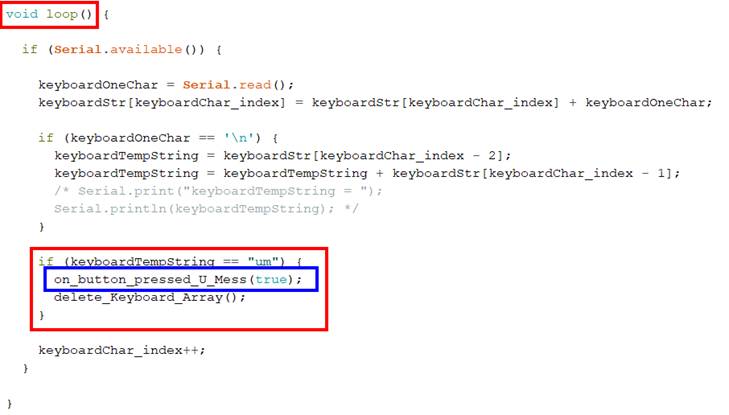
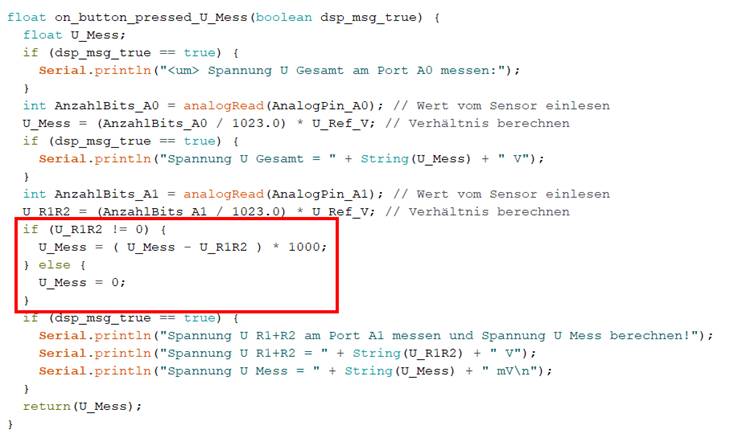
(Zum Vergrößern bitte auf das Bild klicken!)

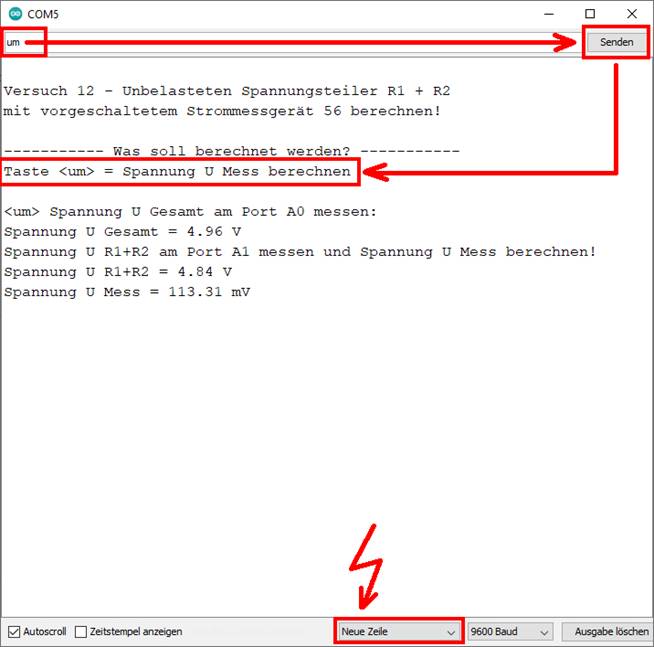
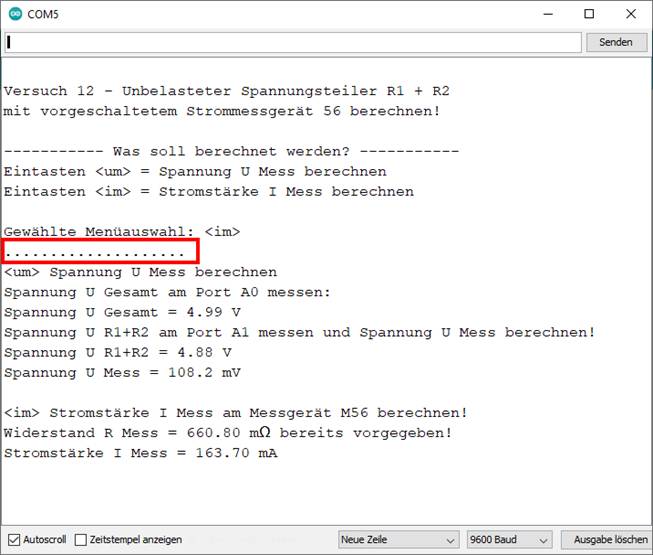
Bei der <if … then>-Abfrage im roten Kasten (siehe im Bild oben) handelt es sich übrigens um die Tastaturabfrage im Arduino-Konsolefenster!

Wenn man dort die Tastenfolge <um> eintastet und mittels <ENTER/RETURN>-Taste bestätigt, dann wird die Menüauswahl „Taste <um> = Spannung U Mess berechnen“ wie folgt ausgeführt (siehe roter Kasten):

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_01.ino)

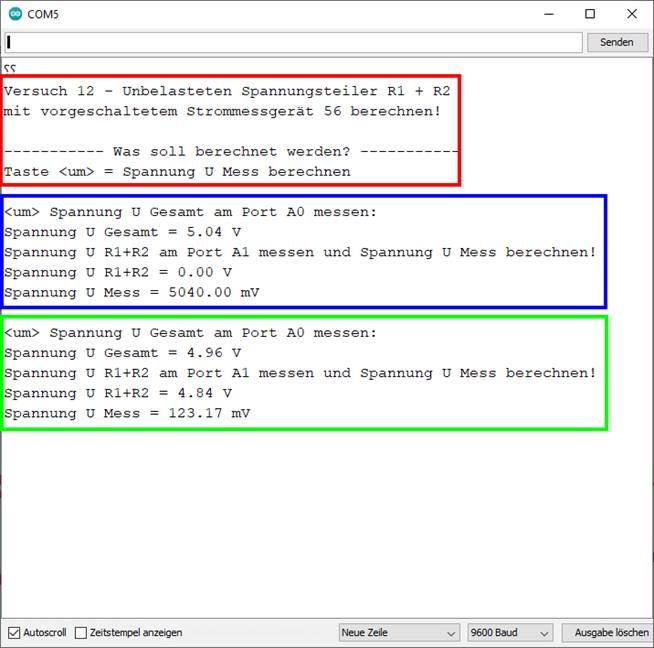
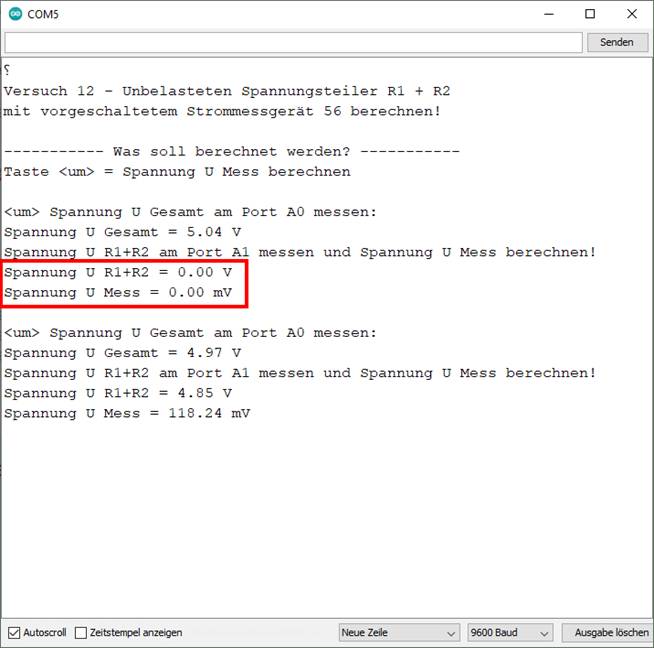
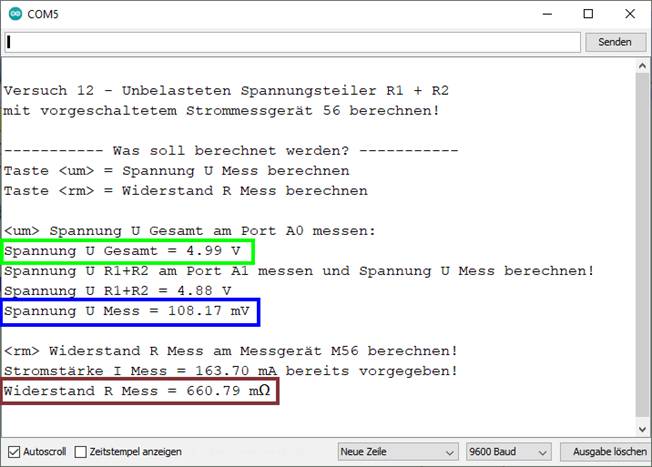
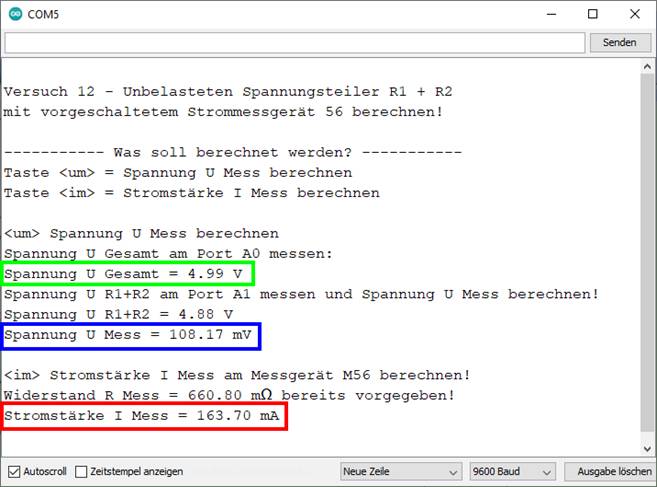
Im obenstehenden blauen Kasten sieht man die Textanzeige der aufgerufenen „<um>“-Funktion „on_button_pressed_U_Mess(true)“ (siehe weiter oben). Dabei bedeutet der Übergabeparameter „true“ beim Funktionsaufruf, dass der angezeigte Ausgabetext nebst der gemessenen bzw. berechneten Werte auch tatsächlich im Arduino-Konsolefenster angezeigt wird.

Wie man im obenstehenden blauen Kasten sieht, gibt es einen Mess- bzw. Rechenfehler! Dieser fällt aber hauptsächlich nur dann auf, wenn man die angezeigten Mess- bzw. Rechenergebnisse im blauen Kasten mit denen im grünen Kasten vergleicht.

Bei der Anzeige im grünen Kasten fällt auf, dass es einen Spannungsabfall U_R1+R2 = 4,84 V gegen Masse „Pin GND“ („┴“) an der Reihenschaltung der beiden Lastwiderständen R_{Lampe 1} und R_{Lampe 2} gibt, während dies bei der Anzeige im blauen Kasten nicht der Fall ist: Spannungsabfall U_R1+R2 = 0,00 V, sodass sich die Frage stellt, weshalb es im blauen Kasten keinen Spannungsabfall U_R1+R2 gibt!

Wenn man sich den Schaltungsaufbau im Bild oder Bild ansieht, dann stellt man fest, dass sich mit dem (Schiebe-) Ein-Aus-Schalter 14 die Stromzufuhr zum Spannungsteiler der beiden in Serie geschalteten Lastwiderstände R_{Lampe 1} und R_{Lampe 2} ein- bzw. ausschalten lässt.

Demzufolge ist der (Schiebe-) Ein-Aus-Schalter 14 bei den angezeigten Werten im grünen Kasten eingeschaltet, sodass die Reihenschaltung der beiden Lastwiderstände R_{Lampe 1} und R_{Lampe 2} mit Strom „versorgt“ wird und sich am Port „Pin A1“ gegen Masse „Pin GND“ („┴“) der Spannungsabfall U_R1+R2 = 4,84 V einstellt (siehe Bild ).

Im Gegensatz dazu ist der (Schiebe-) Ein-Aus-Schalter 14 bei den angezeigten Werten im blauen Kasten ausgeschaltet, sodass die Reihenschaltung der beiden Lastwiderstände R_{Lampe 1} und R_{Lampe 2} nicht mit Strom „versorgt“ wird und sich am Port „Pin A1“ gegen Masse „Pin GND“ („┴“) kein Spannungsabfall U_R1+R2 = 0,00 V einstellt.

Wegen der Differenzbildung im

· Statement < U_Mess = ( U_Mess - U_R1R2 ) * 1000; >

ergibt sich aber trotzdem rechnerisch ein vermeintlicher Spannungsabfall U_Mess parallel zum Strommessgerät 56,

U_Mess = ( U_Mess - U_R1R2 ) * 1000

= ( 5,04 V - 0,00 V ) * 1000 = 5,04 V * 1000 = 5040 mV

der so nicht zutreffend ist!

Wir korrigieren gleich die fehlerhafte Berechnung des Spannungsabfalls U_Mess parallel zum Strommessgerät 56 in folgender Weise (siehe roter Kasten):

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_02.ino)

Schauen wir uns gleich noch die korrigierte Berechnung des Spannungsabfalls U_Mess parallel zum Strommessgerät 56 wie folgt an (siehe roter Kasten):

(Zum Vergrößern bitte auf das Bild klicken!)

Bevor wir in der elektrotechnischen Programmierung, d.h. im Berechnen von weiteren Spannungen, Strömen oder Widerständen fortfahren, möchte ich nachfolgend noch die Tastatureingabe, d.h. das Eintasten einzelner Zeichen in der Eingabezeile der Arduino-Konsole nebst Auswertung programmiertechnisch besprechen.

Dazu muss man wissen, dass das Eintasten einzelner Zeichen, Zeichenketten oder ganzer Sätze z.B. in eine Datei, eine Datenbank, eine Textverarbeitung oder ganz einfach zu Bedienzwecken (= Menüauswahl) unseres Programms immer mittels der <RETURN>- oder <ENTER>-Taste abgeschlossen werden muss, sodass am Ende des Eingabetextes ein <EOL>-Steuerzeichen, das übrigens nicht angezeigt wird, hinzugefügt wird. Dabei steht die engl. Abkürzung „EOL“ für „End of Line“, d.h. Ende der Textzeile bzw. der Texteingabe!

Beim Schreiben eines Textes mit der herkömmlichen Schreibmaschine ist das „EOL“-Textende immer dort, wo ich zuletzt einen Buchstaben, eine Ziffer, ein Komma, ein Semikolon, einen Punkt, ein Ausrufe- oder Fragezeichen eingetippt habe. Dabei kann man das „EOL“-Textende auch an der Wagenposition der Druckwalze oder ganz einfach am Papierrand ausfindig machen.

Bei einer Kugelkopfschreibmaschine erkennt man die aktuelle oder abschließende Schreibposition einer Textzeile an der Position des Kugelkopfes, da die Kugelkopfschreibmaschine keinen beweglichen Wagen mit der Druckwalze besitzt. Ähnlich verhält es sich bei der Typenradschreibmaschine.

Bei der Textverarbeitung am Computer mit entsprechender Textverarbeitungs-Software wie z.B. „Libre Office“, aber auch bei der Schreibmaschine macht das „EOL“-Textende für sich allein noch nicht so viel Sinn, da der Schreiber am Ende einer Textzeile bzw. des Papierrandes ohne Unterbrechung in einer neuen Textzeile weiter schreiben möchte.

Um bei der herkömmlichen Schreibmaschine mit sich bewegendem Transportwagen nebst Druckwalze eine neue Textzeile anzufangen, muss man deshalb zuvor eine Zeilenschaltung (= Zeilenvorschub in eine neue Textzeile), engl. „Line Feed (LF)“ und einen entsprechenden Wagenrücklauf, engl. „Carriage Return (CR)“, an die linke Startposition des Transportwagens mit der DinA4-Seite veranlassen und durchführen, indem man den langen und großen Transporthebel am Transportwagen der Schreibmaschine betätigt. Bei einer Absatzschaltung muss man dann bei der Schreibmaschine den langen und großen Transporthebel ein weiteres Mal betätigen, damit das Papier weiter nach oben geschoben wird und eine Leerzeile quasi „eingefügt“ wird.

Bei der Textverarbeitung auf dem Personal Computer gibt es übrigens eine einfache Zeilenschaltung mittels der Tastenfolge <Umschalttaste> auf Großschreibung & <RETURN/ENTER>.

Wenn man sich dabei in der Textverarbeitung die sogenannten Kapitälchen anzeigen lässt, dann zeigt sich die einfache Zeilenschaltung in Form eines „Häkchens nach links“, sozusagen als Symbol für die <RETURN/ENTER>-Taste . Heutzutage werden Kapitälchen für die ersten Wörter eines Absatzes nach einer Überschrift verwendet.

Mittels der einfachen Zeilenschaltung, veranlasst durch die Tastenfolge <Umschalttaste> & <RETURN/ENTER>, lassen sich in der Eingabezeile von Chat-, SMS-, Messenger-Programmen oder bei Formulareingaben auf einfache Weise Zeilenumbrüche ohne Absatzschaltung durchführen! Die einfache Zeilenschaltung mittels der Tastenfolge <Umschalttaste> & <RETURN/ENTER> entstand meines Wissens mit dem Webdesign von Webseiten, dem Ausfüllen von Textfeldern bei Online-Formularen sowie der Online-Textverarbeitung wie z.B. Writely, dem heutigen Google Docs.

Die herkömmliche, d.h. klassische Zeilenschaltung mit dem sogenannten Kapitälchen ist die wesentlich ältere, entstammt der herkömmlichen Textverarbeitung und zwar zu Zeiten noch lange bevor es das Internet mit den Webseiten gab.

So wurde erstmals im April 1979 auf der West Coast Computer Faire in San Francisco die Textverarbeitung „WordStar 1.0“ gezeigt, die damals unter dem „CP/M“-Betriebssystem lief. >> Das 1987 erschienene WordStar 4 war die letzte größere kommerzielle Software für das CP/M-Betriebssystem. Ende der 80er Jahre wurde dann WordStar 7 für DOS entwickelt: mit Maus-Unterstützung, mit einer Makrosprache und später mit Zugriff auf die Zwischenablage von Windows 3. Jedoch konnte WordStar ab 1990 den Vorsprung von WordPerfect und später zu Microsoft Word nicht mehr aufholen. Außerdem wurden in dieser Zeit auch für weniger anspruchsvolle Textverarbeitungsaufgaben integrierte Programmpakete wie Microsoft Works und weitere Programme, die nach dem WYSIWYG-Prinzip arbeiten, immer populärer. << (Quelle: Wikipedia)

Interessant ist in diesem Zusammenhang noch, dass in der Textverarbeitung „WordStar 3.0“ die Zeilenschaltung mittels der <RETURN/ENTER>-Taste als engl. „End paragraph“, d.h. „Absatz beenden“ bezeichnet wird. -

Wenn man in der Textverarbeitung eine „Kapitälchen“-Zeilenschaltung mittels <RETURN/ENTER>-Taste auslöst, dann wird der laufende, aktuelle Textabsatz beendet, indem die betreffende Textzeile beendet und eine Zeilenschaltung (= Line Feed, „LF“) nebst Wagenrücklauf (= Carriage Return, „CR“) ausgeführt wird, sodass der Textcursor wieder links am Anfang der neuen Textzeile steht. Dabei wird die bis dahin wirksame Textformatierung wie z.B. Blocksatz in der zuletzt bearbeiteten Textzeile nicht mehr umgesetzt, sodass der zuletzt eingetastete Text linksbündig formatiert angezeigt wird!

Im Gegensatz dazu wird bei der einfachen Zeilenschaltung, veranlasst durch die Tastenfolge <Umschalttaste> & <RETURN/ENTER>, die aktuell wirksame Textformatierung wie z.B. Blocksatz in der zuletzt bearbeiteten Textzeile weiterhin umgesetzt, sodass der zuletzt eingetastete Text über die komplette Textzeile als Blocksatz formatiert aufgeteilt wird. Und zwar wegen der Blocksatzformatierung von ganz links bis ganz rechts bis zur Randbegrenzung. Dabei werden die Buchstaben- und Textabstände mit mehreren Leerzeichen aufgefüllt. Das kann dann schon

Aber bezüglich der einfachen Zeilenschaltung, veranlasst durch die Tastenfolge <Umschalttaste> & <RETURN/ENTER>, gibt es noch ein weiteres Phänomen. Und zwar dann, wenn man das Textdokument als Webseite abspeichert, auf einem Webserver publiziert und sich im Browser anzeigen lässt. Dann erscheint die vorherige Textpassage plötzlich als linksbündig formatierter Text:

Praktisch bedeutet dies, dass das sogenannte „WYSIWYG“ (= engl. „What you see is what you get!“), d.h. „Das was du siehst, ist das, was du bekommst.“ nicht mehr funktioniert, weil der ursprünglich im Blocksatz formatierte Text nun plötzlich linksbündig formatiert angezeigt wird.

>> Der Begriff entstand während der späten 1970er am Xerox Palo Alto Research Center, als der erste WYSIWYG-Editor, Bravo, auf dem Alto von Charles Simonyi entwickelt wurde. Der Bildschirm des Alto war in der Lage, eine ganze Seite Text darzustellen und diese auf den damals ersten Laserdruckern auszudrucken. Für die Darstellung von Text auf dem Bildschirm wurden 72-PPI-Zeichensätze verwendet. Der Druck erfolgte jedoch mit 300 DPI. Dadurch kam es zu Abweichungen zwischen der Darstellung auf dem Bildschirm und dem Ausdruck – ein Problem, das bis heute besteht. Die Forscher am Xerox Palo Alto Research Center benutzten mit WYSIWYG eine Abkürzung für ein damals populäres Schlagwort, das von Geraldine, einer Figur aus der The Flip Wilson Show, ins Leben gerufen wurde: „What you see is what you get!“.

Das Apple-Macintosh-System war damals so konzipiert, dass die Auflösung den Bildschirmen und Matrixdruckern von Apple entsprach. Bildschirme verfügten über eine Auflösung von 72 PPI. Die Drucker arbeiteten mit einer Auflösung von 144 DPI. So konnte die Ausgabe von Programmen wie MacWrite und MacPaint durch Verdoppelung gut an die Auflösung der Drucker angepasst werden. WYSIWYG war somit einfach möglich. Mit der Einführung der Laserdrucker verschwand auch das echte WYSIWYG, weil die Auflösung nicht mehr dem doppelten Wert der Bildschirmauflösung entsprach. << (Quelle: Wikipedia)

Das „WYSIWYG“ wurde also gut zwanzig Jahre vor dem kommerziellen Internet Anfang der 1990er Jahre entwickelt und diente ausschließlich dazu, Textdokumente in der Textverarbeitung am Bildschirm möglichst so darzustellen wie sie später als Ausdruck auf dem Laserdrucker mit höherer Auflösung von 300 DPI (= Dots per Inch) ausgedruckt wurden. Da die meisten PC-Anwender zu dieser Zeit noch über keine hochauflösende Grafikkarte nebst Monitor sowie einen Laserdrucker verfügten, gab es mit dem „WYSIWYG“ öfters Probleme, sahen die ausgedruckten Textdokumente deutlich anders aus als im Original auf dem Bildschirm.

Bezüglich des Internets bzw. der Gestaltung von Webseiten mit der Textverarbeitung - jawohl, Webseiten lassen sich z.B. auch mit der Textverarbeitung von Microsoft „Word“ oder „Writer“ von LibreOffice gestalten - gibt es kein „WYSIWYG“, da diese über ihre eigene HTML-Designsprache verfügen, die wiederum vom Webbrowser interpretiert, ausgeführt und zur Anzeige gebracht werden.

Die vereinfachte Zeilenschaltung mittels der Tastenfolge <Umschalttaste> & <RETURN/ENTER> ist also dem Webdesign von Webseiten geschuldet und hat mit dem „WYSIWYG“ nicht das Geringste zu tun.

In diesem Zusammenhang bleibt jetzt nur noch die Frage zu klären, ob sich die beiden Zeilenschaltungen, und zwar die mittels der Tastenfolge <Umschalttaste> & <RETURN/ENTER> und die „Kapitälchen“-Zeilenschaltung mittels <RETURN/ENTER>-Taste, hinsichtlich des Steuerkodes voneinander unterscheiden oder eben nicht!

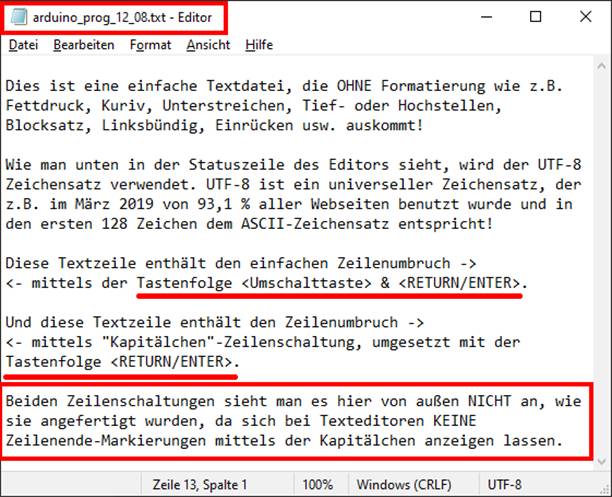
Um das herauszufinden, starten wir den Windows eigenen Editor mittels der Tastenfolge <Start>, <Windows-Zubehör>, <Editor> oder den „Notepad++“-Editor (mehr als 6,2 Mio. Downloads beim Computer-Portal Chip) für Programmierer und fertigen eine kleine Textdatei „arduino_prog_12_08.txt“ an, bei der wir die beiden unterschiedlichen Zeilenschaltungen

· vereinfachte Zeilenschaltung

mittels der Tastenfolge <Umschalttaste> & <RETURN/ENTER> sowie

· die „Kapitälchen“-Zeilenschaltung

mittels <RETURN/ENTER>-Taste

verwenden (siehe Pfeile „->“ und „<-“):

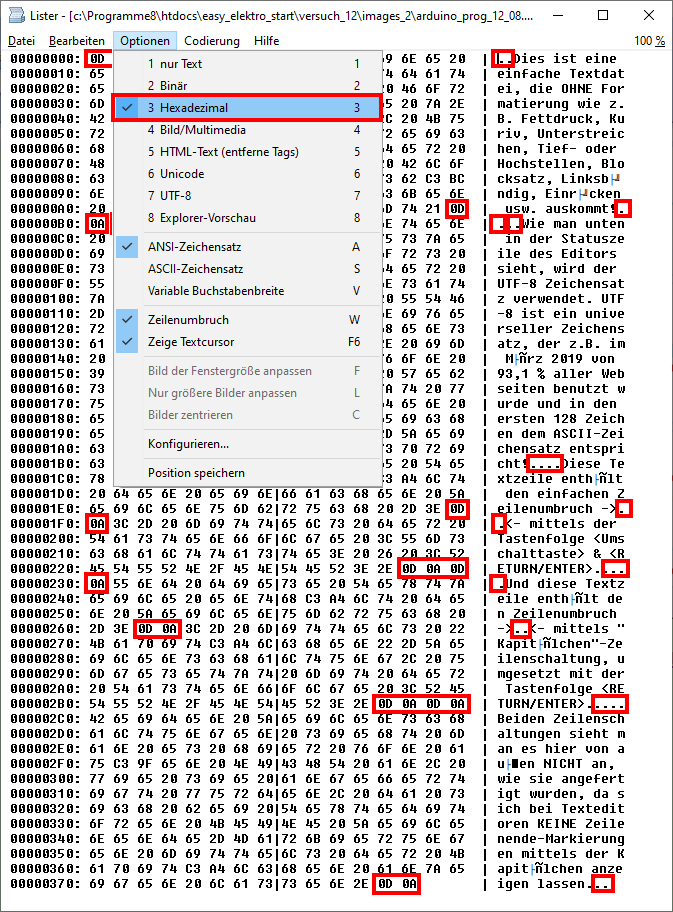
(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_08.txt)

Um die in der einfachen Textdatei enthaltenen, hexadezimal kodierten Zeilenschaltungen sichtbar zu machen, müssen wir uns diese in einem speziellen Texteditor anzeigen lassen, der sich optional auf die Darstellung mit hexadezimalen Zahlen umstellen lässt:

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_08.txt)

Wie man im obenstehenden Bild sieht, setzt sich die Wagenrücklauf- und Zeilenschaltung, engl. „Carriage Return“ (CR) und „Line Feed“ (LF), aus den beiden hexadezimalen Zahlen „0D₁₆“ und „0A₁₆“ zusammen (siehe rote Kästen)!

Ferner wissen wir jetzt, dass es zwischen den beiden unterschiedlichen Zeilenschaltungen

· vereinfachte Zeilenschaltung

mittels der Tastenfolge <Umschalttaste> & <RETURN/ENTER> sowie

· die „Kapitälchen“-Zeilenschaltung

mittels <RETURN/ENTER>-Taste

hinsichtlich der hexadezimalen Kodierung „0D₁₆“ und „0A₁₆“ keinen Unterschied gibt!

Ferner wissen wir jetzt, dass die hexadezimale Kodierung „0D₁₆“ und „0A₁₆“ bei einer Absatzschaltung einfach nur doppelt angewendet werden muss (siehe rote Vierfachkästen „0D 0A 0D 0A“ im obenstehenden Bild)!

Gemäß der ASCII-Zeichentabelle mit der hexadezimalen Nummerierung handelt es sich bei der hexadezimalen Kodierung „0D₁₆“ um den „Carriage Return“ (CR), d.h. den Wagenrücklauf und bei „0A₁₆“ um das „Line Feed“ (LF), d.h. die Zeilenschaltung. In der „Sketch“-Programmierung kurz „\n“.

Damit wäre dann das Geheimnis um die Zeilenschaltung „\n“ mit dem Hexkode „0A₁₆“, d.h. engl. „Line Feed“ (LF), gelöst! -

Bei dem obenstehenden Screenshot wurde der integrierte Texteditor des sogenannten „Total Commander“ (= Zwei-Fenster-Dateimanager) verwendet, der sich im Programm mittels der Funktionstaste <F3 Anzeigen> aufrufen lässt. Beim Computerportal „Chip“ wurde der Total Commander bisher mehr als 10 Millionen mal heruntergeladen. In der neuesten Version 9.51 vom 26.03.2020 insgesamt mehr als 2,6 Millionen mal. Den Zwei-Fenster-Dateimanager gibt es inzwischen seit geraumer Zeit auch für Smartphones! Bei der Software handelt es sich um eine Shareware, die nach der Testphase von 30 Tagen käuflich erworben werden sollte, sodass die Werbeeinblendung mit der Zahlungsaufforderung beim Programmstart nicht mehr erscheint.

Das Programm ist extrem leistungsfähig und deshalb für Einsteiger und Anfänger anfangs gewöhnungsbedürftig. Besonders beim Kopieren, Verschieben und Umbenennen von Dateien sollte man deshalb höllisch aufpassen und nicht überstürzt klicken, da gelöschte Dateien wider Erwarten nicht im Windows-Papierkorb landen. Gelöscht ist deshalb unwiderruflich gelöscht! -

Wenn man also am Ende der Zeicheneingabe in der Eingabezeile der Arduino-Konsole auf die Schaltfläche <Senden> klickt, dann wird der Hexkode „0A₁₆“ = „10₁₀“ = engl. „Line Feed“ (LF), d.h. Zeilenschaltung gesesendet:

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_02.ino)

Texteingaben wie die im obenstehenden Bild zu sehende Menüauswahl <um> (= Messspannung U_Mess am analogen Port „Pin A0“ des „Arduino UNO“ erfassen) lassen sich nur mittels der <RETURN/ENDER>-Taste oder durch Mausklick auf die Schaltfläche <Senden> abschicken, wenn zuvor im Arduino-Konsolefenster die Einstellung <Neue Zeile> vorgenommen wurde (siehe roter Blitz)!

Dabei entspricht das Betätigen der <RETURN/ENDER>-Taste oder der Mausklick auf die Schaltfläche <Senden> dem Erzeugen des hexadezimalen Kodes „0A₁₆“ (= dezimal „10₁₀“), der wiederum abschließend der bereits eingetasteten Texteingabe „um“ hinzugefügt bzw. vorangestellt wird, sodass nach dem Betätigen der <RETURN/ENDER>-Taste oder des Mausklicks auf die Schaltfläche <Senden> die komplette, hexadezimale Zeichenfolge „75₁₆ 6d₁₆ 0A₁₆“ an die serielle Schnittstelle des „Arduino UNO“ übertragen wird!

Dabei entspricht der hexadezimale Kode „0A₁₆“ (= Zeilenschaltung!) dem alphanumerischen Steuerzeichen(!) „n“ von nur 1 Byte Größe mit dem hexadezimalen Wert „0A₁₆“.

Damit das alphanumerischen Steuerzeichen(!) „n“ von nur 1 Byte Größe mit dem hexadezimalen Wert „0A₁₆“ auch als Steuerzeichen(!) erkannt und interpretiert werden kann, muss man bei der Programmierung noch den Backslash „\“ (= Schrägstrich nach links) voranstellen (siehe dunkelgrüner Kasten):

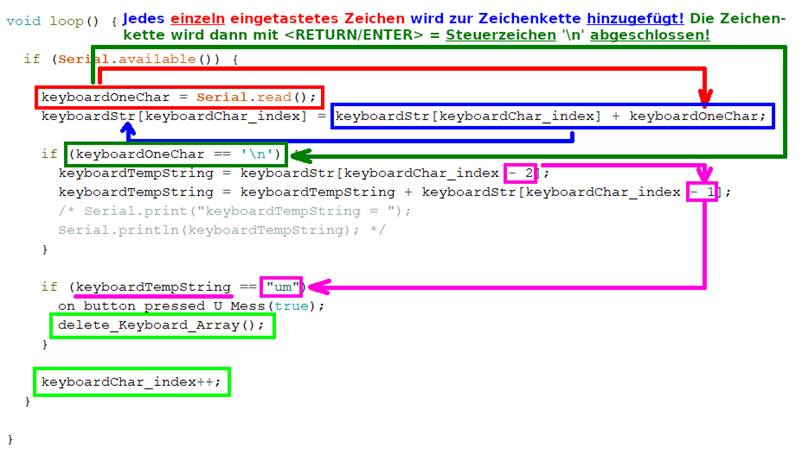
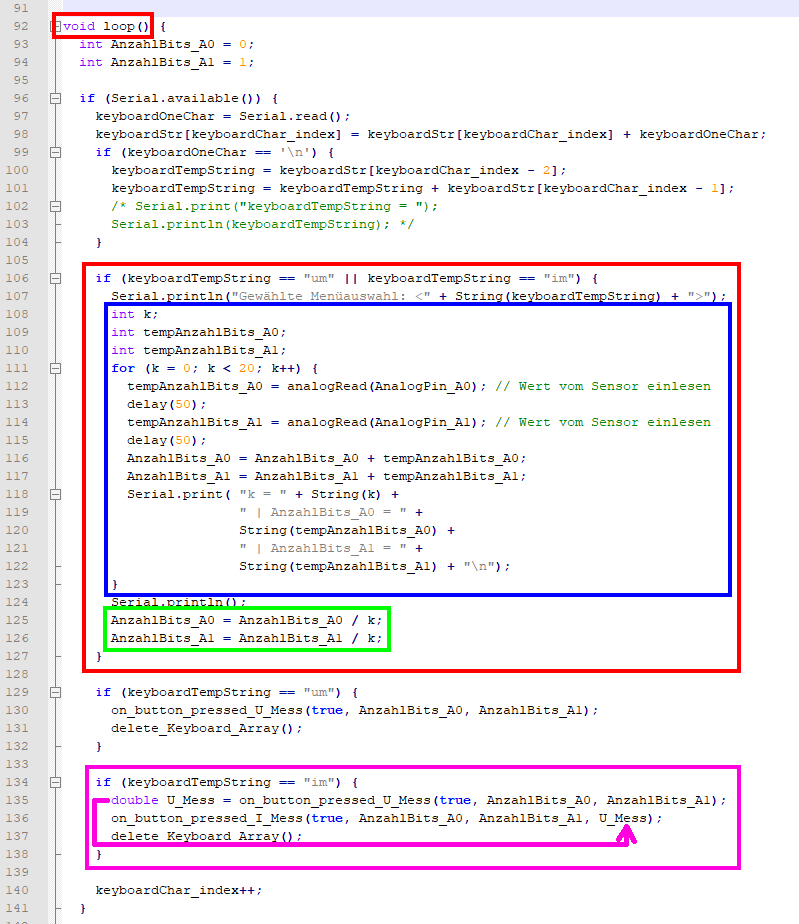
(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_02.ino)

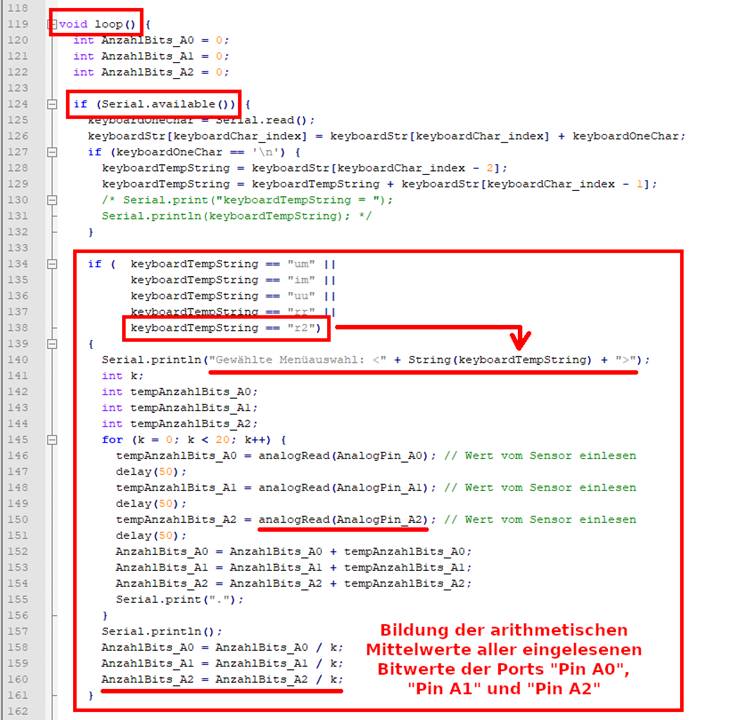
Um herauszufinden und zu verstehen, wie der im obenstehenden Bild zu sehende Programmkode der Funktion „void loop()“ funktioniert, gehen wir „top down“, d.h. von oben nach unten vor.

Mittels des

· Statements < if (Serial.available()) { … } >

wird abgefragt, ob die serielle Schnittstelle verfügbar, engl. „available“, ist.

Zur Erinnerung: Damit die serielle Schnittstelle verfügbar und ansprechbar ist, muss diese zuvor initialisiert werden. Das aber ist einfacher als man denkt. Man muss dieser nämlich nur mitteilen mit welcher Baud-Übertragungsrate (= Anzahl der Symbole(!) pro Sekunde) man arbeiten und Daten in Form von Symbolen(!) empfangen und senden will:

· Statement < Serial.begin(9600); >

Während die Verfügbarkeit der seriellen Schnittstelle innerhalb der Funktion „void loop()“ fortwährend abgefragt wird, muss die Initialisierung nur einmalig und zwar in der „Start“-Funktion „void setup()“ vorgenommen werden!

Innerhalb der Funktion „void loop()“ müssen ferner auch die Tastatureingaben in der Eingabezeile der Arduino-Konsole abgefragt werden. Dabei werden diese zeichenweise, engl. „character“, eingelesen und nicht als Ganzes im Sinne einer einzelnen Zeichenkette, engl. „string“. Tatsächlich eingelesen werden die Tastatureingaben in der Eingabezeile der Arduino-Konsole aber erst dann, wenn die <RETURN/ENDER>-Taste betätigt oder der Mausklick auf die Schaltfläche <Senden> vorgenommen wurde!

Wenn man wissen will, ob es in der Eingabezeile der Arduino-Konsole entsprechende Tastatureingaben gibt, dann muss man die Eingabezeile der Arduino-Konsole fortwährend, d.h. ununterbrochen abfragen und zwar auch dann, wenn keine Tastatureingaben nebst <RETURN/ENDER>-Taste vorgenommen wurden! Dadurch, dass sich das

· Statement < keyboardOneChar = Serial.read(); >

innerhalb der Funktion „void loop()“ befindet, ist das fortwährende Abfragen der Eingabezeile der Arduino-Konsole gewährleistet (siehe roter Kasten im obenstehenden Bild).

Dabei verhält es sich so, dass eine leere Abfrage der Eingabezeile der Arduino-Konsole nicht ins Leere führt, sondern zu einer leeren, .d.h. nicht vorhandenen Eingabe in der Arduino-Konsole. Demzufolge wird in der Variablen „keyboardOneChar“ vom Typ „char“ auch nichts gespeichert, wird dieser der Wert „0“ zugewiesen:

· Statement < keyboardStr[keyboardChar_index] = keyboardStr[keyboardChar_index] + keyboardOneChar; >

Wenn man also der „String“-Variablen keyboardStr[keyboardChar_index] etwas Leeres, d.h. den Wert „0“ der „Character“-Variablen „keyboardOneChar“ hinzufügt, dann bleibt deren Variableninhalt unverändert (siehe blauer Kasten im obenstehenden Bild)!

Anders verhält es sich, wenn mittels des

· Statements < keyboardOneChar = Serial.read(); >

der hexadezimale Wert „0A₁₆“, d.h. der Steuerkode „Zeilenschaltung“ (= ’\n’ ) von der Eingabezeile der Arduino-Konsole aus eingelesen wird (siehe dunkelgrüner Kasten im obenstehenden Bild).

Wenn also die „if“-Abfrage im

· Statement < if (keyboardOneChar == '\n') { } >

den hexadezimalen Wert „0A₁₆“ als Steuerkode „Zeilenschaltung“ (= ’\n’ ) vorfindet, dann wird die „String“-Variable „keyboardStr[ ]“ ausgelesen, aber nur zum Teil, d.h. nur die beiden vor- und vorvorletzten Zeichen (siehe pinkfarbene Kästchen im obenstehenden Bild) und der temporären „String“-Variablen „keyboardTempString“ zwecks Auswertung zugewiesen, da die „String“-Variable „keyboardStr[ ]“ bereits vor dem nächsten Durchlauf der Endlosschleife „void loop()“ wieder gelöscht werden muss (siehe hellgrüner Kasten im obenstehenden Bild):

· Funktionsaufruf < delete_Keyboard_Array(); >

Wenn sich in der temporären „String“-Variablen „keyboardTempString“ der Ausdruck „um“ (= Abkürzung für „U_Mess“) für die Menüauswahl „Taste <um> = Spannung U Mess berechnen“ befindet, dann wird die

· Funktion < on_button_pressed_U_Mess(true) >

ausgeführt. Dabei bedeutet der Übergabeparameter “true”, dass die in der Funktion programmierten Textanzeigen angezeigt werden, sich also an- und abschalten lassen.

Der Grund für die zuschaltbaren Textanzeigen ist der, dass die Berechnungsfunktionen und deren Ergebnisse für Spannungen, Ströme und Widerstände zum Versuch 12 „Ein Strom für zwei Lampen“ von einer Funktion an die nächste weitergegeben werden. Dabei ist es dann nicht sinnvoll, dass alle Textanzeigen der Vorgängerfunktion angezeigt werden, da bei der Werteweitergabe nur diese interessieren, nicht aber wie diese im Einzelnen zustande gekommen sind. Deshalb müssen sich die Textanzeigen abschalten lassen.

Nach der Auswertung des Dateninhalts „um“ (= Menüauswahl „Taste <um> …“) der temporären „String“-Variablen „keyboardTempString“ und des Funktionsaufrufs der

· Funktion < on_button_pressed_U_Mess(true) >

müssen sowohl die temporäre „String“-Variable „keyboardTempString“ als auch die „String“-Variable „keyboardStr[ ]“ gelöscht werden (siehe Funktion < delete_Keyboard_Array() > ).

Ferner muss der laufende Index, d.h. der Variableninhalt der Variablen keyboardChar_index um +1 erhöht werden (= Endlosschleife der fortwährenden Tastaturabfrage am Ende der Funktion void loop() ):

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_02.ino)

Abschließend möchte ich noch einen kleinen Trick verraten, wie man sich den Sourcecode des obenstehenden Programms farbig in der Notation der Programmiersprache „C++“ im Programmiereditor „Notepad++“ anzeigen lassen kann.

Da wir das obenstehende Programm des „Arduino UNO“ in „Sketch“, d.h. in einer speziell auf den Arduino abgestimmten, angepassten und vereinfachten Version der Programmiersprache „C++“, programmieren und dabei den Dateierweiterungsnamen *.ino (in Ahnlehnung an den Arduino) verwenden, kennt der „Notepad++“-Editor die Programmiersprache „Sketch“ wider Erwarten nicht und kann diese demzufolge auch nicht farbig in der Notation von „C++“ darstellen.

Um den obenstehenden Sourcecode trotzdem farbig in der Notation der Programmiersprache „C++“ im Programmiereditor „Notepad++“ angezeigt zu bekommen, muss man die Datei „sketch_prog_12_02.ino“ einfach im „Windows-Explorer“-Dateimanager oder noch besser im „Total Commander“-Dateimanager auf sich selbst kopieren und dabei den Dateierweiterungsnamen *.ino einfach auf *.cc oder *.cpp abändern, sodass der „Notepad++“-Editor beim Aufrufen der Datei „sketch_prog_12_02.cc“ meint, es mit einer „C++“-Sourcecode-Datei zu tun zu haben und den obenstehenden Sourcecode in der Notation der Programmiersprache „C++“ anzeigt! -

[ zurück ] zum Versuch 12 und dem Experimentieren! -

Die Berechnung des Messwiderstandes R_Mess programmieren

Da sich mit dem „Sketch“-Programm „sketch_prog_12_02.ino“ bisher nur der Spannungsabfall U_Mess am Messwiderstand R_Mess in Form der Spannungsdifferenz ∆U_Mess = U_{Pin A0} - U_{Pin A1} sowie die verbleibende Spannung U_Pin A1 = U_R1+R2 = an den in Reihe geschalteten Glühlampen 18 messen ließ, erweitern wir das bisherige Programm dahingehend, sodass sich mit dem „Sketch“-Programm „sketch_prog_12_03.ino“ jetzt auch der Messwiderstand R_Mess berechnen lässt:

R_Mess = U_Mess / I_Mess

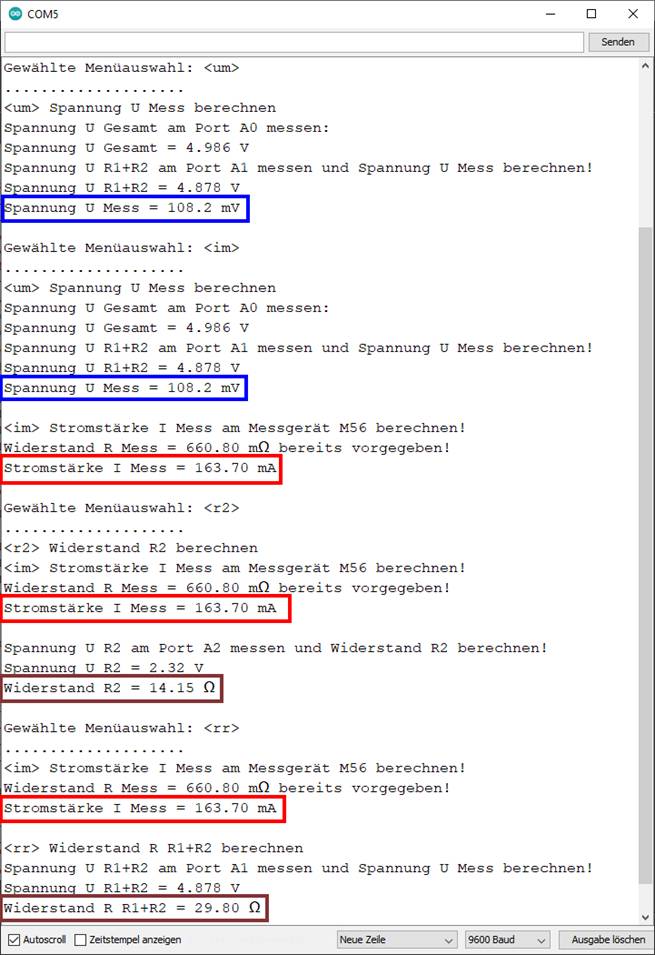
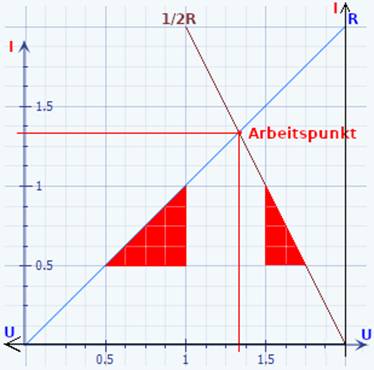
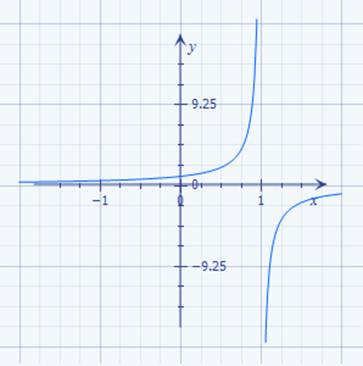
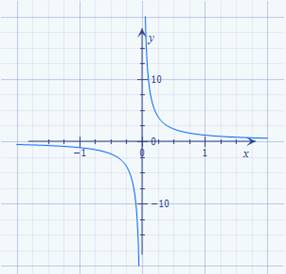
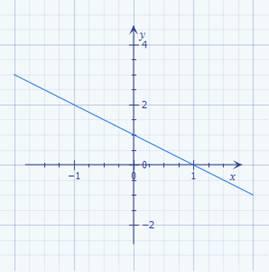
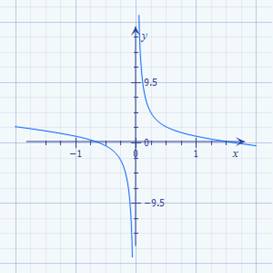
= 108,17 mV / 163,17 mA = 0,662928 Ω = 662,93 mΩ

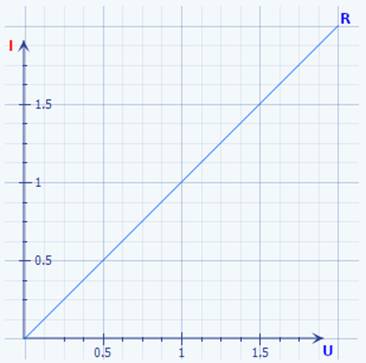
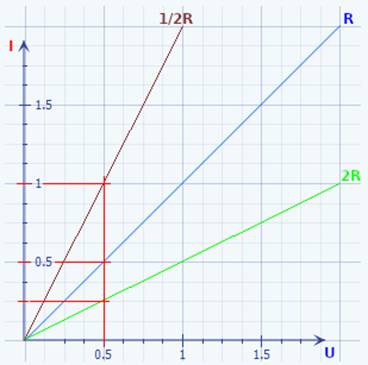
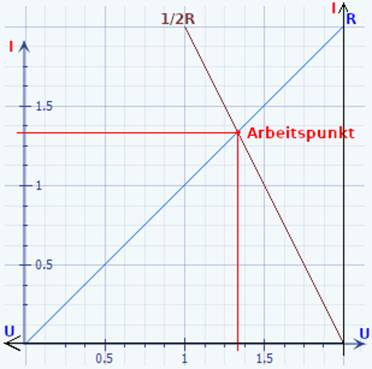
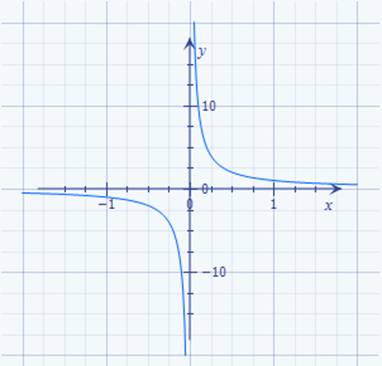
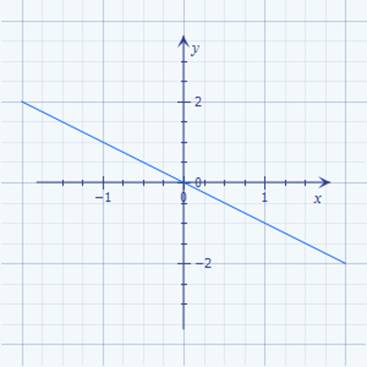
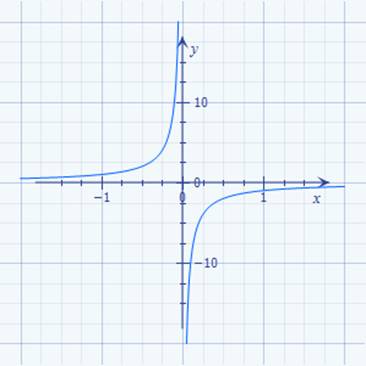
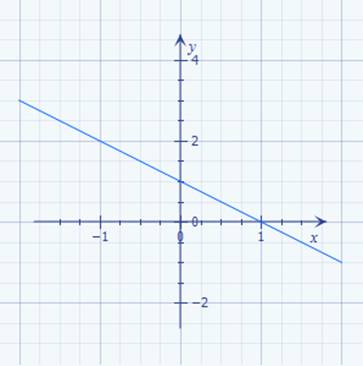
Wie man im nachfolgenden Screenshot des Arduino-Konsolefensters sieht, muss dazu allerdings bereits die Stromstärke I_Mess bekannt sein, da sich in der Mathematik stets nur Gleichungen, wie z.B. unsere

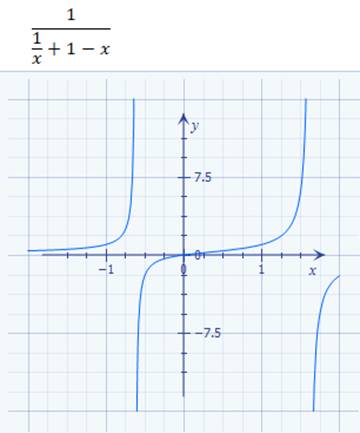
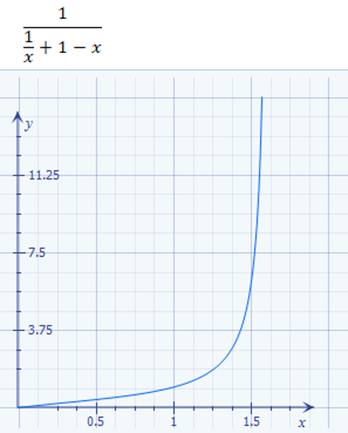
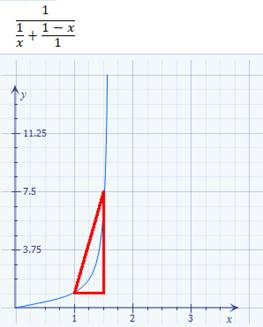
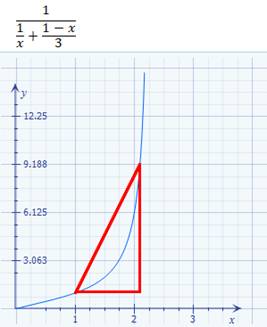
· Geradengleichung mit I = f(U) = 1 / R * U, →

R = U / I = ∆U / ∆I = ( U_{Pin A0} – U_{Pin A1} ) / ∆I = U_Mess / ∆I

= 108,17 mV / ∆I = 108,17 mV / 163,70 mA = 0,660782 Ω = 660,78 mΩ

nur mit einer Unbekannten ( = ∆I ) lösen lassen:

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_03.ino)

Nachdem der Messwiderstand R_Mess ≈ 660,8 mΩ berechnet wurde und fortan bekannt ist, lässt sich nun mit dem „Sketch“-Programm „sketch_prog_12_04.ino“ die Stromstärke I_Mess = I_{Lampe 1+Lampe 2} durch das (Strom-) Messgerät 56 sowie durch den Spannungsteiler R_{Lampe 1} + R_{Lampe 2} berechnen:

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_04.ino)

Bei den bisherigen Spannungsmessungen mit den Ports „Pin A0“ und „Pin A1“ stellte es sich immer wieder heraus, dass diese unerwartet ungenau sind. Dabei zeigte es sich, dass bei mehreren nacheinander durchgeführten Messungen immer wieder unterschiedliche Messergebnisse angezeigt wurden, sodass sich oftmals eine durchgeführte Spannungsmessung nicht reproduzieren ließ, weil bei jeder erneuten, nachfolgenden Messung wider Erwarten ein anderes Messergebnis angezeigt wurde. Dabei beliefen sich die Abweichungen bei den Spannungsmessungen teilweise auf bis zu +/- 20 mV (= +/- 18,5 %), was bei einem Spannungsabfall U_Mess = 108,17 mV am Messgerät 56 bei der Stromstärkemessung mit dem Messbereichsendwert (MBE) von I_{Mess, MBE} = 1 A schon recht viel ist.

Für die fehlerhaften Spannungsmessungen gibt es verschiedene, mögliche Ursachen:

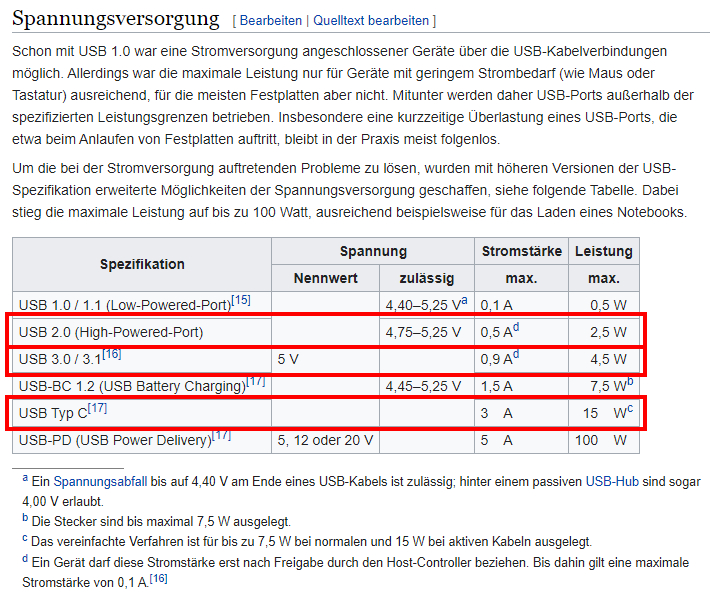
1. So stellen die beiden in Reihe geschalteten Glühlampen 18 mit den Nenn-Betriebsdaten von 3 V und 0,2 A je Glühlampe und einem Stromverbrauch von I_Mess = I_R1+R2 ≈ 164 mA bezüglich der 5 Volt USB-Spannungsversorgung des „Arduino UNO“ schon eine nicht zu vernachlässigende Belastung dar, sodass man mit einem Absinken der Versorgungsspannung nebst einer gewissen Instabilität am USB-Anschluss rechnen muss.

Definitionsgemäß soll zwar der USB 2.0 Anschluss eine maximale Stromstärke von bis zu 500 mA zur Verfügung stellen, wovon dann netto bis zu 400 mA beim Arduino-Port „Pin 5V“ verfügbar sein sollen, aber wegen der Belastung mit einer Spannung von deutlich weniger als 5 Volt!

Wenn aber die Versorgungsspannung des „Arduino UNO“ deutlich in die Knie geht, dann dürfte auch die Spannungsmessung mit der A/D-Wandlung am Port „Pin A0“ und „Pin A1“ davon betroffen sein, sodass sich abweichende Messergebnisse einstellen.

Um dem vorzubeugen, müsste man die Versorgungsspannung des „Arduino UNO“ am Port „Pin 5V“ durch eine extern eingespeiste Spannungsversorgung am Port „Pin Vin“ nebst Spannungsstabilisierung z.B. durch ein stabilisiertes Labornetzteil vornehmen!

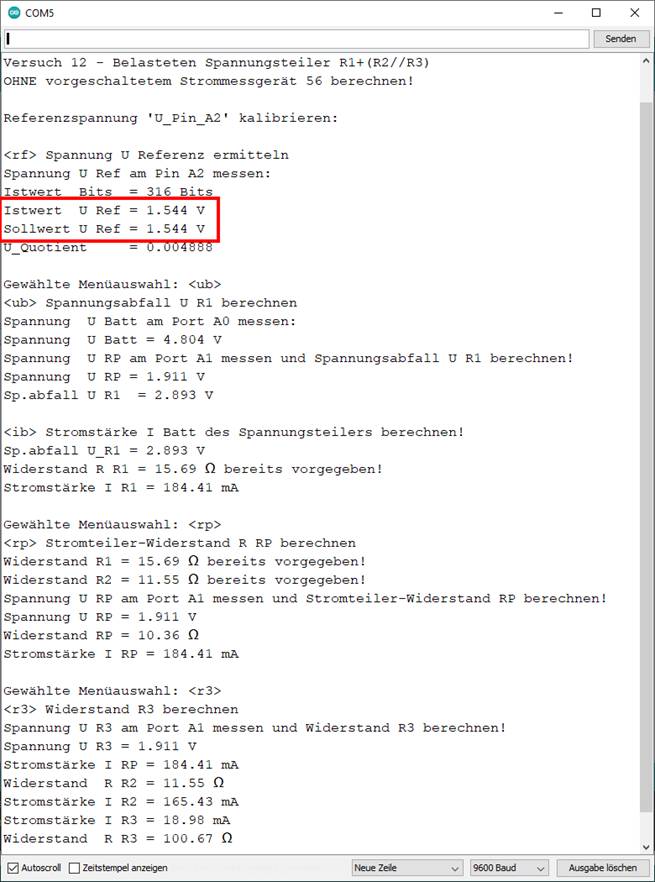
Darüber hinaus müsste man die sogenannte Referenzspannung, die im „Sketch“-Programm der Variablen „U_Ref_V“ mit U_Ref_V = 5,03 V zugewiesen wird, durch eine externe Referenzspannungsquelle z.B. in Form einer kleinen 1,5 Volt Batterie ersetzen, deren Leerlaufspannung über einen separaten Arduino-Port nebst A/D-Wandlung gemessen und auf 5,0 V hochgerechnet wird.

2. Wie man dem nachfolgenden Bild vom „Arduino UNO“ entnehmen kann, verfügt dieser über insgesamt sechs analoge Eingänge A0 bis A5, die der Reihe nach im Multiplexverfahren abgefragt werden:

(Zum Vergrößern bitte auf das Bild klicken!)

Dabei stellt sich die Frage, ob die Multiplexabfragen der analogen Ports „Pin A0“ bis „Pin A5“ zeitlich synchronisiert erfolgen oder nicht.

Das zeitlich synchronisierte Abfragen der analogen Ports „Pin A0“ bis „Pin A5“ hätte nämlich zur Folge, dass die Reihenfolge der Portabfragen stets die gleiche ist und die Abfrage demzufolge immer beim Port „Pin A0“ startet, während es bei einer asynchronen Abfrage der analogen Ports „Pin A0“ bis „Pin A5“ immer dem Zufallsprinzip überlassen bleibt mit welcher Portabfrage begonnen wird. Demzufolge wäre es bei der asynchronen Abfrage der analogen Ports mal der „Pin A3“ mit dem gestartet wird, während ein anderes Mal mit dem „Pin A1“ oder dem „Pin A5“ gestartet werden würde. Dabei kämme es bei den asynchronen Portabfragen auch zu entsprechenden Laufzeitunterschieden, sodass sich die bei der A/D-Wandlung ermittelten Werte u.U. nicht mehr 1:1 reproduzieren ließen. Dies könnte dann dazu führen, dass bei ansonsten unveränderten Eingangsspannungen teils differierende Werte ausgegeben würden.

In diesem Zusammenhang stellt sich dann auch die Frage, ob die Abtastfrequenz der A/D-Wandlung nebst Taktung synchron zum Multiplexen der Portabfragen erfolgt oder nicht. Für den Fall, dass die Abtastfrequenz der A/D-Wandlung nicht im harmonischen, synchronen Verhältnis zu den Multiplexabfragen der Ports steht, könnte es nämlich bei der A/D-Wandlung zu teils unterschiedlichen Messwerten kommen, weil sich die Zeitbasis wegen der Asynchronität nebst der Start-/Stoppzeiten für die A/D-Wandlung aufgrund der Phasenverschiebung immer wieder geringfügig verschiebt.

3. Der „Arduino UNO“ hat intern nicht nur A/D-Wandler verbaut, sondern verfügt u.a. auch über einen sogenannten Komparator, d.h. Vergleicher, der es erlaubt, zwei nahezu gleiche oder voneinander abweichende Spannungen miteinander zu vergleichen. Dabei werden Komparatoren hardwaremäßig meistens mittels sogenannter Operationsverstärker, auch OPVs genannt, realisiert.

In der PDF-Datei „ATmega48A-PA-88A-PA-168A-PA-328-P-DS-DS40002061A.pdf“ findet sich auf der Seite 247 ein Blockdiagramm zum Analog-/Digital Converter (= ADC). Auf Seite 246 ff beginnt das Kapitel „24. Analog-to-Digital Converter“ wo alles genauer beschrieben wird. Dabei kann man sich in der PDF-Datei Textabschnitte markieren und mittels „Copy-and-paste“ in die Google Übersetzung übernehmen und dort ins Deutsche übersetzen lassen.

Auf der Homepage von Henrik Haftmann befindet sich der Abschnitt „24. Der Analog-Digital Wandler“ zum „ATmega“-Mikrocontroller. Selbstverständlich gibt es auch eine Startseite mit Inhaltsverzeichnis in der linken Spalte! -

4. Da sich mit Mikrocontrollern und Einplatinenrechnern nicht nur analoge, sondern eben auch digitale Signale messen, verarbeiten, berechnen und auch wieder ausgeben lassen, arbeiten die meisten A/D-Wandler von diesen nur mit einer Betriebs- und Messbereichsspannung von bis zu 3,3 V, sodass sich die zum Messen zur Verfügung stehenden 1024 Bit im Bereich von [ 0, …, 1023 ] eben nur auf die 3,3 V verteilen und nicht wie beim „Arduino UNO“ auf insgesamt 5 V:

1023 Bit → 5,0 V

2 Bit → x V

x = 5,0 V / 1023 Bit * 2 Bit = 0,009775 V = 9,78 mV absoluter Messfehler bei +/- 1 Bit = 2 Bit (= +51,6 %)

1023 Bit → 3,3 V

2 Bit → x V

x = 3,3 V / 1023 Bit * 2 Bit = 0,0064516 V = 6,45 mV absoluter Messfehler bei +/- 1 Bit = 2 Bit

Demzufolge ergibt sich bei dem „Arduino UNO“ mit einer Betriebs- und Messbereichsspannung von 5,0 V wegen der höheren Spannung und dem größeren Messbereich gegenüber der 3,3 V Messbereichsspannung eine um +51,6 % höhere Messungenauigkeit!

Diesbezüglich bleibt festzustellen, dass wir bei der A/D-Wandlung des „Arduino UNO“ stets mit einer Fehlerrate von bis zu 2 Bit rechnen müssen, sodass angezeigte Spannungen im Millivoltbereich schon mal um bis zu rund +/- 10 mV voneinander abweichen können!

Wenden wir uns nun wieder der Programmierung zu. Beim „Sketch“-Programm „sketch_prog_12_05.ino“ wird jetzt erstmals nicht mehr nur ein einziger Messwert je A/D-Wandler-Port „Pin A0“ und „Pin A1“ eingelesen, sondern bis zu zwanzig, aus deren eingelesenen Bitwerten dann der arithmetische Mittelwert gebildet wird, um eventuelle Ausreißer, d.h. vereinzelte Maximal- oder Minimalwerte zu nivellieren:

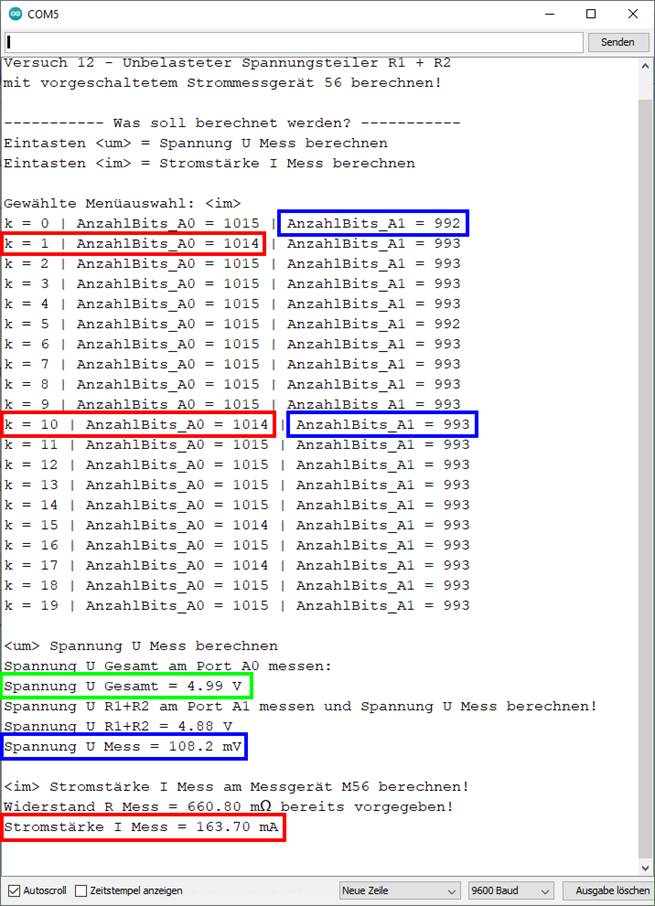
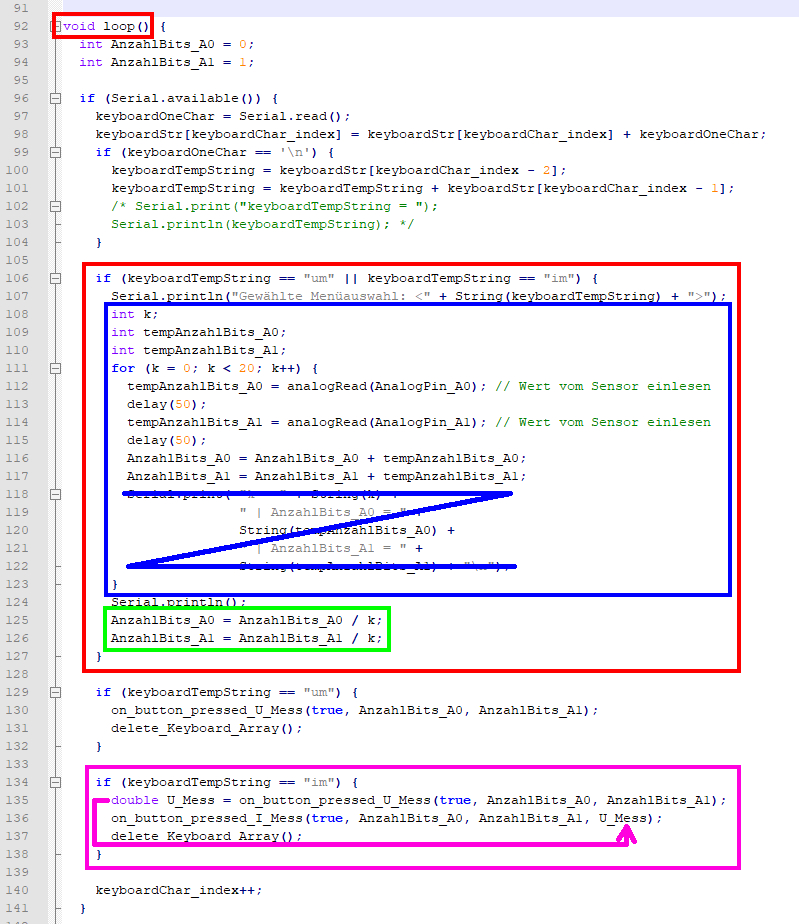
(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_05.ino)

Damit es bei der Messwerterfassung zu keinen Verzögerungen in Form von Laufzeitunterschieden kommt, werden die Portabfragen „Pin A0“ und „Pin A1“ nicht nach „extern“ in eine diesbezügliche Funktion ausgelagert, sondern verbleiben viel mehr innerhalb der Funktion „void loop()“ (siehe roter Kasten):

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_05.ino)

Dabei erfolgt das Einlesen der zwanzig Messwerte an den Ports „Pin A0“ und „Pin A1“ in der „for … next“-Schleife

· for (k = 0; k < 20; k++) { … }

und zwar von k = 0 bis k = 19, macht zusammen k = 20 verschiedene Messungen (siehe blauer Kasten im obenstehenden Bild).

Die Mittelwertbildung selbst erfolgt dann im nachfolgenden grünen Kasten (siehe im Bild oben).

Dabei gilt es zu beachten, dass das Deklarieren der Zählvariablen „k“ außerhalb der „for … next“-Schleife erfolgt, damit deren Wert k = 20 anschließend zur Mittelwertbildung zur Verfügung steht (siehe grüner Kasten im obenstehenden Bild)!

Neu bei der Programmierung hinzugekommen ist der

· Funktionsaufruf double U_Mess = on_button_pressed_U_Mess(true, AnzahlBits_A0, AnzahlBits_A1);

mit der Übergabe der Variablenwerte der Variablen „AnzahlBits_A0” und „AnzahlBits_A1” an die aufzurufende

· Funktion „on_button_pressed_U_Mess()“

und die Rückgabe des Ergebniswertes der Variablen „U_Mess“ an die

· Funktion „void loop()“,

sodass sich der Ergebniswert der Variablen „U_Mess“ an den nächsten

· Funktionsaufruf on_button_pressed_I_Mess(true, AnzahlBits_A0, AnzahlBits_A1, U_Mess);

weitergeben lässt (siehe pinkfarbener Kasten im obenstehenden Bild).

Das „Sketch“-Programm „sketch_prog_12_06.ino“ im Webverzeichnis unterscheidet sich von seinem Vorgänger lediglich darin, dass das Auflisten der zwanzig Bitwerte der Ports „Pin A0“ und „Pin A1“ weggelassen

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_06.ino)

und durch einen Fortschrittsbalken „…“ bei der Messwerterfassung ersetzt wurde. Dabei werden nacheinander bis zu 20 Einzelpunkte als Laufband angezeigt (siehe roter Kasten):

(Zum Vergrößern bitte auf das Bild klicken!)

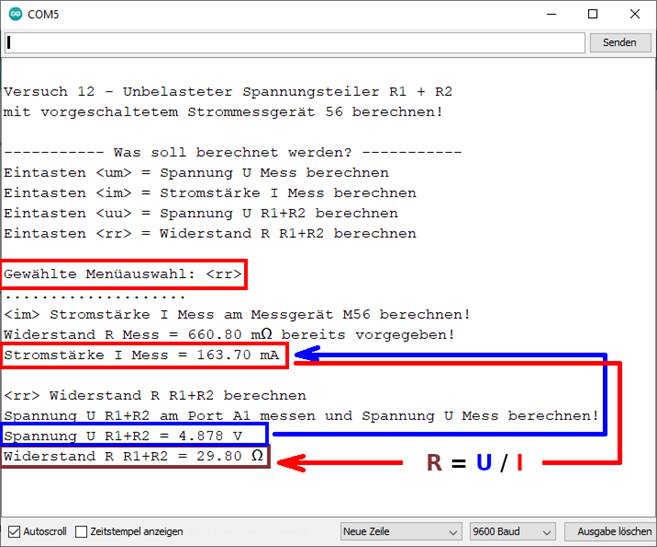
[ zurück ] zum Versuch 12 und dem Experimentieren! -

Gesamtwiderstand des Spannungsteilers berechnen

Als nächstes erweitern wir das bisherige Programm um die Berechnung des Gesamtwiderstandes des unbelasteten Spannungsteilers mit

R_ges = R_R1+R2

= U / I = U_ges / I_R1+R2 = ( U_5V – U_Mess ) / I_Mess = U_R1+R2 / I_Mess

= 4,88 V / 163,70 mA = 4,88 V / 0,1637 A = 29,81 Ω → die Werte wurden dem obenstehenden Bild entnommen!

Erinnern wir uns an die Nenn-Betriebsdaten der Glühlampe 18 mit U_Nenn = 3,2 V mit I_Nenn = 0,2 A und berechnen dazu den Widerstand R_Lampe:

R_Lampe = U_Nenn / I_Nenn =

= 3,2 V / 0,2 A = 16,0 Ω

Für zwei in Reihe geschaltete Glühlampen 18 folgt dann:

R_ges = R_{Lampe 1} + R _{Lampe 2} = 2 * R_{Lampe 1} = 2 * 16,0 Ω = 32,0 Ω

Vergleicht man den rechnerischen Gesamtwiderstand R_ges = 32,0 Ω mit dem des vom obenstehenden Programm R_ges = R_R1+R2 = 29,81 Ω, so darf richtig vermutet werden, dass die beiden Glühlampen 18 nicht zu 100 % identisch sind. Da aber die Abweichung nur -6,84 % gegenüber den 32,0 Ω beträgt, scheint es sich wohl so zu verhalten, dass die beiden Glühlampen 18 nicht der gleichen Produktion mit dem gleichen Herstellungsdatum entstammen.

Diesbezüglich könnte es aber auch sein, dass die Glühlampe 18 mit dem geringeren Einzelwiderstand R_Lampe < 16,0 Ω bereits längere Zeit in Betrieb war, sodass sich die Heizwendel bereits stärker abgenutzt und dabei den Widerstand der Heizwendel entsprechend verringert hat! Eine stärkere Abnutzung einer der beiden Glühlampe 18 könnte man dann an dem stärkeren metallischen Niederschlag der abgenutzten Heizwendel an dem Glaskolben erkennen, der dann dunkler eingefärbt wäre.

Außerdem würde man die stärker verschlissene Glühlampe 18 an dem etwas helleren Leuchten erkennen, da sie wegen des kleineren (Heizwendel-) Widerstandes mehr Strom zieht und dadurch auch mehr elektrische Energie in Wärme und sichtbares Licht umwandelt. Wegen der durch den Verschleiß immer dünner werdenden Heizwendel und der damit größer werdenden Stromstärke würde also die Glühlampe 18 noch stärker verschleißen und entsprechend früher das Zeitliche segnen, wenn eines Tages die Heizwendel vorzeitig zerbricht. Um die Lebensdauer der stärker verschlissenen Glühlampe 18 trotzdem zu verlängern, müsste man also die Nenn-Betriebsspannung von vormals U_Nenn = 3,2 V auf z.B. nur noch 3,0 V herabsetzen!

Immer dann, wenn der mit dem „Sketch“-Programm „sketch_prog_12_07.ino“ berechnete Gesamtwiderstand R_R1+R2 kleiner als der Gesamt-Nennwiderstand von R_{Nenn, ges} < 32 Ω ist,

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_07.ino)

sind die beiden Glühlampe 18 nicht zu 100 % identisch, könnte es sein, dass eine von den beiden stärker verschlissen ist!

Aber noch wissen wir gar nicht, welche von den beiden Glühlampe 18 bereits stärker verschlissen ist bzw. einen kleineren Lampenwiderstand hat. Um das herauszufinden, müssen wir zunächst den Lampenwiderstand einer der beiden in Reihe geschalteten Glühlampe 18 bestimmen. Welchen Lampenwiderstand R_{Lampe 1} oder R_{Lampe 2} wir als Ersten bestimmen, spielt im Prinzip keine Rolle, da wir später auch noch den zweiten Lampenwiderstand berechnen müssen, um die beiden Lampenwiderstände miteinander vergleichen zu können.

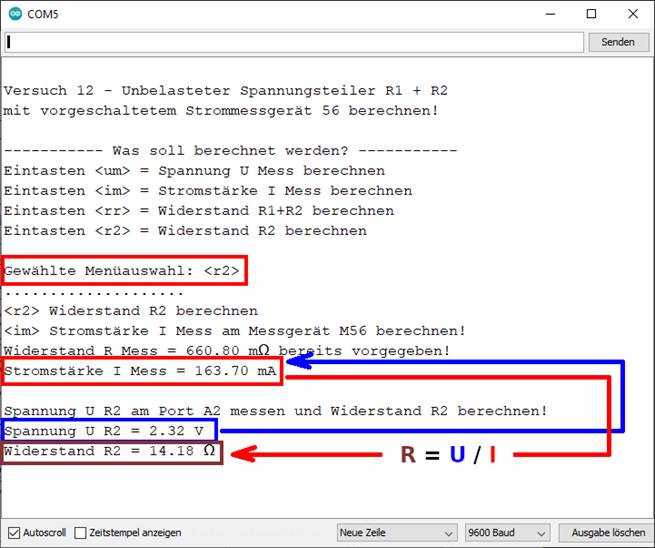
Aus elektro- und messtechnischer Sicht macht es Sinn, den zweiten Lampenwiderstand R_{Lampe 2} des Spannungsteilers R_{Lampe 1} + R_{Lampe 2} als Erstes von den beiden zu berechnen, da dieser direkt auf Masse „GND“ („┴“) führt, so dass man nur den Spannungsabfall U_{Lampe 2} parallel zum Lampenwiderstand R_{Lampe 2} erfassen

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_08.ino)

und über die Stromstärke I = I_Mess = I_R1+R2 = I_R2 den Lampenwiderstand R_{Lampe 2} wie folgt berechnen kann:

R_{Lampe 2} = U_{Lampe 2} / I_{Lampe 2} = U_R2 / I_Mess

= 2,32 V / 163,70 mA = 2,32 V / 0,1637 A = 14,1723 Ω ≈ 14,17 Ω (siehe im obenstehenden Bild)

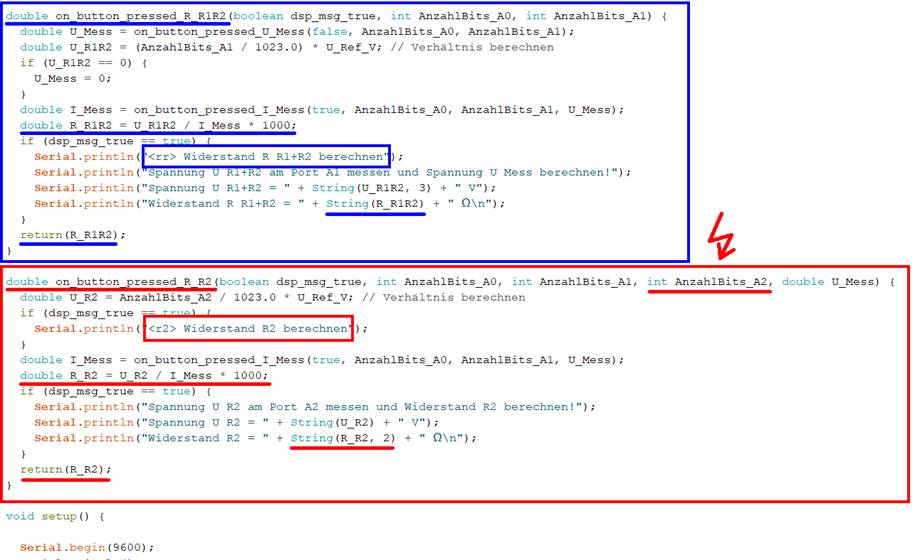
Programmierung der Berechnung der Teilwiderstände des Spannungsteilers

Werfen wir zum besseren Verständnis noch einen Blick auf den Sourcecode des „Sketch“-Programms „sketch_prog_12_08.ino“. Im blauen Kasten sehen wir Berechnung des Gesamtwiderstandes R_R1R2 = des Spannungsteilers mit den beiden in Reihe geschalteten Glühlampen 18 zu denen der Spannungsabfall U_R1R2 = 4,878 V gehört (siehe weiter oben).

Um den Gesamtwiderstand R_R1R2 = 29,81 Ω des Spannungsteilers mit den beiden in Reihe geschalteten Glühlampen 18 gemäß dem Ohmschen Gesetz mit R = U / I berechnen zu können, benötigen wir noch die Stromstärke I_R1+R2 = I_Mess = 163,70 mA ( siehe weiter oben).

Damit wir die Stromstärke I_R1+R2 = I_Mess nicht extra neu berechnen müssen, holen wir uns diese als Return-Wert (= Rückgabewert) I_Mess von der Funktion „I_Mess = on_button_pressed_I_Mess( )“ (siehe im blauen Kasten):

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_08.ino)

Wie man im obenstehenden Bild im roten Kasten sieht, wird dort der zweite Widerstand R_R2 = 14,18 Ω berechnet, indem man gemäß dem Ohmschen Gesetz mit R = U / I den Quotienten U_R2 / I_Mess bildet. Und da die Stromstärke mit I = I_Mess = I_R1+R2 = I_R2 = 163,70 mA in Milliampere ausgegeben und angezeigt wird, muss man den Quotienten U_R2 / I_Mess wegen der Maßeinheit der Stromstärke in [mA] noch mit dem Faktor 1000 multiplizieren, damit sich der Widerstandswert des zweiten Widerstandes R_R2 = 14,18 Ω wieder in der Grundmaßeinheit [Ω] ausgeben und anzeigen lässt (siehe im obenstehenden Bild im roten Kasten).

Damit sich der Quotient U_R2 / I_Mess auch wirklich berechnen lässt, benötigt man noch den Spannungsabfall U_R2 = 2,32 V am zweiten Widerstand, d.h. der zweiten Glühlampe 18 des Spannungsteilers, der zuvor eigens über den Port „Pin A2“ und der Variablen „AnzahlBits_A2“ eingelesen wurde:

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_08.ino)

Werfen wir der Vollständigkeit halber noch einen Blick auf die bisher gemessenen und berechneten Werte des „Sketch“-Programms „sketch_prog_12_08.ino“:

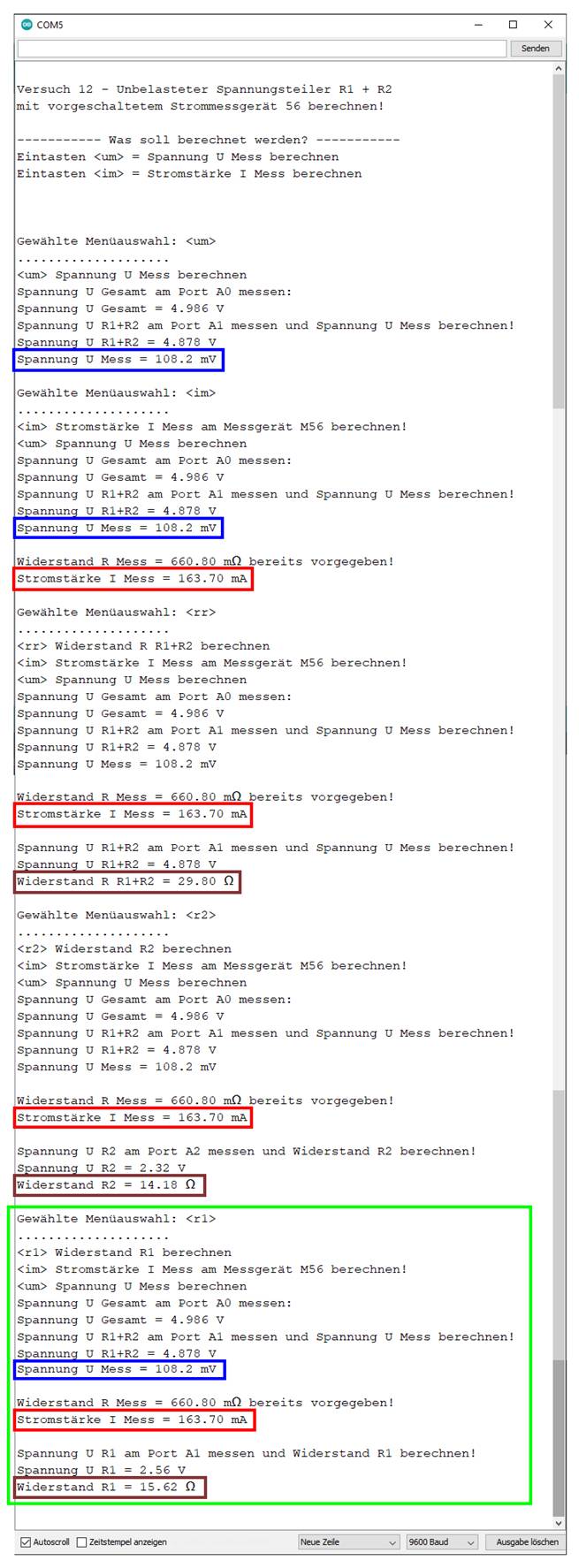
(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_08.ino)

Werfen wir schon mal einen vorauseilenden Blick auf die Mess- und Rechenergebnisse des „Sketch“-Programms „sketch_prog_12_09.ino“, um zu sehen, ob wir bisher richtig gerechnet haben und um zu sehen, dass das Programm zur Berechnung des ersten Lampenwiderstandes R_Lampe 1 = R₁ mittels der Spannungsteilerformel wie erwartet funktioniert (siehe hellgrüner Kasten):

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_09.ino)

Wie man im obenstehenden Bild ganz zu Anfang sieht, klafft bei der Menüauswahl <Was soll berechnet werden?> eine große weiße Lücke von Leerzeilen in denen es eigentlich heißen müsste:

Eintasten <rr> = Widerstand R1+R2 berechnen

Eintasten <r1> = Widerstand R1 berechnen

Eintasten <r2> = Widerstand R2 berechnen

Der Grund für die fehlerhafte Menüauswahlanzeige ist der, dass der Speicherplatz von 32 KByte langsam knapp wird, sodass der „Arduino UNO“ anfängt, nicht mehr fehlerfrei zu arbeiten!

Aber zum Glück ist das neue „Sketch“-Programm „sketch_prog_12_09.ino“ zwecks Berechnung von Spannungen, Stromstärken und Widerständen des unbelasteten Spannungsteilers, der aus zwei in Reihe geschalteten Glühlampen 18 besteht, inzwischen ausgereift und vollständig:

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_09.ino)

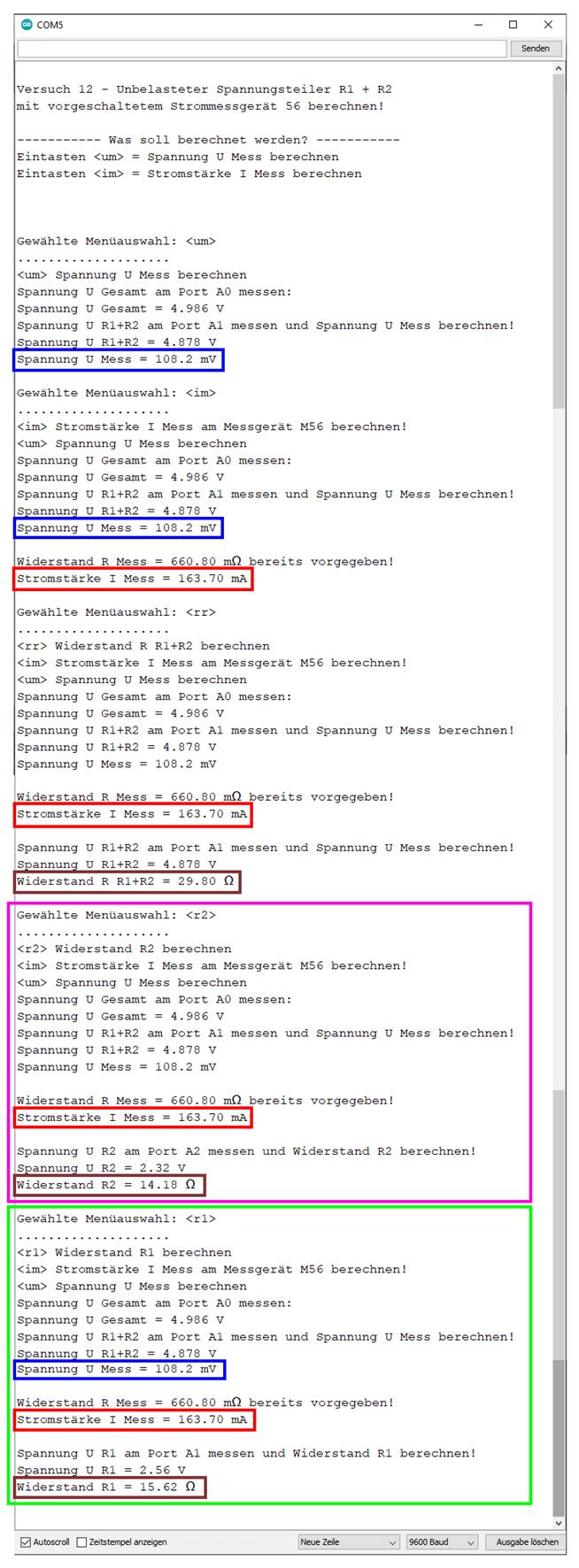
Die im obenstehenden Bild zu sehenden braunen Kästen beziehen sich alle auf die Programmierung der Berechnung des ersten Lampenwiderstandes R_Lampe 1 = R₁ mittels der Spannungsteilerformel beim unbelasteten Spannungsteiler!

Wie man im nachfolgenden Screenshot des „Arduino UNO“-Konsolefensters im pinkfarbenen Kasten sieht, lässt sich mit dem „Sketch“-Programm „sketch_prog_12_09.ino“ auch der zweite Lampenwiderstand R_Lampe 2 = R₂ mittels der Spannungsteilerformel beim unbelasteten Spannungsteiler berechnen und anzeigen:

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_09.ino)

Dabei lässt sich auch feststellen, dass die beiden in Reihe geschalteten Glühlampen 18 mit ihren Lampenwiderständen R_Lampe 1 = R₁ = 15,62 Ω und R_Lampe 2 = R₂ = 14,18 Ω voneinander abweichen!

Der Grund dafür dürfte der sein, dass die beiden Glühlampen 18 nicht aus der selben Produktion stammen, also an unterschiedlichen Produktionstagen hergestellt wurden oder aber eine von den beiden Glühlampen 18 bei Versuchen bereits längere Zeit in Betrieb war, sodass die Glühwendel bereits stärker verschlissen ist und als Folge dessen einen geringeren Widerstand aufweist. Demzufolge müsste also die Glühwendel der Glühlampen 18 mit dem geringeren Lampenwiderstand R_Lampe 2 = R₂ = 14,18 Ω bereits stärker abgenutzt sein.

Deshalb sollte man bei seinem Auto stets beide (Halogen-) Glühlampen gleichzeitig auswechseln, falls eine bereits vorzeitig ihren Dienst aufgegeben und das Zeitliche gesegnet hat, da man auf diese Weise halbwegs sicher sein kann, dass beide neuen (Halogen-) Glühlampen am gleichen Tag hergestellt wurden, der gleichen Produktionslinie entstammen, demzufolge hinsichtlich der elektrischen Daten einander identisch sind und statistisch über die gleiche Lebens- bzw. Leuchtdauer verfügen!

Das „Sketch“-Programm „sketch_prog_12_10.ino“ zwecks Berechnung von Spannungen, Stromstärken und Widerständen des unbelasteten Spannungsteilers ist mit dem „Sketch“-Programm „sketch_prog_12_09.ino“ identisch. Allerdings wird beim „sketch_prog_12_10.ino“-Programm nicht mehr der zweite Lampenwiderstand R_Lampe 2 = R₂ mittels der Spannungsteilerformel berechnet, sondern der dritte Widerstand R₃ = R_Last = 165,86 Ω:

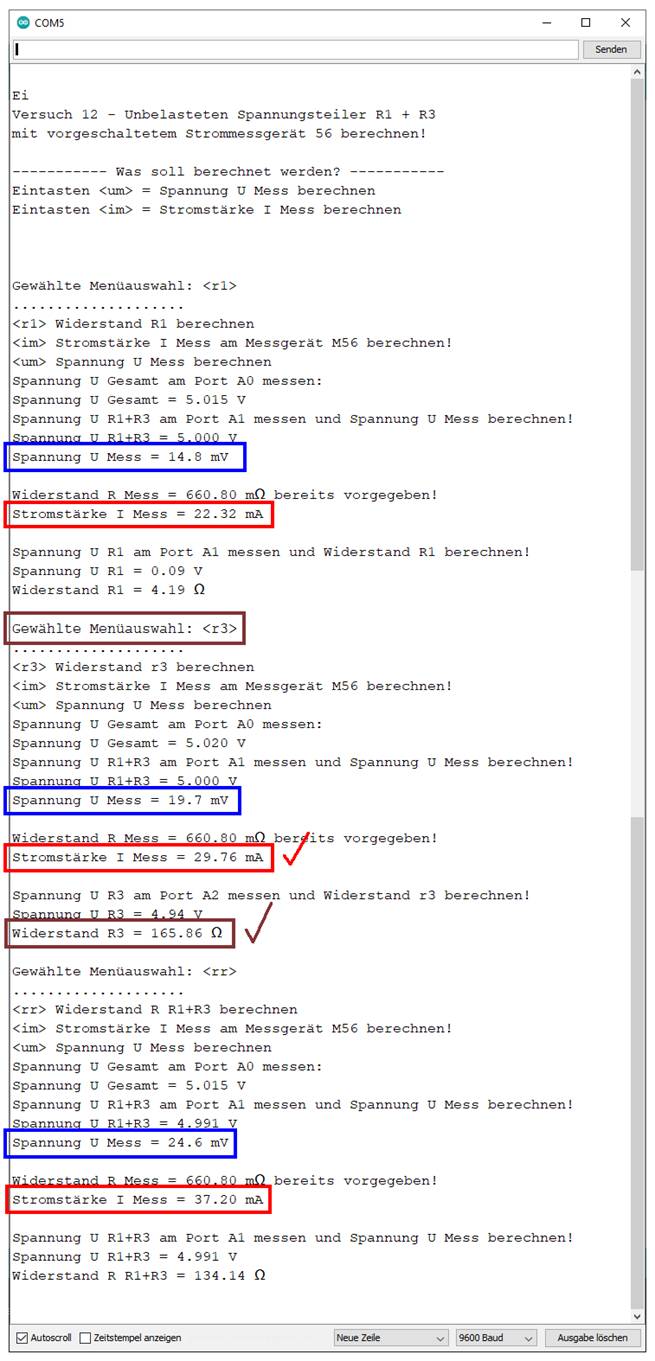
(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_10.ino)

Wie man im obenstehenden Screenshot des „Arduino UNO“-Konsolefensters sieht, stellen sich bei jeder der drei Messungen sowohl unterschiedliche Spannungen als auch Stromstärken ein.

Was aber bedeutet es, wenn man bei ein und demselben unbelasteten Spannungsteiler am Messwiderstand R_Mess = R_{Messgerät 56} = 660,80 Ω drei verschiedene Spannungen misst und daraus auch noch drei verschiedene Stromstärken errechnet?

Da alle drei Spannungen unabhängig voneinander an drei verschiedenen Widerständen (Reihenwiderstand R_{Lampe 1}, Reihenwiderstand R_Last und Reihenschaltungswiderstand R_{Lampe 1} + R_Last) gemessen wurden, würden sich normalerweise auch drei verschiedene Spannungen bzw. Spannungsabfälle und an diesen auch drei verschiedene Stromstärken einstellen. Da aber die beiden Widerstände R_{Lampe 1} und R_Last als unbelasteter Spannungsteiler geschaltet sind, müssten diese von ein und derselben Stromstärke I_Mess = I_{Lampe 1} = I_Last durchflossen werden!

Wenn man sich noch die anderen Spannungswerte der drei Widerstandsmessungen <r1>, <r3> und <rr> anschaut, dann fällt auf, dass der

· Spannungsabfall am unbelasteten Spannungsteiler
mit U_R1+R3 = [ 5,000 V, 5,000 V , 4,991 V ] praktisch konstant bleibt, während der

· Spannungsabfall am (Strom-) Messgerät 56
mit U_Mess = [ 14,8 mV, 19,7 mV , 24,6 mV ] von Messung zu Messung um bis zu 66,22 % ansteigt!

Jetzt wissen wir, dass das (Strom-) Messgerät 56 die Ursache dafür ist, dass es von Messung zu Messung zu ansteigenden Spannungsabfällen nebst der korrespondierenden Stromstärkeanstiegen I_Mess = [ 22,32 mA, 29,76 mA, 37,20 mA ] kommt.

Dies bedeutet praktisch, dass das (Strom-) Messgerät 56 ebenfalls wie die Glühlampen 18 und der Summer 10 (= Lastwiderstand R_Last) über eine Kennlinie verfügt, die oftmals nur abschnittsweise linear verläuft, sodass das Messgerät 56 nur in einem bestimmten Arbeitsbereich (der Kennlinie) korrekte Messergebnisse liefert. Im vorliegenden Fall scheint das Messgerät 56 nur dann richtige Strommessergebnisse anzuzeigen, wenn der Spannungsabfall parallel zum Messgerätewiderstand R_Mess entsprechend größer als mindestens U_Mess > 50 mV ist! Aber so genau wissen wir das nicht, müssten wir zum Messgerät 56 noch die entsprechende Kennlinie in Form einer Wertetabelle aufnehmen.

R_Last = U_Last / I_Last = 5,0 V / 29,76 mA = 168,0 Ω

Zum Lastwiderstand R_Last bei dem es sich ja um den Summer 10 , d.h. einen elektronischen Buzzer handelt, gibt es seitens des Herstellers ein entsprechendes Datenblatt u.a. mit den Nenn-Betriebsdaten zur Nenn-Betriebsspannung von U_{Last, Nenn} = 5 V und des Nennstroms von I_Last, Nenn = 30 mA , sodass sich der Nenn-Widerstand zu R_Last, Nenn = 166,67 Ω ≈ 167 Ω berechnet.

Demzufolge würde es sich bei der mittleren Widerstandsmessung <r3> um die richtige handeln (siehe obenstehendes Bild mit dem roten und braunen Haken). -

In diesem Zusammenhang sei nochmals daran erinnert, dass man bei der Verwendung von (analogen) Drehspulmessgeräten stets nur dann verlässliche Messwerte angezeigt bekommt, wenn man diese im oberen Drittel der Messskala misst!

Demzufolge muss man bei Messwerten, die sich im unteren Drittel der Messskala abspielen, mit ungenauen und teils falschen Werten rechnen! -

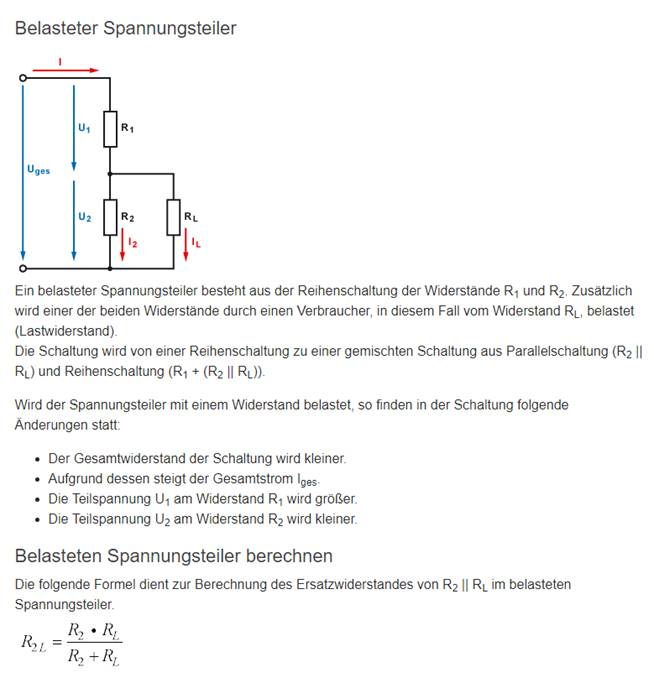
[ zurück ] zur Berechnung des belasteten Spannungsteilers.

Unbelasteter versus belasteter Spannungsteiler

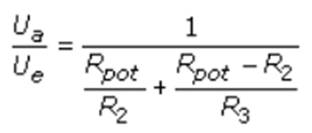
Während es sich bei einem unbelasteten Spannungsteiler um eine einfache Reihenschaltung von mindestens zwei in Serie geschalteten Widerständen R_{Lampe 1} = R₁ und R_{Lampe 2} = R₂ handelt, sodass auf diese z.B. die Spannungsteilerformel anwenden lässt, handelt es sich beim belasteten Spannungsteiler um eine gemischte Schaltung, die sich aus einem Spannungsteiler in Kombination mit einem Stromteiler zusammensetzt:

(Bild vergrößern: auf Bild klicken! Quelle: Elektronik-Kompendium)

Bei der oben im Bild stehenden Berechnungsformel für den Gesamtwiderstand R_2L = R₂ * R_L / ( R₂ + R_L ) des Stromteilers R₂ // R_L handelt es sich um eine Spezialformel für zwei parallel geschaltete Widerstände R₂ // R_L, die sich wie folgt ableitet:

1 / R_2L = 1 / R₂ + 1 / R_L = R_L + R₂ / ( R₂ * R_L ) → Kehrwert bilden!

R_2L = R₂ * R_L / ( R_L + R₂ ) = R₂ * R_L / ( R₂ + R_L )

Bevor sich also der belastete Spannungsteiler als Ganzes berechnen lässt, muss man zuvor den Gesamtwiderstand R_2L des Stromteilers berechnen! Erst danach lässt sich mit dem Gesamtwiderstand R_2L des Stromteilers auch der Gesamtwiderstand R_ges = R₁ + R_2L des belasteten Spannungsteilers berechnen!

Mit dem weiter entwickelten „Sketch“-Programm „sketch_prog_12_11.ino“ lässt sich der Stromteilerwiderstand R₃ = R_Last = R_{Summer 10} berechnen, wenn mit dem Programm zuvor der Stromteilerwiderstand R_{Lampe 2} = R₂ = 12,26 Ω ermittelt wurde:

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_11.ino)

Im Moment müssen wir aber noch den Stromteilerwiderstand R₃ = R_Last = R_{Summer 10} des elektronischen Summers 10 wie folgt zu Fuß ausrechnen:

1 / R_RP = 1 / R₂ + 1 / R_Last → Nach 1 / R_Last umstellen und auf der rechten Seite den Hauptnenner bilden!

1 / R_Last = 1 / R_RP - 1 / R₂ = ( R₂ - R_RP ) / R_RP * R₂ → Den Kehrwert bilden!

R_Last = R_RP * R₂ / ( R₂ - R_RP )

= 10,93 Ω * 12,26 Ω / ( 12,26 Ω - 10,93 Ω )

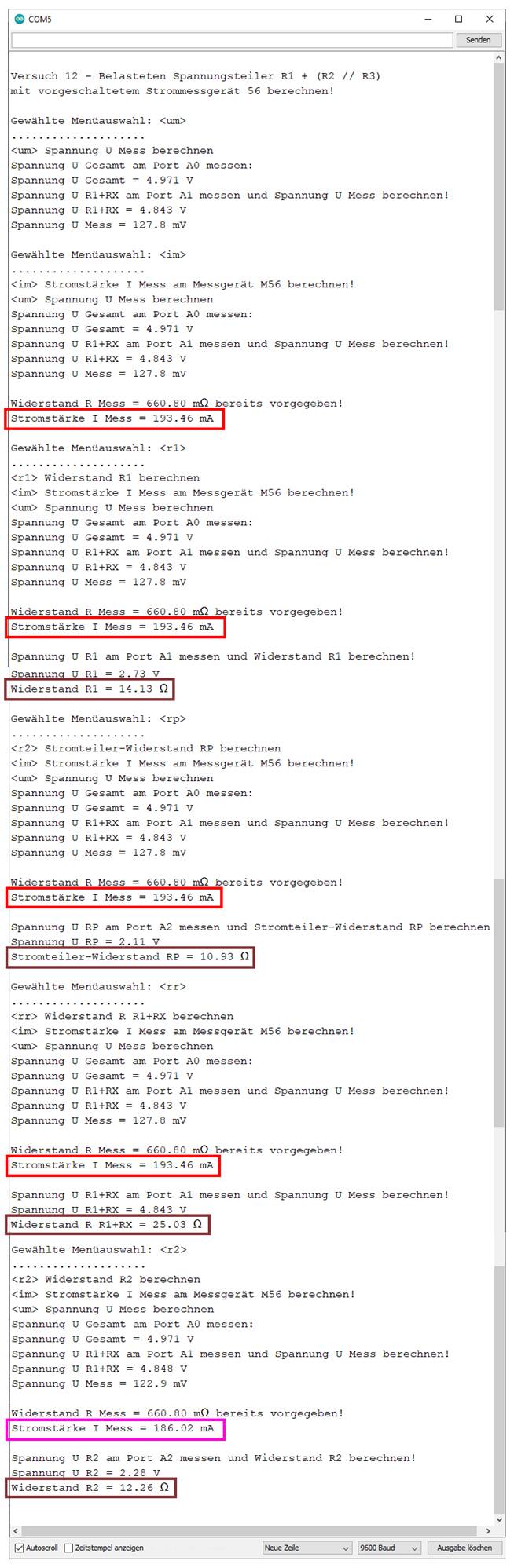
= 134,00 Ω / ( 1,33 Ω ) = 100,75 Ω

Bei der nachfolgenden Messung wenden wir den Trick an und berechnen zunächst nur die Stromstärke und Widerstandswerte für den unbelasteten Spannungsteiler, indem wir den Stromteilerwiderstand R₃ = R_Last = R_{Summer 10} des elektronischen Summers 10 außen vorlassen (siehe pinkfarbener großer Kasten):

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_11.ino)

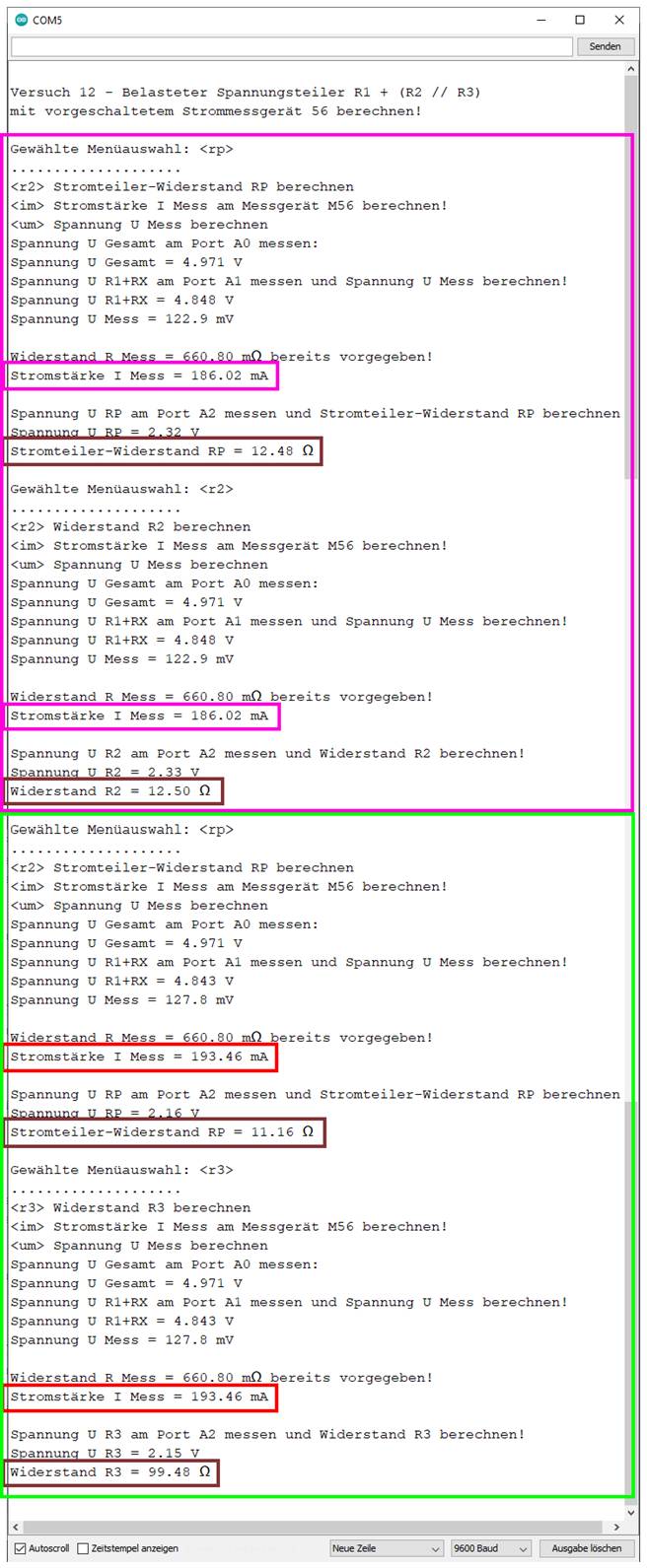
Im zweiten Schritt der obenstehenden Messung berechnen wir die Stromstärke und Widerstandswerte für den belasteten Spannungsteiler, indem wir den Stromteilerwiderstand R₃ = R_Last = R_{Summer 10} des elektronischen Summers 10 hinzufügen (siehe hellgrüner großer Kasten).

Da das „Sketch“-Programm „sketch_prog_12_11.ino“ über keine künstliche Intelligenz bzw. maschinelles Lernen verfügt, weiß das Programm natürlich nicht, ob wir dieses mit einem unbelasteten oder belasteten Spannungsteiler betreiben. Demzufolge weiß das Programm auch nicht, ob wir zum Stromteilerwiderstand R₂ = R_{Glülampe 2} noch zusätzlich den Stromteilerwiderstand R₃ = R_Last = R_{Summer 10} parallel geschaltet haben oder nicht.

Nur deshalb ist es möglich, dass wir mit dem „Sketch“-Programm „sketch_prog_12_11.ino“ zunächst den Stromteilerwiderstand R₂ = R_{Glülampe 2} des unbelasteten Spannungsteilers berechnen und im Anschluss daran den gesamten Stromteilerwiderstand R_{gesamt, parallel} = R_RP, sodass sich aus diesem dann abschließend auch noch der Stromteilerwiderstand R₃ = R_Last = R_{Summer 10} berechnen lässt.

Der Stromteilerwiderstand R₃ = R_Last = R_{Summer 10} lässt sich einerseits herkömmlich wie folgt berechnen

1 / R_RP = 1 / R₂ + 1 / R_Last → Nach 1 / R_Last umstellen und auf der rechten Seite den Hauptnenner bilden!

1 / R_Last = 1 / R_RP - 1 / R₂ = ( R₂ - R_RP ) / R_RP * R₂ → Den Kehrwert bilden!

R_Last = R_RP * R₂ / ( R₂ - R_RP )

= 11,16 Ω * 12,50 Ω / ( 12,50 Ω - 11,16 Ω )

= 139,50 Ω / ( 1,34 Ω ) = 104,1 Ω

und andererseits auch mittels Stromteilerformel:

R_Last / R_RP = I_RP / I_Last →

R_Last / R_{Lampe 2} = I_{Lampe 2} / I_Last →

R_RP / R_{Lampe 2} = I_{Lampe 2} / I _RP → Stromteilerformel → ist richtig!

R_RP = I_{Lampe 2} / I_RP * R_{Lampe 2}

= 168,02 mA / 193,46 mA * 12,50 Ω

= 0,868 mA * 12,50 Ω = 10,85 Ω → FALSCH!

Probe:

R_RP = U_RP / I_RP

= 2,15 V / 193,46 mA = 2,15 V / 0,194 A = 11,08 Ω → RICHTIG!

Jetzt stellt sich die berechtigte Frage, was wir bei der Berechnung mit der Stromteilerformel falsch gemacht haben!

Was man beim Anwenden der Stromteilerformel stets beachten muss, ist, dass sich die Teilströme des Stromteilers, d.h. der Parallelschaltung, immer auf ein und dieselbe Teilspannung, d.h. den gemeinsamen Spannungsabfall des Stromteilers bzw. der Parallelschaltung beziehen!

Demzufolge bezieht sich die Stromstärke I_{Lampe 2} = 168,02 mA der Glühlampe 18 auf die Teilspannung U_{Lampe 2} = 2,33 V des unbelasteten Spannungsteilers! Und genau das ist der Fehler!

Beim Anwenden der Stromteilerformel in Verbindung mit dem belasteten Spannungsteilers müssen wir stets mit dessen Teilspannung am Stromteiler bzw. der Parallelschaltung rechnen:

U_{Lampe 2} = U_RP = 2,15 V

I_{Lampe 2} = U_{Lampe 2} / R_{Lampe 2}

= U_RP / R_{Lampe 2}

= 2,15 V / 12,5 Ω = 0,172 A = 172 mA

R_RP / R_{Lampe 2} = I_{Lampe 2} / I _RP → Stromteilerformel → ist richtig!

R_RP = I_{Lampe 2} / I_RP * R_{Lampe 2}

= 172 mA / 193,46 mA * 12,50 Ω

= 0,8891 * 12,50 Ω = 11,11 Ω → RICHTIG! þ

R_Last = R_RP * R₂ / ( R₂ - R_RP )

= 11,11 Ω * 12,50 Ω / ( 12,50 Ω - 11,11 Ω )

= 138,88 Ω / ( 1,39 Ω ) = 99,91 Ω

I_Last = U_Last / R_Last = U_RP / R_Last

= 2,15 V / 99,91 Ω = 0,02152 A = 21,52 mA

Obwohl die obenstehende Berechnung jetzt richtig ist, gibt es trotzdem elektro- und programmiertechnisch noch etwas Entscheidendes zu verbessern. Der Knackpunkt dabei ist der, dass sich im Moment quasi alles um den Stromteiler und die Stromteilerformel dreht. Und zwar mit dem Problem, dass sich der Lastwiderstand R_Last nur dann berechnen lässt, wenn der Parallelwiderstand R_Lampe 2 oder dessen Stromstärke durch diesen bekannt ist und demzufolge zuvor berechnet werden muss, bevor sich die Stromteilerformel anwenden lässt. Beide aber, d.h. der Parallelwiderstand R_Lampe 2 oder dessen Stromstärke lassen sich zuvor nur mittels des unbelasteten Spannungsteilers berechnen.

Sobald man aber zum zuvor berechneten Parallelwiderstand R_Lampe 2 den Lastwiderstand R_Last parallel hinzuschaltet, sodass sich daraufhin erst der Stromteiler einstellt, ist jeder Widerstand, jeder Spannungsabfall, jeder Strom mit jedem anderen Widerstand, mit jedem anderen Spannungsabfall, mit jedem anderen Strom des belasteten Spannungsteilers verknüpft! Alles ist also mit allem verbunden, alles steht mit allem in Verbindung. Und genau das war das bisherige Problem. Nämlich, dass wenn sich etwas beim Stromteiler ändert, ändert sich auch alles andere beim belasteten Spannungsteiler.

Der eingeprägte Strom beim belasteten Spannungsteiler

Beim belasteten Spannungsteiler mit dem integrierten, d.h. quasi nachgeschalteten Stromteiler wird der Teilwiderstand R₂ = R_Lampe 2 mit der Teilspannung U_R2 des vormals unbelasteten Spannungsteilers zum Stromteilerwiderstand R_RP mit R_RP = R₂ // R_Last und der gemeinsamen Teilspannung U_RP.

Wenn beim belasteten Spannungsteiler die Stromstärke I_{Lampe 2} = 172 mA durch den Teilwiderstand R_Lampe 2 = 12,50 Ω des Stromteilers um das Vielfache, mindestens aber um das Doppelte größer ist als die Stromstärke I_Last = 21,52 mA durch den Teilwiderstand R_Last = 99,91 Ω des Stromteilers, dann spricht man beim sogenannten Querstrom I_Lampe 2 = 172 mA vom „eingeprägten Strom“, sodass die Stromstärke des Querstroms I_Lampe 2 in einem weiten Bereich unabhängig vom parallel geschalteten Lastwiderstand R_Last ist!

Dass es beim eingeprägten Strom, d.h. dem Querstrom I_Lampe 2 durch die zweite Glühlampe 18 des belasteten Spannungsteilers, in einem weiten Bereich nicht auf den parallel geschalteten Lastwiderstand R_Last des Stromteilers ankommt, dieser also praktisch keine Rolle spielt, bedeutet dies elektrotechnisch, dass es sich beim gemeinsamen Spannungsabfall U_RP am Stromteiler um eine stabilisierte Spannung U_{RP, stabil} = 2,15 V handelt (siehe oben)!

Wenn man also dafür sorgt, dass der Querstrom I_Lampe 2 mindestens doppelt, besser noch vier Mal so groß ist als der Laststrom I_Last durch den parallel geschalteten Lastwiderstand R_Last, dann arbeitet der belastete Spannungsteiler am Stromteiler quasi als Konstant-Spannungsquelle bzw. als sogenannter Spannungsregler.

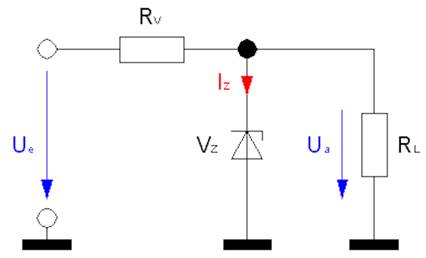
Dabei würde sich ein noch besserer Stabilisierungseffekt einstellen, wenn man den Teilwiderstand R₂ = R_{Lampe 2} durch eine sogenannte Zener-Diode („V_Z“) ersetzt:

(Zum Vergrößern bitte auf das Bild klicken!)

Da die Zener-Diode V_Z in Sperrrichtung betrieben wird und nur über eine bestimmte (Regel-) Leistung wie z.B. P_VZ = U_VZ * I_Z = 2,15 V * 40 mA = 2,15 V * 0,04 A = 0,086 W ≈ 90 mW verfügt, muss die überschüssige Energie mittels des Vorwiderstandes R_V „vernichtet“, d.h. in Wärmeverlustleistung umgewandelt werden:

P_RV = U_RV * I_RV

= ( U_e – U_a ) * ( I_Z + I_L ) = ( U_e – U_a ) * ( I_Z + ½ I_Z )

= ( U_e – U_a ) * ( 1,5 I_Z ) = ( 5,0 V – 2,15 V )* 1,5 * 40 mA = 2,85 V * 60 mA = 171 mW

P_RV = U_RV * I_RV = R_V * I_RV * I_RV = R_V * I_RV² →

R_V = P_RV / I_RV² = 171 mW / 3600 (mA)² = 171 mVA / 3600 (mA)² = 0,0475 V mA / (mA)²

= 0,0475 V / mA = 0,0475 V / 10^-3 A = 0,0475 * 10³ V/A = 0,0475 kΩ = 47,5 Ω

Probe:

I_RV² = P_RV / R_V →

I_RV = ( P_RV / R_V )^½ = ( 171 mW / 47,5 Ω )^1/2 = ( 0,171 VA / 47,5 V/A )^1/2 = 0,06 A = 60 mA

Als nächstes ersetzen wir im „Sketch“-Programm „sketch_prog_12_11.ino“ den bisherigen Summer 10 mit Piezoschallwandler und dem Widerstandswert R_Last = 99,91 Ω (siehe weiter oben) durch einen praktisch gleich großen ohmschen Widerstand R_Last = 100 Ω aus dem KOSMOS-Experimentierkasten „Easy Electronic 200“. Und zwar aus dem einfachen Grund, weil mir das laute und klägliche Piepsen des bisher verwendeten Summers 10 auf die Nerven ging:

(Zum Vergrößern bitte auf das Bild klicken!)

Als nächstes starten wir das „Sketch“-Programm „sketch_prog_12_11.ino“ und führen mit diesem nachfolgende Messung aus:

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_11.ino)

Damit das Programm alle Messungen und Berechnungen der Menüauswahlen <im>, <rr>, <r1>, <rp>, <r2> und <r3> richtig durchführt, müssen diese alle mit der gleichen Stromstärke I_Mess = I_R1 = I_RP = 215,78 mA durchgeführt werden (siehe obenstehendes Bild).

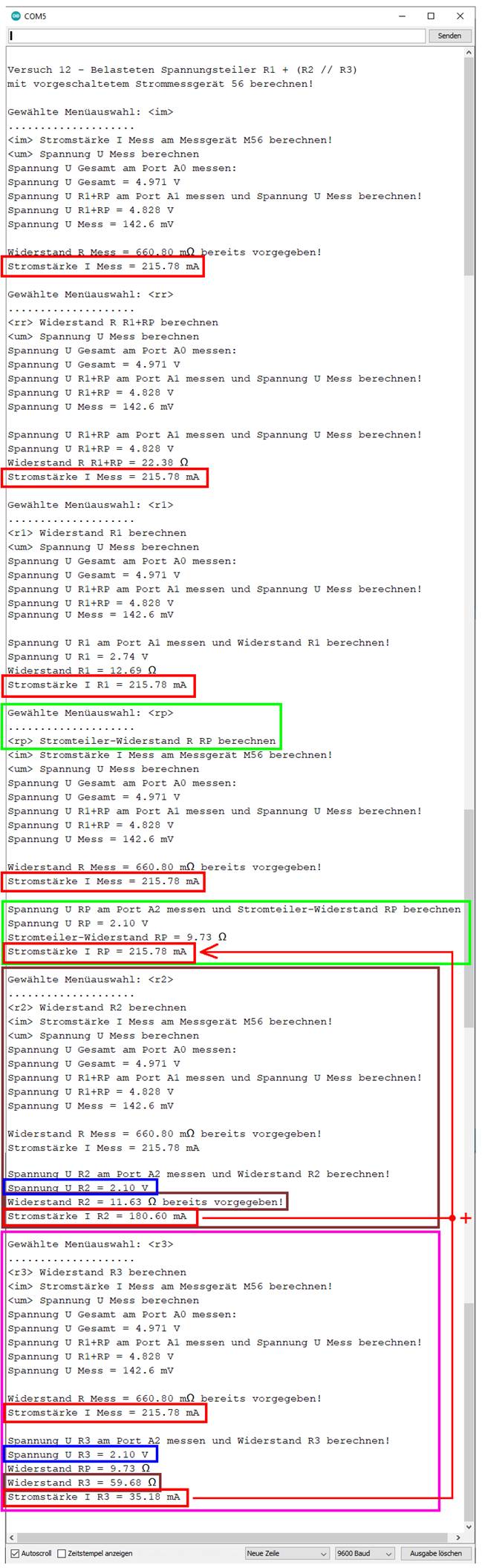
Außerdem muss für den Stromknoten des Stromteilers die Summe der beiden Teilströme I_R2 + I_Last gleich der Stromstärke I_Mess = I_R1 = I_RP durch den belasteten Spannungsteiler sein:

I_Mess = I_R1 = I_RP = I_R2 + I_Last = 180,60 mA + 35,18 mA = 215,78 mA (siehe obenstehendes Bild)

Sollte bei einer der Messungen wider Erwarten eine abweichende Stromstärke als 215,78 mA angezeigt werden, so muss diese wiederholt werden, da nur so sichergestellt werden kann, dass alle Messungen und Berechnungen der Menüauswahlen <im>, <rr>, <r1>, <rp>, <r2> und <r3> richtig gemessen und berechnet werden!

Da der verfügbare Speicherplatz in Form des sogenannten Flash-Speichers beim „Arduino UNO“ leider zu knapp bemessen ist, lassen sich im „Sketch“-Programm „sketch_prog_12_11.ino“ u.a. die Menüauswahlen <im>, <rr>, <r1>, <rp>, <r2> und <r3> leider nicht mehr anzeigen, sodass man diese vielmehr dem Quellkode wie folgt entnehmen muss:

(Bild vergrößern: auf Bild klicken! Webverzeichnis | sketch_prog_12_11.ino)

Bei der letzten Messung und Berechnung des Lastwiderstandes R₃ = R_Last = 100 Ω gemäß der Menüwahl <r3> fällt auf, dass dieser nicht wie physisch und physikalisch auf dem Montagebrett des Widerstandes 40 angegeben 100 Ω groß ist,

(Zum Vergrößern bitte auf das Bild klicken!)

sondern wider Erwarten nur R₃ = R_Last = 59,68 Ω!

Wie kann das sein, wie ist das möglich? Wurde etwa das Ohmsche Gesetz außer Kraft gesetzt?! Gibt es im „Sketch“-Programm „sketch_prog_12_11.ino“ etwaige Rechen- oder Programmierfehler?!

Auf der Webseite „Spannungsteiler belastet berechnen“ lassen sich alle zur Berechnung erforderlichen Widerstands-, Spannungs- und Stromwerte einpflegen und wie folgt berechnen:

(Bild vergrößern: auf Bild klicken! Quelle: „Electronics Planet“)

Leider hat das Programm „Spannungsteiler belastet berechnen“ den Nachteil, dass es den Anwender im Unklaren darüber lässt, wie es rechnet und welche Formeln wie z.B. Ohmsches Gesetz, Spannungsteilerformel, Stromteilerformel usw. dazu angewendet werden.

Um aber trotzdem nachvollziehen zu können, welche Formeln und Berechnungen im „Sketch“-Programm „sketch_prog_12_11.ino“ angewendet und programmiert wurden, reproduzieren wir diese anhand der Tabellenkalkulation „Calc“ vom kostenlosen „LibreOffice“-Programm:

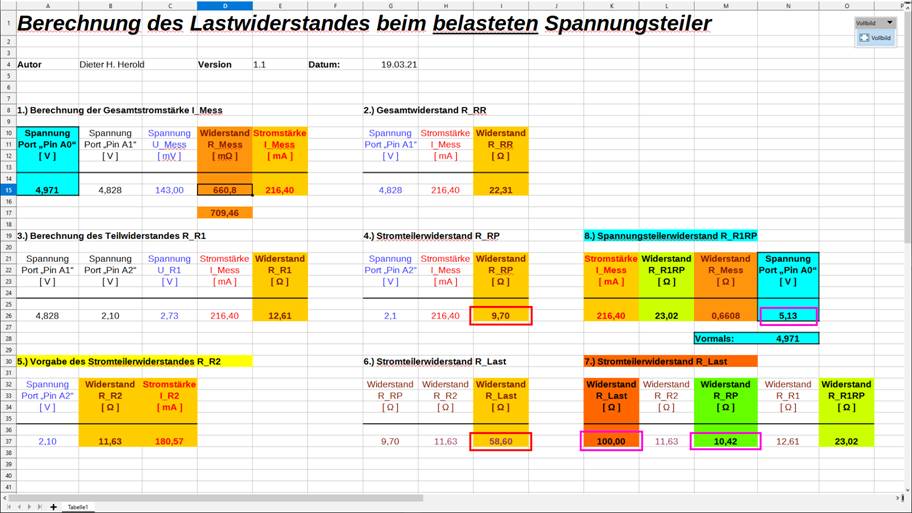
(Bild vergrößern: auf Bild klicken! Tabellenkalkulation: ..\images_2\arduino_prog_12_40.ods)

Wie man im Screenshot der obenstehenden Tabellenkalkulation unter „6.) Stromteilerwiderstand R_Last“ sieht, wurde der Lastwiderstand R_L = R_Last = 58,60 Ω tatsächlich richtig berechnet (siehe auch Konsoleanzeige weiter oben), obwohl der physische (= körperliche) Widerstand 40 physikalisch nach wie vor einen Widerstandswert von R₄₀ = 100 Ω hat!

Wie soll man sich das erklären?! Obwohl die Berechnung sowohl im „Sketch“-Programm „sketch_prog_12_11.ino“ als auch in der Tabellenkalkulation mathematisch richtig ist, ist sie trotzdem falsch! Und zwar elektrotechnisch!

Um herauszufinden, was an der Berechnung nebst Programmierung falsch sein könnte, müssen wir uns das Ohmsche Gesetz wieder in Erinnerung rufen: R = U / I = ∆U / ∆I = konstant!

In Worten: Jede Spannungsänderung ∆U führt sofort zu einer Stromänderung ∆I am Widerstand R! Dabei hat der Widerstand R stets einen konstanten Wert!

Im vorliegenden Fall führt aber eine kleine Spannungsänderung ∆U = ∆U_Pin A0 am Eingang des belasteten Spannungsteilers zu einer großen Widerstandsänderung ∆R_Last am Ausgang desselben, d.h. am Stromteiler. Und genau das dürfte gemäß dem Ohmschen Gesetz nicht passieren, müsste eine Spannungsänderung ∆U stets zu einer Stromänderung ∆I am konstanten Widerstand R_Last führen!

Um herauszufinden, wie es zu dem elektronischen Phänomen kommt, dass eine kleine Spannungsänderung ∆U = ∆U_Pin A0 am Eingang des belasteten Spannungsteilers zu einer großen Widerstandsänderung ∆R_Last am Ausgang desselben führt und dabei das Ohmsche Gesetz scheinbar außer Kraft setzt, gehen wir sozusagen den umgekehrten Weg, zäumen wir das Pferd von hinten, d.h. rückwärts auf!

Da wir wissen, wie groß der ohmsche Lastwiderstand tatsächlich ist, nämlich R_Last = 100 Ω, berechnen wir sozusagen im Umkehrschluss mit welcher (Versorgungs-) Spannung der belastete Spannungsteiler betrieben werden muss, damit sich am Ende wieder der ohmsche Lastwiderstand R_Last = 100 Ω einstellt!

Beginnen wir mit dem Stromteilerknoten für den die Stromteilerformel gilt:

I_RP = I_R2 + I_R3

= U_RP / R₂ + U_RP / R₃ = U_RP * ( 1 / R₂ + 1 / R₃ ) = U_RP * 1 / R_RP

1 / R_RP = 1 / R₂ + 1 / R₃ = 1 / R₂ + 1 / R_Last →

R_RP = 1 / ( 1 / R₂ + 1 / R_Last ) = R₂ * R_Last / R₂ + R_Last

= 11,63 Ω * 100 Ω / ( 11,63 Ω + 100 Ω ) = 1 136 / 111,63 Ω = 10,18 Ω

R_RR = R_R1RP = R₁ + R_RP

= 12,69 Ω + 10,18 Ω = 22,87 Ω

U_{Pin A1} = U_R1RP = I_ges * R_ges = I_Mess * R_RR

= 215,78 mA * 22,87 Ω

= 0,2158 A * 22,87 Ω = 4,935 V → gegenüber U_{Pin A1} = 4,828 V siehe weiter oben!)

U_{Pin A0} = U_Mess = I_ges * ( R_Mess + R_RR ) = I_Mess * ( R_Mess + R_RR )

= 215,78 mA * ( 660,80 mΩ + 22,87 Ω )

≈ 0,2158 A * ( 0,661 Ω + 22,87 Ω )

= 0,2158 A * 23,531 Ω = 5,078 V → gegenüber U_{Pin A0} = 4,971 V siehe weiter oben!)

So, nun wissen wir mit welcher Spannung der belastete Spannungsteiler betrieben werden muss, damit sich rechnerisch der ohmsche Lastwiderstand R_Last = 100 Ω einstellt! Nämlich mit U_{Pin A0} = U_Mess = 5,078 V !

Was passiert aber, wenn sich die erforderliche (Versorgungs-) Spannung U_{Pin A0} = U_Mess = 5,078 V, mit der der belastete Spannungsteiler betrieben werden muss, nicht bereitstellen lässt bzw. nicht zur Verfügung steht? Nämlich genau so, wie im vorliegenden Fall, wo uns die USB-Spannungsversorgung vom Desktop-PC nebst der internen Spannungsversorgung des „Arduino UNO“ am Port „Pin 5V“ nur eine Spannung U_{Pin 5V} = 5,03 V zur Verfügung stellt!

Dann passiert genau das, was nicht passieren soll, was eigentlich nicht passieren darf, aber eben doch passiert! Dann wird der zu berechnende Lastwiderstand R_Last = 100 Ω von unserem Programm falsch berechnet:

1 / R_RP = 1 / R₂ + 1 / R_Last →

1 / R_Last = 1 / R_RP - 1 / R₂ = R₂ - R_RP / ( R_RP * R₂ ) →

R_Last = R_RP * R₂ / ( R₂ - R_RP )

R_RP = U_RP / I_RP = U_{Pin A2} / I_R1 = U_{Pin A2} / I_Mess

= 2,10 V / 215,78 mA = 2,10 V / 0,21578 A = 9,732 Ω

R_Last = R_RP * R₂ / ( R₂ - R_RP )

= 9,732 Ω * 11,63 Ω / ( 11,63 Ω - 9,732 Ω ) = 113,183 Ω² / 1,898 Ω = 59,63 Ω

Die in der bisherigen Berechnung verwendeten Messwerte wurden dem Screenshot vom Programm „sketch_prog_12_11.ino“ im Webverzeichnis entnommen.

Alternativ lassen der (Spannungsteiler-) Widerstand R_RP als auch der Lastwiderstand R_Last mittels der Spannungsteilerformel beim belasteten Spannungsteiler wie folgt berechnen:

R_RP / R_M56 = U_RP / U_M56

= U_{Pin A2} / ( U_{Pin A0} - U_{Pin A1} )

= 2,10 V / ( 4,971 V - 4,828 V ) = 2,10 V / 0,143 V = 14,685

R_RP = 14,685 * R_M56 = 14,685 * 660,80 mΩ = 14,685 * 0,6608 Ω = 9,704 Ω

R_Last = R_RP * R₂ / ( R₂ - R_RP )

= 9,704 Ω * 11,63 Ω / ( 11,63 Ω - 9,704 Ω ) = 112,858 Ω² / 1,926 Ω = 58,6 Ω

So, nun haben wir den Beweis, dass sich der Lastwiderstand R_Last immer nur dann von unserem „Sketch“-Programm „sketch_prog_12_11.ino“ richtig berechnen lässt, wenn uns für den Betrieb des belasteten Spannungsteilers eine hinreichend große Versorgungsspannung von U_{Pin A0} = U_Mess > 5,078 V zur Verfügung steht!

Wenn man also in der Praxis an einem belasteten Spannungsteiler eine Spannungsmessung vornimmt, die beiden Parallelwiderstände R_PR = R₂ // R_Last mit z.B. R₂ = 11,63 Ω sowie R_Last = 100 Ω bekannt sind und das „Sketch“-Programm „sketch_prog_12_11.ino“ dabei den Lastwiderstand R_Last mit R_Last ≠ 100 Ω wider Erwarten falsch berechnet und anzeigt, dann bedeutet dies praktisch, dass für den Betrieb des belasteten Spannungsteilers keine hinreichend große Versorgungsspannung von U_{Pin A0} = U_Mess = 5,078 V zur Verfügung steht, die Spannungsversorgung des belasteten Spannungsteilers demzufolge mehr oder weniger zusammengebrochen ist, sodass sich keine korrekten Widerstands-, Spannungs- oder Stromstärkeberechnungen mehr anstellen lassen! -

Bezüglich der Spannungsversorgung des belasteten Spannungsteilers gibt es zwei Möglichkeiten. Und zwar beim Einspeisungspunkt vor dem Strommessgerät 56 am Port „Pin A0“ mit der Spannung U_{Pin A0} = 5,078 V und nach dem Strommessgerät 56 am Port „Pin A1“ mit der Spannung U_{Pin A1} = 4,935 V.

Da die interne Spannungsversorgung des „Arduino UNO“ nur eine Spannung von U_{Pin A0} = U_{Pin 5V} < 4,971 V bereit stellt, verwenden wir nachfolgend eine externe Spannungsversorgung in Form eines sogenannten „Lithium-Ionen-Akkus“, auch „Powerbank“ genannt.

>> Eine Powerbank ist ein mobiler Zusatzakku insbesondere für Smartphones und Tablets, größere Exemplare versorgen auch Notebooks.^[1] Es ist ein mobiler Energiespeicher mit einem Schaltwandler, der eine konstante Ausgangsspannung, meist 5 Volt, bereitstellt.

Allgemeines

Die fortschreitende Miniaturisierung und die Entwicklung zu immer flacheren mobilen Endgeräten setzt der Kapazität der in die Geräte integrierbaren Akkus technische Grenzen. Um die Verwendungsdauer der Geräte zu verlängern, gibt es daher diese zusätzlichen, extern anschließbaren Speicher.

Technisches

Eine Powerbank ist gewöhnlich mit einer oder mehreren Lithium-Ionen-Akkuzellen ausgerüstet, daher ist die Mitnahme im Flugzeug aufgrund der Brandgefahr an Bedingungen geknüpft.^[1] Sie enthält einen Schaltregler zur Stabilisierung der Ausgangsspannung und Strombegrenzung sowie oft Leds zur Anzeige des Betriebs- bzw. Ladezustands. Die Stromabgabe erfolgt über einen oder mehrere USB-Anschlüsse (meist Typ A), geladen wird die Powerbank meist über einen Micro-USB-Anschluss. Die möglichen Lade- und Entladeströme sind nicht standardisiert und können von den USB-Spezifikationen abweichen. Daher ist nicht jede Powerbank für Apple-Geräte geeignet oder sie funktioniert nur mit einem proprietären Ladekabel dieses Herstellers. Manche Powerbanks weisen zwei oder mehr Ausgänge auf, von denen oft einer dediziert für iPhones oder iPads vorgesehen ist.

Powerbanks mit anderen Ausgängen, z.B. für FireWire oder Thunderbolt, wären technisch möglich, sind jedoch in der Praxis nicht anzutreffen.

Die Akkus in Powerbanks mit USB-Ausgang haben Kapazitäten (=elektrische Ladungsmenge) zwischen unter 1.000 mAh bis über 20.000 mAh. Die Angaben beziehen sich auf den verbauten Akku, nicht auf die entnehmbare elektrische Energie, denn die Akkuspannung von 3,7 Volt muss auf 5 Volt angehoben werden und der Wirkungsgrad des Schaltwandlers abgezogen werden. Zusätzlich sind die Angaben oft deutlich zu optimistisch. Es ergibt sich ein reales Energiespeichervermögen von ca. 3 Wh bis 70 Wh.^[2] (Zum Vergleich, ein Elektro-Leichtfahrzeug wie der Renault Twizy stellt mit seinen Zellen real nutzbare 6.100 Wh zur Verfügung.) Der maximale Strom kann zwischen 500 mA und über 3 A variieren.

Für Laptops werden aber entsprechend größere Geräte angeboten, die über Adapter Notebooks mit den dort üblichen Spannungen von z. B. 12 V oder 19 V versorgen.^[1] << (Quelle: Wikipedia)

Jetzt wissen wir, dass die interne Spannung der Powerbank mit den Lithium-Ionen-Akkus von 3,7 V mittels des internen Spannungswandlers auf 5 V angehoben wird. Dazu muss man wissen, dass Lithium-Ionen-Akkus über einen kleinen Innenwiderstand verfügen und demzufolge größere Stromstärken nach außen an die USB-Buchse abzugeben vermögen. Bei einer Powerbank mit der Kapazität von 10 000 mAh = 10 Ah entspricht das einer Stromstärke von bis zu I_Entlade = 2 A. Zum Vergleich: Die 12 V Starterbatterie eines Mittelklasse-PKWs verfügt z.B. über eine Kapazität von 44 Ah beim Benziner und beim Diesel sind es 66 Ah. Dabei beträgt der Anlasserstrom beim Starten des Motors bis zu 200 A.

>> Statischer Innenwiderstand

In jedem elektrischen Gerät läuft der Strom durch Kupferdrähte, die zum Innenwiderstand beitragen. In einem dynamischen Mikrofon kann er 200 Ω betragen, in einem Leistungstrafo aber nur 0,01 Ω. Bei Batterien läuft der Strom durch Leiter mit wesentlich schlechterer Leitfähigkeit als Kupfer, die zudem absinken kann, wenn die Batterie entladen wird. Präzise ausgedrückt, wird eine Batterie nicht „leer“, sondern der Innenwiderstand wird durch chemische Vorgänge so groß, dass der benötigte Strom nicht mehr entnommen werden kann.

Differentieller Innenwiderstand

Siehe auch: Differentieller Widerstand

Überwacht man die Ausgangsspannung elektronisch, kann diese recht gut konstant gehalten werden, wenn eine Regelung als Folge der Abweichung gegensteuert und den statischen Innenwiderstand schnell genug ändert. Dafür gibt es beispielsweise preiswerte Festspannungsregler. Der Innenwiderstand von Labornetzgeräten kann in extremen Fällen sogar schwach negative Werte erreichen, was bedeutet, dass die Ausgangsspannung mit steigender Belastung etwas ansteigt und den Spannungsverlust durch den ohmschen Widerstand längerer Verbindungsleitungen zur Last kompensiert. Ein übertriebener negativer Widerstand kann allerdings für unerwünschte Oszillationen sorgen.

Bei Labornetzgeräten ist der Innenwiderstand stromabhängig: Bis zu einem gewissen Maximalstrom ist er sehr klein, damit sich die abgegebene Spannung bei Belastung kaum ändert. Wird dieser überschritten, verändert eine interne Überwachungsschaltung den Innenwiderstand zu sehr großen Werten. Labor-Netzgeräte arbeiten dann als Konstantstromquelle, wobei bei sinkendem Außenwiderstand (bis zum Kurzschluss) die abgegebene Spannung immer kleiner wird, ohne das Netzgerät zu zerstören.

Dynamischer Innenwiderstand

Der Strombedarf ist selten konstant, insbesondere nicht bei elektronischen Schaltungen. In Computern kann sich der Strombedarf einzelner Integrierter Schaltkreise im Nanosekundentakt ändern. Weil das einer Frequenz im Gigahertzbereich entspricht, kann die Induktivität der Stromversorgungsleitungen nicht ignoriert werden, auch wenn sie nur wenige Zentimeter kurz sind. Der induktive Widerstand des Drahtes vergrößert den Innenwiderstand der Spannungsquelle mit steigender Frequenz ganz erheblich. Als Folge kann die Spannung am Bauelement selbst bei Stromänderungen beispielsweise zwischen 2 V und 10 V schwanken und den IC stören, möglicherweise sogar zerstören. Eine Regelung reagiert nicht schnell genug, deshalb werden als Gegenmittel induktionsarme Kondensatoren unmittelbar an den IC-Anschlüssen eingesetzt. Da auch Kondensatoren eine gewisse Eigeninduktivität besitzen und nicht im gesamten Frequenzbereich zwischen null und 5 GHz gleich gut filtern, schaltet man meist Elkos und keramische Kondensatoren mit möglichst verschiedenen Dielektrika parallel. << (Quelle: Wikipedia)

So, jetzt sind wir schon mittendrin in der Elektronik. Und das alles nur wegen der internen Spannungsversorgung U_Pin 3.3V bzw. U_{Pin 5V} des „Arduino UNO“.

Aber jetzt wissen wir immerhin, dass Labornetzgeräte einen stromabhängigen Innenwiderstand haben, der beim kleiner werdenden Lastwiderstand immer größer wird, sodass die am Lastwiderstand verfügbare Ausgangsspannung bis zum Kurzschluss immer kleiner wird.

Praktisch bedeutet dies, dass die Stromstärke durch den Lastwiderstand bis zum Kurzschluss konstant groß bleibt, während gleichzeitig die Ausgangsspannung abgesenkt wird, sodass sich die Ausgangsleistung am Lastwiderstand entsprechend verringert. Demzufolge verhält sich die Leistungselektronik bei größeren Stromstärken bis hin zum Kurzschluss wie eine Konstantstromquelle I₀.

>> Stromquelle mit NPN Transistor

Diese Seite zeigt die Grundschaltung für die Konstantstromquelle mit dem NPN Transistor

Von der Spannungsquelle zur Stromquelle...

Im Gegensatz zur Konstantspannungsquelle gibt die Konstantstromquelle immer denselben Strom ab. Und zwar unabhängig vom angeschlossenen [ Last- ] Widerstand. Ändert man bei einer Stromquelle den Lastwiderstand, ändert sich anstatt des Stroms die Spannung. Der einfachste Weg, eine Stromquelle mit konstantem Ausgangsstrom aufzubauen, ist die Kombination einer Spannungsquelle mit einer Stromstabilisierungsschaltung. Nach diesem Prinzip funktioniert auch die Stromquellenschaltung mit dem NPN Transistor. << (Quelle: Electronics Planet)

Obwohl wir noch nicht wissen, ob die interne Spannungversorgung U_3.3V bzw. U_5V des „Arduino UNO“ über eine interne Spannungsstabilisierung nebst Kurzschlussstrombegrenzung verfügt, dies aber vermuten, wissen wir dennoch, dass das „Sketch“-Programm „sketch_prog_12_11.ino“ bei der Verwendung des Summer 10 als Lastwiderstand R_Last beim Stromteiler ordnungsgemäß funktioniert und diesen richtig berechnet:

Summer 10	Widerstand 40 – 100 Ω
U_Gesamt =4,971 V	U_Gesamt =4,971 V
I_Mess = 193,46 mA	I_Mess = 215,78 mA
Widerstand R3 = 99,48 Ω	Widerstand R3 = 59,68 Ω
Spannung U_R3 = 2,15 V	Spannung U_R3 = 2,10 V
Siehe Bild „arduino_prog_12_31“	Siehe Bild „arduino_prog_12_34“

Wie man beim direkten Vergleich zwischen Summer 10 und Widerstand 40 sieht, scheint es zwischen der Stromstärke I_Mess = 193,46 mA und 215,78 mA einen Kipppunkt zu geben, bei dem plötzlich die elektronische Regelung bei der internen Spannungsversorgung U_{Pin 5V} einsetzt. Ob es sich dabei um eine Spannungs- oder eine Stromstabilisierung handelt, lässt sich dabei im Moment noch nicht sagen.

Fest steht aber, dass die zur Verfügung stehende Ausgangsleistung am Port „Pin 5V“ des „Arduino UNO“ gemäß Herstellerangabe auf 1 W bzw. 200 mA begrenzt ist:

P_{Pin 5V} = U_{Pin 5V} * I_{Pin 5V} = 5,0 V * 200 mA = 5,0 V * 0,2 A = 1 W

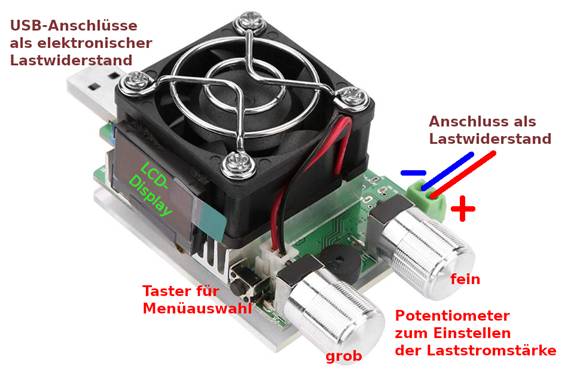
Demzufolge müsste das Abregeln der Ausgangsleistung bei einer Stromstärke I_{Pin 5V} > 200 mA beginnen! Um das überprüfen und feststellen zu können, bräuchten wir jetzt einen veränderlichen, einstellbaren elektronischen Lastwiderstand:

>> Eine elektronische Last ist ein Gerät oder eine Baugruppe, die als Ersatz für einen konventionellen (ohmschen) Lastwiderstand (Eingangswiderstand, Abschlusswiderstand, Außenwiderstand) eingesetzt wird. Im Schaltbild wird sie wie ein Widerstandsbauelement mit einem Rechteck dargestellt und meist als 'R' ohne Index bezeichnet, was für eine beliebige, nicht näher spezifizierte Last steht.

Als Gegenstück zur Stromquelle handelt es sich bei der elektronischen Last um eine Stromsenke. Während beim Belasten einer Stromquelle mit einem Festwiderstand immer nur ein bestimmter Laststrom bei einem bestimmten Widerstandswert eingestellt werden kann, ist die Besonderheit der elektronischen Last, dass der Laststrom in einem definierten Bereich einstellbar ist, er wird elektronisch geregelt.

Die von der elektronischen Last aufgenommene elektrische Leistung wird meistens in Wärme umgewandelt, zur Kühlung und Abführung der Abwärme werden Lüfter oder wassergekühlte Elemente verwendet. Auch eine Rückspeisung in das öffentliche Stromversorgungsnetz ist unter bestimmten Voraussetzungen möglich. Elektronische Lasten werden in verschiedensten Applikationen eingesetzt, vor allem zur Prüfung von Netz- und Steuergeräten, Batterien, Brennstoff- und Solarzellen, Generatoren. Wechselstromlasten werden zum Testen von Transformatoren, Unterbrechungsfreien Stromversorgungen (USVs) oder Bordnetzen verwendet.

Das Leistungs- und Ausstattungsspektrum dieser Geräte beginnt bei einfachsten Schaltkreisen, die im Wesentlichen aus einem Potentiometer zur Sollwerteinstellung und einem Lastkreis bestehen. Der Lastkreis wird beispielsweise aus einem Leistungs-MOSFET gebildet, welcher die aufgenommene Leistung in Wärme umsetzt. Bei weiterentwickelten elektronischen Lasten sind mehrere Betriebsarten vorhanden, meistens sind dieses Konstantstrom, -spannung, -leistung und -widerstand. Außerdem gehört heutzutage die Ansteuerbarkeit über analoge oder digitale Steuersignale von einem Steuergerät wie speicherprogrammierbare Steuerung oder PC zum Betriebsumfang. Damit können auch spezielle Lastformen wie kurzzeitige Impulslasten oder bestimmtes Einschaltverhalten mit unterschiedlichen Lastverläufen von Verbrauchern wiederholbar nachgebildet werden. Sollwerte und gemessene Größen wie Eingangsspannung und tatsächlicher Laststrom werden analog oder digital angezeigt bzw. über die Kontrollschnittstellen übermittelt. << (Quelle: Wikipedia)

Den nachfolgenden elektronischen Lastwiderstand und Batterietester namens „DROK DC 3-21V Load Battery Tester“ kann man beim Amazon für um die 25,- € bestellen:

(Zum Vergrößern bitte auf das Bild klicken!)

Die englischsprachige Bedienungsanleitung gibt es Internet.

Den elektronischen Lastwiderstand und Batterietester mit deutschsprachiger Artikelbeschreibung gibt es bei Amazon auch unter dem Namen „Akozon USB Load Tester Modul 35 Watt“ und „Walfront 35W einstellbare USB Konstante Strom“.

Wir setzen den elektronischen Lastwiderstand „DROK DC 3-21V“ als zusätzlichen Lastwiderstand ein und schalten diesen parallel zur internen Spannungsversorgung U_{Pin 5V} („+“ Pol) und U_{Pin GND} („-“ Pol).

Dabei lässt sich das „DROK DC 3-21V“-Gerät auch als Spannungsmessgerät einsetzen, sofern man beide Potentiometer „grob“ und „fein“ auf null, d.h. auf den linken Anschlag gestellt hat!

Wenn man mit dem Spannungsmessgerät „DROK DC 3-21V“ die interne Spannungsversorgung U_{Pin 5V} („+“ Pol) und U_{Pin GND} („-“ Pol) des „Arduino UNO“ im Leerlauf, d.h. ohne Belastung misst, wobei der Schiebeschalter 14 der Versuchsanordnung nach links auf „AUS“ gestellt ist, dann stellt man fest, dass die Versorgungsspannung U_{Pin 5V} ständig im Sekundentakt(!) zwischen 4,89 V, 4,91 V, 4,93 V, 4,95 V und 4,96 V usw. schwankt, wobei der Mittelwert bei

Auch wenn man den Schiebeschalter 14 der Versuchsanordnung nach rechts auf „EIN“ stellt und die Versorgungsspannung U_{Pin A1} unter Last misst, stellt man fest, dass diese ebenfalls ständig im Sekundentakt(!) zwischen 4,34 V, 4,35 V, 4,37 V und 4,39 V usw. schwankt!

Da der „Arduino UNO“ über das USB-Kabel vom Desktop-PC mit Strom und (Programm-) Daten versorgt wird, überprüfen wir mit dem Spannungsmessgerät „DROK DC 3-21V“ als nächstes die USB-Spannungsversorgung, indem wir den Spannungsmesser mittels USB-Kabel mit der USB-Buchse des PCs verbinden.

Und siehe da, da staunt der Fachmann und es wundert sich der Laie, schwankt die USB-Spannungsversorgung des Desktop-PCs im Leerlauf, d.h. ohne Last, ebenfalls, aber nur unwesentlich.

Während also die USB-Spannung am Desktop-PC im Leerlauf U_{USB PC, Leer} = 5,07 V beträgt, sinkt sie bei Belastung, d.h. beim Hinzuschalten des „Arduino UNO“ nebst der Versuchsanordnung mit den beiden eingeschalteten Glühlampen 18 und dem zugeschalteten Lastwiderstand R_Last = 100 Ω ab auf U_{USB PC, Last} = 4,94 V bei einem Laststrom von I_{USB PC, Last} = 0,22 A, was einem Gesamtwiderstand der Schaltung von R_ges = 22,45 Ω entspricht. Dabei schwankt die USB-Spannung am Desktop-PC zwischen 4,94 V und 4,95 V nur unwesentlich.

Auch wenn die Spannungsschwankungen der USB-Spannung am Desktop-PC nur sehr gering sind, werden diese trotzdem an den „Arduino UNO“ weitergegeben, muss man damit rechnen, dass sich diese auch auf den Einplatinenrechner auswirken. Zwar nicht digital, aber analog auf die interne Versorgungsspannung U_{Pin 5V}, sodass sich die vormals geringen Spannungsschwankungen der USB-Spannung jederzeit auch noch verstärken können!

Und tatsächlich schwankt die Versorgungsspannung U_{Pin A0} unter Last weiterhin im Sekundentakt(!) zwischen 4,46 V, 4,47 V, 4,49 V und 4,51 V usw., was einer Differenz von 50 mV entspricht.

Dazu muss man wissen und sollte man damit rechnen, dass >> der Strombedarf selten konstant (ist), insbesondere nicht bei elektronischen Schaltungen. In Computern kann sich der Strombedarf einzelner Integrierter Schaltkreise im Nanosekundentakt ändern. Weil das einer Frequenz im Gigahertzbereich entspricht, kann die Induktivität der Stromversorgungsleitungen nicht ignoriert werden, auch wenn sie nur wenige Zentimeter kurz sind. Der induktive Widerstand des Drahtes vergrößert den Innenwiderstand der Spannungsquelle mit steigender Frequenz ganz erheblich. Als Folge kann die Spannung am Bauelement selbst bei Stromänderungen beispielsweise zwischen 2 V und 10 V schwanken und den IC stören, möglicherweise sogar zerstören. Eine Regelung reagiert nicht schnell genug, deshalb werden als Gegenmittel induktionsarme Kondensatoren unmittelbar an den IC-Anschlüssen eingesetzt. << (Quelle: Wikipedia)

Auch wenn wir es wie im vorliegenden Fall beim „Arduino UNO“ nicht mit einem Personal Computer zu haben, dessen Intel- oder AMD-Prozessor mit 5 GHz (= Gigahertz) getaktet ist und dessen Stromversorgungsleitungen aufgrund der 5 GHz Prozessor-Taktung hochfrequente Störstrahlungen und Störspannungen an anderen ICs induzieren, so bleibt trotzdem festzuhalten, dass man bei elektronischen Schaltungen, wie die vom „Arduino UNO“, jederzeit damit rechnen muss, dass der Strombedarf selten konstant ist und diesbezügliche analoge Spannungs- oder Stromregelungen oftmals nicht schnell genug sind, um etwaige Schwankungen in der Stromversorgung auszugleichen.

Deshalb ist man gut beraten, wenn man die Stromversorgung zu den Experimentalversuchen von der des „Arduino UNO“ trennt und durch eine zweite und unabhängige Spannungsversorgung wie z.B. mit der Powerbank realisiert!

Selbstverständlich könnte man anstelle der 5-Volt-Powerbank auch ein entsprechendes 5-Volt-USB-Steckernetzteil verwenden, wobei die meisten preiswerten Steckernetzteile nur über eine maximale Stromstärke von I_{USB max} < 1 A verfügen, was im vorliegenden Fall beim Betrieb der beiden Glühlampen 18 eventuell dazu führen könnte, dass die Ausgangsspannung auf deutlich weniger als U_{USB max} = 5,0 V zusammenbricht. Deshalb sollte man bei der Anschaffung eines 5-Volt-USB-Steckernetzteils etwas mehr Geld in die Hand nehmen und sich ein solches, das eine maximale Stromstärke von bis zu I_{USB max} = 2 A bereit stellt, zulegen.

Diesbezüglich gilt es noch zu beachten, dass sich eine 5-Volt-Powerbank hinsichtlich der Stromversorgung potentialfrei betreiben lässt, während man das 5-Volt-USB-Steckernetzteil stets auf der gleichen Masse („┴“) anschließen muss wie den „Arduino UNO“ mit seiner Masse („GND“).

Langer Rede kurzer Sinn, wir nehmen die 5-Volt-Powerbank und setzen diese als Spannungsquelle für die Stromversorgung des belasteten Spannungsteilers ein. Wie bei jeder anderen Spannungsquelle auch interessiert uns als Elektrotechniker/Elektroniker dabei die sogenannten Leerlaufspannung.

>> Die Leerlaufspannung (englisch open-circuit voltage, OCV) ist in der Elektrotechnik die an den Klemmen einer offenen Spannungsquelle gemessene elektrische Spannung. Das heißt, die Leerlaufspannung ist die Spannung auf der Ausgangsseite, wenn kein Verbraucher angeschlossen ist. Es fließt kein elektrischer Strom, wodurch keine Spannung über den Innenwiderstand der Spannungsquelle abfällt.

Die Leerlaufspannung ist genau dann gleich der Quellenspannung U_Q, wenn innerhalb der Spannungsquelle, wie bei einem Generator oder einer galvanischen Zelle, keine parallelen Strompfade existieren, die zum Beispiel Leckströme verursachen, welche die Leerlaufspannung verringern. Fließt ein nicht mehr zu vernachlässigender Strom und kommt es zu einem Spannungsabfall am Innenwiderstand der Spannungsquelle, so stellt sich an den Klemmen die sogenannte Klemmenspannung ein, welche vom Betrag her immer kleiner als die Leerlaufspannung ist. (…)

Zur Messung der Leerlaufspannung ist ein Spannungsmessgerät erforderlich, das einen wesentlich höheren Innenwiderstand als die Quelle hat. Damit wird gewährleistet, dass die Belastung der Spannungsquelle durch das Messgerät und die daraus resultierende Rückwirkungsabweichung vernachlässigbar klein ist. Der Innenwiderstand marktüblicher Digitalmultimeter liegt im Bereich einiger Megaohm, so dass diese Bedingung bei vielen Spannungsquellen gegeben ist. << (Quelle: Wikipedia)

Soweit also zur Theorie der Spannungsmessung einer Leerlaufspannung mit U_leer = I_leer * R_i. Bei der Messung der Leerlaufspannung mit einem Digitalvoltmeter gibt es aber wider Erwarten das Problem, dass sich diese nicht so ohne Weiteres vornehmen lässt.

Der Grund dafür ist der in der 5-Volt-Powerbank verbaute DC/DC-Wandler, der die interne Spannung von 3,7 V der verbauten Lithium-Ionen-Akkus auf die externe Klemmenspannung von 5 V anheben muss, dies aber nur tut, wenn ein entsprechender Lastwiderstand R_Last als (Strom-) Verbraucher angeschlossen wird! Das Digitalvoltmeter ist aber am Messeingang so hochohmig (R_Mess > 10 MΩ = 10 * 10⁶ Ω → 10 * 10^-6 A = 10 µA), dass bei der Messung der Leerlaufspannung der winzig kleine Messstrom den DC/DC-Wandler wider Erwarten nicht einzuschalten vermag!

Um aber trotzdem eine Messung der Ausgangsspannung der 5-Volt-Powerbank vornehmen zu können, verwenden wir deshalb den 100-Ohm-Lastwiderstand R_Last = 100,8 Ω (mit dem Vielfachmessgerät gemessen!), um die zum „Messwiderstand“ zugehörige Spannung U_Last = 5,06 V wie folgt zu messen und zu berechnen:

I_Mess = I_Last = U_Mess / R_Mess = U_Mess / R_Last = 5,06 V / 100,8 Ω = 0,0502 A = 50,2 mA

Diesbezüglich stellt sich gleich die Frage, wie groß der Messwiderstand wäre, wenn der Messstrom gerade einmal 50,2 µA groß wäre:

R_Mess = U_Mess / I_Mess = 5,06 V / 50,2 µA = 5,06 V / 50,2 * 10^-6 A = 0,1007968 * 10⁶ Ω = 100,8 * 10³ Ω = 100,8 kΩ

Aber auch, wenn sich der Messwiderstand R_Mess = 100,8 kΩ theoretisch berechnen lässt, heißt das praktisch nicht automatisch, dass die Messspannung U_Mess in Wirklichkeit nicht doch größer als 5,06 V wäre!

Interessant wird es gleich, wenn wir den belasteten Spannungsteiler in Betrieb nehmen und an die Spannungsversorgung mit der 5-Volt-Powerbank anschließen und dabei erstaunt feststellen, dass die Leerlaufspannung der 5-Volt-Powerbank wegen der hohen Belastung in Form des Laststroms I_Last = 179,0 mA auf nur noch U_Last = 4,80 V absinkt.

R = ∆U / ∆I

= ( U₂ - U₁ ) / ( I₂ – I₁ ) = ( U_{100 Ω} - U_Last ) / ( I_{100 Ω} – I_Last )

= ( 5,06 V - 4,80 V ) / ( 50,2 mA - 179,0 mA )

= ( 0,26 V ) / ( -128,8 mA ) = - 2,02 Ω

Immer dann, wenn der Differenzenquotient ∆U / ∆I im Ergebnis negativ wird, dann handelt es sich dem berechneten Widerstand R = ∆U / ∆I nicht um einen ohmschen Verbraucher, sondern um einen (Gleichstrom-) Generator, der an seinen Anschlussklemmen einen Gleichstrom liefert. Im vorliegenden Fall handelt es sich bei dem Gleichstromgenerator um die 5-Volt-Powerbank als Energielieferant.

Wenn man die 5-Volt-Powerbank als Energielieferant an die elektronische Last bzw. den elektronischen Lastwiderstand anschließt (siehe Bild), dann lassen sich z.B. die beiden Messwerte ( U₂ = 4,81 V, I₂ = 10 mA ) und ( U₁ = 4,79 V, I₁ = 180 mA ) mittels der Drehregler aufnehmen, d.h. als elektronische Last einstellen, sodass für den Differenzenquotient ∆U / ∆I folgt:

R = ∆U / ∆I

= ( U₂ - U₁ ) / ( I₂ – I₁ )

= ( 4,81 V - 4,79 V ) / ( 10 mA - 180,0 mA )

= ( 0,02 V ) / ( -170,0 mA ) = - 0,11765 Ω

Wenn man den Differenzenquotient ∆U / ∆I bildet, dann muss es sich bei den beiden Messungen ∆U / ∆I = ( U₂ - U₁ ) / ( I₂ - I₁ ) stets um ein und denselben (Last-) Widerstand handeln. Anderen falls stellt sich ein falsches Ergebnis ein!

Was uns bei der 5-Volt-Powerbank als Energielieferant wirklich interessiert, ist aber nicht so sehr der differentielle Widerstand R = ∆U / ∆I, sondern der Innenwiderstand R_i:

R_i = U_Leer / I_Kurz →

I_Kurz = U_Leer / R_i

= 5,06 V / 2,02 Ω = 2,505 A

Auch wenn sich die Leerlaufspannung U_Leer der 5-Volt-Powerbank nicht exakt bestimmen lässt, weil der DC/DC-Wandler der Powerbank bei einer hochohmigen Spannungsmessung (R_{i, Multimeter} = 10 MΩ pro 1 V, d.h. 10 µA Stromaufnahme bei 1 V Vollausschlag) nicht anspringt, wissen wir jetzt trotzdem, dass der Innenwiderstand R_i der Powerbank - genau genommen der des DC/DC-Wandlers - sehr klein ist und rechnerisch/theoretisch einen Kurzschlussstrom von I_Kurz= U_Leer / R_i ≈ 2,5 A zu liefern vermag.

Trotzdem ist man natürlich gut beraten, bei der 5-Volt-Powerbank keinen Kurzschluss zu provozieren oder durchzuführen, weil Lithium-Ionen-Akkus im Falle eines Kurzschlusses im Inneren sehr hohe Temperaturen von einigen Tausend Grad Celsius entwickeln, die dazu führen, dass sich auch Nachbarzellen im Akku entzünden und Feuer fangen, sodass sich der Akku auf herkömmliche Weise nicht mehr löschen lässt! -

Darauf, dass Lithium-Ionen-Akkus intern über eine elektronische Überstromsicherung verfügen, die den Akku im Falle des Kurzschlusses abschalten, sollte man sich nicht unbedingt verlassen!

Wer auf Nummer sicher gehen will, müsste den Lithium-Ionen-Akkus öffnen und nachschauen, ob vor den Ausgangsanschlüssen eine entsprechende Leistungselektronik mittels MOS-FET-Transistoren verbaut ist, die die Ausgangsspannung im Falle einer Überlastung herunter regelt oder ganz abschaltet. -

Im Zusammenhang mit der 5-Volt-Powerbank sei daran erinnert, dass diese die in ihr gespeicherte Energie ein- und ausgangsseitig über USB-Buchsen bezieht, d.h. über einen USB-2.0-Micro-B-Stecker-Kabel oder USB-3.1-Typ-C-Stecker-Kabel aufgeladen und über bis zwei USB-1.0-/2.0-Typ-A-Stecker-Kabel entladen wird:

(Zum Vergrößern bitte auf das Bild klicken!)

(Zum Vergrößern bitte auf das Bild klicken!)

Interessant ist noch, dass sich die 5-Volt-Powerbank über die „USB 3.1-Typ-C“-Buchse eingangsseitig mit einer Stromstärke von bis zu 3 A aufladen lässt,

(Zum Vergrößern bitte auf das Bild klicken!)

während sie sich ausgangsseitig mittels der beiden „USB 2.0“-Buchsen mit einer Stromstärke von bis zu 2 x 2 A entladen lässt.

Gemäß der Technischen Daten der Bedienungsanleitung des Herstellers „GRIXX“ beträgt aber die Gesamtleistung nur 2,1 A (max), sodass sich jede einzelne der beiden „USB 2.0“-Buchsen mit einer Stromstärke von bis zu 2,1 A entladen lässt, während alle beiden „USB 2.0“-Buchsen zusammen insgesamt ebenfalls nur eine Stromstärke von bis zu 2,1 A liefern. -

Den unbelasteten Spannungsteiler grafisch darstellen und berechnen

Wie sich die Kennlinie eines linearen, ohmschen Widerstandes R als Funktion I = f(U) = 1/R * U darstellen und berechnen lässt, wissen wir bereits (siehe linkes Diagramm):

(Zum Vergrößern bitte jeweils auf das Bild klicken!)

Wenn man den linearen, ohmschen Widerstand R auf 2R verdoppelt, d.h. um den Faktor 2 vergrößert, dann halbiert sich die Stromstärke von I = 0,5 A auf ½ I = 0,25 A (siehe rechtes Diagramm).

Wenn man den linearen, ohmschen Widerstand R auf 1/2 R halbiert, d.h. um den Faktor 1/2 verkleinert, dann verdoppelt sich die Stromstärke von I = 0,5 A auf 2 I = 1,0 A (siehe rechtes Diagramm).

Im nachfolgenden Diagramm verwenden wir die beiden, in Reihe geschalteten Widerstände R und ½ R des unbelasteten Spannungsteilers (siehe rechtes Bild oben).

Um den sogenannten Arbeitspunkt des unbelasteten Spannungsteilers grafisch zu ermitteln, wird das Koordinatensystem des Widerstandes ½ R wie folgt gespiegelt, sodass sich beide Widerstandsgeraden im Arbeitspunkt schneiden:

(Zum Vergrößern bitte auf das Bild klicken!)

Selbstverständlich lässt sich der Arbeitspunkt auch rechnerisch ermitteln. Doch dazu ist es erforderlich, dass man zuvor die beiden Widerstände R und ½ R mittels des Steigungsdreiecks wie folgt berechnet (siehe rechtes Bild oben):

R = ∆U / ∆I

= ( 1,0 V - 0,5 V ) / ( 1 mA - 0,5 mA ) = 0,5 V / 0,5 mA = 1 KΩ = 1000 Ω

½R = ∆U / ∆I

= ( 0,5 V - 0,25 V ) / ( 1 mA - 0,5 mA ) = 0,25 V / 0,5 mA = 0,5 KΩ = 500 Ω

Mit der Geradengleichung I_R = 1 / R * U_R und R = 1000 Ω folgt:

I_R = 1 / R * U_R = U_R / R

= U_R / 1000 Ω → Geradengleichung 1

Mit der Geradengleichung I_1/2R = 1 / ½R * U_1/2R und ½R = 500 Ω folgt:

I_1/2R = 1 / ½R * U_1/2R = U_1/2R / ½R

= U_1/2R / 500 Ω

= 2 U_1/2R / 1000 Ω → Geradengleichung 2

Im gemeinsamen Schnittpunkt I_A müssen beide Stromstärken I_R und I_1/2R gleich groß sein:

I_R = U_R / R = U_R / 1000 Ω

= ( 1,25 + 0,125 * 2/3 ) V / 1000 Ω = ( 1,25 + 0,08333 ) V / 1000 Ω

= ( 1,33333 ) V / 1000 V/A = 1,3333 mA ≈ 1,33 mA

I_1/2R = U_1/2R / ½R = U_1/2R / 500 Ω

= ( 0,5 + 0,125 + 0,125 * 1/3 ) V / 500 Ω = ( 0,625 + 0,0417 ) V / 500 Ω

= 2 * ( 0,6667 ) V / 1000 V/A = 1,3334 mA ≈ 1,33 mA

Mathematische Lösung:

Geradengleichung 1 = Geradengleichung 2

U_R / 1000 Ω = 2 U_1/2R / 1000 Ω

U_R = 2 U_1/2R = 2 * 0,6667 V = 1,3334 V ≈ 1,33 V

Einsetzen in die Geradengleichung 1 liefert:

I_R = 1 / R * U_R = U_R / R

= U_R / 1000 Ω = 1,33 V * 1000 Ω = 1,33 V * 1000 V/A = 1,33 mA

→ Schnittpunkt S = Arbeitspunkt A = ( 1,33 V, 1,33 mA )

Den belasteten Spannungsteiler grafisch darstellen und berechnen

Der belastete Spannungsteiler unterscheidet sich vom unbelasteten einfach dadurch, dass parallel zum Spannungsteilerwiderstand R₂ (= Glühlampe 18) noch der Lastwiderstand R_Last = R₃ = 100,8 Ω hinzugeschaltet wird (siehe Bild):

(Bild vergrößern: auf Bild klicken! Belasteter Spannungsteiler: Elektronik-Kompentium)

Wie man im obenstehenden Bild des belasteten Spannungsteilers sieht, sind der Spannungsteilerwiderstand R₂ (= Glühlampe 18) und der Lastwiderstand R_Last = R₃ = 100,8 Ω parallel geschaltet, sodass sich der Ersatzwiderstand wie folgt berechnet:

Parallelschaltung zweier Widerstände

R_ers = R₂ // R_Last = R₂ // R₃

1/R_ers = 1/R₂ + 1/R₃

R_ers = 1 / ( 1/R₂ + 1/R₃ )

Reihenschaltung zweier Widerständen inkl. Ersatzwiderstand

R_ges = R_pot = R₁ + R_ers = R₁ + 1 / ( 1/R₂ + 1/R₃ ) →

R_pot = R₁ + 1 / ( 1/R₂ + 1/R₃ )

Spannungsteilerformel

U_ers = U_R2//R3 = U_2L

U_2L / U_ges = U_a / U_e

U_a / U_e = R₂ // R₃ / ( R₁ + R₂ // R₃ )

= R₂ * R₃ / ( R₂ + R₃ ) / ( R₁ + R₂ * R₃ / ( R₂ + R₃ ) ) → Im Nenner den Hauptnenner bilden →

= R₂ * R₃ / ( R₂ + R₃ ) / [ ( R₁ * ( R₂ + R₃ ) + R₂ * R₃ ) / ( R₂ + R₃ ) ]

= R₂ * R₃ / ( R₂ + R₃ ) * 1 / [ ( R₁ * ( R₂ + R₃ ) + R₂ * R₃ ) / ( R₂ + R₃ ) ] → ( R₂ + R₃ ) in den Zähler bringen!

= R₂ * R₃ / ( R₂ + R₃ ) * ( R₂ + R₃ ) / [ ( R₁ * ( R₂ + R₃ ) + R₂ * R₃ ) ]

→ Nenner / ( R₂ + R₃ ) gegen Zähler * ( R₂ + R₃ ) / kürzen!

= R₂ * R₃ / ( R₂ + R₃ ) * ( R₂ + R₃ ) / [ ( R₁ * ( R₂ + R₃ ) + R₂ * R₃ ) ]

= R₂ * R₃ / [ ( R₁ * ( R₂ + R₃ ) + R₂ * R₃ ) ] → Im Nenner R₁ = R_pot - R₂ einsetzen!

→ R_pot bezeichnet den Widerstand des Potentiomenters mit R_pot = R₁ + R₂

→ Der Lastwiderstand R_Last = R₃ spielt beim Potentiomenter-Widerstand R_pot keine Rolle!

= R₂ * R₃ / [ ( R_pot - R₂ ) * ( R₂ + R₃ ) + R₂ * R₃ ] → Nenner, d.h. runde Klammern ( ) ausmultiplizieren!

= R₂ * R₃ / [ R_pot * R₂ + R_pot * R₃ - R₂² - R₂ * R₃ + R₂ * R₃ ]

= R₂ * R₃ / [ R_pot * R₂ + R_pot * R₃ - R₂² - R₂ * R₃ + R₂ * R₃ ]

= R₂ * R₃ / [ R_pot * R₂ + R_pot * R₃ - R₂² ]

= 1 / [ ( R_pot * R₂ + R_pot * R₃ - R₂² ) ./. R₂ * R₃ ]

= 1 / [ ( R_pot * ( R₂ + R₃ ) - R₂² ) ./. R₂ * R₃ ]

= 1 / [ ( R_pot / R₃ + R_pot / R₂ ) - R₂ / R₃ ]

= 1 / [ ( R_pot / R₂ + R_pot / R₃ ) - ( R₂ / R₃ ) ]

= 1 / [ R_pot / R₂ + R_pot / R₃ - R₂ / R₃ ]

U_a = 1 / [ R_pot / R₂ + ( R_pot - R₂ ) / R₃ ] * U_e → Geradengleichung U_a = f( U_e )

Wenn man den Potentiometerwiderstand R_pot durch den Einheitswert R_pot = 1 ersetzt, folgt mathematisch:

f(x) = 1 / [ 1 / R₂ + ( 1 - R₂ ) / R₃ ]

Wenn man den Potentiometerwiderstand R₂ durch die Unbekannte x und den Lastwiderstand R_Last = R₃ durch den Parameter a ersetzt, dann folgt abschließend:

f(x) = 1 / ( 1 / x + ( 1 - x ) / a ) →

Mathematisch lautet die Funktion y = f(x) = U_a mit x = R₂ und a = R₃ wie folgt:

Im Zusammenhang mit der obenstehenden Funktionsgleichung y = f(x) = 1 / ( 1 / x + ( 1 - x ) / a ) stellt sich die Frage, wie sich diese grafisch darstellen lässt bzw. grafisch Stück für Stück zusammensetzt!

Die nachfolgenden Grafiken bzw. Funktionsgraphen wurden mit dem kostenlosen Programm „Microsoft Mathematics“ in der „64 Bit“-Version 4.0 für Windows 7,8 und 10 erstellt. Das Programm gibt es auf der Webseite weiter unten auch in der „32 Bit“-Version. -

Interessant und sehr zu empfehlen ist auch die Webseite „Microsoft Math Solver“. Den mathematischen (Problem-) Löser, engl. „solver“, gibt es auch als Mobile App für das Smartphone. -

Wenn man die Funktion einer Geraden mit y = f(x) = x (siehe linkes Bild unten) invertiert, dann folgt für die Funktion y’ = f(x)’ = x^-1 = 1 / x (siehe rechtes Bild unten):

(Zum Vergrößern bitte jeweils auf das Bild klicken!)

Die Funktion y = f(x) = 1 / x nennt man gleichseitige Hyperbel (siehe rechtes Bild oben).

Wenn man die Funktion y = f(x) = x (siehe linkes Bild oben) direkt an der y-Achse spiegeln will, dann muss man die Funktionsgleichung nur mit (-1) multiplizieren → y = f(x) = - x (siehe linkes Bild unten):

(Zum Vergrößern bitte jeweils auf das Bild klicken!)

Die Funktion y = f(x) = - x lässt sich natürlich auch invertieren, sodass eine um 90 Grad gegen den Uhrzeigersinn gedrehte, invertierte Hyperbel mit der Funktion y = f(x) = - 1 / x entsteht (siehe rechtes Bild oben).

Die an der y-Achse gespiegelte Funktion y = f(x) = - x lässt sich problemlos um +1 nach rechts entlang der x-Achse verschieben, sodass die Funktion jetzt y = f(x) = - x + 1 lautet. Damit das Ganze dann auch richtig mathematisch professionell aussieht (und sich nicht mehr auf Anhieb verstehen lässt), lassen sich die beiden Summanden auch entsprechend vertauschen y = f(x) = - x +1 = 1 - x. An der Stelle x = 1 entsteht dann eine Nullstelle mit

y(1) = f(x=1) = f(1) = 0 (siehe linkes Bild unten):

(Zum Vergrößern bitte jeweils auf das Bild klicken!)

Die neue, um +1 nach rechts entlang der x-Achse verschobene Geradengleichung y = f(x) = -x + 1 = 1 - x lässt sich wie gehabt ebenfalls invertieren, sodass sich die neue Funktion jetzt wie folgt darstellt: y = f(x) = ( 1 - x )^-1 = 1 / ( 1 - x ) (siehe rechtes Bild oben).

Als nächstes lassen sich die beiden Funktionen y = f(x) = 1 / x und y = f(x) = 1 - x wie folgt addieren:

y = f(x) = 1 / x

+

y = f(x) = -x + 1 = 1 - x

=

y = f(x) = 1 / x + ( 1 - x )

(Zum Vergrößern bitte jeweils auf das Bild klicken!)

Die logarithmische Kennlinie des linearen Potentiometers stellt sich ein, wenn man die Funktion y = f(x) = 1 / x + ( 1 - x ) abschließend wie folgt invertiert mit y = f(x) = 1 / [ 1 / x + ( 1 - x ) ] :

(Zum Vergrößern bitte jeweils auf das Bild klicken!)

Von den vier Graphen in allen Quadranten des Koordinatensystems (siehe linkes Bild oben) interessiert uns bezüglich des Potentiometers nur der Graph im ersten Quadranten des Koordinatensystems (siehe rechtes Bild oben).

Da es beim Potentiometer elektrisch betrachtet auf den Stromteiler R2 // R3 ankommt, bringen wir den Parameter a noch wie folgt in die bisherige Formel ein:

f(x) = 1 / [ 1 / x + ( 1 - x ) ]

= 1 / [ 1 / x + ( 1 - x ) / 1 ]

= 1 / [ 1 / x + ( 1 - x ) / a ] → mit a aus dem Intervall [ 1 < a < 10 ]:

Nachfolgend sieht man anhand der Diagramme nebst Steigungsdreiecken wie sich Veränderungen des Parameters a auf den Kurvenverlauf und das elektrische Verhalten des Potentiometers auswirken:

f(x) = 1 / [ 1 / x + ( 1 - x ) / 1 ]

f(x) = 1 / [ 1 / x + ( 1 - x ) / 3 ]

f(x) = 1 / [ 1 / x + ( 1 - x ) / 10 ]

(Zum Vergrößern bitte jeweils auf das Bild klicken!)

Wenn man das links obenstehende Diagramm betrachtet, dann stellt man fest, dass der Graph der Funktion 1 / [ 1 / x + ( 1 - x ) / 1 ] schon bei einer kleinen x-Auslenkung von x = 1,5 sehr steil nach oben verläuft. Praktisch bedeutet dies, dass der Verstellwiderstand R₂ bereits bei einem sehr kleinen Widerstandswert von R₂ = 1,5 kΩ eine sehr große Ausgangsspannung U_a = 7,5 V zur Folge hat. Demzufolge reagiert das Potentiometer sehr empfindlich auf kleinste Änderungen ∆x = ∆R₂ und ∆y = ∆U_a wobei der eigentliche Regelbereich dementsprechend sehr klein und schmal ausfällt. Für den Anwender, der am Potentiometer eine bestimmte Ausgangsspannung U_a einstellen soll, wird es dann wegen des sehr kleinen Regelbereichs richtig stressig, diesen mit viel Fingerspitzengefühl einstellen zu müssen!

Wenn man das mittlere obenstehende Diagramm betrachtet, dann stellt man fest, dass der Graph der Funktion 1 / [ 1 / x + ( 1 - x ) / 3 ] erst nach einer größeren x-Auslenkung von x = 3 steil nach oben verläuft. Praktisch bedeutet dies, dass der Verstellwiderstand R₂ erst bei einem größeren Widerstandswert von R₂ = 2,12 kΩ eine größere Ausgangsspannung U_a = 9,188 V zur Folge hat. Demzufolge reagiert das Potentiometer weniger empfindlich auf kleinste Änderungen ∆x = ∆R₂ und ∆y = ∆U_a wobei der eigentliche Regelbereich dementsprechend größer und breiter ausfällt. Für den Anwender, der am Potentiometer eine bestimmte Ausgangsspannung U_a einstellen soll, wird es dann wegen des größeren Regelbereichs weniger stressig, diesen mit viel Fingerspitzengefühl einstellen zu müssen!

Wenn man das rechts obenstehende Diagramm betrachtet, dann stellt man fest, dass der Graph der Funktion 1 / [ 1 / x + ( 1 - x ) / 10 ] erst nach einer sehr großen x-Auslenkung von x = 10 steil nach oben verläuft. Praktisch bedeutet dies, dass der Verstellwiderstand R₂ erst bei einem größeren Widerstandswert von R₂ = 3,25 kΩ eine größere Ausgangsspannung U_a = 12,2 V zur Folge hat. Demzufolge reagiert das Potentiometer unempfindlich auf kleinste Änderungen ∆x = ∆R₂ und ∆y = ∆U_a wobei der eigentliche Regelbereich dementsprechend doppelt so groß und breit ausfällt. Für den Anwender, der am Potentiometer eine bestimmte Ausgangsspannung U_a einstellen soll, wird es dann wegen des größeren Regelbereichs zum Kinderspiel, diesen auch als Grobmotoriker einstellen zu müssen!

Auf dem Webportal „Informations- und Kommunikationstechnik“ mit dem Elektroniktutor gibt es den

· Menüpunkt „R, L, C-Schaltungen an Gleichspannung“ mit dem

· Kapitel „Ohmscher Spannungsteiler“ und dem

· Abschnitt „Lineares Poti mit logarithmischer Kennlinie“.

Dort wird anhand der nachfolgenden Grafik anschaulich dargestellt, wie sich der Parameter a = R₃ auf die Charakteristik, d.h. das Regelverhalten des Potentiometerwiderstandes R₂ mit U_a = f(R₂) auswirkt:

(Bild vergrößern: auf Bild klicken! Belasteter Spannungsteiler: Elektroniktutor)

In der obenstehenden Grafik finden sich drei Graphen zur Funktion

· y = f(x) = 1 / [ 1/x + ( 1-x ) / a ] = 1 / [ 1/x - ( x + 1 ) / a ] mit a aus dem Intervall [ 3 / 0,2 / 0,1 ] bzw.

· U_a = f(R₂) = 1 / R_ges * U_e mit

· R_ges = [ R_pot / R₂ + ( R_pot - R₂ ) / R₃ ]

R_ges = [ R_pot * ( 1 / R₂ + 1 / R₃ ) - R₂ / R₃ ] → R_ers = R₂ // R₃ → 1 / R_ers = 1 / R₂ + 1 / R₃

Dass sich die beiden parallel geschalteten Widerstände R₂ und R₃ gegenseitig beeinflussen und damit die Steilheit bzw. Empfindlichkeit des Regelungsverhaltens (nicht Steuerung) beeinflussen, dürfte unbestritten sein.

Demzufolge verhält es sich bei der grünen Kennlinie so, dass der Lastwiderstand R_Last = R₃ = 30 kΩ gegenüber dem Potentiometerwiderstand R₂ = 10 kΩ absolut dominierend ist und den sogenannten Querstrom des belasteten Spannungsteilers festlegt. Und zwar mit der Folge, dass sich nur ein ganz kleiner Regelbereich mit a = 3 am Potentiometer selbst einstellt.

Bei der roten Kennlinie verhält es sich so, dass der Lastwiderstand R_Last = R₃ = 2 kΩ gegenüber dem Potentiometerwiderstand R₂ = 10 kΩ immer noch dominierend ist und den sogenannten Querstrom des belasteten Spannungsteilers festlegt. Und zwar mit der Folge, dass sich nun ein etwas größerer Regelbereich mit a = 0,2 am Potentiometer selbst einstellt.

Bei der blauen Kennlinie verhält es sich so, dass der Lastwiderstand R_Last = R₃ = 1 kΩ gegenüber dem Potentiometerwiderstand R₂ = 10 kΩ nicht mehr dominierend ist und der Querstrom des belasteten Spannungsteilers jetzt durch den Potentiometerwiderstand R₂ = 10 kΩ bestimmt wird. Und zwar so, dass sich nun ein großer Regelbereich mit a = 0,1 am Potentiometer einstellt. Demzufolge verhält sich das Potentiometer beim Aufdrehen desselben wegen der verringerten Empfindlichkeit (= größeres Steigungsdreieck) etwas träge und behäbig, sodass sich die gewünschte Ausgangsspannung U_a sehr gut und bequem einstellen lässt. Dabei beträgt der Querstrom des belasteten Spannungsteilers durch den Potentiometerwiderstand R₂ = 10 kΩ exakt das Dreifache des Laststroms I_Last = I₃.

Bezüglich des Querstroms beim belasteten Spannungsteiler sei daran erinnert, dass sich immer dann eine halbwegs stabile Ausgangsspannung U_a einstellt, wenn der Querstrom das Vier- bis Zehnfache (a = 4 … 10) des Laststroms I_Last = I₃ beträgt.

Das obenstehende Diagramm beschreibt mit der mathematischen Funktion y = f(x) = 1 / [ 1 / x + ( 1 - x ) / a ] und mit der äquivalenten elektrotechnischen Widerstandsgeraden U_a = 1 / [ R_pot / R₂ + ( R_pot - R₂ ) / R₃ ] * U_e grafisch und rechnerisch den belasteten Spannungsteiler R_ges = [ R_pot / R₂ + ( R_pot - R₂ ) / R₃ ].

Während der Lastwiderstand R_Last = R₃ nebst Parameter a verschiedene Werte aus dem Intervall [ 3 / 0,2 / 0,1 ] annimmt und z.B. für den Wert a = 0,1 mit R₃ = 1 kΩ aber konstant bleibt, ändert sich der Potentiometerwiderstand R₂ entlang der dünnen grünen Kennlinie fortwährend. Und zwar durch Drehen des beweglichen Schleifers am Potentiometer:

(Bild vergrößern: auf Bild klicken! Belasteter Spannungsteiler: Elektroniktutor)

Wenn man nun wissen will, wie groß der Potentiometerwiderstand R₂ maximal ist, d.h. bei Drehung des Potentiometer-schleifers bis zum 270^o Endanschlag, dann muss man aus dem Diagramm zwei Wertepaare ( P1, P2 ) = ( x_b / y_b, x_a / y_a ) mit jeweils x_b > x_a, y_b > y_a wie z.B. ( P1, P2 ) = ( x_b / y_b, x_a / y_a ) = ( 10 / 10, 5 / 5 ) ablesen und diese in die Zweipunkteform wie folgt einsetzen:

( y - y₁ ) / ( x - x₁ ) = ( y₂ - y₁ ) / ( x₂ - x₁ ) → Zweipunkteform

( y – y_a ) / ( x – x_a ) = ( y_b – y_a ) / ( x_b – x_a ) = ∆y / ∆x → Steigung m = ∆y / ∆x

( y – 5 ) / ( x – 5 ) = ( 10 – 5 ) / ( 10 – 5 ) →

( y – 5 ) / ( x – 5 ) = ( 5 ) / ( 5 ) →

( y – 5 ) / ( x – 5 ) = 1 → Steigung m = ∆y / ∆x = 1 →

y = ( x – 5 ) + 5 →

y = m x → Geradengleichung der Widerstandsgeraden R₂ mit der Steigung m = 1 und Steigungswinkel α = 45^o

Die Geradengleichung entspricht der dunkelgrünen Kennlinie nebst Steigungsdreick im obenstehenden Bild!

In die Geradengleichung y = m x der Widerstandsgeraden R₂ lassen sich nun für x beliebige Werte einsetzen wie z.B. die von den beiden Punkten ( P1, P2 ) = ( x_b / y_b, x_a / y_a ) = ( 10 / 10, 5 / 5 ) der Zweipunkteform.

Für den Punkt P1 = ( x_b / y_b ) = ( 10 / 10 ) folgt:

y_b = f(x_b) = f(x_b = 10) = m x_b = 1 * 10 = 10

Und für den Punkt P2 = ( x_a / y_a ) = ( 5 / 5 ) folgt:

y_a = f(x_a) = f(x_a = 5) = m x_a = 1 * 5 = 5

Auch wenn das obenstehende Diagramm sowohl mathematisch für die Funktion y = f(x) = 1 / [ 1 / x + ( 1 - x ) / a ] als auch elektrotechnisch für den Potentiometerwiderstand R₂ und die Ausgangsspannung U_a mit U_a = f(R₂) ausgelegt ist, darf man trotzdem nicht den Fehler machen und die Geradengleichung y = m x der Widerstandsgeraden R₂ direkt auf die Funktion der Ausgangsspannung U_a mit U_a = f(R₂) wie folgt übertragen:

y = m x → Die mathematisch unabhängige Variable x wird dem Potentiometerwiderstand R₂ zugeordnet und die mathematisch abhängige Variable y wird der Ausgangsspannung U_a zugeordnet: U_a = f(R₂)

Der Knackpunkt der Funktion U_a = f(R₂), ist nämlich der, dass sich die Ausgangsspannung U_a gemäß dem Ohmschen Gesetz wie folgt berechnet:

U = R * I → U_a = R_ges * I_ges

U_a / U_e = 1 / [ R_pot / R₂ + ( R_pot - R₂ ) / R₃ ] → Spannungsteilerformel für belasteten Spannungsteiler →

U_a = R_ges * I_ges = 1 / [ R_pot / R₂ + ( R_pot - R₂ ) / R₃ ] * U_e

Wenn man aber davon ausgeht, dass der Potentiometerwiderstand R_pot = 10 kΩ, der Lastwiderstand R_Last = R₃ = 30 kΩ und die Eingangsspannung U_e = 10 V allesamt konstante, d.h. unveränderliche Werte aufweisen, dann bleibt nur noch die Widerstandsgerade R₂ als unabhängige Variable übrig, sodass gilt: U_a = f(R₂) womit die Welt wieder in Ordnung wäre!

Diesbezüglich lässt sich die Geradengleichung der dunkelgrünen Widerstandsgeraden z.B. mittels der Punktsteigungsform

y = f(x) = m * (x + x₁) + y₁ = ∆y/∆x * (x + x₁) + y₁ → Steigungsdreieck mit m = ∆y/∆x → m = ∆U_a / ∆R₂

und mit

∆x → ∆R₂ = 4 Kästchen * 0,5 kΩ = 2 kΩ,

∆y → ∆U_a = 4 Kästchen * 0,5 V = 2 V und

m → ∆U_a / ∆R₂ = 2 V / 2 kΩ = 10^-3 V / V/A = 10^-3 A = 1 mA

wie folgt berechnen:

y = f(x) = m * (x - x₁) + y₁

= f(x) = ∆y/∆x * (x - x₁) + y₁ →

U_a = f(R₂) = ∆U_a / ∆R₂ * ( R₂ - ∆R₂ ) + ∆U₂ → Geradengleichung zur Funktion U_a = f(R₂)

= 1 mA * ( 10 kΩ - 2 kΩ ) + 2 V

= 1 mA * ( 8 kΩ ) + 2 V = 1 A * ( 8 V/A ) + 2 V = 10 V

Wenn man auch die Werte des Mittelpunktes M = ( R_2M / U_aM ) = ( 8,0 kΩ / 3,0 V ) in die Geradengleichung zur Funktion U_a = f(R₂) einsetzen will, dann muss man diese zuvor in die parallel nach unten verschobene Widerstandsgerade der Funktion U_aM = f(R_2M) umwandeln!

Und zwar z.B. mittels der Zweipunkteform und den beiden Wertepaaren ( P3, P4 ) = ( x_b / y_b, x_a / y_a ) mit jeweils x_b > x_a, y_b > y_a wie z.B. = ( P3, P4 ) = ( x_b / y_b, x_a / y_a ) = ( 10 / 5, 5 / 0 ):

( y - y₁ ) / ( x - x₁ ) = ( y₂ - y₁ ) / ( x₂ - x₁ ) → Zweipunkteform

( y – y_a ) / ( x – x_a ) = ( y_b – y_a ) / ( x_b – x_a ) = ∆y / ∆x → Steigung m = ∆y / ∆x

( y – 0 ) / ( x – 5 ) = ( 5 – 0 ) / ( 10 – 5 ) →

y / ( x – 5 ) = ( 5 ) / ( 5 ) →

y / ( x – 5 ) = 1 → Steigung m = ∆y / ∆x = 1 →

y = ( x – 5 ) →

y = x - 5 → Geradengleichung der Widerstandsgeraden R_2M mit der Steigung m = 1 und Steigungswinkel α = 45^o

Die Geradengleichung y = x - 5 entspricht dabei der parallel nach unten verschobenen dunkelgrünen Kennlinie, die im obenstehenden Bild durch den Mittelpunk M verläuft!

In die Geradengleichung y = x - 5 der Widerstandsgeraden R_2M lassen sich nun für x beliebige Werte einsetzen wie z.B. die von den beiden Punkten ( P3, P4 ) = ( x_b / y_b, x_a / y_a ) = ( 10 / 5, 5 / 0 ) der Zweipunkteform.

Für den Punkt P3 ( x_b / y_b ) = ( 10 / 5 ) folgt:

y_b = f(x_b) = f(x_b = 10) = m x_b - 5 = 1 * 10 – 5 = 5

Und für den Punkt P4 ( x_a / y_a ) = ( 5 / 0 ) folgt:

y_a = f(x_a) = f(x_a = 5) = m x_a - 5 = 1 * 5 - 5 = 0

Selbstverständlich lässt sich die Geradengleichung y = x - 5 der Widerstandsgeraden R_2M auch mittels der Punktsteigungsform wie folgt ermitteln:

y = f(x) = m * ( x - x₁ ) + y₁ → Steigung m = ∆y / ∆x → Punkt P ( x₁ + y₁ )

Für den Punkt P4 ( x₁ / y₁ ) = ( 5 / 0 ) folgt:

y = f(x) = m * ( x - x₁ ) + y₁

= 1 * ( x - 5 ) + 0

y = f(x) = x - 5 → Geradengleichung der Widerstandsgeraden R_2M mit der Steigung m = 1

Diesbezüglich lässt sich die Geradengleichung der Widerstandsgeraden R_2M rechnerisch auch auf die Werte des Mittelpunktes M = ( x_2M / y_2M ) = ( 8,0 / 3,0 ) wie folgt anwenden:

y_2M = f(x_2M) = x_2M - 5 = 8,0 - 5 = 3,0

In der Mathematik - hier konkret in der Algebra - lassen sich Funktionen und deren (Funktions-) Gleichungen stets grafisch darstellen und lösen, aber auch in Form einer Gleichung rechnerisch lösen. Und umgekehrt!

Wenn man also eine Gleichung und deren rechnerische Lösung besser und grundlegender verstehen will, dann sollte man versuchen, aus der Gleichung nebst Lösung die grafische Darstellung nebst Lösung abzuleiten (siehe Bild 63).

Im vorliegenden Fall führte uns die grafische Darstellung und Lösung (siehe Bild 63 oben) nebst der Spannungsteilerformel für den belasteten Spannungsteiler

U_a / U_e = 1 / [ R_pot / R₂ + ( R_pot - R₂ ) / R₃ ]

zur Funktionsgleichung

U_a = R_ges * I_ges = 1 / [ R_pot / R₂ + ( R_pot - R₂ ) / R₃ ] * U_e = ∆I_R2 * ( R_2M - 5 kΩ )

mit der angenehmen Folge, dass diese auch für den Mittelpunkt M = ( x_2M / y_2M ) = ( 8 / 3 ) mit der Mittelpunktsgleichung

U_a2M = R_2M * I_a2M

= 1 / [ R_pot / R_2M + ( R_pot - R_2M ) / R₃ ] * U_e

= 1 / [ 10 kΩ / 8 kΩ + ( 10 kΩ - 8 kΩ ) / 0,96 kΩ ] * 10 V → Vorwegnahme R₃ = 960 Ω (siehe weißer Kasten!)

= 1 / [ 1,25 + ( 2 ) / 0,96 ] * 10 V

= 1 / [ 1,25 + 2,083 ] * 10 V

= 1 / [ 3,333 ] * 10 V

= 0,300 * 10 V = 3,0 V

I_a2M = U_a2M / R_2M

= 3,0 V / 8 kΩ = 0,375 mA

Interpretation des Ergebnisses von I_a2M = 0,375 mA:

Wie wir wissen, ist der ungeregelte, maximale Potentiometerwiderstand R₂ = R_pot = 10 kΩ groß! Dabei beträgt die Eingangsspannung U_e = 10 V am Eingang des Potentiometers R_pot gegen Masse („┴“), sodass sich eine Stromstärke von I_pot = 1 mA einstellt.

Verstellt man nun den regelbaren Potentiometerwiderstand R₂ auf den Punkt M = ( R_2M / U_aM ) = ( 8 kΩ / 3 V ) mit R₂ → R_2M = 8 kΩ, dann verringert sich nicht nur der regelbaren Potentiometerwiderstand R₂, sondern auch die durch ihn hindurch fließende Stromstärke von vormals I_R2 = 1 mA auf nur noch I_R2M = 0,375 mA sowie der an ihm anliegende Spannungsabfall auf nur noch U_a2M = 3 V (siehe Bild 63 weiter oben)!

U_a2M = R_2M * I_a2M

= 8 kΩ * 0,375 mA = 8 V/A * 0,375 A = 3.0 V

= 1 / [ R_pot / R_2M + ( R_pot – R_2M ) / R₃ ] * U_e

= ∆I_R2 * ( R_2M - 5 kΩ ) → Siehe weiter oben!

= 1 mA * ( 8 kΩ - 5 kΩ ) = 1 mA * 8 kV/A - 1 mA * 5 kV/A = 8 V - 5 V = 3.0 V

Interpretation des Ergebnisses von U_a2M = 3.0 V:

Die bei der Tangente von P3 nach P4 handelt es sich um die parallel nach rechts unten verschobene Widerstands-gerade

y = f(x) = x - 5 → Geradengleichung der Widerstandsgeraden R_2M mit der Steigung m = 1

des verstellbaren Potentiometerwiderstandes R₂.

Dabei lautet die allgemeine, mathematische Form der Geradengleichung wie folgt:

y = f(x) = m * x + b = a * x +b mit m, a = Steigung und b = x₀ Parallelverschiebung aus dem Koordinatenursprung

Elektrotechnisch lautet die aus der Geradengleichung abgeleitete Widerstandsgerade:

I = f(U) = 1 / R * U + I₀ →

I_2M = f(U_2M) = 1 / R_2M * U_2M + I₀

= 1 / 8 kΩ * 3.0 V + 0 mA = 0,125 mV/A * 3.0 V = 0,375 mA (siehe oben!)

Wie aber muss man die mathematische Funktion y = f(x) = x - 5 in die elektrotechnische „übersetzen“?

U_a = f(R₂) = I₂ * ( R₂ - 5 kΩ ) →

U_a2M = f(R_2M) = I_2M * ( R_2M - 5 kΩ )

= 1 mA * ( 8 kΩ - 5 kΩ ) = 1 mA * 8 kV/A - 1 mA * 5 kV/A = 8 V - 5 V = 3.0 V

Gemäß der Funktionszuordnung U_a2M = f(R_2M) verhält es sich so, dass es sich bei dem verstellbaren Potentiometerwiderstand R_2M um die unabhängige Variable, mathematisch „x“, handelt, während es sich bei der Ergebnisgröße, d.h. der Ausgangsspannung U_a2M, um die abhängige Variable, mathematisch „y“, handelt.

Mit anderen Worten: Wenn man den veränderbaren Potentiometerwiderstand R_2M verstellt, dann ändert sich im gleichen Maße die Ausgangsspannung U_a2M. Und zwar linear, d.h. gleichförmig mit konstanter Steigung.

Mathematisch:

m = ∆y / ∆x →

Elektrotechnisch:

∆U_a2M / ∆R_2M mit den Maßeinheiten [ V / Ω ] → U / R = I * R / R = I →

I = 1 / R * U mit der Steigung 1 / R → I_R2M = 1 / R_2M * U_a2M → R_2M = U_a2M / I_R2M = 3.0 V / 0,375 mA = 8 kΩ

Bei der Funktion U_a2M = f(R_2M) = I_R2M * ( R_2M - 5 kΩ ) handelt es sich also um die lineare Funktion

I_R2M = f(U_a2M) = 1 / R_2M * U_a2M, d.h. um die dunkelgrünen Kennlinie, die im nachfolgenden Bild durch den Mittelpunk M verläuft:

(Bild vergrößern: auf Bild klicken! Belasteter Spannungsteiler: Elektroniktutor)

Im nachfolgenden weißen Kasten wird gezeigt, wie man mittels der Spannungsteilerformel

U_aM = U_e / [ R_pot / R_2M + ( R_pot – R_2M ) / R₃ ] = 3.0 V und des Mittelpunktes M = ( R_2M / U_aM ) = ( 8 kΩ / 3.0 V )

den Widerstandswert des bisher noch unbekannten Lastwiderstandes R_Last = R₃ = 960 Ω berechnet:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden weißen Kasten sieht, lassen sich mit der Mittelpunktsgleichung, abgeleitet aus der Spannungsteilerformel und der Widerstandsgerade (= dunkelgrünen Kennlinie durch den Mittelpunk M), jeweils einzeln einer der die beiden Widerstände R_2M ( → x ) oder R_Last = R₃ ( → 0.96 kΩ ) berechnen:

(Zum Vergrößern bitte auf das Bild klicken!)

In der obenstehenden Formel steht dabei die Zahl 10 im Zähler für die Eingangsspannung U_e = 10 V und im Nenner für den Potentiometerwiderstand R_pot = 10 kΩ.

Die Variable x auf der rechten Seite der Gleichung steht ebenfalls für den Potentiometerwiderstand R_2M = 8 kΩ und die Zahl 5 für den Tangentenwiderstand R_Tang = 5 kΩ der Widerstandsgerade (= dunkelgrünen Kennlinie durch den Mittelpunk M).

Da wir mittels der kombinierten Mittelpunktsgleichung (= Spannungsteilerformel auf der linken Seite & Widerstandsgerade durch den Mittelpunkt M auf der rechten Seite) rechnen, muss es sich auf der rechten Seite der Mittelpunktsgleichung elektrotechnisch(!) und von wegen der Maßeinheit [V] um eine Spannung handeln!

Und zwar um die Spannung U_aM im Mittelpunkt M = ( R_2M / U_aM ) = ( 8 kΩ / 3.0 V ), die sich wiederum nur einstellt, wenn man die rechte Seite „x – 5“ der Mittelpunktsgleichung mit der Stromstärke I_R2M = 1 mA multipliziert:

U_a2M = f(R_2M)

= I_R2M * ( R_2M - 5 kΩ )

= 1 mA * ( 8 kΩ - 5 kΩ ) = 1 mA * 3 kΩ = 1 A * 3 V/A = 3.0 V (siehe weiter oben!)

Der belastete Spannungsteiler mit der Mittelpunktsgleichung

Jetzt wo wir unser mathematisches und elektrotechnisches Wissen maßgeblich erweitert und verbessert haben, wissen, wie man den Schnittpunkt M der Tangente mit dem Funktionsgraphen des belasteten Spannungsteilers berechnet, ist es an der Zeit, dass wir das erworbene Wissen auf die Praxis, d.h. den belasteten Spannungsteiler, der aus den beiden in Serie geschalteten Glühlampen 18 (siehe nachfolgend Widerstand R₁ und R₂) sowie aus dem Lastwiderstand R_Last = R₃ besteht, anwenden:

(Zum Vergrößern bitte auf das Bild klicken!)

Nachfolgend geht es dabei darum, den (Potentiometer-) Widerstand R₂ der Glühlampen 18 mittels der nachfolgenden Spannungsteilerformel

(Zum Vergrößern bitte auf das Bild klicken!)

wie folgt

U_a / U_e = 1 / [ R_pot / R₂ + ( R_pot - R₂ ) / R₃ ] →

U_a = 1 / [ R_pot / R₂ + ( R_pot - R₂ ) / R₃ ] * U_e

U_a = U_e / [ R_pot / R₂ + ( R_pot - R₂ ) / R₃ ]

mit den Werten

U_e = U_Batt = 4,804 V

U_a = U_R2 = U_RP = 1,911 V

R_pot = R₁ + R₂ = 15,69 Ω + 11,55 Ω = 27,24 Ω

R_Last = R₃ = 100,67 Ω (siehe Variable x)

zu berechnen:

(Zum Vergrößern bitte auf das Bild klicken!)

Der Widerstandswert R₂ = 11,552 Ω der Glühlampen 18 wurde dem „Sketch“-Programm „sketch_prog_12_12.ino“ entnommen und zuvor experimentell bzw. iterativ ermittelt. Ob es sich bei diesem um den Widerstandswert im Mittelpunkt M (siehe weiter oben) handelt, muss sich noch herausstellen.

Der Potentiometerwiderstand R_pot des unbelasteten Spannungsteilers, d.h. ohne den Lastwiderstand R_Last = R₃, lässt sich aber auch mittels des Ohmschen Gesetzes, der anliegenden Spannung U_pot und der Stromstärke I_pot wie folgt berechnen:

R_pot = U_pot / I_pot = U_e / ( I_ges - I_R3 ) = U_Batt / ( I_RP - I_R3 )

= 4,804 V / ( 184,41 mA - 18,87 mA )

= 4,804 V / 165,54 mA = 29,02 Ω

(Zum Vergrößern bitte auf das Bild klicken!)

Wenn sich der Potentiometerwiderstand R_pot von R_pot = 27,24 Ω auf R_pot = 29,02 Ω vergrößert, dann muss sich auch einer der beiden (Potentiometer-) Teilwiderstände R₁, R₂ entsprechend vergrößern!

Da der (Potentiometer-) Teilwiderstand R₁ in der Spannungsteilerformel nicht vorkommt, muss sich der (Potentiometer-) Teilwiderstand R₂ von R₂ = 11,552 Ω (= obere Berechnung im weißen Kasten) auf R₂ = 12,358 Ω (= untere Berechnung weißen Kasten) entsprechend vergrößern:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden Screenshot sieht, vergrößert sich die Ausgangsspannung U_a = U_R2 = U_R3 = U_RP nur ganz geringfügig, d.h. um 1,911060 V - 1,910998 V = 0,000062 V = 0,062 * 10^-3 V = 62 * 10^-6 = 62 µV = 62 Hundertausendstel!

Der Knackpunkt dabei ist der, dass zwar die Rechengenauigkeit des Rechenwerks, engl. „Arithmetic Logic Unit“ (ALU), des „Arduino UNO“ groß genug ist, nicht aber die Auflösung unseres A/D-Wandlers an einem der Ports „Pin A0“, „Pin A1“ oder „Pin A2“. Früher oder später werden wir also zu einem Trick greifen müssen, um die Auflösung unseres A/D-Wandlers wenigstens um eine Zehnerpotenz bzw. Binärdekade zu vergrößern!

Doch zunächst geht es noch darum, den bereits bekannten Rechenalgorithmus, d.h. die obenstehende Spannungsteilerformel so anzuwenden, sodass sich der Spannungsteilerwiderstand R₂ ≈ 11,522 Ω möglichst exakt berechnen lässt. Und dazu brauchen wir die Mittelpunktgleichung wie z.B.

(Zum Vergrößern bitte auf das Bild klicken!)

Die Spannungsteilerformel lautet, wie inzwischen bekannt,

U_a = U_e / [ R_pot / R₂ + ( R_pot - R₂ ) / R₃ ] (siehe oben)

Dabei bezieht sich die Ausgangsspannung U_a auf die parallel geschalteten Widerstände R_RP = R₂ // R₃ des Stromteilers mit

R_RP = R₂ // R₃ = 1 / [ ( 1 / R₂ + 1 / R₃ ) ] = U_a / I_RP → U_a = 1 / [ ( 1 / R₂ + 1 / R₃ ) ] * I_RP = R_RP * I_RP

Für den Stromknoten gilt:

I_R2 + I_R3 + ( - I_RP ) = 0 → Die Summe aller in den Stromknoten hinein und heraus fließenden Ströme ist gleich Null!

I_R2 = I_RP - I_R3 = U_RP / R_RP - U_RP / R₃ = U_RP * ( 1 / R_RP - 1 / R₃ ) = U_a / [ 1 / ( 1 / R_RP - 1 / R₃ ) ] = U_a / R₂ →

I_RP - I_R3 = I_R2 = U_a / R₂ = U_a * ( 1 / R₂ ) = U_a * ( 1 / R_RP - 1 / R₃ ) →

U_a = I_R2 / ( 1 / R_RP - 1 / R₃ ) = ( I_RP - I_R3 ) / (1 / R₂ ) (siehe Formel im weißen Kasten oben, rechte Seite!)

U_a = ( I_RP - I_R3 ) * R₂ = I_RP * R₂ - I_R3 * R₂

= 184,41 mA * 11,552 Ω - 18,98 mA * 11,552 Ω = 2,1303 V - 0,2193 V = 1,911 V þ

(Zum Vergrößern bitte auf das Bild klicken!)

Das Interessante an der Gleichung U_a = ( I_RP - I_R3 ) * R₂ = I_RP * R₂ - I_R3 * R₂ ist, dass es eine weder eine Spannung I_RP * R₂ = 184,41 mA * 11,552 Ω = 2,1303 V, noch eine Spannung I_R3 * R₂ = 18,98 mA * 11,552 Ω = 0,2193 V gibt. Rechnerisch wie man sieht zwar schon, nicht aber elektrotechnisch bzw. ohmsch!

Denn durch den Widerstand R₂ fließt der Strom I_R2 und nicht der Strom I_RP. Ebenso fließt der Strom I_R3 nicht durch den Widerstand R₂, sondern durch den Widerstand R_Last = R₃.

Das Ausmultiplizieren der Gleichung U_a = ( I_RP - I_R3 ) * R₂ = I_RP * R₂ - I_R3 * R₂ bringt also nichts bzw. keinen zusätzlichen Erkenntnisgewinn. Im Gegenteil: Durch das Ausmultiplizieren geht der strommäßige Zusammenhang ( I_RP - I_R3 ) = I_R2 gemäß Stromknoten I_R2 + I_R3 + ( - I_RP ) = 0 verloren! –

Der Vorteil der Spannungsteilerformel ist ja gerade der, dass für das Berechnen diverser, einzelner Werte nur Spannungs- oder Widerstandswerte erforderlich sind, nicht jedoch einzelne Ströme des Stromknotens!

[ zurück ] zum Versuch 12 und dem Experimentieren! -

[ Easy Elektro Start ] [ Seitenanfang ] [ zurück ]