[ electronic 159 ] [ Seitenende ] [ Programmieren ] [ Versuch 2 ]

electronic 159 – Versuch 1

Elektrischer Strom, der „leuchtet“

Auch in der Natur gibt es elektrische Ströme, die den elektrischen Strom quasi leuchten lassen. Und zwar wesentlich heller als bei der Glühlampe [18] im Stromkreis des ersten Versuches:

(Zum Vergrößern bitte auf das Bild klicken!)

Leider ist die Leuchtdauer in der Natur aber nur von so kurzer Dauer, dass man in der kurzen Zeit keine Zeitung lesen kann.

Aber die beim Leuchten des elektrischen Stromes übertragene elektrische Energie wäre immerhin so groß, nämlich ca. 280 Kilowattstunden [kWh], sodass man dafür an der Tankstelle etwa 31 Litern Benzin zum Antrieb eines Personenkraftwagens mit Ottomotor bekäme.

Weißt du nun, worum es sich in der Natur beim Leuchten des elektrischen Stromes handelt?

Richtig, um einen Blitz beim Gewitter!

>> Unter der Nutzung von Blitzenergie werden Versuche verstanden, die in Blitzen steckende Energie technisch nutzbar zu machen. Dies wird seit Ende der 1980er Jahre versucht. In einem einzelnen Blitz entlädt sich elektrische Energie von ca. 280 kWh. Dies entspricht ca. 1 GJ oder der Energie von etwa 31 Litern Benzin.^[1] Allerdings kommt am Boden weniger als ein Zehntel an,^[2] zudem nur sporadisch in Raum und Zeit.^[3] Es wurde vorgeschlagen, mit der Energie von Blitzen Wasserstoff aus Wasser herzustellen, das durch den Blitz schnell erhitzte Wasser zur Stromerzeugung zu nutzen^[4] oder durch in der Nähe platzierte Induktoren einen sicheren Bruchteil der Energie einzufangen.^[5]

Eine Technologie, welche fähig ist, die Energie von Blitzen zu nutzen, müsste diese Energie in kurzer Zeit speichern können. Verschiedene Ideen wurden schon ausprobiert, aber die sich immer ändernde Intensität der Blitze macht die Nutzung von Blitzenergie am Boden unpraktisch. Zu hohe Energiemengen zerstören die Speicher und zu niedrige Energiemengen lassen sich nicht speichern. Zudem treten Blitze nur sporadisch auf, sodass die Energie eingesammelt und längerfristig gespeichert werden müsste. Außerdem müsste man die extrem hohen Spannungen in speicherbare, niedrigere umwandeln. << (Quelle: Wikipedia)

Ein Blitz mit dem zeitlich nachfolgenden Donner entsteht immer dann, wenn warme und kalte Luftschichten aufeinander treffen und sich die in den Gewitterwolken enthaltenen Wasserdampftröpfchen nebst Staubpartikel aneinander reiben und dabei sogenannte Reibungselektrizität entstehen lassen.

>> Ein Blitz ist in der Natur eine Funkenentladung oder ein kurzzeitiger Lichtbogen zwischen Wolken oder zwischen Wolken und der Erde. In aller Regel tritt ein Blitz während eines Gewitters infolge einer elektrostatischen Aufladung der wolkenbildenden Wassertröpfchen oder der Regentropfen auf. Er wird dabei vom Donner begleitet und gehört zu den Elektrometeoren. Dabei werden elektrische Ladungen (Elektronen oder Gas-Ionen) ausgetauscht, das heißt, es fließen elektrische Ströme. Blitze können, je nach Polarität der elektrostatischen Aufladung, auch von der Erde ausgehen.

Künstlich im Labor mit Hochspannungsimpulsen erzeugte Blitze dienen deren Studium oder der Überprüfung von Einrichtungen des Stromnetzes hinsichtlich der Effekte von Blitzeinschlägen und der Wirksamkeit von Schutzmaßnahmen.

Eine Blitzentladung ist deutlich komplexer als eine reine Funkenentladung. Die der natürlichen Blitzentstehung zugrunde liegenden physikalischen Gesetzmäßigkeiten sind bis heute nicht abschließend erforscht. << (Quelle: Wikipedia)

Wenn sich also Gewitterwolken mittels elektrischer Ladungen aufladen, dann enthält eine Wolke positive Ladungsträger und die andere negative, sodass zwischen beiden Wolken ein Potentialunterschied, d.h. ein elektrisches Potentialgefälle entsteht.

Wenn das Potentialgefälle, man spricht auch von dem Spannungsunterschied, zu groß wird, dann versuchen die elektrischen Kräfte der Ladungsträger einen Ausgleich zwischen den unterschiedlichen positiven und negativen Ladungsträgern herbeizuführen, sodass beide sich durch einen Blitz von Wolke zu Wolke entladen, d.h. elektrisch ausgleichen!

Dabei breitet sich der Blitz in dem sogenannten Blitzkanal mit Lichtgeschwindigkeit c = v_Licht = 300 000 km/h aus, während die durch den Blitz getrennten Luftmassen der Wolken mit Schallgeschwindigkeit c_S = v_Schall = 340 m/s aufeinandertreffen und das Donnergrollen bewirken.

Während sich also der Schall recht langsam mit nur

c_S = v_Schall = 340 * 1 m/s = 340 * 1/1000 km / 1/3600 h = 340 * 3600/1000 km/h = 340 * 3,6 km/h = 1 224 km/h

ausbreitet, geht es beim Blitz mit 300 000 km/h wortwörtlich blitzschnell!

Wegen der unterschiedlichen Ausbreitungsgeschwindigkeit von Blitz und Donner lässt sich die Entfernung eines Gewitters vom heimischen Standort aus recht einfach aus der Zeitdifferenz von Blitz und Donner wie z.B. ∆t = 3 s wie folgt berechnen:

Geschwindigkeit v = Strecke s / Zeit t → Strecke s = Geschwindigkeit v * Zeit t

s_Entfernung = v_Donner / t_Donner → ∆s_Entfernung= v_Donner / ∆t = 340 m/s * 3 s = 1 020 m ≈ 1,0 km

Wenn also zwischen Blitz und dem zeitlich nachfolgenden Donner eine Zeitdifferenz von ∆t = 3 s verstreicht, dann befindet sich das Gewitter mit nur einem Abstand von ∆s_Entfernung= 1,0 km unmittelbar über den Bewohnern! Höchste Zeit also, sich in Sicherheit zu bringen und das Haus, eine mit Blitzschutz versehene Schutzhütte oder das Auto als Faradayscher Käfig aufzusuchen!

Auf keinen Fall sollte man sich im Wald unter einen Baum stellen oder auf einer Wiese der Länge nach hinlegen, sondern wegen der sogenannten lebensgefährlichen Schrittspannung auf der Wiese hinhocken, damit man nicht aus dem Geländeprofil herausragt und den Blitz förmlich auf sich zieht. Dabei sollten dann die Beine beim Hinhocken unbedingt geschlossen sein, sodass sich die gefährliche Schrittspannung im Falle eines Blitzeinschlagens nur zwischen den Füßen und den Schuhsohlen aufbauen kann.

Wenn man im Wald oder in Feld und Flur mit dem Fahrrad unterwegs ist, sollte man das Fahrrad, das ja metallisch elektrisch leitend ist, keinen Faradayschen Käfig darstellt und deshalb den Blitz auf sich lenkt, möglichst weit weg von sich, d.h. im Abstand von 150 m oder mehr abstellen! Je weiter weg, desto besser! Wer Angst hat, dass das Fahrrad im Wald gestohlen wird, kann es ja mit einem Schloss absperren! Ach ja, einen Regenschirm mit metallischen Streben sollte man natürlich auch nicht aufspannen, egal wie stark es regnet.

Blitz und Donner [ programmieren ]

Formelbuchstaben und Maßeinheiten der Elektrizitätslehre (Klasse 9 im Physikunterricht)

Wie lautet noch einmal die Formel zur Berechnung der Geschwindigkeit v, was ist überhaupt Geschwindigkeit?

Geschwindigkeit v ist die in einer Zeitspanne t zurückgelegte Wegstrecke s: v = s / t mit der Maßeinheit [Kilometer pro Stunde] = [km/h] oder [Meter pro Sekunde] = [m/s]

Mit anderen Worten: Je größer die zurückgelegt Wegstrecke in einer kleinen Zeitspanne ist, umso größer ist die Geschwindigkeit!

Während sich der elektrische Stromimpuls(!) in einem Stromkreis (siehe Schaltung im Versuch 1) mit Lichtgeschwindigkeit c = v_Licht = 300 000 km/h ausbreitet, beträgt die Fortbewegung der Ladungsträger (= Elektronen) im Kupferdraht bzw. in den Leitungen eines elektrischen Stromkreises nur wenige Meter pro Sekunde [m/s].

Blitz und Donner [ programmieren ]

Übrigens: Weiß du, wie der Kupferdraht als elektrische Leitung bzw. elektrisches Kabel im Stromkreis erfunden wurde?

Einem von zwei geizigen Schotten fiel eine Kupfermünze zu Boden. Während sich beide Schotten gleichzeitig bückten, um die Kupfermünze aufzuheben und sich dabei stritten, wem denn nun die Kupfermünze gehöre, dehnte sich diese zum dünnen Kupferdraht.

Wenn man aber zu viele Ladungsträger in Form von negativ geladenen Elektronen und einem entsprechend großen Strom I durch einen dünnen Kupferdraht zwängen will, sodass durch diesen ein Strom I von z.B. von I = 16 Ampere [A] fließt, dann behindern sich die Elektronen in der Leitung gegenseitig, sodass sich der Kupferdraht entsprechend stark erwärmt, „rote Bäckchen“ bekommt, d.h. zu glühen anfängt, durchschmort und einen Zimmerbrand auslöst. Deshalb sollte man z.B. einen Heizstrahler, Öl-Wärmeradiator, Heizlüfter, Bügeleisen oder einen Wasserkocher mit einer (Wärme-) Leistung P von z.B. P = 2000 Watt [W] niemals mittels einer Verlängerungsschnur oder Kabeltrommel verlängern!

Leistung P ist gleich Spannung U multipliziert mit dem Strom I

Ein handlicher Autostaubsauger verfügt über einen 400 Watt [W] starken Motor, der über die Autosteckdose in Form eines herausnehmbaren Zigarettenanzünders mit elektrischer Energie W bei einer Spannung von U_Batterie = 12 V betrieben wird.

Frage: Wie groß ist der Strom I bzw. die Stromstärke I in Ampere [A], die durch das Netzkabel fließt?

P = U * I → I_Motor = P_Staubsauger / U_Batterie = 400 W / 12 V = 33,33 A

Demzufolge wäre das Netz-/Stromkabel des Autostaubsaugers im Vergleich zu einem Haushalts-Verlängerungskabel für einen max. zugelassenen Strom I von I = 16 A gut und gern doppelt so dick, müsste der Querschnitt, d.h. die Querschnittsfläche des Kupferkabels bzw. des Netz-/Stromkabels des Autostaubsaugers doppelt so groß sein, damit sich über die größere Querschnittsfläche des dickeren Kabels auch zahlenmäßig mehr Ladungsträger in Form von Elektronen transportieren lassen!

Demzufolge steht die zu transportierende Ladungsmenge Q in [Amperestunden] = [Ah] mit Q ist gleich Stromstärke I in [Ampere] = [A] multipliziert mit der Zeit(dauer) t in [Stunden] = [h] direkt im Verhältnis zueinander:

Q = I * t → t = Q_Batterie / I_Staubsauger = 44 Ah / 33,33 A = 1,32 h

Bei einer herkömmlichen Autobatterie mit der verfügbaren Ladungsmenge Q von z.B. Q = 44 Ah ließe sich der Autostaubsauger mit einem Motorstrom I_Staubsauger = 33,33 A bis zu 1,32 Stunden lang betreiben!

Diesbezüglich lässt sich eine etwa vier Jahre alte Autobatterie, die sich im Stadtverkehr wegen der kurzen Wege zum Bäcker und Lebensmittelmarkt oftmals nicht vollständig aufladen lässt und wegen der Alterung auch noch über eine verringerte Ladungsmenge Q von z.B. Q = 22 Ah verfügt, mit dem Autostaubsauger nur noch ? Stunden betreiben:

t = Q_Batterie / I_Staubsauger = 22 Ah / 33,33 A = 0,66 h = 66/100 h = 66/100 * 60 min = 39,6 min ≈ 40 min

Und, das ist mir vor Jahren tatsächlich passiert: nach knapp 35 Minuten war die gealterte und nicht vollständig aufgeladene Autobatterie so weit durch den Autostaubsauger entladen, dass sich das Auto wider Erwarten nicht mehr starten ließ.

Die Ladungsmenge Q einer Batterie von z.B. Q = 44 Ah gibt also an, wie lange sich der Entladestrom I = 44 A der Batterie entnehmen lässt, nämlich gerade einmal eine Stunde lang:

Q = I * t → t = Q / I = 44 Ah / 44 A = 1 h

Beim Starten des Motors zieht der Anlasser (= Elektromotor) während des Anlassens einen Strom von bis zu I = 200 A.

Wie oft darf der Anlasser betätigt werden, wenn der Startvorgang bis zu t = 5 Sekunden dauert und die Autobatterie über eine Kapazität (= Ladungsmenge Q) von Q = 50 Ah verfügt?

t = Q / I = 55 Ah / 200 A = 0,275 h = 275/1000 * 60 min = 16,5 min = 16,5 * 60 s = 990 s

Berechnung der Anzahl n der Startvorgänge

n = 990 s / 5 s = 198

Bis die (Starter-) Batterie des Auto komplett leer ist und über keine Ladungsmenge Q mehr verfügt, ließe sich das Auto theoretisch bis zu 198 mal starten.

Da man eine wieder aufladbare Autobatterie (= Akku) aber niemals tief entladen soll, beschränken wir uns auf nur n_max = 150 Startvorgänge, sodass als Restladungsmenge Q_Rest noch Q_Rest = ? Ah zur Verfügung stehen.

Berechne die verbleibende Restladungsmenge Q_Rest für n_Rest = 48 Startvorgänge!

n_Rest = 48 → t_Rest = n_Rest * t_Start (5 s für einen Startvorgang, siehe oben)

t_Rest = n_Rest * t_Start = 48 * 5 s = 240 s = 240 * 1/60 min = 4 min = 4 * 1/60 h = 0,067 h

Berechnung der restlichen Ladungsmenge Q_Rest:

Q_Rest = I * t = 200 A * 0,067 h = 0,067 Ah = 67/1000 Ah = 67 mAh [ Milliamperestunden ] = [ 1/1000 Amperestunden ]

Die verbleibende Restladungsmenge von gerade mal Q_Rest = 67 mAh ist verdammt wenig, sodass es tatsächlich fraglich ist, ob die Autobatterie dabei nicht doch schon so tief entladen wurde, dass sie Schaden genommen hat.

Um das beurteilen zu können, müssen wir noch die verbleibende (Batterie-) Spannung U_Batt in die Berechnung mit einbeziehen:

C = Q / U → Kapazität, gemessen in [ Amperestunden pro Volt ] = [ Ah / V ]

C_Batt = Q_Batt / U_Batt = 55 Ah / 12 V = 4,583 Ah/V bei einer voll aufgeladenen Autobatterie!

C_Rest = Q_Rest / U_{Batt, Rest} → U_{Batt, Rest} = Q_Rest / C_Rest

Elektrische Energie W ist gleich dem Produkt von elektrischer Leistung P multipliziert mit der Zeit t

Um das beurteilen zu können, müssen wir noch die verbleibende (Batterie-) Spannung U_Batt in die Berechnung mit einbeziehen. Und zwar in Bezug auf die noch als Restmenge in der Autobatterie gespeicherte Energie W, gemessen in [ Wattstunden ] = [ Wh ] oder [ Kilowattstunden ] = [ kWh ].

Der Formelbuchstabe W stammt aus dem Englischen und steht für engl. „work“, d.h. Arbeit.

Wenn der Anlassermotor unseres Autos den Motor fünf Sekunden lang startet, d.h. die Kurbelwelle des Ottomotors fünf Sekunden lang dreht bis die Zündung den Motor startet, dann „verbraucht“ der Anlassermotor in dieser Zeitspanne t = 5 s eine elektrische Energie W von

W_Anlasser = P_Anlasser * t = U_Anlasser * I_Anlasser * t

= 12 V * 200 A * 5 s = 12 000 Ws = 12 000 * 1/1000 kWs = [ Kilowattsekunden ]

= 12 000 * 1/1000 kWs = 12 000 * 1/1000 kWs = 12 kWs = 12 kW * 1/3600 h

= 12 000 / 3600 Wh = 120 / 36 Wh = 3,33 Wh = [ Wattstunden ]

Im Vergleich dazu berechnet sich die in der voll aufgeladenen Autobatterie gepeicherte Energie W_Batt wie folgt:

W_Batterie = P_Batterie * t = U_Batterie * I_Anlasser * t_gesamt = U_Batterie * I_Anlasser * n * t_Start

= 12 V * 200 A * 198 * 5 s = 2 376 000 VAs = 2 376 000 Ws

= 2 376 000 W * 1/3600 h = 23 760 W * 1/36 h = 23 760 / 36 Wh = 660 Wh = [ Wattstunden ]

Mit anderen Worten:

Die in der vollständig aufgeladenen Autobatterie gepeicherte Energie W_Batterie = 660 Wh ist in der Lage, die elektrische Arbeit A von A_Batterie = W_Batterie = 660 Wh zu verrichten, wobei die Arbeit A der Arbeit W, engl. „work“ entspricht!

Damit das Ganze noch verständlicher und anschaulicher wird, kann man auch formulieren:

Die in der vollständig aufgeladenen Autobatterie gepeicherte elektrische Energie W_Batterie = 660 Wh ist in der Lage, einen Elektromotor der Leistung P_Motor = 660 W eine Stunde lang arbeiten zu lassen:

W_Motor = P_Motor * t = 660 W * 1 h = 660 Wh = [ Wattstunden ]

Alternativ:

Die in der vollständig aufgeladenen Autobatterie gepeicherte elektrische Energie W_Batterie = 660 Wh ist in der Lage, eine Halogen-Glühlampe der Leistung P_Halogen = 60 W elf Stunden lang hell leuchten zu lassen:

W_Halogen = P_Halogen * t = 60 W * 11 h = 660 Wh = [ Wattstunden ]

Zur Kontrolle, ob wir bisher auch richtig gerechnet haben, mach wir die Probe:

W_Batterie = P_Batterie * t = U_Batterie * I_Anlasser * t_gesamt = U_Batt * Q_Batterie →

Q_Batterie = W_Batterie / U_Batterie = 660 Wh / 12 V = 660 VAh / 12 V = 55 Ah = [ Amperestunden ] þ

Jetzt kennen wir nicht nur den Unterschied zwischen elektrischer Energie (= Arbeit) W und elektrischer Leistung P, sondern auch den Zusammenhang mit der während der Zeit t bereitgestellten Ladungsmenge Q:

W = P * t = U * I * t = U * Q

… mit der Umrechnung P = W / t bzw. Q = W / U

In diesem Zusammenhang muss noch erwähnt werden, dass Energie niemals „verbraucht“ wird, im Sinne von verloren gehen, sondern stets nur von einer Energieform in eine andere wie z.B. Wärme W_Wärme, den mechanischen Antrieb W_mech eines Motors mit dem Drehmoment M oder in die beschleunigte Bewegung W_kin eines Körpers der Masse m umgewandelt wird!

In diesem Zusammenhang bleibt bei dieser Gelegenheit noch der Sachverhalt zwischen der elektrischen Spannung U, die in [ Volt ] = [ V ] gemessen wird und dem elektrischen Strom I bzw. der elektrischen Stromstärke, die in [ Ampere ] = [ A ] gemessen wird, zu klären.

Am besten kann man sich das bildlich klarmachen. Zum Beispiel an einem (Wasser-) Hochbehälter oder einem Wasserturm. Dabei entspricht der Wasserdruck im Hochbehälter dem Wert der elektrischen Spannung U, wie z.B. U = 230 V bei der „Strom“-Versorgung im Haushalt und der jeweilige Wasserdruck in 1 m, 5 m oder 10 m Höhe der Stromstärke I, wie z.B. I_Erdgeschoss = 16 A, I_{Erster Stock} = 10 A oder I_Dachgeschoss = 5 A.

Während aber der Wasserdruck als Funktion vom Rohrquerschnitt und der Fallhöhe im Fallrohr (= Abflussrohr) abhängt, sich also mit zunehmender Höhe verringert, verhält sich das bei der elektrischen Stromstärke anders, ist diese überall gleich groß bzw. richtet sich diese ausschließlich nach dem angeschlossenen Verbraucher.

So „verbraucht“ eine 60 Watt Glühlampe im Erdgeschoss eben so viel Strom wie im Dachgeschoss. Ähnlich verhält es sich bei einem Wäschetrockner mit 2000 Watt Anschlussleistung; auch dessen Strom“verbrauch“ ist überall gleich groß, egal ob sich der Wäschetrockner im Erdgeschoß oder Dachgeschoß befindet.

Das Ohmsche Gesetz als Beziehung zwischen Strom I und Spannung U

Georg Simon Ohm ist es zu verdanken, dass er in Jahre langer Arbeit herausgefunden hat, dass es zwischen Spannung U und Strom I eine Beziehung, einen Zusammenhang gibt:

>> Ohms Name ist in die Terminologie der Elektrizitätslehre eingegangen. Als Ohmsches Gesetz wird die Proportionalität zwischen Stromstärke und Spannung in einem elektrischen Leiter bezeichnet, die Ohm im Frühjahr 1826 gefunden hatte. Die Proportionalitätskonstante wird als elektrischer Widerstand bezeichnet, dessen SI-Einheit das Ohm (Symbol Ω) ist. << (Quelle: Wikipedia)

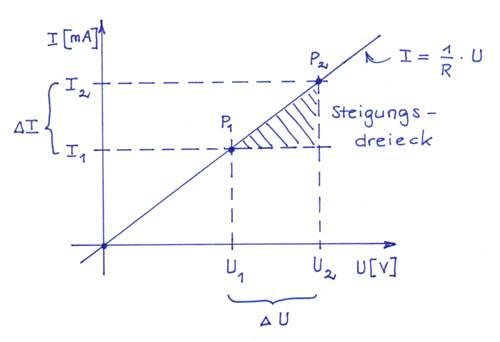
Die Stromstärke I in einem elektrischen Leiter ist proportional der Spannung U: I ~ U

Demzufolge ist die Stromstärke I eine Funktion der Spannung U: I = f(U)

I ~ U → I = k * U → k = Konstante → k = I / U → 1 / k = U / I mit der Maßeinheit [ V/A ] = [ Ω ]

Dabei bezeichnet man den Quotienten U / I als Ohmschen Widerstand R mit der Maßeinheit [ Ohm ] = [ Ω ]

Demzufolge definiert sich der elektrische Widerstand R zu

R = U / I = ∆U / ∆I → Spannungsänderung zu Stromänderung

Das Ohmsche Gesetz und die nach I umgestellte Formel

I = f(U) = 1 / R * U → ∆I = f(U) = 1 / R * ∆U → Steigungsdreieck!

lässt sich auch wie folgt grafisch darstellen:

(Zum Vergrößern bitte auf das Bild klicken!)

Von Spannungs- und Stromquellen

Was Georg Simon Ohm bei seinen Messreihen und Experimenten in den Jahren 1825 bis 1926 zur Entwicklung des heutigen Ohmschen Gesetzes nicht wusste, nicht wissen konnte, ist, dass es nicht nur Spannungsquellen U₀ wie z.B. Batterien, Akkus oder Netzteile gibt, sondern eben auch Stromquellen I₀, die man aber hauptsächlich nur in Laber-Netzgeräten vorfindet. Dabei handelt es sich bei einer Stromquelle I₀ um eine sogenannte Konstant-Stromquelle.

Was aber unterscheidet eine Spannungsquelle U₀ von einer (Konstant-) Stromquelle I₀?

Eine Spannungsquelle U₀ liefert bei einer konstanten Spannung U₀ wie z.B. bei einer „Mignon AA“-Rundzelle mit U₀ = 1,5 V je nach angeschlossener Last (Glühlampe, Motor, Widerstand) wie z.B. R_Last = 100 Ω einen von der Last abhängigen Laststrom I_Last = U₀ / R_Last = 1,5 V / 100 Ω = 0,015 A = 15 mA

Eine Stromquelle I₀ liefert bei einem konstanten Strom I₀ mit z.B. I₀ = 15 mA je nach angeschlossener Last (Glühlampe, Motor, Widerstand) mit z.B. R_Last = 100 Ω eine dazugehörige, resultierende Klemmenspannung

U_Klemme = I₀ * R_Last = 15 mA * 100 Ω = 0,015 A * 100 V/A = 15 V

Bei einem Lastwiderstand von R_Last = 10 KΩ stellt sich bei der (Konstant-) Stromquelle I₀ bereits eine Klemmenspannung ein von U_Klemme = I₀ * R_Last = 15 mA * 10 KΩ = 15 * 10^-3 A * 10 * 10³ Ω = 15 * 10 A * V/A = 150 V

Bei einem Lastwiderstand von R_Last = 100 KΩ stellt sich bei der (Konstant-) Stromquelle I₀ bereits eine Klemmenspannung ein von U_Klemme = I₀ * R_Last = 15 mA * 100 KΩ = 15 * 10^-3 A * 100 * 10³ Ω = 15 * 100 A * V/A = 1 500 V

Bei einem Lastwiderstand von R_Last = 1 MΩ stellt sich bei der (Konstant-) Stromquelle I₀ bereits eine Klemmenspannung ein von U_Klemme = I₀ * R_Last = 15 mA * 1 MΩ = 15 * 10^-3 A * 100 * 10⁶ Ω = 15 * 100 * 1000 A * V/A = 100 000 V

Da sich bei der (Konstant-) Stromquelle I₀ die an den (Batterie-) Klemmen anliegende Spannung U_Klemme stets nach dem angeschlossenen Lastwiderstand R_Last richtet, kann die Klemmenspannung der (Konstant-) Stromquelle I₀ bei einem unendlich großen Lastwiderstand R_Last = ∞ theoretisch auch unendlich groß werden mit U_Klemme = ∞, was natürlich lebensgefährlich wäre und bei normaler Raumtemperatur mit einer Luftfeuchtigkeit von z.B. 60 % sofort zum Spannungsüberschlag führen würde.

Aus dem Grund, dass an einer im Leerlauf, d.h. ohne Lastwiderstand mit R_Last = ∞, betriebenen (Konstant-) Stromquelle I₀ an den (Batterie-) Klemmen eine lebensgefährlich unendlich hohe Leerlaufspannung U_Leer mit U_Leer = ∞ entstehen kann, darf diese in der Praxis niemals ohne einen entsprechenden Lastwiderstand R_Last mit von z.B. R_Last = 100 Ω betrieben werden, sodass die Klemmenspannung mit U_Klemme = 15 V absolut ungefährlich ist (siehe oben)!

Bei den in Labor-Netzgeräten verbauten (Konstant-) Stromquellen I₀ mittels Operationsverstärker verhält es sich allerdings so, dass die intern verbaute, elektronische (Konstant-) Stromquelle I₀ meistens nur eine maximale Klemmenspannung U_Klemme von deutlich weniger als die interne Versorgungsspannung U_Vor < 60 V zur Verfügung stellt, sodass unter keinen Umständen Lebensgefahr besteht. –

In der Praxis aber, wenn wir es mit zunächst unbekannten elektronischen Geräten und Schaltungen zu tun haben, müssen wir stets daran denken und damit rechnen, dass in diesen auch eine (Konstant-) Stromquellen I₀ verbaut sein kann, die von außen durchgeführte Spannungs- und Strommessungen verfälschen kann („Unverhofft, kommt oft!“).

Das Ohmsche Gesetz in seiner allgemeinsten Form mit (Konstant-) Stromquelle I₀

Da in der bisherigen Abhandlung und Herleitung des Ohmschen Gesetzes mit

R = U / I = ∆U / ∆I → I = f(U) = 1/R * U → ∆I = f(U) = 1/R * ∆U → Steigungsdreieck!

eben keine (Konstant-) Stromquelle I₀ vorkam, diese demzufolge auch in der Formel R = U / I bzw. in der Funktion I = f(U) = 1/R * U keine Berücksichtigung fand, gilt das Ohmsche Gesetz wider Erwarten nicht in seiner allgemeinsten Form, sondern vielmehr nur für den Spezialfall, dass die Widerstandsgerade, d.h. der Graf der Funktion I = f(U) = 1/R * U, immer durch den Ursprung des Koordinatenkreuzes geht bzw. gehen muss (siehe oben)!

Das Ohmsche Gesetz in seiner allgemeinsten Form mit (Konstant-) Stromquelle I₀ und die nach I umgestellte Formel

I = f(U) = 1 / R * U + I₀ → ∆I = f(U) = 1 / R * ∆U + I₀ → Steigungsdreieck!

lässt sich auch wie folgt grafisch darstellen:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im Grafen der obenstehenden Funktion I = f(U) = 1 / R * U + I₀ unschwer sieht, geht die sogenannte Widerstandsgerade ( = Graf der Funktion I = f(U) ) jetzt nicht mehr durch den Ursprung des Koordinatenkreuzes!

Vielmehr verhält es sich beim Vorhandensein einer (Konstant-) Stromquelle I₀ mit I₀ > 0 so, dass die Widerstandskennline (= Kennlinie, Kennlinienverlauf des Stromes als Funktion der Spannung) aus dem Ursprung des Koordinatenkreuzes heraus parallel nach oben (oder unten für I₀ < 0) verschoben ist! -

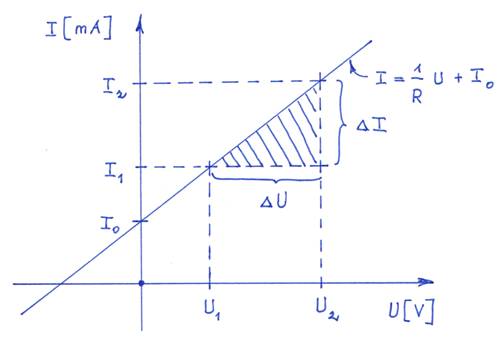
Auch wenn wir es in der Praxis äußerst selten in einer Schaltung mit einer (Konstant-) Stromquelle I₀ zu tun haben werden, so sollten wir trotzdem wissen, dass es nicht nur Spannungsquellen U₀, sondern eben auch Stromquellen I₀ gibt!

Aufgabe

Gegeben ist die nachfolgende Wertetabelle mit dem Strom I als Funktion der Spannung U mit I = f (U):

U [ V ]	-2	-1	0	1	2	3
I [ mA ]	-5	0	5	10	15	20

Berechne den Widerstand R der Widerstandsgeraden!

Lösung

Wie man anhand der Wertetabelle

U [ V ]	-2	-1	0	1	2	3
I [ mA ]	-5	0	5	10	15	20

sieht, ist die Widerstandsgerade mit I = f(U) = 1 / R * U + I₀ bei U = 0 V parallel nach oben aus dem Ursprung des Koordinatenkreuzes heraus verschoben, sodass sich bereits bei der Spannung U = 0 die Stromstärke I = f(U) = f(U₀) = 5 mA einstellt!

Setzt man in die Funktion I = f(U) = 1 / R * U + I₀ den Wert für die Spannung U = U₀ = 0 V ein, so folgt gemäß der Wertetabelle:

I = 1/R * U + I₀ →

I₀ = I – ( 1/R * U )

= 5 mA – ( 1/R * 0 V ) = 5 mA – 0 = 5 mA

Mit

R = U / I = ∆U / ∆I = ( U₂ – U₀ ) / ( I₂ – I₀ )

= ( 2 V – 0 V ) / ( 15 mA – 5 mA ) = 2 V / 10 mA = 2 V / 0,01 A = 2 V / 1/100 A = 2 * 100 V/A = 200 Ω

Das selbe Ergebnis stellt sich ein, wenn wir die allgemeingültige Funktion bzw. Formel

I = 1/R * U + I₀

nach R wie folgt umstellen, sodass folgt:

1/R * U = I – I₀ → 1/R = (I – I₀) / U →

R = 1 / [ (I – I₀) / U ] = 1 / [ (I – I₀) ] * U = U / (I – I₀) = U₂ / (I₂ – I₀)

= 2 V / ( 15 mA – 5 mA ) = 2 V / 10 mA = 0,2 KΩ = 200 Ω þ

Würden wir einfach nur das herkömmliche, nicht allgemein gültige Ohmsche Gesetz R = U / I, d.h. ohne Berücksichtigung der (Konstant-) Stromquelle I₀ verwenden, bekämen wir ein falsches Ergebnis für den Ohmschen Widerstand R:

R = U / I

= U₂ / I₂ = … = U_x / I_x

= U₃ / I₃

= 3 V / 20 mA = 0,15 KΩ = 150 Ω FALSCH!

Wem die allgemein gültige Funktion des Ohmschen Gesetzes mit

R = 1 / [ (I – I₀) / U ] = U / (I – I₀)

zu kompliziert erscheint, der sollte wegen des stets gültigen Steigungsdreiecks und der Geradengleichung (= Widerstandsgeraden) stattdessen das

allgemein gültige Ohmsche Gesetz

R = ∆U / ∆I

mit ∆U = U und ∆I = (I – I₀)

verwenden bei dem man nichts falsch machen kann! -

Jetzt wissen wir, dass in einem elektrischen Stromkreis auch bei einer Spannung von null Volt ein Strom von 5 mA fließen kann!

Nämlich dann, wenn sich im Stromkreis eine (Konstant-) Stromquelle I₀ mit z.B. I₀ = 5 mA befindet!

Das allgemein gültige Ohmsche Gesetzes in der Praxis

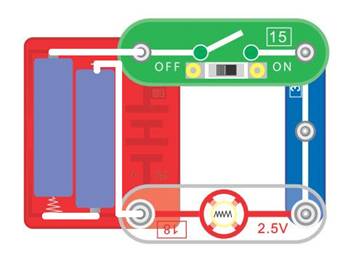
„Grau ist alle Theorie“ könnte man meinen. Dem ist aber nicht so, wenn man der Theorie in der Praxis begegnet bzw. die Theorie auf die Praxis anwendet! Was aber ist die Praxis?

Ganz einfach, unser erster Versuch, d.h. der Stromkreis, der im Gegenuhrzeigersinn (von rechts nach links) aus

· der Batteriehalterung [19],

· der Glühlampe [18],

· dem Einfach-Druckknopf [1] als Verbindungsglied und

· dem Gleit-/Schiebeschalter [15]

besteht.

Aus elektrischer Sicht sind dabei alle Bauelemente in Reihe sozusagen hintereinander in Serie miteinander verbunden/verschaltet,

(Zum Vergrößern bitte auf das Bild klicken!)

sodass der elektrische Strom I der Reihe nach alle Bauelemente nacheinander durchfließt.

Dabei verhält es sich so, dass die einzelnen Elektronen als negativ geladene Ladungsträger den Stromkreis selbst nur ganz langsam mit wenigern Metern pro Sekunde [m/s] durchwandern, während sich der Stromimpuls zusammen mit der Stromstärke und dem Strom I mit Lichtgeschwindigkeit (c = 300 000 Kilometer pro Stunde [km/h]) durch den Stromkreis ausbreitet, sodass die elektrische Stromstärke an jeder Stelle im Stromkreis und zu jeder Zeit gleich groß ist!

Demzufolge fließt durch die Glühlampe [18], dem Gleit-/Schiebeschalter [15] und der Batteriehalterung [19] stets derselbe Strom I mit der gleichen Stromstärke I, sodass gilt:

I = I_Glühlampe = I_Batterie = I_{Schiebeschalter}

Dabei geht unterwegs in der Schaltung kein Strom „verloren“, noch „stauen“ sich in der Glühlampe [18] oder einem anderen Bauelement etliche Ladungsträger in Form von Elektronen.

Würden sich nämlich irgendwo im Stromkreis Ladungsträger in Form der Elektronen - bildlich gesprochen - „versammeln“ oder „stauen“, dann würde z.B. der Einfach-Druckknopf [1] als Verbindungsglied zu glühen anfangen und durchschmoren (Brandgefahr) oder die Glühwendel der Glühlampe [18] würde durchbrennen, sodass diese nicht mehr leuchtet!

Das Ohmschen Gesetz in der

· speziellen Form R = U / I (ohne Stromquelle I₀) und

· Funktionsgleichung I = f(U) = 1/R * U

beherbergt aber in der obenstehenden Schaltung noch diverse weitere Spannungen U und Widerstände R als da sind

· die Batteriespannung U_Batterie,

· die Glühlampenspannung U_Glühlampe,

· den Widerstand in der Glühlampe R_Glühlampe und

· den Innen-Widerstand in der Batterie R_i.

Wenn wir die Wirkungsweise der Schaltung mit den Spannungen und Widerständen verstehen wollen, dann müssen wir diese zunächst horizontal spiegeln, da wir in der westlichen Welt, d.h. in den USA sowie in Ost- und West-Europa, von links nach rechts schreiben und lesen.

Außerdem muss der Gleit-/Schiebeschalter [15] die Stromzufuhr auf dem „Hinweg“ vom „+“-Pol der Batteriehalterung [19] zur Glühlampe [18] unterbrechen, d.h. ein- oder ausschalten, und nicht auf dem „Rückweg“ zum „-“-Pol Batteriehalterung [19].

Schließlich geht es aus Sicherheitsgründen prinzipiell darum, dass die Schaltung beim Ausschalten nicht mit der Stromzuführung („+“-Pol der Batteriehalterung [19]) verbunden bleibt:

(Zum Vergrößern bitte auf das Bild klicken!)

Bezüglich der Batteriehalterung [19] verhält es sich so, dass diese zwei 1,5 Volt Batterien vom Typ „Mignon AA“ enthält, die in Reihe geschaltet sind, sodass sich die einzelnen Teilspannungen U_Batt1 und U_Batt2 zur Gesamtspannung U_Batterie wie folgt addieren:

U_Batterie = U_Batt1 + U_Batt2 = 1,5 V + 1,5 V = 3,0 V

Im vorliegenden Fall kommen zwei Alkali-Mangan-Batterien der ISO-Norm „LR6“ zum Einsatz, die jeweils über eine Nennspannung U_Nenn von U_Nenn = 1,5 V verfügen. Dabei wird die Nennspannung U_Nenn = 1,5 V in der Praxis meist nur dann erreicht, wenn die Batterie noch unbenutzt ist und nicht zu lange auf dem Transportweg oder beim Händler im Regal zwischengelagert wurde. Dazu muss man wissen, dass es sich bei Batterien um kleine Chemiefabriken handelt, deren chemische Komponenten auch Alterungsprozessen unterliegen, sodass sich die in der Batterie gespeicherte Ladung im Laufe der Zeit verringert.

Wie man der obenstehenden Schaltung aus dem Versuch 1 entnehmen kann, darf die Glühlampe [18] nur mit einer Spannung von U_Glühlampe = 2,5 V betrieben werden. Da die beiden 1,5 Volt Batterien in der Batteriehalterung [19] aber in Serie zusammengeschaltet sind, liefern sie eine Gesamtspannung von

U_Batterie = U_Batt1 + U_Batt2 = 1,5 V + 1,5 V = 3,0 V.

Demzufolge würde beim Einschalten des Schiebeschalters [15] an die 2,5 Volt Glühlampe [18] eine um +20 % höhere Spannung von U_Batterie = U_Glühlampe + 0,5 V = 2,5 V + 0,5 V = 3,0 V gelangen, sodass die Gefahr besteht, dass die Glühlampe durchbrennt.

Eine diesbezüglich Rückfrage beim Hersteller und Lieferanten der Fa. Eichsfelder Technik, eitech GmbH, ergab aber, dass es noch nie Reklamationen wegen des Durchbrennens der Glühlampe [18] gegeben hätte.

Dass die Glühlampe [18] trotz höherer Spannung von 3,0 V nicht durchbrennt, liegt einerseits daran,

· dass Glühlampen mit einer (Spannungs-) Toleranz von bis zu +10 %

hergestellt werden und andererseits daran,

· dass die beiden 1,5 V Batterien der Batteriehalterung [19] selbst

über einen internen (Batterie-) Innenwiderstand R_i von z.B. R_i = 1,543 Ω verfügen.

Und bei zwei in Serie geschalteten 1,5 Volt Batterien vom Typ „Mignon AA“ beträgt dann der gesamte Innenwiderstand schon R_{i, ges} = 2 * 1,543 Ω = 3,086 Ω.

Was aber bewirkt der gesamte Innenwiderstand R_{i, ges} der beiden in Serie geschalteten 1,5 Volt Batterien?

Ganz einfach, sowohl die Glühlampe [18] mit der Glühlampenspannung U_Glühlampe = 2,5 V als auch der in Serie befindliche Innenwiderstand R_{i, ges} = 3,086 Ω mit dem Spannungsabfall U_{i, ges} = 0,5 werden von ein- und demselben Strom I = I_Batterie = I_{Schiebeschalter} = I_Glühlampe durchflossen, sodass die Glühlampe [18] leuchtet und sich die beiden in Serie geschalteten 1,5 Volt Batterien im Inneren des gesamten Innenwiderstandes R_{i, ges} entsprechend geringfügig erwärmen!

Diesbezüglich berechnet sich die im gesamten Innenwiderstand R_{i, ges} entstehende Wärmeverlustleistung P_{i, ges} wie folgt:

P_{i, ges} = U * I = U_{i, ges} * I = U_{i, ges} * U_{i, ges} / R_{i, ges} = ( U_{i, ges} )² / R_{i, ges}

= ( 0,5 V )² / 3,086 Ω = 0,25 V² / 3,086 V/A = 0,25 / 3,086 VA = 0,081 W = 81 mW

Die resultierende Stromstärke I, die durch die gesamte Schaltung als auch durch den gesamten Innenwiderstand R_{i, ges} fließt, berechnet sich wie folgt:

P_{i, ges} = U * I = U_{i, ges} * I → I = P_{i, ges} / U_{i, ges} = 81 mW / 0,5 V = 0,081 VA / 0,5 V = 0,162 A = 162 mA

Energieverschwendung der Glühlampe [18] als Heizstrahler

Herkömmliche Glühlampen mit einer Heizwendel aus Wolfram, einem Edelmetall, verfügen nur über einen geringen Wirkungsgrad von 5 % bei der Lichtausbeute, sodass 95 % der zugeführten elektrischen Energie als Wärme abgestrahlt werden.

Der schlechte Wirkungsgrad und die damit verbundene hohe Wärmeverlustleistung waren es dann auch, die dazu führten, dass die Glühlampen seitens der Europäischen Union ab 2008 verboten wurden. -

Jetzt wo wir den Strom I = 162 mA, der durch die gesamte Schaltung fließt, kennen, lässt sich die (Wärmeverlust-) Leistung P_Glühlampe der Glühlampe [18] ganz leicht wie folgt berechnen:

P_Glühlampe = U * I = U_Glühlampe * I = 2,5 V * 162 mA = 2,5 V * 0,162 A = 0,405 W ≈ 400 mW

Vergleicht man die (Wärmeverlust-) Leistung P_{i, ges} = 81 mW in den beiden Innenwiderständen der in Serie geschalteten 1,5 Volt Batterien vom Typ „Mignon AA“ mit der (Wärmeverlust-) Leistung P_Glühlampe = 400 mW der Glühlampe [18], so stellt man unschwer fest, dass die (Wärmeverlust-) Leistung der Glühlampe um rund das Fünffache größer ist als die in den Innenwiderständen der beiden 1,5 Volt Batterien! Und das ist gut so, schließlich soll ja die Glühlampe [18] glühen, d.h. leuchten und nicht die beiden 1,5 Volt Batterien!

Formeln zur Leistungsberechnung

>> Die Leistung als physikalische Größe bezeichnet die in einer Zeitspanne umgesetzte Energie bezogen auf diese Zeitspanne. Ihr Formelzeichen ist meist P (von englisch power), ihre SI-Einheit das Watt mit dem Einheitenzeichen W.

Im physikalisch-technischen Zusammenhang wird der Begriff Leistung in verschiedenen Bedeutungen verwendet:

· als installierte oder maximal mögliche Leistung (Kennzeichen eines Gerätes oder einer Anlage; auch Nennleistung genannt)

· als tatsächliche Leistung in einer Anwendung

· die zugeführte Leistung

· die im Sinne der Aufgabenstellung abgegebene Leistung.

Die Leistungsaufnahme und die für eine bestimmte Anwendung nutzbringende Leistungsabgabe können je nach Wirkungsgrad bzw. Abwärme erheblich voneinander abweichen. << (Quelle: Wikipedia)

>> Die physikalische Größe Leistung (Formelzeichen P von englisch power, Einheit Watt, Einheitenzeichen W) ist die in einer Zeitspanne umgesetzte Energie bezogen auf diese Zeitspanne. Sie wird dann als elektrische Leistung bezeichnet, wenn die bezogene oder gelieferte Energie eine elektrische Energie ist. (Quelle: Wikipedia)

Bei Gleichstrom ist die tatsächliche elektrische Leistung P das Produkt der elektrischen Spannung U und der elektrischen Stromstärke I:

P = U * I

Verhält sich der Verbraucher als ohmscher Widerstand R, so lässt sich die Leistung P durch Anwenden des Ohmschen Gesetzes auch wie folgt ausdrücken:

R = U / I → U = R * I → P = R * I²

R = U / I → I = 1/R * U → P = 1/R * U²

Berechnung des Innenwiderstands R_i einer realen Spannungsquelle

Während eine ideale Spannungsquelle über keinen Innenwiderstand R_i verfügt, besitzt eine reale Spannungsquelle sehr wohl einen Innenwiderstand R_i, der sich unglücklicherweise auch noch kontraproduktiv verhält, weil sich dieser mit zunehmender Entladung der Batterie auch noch vergrößert, sodass der Batterie immer weniger Energie entnommen werden kann und sich die für den angeschlossenen Verbraucher zur Verfügung stehende Stromstärke der Batterie I_Batterie mehr und mehr verringert!

Wenn man den Innenwiderstand R_i einer fabrikneuen Batterie ermitteln und berechnen will, dann muss man die Batterie an ihren Batteriepolen kurzschließen, diese mit einem dicken Kupferkabel überbrücken. Der dabei fließende Strom nennt man Kurzschlussstrom I_K, der übrigens ein Vielfaches des Nennstromes I_Nenn bei Dauerbetrieb betragen kann.

Da der teils extrem große Kurzschlussstrom I_K bei der kurzgeschlossenen Batterie ausschließlich über den Innenwiderstand R_i der Batterie fließt, erwärmen sich Batterie und Innenwiderstand R_i innerhalb kürzester Zeit sehr stark, sodass sich die Batterie stark ausdehnt, eventuell aufplatzt, die Chemikalien auslaufen und zu Verätzungen führen. Deshalb sollte man zur Messung des Kurzschlussstromes nur wenige Sekunden lang kurzschließen!

Zur Berechnung des Innenwiderstandes R_i einer Batterie benötigt man neben dem Kurzschlussstrom I_K auch noch die sogenannte Leerlaufspannung U_Leer.

Dabei handelt es sich bei der Leerlaufspannung U_Leer um diejenige Spannung, die sich an den Batteriepolen messen lässt, wenn kein Verbraucher (= Lastwiderstand R_Last → ∞) angeschlossen ist.

Wie wir bereits wissen, hat eine einzelne der beiden in Serie geschalteten 1,5 Volt Batterien vom Typ „Mignon AA“ eine Leerlaufspannung U_Leer von U_Leer = 1,5 V.

Demzufolge berechnet sich der Innenwiderstand R_i einer einzelnen 1,5 Volt Batterie bei einem Kurzschlussstrom I_K von I_K = 310 mA = 0,31 A zu:

I_K = U_Leer / R_i →

R_i = U_Leer / I_K = 1,5 V / 0,31 A = 4,839 Ω ≈ 4,8 Ω

Vergleicht man den Kurzschlussstrom I_K = 310 mA mit dem Laststrom I_Glühlampe = 162 mA der Glühlampe [18], so wäre der Kurzschlussstrom I_K um das 1,9-fache größer!

Da der Kurzschlussstrom I_K die Batterie stark belastet, wenn auch nur für ein paar Sekunden, so wird diese bei der Kurzschlussmessung mit einem entsprechenden Amperemeter (= Strommessgerät) trotzdem stark entladen! Deshalb sollte man eine Kurzschlussstrommessung nicht mehrmals nacheinander durchführen!

In diesem Zusammenhang stellt sich daher noch die Frage, ob man zur Berechnung des (Batterie-) Innenwiderstandes R_i nicht doch auf die Kurzschlussstrommessung verzichten kann, schließlich kennen wir von der Alkali-Mangan-Batterie noch zwei weitere (Hersteller-) Angaben als da sind:

Kapazität: 2,0 Ah

Energie: 3,0 Wh

Q = I * t = 2,0 Ah

W = P * t = 3,0 Wh = 3,0 W * 1 h = 0,3 W * 10 h →

Die Entladezeit der beiden in Serie geschalteten 1,5 Volt Batterien vom Typ „Mignon AA“ bezüglich der angeschlossenen Glühlampe [18] mit der Spannung U_Glühlampe = 2,5 V und dem Strom I_Glühlampe = 162 mA berechnet sich dann wie folgt:

t_Entlade = W / P = W / ( U * I ) = W / U * I

= 2 * 3,0 Wh / 2,5 V * 0,162 A = 6,0 VAh / 2,5 V * 0,162 A = 14,8 h

Die an die Batteriehalterung [19] angeschlossenen Glühlampe [18] lässt sich bis zu 14,8 Stunden lang betreiben!

In einer der beiden in Serie geschalteten 1,5 Volt Batterien ist die elektrische Energie W = 3,0 Wh mit der Ladungsmenge Q = 2,0 Ah gespeichert (siehe oben).

Demzufolge lässt sich die Angabe „Energie: 3,0 Wh“ mit der Formel W = P * t = U * I * t = U * Q berechnen.

W = P * t = U * I * t = U * Q →

W = Q * U Mit Q = I * t und durch entsprechendes Umstellen der neuen Formel lässt sich nun auch der adäquate Entladestrom berechnen:

I = W / ( U * t ) Bestätigung der Formel durch Probe der Maßeinheiten: [ A ] = [ Ws / ( V * s) ] = [ VAs / ( Vs ) ] þ

Q = W / U Die ist eine neue Formel zur Berechnung

der Ladungsmenge Q als Funktion der gespeicherten Energie W

U = W / Q Und die ist die interessantere Formel zur Berechnung der Nennspannung U_Nenn, wenn

es darum geht, mittels der beiden Angaben „Kapazität: 2,0 Ah“ und „Energie: 3,0 Wh“

die Nennspannung der 1,5 Volt Batterie zu berechnen!

Probe:

Q = W / U = P * t / U = U * I * t / U = I * t þ

Setzt man die beiden (Hersteller-) Angaben „Kapazität: 2,0 Ah“ und „Energie: 3,0 Wh“ zur 1,5 Volt Batterie vom Typ „Mignon AA“ in die umgestellte, neue Formel zur Berechnung der Nennspannung ein, dann lässt sich die Nennspannung U_Nenn der „Mignon AA“-Batterie wie folgt berechnen:

U = W / Q

= 3,0 Wh / 2,0 Ah = 3,0 VAh / 2,0 Ah = 1,5 V Nennspannung der „Mignon AA“-Batterie

Ersetzt man Q durch Q = I * t in der Formel U = W / Q = W / ( I * t ), so lässt sich der Nennstrom I_Nenn der 1,5 Volt „Mignon AA“-Batterie wie folgt berechnen:

U_Nenn = W / Q = W / ( I * t ) → I * t = W / U → [ Ah ] = [ VAh / V ] bezüglich der Maßeinheiten þ

I_Nenn = ( W / U_Nenn ) / t ) = W / ( U_Nenn * t ) → [ A ] = [ VAh / V / h ] bezüglich der Maßeinheiten þ

Hier an dieser Stelle stellt sich die Frage, welche Zeitdauer t wir für die Stromentnahme einsetzen müssen,

um auf diese Weise den Nennstrom I_Nenn berechnen zu können mit dem sich die 1,5 Volt „Mignon AA“-Batterie am längsten bzw. optimal betreiben lässt.

Diesbezüglich orientieren wir uns an der Angabe der Ladungsträgermenge Q = 2,0 Ah entsprechend der Herstellerangabe (siehe oben): Q = 2,0 Ah = 2 A * 1 h = 0,2 A * 10 h = 200 mA * 10 h = 2 000 mAh

I_Nenn = 3,0 Wh / ( 1,5 V * 10 h ) = 3,0 VAh / 1,5 V / 10 h = 2 / 10 A = 0,2 A = 200 mA

Da die in der 1,5 Volt „Mignon AA“-Batterie gespeicherte Ladungsträgermenge Q nicht auf einen Schlag „verbraucht“ werden soll, was nämlich einem Kurzschluss der Batterie gleich käme, sondern vielmehr kontinuierlich über einen längeren Zeitraum von mehreren Stunden und wir bereits wissen, wie groß die Stromstärke der Glühlampe [18] ist, entscheiden wir uns bei der Berechnung für Q = 2,0 Ah = 0,2 A * 10 h = 200 mA * 10 h.

Selbstverständlich lässt sich der Strom durch die Glühlampe [18] und dessen Stromstärke auch für die beiden in Serie geschalteten 1,5 Volt Batterien mit der doppelten Ladungsmenge von Q = 2 * 3,0 Wh, der gesamten Batteriespannung von U_{Batt, ges} = 2,5 V und der bereits berechneten Entladezeit t_Entlade = 14,8 h wie folgt berechnen:

I_Glüh = ( W / U_Nenn ) / t ) = W / ( U_Nenn * t )

= 2 * 3,0 Wh / ( 2,5 V * 14,8 h ) = 6,0 VAh / 2,5 V / 14,8 h = 0,162 A = 162 mA þ

Zur Erinnerung: die geringere Stromstärke von „nur“ 162 mA der Glühlampe [18] stellt sich deshalb ein, weil an den beiden Innenwiderständen der in Serie geschalteten 1,5 Volt Batterien ein Spannungsabfall von insgesamt 0,5 V auftritt, sodass sich der resultierende Strom I_Glühlampe der in Serie geschalteten Widerstände entsprechend verringert, während sich gleichzeitig die max. Stromentnahmezeit bzw. Entladezeit der 1,5 Volt Batterien entsprechend vergrößert!

>> Aufgrund des positiven Temperaturkoeffizienten (Kaltleiter) fließt beim Einschalten einer Metalldraht-Glühlampe ein sehr hoher Einschaltstrom (das Fünf- bis Fünfzehnfache des Nennstromes), der die Glühwendel schnell auf die Betriebstemperatur aufheizt. Mit der Zunahme des elektrischen Widerstands bei steigender Temperatur sinkt der Strom auf den Nennwert. Die früher gebräuchlichen Kohlenfadenlampen zeigten dagegen eine sanfte Zunahme des Stromes beim Einschalten, da erst mit steigender Temperatur genügend Ladungsträger für den Stromtransport freigesetzt werden (Kohle ist ein Heißleiter).

Der hohe Einschaltstrom ist die Ursache für Ausfälle von Glühlampen unmittelbar beim Einschalten (siehe unten). Dabei kann (bei höheren Betriebsspannungen) ein Lichtbogen zünden, was zum Auslösen der Sicherung und/oder zum Bersten des Glaskolbens führen kann. Glühlampen für Netzspannung sind daher im Sockel mit einer Schmelzsicherung in Form eines dünnen Anschlussdrahtes versehen.

Der hohe Einschaltstrom von Metalldrahtglühlampen belastet das Energieversorgungssystem des Leuchtmittels. << (Quelle: Wikipedia)

Jetzt wissen wir, dass der hohe Einschaltstrom einer Glühlampe I_Einschalt ≥ 5 * I_Nenn = 5 * 200 mA = 1 000 mA = 1,0 A und mehr betragen kann, unsere beiden in Serie geschalteten 1,5 Volt Batterien für einen kurzen Moment extrem belasten und kurzschließen, sodass für die Berechnung des gesamten Innenwiderstandes R_{i, ges} der beiden Batterien folgt:

R_i = U_Leer / I_K → R_{i, ges} = U_Leer / I_K = U_Leer / ( 5 * I_Nenn ) = 3,0 V / ( 5 * 0,2 A ) = 3,0 V / 1 A = 3 Ω

Dass beim Einschalten der Glühlampe tatsächlich durch die beiden in Serie geschalteten 1,5 Volt Batterien ein Einschaltstrom von bis zu 1,0 A fließt bzw. fließen kann, kann ich mir praktisch nicht vorstellen, da sich der gesamte Innenwiderstand der 1,5 V Batterien wegen der Reihenschaltung verdoppelt, während sich die Stromstärke gleichzeitig halbiert!

Ferner gilt es zu bedenken, dass sich der hohe Einschaltstrom der Glühlampe kurz nach dem Einschalten nur für wenige Millisekunden einstellt, sodass sich dieser wegen der Trägheit von analogen und auch digitalen Strommessgeräten nicht messen und anzeigen lässt. Trotzdem gibt es durch den hohen Einschaltstrom der Glühlampe natürlich einen verstärkten Verschleiß der Glühwendel mit der Folge, dass diese nur eine begrenzte Lebensdauer hat.

>> Eine Möglichkeit, die Lebensdauer zu verlängern, ist daher die Begrenzung des Einschaltstroms oder die in der Veranstaltungstechnik häufig angewandte Vorheizung (engl. Pre Heat) durch einen permanenten Stromfluss knapp unterhalb der Leuchtschwelle. << (Quelle: Wikipedia)

Berechnen des Widerstandes der Glühlampe [18] mittels Differenzenquotient

„Differenzquotient“ hört sich sehr mathematisch und kompliziert an, ist es aber nicht wirklich. Was eine Differenz ist, wissen wir bereits und zwar die Spannungs- oder Stromdifferenz mit ∆U oder ∆I:

∆U = U₂ – U₁ mit der Bedingung U₂ > U₁

∆I = I₂ – I₁ mit der Bedingung I₂ > I₁

Ein Quotient ist nichts anderes als ein Verhältnis im Sinne eines Bruches mit Zähler und Nenner. Dabei legt der Nenner das Teilungsverhältnis fest und der Zähler zählt bzw. legt fest, wie oft das Teilungsverhältnis angewendet werden soll:

Eine drei Viertel ( = ¾ ) Erdbeertorte ist gleich eine ganze Torte, die in Viertelstücke mit dem Küchenmesser aufgeteilt wird.

Demzufolge hat der Nenner, der unter dem Bruchstrich steht, den Wert 4 im Sinne von einem Viertel ( = ¼):

¾ Erdbeertorte = 3 Kuchenstücke Erdbeertorte zu je einem Viertel ( = ¼ )

= 3 * ¼ = ¾ einer ganzen, d.h. 4/4 Erdbeertorte.

Wie man sieht, hat der Zähler, der über dem Bruchstrich steht, den Wert 3 und der Nenner, der unter dem Bruchstrich steht und das Teilungsverhältnis festlegt, den Wert 4.

Eine drei Viertel ( = ¾ ) Erdbeertorte hat also den Quotienten ¾, sozusagen als Bruch mit dem Zähler 3 über dem Bruchstrich und dem Nenner 4 unter dem Bruchstrich!

Für den Differenzenquotient von Spannungs- und Stromdifferenz folgt:

Differenzenquotient = Spannungsdifferenz / Stromdifferenz = ∆U / ∆I = U₂ – U₁ / I₂ – I₁

Was aber ist der Differenzenquotient ∆U / ∆I ?

Tipp:

Wie lautet das allgemein gültige Ohmsche Gesetz? (Siehe weiter oben!)

Es lautet nicht: R = U / I, sondern …

Kehren wir zurück Glühlampe [18] und deren Berechnung mittels des Differenzenquotienten ∆U / ∆I = U₂ – U₁ / I₂ – I₁

Wie wir wissen, werden in der Batteriehalterung [19] zwei 1,5 Volt Batterien vom Typ „Mignon AA“ in Serie, d.h. in Reihe hintereinander geschaltet:

U_Batterie = U_ges = U_{Batt 1} + U _{Batt 2} mit U _{Batt 1} = U _{Batt 2} = 1,5 V → U₂ = U _{Batt 1} + U _{Batt 1} = 2 * U _{Batt 1} = 2 * 1,5 V = 3,0 V

Da wir zwecks Berechnung des Differenzenquotienten ∆U / ∆I = U₂ – U₁ / I₂ – I₁ noch eine weitere Spannung, nämlich die Spannung U₁ mit U₁ < U₂ benötigen, entfernen wir bei der zweiten Messung eine der beiden 1,5 Volt Batterien, sodass die Batteriehalterung [19] nur noch mit einer 1,5 Volt Batterie betrieben wird.

Damit die Batteriehalterung [19] mit jetzt nur noch mit einer 1,5 Volt Batterie auch funktioniert, müssen wir die entfernte zweite 1,5 Volt Batterie elektrisch mittels eines kurzen, z.B. blauen Kabels überbrücken:

(Zum Vergrößern bitte auf das Bild klicken!)

Achtung:

Was man auf keinen Fall machen sollte, ist, die zweite Batterie rechts im Batteriefach zu belassen und mit einem Kabel überbrücken, da diese dann kurzgeschlossen wird, sich im Falle des Kurzschlusses stark erhitzt, sodass das Gehäuse aufplatzt und die ätzende Batterieflüssigkeit ausläuft.

Wenn wir jetzt also die Batteriehalterung [19] nur noch mit einer 1,5 Volt Batterie betreiben, dann folgt für die Batteriespannung:

U_Batterie = U_ges = U_{Batt 1} → U₁ = U _{Batt 1} = 1,5 V

Für die Berechnung der Spannungsdifferenz ∆U folgt dann:

∆U = U₂ – U₁ = 3,0 V – 1,5 V = 1,5 V → Die Bedingung U₂ > U₁ ist erfüllt!

Für die Stromdifferenz ∆I folgt durch Einsetzen der Werte (siehe weiter oben):

∆I = I₂ – I₁ = 200 mA – 100 mA = 0,2 A – 0,1 A = 0,1 A → Die Bedingung I₂ > I₁ ist erfüllt!

Dabei beträgt die Stromstärke I₂ = I_Nenn = 200 mA beim Betrieb der Batteriehalterung [19] mit zwei 1,5 Volt Batterien vom Typ „Mignon AA“ in Serie und einer Entladedauer von t = 10 h (siehe weiter oben!).

Demzufolge beträgt die Stromstärke I₁ beim Betrieb der Batteriehalterung [19] mit nur noch einer 1,5 Volt Batterie wegen der hälftigen Batteriespannung nur noch (ungefähr) die Hälfte des Nennstromes I₂:

I₁ ≈ ½ I₂ = 0,5 * 200 mA = 100 mA = 0,1 A

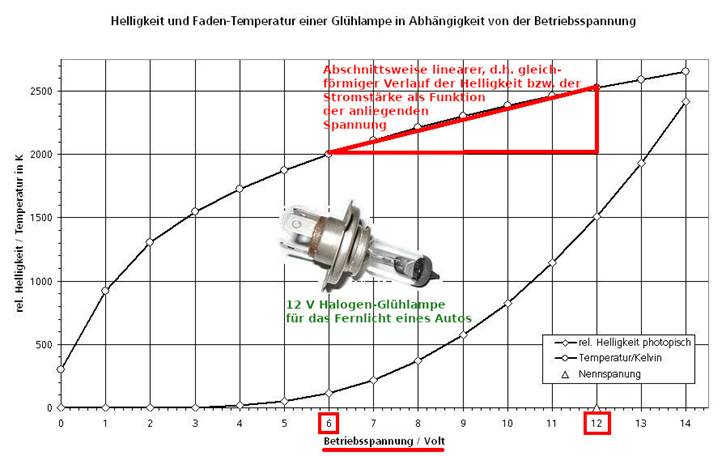
Die Stromstärke I₁ beträgt nur ungefähr die Hälfte des Nennstromes I₂, da dieser von der jeweiligen (Glühlampen-) Spannung U₂ bzw. U₁ abhängt: I₂ = f (U₂), I₁ = f (U₁)

Außerdem ist der Helligkeitsverlauf bzw. der Verlauf der Stromstärke durch die Glühlampe nur abschnittsweise linear, d.h. gleichförmig (= konstante Steigung m mit y = m x +b bei der Geradengleichung bzw. I = f(U) = 1 / R * U + I₀ mit I₀ = 0).

Als Beispiel sei hier der Helligkeits- bzw. Stromverlauf einer 12 Volt Halogenlampe erwähnt (Quelle: Wikipedia)

(Zum Vergrößern bitte auf das Bild klicken!)

Der Helligkeits- bzw. Stromverlauf unserer 2,5 Volt Glühlampe [18] mit Wolfram-Glühwendel verhält sich ähnlich wie der der 12 Volt Halogen-Glühlampe beim Auto, d.h. abschnittsweise linear, allerdings nur im Spannungsbereich vom [ 1,5 … 3,0 V ].

Für die Berechnung des Differenzenquotienten ∆U / ∆I = U₂ – U₁ / I₂ – I₁ der Glühlampe [18] folgt:

∆U / ∆I = U₂ – U₁ / I₂ – I₁ = 3,0 V – 1,5 V / 0,2 A – 0,1 A = 1,5 V / 0,1 A = 15 V/A = 15 Ω

Spätestens jetzt wissen wir, dass es sich beim Differenzenquotienten ∆U / ∆I in Wirklichkeit um den ohmschen Widerstand R_Glühlampe der Glühlampe [18] handelt!

Selbstverständlich lassen sich bei der Berechnung des Differenzenquotienten ∆U / ∆I auch die gemessenen Werte aus dem Abschnitt „Energieverschwendung der Glühlampe [18] als Heizstrahler“ mit

U_Glühlampe = 2,5 V und I = 162 mA wie folgt einsetzen und berechnen:

R_Glühlampe = ∆U / ∆I = U / I = U_Glühlampe / I_Glühlampe

= 2,5 V / 162 mA = 2,5 V / 0,162 A = 15,4 Ω ≈ 15 Ω

Der gesamte Innenwiderstand R_{i, ges} der beiden in Serie geschalteten 1,5 Volt Batterien der Batteriehalterung [19] lässt nun ebenfalls wie folgt berechnen:

R_{i, ges} = ∆U / ∆I = U_{Ri, ges} / I_Glühlampe

= 0,5 V / 162 mA = 0,5 V / 0,162 A = 3,086 Ω ≈ 3 Ω

Siehe weiter oben im Abschnitt „Das allgemein gültige Ohmsche Gesetzes in der Praxis“.

Zur Erinnerung: der Spannungsabfall U_{Ri, ges} = 0,5 V im Inneren des gesamten Innenwiderstandes R_{i, ges} lässt sich von außen, d.h. an den Anschlussklemmen der Batteriehalterung [19] wider Erwarten nicht messen, sondern nur berechnen!

Erste Messung von Spannung U₂ und Stromstärke I₂ in der Praxis

mittels der beiden in Serie geschalteten 1,5 Volt Batterien vom Typ „Mignon AA“ in der Batteriehalterung [19]

(Zum Vergrößern bitte auf das Bild klicken!)

Für den Differenzenquotienten messen wir das erste Wertepaar P₂ = ( U₂ / I₂ ) = ( 2,53 V / 162 mA )

Zweite Messung von Spannung U₁ und Stromstärke I₁ in der Praxis

mittels nur noch einer 1,5 Volt Batterie vom Typ „Mignon AA“ in der Batteriehalterung [19]

(Zum Vergrößern bitte auf das Bild klicken!)

Für den Differenzenquotienten messen wir das zweite Wertepaar P₁ = ( U₁ / I₁ ) = ( 1,3 V / 112 mA )

Für die Berechnung des Differenzenquotienten R = ∆U / ∆I = U₂ – U₁ / I₂ – I₁ der Glühlampe [18] folgt:

R = ∆U / ∆I = U₂ – U₁ / I₂ – I₁

= 2,53 V – 1,3 V / 162 mA – 112 mA = 1,23 V / 50 mA = 0,0246 KΩ = 24,6 Ω

I = f(U) = 1 / R * U + I₀ → mit I₀ = 0, da im Stromkreis keine (Konstant-) Stromquelle I₀ verhanden ist!

Für die Spannung U₂ = 2,53 V folgt:

I₂ = f(U₂) = 1 / R * U₂

= 1 / 24,6 Ω * 2,53 V = 0,103 A = 103 mA

Und für die Spannung U₁ = 1,3 V folgt:

I₁ = f(U₁) = 1 / R * U₁

= 1 / 24,6 Ω * 1,3 V = 0,0528 A = 52,8 mA

Da die Geradengleichung (mathematisch) bzw. die Widerstandsgerade (physikalisch, elektrotechnisch)

I = f(U) = 1 / R * U + I₀ mit I₀ = 0

für alle beliebigen Spannungen U im Bereich von [ 0 V … 3 V ] gilt, müsste sich der Strom I₁ bei der Verwendung nur einer 1,5 Volt Batterie exakt halbieren, so dass gilt:

I₁ = ½ * I₂ = 0,5 * 103 mA = 51,5 mA

Wie man aber sieht, ist dem aber nicht so hundertprozentig, ist der Strom I₁ mit I₁ = 52,8 mA mit + 2,5 % etwas größer als halb so groß!

Ähnlich verhält es sich übrigens bei den (Batterie-) Spannungen U₂ = 2,53 V und U₁ = 1,3 V! Auch hier ist die Spannung U₁ mit U₁ = 1,3 V nicht hundertprozentig halb so groß, sondern mit + 2,8 % ebenfalls etwas größer als halb so groß:

U₁ = ½ * U₂ = ½ * 2,53 V = 1,265 V

In diesem Zusammenhang stellt sich nun die Frage, was die Ursachen dafür sind, schließlich bewegen sich die hälftigen Werte für Spannung und Strom noch im Toleranzbereich!

Diesbezüglich sind es hauptsächlich zwei Gründe für die geringen Abweichungen bei der Berechnung der hälftigen Werte:

1. die beiden 1,5 Volt Batterien vom Typ „Mignon AA“ sind nicht 100%tig gleichartig, d.h. identisch!

Der Grund dafür kann sein, dass es bei der Herstellung der Batterien geringe chemische und damit elektrische Unterschiede im Sinne von Toleranzen gibt. Insbesondere dann, wenn die Batterien aus unterschiedlichen Produktionsserien stammen!

Tatsächlich verhält es sich aber so, dass eine der beiden 1,5 Volt Batterien vom Typ „Mignon AA“ bereits stärker als die andere entladen wurde und deshalb eine geringere Ladungsmenge Q von Ladungsträgern, d.h. Elektronen, enthält.

2. die Glühdrahttemperatur (= Helligkeitsverlauf) als Funktion der Spannung an der Glühlampe verläuft wie bereits erwähnt nur abschnittsweise gleichförmig, d.h. linear im Sinne einer Geraden mit konstanter Steigung!

Ob dabei der linear ansteigende Bereich der Glühdrahttemperatur bzw. Helligkeit tatsächlich bei U₁ = 1,5 V beginnt oder vielleicht doch erst oberhalb von U₁ > 1,5 V und darüber hinaus, lässt sich nicht so ohne Weiteres feststellen.

Demzufolge muss man damit rechnen, dass der linear ansteigende Bereich der Glühdrahttemperatur bzw. Helligkeit im wesentlich kleineren Bereich von [ 2,0 V … 3,0 V ] stattfindet als wie bisher angenommen im Bereich von [ 1,5 V … 3,0 V ].

Eben weil die Kennlinie des Verlaufs der Glühdrahttemperatur bzw. Helligkeit nicht durchgehend linear verläuft, müssen wir jederzeit damit rechnen, dass sich aufgrund eines nichtlinearen Verlaufs der Kennlinie, rechnerische Abweichungen einstellen.

Zu guter Letzt muss man also wissen, dass es sich bei Glühlampen und Batterien nicht um lineare Bauteile handelt, die sich wie Ohmsche Widerstände mit linear ansteigender Kennlinie verhalten und berechnen lassen.

Siehe auch „Entladung“ einer Alkali-Mangan-Zelle wie die 1,5 V Batterien in der Batteriehalterung [19]. –

Reihenschaltung elektrischer Bauelemente und deren Spannungen

Hier im ersten Versuch setzt sich die Schaltung aus insgesamt vier Bauteilen zusammen (im Uhrzeigersinn):

1. Schiebeschalter [15],

2. Dreifach-Druckknopf [3] (= Verbindungsleiter),

3. Glühlampe [18] mit 2,5 V und

4. Batteriehalterung [19]

zwecks Aufnahme zweier in Reihe geschalteten

1,5 Volt Batterien vom Typ „Mignon AA“.

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man oben in der Schaltung sieht, sind die beiden 1,5 Volt Batterien nacheinander, d.h. in Reihe, geschaltet.

Dabei addieren sich die beiden Teilspannungen U_{Batt_1} = 1,3 V (siehe oben) und U_{Batt_2} = U₂ – U₁ = 2,53 V – 1,3 V = 1,23 V (siehe oben, Abschnitt „Berechnen des Widerstandes der Glühlampe [18] mittels Differenzenquotient“) zur Gesamtspannung von U_{Batt_ges} = U_{Batt_1} + U_{Batt_2} = 1,3 V + 1,23 V = 2,53 V

Eigentlich müssten, wie bereits besprochen, die beiden Teilspannungen U_{Batt_1} und U_{Batt_2} der beiden baugleichen und ansonsten identischen 1,5 Volt Batterien vom Typ „Mignon AA“ gleich groß sein! Sind sie aber nicht, da die zweite 1,5 Volt Batterie offensichtlich bereits stärker entladen wurde!

Reihenschaltung – von der Addition von Teilspannungen zur Gesamtspannung

Allgemein gilt, dass sich alle (Batterie-) Teilspannungen zur Gesamtspannung U_ges addieren:

U_ges = U₁ + U₂ + … + U_n

Wenn alle in Reihe geschalteten Batterien vom gleichen Typ wie z.B. „Mignon AA“ sind, über die gleich große Batteriespannung und darüber hinaus die gleiche Ladungsmenge Q enthalten, dann lässt sich die Addition der Teilspannungen mit U₁ = U₂ = … = U_n wie folgt vereinfachen:

U₁ = U₂ = … = U_n = U_ges / n →

U_ges = U_n * n

Dabei verhält es sich so, dass beide 1,5 Volt Batterien wegen der Reihenschaltung von ein- und demselben Strom, dessen Größe I_Glühlampe von der Größe der gesamten Batteriespannung U_{Batt_ges} = 2,53 V bestimmt wird, durchflossen werden:

I = I_Glühlampe = U_Glühlampe / R_Glühlampe

Da der gleich große Strom I_Glühlampe durch alle Bauteile der Schaltung fließt, folgt:

I = I_Batterie = I_Glühlampe

Setzt man zwecks Überprüfung die entsprechenden Werte ein, so folgt für die Stromstärke I im Stromkreis:

I = U_{Batt_ges} / R_Glühlampe

= 2,53 V / 24,6 Ω = 2,53 V / 24,6 V/A

= 0,103 A = 103 mA (siehe oben beim “Differenzenquotienten R”!)

Von der Reihenschaltung zum Spannungsteiler

Dass sich elektrische Bauelemente einer Schaltung, eines Stromkreises, zu denen auch die beiden in Serie geschalte-ten 1,5 Volt Batterien vom Typ „Mignon AA“ gehören, in Reihe schalten lassen und sich dabei die jeweiligen Teilspannung zur Gesamtspannung addieren, wissen wir nun.

Aber dass sich eine Teilspannung auch zu einer weiteren Teilspannung oder zur Gesamtspannung ins Verhältnis setzen lässt, wissen wir noch nicht bzw. werden wir gleich sehen.

Erinnern wir uns daran, dass eine reale Spannungsquelle wie z.B. unsere 1,5 Batterie in ihrem Inneren, d.h. in der kleinen chemischen Fabrik zur Stromerzeugung, einen sogenannten Innenwiderstand R_i besitzt, den man allerdings nicht sehen, dafür aber wie folgt berechnen kann:

R_{i, Batt_1} = U_{Batt_1} / I = U_{Batt_1} / I_Glühlampe

= 1,3 V / 103 mA = 1,3 V / 0,103 A = 12,62 Ω

R_{i, Batt_2} = U_{Batt_2} / I = U_{Batt_2} / I_Glühlampe =

= 1,23 V / 103 mA = 1,23 V / 0,103 A = 11,94 Ω

R_{i, ges} = ( U_{Batt_1} + U_{Batt_2} ) / I = ( U_{Batt_1} + U_{Batt_2} ) / I_Glühlampe

= ( 1,3 V + 1,23 V ) / 103 mA = 2,53 V / 0,103 A = 24,56 Ω þ

Setzen wir nun also die verschiedenen Innenwiderstände

R_{i, Batt_1} = U_{Batt_1} / I

R_{i, ges} = ( U_{Batt_1} + U_{Batt_2} ) / I = U_{Batt, ges} / I

zueinander ins Verhältnis, indem wir den Quotienten wie folgt bilden:

R_{Batt_1} / R_{i_ges} = ( U_{Batt_1} / I ) / ( U_{Batt, ges} / I )

= U_{Batt_1} / U_{Batt, ges}

Setzen wir nun zur Kontrolle die obenstehende Werte ein, sodass folgt:

R_{Batt_1} / R_{i_ges} = 12,62 Ω / 24,56 Ω = 0,5138

= U_{Batt_1} / U_{Batt, ges} = 1,3 V / 2,53 V = 0,5138

R_{Batt_1} / R_{i_ges} = U_{Batt_1} / U_{Batt, ges} þ

>> Ein Spannungsteiler besteht im Regelfall aus zwei Widerständen [ oder wie im vorliegenden Fall aus zwei Spannungsquellen U_{Batt_1,2} (nebst internen Innenwiderständen R_i) ], an denen sich die Gesamtspannung U_ges in zwei Teilspannungen aufteilt. Die Grundform ist der unbelastete Spannungsteiler, der einer Reihenschaltung aus zwei Widerständen entspricht.

Spannungsteiler werden verwendet, um Arbeitspunkte (Spannungsverhältnisse) an aktiven Bauelementen einzustellen. Zum Beispiel bei einer Transistor-Verstärkerschaltung. Dabei wird nur ein kleiner Stromfluss erzeugt. Hauptsächlich werden mit einem Spannungsteiler Spannungspotentiale erzeugt, die geringer sind als die Gesamtspannung.

Sobald man einen unbelasteten Spannungsteiler mit einem Verbraucher beschaltet [ d.h. belastet ], verändert sich die Spannungsverteilung im Spannungsteiler. << (Quelle: Elektronik-Kompendium)

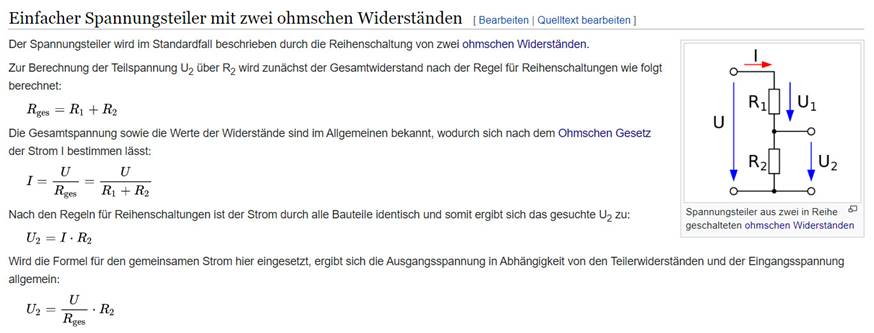
>> Der Spannungsteiler ist eine Reihenschaltung aus passiven elektrischen Zweipolen, durch die eine elektrische Spannung aufgeteilt wird. (…)

(Zum Vergrößern bitte auf das Bild klicken!)

<< (Quelle: Wikipedia)

Wie man oben sieht, ist die Definition des Spannungsteilers von Wikipedia wesentlich präziser:

„Der Spannungsteiler ist eine Reihenschaltung aus passiven elektrischen Zweipolen,

durch die eine elektrische Spannung aufgeteilt wird.

„Passive elektrische Zweipole“ sind z.B. Widerstände, Glühlampen, (Gleichrichter-) Dioden, Leuchtdioden, aber auch Batterien, (Kupfer-) Spulen oder Kondensatoren. Sozusagen alles was zwei „Beinchen“, d.h. Anschlüsse bzw. Anschlussdrähte hat.

Dabei können das auch Halbleiter wie z.B. unterschiedlich farbige Leuchtdioden sein (siehe Versuch 14 - Der Gebrauch einer Leuchtdiode).

Wichtig dabei ist, dass der Halbleiter, der übrigens über keine linear ansteigende Kennlinie bzw. Kennlinien verfügt, keine Verstärkung von Spannungen und/oder Strömen aufweist!

Bei unserem Spannungsteiler, der aus den beiden in Serie geschalteten 1,5 Volt Batterien vom Typ „Mignon AA“ nebst der integrierten Innenwiderständen R_i besteht, handelt es sich sozusagen um einen Spezial-Spannungsteiler, dessen Einzelkomponenten sich jeweils

1. aus einem integrierten Innenwiderstand R_i und

2. einer in Reihe dazu geschalteten 1,5 Volt Spannungsquelle in Form der 1,5 Volt Batterie

zusammensetzen!

Dabei begrenzt der Innenwiderstand R_i den Stromfluss in der 1,5 Volt Batterie und die Stromstärke I = I_Glühlampe im Stromkreis, während die in Serie befindliche Spannungsquelle jeweils eine Teilspannung im Spannungsteiler definiert!

Diesbezüglich verhält es sich bei der einzelnen (Teil-) Spannung an den Anschlussklemmen der 1,5 Volt Batterie so, dass diese die treibende Kraft darstellt, ähnlich wie das Gefälle bei einem Fluss, während sich der durch den Stromkreis fließende Strom und dessen Stromstärke I = I_Glühlampe = I_Batterie mit der Breite des Flusses (= Stromstärke) und der Breite des Flussbettes (= Leiterquerschnitt) vergleichen lässt. Denn zu einem „dicken“ Strom gehört auch ein „dickes Flussbett“ im Sinne eines entsprechenden Kupferdrahtes bzw. Leiters nebst maßgeblicher Leiterquerschnittsfläche A = π r² [ mm² ] wie z.B. in Form des blauen Verbindungsstückes [3].

Der sogenannte elektrische Leitwert G ist uns bereits schon begegnet, nur haben wir ihn bisher noch nicht bemerkt, weil er sich hinter dem Ohmschen Gesetz versteckt hat:

R = 1 / G = U / I →

G = 1 / R = 1 / U / I = 1 / U * I = I / U

G = I / U

Für die [ Maßeinheiten ] folgt:

[ A / V ] = [ S ], wobei [ S ] für Siemens steht.

Nehmen wir mal an, wir haben es mit dem vierfachen Leitwert im Sinne der Leitfähigkeit zu tun: 4G, wobei 4G (LTE) kein Mobilfunkstandard ist und G auch nichts mit der Erdanziehungskraft g = 9,81 kg m/s² zu tun hat. 4G bedeutet einfach nur vierfacher Leitwert.

Setzen wir 4G = 4 * 1 G ein in das Ohmsche Gesetz R = U / I = 1 / G ein, so folgt:

4G = 4 G = 4 * G = 4 * 1 / R = 4 / R = 4 * 1 / R = 1 / ¼ R → 4 G = 1 / ¼ R → G = 1 / R þ

Wenn also der Leitwert G um das Vierfache größer ist, dann bedeutet dies zugleich auch, dass die Leitfähigkeit um das Vierfache größer ist, sodass der Leiter mit 4G den elektrischen Strom um das Vierfache besser leitet.

Demzufolge muss der Widerstand R des Leiters um das Vierfache kleiner sein, sodass dieser nur noch ein Viertel beträgt: 4G = 1 / ¼ R

Jetzt wissen wir zwar wie es um den formelmäßigen Zusammenhang zwischen dem Ohmschen Widerstand R und dem Leitwert G mit G = 1 / R bestellt ist, wissen aber immer noch so nicht richtig, wie sich der Leitwert bzw. Leitfähigkeit physikalisch definiert.

Der spezifische Widerstand

Während es beim Ohmschen Gesetz R = U / I formal keine Rolle spielt, ob wir es mit einem „dünnen“ oder „dicken“ Stromkabel aus Aluminium, Kupfer, Platin, Silber oder Gold zu tun haben, spielt die Beschaffenheit des als Stromkabel verwendeten Materials z.B. bei der elektrischen Hausinstallation, d.h. der Verlegung der Stromkabel im Haus, für den Bauherrn schon ein maßgebliche Rolle, da die Kabeltrommel mit dem Stromkabel aus Platin, Silber oder Gold ein Vielfaches kostet, als eine Kabeltrommel mit Kupferkabel! -

Betrachten wir einmal die [ Maßeinheit ] = [ Ω mm² / m ] → R * A / l → R = Widerstand, A = Fläche und l = Länge

Bei dem nachfolgenden Fragezeichen „?“ handelt es sich um eine physikalische Konstante, d.h. einen feststehenden, unveränderlichen Wert:

? = R * A / l →

R = ? / A * l →

· Der Widerstand R ist umso kleiner, je größer die Fläche (= Nenner, Divisor) ist.

Mathematisch: Wenn man einen bestimmten Wert durch einen noch viel größeren Wert dividiert, dann ist das Ergebnis der Division noch viel kleiner als der ursprüngliche (Ausgangs-) Wert selbst!

· Der Widerstand R ist umso größer, je größer die Länge l (= Zähler, Multiplikator) ist.

Mathematisch: Wenn man einen bestimmten Wert mit einem noch viel größeren Wert multipliziert, dann ist das Ergebnis der Multiplikation um ein großes Vielfaches größer als der ursprüngliche (Ausgangs-) Wert selbst!

Jetzt stellt sich nur noch die Frage, was mit der Fläche A und der Länge l gemeint ist! Ganz einfach: A ist die Querschnittsfläche z.B. des verwendeten Kupferkabels bzw. des Kupferdrahtes und l die Länge des verwendeten Kabels bzw. Drahtes.

Also: Je länger die Länge l des „dünnen“ Kupferdrahtes ist und umso kleiner seine entsprechende Querschnittsfläche A ist, umso größer ist der elektrische Widerstand R = ? / A * l

? = R * A / l →

[ Ω mm² / m ] → 1 mm = 10^-3 m = 0,001 m → 1 mm² = (10^-3)² m² = 10^-6 m² = 0,000 001 m²

[ Ω * mm² / m ] → [ Ω * 0,000 001 m² / m ] = [ Ω * 0,000 001 m ] = 0,000 001 [ Ω m ] → ϱ

Das komische, d.h. griechische Formelzeichen „ϱ” steht im Deutschen für „Rho“ und bezeichnet den spezifischen Widerstand ϱ mit

ϱ = R * A / l → [ Ω * mm² / m ] → [ Ω m ]

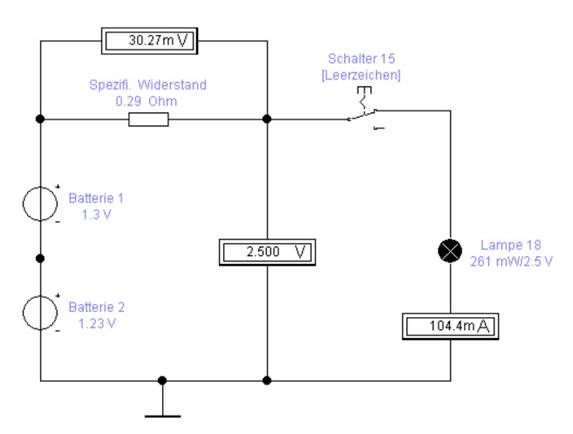
(Zum Vergrößern bitte auf das Bild klicken!)

(Quelle: Wikipedia)

Wenn uns die nachfolgenden Werte

· Ohmscher Widerstand R = 0,29 Ω

aller im Stromkreis vorhandenen Leitungen,

d.h. Anschlussdrähte zu den Bauelementen,

· Querschnittsfläche A = π r² = π ( d/2 )² mit dem Drahtdurchmesser d = 0,5 mm

und dem Radius r = d / 2 des verwendeten Anschlussdrahtes zu den Bauelementen,

· Länge l = 1,27 cm des jeweils verwendeten Anschlussdrahtes und

· Anzahl 4 der verdrahteten Bauelemente

bekannt wären, dann ließe sich der spezifische Widerstadt ϱ wie folgt berechnen:

ϱ = R * A / l →

= R * π * r² / l = R * π * ( d / 2 )² / l

= 0,29 Ω * 3,14 * ( 0,5 mm / 2 )² / 4 * 1,27 cm = 0,29 Ω * 3,14 * 0,0625 mm² / 5,08 cm

= 0,29 Ω * 3,14 * 0,0625 mm² / 50,8 mm = 0,0569125 Ω mm / 50,8

= 0,00112 Ω mm = 0,00112 Ω * 10^-3 m = 1,12 Ω * 10^-6 m = 1,12 Ω * µm = 1,12 Ω µm

Wie man sieht, ist der spezifische Widerstadt ϱ mit ϱ = 1,12 Ω µm, d.h. der Leiterwiderstand aller 4 Verbindungs- bzw. Anschlussleitungen zu den Bauelementen der Schaltung bzw. des Stromkreises extrem klein, nämlich nur 1,12 Millionstel Ohm entlang eines Meters oder 1,12 Ohm entlang eines Millionstel Meters

Demzufolge könnte man auch sagen, dass der Leitungswiderstand aller Anschlussleitungen zu den Bauteilen nicht nur extrem niedrig ist, sondern die Leitfähigkeit im Umkehrschluss extrem gut ist. Die Leitfähigkeit selbst mit dem griechischen Formelzeichen „ϰ” steht im Deutschen für „Kappa“, werden wir gleich kennenlernen! -

Gegenprobe:

R_Spez = ϱ * l / A

= 1,12 Ω µm * 5,08 cm / 3,14 * 0,0625 mm² = 1,12 Ω * 10^-6 m * 50,8 mm / 0,19625 mm²

= 1,12 Ω * 10^-3 mm * 50,8 / 0,19625 mm = 0,00112 Ω * mm * 50,8 / 0,19625 mm

= 0,2899 Ω ≈ 0,29 Ω

Abschließend bleibt noch die Frage zu klären, wie wir eingangs auf den Wert des spezifischen Widerstandes mit R_Spez = 0,29 Ω gekommen sind.

Ganz einfach durch Probieren bzw. „Iteration“. Dabei bezieht sich der spezifische Widerstand mit R_Spez = 0,29 Ω auf den in Serie geschalteten Widerstand namens „Spezifi. Widerstand“ im Sinne eines Vorwiderstandes an dem einer kleiner Spannungsabfall entsteht:

U_{Spez. Widerstandt} = I * R_Spez = 104,4 mA * 0,29 Ω = 30,276 * 10^-3 A * V/A = 30,276 * 10^-3 V = 30,276 mV ≈ 30,28 mV

(Bild vergrößern: auf Bild klicken! Webverzeichnis schaltung_01-01.ewb)

Schaltungsbeschreibung der Schaltung „schaltung_01-01.ewb“:

Bei der obenstehenden Schaltung wird die elektronische Schaltungssimulation „Electronics Workbench“ verwendet.

Beginnen wir bei der obenstehenden Schaltung von links nach rechts, so wie wir auch lesen und schreiben. Wie man sieht, sind die beiden Spannungsquellen „Batterie 1“ mit U_{Batt_1} = 1,3 V und „Batterie 2“ mit U_{Batt_1} = 1,23 V in Serie, d.h. in Reihenschaltung, geschaltet. Dabei fällt auf, dass die beiden Batterien über unterschiedliche Klemmenspannungen verfügen. Dies ist dem Umstand geschuldet, dass es sich bei den beiden Spannungsquellen im Versuch 1 in Wirklichkeit um 1,5 Volt Batterien vom Typ „Mignon AA“ handelt, die im Laufe der Zeit teils unterschiedlich entladen wurden, sodass sich unterschiedliche Klemmenspannungen einstellen.

Für die in Serie geschalteten Spannungsquellen bzw. 1,5 Volt Batterien folgt für die Gesamtspannung U_{Batt, ges}:

U_{Batt, ges} = U_{Batt_1} + U_{Batt_2} = 1,3 V + 1,23 V = 2,53 V ≈ 2,5 V (siehe Voltmeter oben in der Schaltung )

Wie man in der obenstehenden Schaltung sieht, verfügt die Glühlampe [18] über folgende elektrische Betriebsdaten:

· U_Glühlampe = 2,5 V und

· der (Wärme-/Licht-) Leistung P_Glühlampe = 261 mW

Der durch die Glühlampe [18] fließende Strom bzw. Stromstärke berechnet sich dann zu:

P_Glühlampe = U_Glühlampe * I_Glühlampe →

I_Glühlampe = P_Glühlampe / U_Glühlampe

= 261 mW / 2,5 V = 261 * 10^-3 VA / 2,5 V = 104,4 mA (siehe Amperemeter oben in der Schaltung )

Wie wir bereits gelernt haben, ist die Stromstärke I wegen der Reihenschaltung aller Bauelemente überall im Stromkreis gleich groß, sodass folgt:

I = I_{Spezifi. Widerstand} = I_Schalter[15] = I_Glühlampe = I_{Batterie_1+2}

Bleibt noch die Frage zu klären, wozu und weshalb es den Vorwiderstand in Form des spezifischen Widerstandes R_{Spezifi. Widerstand} = 0,29 Ω braucht.

Wie man anhand des Voltmeters (= Spannungsmesser) parallel zum spezifischen Widerstand sieht, liegt am spezifischen Widerstand eine Spannung (= Spannungsabfall ) U_{Spezifi. Widerstand} = 30,27 mV an:

R = U / I → I = U / R = 1 / R * U

I_{Spezifi. Widerstand} = U_{Spezifi. Widerstand} / R_{Spezifi. Widerstand} = 1 / R_{Spezifi. Widerstand} * U_{Spezifi. Widerstand}

= 1 / 0,29 Ω * 30,27 mV = 3,448 A/V * 30,27 * 10^-3 V = 104,37 * 10^-3 A ≈ 104,4 mA (siehe oben!)

Der spezifischen Widerstand R_{Spezifi. Widerstand} = 0,29 Ω wird als Vorwiderstand gebraucht, damit an diesem ein kleiner Spannungsabfall von U_{Spezifi. Widerstand} = 30,27 mV entsteht, sodass an der Glühlampe [18] nur noch eine Spannung von

U_Glühlampe = U_{Batt, ges} - U_{Spezifi. Widerstand}

= 2,53 V - 30,27 mV = 2,53 * 10³ mV - 30,27 mV

= 2 530 mV - 30,27 mV = 2.499,73 mV = 2,4997 V ≈ 2,5 V anliegt!

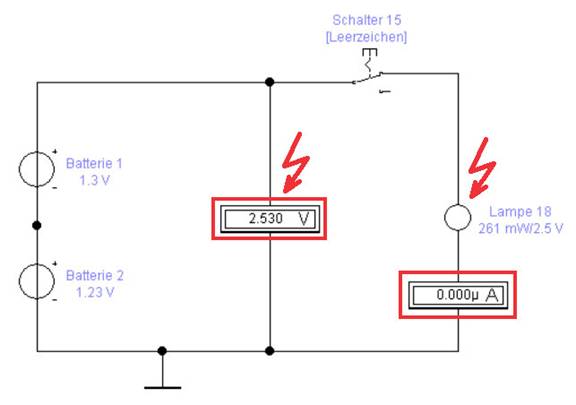
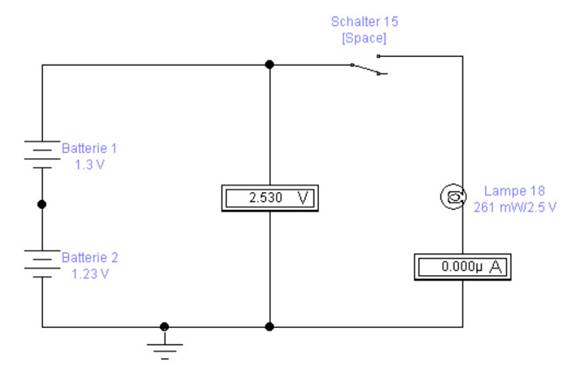
Wie man oben in der Schaltung „schaltung 01-01.ewb“ sieht, wird die Glühlampe [18] exakt mit der Spannung von 2,5 Volt versorgt, die die Glühlampe als Nennspannung „verträgt“ ohne durchzubrennen!

Entfernt man den Vorwiderstand in Form des spezifischen Widerstand R_{Spezifi. Widerstand} = 0,29 Ω aus der Schaltung, dann brennt die Glühlampe [18] wegen der zu hohen Betriebsspannung von U_Glühlampe = 2,53 V einfach durch:

(Bild vergrößern: auf Bild klicken! Webverzeichnis schaltung_01-02.ewb)

Da es sich bei dem vorliegenden Simulationsprogramm „Electronics Workbench“

· um die Version 5.12 aus dem Jahr 1997 handelt,

· das ursprünglich von Interactive Image Technologies
auf der Basis von Berkeley SPICE entwickelt wurde,

· 2005 von National Instruments übernommen,
in National Instruments Electronics Workbench Group umbenannt wurde und

· heutzutage unter dem Namen „NI Multisim“
vom US-amerikanischen Hersteller National Instruments weiterentwickelt und vertrieben wird,

wird man selbst bei der deutschsprachigen Version, das in 2002 vom Franzis-Verlag auf zwei CD-ROM zusammen mit dem Buch „Grundlagen der Elektrotechnik und Elektronik“ von Herbert Bernstein, ISBN 3-7723-5108-5, zum Preis von damals 49,95 € in Deutschland vertrieben wurde und das man sich bei Momox noch gebraucht für kleines Geld kaufen kann, vergeblich nach deutschen DIN-Symbolen für das Schaltungssymbol einer Batterie, einer Spannungs- oder Stromquelle, eines Spannungs- oder Strommessgerätes usw. suchen.

Wie man im nachfolgenden Screenshot der (gecrackten) englischen Sprachversion von „Electronics Workbench 5.12“ sieht, entspricht das Batterie-Schaltsymbol der deutschen DIN-Norm, während das Schaltsymbol für die Glühlampe schon nicht mehr der deutschen DIN-Norm entspricht:

(Bild vergrößern: auf Bild klicken! Webverzeichnis schaltung_01-02.ewb)

Vom spezifischen Widerstand ϱ zur spezifischen Leitfähigkeit ϰ

Die Leitfähigkeit mit dem griechischen Formelzeichen „ϰ” steht im Deutschen für „Kappa“ und ist uns bereits weiter oben begegnet, aber nur indirekt, das die spezifischen Leitfähigkeit ϰ mathematisch nichts anderes als die Umkehrung des spezifischen Widerstand ϱ ist:

ϱ = R * A / l → [ Ω * mm² / m ] → [ Ω m ]

Mit ϰ = 1 / ϱ folgt:

ϰ = 1 / ϱ = 1 / ( R * A / l ) = 1 / R * I / A = G * I / A

ϰ = G * I / A → [ S * m / mm² ] → [ S * m / 10^-6 m² ] → [ S m^-1 ]

Wenn wir die Werte von weiter oben, d.h. der

Gegenprobe:

R_Spez = ϱ * l / A

= 1,12 Ω * µm * 5,08 cm / 3,14 * 0,0625 mm² = 1,12 Ω * 10^-3 mm * 50,8 mm / 0,19625 mm²

= 0,00112 Ω * 50,8 / 0,19625 = 0,2899 Ω ≈ 0,29 Ω þ

einsetzen, um den spezifischen Leitwert G zu berechnen, so folgt:

G_Spez = 1 / R_Spez = 1 / 0,29 Ω = 3,448 A/V = 3,448 S

= 1 / ( ϱ * l / A ) = 1 / ϱ * 1 / ( l / A )

= 1 / ϱ * A / I

= 1 / ( 1,12 Ω µm ) * 3,14 * ( 0,5 mm / 2 )² / 4 * 1,27 cm

= 0,892857 A/V * 10⁶ m^-1 * 0,19625 mm² / 5,08 cm

= 0,892857 A/V * 10⁶ 10^-3 mm^-1 * 0,19625 mm² / 50,8 mm

= 0,892857 A/V * 10³ * 0,19625 / 50,8

= 892,857 A/V * 0,19625 / 50,8 = 3,449275 S ≈ 3,45 S þ

Probe:

R_Spez = 1 / G_Spez = 1 / 3,45 S = 0,289855 Ω ≈ 0,29 Ω þ

Die spezifische Leitfähigkeit ϰ berechnet sich dann wie folgt:

ϰ = G_Spez * I / A

= 3,45 S * 4 * 1,27 cm / 3,14 * ( 0,5 mm / 2 )² = 3,45 S * 50,8 mm / 0,19625 mm²

= 893,0446 S/mm ≈ 893 S/mm = 893 S / 10^-3 m

= 893 S * 10³ m = 893 S * 10³ 10³ mm = 893 S * 10⁶ mm = 893 S * 10⁶ 10^-3 m

= 893 S * 10³ m = 893 S * mm = 0,893 S 10^-6 m = 0,893 S µm

= 0,893 S µm = 1,12 Ω µm þ

Probe:

R_Spez = 1 / G_Spez = 1 / ( ϰ * A / I )

= 1 / ( 0,893 S µm * 3,14 * ( 0,5 mm / 2 )² / 4 * 1,27 cm )

= 1 / ( 893 S/mm * 3,14 * ( 0,5 mm / 2 )² / 4 * 1,27 cm )

= 1 / ( 893 S/mm * 0,19625 mm² / 50,8 mm )

= 1 / ( 893 A/V * 0,19625 / 50,8 ) = 1 / ( 3,4498 A/V ) = 0,28987 V/A ≈ 0,29 Ω þ

Wie man oben anhand der Berechnungen, des Umstellens von Formeln sowie das Umrechnen von Maßeinheiten sieht, muss man sich ziemlich konzentrieren, braucht es entsprechende Übung, damit man keine Fehler macht.

Deshalb ist das Berechnen des spezifischen Widerstandes ϱ und der spezifischen Leitfähigkeit ϰ eine gute und herausfordernde Gelegenheit, das Umrechnen von Maßeinheiten und abgeleiteten Maßeinheiten wie z.B.

1 mm = 10^-3 m oder

( 1 mm )² = ( 10^-3 m )² = 10^-6 m² = 1 µm²

zu üben! -

[ electronic 159 ] [ Seitenanfang ] [ Programmieren ] [ Versuch 2 ]