|
|
[ electronic
159 ] [ Seitenende ] [ Programmieren ] [ Versuch 2 ] [ Versuch 4 ] |
|
||||||||||||||||||||
|
|
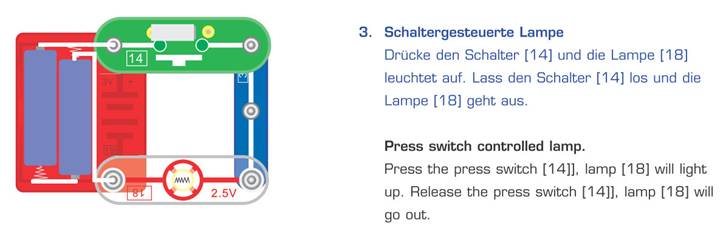
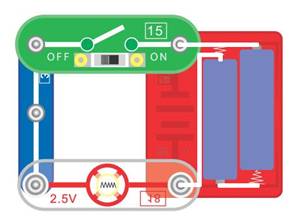
electronic 159 – Versuch 3 Elektrischen
Strom mit Strom ein-
und ausschalten Der Versuch
3 „Schaltergesteuerte Lampe“ müsste eigentlich „Tastergesteuerte Lampe“ heißen, weil es sich bei dem Bauteil Schalter [14] um einen Taster handelt. Der Schalter
[14], der als Taster arbeitet, muss per
Fingerdruck so lange gedrückt werden, wie die Glühlampe [18] leuchten soll. Nur das Drücken und gedrückt halten des
Schalters [14] (= Taster) sorgt dafür, dass die Glühlampe [18] leuchtet. Lassen wir den Taster
bzw. Schalter [14] los, wird der Stromkreis,
der aus Batterie, Glühlampe und Taster besteht, elektrisch unterbrochen,
sodass durch die Glühlampe [18] kein
Strom mehr fließt und diese erlischt. (Zum Vergrößern bitte
auf das Bild klicken!) Wenn wir die Wirkungsweise der Schaltung mit
den Spannungen und Widerständen verstehen wollen, dann müssen wir diese
zunächst horizontal spiegeln, da wir in der westlichen Welt, d.h. in den USA
sowie in Ost- und West-Europa, von links nach rechts schreiben und lesen. Außerdem muss der Schalters [14] (= Taster) die Stromzufuhr auf
dem „Hinweg“ vom „+“-Pol der Batteriehalterung [19] zur Glühlampe [18]
unterbrechen, d.h. ein- oder ausschalten, und nicht auf dem „Rückweg“
zum „-“-Pol Batteriehalterung [19]. Schließlich geht es aus Sicherheitsgründen prinzipiell darum,
dass die Schaltung beim Ausschalten nicht mehr mit der Stromzuführung
(„+“-Pol der Batteriehalterung [19]) verbunden bleibt: (Zum Vergrößern bitte
auf das Bild klicken!) Weshalb ist der Taster (=
Schalter [14])
sehr ökologisch (umweltfreundlich), ökonomisch (wirtschaftlich) und auch
energiesparend? Der Taster (=
Schalter [14])
ist deswegen ökologisch, d.h. umweltfreundlich, weil die Glühlampe [18] immer nur dann leuchtet, wenn man den Taster drückt, damit den Stromkreis schließt und die Glühlampe „unter Strom setzt“, sodass
diese leuchtet. Da also die Glühlampe immer nur dann leuchtet,
wenn man den Taster betätigt bzw. wenn man Licht benötigt, um im Winter im
Dunklen die Zeitung lesen zu können, wird keine Energie verschwendet, weshalb Taster auch ökonomisch, d.h. wirtschaftlich,
bezeichnet werden können. Auch wenn man mit dem Taster Energie sparen kann, so hat er doch auch
einen entscheidenden Nachteil! Wenn in einem Zwei-Personen-Haushalt im Winter
an dunklen Abenden beide Bewohner im Dunkeln die Zeitung lesen wollen,
indem sie diese untereinander aufteilen (der Mann ließt die Fußballseiten und
die Frau die Seite mit dem neuen Kochrezept und den Kreuzworträtseln) und
dabei das Licht, d.h. unsere Glühlampe
[18],
einschalten müssen, dann kann immer nur eine Person die Zeitung lesen,
weil die zweite Person dazu den Taster
drücken und gedrückt halten muss, damit die Glühlampe [18] mit Strom
„versorgt“ wird und leuchtet. Könnte man den Taster
mechanisch verriegeln, sodass dieser ständig eingeschaltet bleibt,
dann könnten in unserem Zwei-Personen-Haushalt beide Bewohner beim
Lichte der Glühlampe
[18]
Zeitung lesen. Vorausgesetzt natürlich, man streitet sich nicht darüber, wer
den Sportteil in der Zeitung zu erst lesen darf! Man kann den Taster
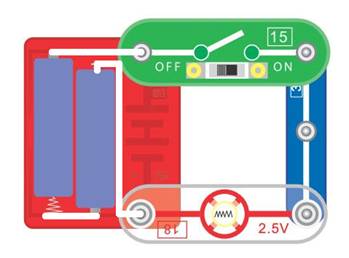
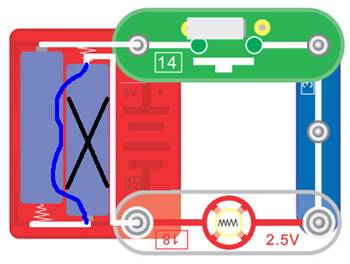
aber auch elektrisch verriegeln, sodass unsere Glühlampe [18] andauernd leuchtet! Dazu muss man nur den Taster (= Schalter [14]) durch den Schiebeschalter (= Gleitschalter
[15]),
wie in Versuch 1, ersetzen: (Zum Vergrößern bitte
auf das Bild klicken!) Jetzt lässt sich die Glühlampe [18] zwar wieder mit dem Schiebeschalter (=
Gleitschalter [15])
dauerhaft ein- oder ausschalten, sodass keine Person mehr benötigt wird,
die den Taster (= Schalter [14])
dauerhaft gedrückt hält, damit man in Ruhe Zeitung lesen kann. Aber wenn wir unsere Glühlampe [18] wieder energiesparend
betreiben wollen, dann geht das nur, wenn wir wieder den Taster (= Schalter [14]) einsetzen. Auf Dauer aber
dürfte das fortwährende Auswechseln des Tasters (= Schalter [14]) gegen den Schiebeschalter (=
Gleitschalter [15]) und umgekehrt ziemlich nervig und umständlich sein! Schön und ergonomisch
(= effizient, optimal, mit wenig Aufwand) wäre es deshalb, wenn sich der
jeweilige Vorteil der Schaltung aus Versuch 1 (= Schiebeschalter) mit dem Vorteil der
Schaltung aus Versuch 3 (=
Taster) kombinieren ließen, sodass man nicht ständig die
Bauteile Schiebeschalter (= Gleitschalter [15]) und Taster (= Schalter [14]) gegeneinander auswechseln
muss! Frage: Geht das? Und falls ja, wie? Wenn wir einen Blick in den
Elektronikbaukasten „electronic 159“ oder in die Materialliste werfen, dann fällt uns
auf, dass es die Batteriehalterung
[19]
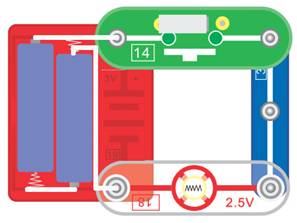
in zweifacher Ausfertigung gibt, (Zum Vergrößern bitte
auf das Bild klicken!) sodass wir sowohl den Versuch 3 (siehe unten links) als auch den Versuch 1 (siehe unten rechts) zusammen auf ein
Montagebrett aufbauen können: (Zum Vergrößern bitte
jeweils auf das Bild klicken!) Zwar gibt es im Elektronikbaukasten
„electronic 159“ insgesamt zwei Batteriehalterungen [19], leider aber nur eine Glühlampe [18], sodass wir immer nur eine
Schaltung, entweder Versuch 3 (siehe oben links)
oder Versuch 1 (siehe oben rechts),
aufbauen können. Aber das ist natürlich kein Grund zur Verzweiflung,
schließlich sind wir ja auf dem Weg zum Ingenieur! Und wie heißt es in dem
Film „Feuerzangenbowle“ mit Heinz Rühmann? Richtig: „Einem Ingenieur ist
nichts zu schwör!“ im Sinne von schwer! „Geht nicht, gibt’s nicht!“ – Wie man nämlich oben in den beiden Schaltungen
von Versuch 3 (siehe oben links)
oder Versuch 1 (siehe oben rechts)
sieht, werden in beiden Versuchen ein- und dieselbe Glühlampe [18] verwendet! Und das auch noch im Stromrückflusszweig zum Minuspol der beiden 1,5 Volt Batterien, die ja
bekanntlich in den Batteriehalterungen
[19] hintereinander,
d.h. in Serie geschaltet sind. Darüber hinaus verhält es sich so, dass beide
Schaltungen von Versuch 3 (siehe oben links)
und Versuch 1 (siehe oben rechts)
aufgrund der gleichen Batteriehalterung
[19]
mit jeweils 3,0 Volt
Versorgungsspannung
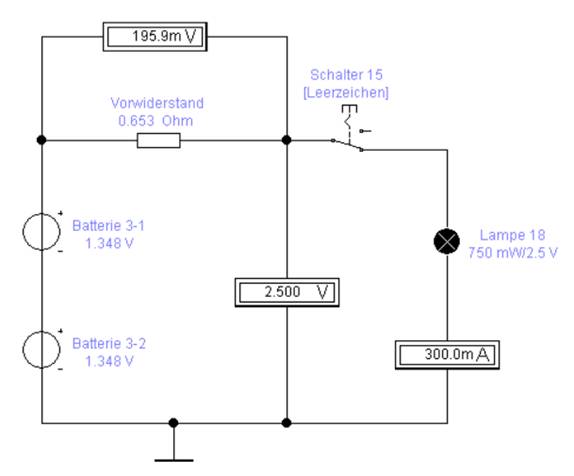
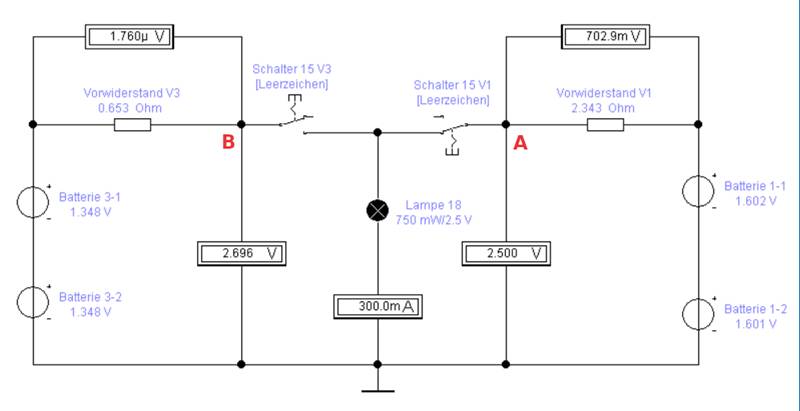
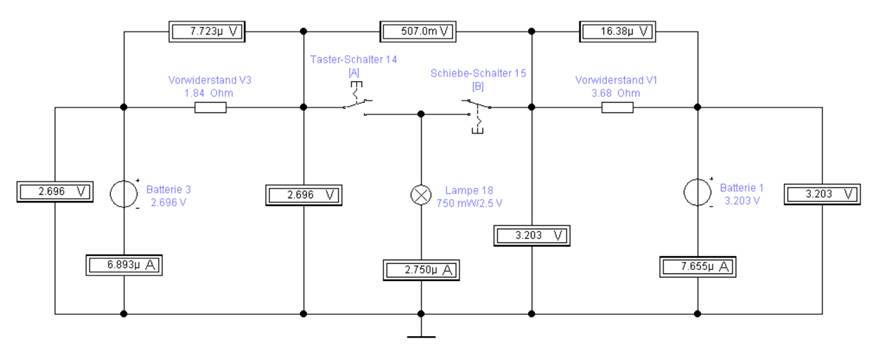
betrieben werden mit der angenehmen Folge, dass beide Pluspole „+“ im Versuch 3 (siehe oben links) und Versuch 1 (siehe oben rechts) über nahezu das gleiche Spannungspotential verfügen. Da die Spannungsdifferenz mit UDifferenz = 0,51 V > 0 V
größer null Volt, d.h. positiv ist, verläuft der Spannungspfeil der Differenzspannung UDifferenz von rechts
nach links, d.h. von Versuch 1 mit der
Batteriespannung UBatt_2
= 3,203 V
(siehe oben rechts) zu Versuch 3 mit der kleineren
Batteriespannung UBatt_1
= 2,696 V
= (siehe oben links): (Zum Vergrößern bitte
auf das Bild klicken!) Wenn es aber zwischen beiden Pluspolen „+“ im Versuch 3 (siehe oben links) und Versuch 1 (siehe oben rechts) über nahezu das gleiche Spannungspotential gibt, die
Spannungsdifferenz (= Potentialunterschied) nahezu null Volt beträgt, UDifferenz = UBatt_2 - UBatt_1 → mit UBatt_2 > UBatt_1 = ( 1,602 V + 1,601 V ) - ( 1,348 V + 1,348 V ) = ( 3,203 V ) - ( 2 * 1,348 V ) = ( 3,203 V ) - ( 2,696 V ) = 0,507 V ≈ 0,51 V dann lassen sich beide Schaltungen von Versuch 3 (siehe oben links) oder Versuch 1 (siehe oben rechts) wie folgt zusammenschalten,
indem sich beide die gemeinsame Glühlampe [18] teilen: (Zum Vergrößern bitte
auf das Bild klicken!) Das Zusammenschalten der beiden Schaltungen
von Versuch 3 (siehe oben links) und
von Versuch 1 (siehe oben rechts)
nennt man Superposition, d.h. Überlagerung mehrerer Schaltungen
(Elektrotechnik) bzw. mehrerer Gleichungen (Mathematik). Dabei darf man dass mit dem „Überlagern“ ruhig wörtlich nehmen, da eventuell
vorhandene Potentialunterschiede, d.h. Spannungsunterschiede ∆U zwischen den Stromversorgungen beim Versuch 3 (siehe oben links) und Versuch 1 (siehe oben rechts) immer bestrebt
sind sich auszugleichen, wobei dann auch entsprechende Ausgleichströme ∆I fließen können! Wie beispielsweise beim Gewitter, wo
sich große Potentialunterschiede unterschiedlicher Aufladungen zwischen
Himmel und Erde durch Blitze auszugleichen versuchen. Beim Einschlagen eines
Blitzes in die Erde entstehen deshalb nicht nur hohe Spannungen von einigen Millionen Volt, sondern es fließen auch dicke Ströme von einigen tausend Ampere in Form von Lichtbögen mit Temperaturen von bis zu tausend Grad Celsius und mehr, sodass Gebäude, in die der Blitz
einschlägt, Feuer fangen können! Mit Potentialunterschieden in Form von Spannungsunterschieden ∆U und entsprechenden (Potential-) Ausgleichströmen ∆I haben wir es auch zu tun, wenn wir im Winter
ein Auto, das nicht anspringt, weil die altersschwache Starterbatterie (die
in Wirklichkeit ein Akku ist) keinen „Saft“ mehr hat mit Fremdstarthilfe durch die
Starterbatterie eines anderen Autos wieder zum Laufen bringen wollen. Damit die Starterbatterie des helfenden
Autos beim Fremdstarten keinen Schaden nimmt, sollte bei diesem zwecks
Unterstützung der Batterie stets der Motor laufen, damit die Lichtmaschine
zusätzlich elektrische Energie bereitstellt! Wegen der stark entladenen Batterie im liegen
gebliebenen Auto hat diese oftmals nur noch eine Batteriespannung von
deutlich weniger als 12 Volt, sodass beim Verbinden der beiden
Autobatterien sofort ein entsprechend dicker Ausgleichsstrom von etlichen Ampere Stromstärke fließt, der
beim Verbinden mit der roten Verbindungszange („+“ Pol) zu einem mehr oder
weniger starken Funkenregen führen kann! - Doch
zurück zum Versuch 3 (siehe oben links) und
Versuch 1 (siehe oben rechts)
nebst Potentialunterschied, den es ja nur
deswegen gibt, weil die beiden 1,5 Volt Batterien in der linken Batteriehalterung [19] bereits teilweise
entladen sind, während die beiden 1,5 Volt Batterien in der rechten
Batteriehalterung [19] noch fabrikneu
und „taufrisch“ sind, d.h. über eine Leerlaufspannung von zusammen UBatt_2 = 3,203 V > UBatt_1 = 2,696 V verfügen!
Um zu einem weitergehenden Verständnis zu
kommen, bemühen wir als nächstes die Elektroniksimulation „Electronics
Workbench“ mit der wir schon gearbeitet haben. Der Knackpunkt dabei ist
der, dass die Elektroniksimulation sehr empfindlich ist. Wenn wir die Glühlampe [18] anstatt mit einer
Nennspannung von UNenn = 2,5 V mit 3,0 V betreiben, dann brennt
diese sofort durch! Deshalb müssen wir mittels eines Vorwiderstandes RVor
für einen entsprechenden Spannungsabfall ∆UVor sorgen, sodass die Glühlampe [18]
tatsächlich nur mit der Nennspannung UNenn = 2,5 V betrieben wird
und die Glühlampe eben nicht durchbrennt! Dabei bilden der Vorwiderstand RVor und die Glühlampe [18] einen Spannungsteiler. Auf dem Glühlampengewinde befindet sich am
oberen Rand der Aufdruck 0,3 A womit die Nennstromstärke der Glühlampe
gemeint ist. Der davor befindliche Aufdruck, der die Nennspannung von 2,5 V
der Glühlampe benennt, ist leider nicht lesbar. Betriebsdaten
der Glühlampe [18]: UNenn = 2,5 V INenn = 0,3 A Berechnung der elektrischen (Wärmeverlust-)
Leistung PGlühlampe: P = U *
I → PGlühlampe = UNenn * INenn = 2,5 V * 0,3 A = 0,75 W = 750 mW Auf der roten Lampenhalterung mit der Glühlampe [18] befindet sich inzwischen der Aufdruck „750 mW“ als Hinweis darauf,
dass nur eine (Ersatz-)
Glühlampe
bis zur Leistung von PGlühlampe = 0,75 W = 750 mW verwendet werden
darf! Für die Berechnung des ohmschen Widerstandes
der Glühlampe [18] folgt dann: R = U /
I → RGlühlampe = UNenn / INenn = 2,5 V / 0,3 A = 8,33 Ω Wenn nun die beiden 1,5 Volt Batterien
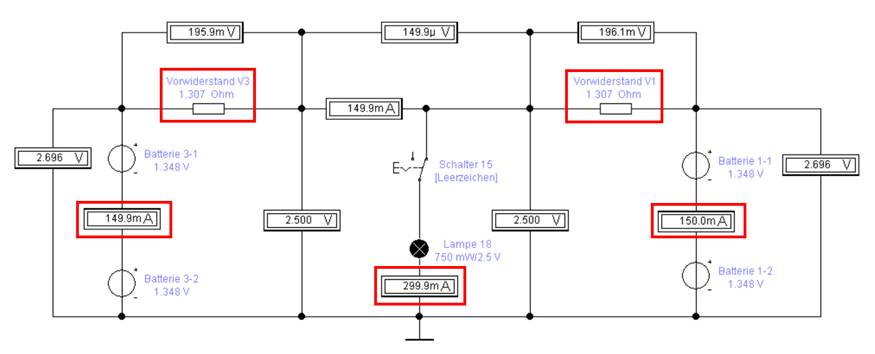
vom Typ “Mignon AA” über eine Gesamtspannung von UBatt_3, ges = UBatt_3-1 + UBatt_3-2
= 1,348 V + 1,348 V = 2 * 1,348
V = 2,696 V verfügen, dann muss am Vorwiderstand RVor V3 ein Spannungsabfall von UR
Vor V3 = UBatt_3, ges - UNenn = 2,696 V - 2,5 V =
0,196 V = 196 mV anliegen, sodass sich der Vorwiderstand RVor V3 selbst wie folgt berechnet: R = U /
I → RVor V3 = UR Vor / INenn = 196 mV / 0,3 A =
196 (Bild vergrößern: auf
Bild klicken! Webverzeichnis schaltung_03-01.ewb) Probieren wir bei dieser Gelegenheit noch die
Berechnung des Vorwiderstandes
anhand der Spannungsteilerformel aus: RVor V3 / RGlühlampe = UR
Vor V3 / UNenn → RVor V3 = UR Vor V3 / UNenn * RGlühlampe = 196 mV / ( 2,5 V * 8,33 Ω
) = 0,196 Weiter geht’s mit der Berechnung des
Vorwiderstandes RVor V1 der Schaltung von Versuch 1 auf der
rechten Seite. Wenn nun die beiden 1,5 Volt Batterien
vom Typ “Mignon AA” über eine Gesamtspannung von UBatt_1, ges = UBatt_1-1 + UBatt_1-2
= 1,602 V + 1,601 V = 3,203 V verfügen, dann muss am Vorwiderstand RVor V1 ein Spannungsabfall von UR
Vor V1 = UBatt_1, ges - UNenn = 3,203 V - 2,5 V =
0,703 V = 703 mV anliegen, sodass sich der Vorwiderstand RVor V1 selbst wie folgt berechnet: R = U /
I → RVor V1 = UR Vor V1 / INenn = 703 mV / 0,3 A =
703 (Bild vergrößern: auf
Bild klicken! Webverzeichnis schaltung_03-02.ewb) Nun ist die Zeit gekommen, wo sich beide
Schaltungen und zwar die Schaltung aus dem Versuch 3 und dem Versuch 1 wie
folgt zusammenschalten lassen, wobei sich diese die gemeinsame Glühlampe [18]
teilen: (Bild vergrößern: auf
Bild klicken! Webverzeichnis schaltung_03-03.ewb) Jetzt wurden die Schaltung aus Versuch 3 (links) und die Schaltung aus
Versuch 1
(rechts)
zwar zusammengefügt, sind aber wegen der beiden Wechselschalter „Schalter 15
V3“
und „Schalter 15 V1“ noch nicht superpositioniert, d.h. noch nicht
überlagert, sodass sich immer nur ein Schaltungsteil, nämlich die
Schaltung von Versuch 3 (links) oder die Schaltung von Versuch 1
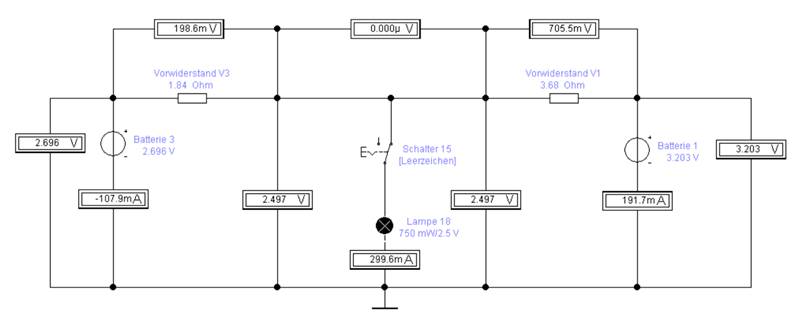
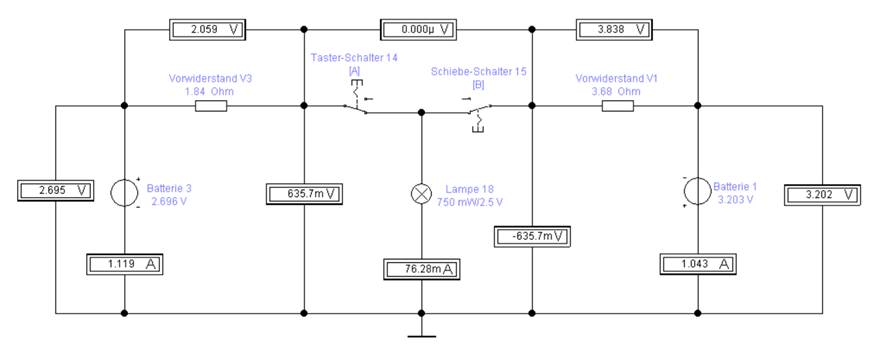
(rechts) einschalten und in Betrieb nehmen lässt! Da die Batteriehalterung [19] mit den beiden 1,5 Volt Batterien aus dem Versuch 1 (rechts) über eine Batteriespannung von Uges, V1
= 3,203 V verfügt und die Batteriespannung von Versuch 3 (links) nur Uges, V3 = 2,696 V beträgt,
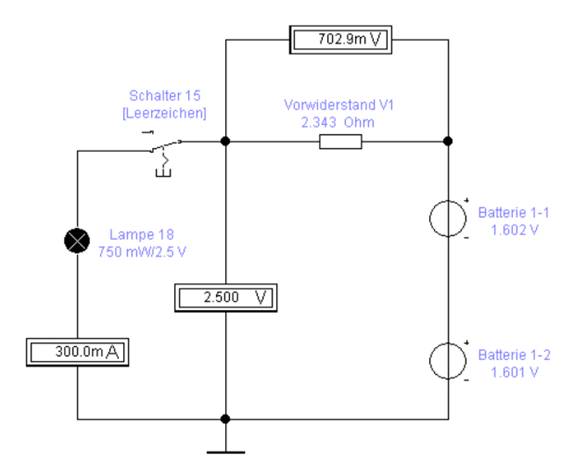
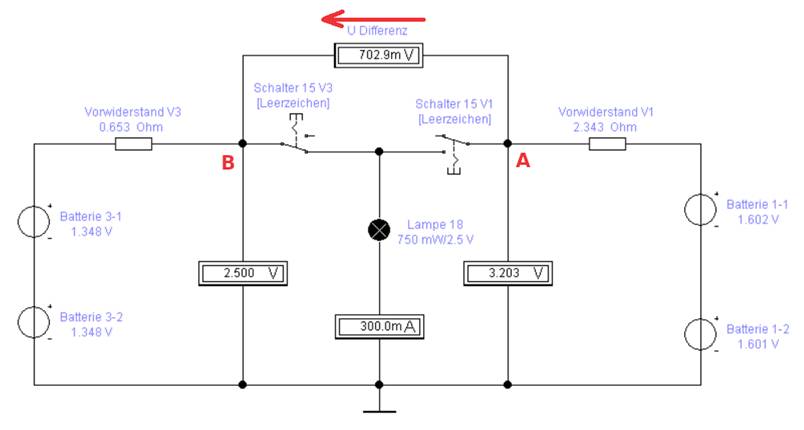
entsteht zwischen den Punkten A und B, d.h. von rechts nach links, ein
entsprechendes Spannungsgefälle von UDifferenz = 702,9 mV
als treibende Kraft: (Bild vergrößern: auf
Bild klicken! Webverzeichnis schaltung_03-04.ewb) Das große Potentialgefälle von UDifferenz = 702,9 mV
sorgt als treibende Kraft dafür, dass die Batteriespannung aus Versuch 1 (rechts) die beiden 1,5 Volt Batterien aus Versuch 3 (links) aufzuladen versucht. Und zwar mit
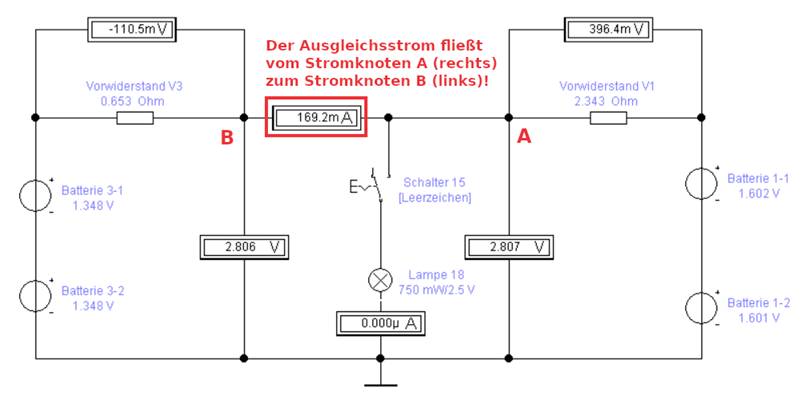
einem Auflade-/Ausgleichsstrom von IAB
= 169,2 mA, der schon ziemlich groß ist: (Bild vergrößern: auf
Bild klicken! Webverzeichnis schaltung_03-05.ewb)
Als nächstes gehen wir der Frage nach, was
passiert, wenn man den Schalter [15] betätigt, um den Stromfluss durch die
Glühlampe [18] einzuschalten, sodass die Glühlampe leuchtet (siehe
obenstehendes Bild). Es wundert sich der Laie und es staunt der
Fachmann: die Glühlampe [18] brennt sofort nach dem Einschalten des Schalters
[15] durch! Und das, obwohl wir doch zuvor die beiden Vorwiderstände RVor V3 (links) und RVor V1 (rechts) extra so
berechnet haben, dass die Glühlampe nicht durchbrennt! Na ja, ganz so wunderlich ist es dann doch
nicht! Gilt es doch zu beachten, dass wir die beiden Vorwiderstände RVor V3 (links) und RVor V1 (rechts) zwar
berechnet haben, aber eben für jeden Schaltungsteil gemäß Versuch 3 (links)
und Versuch 1 (rechts) einzeln und noch nicht in der Zusammenschaltung gemäß Superposition, d.h. Überlagerung beider Schaltungen! In dem Moment aber, wo wir beide
Schaltungen zusammen schalten, d.h. die Potentialpunkt A und B
über das Amperemeter (= Strommessgerät) miteinander
verbinden und die Schaltung „schaltung_03-06.ewb“ durch Einschalten
der Glühlampe [18] belasten, sodass durch die Glühlampe ein Querstrom von IGlühlampe ≈ 300 mA gegen Masse
„┴ “ in die 1,5 Volt
Batterien der beiden Batteriehalterungen
[19]
links und rechts zurück fließt, beeinflussen sich die Schaltungen
gemäß Versuch 3 (links) und Versuch 1 (rechts) gegenseitig! Dabei handelt es sich bei dem Querstrom durch die Glühlampe [18] um einen resultierenden, d.h. gemischten
Strom, da beide Stromquellen gemäß Versuch 3 (links) und Versuch 1
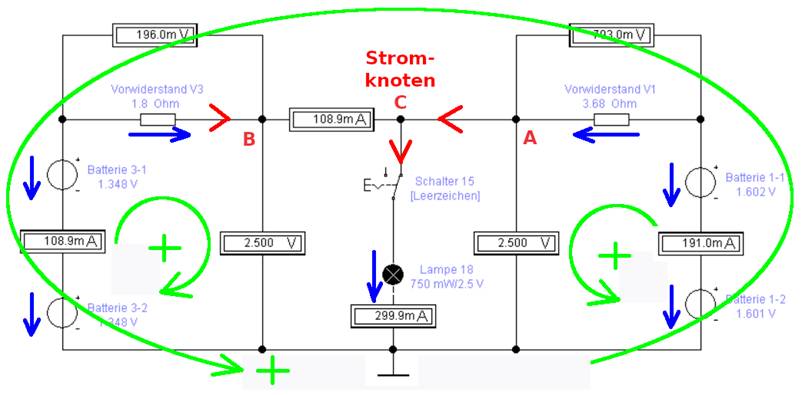
(rechts) eine anteilige Stromstärke zu IGlühlampe ≈ 300 mA beisteuern (siehe „Stromknoten C“): (Bild vergrößern: auf
Bild klicken! Webverzeichnis schaltung_03-06.ewb) Wie man im obenstehenden Bild sieht, gibt es
insgesamt drei grüne
Maschenumläufe
und zwar zwei im Inneren der Schaltung und
einen äußeren um die Schaltung
herum. Dabei gibt die grüne Pfeilspitze jeweils die Umlaufrichtung für den Maschenumlauf an. Und das grüne Pluszeichen „+“ legt fest, wie herum die blauen Spannungspfeile der Reihe nach aufaddiert
werden. Wenn ein blauer Spannungspfeil entgegengesetzt zur Umlaufrichtung „+“ verläuft, dann wird
er negativ gezählt(!) und zu den anderen Spannungen addiert! Die Summe aller positiv oder
negativ gezählten Spannungen ist dann gleich null! Spannungsumlauf Versuch 3 (links): UR Vor V3 +ULampe 18
+ ( - UBatt_3-2 ) + ( -UBatt_3-1 ) = 0 → UR Vor V3 +ULampe 18
- ( UBatt_3-2 + UBatt_3-1
) = 0 → UR Vor V3 = ( UBatt_3-2 + UBatt_3-1
) - ULampe 18 = ( 1,348 V + 1,348 V ) - 2,5 V = ( 2 * 1,348 V ) -
2,5 V = 0,196 V = 196 mV Spannungsumlauf Versuch 1 (rechts): UR Vor V1 + ULampe 18
+ ( - UBatt_1-2
) + ( - UBatt_1-1 ) = 0
→ UR Vor V1 + ULampe 18
- ( UBatt_1-2 + UBatt_1-1
) = 0 → UR Vor V1 = ( UBatt_1-2 + UBatt_1-1
) - ULampe 18 = ( 1,601 V + 1,602 V
) - 2,5 V = 3,203 V - 2,5 V = 0,703 V = 703
mV Äußerer Spannungsumlauf: ( - UBatt_1-2
) + ( - UBatt_1-1 ) + UR
Vor V1
+ ( - UR Vor V3 ) + UBatt_3-1
+ UBatt_3-2 = 0 → - ( UBatt_1-2 + UBatt_1-1
) + UR Vor V1 - UR
Vor V3
+ UBatt_3-1 + UBatt_3-2 = 0 → - ( 1,601 V + 1,602 V ) + 0,703 V - 0,196 V + 1,348 V + 1, 348 V = 0 þ Stromknoten C: IVor 1 + IVor 3 + ( - ILampe 18 ) = 0
→ IVor
1 + IVor 3 - ILampe 18
= 0 191 mA + 108,9 mA - 299,9 mA = 0 þ Jetzt wissen wir, dass alle Spannungsumläufe sowie der Stromknoten C richtig aufgestellt wurden. Aber da
wir alle Werte aus der Simulation übernommen
haben, wissen wir noch nicht, wie man z.B. den Vorwiderstand RVor V1 (rechts) berechnet, obwohl dieser vom
gleich großen Batteriestrom
IBatterie V1 (rechts) durchflossen wird: IBatt_1-1 = IBatt_1-2 =
IR Vor 1 = UR Vor V1 / RVor V1 → RVor V1 = UR Vor 1 / IR Vor 1 = UR Vor 1 / IBatt_1-1 = ( UBatterie V1 - UGlühlampe
) / IBatt_1-1 Der Vorwiderstand RVor V3 (links) berechnet sich wie der Vorwiderstand RVor V1 (rechts), nur mit
anderen Werten: RVor V3 = UR Vor 3 / IR Vor 3 = UR Vor 3 / IBatt_3-1 = ( UBatterie V3 - UGlühlampe
) / IBatt_3-1 Die beiden Ströme IR Vor V1 und IR Vor V3 sind aber wiederum durch den Stromknoten C und den Strom durch die Glühlampe [18] mit IGlühlampe = 0,3 A verbunden:
Wie aber überführt man mathematisch
eine Gleichung mit zwei Unbekannten in eine solche mit nur einer
Unbekannten? Und
wie überführt man elektrisch eine Gleichung,
d.h. Maschenumlauf oder Stromknoten mit zwei Unbekannten in eine Gleichung mit nur einer
Unbekannten? Erinnern wir uns daran, dass unsere beiden Unbekannten die Ströme IR
Vor 3
(links) und IR
Vor 1
(rechts) durch die beiden Vorwiderstände
RVor 3 (links) und RVor 1 (rechts) sind! Wenn wir dafür sorgen, dass der Strom IR Vor 3 (links) gleich dem IR Vor 1 (rechts) ist, sodass beide
Ströme gleich groß sind, dann haben wir aus zwei unbekannten
Variablen nur noch eine gemacht: IR Vor 3 (links) = IR Vor 1 (rechts)
→ Wenn aber die beiden Ströme durch die
Vorwiderstände gleich groß sind, dann bedeutet das nichts anderes als dass
wir es in der Schaltung mit einer Parallelschaltung der beiden Vorwiderstände (aber auch der
Spannungsquellen links und rechts in der Schaltung) zu tun haben: IGlühlampe = IR Vor 3 + IR Vor 1 = 2 * IR Vor 3 = 2 * IR Vor 1 = 2 * IR Vor → IR Vor = ½ IGlühlampe Damit sich aber die (Quer-) Ströme IR Vor durch die
betreffenden Vorwiderstände
RVor
halbieren können, müssen sich elektrisch, d.h. aufgrund des Ohmschen
Gesetzes, die Widerstandswerte der jeweiligen Vorwiderstände RVor verdoppeln!
Stromknoten C: IVor 1 + IVor 3 + ( - ILampe 18 ) = 0
→ IVor 1 + IVor 3 - ILampe 18 = 0 Wegen der Parallelschaltung der beiden Vorwiderstände folgt jetzt mit IVor 1 = IVor 3 : IVor
1 + IVor 3 - ILampe 18
= 0 IVor
+ IVor + - ILampe 18
= 0 2 * IVor = ILampe 18 → IVor = ½ ILampe 18 = ½
* 0,3 A = 0,15 A Für jeden der beiden Vorwiderstände
folgt jetzt: IR Vor = UR
Vor
/ RVor → RVor = UR
Vor
/ IR Vor = ( UBatterie - UGlühlampe
) / IR Vor → mit gleich
großen Batteriespannungen UBatterie V3 = UBatterie V1 =
( UBatterie - UGlühlampe
) / (½
ILampe 18 ) = ( 2,696 V – 2,5 V ) / 0,15 A
= 0,196 V / 0,15 A = 1,30667 Ω ≈ 1,307 Ω Übrigens: Eine unbekannte Variable ist
„doppelt gemoppelt“, weil eine Variable eine Unbekannte ist! Nachfolgend noch die Elektroniksimulation
„Electroncis Workbench“ mit der Schaltung „schaltung_03-07.ewb“ mit der sich
zeigen lässt, dass die beiden Versuchsschaltungen Versuch 1 (links) und
Versuch 3 (rechts) nicht nur identisch, sondern eben auch parallel
geschaltet sind: (Bild vergrößern: auf Bild
klicken! Webverzeichnis schaltung_03-07.ewb) Jetzt haben wir einen Weg gefunden, wie man
eine Gleichung mit zwei Unbekannten auf eine Gleichung mit nur noch einer Unbekannten überführt! Nämlich durch das Parallelschalten von gleichartigen Maschen, indem man diese widerstandsmäßig und spannungsmäßig aneinander angleicht! Jetzt stellt sich allerdings noch die Frage,
ob es auch einen Weg zurück gibt, d.h. wieder hin zu einem Gleichungssystem mit zwei Unbekannten. Ja gibt es, allerdings nur quasi mit zwei
Unbekannten und zwar mit einer echten Unbekannten und einer zweiten unechten
Unbekannten, die sich aus der ersten, echten Unbekannten über einen Umrechnungsfaktor ableitet,
sodass wir es mathematisch immer noch mit nur einer Unbekannten zu tun haben! - Wir erhöhen in der Schaltung
„schaltung_03-07.ewb“, Versuch 3 (links), die Batteriespannung von vormals UBatt_3-1
= 1,348 V auf nunmehr UBatt_3-1 = 1,602 V mit ∆UBatt_3 = 1,602 V - 1,348 V = 0,254 V, d.h. den
Faktor k = 100 / 1,348 V * 1,602 V - 100 =
118,84 – 100 = + 18,84 % → Einfacher
Dreisatz! Was bedeutet die Erhöhung der Batteriespannung
um 18,84 % für die Schaltung „Versuch 1“ (rechte Seite)? Wie reagiert die
Schaltung auf die Spannungserhöhung? Jede Erhöhung der Batteriespannung um +18,84 %, d.h. UBatt_3-1 neu = UBatt_3-1
+ ∆UBatt_3 =
1,348 V + 0,254 V = 1,602 V führt sofort dazu, dass sich die Stromstärke sowohl durch den Vorwiderstand RVor_1
als auch durch die Glühlampe [18] maßgeblich erhöht, sodass die Glühlampe sofort durchbrennt! Selbst wenn man den bisherigen Vorwiderstand von RVor_V1 = 1,307 Ω auf RVor_V1=
3,68 Ω mehr als
verdoppelt, brennt die Glühlampe sofort wieder durch (siehe
Schaltung „schaltung_03-08.ewb“). Der Grund dafür, weshalb die Glühlampe [18] wieder und wieder durchbrennt
ist der, und das hatten wir bereits schon festgestellt, dass sich die
einzelnen Maschen, bestehend aus der Parallelschaltung von Versuch 3 (linke Seite) und Versuch 1
(rechte Seite) wechselseitig beeinflussen. Wenn ich auf der rechten
Seite beim Versuch 1 weniger Energie, d.h. weniger Stromstärke einspeise, dann gleicht das die
linke Seite beim Versuch 3 sofort wieder aus, sodass die
Glühlampe sofort wieder durchbrennt! Deshalb kann man die Parallelschaltung von Versuch 3 (linke
Seite) und Versuch 1 (rechte Seite) durchaus mit einer Balkenwaage oder noch
besser mit einer kommunizierenden
Röhre vergleichen, die sich immer im Gleichgewicht befindet bzw. die von sich aus immer versucht, ein
bestehendes Ungleichgewicht selbst- und eigenständig auszugleichen! Elektrotechnisch hängt das damit zusammen,
dass sich eine Potentialdifferenz bzw. ein Potentialgefälle stets auszugleichen
versucht und „nicht eher Ruhe gibt, bis dieses ausgeglichen ist!“ Bildlich
gesprochen sucht sich das Wasser immer den geringsten Widerstand und das
stärkste Gefälle. So sucht sich auch der elektrische Strom immer den Weg des geringsten elektrischen Widerstandes und des größten
Potentialgefälles bzw. der größten Spannungsdifferenz! So, nun wird es langsam Zeit, dass wir uns zum
zweiten Mal mit der Superposition,
d.h. dem Überlagerungsverfahren auseinandersetzen.
Und zwar mit den nachfolgenden Regeln. Was uns nämlich bei der Parallelschaltung ständig zu schaffen
macht, sind die beiden Spannungsquellen im Versuch 3 (links)
und Versuch 1 (rechts), die sich elektrisch gegenseitig beeinflussen und
dafür „verantwortlich“ sind, dass wir es rechnerisch stets mit zwei
Unbekannten (= Variablen) zu tun haben! >>
Überlagerungsverfahren nach Helmholtz Das
Überlagerungsverfahren beruht auf dem Superpositionsprinzip
bei
linearen Systemen. Vorgehen: · Bis auf eine Quelle werden alle anderen entfernt.
· Die gesuchten
Teilströme mit der
verbliebenen Quelle werden
berechnet. · Das Vorgehen wird für jede andere
Quelle wiederholt. · Zum Schluss wird die vorzeichenrichtige
Addition der errechneten Teilströme für die betrachteten Zweige
durchgeführt. Ergebnis: Der gesuchte Teilstrom wurde ermittelt. <<
(Quelle: Wikipedia) Maschenumläufe und Stromknoten sind das eine,
Superposition das andere Ding. Wenn wir es z.B. mit einer Schaltung mit
insgesamt drei Spannungsquellen zu tun haben, dann werden wir mit drei
Unbekannten konfrontiert, sodass sich ein Maschenumlauf mit drei
Unbekannten nicht lösen lässt. Mit dem „Trick“, dass wir alle
Spannungsquellen bis auf eine, sodass die erste übrig bleibt,
entfernen, haben wir es nur noch mit einer Unbekannten und dem
dazugehörigen ersten Maschenumlauf zu tun. Mit dem „Trick“, dass wir alle
Spannungsquellen bis auf eine, sodass die zweite übrig bleibt,
entfernen, haben wir es nur noch mit einer Unbekannten und dem
dazugehörigen zweiten Maschenumlauf zu tun. Mit dem „Trick“, dass wir alle Spannungsquellen
bis auf eine, sodass die dritte übrig bleibt, entfernen, haben wir es
nur noch mit einer Unbekannten und dem dazugehörigen dritten
Maschenumlauf zu tun. Demzufolge wird eine Schaltung mit drei
Spannungsquellen und demzufolge drei Unbekannten in insgesamt drei
einzelne Schaltungen, d.h. Maschenumläufen, mit nur einer
Spannungsquelle und einer Unbekannten aufgeteilt! Alle drei Maschengleichungen werden
dann nach ein- und derselben Unbekannten aufgelöst bzw. umgestellt,
wobei alle ein- und dieselben Unbekannten in den drei
Maschengleichungen das gleiche Vorzeichen (meistens „+“) aufweisen
müssen! Ist dies der Fall, dann lassen sich alle drei
Maschengleichungen mit ein- und dieselben Unbekannten addieren,
sodass sich diese durch die Addition abschließend berechnen lassen! Damit
wäre dann auch die Superposition abgeschlossen. - Im vorliegenden Fall, d.h. der Schaltung „schaltung_03-08.ewb“, haben wir es mit zwei
Spannungsquellen „Batterie_1“ (rechts) „Batterie _3“ (links) und demzufolge
mit zwei Unbekannten zu tun, (Bild vergrößern: auf
Bild klicken! Webverzeichnis
schaltung_03-08.ewb) sodass
wir die Schaltung „schaltung_03-08.ewb“ gemäß den Regeln der Superposition in zwei
Schaltungen mit nur noch je einer Spannungsquelle nebst Maschenumlauf
aufteilen. Nachfolgend die erste Schaltung „schaltung_03-09.ewb“ der Superposition bei der die Spannungsquelle UBatt_3
vom Versuch 3 (links) durch einen Kurzschluss ersetzt wurde: (Bild vergrößern: auf
Bild klicken! Webverzeichnis
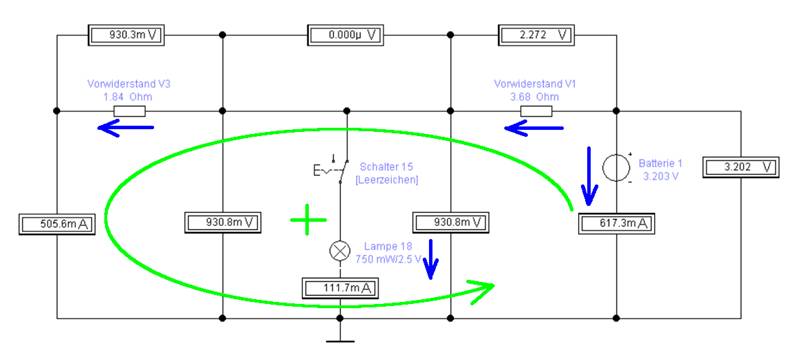
schaltung_03-09.ewb) Wenn man in der obenstehenden Schaltung „schaltung_03-09.ewb“ von
der Spannungsquelle „Batterie 1“ aus nach links in die Schaltung hinein
schaut, dann sieht man als erstes den Vorwiderstand
RVor_V1, der in Reihe geschaltet ist mit
den beiden parallel geschalteten Widerständen ( RVor_V3 // RLampe_18 ), sodass sich der Gesamtwiderstand
Rges_V1 wie folgt berechnen
lässt: Rges_V1 = RVor_V1 + ( RVor_V3 // RLampe_18 ) = RVor_V1 + [ RVor_V3 * RLampe_18 / ( RVor_V3 + RLampe_18 ) ] Betriebsdaten der Glühlampe [18]: UNenn = 2,5 V INenn = 0,3 A Gemäß der
Betriebsdaten (= Nennwerte) lässt sich der Widerstand der Glühlampe wie folgt
berechnen: RLampe_18 = ULampe_18 / ILampe_18 = 2,5 V / 0,3 A = 8,33 Ω Rges_V1 = RVor_V1 + [ RVor_V3 * RLampe_18 / ( RVor_V3 + RLampe_18 ) ] = 3,68 Ω + [ 1,84 Ω *
8,33 Ω / (1,84 Ω + 8,33 Ω ) ] = 3,68 Ω + [ 15,327 Ω = 3,68 Ω + [ 1,507 Ω ] = 5,187 Ω Iges = Uges / Rges
= UBatt_V1 / Rges_V1
= 3,203 V / 5,187 Ω
= 0,6175 A = 617,5 mA þ Spannungsumlauf Versuch 1 (rechts), Schaltung „schaltung_03-09.ewb“ UR Vor V1 + ULampe 18
+ ( - UBatt_1 ) = 0 → UR Vor V1 = UBatt_1 - ULampe 18 → Der Wert für ULampe 18 = 0,9308 V wurde der Simulation
entnommen! = 3,203 V - 0,9308 V = 2,2722 V = 2,272 V UBatt_1 = UR Vor V1 + ULampe 18 = 2,272 V + 0,9308 V = 3,2028 V = 3,203 V Probe: ULampe_18 = UBatt_1
- UR Vor V1 =
3,203 V - 2,272 V = 0,931 V þ
ULampe_18 = ILampe_18 * RLampe_18 → ILampe_18 = ULampe_18 / RLampe_18 =
0,931 V / 8,33 Ω = 0,1118 Nachfolgend die zweite Schaltung „schaltung_03-10.ewb“ der Superposition bei der die Spannungsquelle UBatt_1
vom Versuch 1 (rechts) durch einen Kurzschluss ersetzt wurde: (Bild vergrößern: auf
Bild klicken! Webverzeichnis
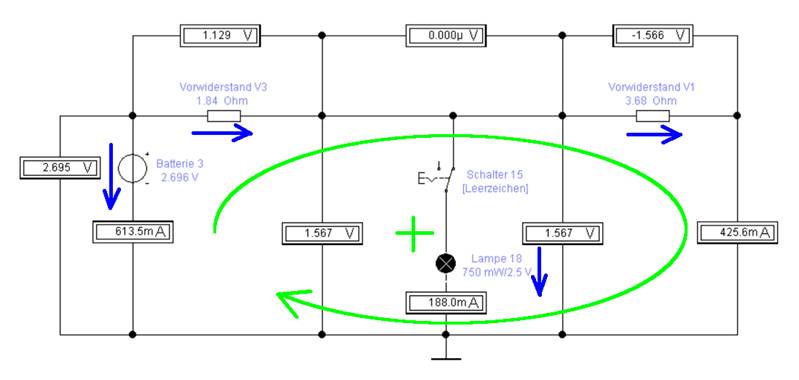
schaltung_03-10.ewb) Wenn man in der obenstehenden Schaltung „schaltung_03-10.ewb“ von
der Spannungsquelle „Batterie 3“ aus nach rechts in die Schaltung
hinein schaut, dann sieht man als erstes den Vorwiderstand RVor_V3, der in Reihe geschaltet ist mit
den beiden parallel geschalteten Widerständen ( RVor_V1 // RLampe_18 ), sodass sich der Gesamtwiderstand
Rges_V3 wie folgt berechnen
lässt: Rges_V3 = RVor_V3 + ( RVor_V1 // RLampe_18 ) = RVor_V3 + [ RVor_V1 * RLampe_18 / ( RVor_V1 + RLampe_18 ) ] Betriebsdaten der Glühlampe [18]: UNenn = 2,5 V INenn = 0,3 A Gemäß
der Betriebsdaten (= Nennwerte) lässt sich der Widerstand der Glühlampe wie
folgt berechnen: RLampe_18 = ULampe_18 / ILampe_18 = 2,5 V / 0,3 A = 8,33 Ω Rges_V3 = RVor_V3 + [ RVor_V1 * RLampe_18 / ( RVor_V1 + R
Lampe_18 ) ] =
1,84 Ω + [ 3,68 Ω * 8,33 Ω / (3,68 Ω + 8,33 Ω )
] =
1,84 Ω + [ 30,6544 Ω =
1,84 Ω + [ 2,5524 Ω
] = 4,392 Ω Iges
= Uges / Rges = UBatt_V3
/ Rges_V3 = 2,696 V / 4,392 Ω =
0,61384 A ≈ 613,8 mA þ Spannungsumlauf Versuch 3 (links), Schaltung „schaltung_03-10.ewb“ UR Vor V3 + ULampe 18
+ ( - UBatt_3 ) = 0 → UR Vor V3 = UBatt_3 - ULampe 18 → Der Wert für ULampe 18 = 1,567 V wurde der Simulation entnommen! = 2,696 V - 1,567 V = 1,129 V þ UBatt_3 = UR Vor V3 + ULampe 18 = 1,129 V + 1,567 V = 2,696 V þ Probe: ULampe_18 = UBatt_3
- UR Vor V3 =
2,696 V - 1,129 V = 1,567 V þ
ULampe_18 = ILampe_18 * RLampe_18 → ILampe_18 = ULampe_18 / RLampe_18 = 1,567 V / 8,33 Ω = 0,1881 Nun wieder zurück zur Superposition bei der es wegen der zwei Spannungsquellen „UBatt_V3“ und „UBatt_V1“ auch zwei Maschenumläufe gibt: Spannungsumlauf Versuch 1 (rechts) , Schaltung „schaltung_03-09.ewb“ UR Vor V1 + ULampe 18 + ( - UBatt_1 ) = 0 → ULampe 18 = UBatt_1 - UR
Vor V1
Spannungsumlauf Versuch 3 (links) , Schaltung „schaltung_03-10.ewb“ UR Vor V3 + ULampe 18 + ( - UBatt_3 ) = 0 → ULampe
18
= UBatt_3 - UR Vor V3 Superposition, d.h. Addition der beiden Spannungsumläufe:
ULampe 18 = ( UBatt_1 - UR
Vor V1
) + ( UBatt_3 - UR
Vor V3
) = ( UBatt_1 + UBatt_3 ) - ( UR Vor V1 + UR Vor V3 ) = ( 3,203 V + 2,696 V ) - ( 2,272 V + 1,129 V ) = ( 5,899
V ) - ( 3,401 V ) = 2,498 V þ Achtung: Die Glühlampenspannungen sind wegen der Superposition nicht identisch bzw. dürfen nicht
gleichgesetzt werden:
ULampe 18 ≠ ULampe 18 ≠ ULampe
18 Zwecks Verifizierung lässt sich die Superposition auch direkt auf den Spannungsabfall der Glühlampe [18] wie
folgt anwenden:
Maschenumlauf 1, Schaltung „schaltung_03-09.ewb“ ULampe 18 = UBatt_1 - UR Vor V1 = 3,203 V - 2,272 V = 0,931 V = 931 mV Maschenumlauf 2, Schaltung „schaltung_03-10.ewb“ ULampe 18 = UBatt_3 - UR Vor V3 = 2,696 V
- 1,129 V
= 1,567 V ULampe 18 = ULampe
18
+ ULampe 18 = 0,931 V + 1,567 V = 2,498 V þ (siehe weiter oben: Electronics Workbench „Schaltung_03-08.ewb“) ILampe_18 = ULampe_18 / RLampe_18 =
2,498 V / 8,33 Ω =
0,29988 = 299,9 mA þ (siehe weiter oben: Electronics Workbench „Schaltung_03-08.ewb“) So, jetzt wo wir wissen, was eine Superposition ist und wie sie funktioniert, wenden
wir uns wieder der Praxis zu (Zum Vergrößern bitte auf
das Bild klicken!) und fragen uns, wozu sich der Versuchsaufbau
aus der Kombination von Versuch 3 (links) und Versuch 1 (rechts)
eignet und sich einsetzen lässt. Schließlich befinden sich die beiden
Batteriepacks „Batterie_V3“ (links) und „Batterie_V1“ (rechts) in Konkurrenz
zueinander. Wenn z.B. das Batteriepack „Batterie_V3“
(links) bereits teilweise entladen ist, während das Batteriepack
„Batterie_V1“ (rechts) sozusagen noch fabrikneu und taufrisch ist,
versucht das Batteriepack „Batterie_V1“ (rechts) das Potentialgefälle zum Batteriepack
„Batterie_V3“ (links) auszugleichen, indem es die Batterien im
Batteriepack „Batterie_V3“ (links) aufzuladen versucht, obwohl es sich
bei den Batterien nicht um aufladbare Akkus handelt! Schließlich kann der Ausgleichstrom vom Batteriepack „Batterie_V1“
(rechts) zum Batteriepack „Batterie_V3“ (links) ziemlich „dick und groß“
werden: IAusgleich = ∆IBatt_V1 = 265 mA - 108 mA = 157 mA. Deshalb darf es zwischen den beiden
Batteriepacks „Batterie_V1“ (rechts) und „Batterie_V3“ (links) keine permanente,
fortwährende Verbindung geben! Dies ist dann auch der Grund dafür, weshalb jeweils
ein Taster (links) und ein Schiebeschalter (rechts) eingesetzt werden (siehe obenstehendes Bild)! Diesbezüglich dient das Batteriepack „Batterie_V1“
(rechts) wegen der vollständigen, fabrikneuen Aufladung als Referenz, d.h. als Bezugs- und Vergleichsquelle für die bereits teilweise
„verbrauchten“ Batterien im Batteriepack „Batterie_V3“ (links). Der
Batterietester als Kombination von Versuch 3 (links) und Versuch 1 (rechts). Wie also lassen sich die bereits teilweise
„verbrauchten“ Batterien im Batteriepack „Batterie_V3“ (links) erkennen,
feststellen und testen? Ganz einfach, indem wir den Taster [14] schließen, sodass die Glühlampe [18] mehr oder weniger hell
leuchtet. Je nach Ladezustand der bereits teilweise
„verbrauchten“ Batterien im Batteriepack „Batterie_V3“ (links). Um zu wissen, wie gering oder wie stark die
Batterien im Batteriepack „Batterie_V3“ (links) bereits „verbraucht“ sind,
müssen wir die Referenz in Form des
Batteriepacks „Batterie_V1“ (rechts) bemühen und durch Betätigen des Schiebeschalters [15] das Batteriepack
„Batterie_V3“ (links) hinzuschalten, sodass die Glühlampe [18] plötzlich deutlich heller leuchtet!
Sozusagen als Indiz
(Hinweis)
dafür, dass das Batteriepack „Batterie_V3“ (links) bereits „verbraucht“ ist! Dabei
kommt es also zwingend auf die Reihenfolge an, welche Tasten (Taster [14], Schiebeschalters [15]) wann gedrückt bzw. betätigt werden, damit der Batterietester wie gewünscht funktioniert! Wenn wir z.B. als erstes den Schiebeschalters [15] (rechts) betätigen
und damit das Batteriepack „Batterie_V1“ (rechts) auf die Glühlampe [18] schalten, dann leuchtet dieses wie erwartet
sehr hell. Wenn wir dann als zweites den Taster [14] (links) betätigen, wird zwar das Batteriepack
„Batterie_V3“ (links) ebenfalls auf die Glühlampe [18] geschaltet, aber ohne sichtbare Auswirkung
bezüglich der hell leuchtenden Glühlampe [18], weil die Batteriespannung des Batteriepacks
„Batterie_V3“ (links) deutlich niedriger ist als die des Batteriepacks
„Batterie_V1“ (rechts), sodass sich auch am Potentialgefälle vom Batteriepack „Batterie_V1“ (rechts) hin
zum Batteriepack „Batterie_V3“ (links) nichts ändert: (Bild vergrößern: auf
Bild klicken! Webverzeichnis
schaltung_03-11.ewb) Bei der obenstehenden Schaltung „schaltung_03-11.ewb“ von Electronics
Workbench, die sich als Batterietester von 1,5 Volt Batterien des Typs „Mignon AA“ - die sich links in der Batteriehalterung [19] „Batterie_3“ des Versuchs 3 (links) befinden - verwenden lässt, verhält es sich im „werksseitigen“
Betriebszustand so, dass beide Schalter Taster [14] (links) und
Schiebeschalter [15] (rechts) geöffnet sind, sodass die Glühlampe [14]
nicht leuchtet und die Batterien in den beiden Batteriehalterungen im Leerlauf betrieben werden. Dabei bedeutet der Betriebszustand „Leerlauf“ der Batterien, dass diese nicht entladen werden und
demzufolge keinen Strom nach außen zur Glühlampe [18] liefern! Die an den Batterieklemmen zwischen dem
jeweiligen „+“ und „-“-Pol anliegende Klemmenspannung nennt man Leerlaufspannung: UKlemme = ULeerlauf >>
Die Leerlaufspannung (englisch open-circuit voltage, OCV)
ist in der Elektrotechnik die an den Klemmen einer
offenen Spannungsquelle gemessene elektrische Spannung. Das heißt, die
Leerlaufspannung ist die Spannung auf der Ausgangsseite, wenn kein
Verbraucher angeschlossen ist. Es fließt kein elektrischer Strom, wodurch keine Spannung
über den Innenwiderstand der Spannungsquelle
abfällt. Die
Leerlaufspannung ist genau dann gleich der Quellenspannung UQ,
wenn innerhalb der Spannungsquelle, wie bei einem Generator oder
einer galvanischen Zelle, keine parallelen
Strompfade existieren, die zum Beispiel Leckströme verursachen, welche die
Leerlaufspannung verringern. Fließt ein nicht mehr zu vernachlässigender
Strom und kommt es zu einem Spannungsabfall am
Innenwiderstand der Spannungsquelle, so stellt sich an den Klemmen die
sogenannte Klemmenspannung ein, welche vom Betrag
her immer kleiner als die Leerlaufspannung ist. (…) Zur Messung der Leerlaufspannung ist ein Spannungsmessgerät erforderlich, das einen wesentlich höheren Innenwiderstand als die Quelle
hat. Damit wird gewährleistet, dass die Belastung der Spannungsquelle durch
das Messgerät und die daraus resultierende Rückwirkungsabweichung vernachlässigbar klein ist. Der Innenwiderstand
marktüblicher Digitalmultimeter liegt im Bereich einiger Megaohm, so dass diese Bedingung bei vielen Spannungsquellen
gegeben ist. << (Quelle: Wikipedia) Wie man bei der obenstehenden Schaltung „schaltung_03-11.ewb“ von Electronics Workbench sieht, ist die
Leerlaufspannung UBatterie_3 = 2,696 V der Batterien in der
Batteriehalterung [19] (links) deutlich niedriger als die Leerlaufspannung UBatterie_1
= 3,203 V der Batterien in der Batteriehalterung [19] (rechts). Der Grund
dafür ist der, dass den Batterien in der Batteriehalterung [19] (links) schon
mehrfach elektrische Energie Wel = Pel * tEntlade
in Form von Ladungsträgern (= Elektronen) entnommen wurden, sodass diese
nicht mehr „taufrisch“ sind! Die bereits entnommene elektrische
Energie der Batterien in der Batteriehalterung [19] (links) lässt sich dabei
im Vergleich zu den noch voll aufgeladenen Batterien in der Batteriehalterung
[19] (rechts) wie folgt berechnen: ∆Wel = Wel, V1 - Wel, V3 =
( Pel, V1 - Pel, V3 ) * ∆tEndlade = ( UBatterie_V1
- UBatterie_V3 ) * IGlühlampe * ∆tEndlade Eine einzelne, voll „aufgeladene“ und
„taufrische“ 1,5 Volt Batterie vom Typ „Mignon AA“ hat nach Herstellerangabe
eine gespeicherte Ladungsmenge Q von Q = 2,0 Ah und enthält eine
gespeicherte elektrische Energie Wel von Wel = 3.0 Wh. In diesem Zusammenhang stellt sich dann gleich
die Frage, ob zwei voll „aufgeladene“ 1,5 Volt Batterien in
Reihenschaltung
dann über die doppelte Ladungsträgermenge Qges = 2 * QBatterie
= 2 * 2,0 Ah = 4,0 Ah verfügen oder nicht! Dabei gilt es zu bedenken, dass das Zusammenschalten zweier 1,5
Volt Batterien in Serie
- eben so wie in der Batteriehalterung
[19]
- zunächst dafür sorgt, dass sich die Batteriespannung auf insgesamt 3,0 Volt verdoppelt: UBatt, ges = UBatt, 1 + UBatt, 2 = 2 * UBatt, 1 = 2 * 1,5 V = 3,0 V → … mit UBatt, 1 = UBatt, 2 Die verdoppelte Batteriespannung UBatt, ges = 3,0 V sorgt wiederum sofort dafür, dass sich
die Stromstärke durch die in Reihe geschalteten 1,5 Volt
Batterien ebenfalls verdoppelt, vorausgesetzt natürlich, dass wir
weiterhin die gleiche Glühlampe
[18]
mit dem gleichen Widerstandswert verwenden! Die Glühlampe [18] wiederum reagiert ebenfalls sofort auf die verdoppelten
Werte von Spannung und Strom,
indem sie praktisch doppelt so hell leuchtet und dabei natürlich auch doppelt
so viel Energie „verbraucht“ bzw. von
den Batterien aufnimmt! Dabei wird also das praktisch doppelt
so helle Leuchten der Glühlampe
[18]
mit dem doppelt so hohen Energieverbrauch „erkauft“ bzw.
stillschweigend akzeptiert mit der Folge, dass die Glühlampe [18] eben nicht doppelt so lange leuchtet
als bisher, obwohl uns ja bei zwei in Reihe geschalteten 1,5 Volt
Batterien die doppelte Energie zur Verfügung steht! Werfen wir zu also einen Blick auf das
Berechnen der elektrischen Energie Wel,
der elektrischen Leistung
Pel
und der Ladungsträgermenge Qel: Wel = Pel * t = U * I * t = UBatt * IEntlade * t = UBatt * QBatt = QBatt * UBatt → QBatt = Wel
/ UBatt = Wel / ( UBatt, 1 + UBatt, 2 ) → Wel = QBatt * UBatt = QBatt * ( UBatt,
1
+ UBatt, 2 ) = 2,0 Ah * ( 1,5 V + 1,5 V ) = 2,0
Ah * 3,0 V = 6,0 VAh þ Wie man sieht, verdoppelt sich die in
den beiden in Reihe geschalteten 1,5 Volt Batterien gespeicherte
Energie Wel tatsächlich
(siehe „Probe“ und roter Kasten weiter unten)! - Neben der Herstellerangabe zur gespeicherten
Energie Wel = 3,0 Wh einer einzelnen 1,5 Volt Batterie vom Typ
„Mignon AA“ aus Alkali-Mangan gibt es noch die Angabe zur gespeicherten
Ladungsträgermenge QBatt = 2 Ah. Wenn man die elektrische Energie Wel einer einzelnen 1,5 Volt Batterie ins
Verhältnis setzt zur Ladungsträgermenge
QBatt,
d.h. den Quotienten Wel / QBatt bildet, dann folgt: UBatt = Wel / QBatt = 3 Wh / 2,0 Ah
= 3 V Probe: UBatt =
Wel / QBatt → Wel =
QBatt UBatt = QBatt, 1 UBatt, 1 = 2,0 Ah * 1,5 V = 3,0 VAh = 3,0 Wh þ Wel, ges = QBatt UBatt = QBatt, 1 UBatt, 1 + QBatt, 2 UBatt,
2 → mit QBatt, 1 = QBatt, 2 und UBatt, 1 = UBatt, 2 = QBatt, 1 ( UBatt, 1 + UBatt, 2 ) = QBatt,
1 ( UBatt, 1 + UBatt, 1 ) = 2 * QBatt,
1 UBatt, 1 = 2 * 2,0 Ah * 1,5 V = 6 Wh þ Reihenschaltung zweier
einzelner 1,5 Volt Batterien Schaltet
man zwei 1,5 Volt Batterien in Serie, so folgt für die Gesamtspannung UBatt, ges UBatt, ges = UBatt, 1 + UBatt,
2 → mit Wel = QBatt UBatt → UBatt = Wel / QBatt → = Wel, 1 / QBatt, 1 + Wel, 2 / QBatt, 2 → mit Wel,
1 = Wel, 2 und QBatt,
1 = QBatt, 2 → = 2 * Wel, 1 / QBatt,
1 → ½ * UBatt, ges = Wel,
1 / QBatt, 1 = UBatt, 1 → Linke und rechte
Seite der Gleichung tauschen! UBatt, 1 =
½ * UBatt, ges → UBatt, ges = 2 * UBatt, 1 = Wel, 1 / QBatt, 1 = 3,0 Wh / 2 Ah = 3,0 V UBatt, ges =
2 * UBatt, 1 = 2 * 1,5 V = 3,0 V þ QBatt, ges =
Wel / UBatt,
ges
= Wel / ( 2 UBatt,
1
) = Wel *
( 1 / 2 UBatt, 1 ) → Wel = Pel * tEinschalt = Uel * Iel tEinschalt = Uel * Iel tEinschalt = Uel * Qel = UBatt,
1 * Qel, 1 → für eine
Batterie! = Wel *
( 1 / 2 UBatt, 1 ) = Wel / 2 UBatt, 1 = Wel / UBatt, ges = UBatt,
1 * Qel, 1 / UBatt, ges = UBatt, 1 * Qel, 1 / UBatt, ges = UBatt,
1 / UBatt, ges * Qel,
1
= 1,5 QBatt, ges =
Wel / UBatt,
ges
= Wel / ( 2 UBatt, 1 ) = ½ Wel / UBatt,
1
= ½ QBatt, 1 = ½ * 2,0 Ah = 1,0 Ah
þ QBatt, 1 =
Wel, 1 / UBatt, 1 = 3 Wh
/ 1,5 V = 3
Wenden wir uns wieder der Schaltung „schaltung_03-11.ewb“ von Electronics
Workbench zu: (Bild vergrößern: auf
Bild klicken! Webverzeichnis
schaltung_03-11.ewb) Gemäß der Herstellerangabe
beträgt die in einer einzelnen 1,5 Volt Batterie vom Typ “Mignon AA,
Alkali-Mangan” gespeicherte Ladungsträgermenge QBatt, 1 = 2,0 Ah. Wie wir bereits wissen, verringert sich
die gesamte Ladungsträgermenge
Qges
= ½ QBatt, 1 um die Hälfte, wenn die zwei
1,5 Volt Batterien in der Batteriehaltung
[19] in Serie geschaltet sind: QBatt, ges = ½ QBatt, 1 = ½ * Wel, 1 / UBatt, 1 = ½
* 3,0 Wh / 1,5 V = 1 Ah QBatt, ges = IBatt * tEntlade → tEntlade = QBatt, ges / IBatt = 1 Ah / 0,3 A = 3,33
h ∆Wel = ( UBatterie_V1 - UBatterie_V3, Leerlauf ) * IGlühlampe
* ∆tEndlade = ( 3,203 V - 2,696 V ) 0,3 A * 3,33 h =
0,507 V * 0,3 A * 3,33 h = 0,5065 Wh Nach Herstellerangabe
beträgt die in einer einzelnen 1,5 Volt Batterie vom Typ “Mignon AA, Alkali-Mangan
” gespeicherte elektrische Energie WHersteller = 3,0 Wh, sodass
dann bei zwei 1,5 Volt Batterien schon bis zu Wel, ges = 6
Wh an elektrischer Energie zur Verfügung stehen. Demzufolge wurden den beiden bereits teilentladenen
1,5 Volt Batterien in der Batteriehalterung [19] (links) Wel,
ges n 100 % ∆
Wel n
x % __________________ x = 100 % /
Wel, ges * ∆ Wel = ( 100 % / 6 der elektrischen Energie entnommen, sodass diese noch über eine verbleibende
elektrische Energie von 100 % - 8,44 % = 91,56 % verfügen! Theoretisch! Aber weshalb nur theoretisch, d.h. nicht
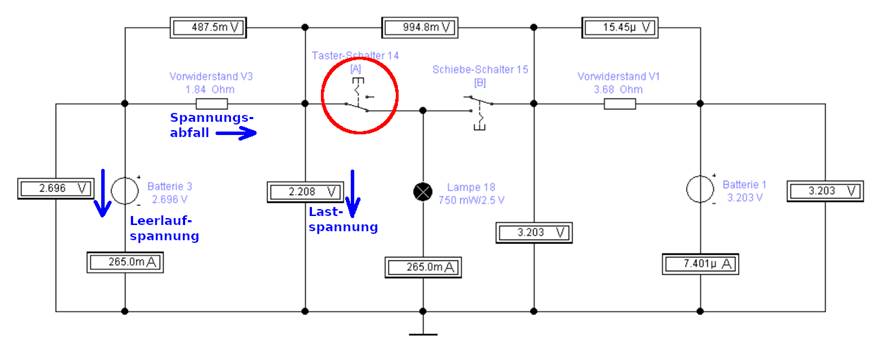
praktisch? Ganz einfach! Weil die Leerlaufspannung von ULeerlauf_V3 = 2,696 V bei
Belastung durch einen ohmschen Verbraucher wie z.B. unsere Glühlampe [18] „in die Knie geht!“, d.h. sich
entsprechend der Belastung maßgeblich verringert!
Bei der obenstehenden Schaltung „schaltung_03-11.ewb“ verringert
sich nämlich die Leerlaufspannung von ULeerlauf_V3 = 2,696 V beim
Schließen des Tasters [14] (links), d.h. durch
das Hinzuschalten der Glühlampe
[18],
wie folgt: ∆Wel = ( UBatterie_V1 - UBatterie_V3, Last ) * IGlühlampe
* ∆tEndlade =
( 3,203 V - 2,208 V ) 0,3 A * 3,33 h = 0,995 V * 0,3 A * 3,33 h =
0,994
Wh Demzufolge wurden den beiden bereits teilentladenen
1,5 Volt Batterien in der Batteriehalterung [19] (links) Wel,
ges n 100 % ∆
Wel n
x % __________________ x = 100 % /
Wel, ges * ∆ Wel = ( 100 % / 6 der
elektrischen Energie entnommen, sodass diese nur noch über eine verbleibende
elektrische Energie von 100 % - 16,57 % = 83,43 % verfügen! Praktisch!
Übrigens: Es gibt im realen Alltag ähnliche
Phänomene (= Erscheinungen), wo man den Unterschied zwischen Leerlauf und Belastung beobachten kann. Verkalkte Wasserleitung Bei einem älteren Wohnhaus z.B. aus den 1950er
Jahren verkalken die Frischwasserleitungen hin zur Küche oder Bad im Laufe
der Jahre oder Jahrzehnte, je nachdem wie kalkhaltig das Leitungswasser im
Stadtteil ist, sodass sich die Wasserleitung mehr und mehr durch
Kalkablagerungen zusetzt und sich der Leitungsquerschnitt maßgeblich
verringert. Mit der unangenehmen Folge, dass sich nicht mehr so viele
Kubikmeter Wasser pro Stunde durch die verkalkte Wasserleitung transportieren
lassen und die Durchfluß-/Transportmenge entsprechend verringert, sodass das
Einlassen des Badewassers in die Badewanne immer mehr Zeit benötigt! Feststellen kann man eine stark verkalkte
Wasserleitung daran, dass wenn man den Wasserhahn in der Küche aufdreht, zunächst,
d.h. die ersten paar Sekunden, das Wasser mit einem starken, dafür aber
dünnen Strahl aus dem Wasserhahn schießt. Aber bereits nach ein bis zwei
Sekunden baut sich der aufgestaute Wasserdruck in der verkalkten
Wasserleitung ab, sodass der Wasserdruck wegen der verringerten
Querschnittsfläche der verkalkten Wasserleitung schlagartig sinkt und sich
nur noch ein schwaches Rinnsal an Wasser in das Waschbecken ergießt. - Altersschwache Autobatterie im Winter Ältere Autobatterien, eigentlich sind es ja
wieder aufladbare Akkus, die z.B. schon mehr als sechs Jahre auf dem Buckel
haben, verschleißen mit der Zeit, wobei die Bleiplatten im Inneren wegen der
Schwefelsäure und den chemischen Vorgängen beim Laden und Entladen immer
dünner werden und sich die Oxidationsprodukte in Form von Bleischlamm auf dem
Boden der Autobatterie absetzen bis dieser sogar die Bleiplatten kurzschließt
und nichts mehr geht! Wenn man z.B. im Winter bei tieferen
Temperaturen ins Auto steigt, dann ist zunächst alles so wie gewohnt: die
Innenraumbeleuchtung leuchtet beim Öffnen der Tür, die
Armaturenbrettbeleuchtung leuchtet beim Einstecken des Zündschlüssels und das
Autoradio funktioniert auch (noch). Fragt sich nur wie lange! Plötzlich aber,
wenn man den Zündschlüssel umdreht, um mit dem Anlasser den Motor zu starten,
gehen die Innenraumbeleuchtung, die Armaturenbrettbeleuchtung und das
Autoradio aus, weil die Autobatterie plötzlich keinen Saft mehr hat.
Plötzlich? Nein, sie hatte bereits auch schon vorher keinen Saft, d.h. in der
Batterie gespeicherte, elektrische Energie. Zwar hat die restliche Energie
noch für die Innenraumbeleuchtung, die Armaturenbrettbeleuchtung und das
Autoradio ausgereicht, nicht aber mehr für den Anlasser! Dazu muss man wissen, dass der Anlasser
zum Starten des Motors kurzzeitig einen Strom von IAnlasser = 400 A zieht und die altersschwache
Autobatterie extrem belastet, sodass diese durch den Anlassvorgang
quasi kurzgeschlossen wird mit der Folge, dass die Batteriespannung
u.a. auch wegen des Verschleiß bedingten höheren Innenwiderstandes „in die Knie geht“ und auf deutlich unter 12
Volt absackt. Hat die Autobatterie nach dem Startversuch des Anlassens nur
noch eine Bordspannung von deutlich weniger als 10 Volt, ist sie defekt! – Nun wieder zurück zum Batterietester!
Im Zusammenhang mit dem Hin und Her um die Leerlaufspannung und der Lastspannung stellt sich jetzt erst recht die
Frage, ob es nicht doch einen verwertbaren Zusammenhang, eine Beziehung oder
eine neue Erkenntnis zwischen beiden gibt bzw. geben könnte. Könnte es sein,
dass wir etwas übersehen haben, was uns eigentlich schon bekannt sein müsste?
Abschließend berechnet
sich der Widerstand der Glühlampe wie folgt: RLampe_18 = ULampe_18 / ILampe_18 = UBatterie_V3, Last
/ IBatt_V3 = 2,208 V / 265 mA =
2,208 V / 0,265
A = 8,33 Ω Nachfolgend noch die zugehörige Schaltung „schaltung_03-11.ewb“ von Electronics Workbench: (Bild vergrößern: auf
Bild klicken! Webverzeichnis
schaltung_03-11.ewb) Da die beiden im Elektronik-Baukasten „electronic
159“
enthaltenen Batteriehalterungen
[19]
jeweils zwei 1,5 Volt Batterien vom Typ „Mignon AA“ aufnehmen, können
wir mit unserem Batterietester immer nur zwei Batterien als Ganzes
testen, ob diese noch zu gebrauchen sind oder bereits so entladen wurden,
dass diese keine elektrische Energie mehr in Form Elektronen als Ladungsträger
gespeichert haben und demzufolge entsorgt werden können. Da die beiden 1,5 Volt Batterien in der Batteriehalterung [19] hintereinander,
d.h. in Serie bzw. in Reihe geschaltet sind und die fabrikneuen und
„frischen“ Batterien bei der Herstellung aus ein- und derselben
Produktionsserie stammen, kann man davon ausgehen, dass diese gleichartig
beschaffen sind, gleiche Eigenschaften aufweisen und demzufolge beide
über die gleiche gespeicherte Energie und Ladungsmenge Q an Elektronen
e- als Ladungsträger verfügen. Dabei beträgt die in einer 1,5 Volt
Batterie vom Typ „Alkali-Mangan“
gespeicherte elektrische Energie Wel = 3.0 Wh; bei zwei im
Batteriepack in Serie geschalteten 1,5 Volt Batterien
beträgt die gespeicherte elektrische Energie Wel = 2 * 3.0 Wh =
6,0 Wh bei einer Gesamtspannung von UBatt_V1, ges = 3,203 V. Früher oder später wird es aber vorkommen,
dass wir zu unserem Elektronik-Baukasten
„electronic 159“ keine Batterien mehr vorrätig haben, weil wir es versäumt
haben, uns rechtzeitig um Nachschub zu kümmern. Dann ist guter Rat teuer. Was
also machen, wo lassen sich doch noch 1,5 Volt Batterien im Haushalt
auftreiben? Dabei erinnern wir uns daran, dass z.B. der
Radiowecker im Schlafzimmer oder die LED-Taschenlampe ja auch zwei 1,5 Volt
Batterien vom Type „Mignon AA“ verwendet, die man ausbauen und als Ersatz für
den Elektronik-Baukasten „electronic 159“ verwenden könnte.
Gesagt getan! Aber wider Erwarten scheinen die beiden 1,5 Volt Batterien aus
der LED-Taschenlampe nicht richtig zu funktionieren, da sich mit diesen
unsere Glühlampe [18] wider Erwarten nicht
zum Leuchten bringen lässt. Da es sich bei den ausgebauten 1,5 Volt
Batterien aus der LED-Taschenlampe um zwei Batterien handelt, stellt
sich die Frage, ob eventuell alle beiden Batterien nicht
funktionieren, d.h. komplett entladen sind, oder nur eine der
beiden. Wenn nämlich von den beiden
Ersatzbatterien nur eine komplett entladen ist, dann können beide
Batterien wegen der Reihenschaltung nicht mehr die
volle Batteriespannung aufbringen, sodass die schwächere Batterie die
stärke „ausbremst“: UBatt, ges = UBatt_1 + UBatt_2
= 1,2 V + 0,75 V = 1,95 V Bei unserem
Batterietester ließe sich zwar auch eine einzelne 1,5 Volt Batterie in
die linke Batteriehalterung
[19]
vom Versuch 3 einsetzen, (Zum Vergrößern bitte
auf das Bild klicken!) was aber das Problem nicht
löst, da wir auch in der rechten Batteriehalterung [19] vom Versuch 1 nur eine einzelne 1,5 Volt (Referenz-) Batterie
einsetzen dürften und noch dazu die 2,5 Volt Glühlampe [18] durch eine 1,5 Volt Glühlampe auswechseln müssten! „Eine Kette ist nur so
stark, wie ihr schwächstes Glied!“ bedeutet bezüglich der linken Batteriehalterung [19] vom Versuch 3, dass wir wegen · der Reihenschaltung der beiden 1,5
Batterien immer · eine fabrikneue
1,5 Volt Batterie und · eine bereits benutzte
oder teilentladene 1,5 Volt Batterie zu Test- und Prüfzwecken einsetzen, sodass wir trotz der Batteriehalterung
[19] für zwei 1,5 Volt Batterien
immer nur eine einzelne 1,5 Volt Batterie testen: UBatt, ges = UBatt_1 + UBatt_2 = 1,25 V + 0,75 V = 1,95 V → Die zweite
Batterie mit 0,75 V sollte ausgewechselt
werden! Ansonsten hilft uns die nachfolgende Tabelle des
Batterietesters „TAKIT
Batterietester Digital“ weiter, der man entnehmen kann, wann eine
1,5 Volt Batterien oder zwei 1,5 Volt in Reihe geschaltete
Batterien, quasi als 3,0 Volt Batterie, ausgewechselt, engl. „replace“,
werden sollte: (Zum Vergrößern bitte
auf das Bild klicken!) Das Interessante an dem „TAKIT
Batterietester Digital“ ist übrigens, dass er der einzige ist, den ich
bei Amazon gefunden habe, der über eine digitale Spannungsanzeige in Volt
verfügt, der sich bis zu einem Spannungsbereich von 9 Volt auch als sehr preiswertes Digitalvoltmeter
verwenden läßt: (Zum Vergrößern bitte
auf das Bild klicken!)
Wer etwa das Doppelte an Euros investieren
kann oder möchte, bekommt bei Amazon für knapp 25,- Euro den sogenannten „UM25C
USB 2.0 Tester“ mit Bluetooth-Datenübertragung
an die entsprechende Android-App
oder die Windows-Software zwecks
Bedienung und Messung von Spannung, Strom, Widerstand, Energie [mWh],
Kapazität [mAh] und vieles mehr: (Zum Vergrößern bitte
auf eines der Bilder klicken!) Vom „cc2tv“-Computerclub, Folge 241 „Bluetooth
(BT) bei Multimetern und USB-Messgeräten“ gibt es bei YouTube
auch ein entsprechendes Video in dem Wolfgang Rudolph das USB-Messgerät
vorstellt: >> Messwertübertragung
per Bluetooth Kaum eine Gerätekategorie bei der nicht in
irgendeiner Art BT im Spiel ist. Auch bei Multimetern für den Hobbybereich
findet man Geräte die Ihre gemessenen Werte per BT verbreiten können. Ein
näherer Blick auf die Möglich- und Fähigkeiten des WON B35T lässt staunen. Er sieht aus wie ein zu fett gewordener
USB-Stick. Allerdings verbirgt sich in diesem Dongle ein komplexes Messgerät
mit dem U, I, P, R, Ah und weitere elektrische Werte bestimmt werden können.
Auch die Spannung auf den Datenleitungen lässt sich messen. Speichern und
grafisches Darstellen beherrscht diese kleine Wunder genauso wie BT. Es kann
sogar bis zu 24V DC anzeigen. Vorgestellt wird hier die Version UM24C.
<< Aber nur das USB 2.0 Messgerät vom Typ „UM25C“ verfügt über die Bluetooth-Messwertübertragung! – Da es sich um ein USB 2.0 Messgerät handelt,
muss man sich zusätzlich zu der Anschaffung eventuell noch einen Messkopf
basteln bei dem z.B. der Micro-USB-Stecker am anderen Ende eines
herkömmlichen USB-Verlängerungskabels abgetrennt wird und die einzelnen am
offenen Kabelende heraustretenden Adern mit einem einadrigen roten und
schwarzen Messkabel nebst Prüfspitze versehen wird. Dazu müssen diese
miteinander verlötet und dann isoliert werden. Bei einem USB-Kabel werden Daten seriell, d.h.
zeitlich nacheinander übertragen, sodass zwei Adern mit „+“ und „-“ Pol
zwecks Stromversorgung, eines für den Output und eines für den Input
serieller Daten verwendet wird. Die beiden Ein- und Ausgangsadern für die
Datenübertragung benutzen dabei den „-“ Pol als gemeinsame Masse „┴“. Insgesamt haben wir
es also mit vier entsprechend farbigen Litzendrähten plus Abschirmung zu tun. Wer nicht basteln und löten möchte, kann sich
auch gleich fertige Prüf-
und Messkabel für den USB-Anschluss bei Amazon mitbestellen! - Batterie-Tester [ programmieren ] Kehren wir wieder zurück zu unserem
„Batterietester“ und der Schaltung „schaltung_03-11.ewb“ bei der mir die
Herstellerangaben einer 1,5 Volt Batterie vom Typ „Mignon AA“, d.h.
einer Alkali-Mangan-Batterie, nicht aus dem Kopf gehen: Kapazität:
2,0 Ah Energie:
3,0 Wh Bei der Angabe
„Kapazität“ handelt es sich gemäß
der Maßeinheit [ Ah ] um die in
der fabrikneuen Batterie gespeicherte Ladungsmenge
Q = I * t = 2 A * 1 h = 0,2 A * 10 h = 200 mA * 10 h = 20 mA * 100 h Bei der Angabe
„Energie“ handelt es sich gemäß der Maßeinheit [ Wh ] um die in der
fabrikneuen Batterie gespeicherte elektrische Energie Wel: Wel
= P * t = U * I * t = I2 R * t = U2 / R * t = U * Q → mit Q = I * t Bildet man den Quotienten von Energie [Wh]
zu Kapazität [Ah], so bekommt man als
Resultat die Spannung
[V]
zurück: UBatt, 1 =
Wel, 1 / QBatt,
1 = 3,0 Wh / 2,0 Ah = 3,0 V Jetzt bestätigt sich, dass sich die obenstehenden
Herstellerangaben tatsächlich auf eine einzelne 1,5 Volt
Batterie beziehen! Im Zusammenhang mit der Batteriehalterung [19] zwecks Aufnahme zweier
1,5 Volt Batterien vom Type „Mignon AA“, die in Reihenschaltung miteinander verbunden sind, müssten die
Herstellerangabe wie folgt lauten: Kapazität:
2,0 Ah Energie:
6,0 Wh Bildet man den Quotienten von Energie [Wh]
zu Kapazität [Ah], so bekommt man als
Resultat die Spannung
[V]
zurück: UBatt =
Wel / QBatt = 6,0 Wh / 2,0 Ah = 6,0 V Da es aber eine 3,0 Volt Batterie vom Typ
“Mignon, AA” nicht gibt, wissen wir, dass zwei 1,5 Volt
Batterien vom Typ „Mignon AA“, die in Reihe
geschaltet sind, eingesetzt werden: UBatt,
ges = UBatt, 1 + UBatt, 2 = Wel, 1 / QBatt, 1 + Wel, 2 / QBatt, 2 → Hauptnenner bilden! = Wel, 1 * QBatt, 2 / QBatt, 1 * QBatt,
2
+ Wel, 2 * QBatt,
1 / QBatt, 2 * QBatt,
1
= Wel, 1 * QBatt, 2 + Wel, 2 * QBatt,
1 / ( QBatt, 1 * QBatt,
2
) Dimensionsprobe: Wel, 2 * QBatt, 1 / ( QBatt, 1 * QBatt,
2
)
→ [ Wh ] * [ = Wel, 1 * QBatt, 1 + Wel, 2 * QBatt,
1 / ( QBatt, 1 * QBatt,
1 ) = = ( Wel, 1 + Wel, 1 ) / QBatt, 1 = 2 * Wel, 1 / QBatt,
1
= 2 * UBatt,
1
= 2 * 1,5 V = 3,0 V þ Jetzt machen wir das Gleiche noch für die Ladungsmenge Q [ Ah ]: UBatt, ges = Wel,
ges / QBatt,
ges → QBatt, ges = Wel, ges / UBatt, ges = Wel,
ges / ( UBatt,
1 + UBatt,
2 ) = Wel, ges / ( UBatt, 1 + UBatt, 1 ) = Wel, ges
/ ( 2 * UBatt, 1 ) = ½ Wel, ges
/ UBatt, 1 → mit UBatt, 1 = UBatt, 2 → Reihenschaltung von zwei
1,5 Volt Batterien! = ½ * 6 Wh / 1,5 V = ½ 6 = Wel, 1 / UBatt,
1 = QBatt, 1 = 3 Wh / 1,5 V = 3
Und weil wir gerade dabei sind, hier noch die
Herstellerangaben zu einem Pedelec-Akku
(= Lithium-Ionen): Kapazität:
12,8 Ah Spannung:
48 V Gemäß diesen beiden Angaben lässt sich zuerst
die Energie Wel wie
folgt berechnen: Wel = P * t = U * I * t =
UBatt * QBatt → mit QBatt = IBatt * tEntlade = 12,8 Ah und UBatt = 48 V = 48 V * 12,8 Ah = 614,4 VAh = 614,4 Wh Berechnung der Akkulaufzeit mit der im Akku gespeicherten Energie Wel = 614,4 Wh: Entsprechend
der gesetzlichen Vorgaben beträgt die Dauerleistung des Pedelec-Motors PMotor = 250 W und
damit verbunden die Akkulaufzeit : tEntlade = Wel / PMotor = 614,4 Wh /
250 W = 2,46 h → PMotor = UBatt * IMotor → IMotor = PMotor / UBatt =
250 W / 48 V = 250 Da
der Pedelec-Motor kurzfristig eine
Spitzenleistung vom Drei- bis Vierfachen
liefert, folgt für den Motorstrom: IMotor = PMotor / UBatt = 250
W * 3,5 / 48 V = 875 Demzufolge
beträgt der durchschnittliche Motorstrom: IMotor Ø = ( 5,21 A + 18,23 A
) / 2 = (
23,44 A ) / 2 = 11,72 A → Berechnung
der durchschnittlichen Antriebsleistung
PMotor Ø: PMotor Ø = UBatt
* IMotor Ø = 48 V * 11,72 A = 562,56 W Wenn
man bedenkt, dass ein untrainierter Radfahrer gerade mal über eine Antriebsleistung von PRadfahrer = 100 W
verfügt, dann ist man mit der durchschnittlich 5,62-fachen Motorunterstützung sehr
gut aufgestellt, lassen sich mit dieser auch größere Steigungen mühelos
erklimmen! - Elektrischen
Strom mit Strom ein-
und ausschalten
Was wir bisher gelernt haben, ist, dass elektrischer
Strom im Prinzip nur in einem geschlossenen Stromkreis „fließen“ kann. Aber
der elektrische Strom „fließt“ nicht wirklich, da sich die Elektronen als
negativ geladene Ladungsträger nur mit der Geschwindigkeit von wenigen Metern
pro Sekunde durch den Leiter, wie z.B. einem Kupferdraht, bewegen. Der
elektrische Strom selbst breitet sich aber mit Lichtgeschwindigkeit
(= 300 000 Km/s) aus, wobei nur der Bewegungsimpuls, wenn zwei oder mehr frei bewegliche
Elektronen aufgrund des Potentialgefälles aneinander stoßen,
weitergegeben wird! Dabei entsteht ein Potentialgefälle bzw. eine Potentialdifferenz
z.B. zwischen dem „+“-Pol und „-“-Pol einer Batterie. Dabei wird das
Potentialgefälle und die Größe der Potentialdifferenz zwischen den
Batteriepolen als elektrische
Spannung U, gemessen in Volt
[ V ], bezeichnet bzw. als solche angegeben. Wenn an dem Minuspol „-“ der Batterie ein Elektronenüberschuss herrscht und am Pluspol „+“ ein entsprechender Elektronenmangel, weil dort frei bewegliche Elektronen fehlen, dann bildet sich ein
entsprechendes Potentialgefälle aus, wobei die unterschiedlichen
Potentiale an den Anschlussklemmen stets bestrebt sind, sich
auszugleichen. Und zwar so lange bis es an dem Minuspol „-“ der Batterie keinen
Elektronenüberschuss und am Pluspol „+“ keinen Elektronenmangel
mehr gibt! Da aber in einer Batterie
beide Batteriepole mit den negativen und positiven Potentialen durch
eine Isolationsschicht von einander getrennt
sind, kann sich eine Batterie nicht selbst entladen. Weil aber eine Batterie
im Inneren eine kleine Chemiefabrik ist, können Alterungsprozesse im Laufe
der Jahre dazu führen, dass die an den Batteriepolen vorhandenen Spannungspotentiale
verringern und abbauen, weil sich die Chemie und die Chemikalien im Inneren
verändern, z.B. oxidieren. Weil sich Batterien wegen der unumkehrbaren chemischen Prozesse im
Inneren verbrauchen, lassen sich diese nicht aufladen, sondern
allenfalls durch elektrisch veranlasste Regeneration etwas auffrischen. Bei den Batterien, wiederaufladbaren Akkus,
Netzgeräten oder (Smartphone-) Steckernetzteilen unterscheidet man im
angeschlossen Stromkreis eines Verbrauchers zwischen der technischen und
physikalischen Stromflussrichtung. Damals als man sich zwischen der technischen
oder physikalischen Stromflussrichtung entscheiden musste, traf man aus der
Unkenntnis heraus die falsche Entscheidung, nämlich die für die technische
Stromflussrichtung vom („+“)-Pol → zum („-“)-Pol, obwohl sich die Elektronen als negativ
geladene Ladungsträger in genau die umgekehrte Richtung bewegen. >> Umgangssprachlich
tauchen die miteinander konkurrierenden Begriffe der sogenannten
„technischen“ und „physikalischen“ Stromrichtung auf. Tatsächlich aber ist
die elektrische Stromrichtung identisch mit der „technischen“ Stromrichtung
und in der Physik und Elektrotechnik genau gleich definiert.[3][4] Der Begriff der „technischen Stromrichtung“ ist in
erster Linie historisch bedingt; er geht von einem Strom von Ladungen aus,
die sich – der Feldlinienrichtung des elektrischen Feldes folgend
– vom positiven zum negativen Spannungspol bewegen. Dass es dagegen in
metallischen Leitern die Elektronen sind, die als
Ladungsträger den Stromfluss bewirken und dabei genau umgekehrt vom negativen
zum positiven Pol fließen, war zur Zeit dieser Begriffsbildung noch
unbekannt.[5] Die
Definition der elektrischen Stromrichtung wurde auch nach der Entdeckung der
Elektronen fast ein Jahrhundert später als einheitliche Konvention
beibehalten. Die Festlegung des Vorzeichens der Stromrichtung ist unmittelbar
verknüpft mit der Festlegung des Vorzeichens der Ladung; die ursprünglich
angenommene einzige Art von Ladungen war positiv. Die Ladung der in
Gegenrichtung bewegten Elektronen wurde dann unter Beibehaltung des elektrostatischen Kraftgesetzes als
negativ erklärt. Im Unterschied dazu bezeichnet der Begriff der „physikalischen
Stromrichtung“ nicht den Strom elektrischer Ladung, sondern einen Massen-,
Volumen-,
Teilchenstrom
oder quantenmechanischen (Aufenthalts-) )Wahrscheinlichkeitsstrom von
elektrischen Ladungsträgern. Er kennzeichnet somit
die Bewegung der elektrischen Ladungsträger unabhängig von ihrer jeweiligen
Ladung. Teilweise wird offen gelassen, um welche Ladungsträger es sich
handelt; oft sind Elektronen in Metallen gemeint, die per Konvention
eine negative Ladung besitzen. Dann ist die Elektronenströmung
(„physikalische Stromrichtung“), wie in der Abbildung verdeutlicht, der
(positiven) Ladungsströmung („technische Stromrichtung“) entgegengerichtet.
<< (Quelle: Wikipedia) Die technische Stromrichtung vom („+“)-Pol zum („-“)-Minuspol
wird bis zum heutigen Tage entsprechend der Konvention angewendet; also
demzufolge auch hier beim Elektronik-Baukasten „electronic
159“. Damit in einem geschlossenen Stromkreis ein elektrischer Strom I,
gemessen in Ampere [A],
„fließen“ kann, bedarf es eines Potentialunterschiedes in Form eines Spannungsgefälles zwischen dem („+“)-Pol und dem („-“)-Minuspol
einer Batterie, die als Spannungsquelle
dient. Damit die Batterie nicht elektrisch
kurzgeschlossen wird, bedarf es außerdem noch eines Verbrauchers, meistens
als ohmscher
Widerstand, der als sogenannter Lastwiderstand (=
Glühlampe [18]) den Stromfluss und die Stromstärke
I auf z.B. IGlühlampe
= 0,3 A
begrenzt. - Die
Glühlampe [18] wechselseitig mit Taster oder Schiebeschalter einschalten Bei der nachfolgenden Schaltung „schaltung_03-13.ewb“ haben wir es wie
bisher im linken Teil mit dem Versuch
3 „Schalter gesteuerte Lampe“ zu tun, wobei es sich bei dem Schalter[14] um einen Taster
handelt! Ein Taster hat die Eigenschaft, dass er nicht
einrastet, um die Glühlampe [18] dauerhaft leuchten zu lassen, sondern nur so
lange wie man den Taster gedrückt hält. Demzufolge wäre der Betrieb,
d.h. das Einschalten der Glühlampe [18] mittels Taster sogar umweltfreundlich
und ökologisch, da diese immer nur dann leuchtet, wenn man den Taster drückt
und gedrückt hält. Im rechten Teil der nachfolgenden
Schaltung haben wir es mit dem Versuch 1, bei dem sich die
Glühlampe [18] mittels des „Gleitschalters [15]“ bzw. des Schiebeschalters
auch dauerhaft einschalten lässt, zu tun. Dabei wurde aber der Versuch 1 dahingehend abgewandelt,
dass die Batteriehalterung [19] (rechts) nun nach links gegen den
Uhrzeigersinn, d.h. um -180 Grad nach links gedreht, eingesetzt wurde! Siehe
im Vergleich dazu auch Bild versuch_03_07.jpg!
Bezüglich des Betriebs der Glühlampe [18]
verhält sich die nachfolgenden Schaltung
„schaltung_03-13.ewb“ auf den ersten
Blick genau so wie die vorherigen Schaltung
„schaltung_03-11.ewb“ (siehe auch Bild versuch_03_07.jpg). Wenn man den Taster [14] (links) drückt und auch etwas länger gedrückt
hält, dann leuchtet die Glühlampe [18] so lange, bis man den Taster wieder
los lässt. Wenn man den Schiebeschalter [15] (rechts) nach rechts schiebt, dann leuchtet
die Glühlampe [18] ebenfalls und zwar so lange, bis man den Schiebeschalter wieder
nach links in seine Ausgangsposition schiebt, d.h. ausschaltet! Beim Einschalten der Glühlampe [18] mittels
des Schiebeschalters [15] wird man allerdings
feststellen, dass die Glühlampe deutlich wahrnehmbar heller leuchtet,
als wenn man diese mit dem Taster [14] einschaltet! Der Grund dafür ist der, dass die beiden 1,5
Volt Batterien vom Typ „Mignon AA“ in der Batteriehalterung [19] (rechts)
bisher weniger elektrische Energie z.B. zum Leuchten der Glühlampe
[18] abgegeben haben als die beiden 1,5 Volt Batterien in der
Batteriehalterung [19] (links)! Würde man die beiden 1,5 Volt Batterien der
linken Seite mit denen der rechten Seite austauschen, dann wäre es
genau umgekehrt, dann würde die Glühlampe 18], die mit dem Taster[14]
eingeschaltet wird, heller leuchten! Demzufolge leuchtet die Glühlampe [18] immer
nur so hell, wie es die beiden 1,5 Volt Batterien in der jeweiligen
Batteriehalterung [19] (links oder rechts) zulassen bzw. wie diese
noch mehr oder weniger fabrikneu mit elektrischer Energie „gefüllt“ sind. (Zum Vergrößern bitte
auf das Bild klicken!) Wenn du deinem Spieltrieb und deiner
Experimentierfreude freien Lauf lässt, dann wird es früher oder später
passieren, dass du die Glühlampe
[18]
mit dem Schiebeschalter [15] (rechts) einschaltest,
länger eingeschaltet lässt und dann aus Neugier, aus Versehen oder
Langeweile auch noch zusätzlich den Taster [14] (links) drückst und gedrückt hältst und
dabei überrascht feststellst, dass die Glühlampe [18] erlischt und wider Erwarten nicht mehr
leuchtet! Aber wie kommt es dazu? Normalerweise schaltet man doch
die Glühlampe [18] mit
dem Taster [14] (links) oder dem Schiebeschalter
[15] (rechts) ein und nicht
aus, oder?
Kann es
sein, dass der Taster [14] (links)
irgendwie verhext ist, einen Wackelkontakt hat oder so gar defekt ist? Nein! Schalte einfach den Schiebeschalter [15] (rechts) wieder aus,
indem du diesen wieder nach links in die Ausgangsposition schiebst und
die Glühlampe [18] leuchtet wieder so
wir es gewöhnt sind bzw. es normalerweise erwarten! Unten in der Elektroniksimulation von
„Electronics Workbench“ lässt sich die Glühlampe [18] mit dem Schiebeschalter
[15] einschalten,
indem du auf der Computer-Tastatur
auf die Taste mit dem Buchstaben „b“ drückst und mit dem Taster [14] wieder ausschalten, indem du
auf der Computer-Tastatur auf die
Taste mit dem Buchstaben „a“ drückst: (Bild vergrößern: auf
Bild klicken! Webverzeichnis
schaltung_03-13.ewb) Wenn man also die Glühlampe [18] mit dem Schiebeschalter
[15]
(rechts) einschaltet und mit dem Taster [14] wieder ausschaltet, dann sorgt man mittels des Tasters [14] dafür, dass man den elektrischen Strom
durch die Glühlampe (des Schiebeschalters [15]) wieder ausschaltet (und
umgekehrt)! Demzufolge
lässt sich die Glühlampe [18]
durch einen elektrischen Strom einschalten und durch einen anderen
elektrischen Strom wieder ausschalten! Wahnsinn! So, jetzt wissen wir zwar, dass man mit einem
Strom einen anderen ausschalten kann (und umgekehrt), haben auch einen
bestimmten Verdacht, dass der eine Strom den anderen Strom
kompensiert, d.h. aufhebt, sodass die Glühlampe nicht mehr mit
elektrischer Energie versorgt wird, demzufolge auch nicht mehr
leuchtet. Aber da wir den elektrischen Strom nicht
sehen, nicht hören und auch nicht fühlen können, es sei denn, man bekommt
einen elektrischen Stromschlag,
der bei der Stromversorgung mit 230(!) Volt in der Wohnung und im Haushalt tödlich
sein kann, sind wir noch unsicher, wie man sich den Effekt „mit einem Strom
einen anderen Strom ausschalten“ erklären soll. Dass man den elektrischen Strom nicht sehen
kann, stimmt nicht so ganz! Zwar können wir den elektrischen Strom, d.h. die
Elektronen als negativ geladene Ladungsträger, nicht im Kupferdraht und den
Verbindungsleitungen unserer Schaltung sehen, aber wenn man ihn über die
Glühlampe [18] fließen lässt, dann eben schon! Und hören können wir den elektrischen Strom
auch, nämlich dann, wenn wir ihn nicht über die Glühlampe [18], sondern über den kleinen Elektromotor [24] fließen lassen,
sodass sich dieser dreht und entsprechende Umdrehungsgeräusche produziert: (Zum Vergrößern bitte
auf das Bild klicken!) In der obenstehenden Schaltung wird der kleine
Elektromotor [24] mit dem Schiebeschalter [15] (rechts) eingeschaltet,
so dass dieser dreht und zu schnurren anfängt. Ob sich der Motor dabei rechts oder links herum dreht,
hängt davon ab, wie herum du den Motor in die Schaltung eingebaut hast! Bei
genauerem Hinsehen auf die gelbe Befestigungsplatte
des Motors kann man nämlich ein Pluszeichen
(„+“)
für den Pluspol des Motors erkennen
und auf der anderen Seite die Beschriftung
„24“
für das Bauteil des kleinen Elektromotors
[24].
In der obenstehenden Schaltung befindet sich
der Pluspol („+“) des Elektromotors [24] von unten aus gesehen
hinter dem Motor und die Beschriftung „24“ vor dem Motor.
Demzufolge könnte man meinen, dass sich der Motor nur in eine Richtung dreht.
Dem ist aber nicht so! Wenn man nämlich den Schiebeschalter [15] (rechts) öffnet,
indem man diesen nach links schiebt und dann den Taster [14] (links) drückt
und gedrückt hält, dann läuft der Elektromotor [24] rechts herum, d.h. im
Uhrzeigersinn! Vorausgesetzt natürlich, dass man hat den Motor
tatsächlich mit der richtigen Polung
und dem Pluspol („+“) nach oben in
die Schaltung eingebaut hat! Da es sich bei dem kleinen Elektromotor [24] um einen Gleichstrommotor handelt, läuft
dieser sowohl rechts als auch links herum! Demzufolge dient das Pluszeichen
(„+“) nur dazu, den Pluspol des Motors zu
kennzeichnen, um zu verdeutlichen, dass sich dieser rechts herum
dreht, wenn man ihn, wie im vorliegenden Fall, über den Taster [14] mit dem Pluspol („+“) der Batteriehalterung
[19] (links) verbindet! Folgerichtig
muss sich der Elektromotor [24] links
herum drehen, wenn man den Schiebeschalter [15] (rechts) einschaltet, d.h. nach rechts schiebt! Der Grund dafür, dass sich der Elektromotor [24] links herum
dreht, wenn man den Schiebeschalter
[15]
(rechts) einschaltet, ist also der, dass die Versorgungsspannung aus der Batteriehalterung [19] (rechts) mit umgekehrter Polung erfolgt, sodass am Pluspol („+“) des Motors
der Minuspol („-“) der Versorgungsspannung aus der Batteriehalterung [19] (rechts) anliegt: (Bild vergrößern: auf
Bild klicken! Webverzeichnis
schaltung_03-14.ewb) Wie man in der obenstehenden Schaltung sieht,
kann man sich durch die Rechts- oder
Linksdrehung des Motors „anzeigen“ lassen, welche der beiden
Batteriehalterungen [19] (links oder rechts) nebst der beiden 1,5 Volt
Batterien zwecks Spannungsversorgung im Zugriff ist. Wenn man hilfsweise noch die rote Leuchtdiode [17], wie oben in der
Schaltung zu sehen ist, parallel zum Elektromotor [24] einbaut, dann leuchtet diese stets
auf, wenn der Taster [14] gedrückt wird
und sich der Elektromotor rechts herum
dreht! Was eine Leuchtdiode (LED),
engl. „light-emitting diode“, ist und wie diese funktioniert, werden wir
später ab dem Versuch 14 „Der Gebrauch einer Leuchtdiode“ noch kennenlernen.
Im Moment reicht es zu wissen, dass es sich bei einer LED um einen
sogenannten Halbleiter handelt,
die den elektrischen Strom nur in eine Richtung, nämlich in Pfeil-
bzw. Dreieck-Pfeilrichtung, durchlässt und in die umgekehrte Richtung sperrt.
Wird also eine Leuchtdiode (LED) in Pfeilrichtung, d.h. in Durchlassrichtung
von „+“ nach „-“ betrieben, dann leuchtet sie je nach Stromstärke mehr oder
weniger hell. - Wenn man zusätzlich zum Taster [14] (links) auch noch den Schiebeschalter [15] (rechts) betätigt,
dann bleibt der Elektromotor
[24] stehen,
weil sich die beiden Batteriehalterungen
[19]
nebst der beiden 1,5 Volt Batterien und der Batterieströme gegeneinander aufheben! - |
|
||||||||||||||||||||
|
|
[ electronic 159 ] [ Seitenanfang ] [ Programmieren ] [ Versuch 2 ] [ Versuch 4 ] |
|