[ electronic 159 ] [ Seitenende ] [ Programmieren ] [ Versuch 3 ]

electronic 159 – Versuch 4

Elektrische Kennlinie des Elektromotors aufnehmen

Wenn man sich den Versuch 4 „Elektrischer Propeller“ mit dem kleinen Elektromotor als Antrieb so anschaut, dann fragt man sich, was sich mit dem Versuch noch so anstellen lässt.

Schließlich gibt es im Alltag, im Haushalt viele Haushaltsgeräte mit Elektromotoren wie z.B. die elektrische Kafféemühle, den Mixer zum Zerkleinern von Früchten, um einen Smoothie herzustellen, den Föhn im Badezimmer zum Trocknen der Haare, die Waschmaschine, den Raumventilator zum Kühlen der Raumluft im Hochsommer, den alten Plattenspieler, den Batterie getriebenen CD-Player usw.

Dabei kommen bei den unterschiedlichen Haushaltsgeräten natürliche verschiedene Elektromotore wie z.B. einfache Wechselstrommotore mit geringer Antriebsleistung (Raumventilator, z.B. bis 60 Watt Leistung, Plattenspieler, z.B. bis 25 Watt Leistung) oder mit größerer Antriebsleistung (Universalmotor bei der Waschmaschine z.B. bis 500 Watt Leistung) zum Einsatz. Besonders interessant ist der digital gesteuerte und geregelte Hochgeschwindigkeits-Gleichstrommotor im Dyson Haarföhn, der mit bis zu 110 000 U/min rotiert, je nach Gebläsestufe.

Da unser kleiner Elektromotor von zwei 1,5 Volt in Serie geschalteten Batterien vom Typ „Mignon AA“ in der Batteriehalterung [19] angetrieben wird, handelt es sich bei diesem um einen Gleichstrommotor:

(Zum Vergrößern bitte auf das Bild klicken!)

Da wir in der westlichen Welt als Rechtshänder stets von links nach rechts schreiben, lesen wir auch den Schaltungsaufbau von links nach rechts, d.h. von der Batteriehalterung [19] links nach rechts zum Schiebeschalter [15] und über den Gleichstrommotor [24] wieder nach links zurück (siehe unten)!

Dabei gilt es aus Sicherheitsgründen zu beachten, dass die Stromzufuhr links vom Pluspol der Batteriehalterung [19] nach rechts zum Schiebeschalter [15] unterbrochen wird:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden Bild sieht, sollte die Unterbrechung der Stromzufuhr mittels Schiebeschalter [15] nicht im Stromrückfluss zur Batteriehalterung [19] hin erfolgen, sondern unmittelbar nach der Stromversorgung, d.h. hinter dem Pluspol der Batterien, sodass die nach dem Schiebeschalter [15] folgenden Bauelemente im ausgeschalteten Zustand immer stromlos sind!

Wenn man den Gleichstrommotor [24] mit der richtigen Polung anschließt, d.h. mit dem Pluspol (+) über den Schiebeschalter [15] an den Pluspol (+) der Batteriehalterung [19], dann sollte dieser sich nach dem Einschalten im Uhrzeigersinn rechts herum drehen.

Selbstverständlich lässt sich der Gleichstrommotor [24] aber auch durch Umpolen so in Betrieb nehmen, dass er sich links herum dreht. Wenn man beim regulären Betrieb des Motors rechts herum befürchtet, dass das Flügelrad bzw. der Propeller bei höherer Drehzahl sich verselbständigt und abhebt, dann muss man den Gleichstrommotor [24] durch Umpolen der Anschlüsse nur links herum laufen lassen, sodass der Luftstrom nach oben geht und der Propeller nicht abheben kann, weil er nach unten auf die Montageplatte gedrückt wird.

Wenn man die obenstehende Schaltung aufbaut und den Gleichstrommotor [24] erstmalig in Betrieb nimmt, indem man diesen am Schiebeschalter [15] einschaltet, dann fragt man sich sofort, wie viel Strom dieser „verbraucht“. Aber als angehende Elektrotechniker, Elektroniker wissen wir natürlich, dass der kleine Motor keinen Strom verbraucht, sondern in Form von elektrischer Energie W_el aufnimmt und diese sofort in mechanische Antriebsenergie W_mech umwandelt, sodass sich der Rotor immer schneller dreht bis dieser abhebt und davon fliegt.

Wie aber lässt sich der volkstümlich sogenannte Stromverbrauch messen? Ganz einfach durch unser selbst gebasteltes Digital-Voltmeter (= Spannungsmesser) in Form des „Calliope mini“- oder des älteren BBC „micro:bit“-Rechners nebst entsprechendem „Python“- oder „JavaScript“-Programm (siehe Webverzeichnis mini-programm_03_19.py).

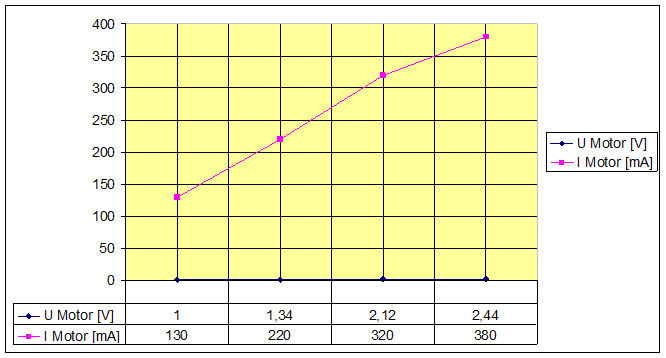
Konkret geht es dabei um das Messen mehrerer unterschiedlicher (Betriebs-) Spannungen am Gleichstrommotor [24] mit dem Ziel eine entsprechende Spannungsmessreihe mit I_Motor = f (U_Motor) aufzunehmen und in einer Wertetabelle zu erfassen:

UMotor [V]	1	1,34	2,12	2,44
IMotor [mA]	130	220	320	380

Dabei bezeichnet U_Motor die unabhängige Variable und die Ergebnisgröße I_Motor die abhängige Variable.

Demzufolge benötigen wir neben dem (Digital-) Voltmeter auch noch ein entsprechendes Amperemeter (= Strommessgerät) zum Messen der Stromstärke I_Motor in Milliampere [mA].

Um die Stromstärke I_Motor des Gleichstrommotor [24] mit dem Amperemeter messen zu können, muss man den Stromkreis auftrennen oder. das Strommessgerät parallel zum Schiebeschalter [15] anschließen, sodass der Stromkreis durch die Strommessung mit dem Amperemeter wieder geschlossen wird und man den Schiebeschalter nicht mehr betätigen muss!

Wenn man noch über kein entsprechendes Amperemeter (= Strommessgerät) zum Messen der Stromstärke I_Motor in Milliampere [mA] verfügt, dann muss man einen wertmäßig bekannten Messwiderstand R_Mess = 205,30 mΩ mit geringer Toleranz, wie z.B. einen Präzisionsmesswiderstand mit 1 % Toleranz, verwenden.

Im vorliegenden Fall benutzen wir deshalb einfach die im Elektronikbaukasten „electronic 159“ vorhandene (Ersatz-) Schmelzsicherung mit dem sehr kleinen Messwiderstand R_Mess = 0,2053 Ω = 205,3 mΩ (Berechnung siehe weiter unten). -

Wenn man die (x, y) bzw. (U, I)-Messpunkte in das untenstehende Koodinatensystem einträgt, dann lässt sich der sogenannte Graph der Funktion mit I_Motor = f (U_Motor) wie folgt zeichnen:

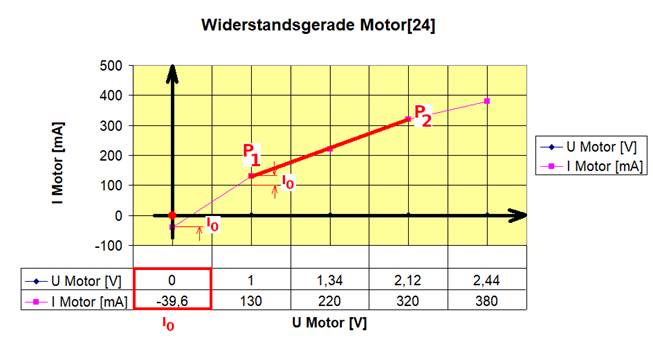
(Zum Vergrößern bitte auf das Bild klicken!)

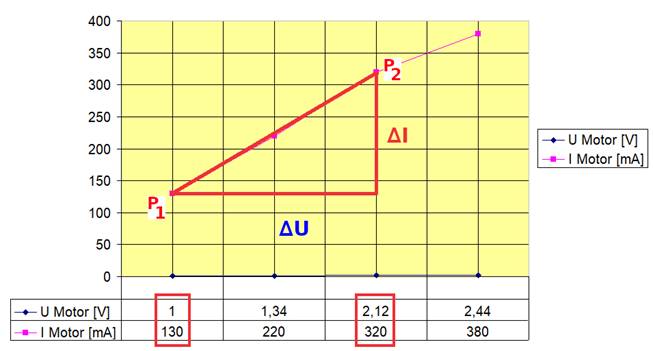
Wie man im obenstehenden Diagramm sieht, flacht die Motorkennlinie I_Motor = f (U_Motor) ab dem dritten Messpunkt, d.h. bei U_Motor = 2,12 V deutlich ab.

Für die ersten drei Messpunkte lässt sich aber trotzdem das entsprechende Steigungsdreieck einzeichnen, da die Kennlinie in diesem Abschnitt nahezu linear (= gleichmäßig, gleichförmig mit konstanter Steigung) verläuft:

(Zum Vergrößern bitte auf das Bild klicken!)

Mittels des Differenzenquotienten ∆U_Motor / ∆I_Motor = 1 / ( ∆I_Motor / ∆U_Motor ) = 1 / G_Steig = R_Steig lässt sich zunächst nur die mathematische Steigung a (= Steilheit der Widerstandsgeraden) gemäß der Zwei-Punkte-Form wie folgt berechnen:

a = y₂ - y₁ / x₂ - x₁ = y₂ - y₁ / ( x₂ - x₁ ) → mit y₂ > y₁ und x₂ > x₁

Einsetzen in die Geradengleichung liefert:

y = f(x) = ax + b → mit b = Parallelverschiebung aus dem Ursprung des Koordinatensystems

Demzufolge berechnet sich die Steigung(!) der Widerstandsgeraden(!) wie folgt:

G_Steig = 1 / R_Steig = 1 / ( ∆U_Motor / ∆I_Motor ) → G_Steig = Leiterwert des Steigungsdreiecks!

R_Steig = ( ∆U_Motor / ∆I_Motor ) → R_Steig = Widerstand des Steigungsdreiecks!

I_Motor = f(U_Motor) = G_Steig * U_Motor + I₀ →

= f(U_Motor) = ( 1 / R_Steig ) * U_Motor + I₀

Geradengleichung der Widerstandsgeraden:

Obwohl die Geradengleichung wegen ihrer mathematischen Schreibweise und wegen I₀ anfangs etwas gewöhnungsbedürftig ist, ist sie dennoch ein mächtiges Werkzeug, das sich praktisch immer und überall anwenden lässt. Demzufolge lässt sich die Geradengleichung nicht nur auf das obenstehende Steigungsdreieck anwenden, sondern auch für Spannungsmessungen jedweder Art wie z.B. beim unbelasteter/belasteter Spannungsteiler, verketteten Spannungen oder bei Spannungsmessungen mit Konstantstromanteil I₀:

I_Motor = 1 / R_ges * U_Motor + I₀ → mit I₀ = Konstantstrom → Parallelverschiebung

→ und R_ges = R_Motor + R_Mess

Wie man bei der Geradengleichung sieht, besteht diese u.a. aus der unabhängigen Variablen U_Motor, d.h. der Spannung, die zwischen den Anschlussklemmen am Motor[24] anliegt.

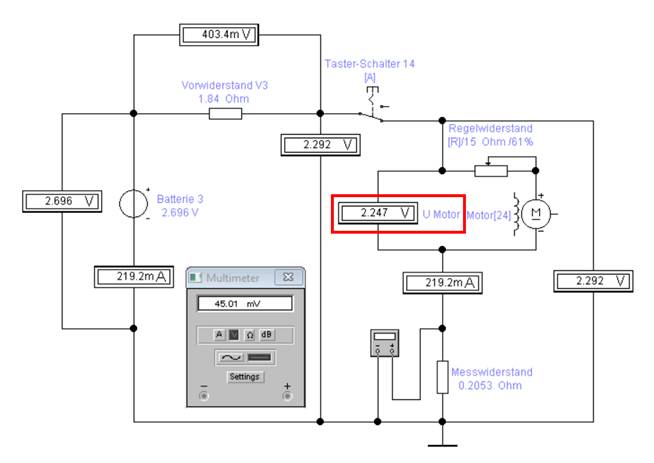
Wegen des in Reihe zum Motor[24] geschalteten Messwiderstandes R_Mess für die spätere Strommessung handelt es sich bei der Spannung U_Motor am Motor um einen sogenannten Spannungsabfall. Dabei wird der Spannungsabfall parallel zum Motor[24] und nicht zwangsläufig gegen Masse („┴“) gemessen:

(Zum Vergrößern bitte auf das Bild klicken!)

In der Praxis verhält es sich aber oftmals so, dass der Kabelanschluss am Motoranschlussklemmbrett des Motors nicht frei zugänglich ist, sodass der Betriebselektriker aus Bequemlichkeit heraus die Spannung am Motor[24] lieber direkt gegen Masse („┴“) misst, und er es dabei sofort mit einer verketteten Spannung zu tun hat, die den Spannungsabfall am Messwiderstand R_Mess mit einbezieht, sodass insgesamt mehr Spannung gemessen wird als der Motor[24] tatsächlich „abbekommt“:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man aber anhand des roten Kastens „Messwiderstand“ erkennt, gibt es im Strompfad des Motors[24], d.h. in Serie nachgeschaltet noch den Messwiderstandes R_Mess zur späteren Strommessung, sodass es sich bei der Spannungsmessung des Motors[24] um eine verkettete Spannung handelt und zwar um die der Spannungsversorgung U_ges = 2,292 V mit U_ges > U_Motor = 2,247 V.

Demzufolge müsste sich der Elektriker vor der Spannungsmessung gegen Masse („┴“) erkundigen, ob es im Strompfad des Motors[24] noch etwaige in Serie nachgeschaltete Verbraucher hin zum Masseanschluss gibt!

Nur wenn der Elektriker weiß, dass es im Strompfad des Motors[24] noch einen in Serie nachgeschalteten Messwiderstand R_Mess gibt, kann er dessen Spannungsabfall aus der verketteten Gesamtspannung U_ges wie folgt herausrechnen:

U_Motor = U_ges - U_Mess → U_ges = U_+3v3 lässt sich beim „Calliope mini“

am Port „Pin +3v3“ („+“) gegen Masse („┴“) bzw. („-“) messen!

→ U_Mess lässt sich beim „Calliope mini“

am Port1 „Pin P1“ gegen Masse („┴“) bzw. („-“) messen!

= 2,292 V - 45,01 mV = 2,292 V - 0,04501 V ≈ 2,247 V → Nicht gegen Masse („┴“) messen!

U_Motor = R_Motor * I_Motor = R_Motor * I_Mess → wegen Reihenschaltung R_Motor + R_Mess mit I_Motor = I_Mess

U_Mess = U_ges - U_Motor

= 2,292 V - 2,247 V = 0,045 V = 45 mV

= I_Mess * R_Mess = I_Motor R_Mess →

I_Motor = U_Mess / R_Mess = 45,01 mV / 0,2053 Ω = 45,01 mV / 205,3 mV/A = 0,21924 A = 219,24 mA

Dabei gilt es zu beachten, dass sich der Motorstrom I_Motor nur berechnen lässt, wenn man die Größe des Messwiderstandes R_Mess kennt! -

Mit der Geradengleichung und dem Konstantstrom I₀ = 0 lässt sich jetzt auch noch der Gesamtwiderstand R_ges wie folgt berechnen:

I_Motor = 1 / R_ges * U_Motor + I₀ = 1 / ( R_Motor + R_Mess ) * U_Motor

Doch was bedeutet es, wenn der Konstantstrom I₀ = 0 ist? Wenn es generell keinen Konstantstrom I₀ gibt, dann gibt es auch keine Konstantstromquelle. Aber ob dem wirklich so ist, wissen wir (noch) nicht.

Wenn es an der Stelle I_Motor = f(U) = f(U_Motor) → I₀ = f(U₀ = 0) = 0 → I₀ = 0

keinen Konstantstrom I₀ gibt, dann folgt für die Geradengleichung:

I_Motor = 1 / R_Motor * U_Motor →

R_Motor = U_Motor / I_Motor = 2,247 V / 221,7 mA = 0,0101353 KΩ ≈ 10,14 Ω

R_ges = R_Motor + R_Mess = 10,14 Ω + 205,30 mΩ = 10,14 Ω + 0,20530 Ω ≈ 10,35 Ω

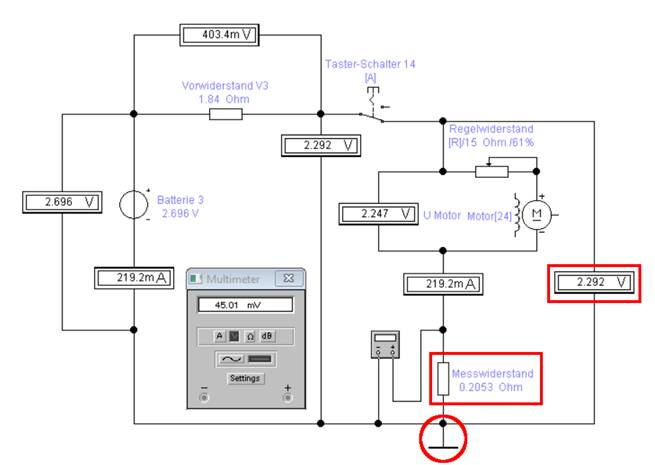
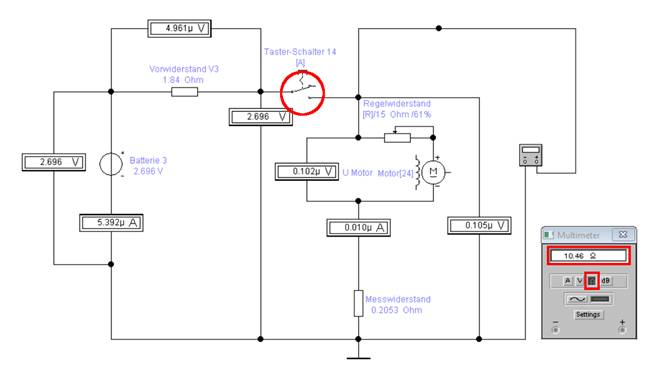
Wir machen die Probe auf’s Exempel, d.h. (Lehr-) Beispiel, indem wir den Taster-/Umschalter [14] durch Tastendruck „A“ öffnen, sodass keine Stromversorgung mehr erfolgt! Anschließend schalten wir die Elektronik-Simulation „Electronics Workbench“ am Netz-/Kippschalter ein (oben rechts) und messen den Gesamtwiderstand der Schaltung, der wegen der vielen Spannungs- und Strommessgeräten etwas höher ausfällt als unser Rechenergebnis von R_ges = 10,35 mΩ:

(Bild vergrößern: auf Bild klicken! Webverzeichnis schaltung_04-05.ewb

Als Zwischenfazit lässt sich festhalten, dass sich Spannungsmessungen auch mit verketteten Spannungen problemlos durchführen lassen. Allerdings sollte man sich bei Spannungsmessungen stets bewusst sein, dass man bei Spannungsgsmessungen gegen Masse („┴“) oftmals auch mit verketteten Spannungen rechnen muss.

Wenn es aber darum geht mit der Geradengleichung I = 1 / R * U + I₀ zu arbeiten, dann kommt man um den Differenzenquotienten R = ∆U / ∆I, d.h. um den Steigungskoeffizienten der Widerstandsgeraden in Form des Leitwerts G = 1 / R = ∆I / ∆U nicht umhin.

Demzufolge kommt man konkret auch nicht um den Messwiderstand R_Mess = 205,3 mΩ umhin, muss dieser wertmäßig bekannt sein, da sich nur mit diesem die Stromstärke I_Motor indirekt über den Spannungsabfall U_Mess berechnen lässt!

Dies gilt dann auch für die ganz oben stehende Wertetabelle, das Steigungsdreieck und den Steigungswiderstand:

R_Steig = ∆U / ∆I = ( U₂ - U₁ ) / ∆I

= ( U_{Pin P2} - U_{Pin P1} ) / ∆I_Motor

= ( 2,12, V – 1,0 V ) / 190 mA → … siehe Wertetabelle sowie Steigungsdreieck weiter oben!

= 0,005895 KΩ = 5,895 Ω

= ( U_{Pin P2} - U_{Pin P1} ) / I_Mess → I_Mess = U_Mess / R_Mess → U_Mess = U_{Pin P1, ┴} gegen Masse („┴“)

= ( U_{Pin P2} - U_{Pin P1} ) / ( U_Mess / R_Mess )

= ( U_{Pin P2} - U_{Pin P1} ) / ( U_{Pin P1, ┴} / R_Mess )

I_Motor = 1 / R_Mess * U_{Pin P1, ┴} →

I_ges = 1 / R_Steig * U_{Pin P1, ┴} + I₀

Berechnung des Konstantstromes I₀ anhand des Steigungsdreiecks (siehe oben)

… am Schnittpunkt mit der senkrechten I_Motor-Achse mit U_Motor = 1 V:

I_{Motor P1} = 1 / R_Steig * U_Motor + I₀ →

I₀ = I _{Motor P1} - 1 / R_Steig * U_Motor

= 130 mA - 1 / 5,895 Ω * 1 V = 0,13 A - 0,1696 A/V * 1 V = 0,13 A - 0,1696 A = - 0,0396 A = -39,6 mA

… am Schnittpunkt mit der senkrechten I_Motor-Achse mit U_Motor = 2,12 V:

I₀ = I _{Motor P2} - 1 / R_Steig * U_Motor

= 320 mA - 1 / 5,895 Ω * 2,12 V = 0,32 A - 0,1696 A/V * 2,12 V = 0,32 A - 0,3596 A = - 0,0396 A = -39,6 mA

Probe:

I_{Motor P2} = 1 / R_Steig * U_{Motor P2} + I₀

= 1 / ( 5,895 V/A ) * 2,12 V + ( -39,6 mA )

= 0,1696 A/V * 2,12 V - 39,6 mA

= 359,55 mA - 39,6 mA = 319,95 mA ≈ 320 mA þ

Jetzt wo wir wissen, wie sich der Konstantstrom I₀ berechnen lässt, nämlich mittels der Geradengleichung im Schnittpunkt mit der senkrechten „I_Motor“-Achse, können wir den Konstantstrom I₀ wie folgt auch im Punkt P₁ berechnen:

I_{Motor P1} = 1 / R_Steig * U_{Motor P1} + I₀ →

I₀ = I_{Motor P1} - 1 / R_Steig * U_{Motor P1} → Messwerte vom Punkt P₁ einsetzen!

= 130 mA - 1 / 5,895 Ω * 1 V = 0,13 A - 0,1696 A/V * 1 V

= 0,13 A - 0,1696 A = - 0,0396 A = - 39,6 mA

Aber das hatten wir ja bereits (siehe oben), d.h. wir haben tatsächlich die richtigen Werte eingesetzt!

Mal sehen, ob sich die Berechnung des rechnerischen Konstantstroms I₀ auch auf den Koordinatenursprung anwenden lässt:

I₀ = I_Motor - 1 / R_Steig * U_Motor → „Messwerte“ vom Koordinatenursprung einsetzen!

= - 39,6 mA - 1 / 5,895 Ω * 0 V = -39,6 mA

Wer hätte das gedacht, dass die Mathematik auch ganz trivial, d.h. einfach, simpel, sein kann! J

Wenn man sich die obenstehende Wertetabelle im linearen Bereich zwischen den Messpunkten P₁ und P₂ betrachtet, dann könnte man auf die Idee kommen und den elektrischen Widerstand R_Motor des Motors - also nicht Steigungswiderstand R_Steig - einfach mittels des Ohmschen Gesetzes (→ohne Konstantstrom I₀ ) wie folgt berechnen:

Punkt P₁ = ( 1 V / 130 mA )

R_Motor = U_Motor / I_Motor = 1 V / 130 mA = 0,00769 KΩ = 7,69 Ω → FALSCH!

Punkt P₂ = ( 2,12 V / 320 mA )

R_Motor = U_Motor / I_Motor = 2,12 V / 320 mA = 0,006625 KΩ = 6,625 Ω → FALSCH!

Wegen des linearen Abschnitts der Widerstandsgeraden zwischen den Messpunkten P₁ und P₂ ist nicht nur der Steigungswiderstand R_Steig, sondern auch der (Gleichstrom-) Widerstand R_Motor des Motors[24] überall gleich groß, d.h. konstant!

Wie wir ja inzwischen wissen, ist das Steigungsdreieck des Motors um den Konstantstrom I₀ = - 39,6 mA nach unten parallel aus dem Koordinatenursprung heraus verschoben, sodass wir eben nicht das Ohmsche Gesetz in seiner Spezialform(!) mit der Widerstandsgeraden durch den Koordinatenursprung sowie mit dem Konstantstrom I₀ = 0 anwenden dürfen:

(Zum Vergrößern bitte auf das Bild klicken!)

Wenn man wie zuvor in der Wertetabelle (siehe weiter oben) aus Bequemlichkeit, Unkenntnis oder wegen der fehlenden Linearität der abknickenden Kennlinie wider Erwarten nicht den Nulldurchgang der Kennlinie berechnet, dann kommt man im Leben nicht darauf, dass das Steigungsdreieck bzw. die Widerstandsgerade im linearen Bereich zwischen den Messpunkten P₁ und P₂ parallel um den Konstantromanteil I₀ wegen I₀ = - 39,6 mA nach unten verschoben ist und man deswegen stets mit der

Geradengleichung I_Motor = 1 / R_Steig * U_Motor + I₀

rechnen muss und eben nicht mit dem Ohmschen Gesetzes (→ohne Konstantstrom I₀ )! -

Berechnung des Motorwiderstandes R_Motor mittels der Geradengleichung:

Punkt P₁ = ( 1 V / 130 mA )

I_Motor = 1 / R_Steig * U_Motor + I₀

= 1 / ( ∆U_Motor / ∆I_Motor ) * U_Motor + I₀

→ Steigungswiderstand R_Steig = ∆U_Motor / ∆I_Motor = 1,12 V / 190 mA = 0,005895 KΩ = 5,895 Ω

= 1 / ( 1,12 V / 190 mA ) * U_Motor - 39,6 mA

= 1 / ( 5,895 V/A ) * 1,0 V - 39,6 mA = 1 / ( 5,895 V/A ) * 1,0 V - 0,0396 A

= 0,1696 A - 0,0396 A = 0,13 A = 130 mA þ

I_Motor = 1 / R_Steig * U_Motor + I₀

I_Motor - I₀ = ( 1 / R_Steig ) * U_Motor

( I_Motor - I₀ ) / U_Motor = 1 / R_Steig

U_Motor / ( I_Motor - I₀ ) = R_Steig þ

U_Motor = R_Steig * ( I_Motor - I₀ )

R_Motor = U_Motor / I_Motor

= R_Steig * ( I_Motor - I₀ ) / I_Motor

R_Motor = R_Steig * ( 1 - I₀ / I_Motor )

= 5,895 Ω * ( 1 + 39,6 mA / 130 mA ) = 5,895 Ω * 1,305 = 7,693 Ω þ

Formel zur Berechnung des Motorwiderstandes R_Motor

R_Motor = R_Steig * ( 1 - I₀ / I_Motor )

Wie man sieht, ist der Motorwiderstand R_Motor = 7,693 Ω des Elektromotors deutlich kleiner ist als der der Glühlampe [18] mit R_Glühlampe = 8,33 Ω. -

Im Zusammenhang mit der Aufnahme der Messreihe in Form der Wertetabelle gilt es noch die Frage zu klären, wie die vier verschiedenen Spannungswerte des Elektromotors zustande gekommen sind. Schließlich gibt es im Elektronik-Baukasten „electronic 129“ kein regelbares Netzgerät für einstellbare Betriebsspannungen im Bereich [ 0 … 6 V ].

Dabei ist die Lösung einfacher als man denkt. Schließlich bastelten wir uns im Versuch 3 und bei der Programmierung 3

nicht nur ein brauchbares Digital-Voltmeter, sondern untersuchten mit diesem auch die (Rest-) Ladekapazität verschiedener mehr oder weniger stark entladener 1,5 V Batterien vom Typ „Mignon AA“.

So kam z.B. beim ersten Messwert ( 1 V / 130 mA ) eine 1,5 V Batterie mit einer Restkapazität von nur 60 % zum Einsatz, beim zweiten Messwert ( 1,34 V / 220 mA ) wurde hingegen eine 1,5 V Batterie mit einer Restkapazität von 86 % verwendet, beim dritten Messwert wurden dann schon zwei 1,5 V Batterien in Serie geschaltet, und zwar die erste 1,5 V Batterie mit 60 % und die zweite mit 86 % Restkapazität. Beim vierten Messwert ( 2,44 V / 380 mA ) kamen dann ebenfalls zwei 1,5 V Batterien in Serie geschaltet zum Einsatz und zwar mit insgesamt 80 % Restkapazität.

Wie man sieht, macht es Sinn, unterschiedlich entladene 1,5 V Batterien bis hin zu einer Restkapazität von 60 % aufzubewahren, da sich mit diesen und auch mit noch fabrikneuen 1,5 Volt Batterien jeweils in Einzelschaltung, Reihenschaltung sowie in Kombination hinsichtlich der Restkapazität teils sehr unterschiedliche Gesamtspannungen realisieren lassen, sodass sich jederzeit verschiedene Messreihen aufstellen lassen (siehe oben). -

Mit der Spannung den Strom messen

Bei der obenstehenden Wertetabelle

UMotor [V]	1	1,34	2,12	2,44
IMotor [mA]	130	220	320	380

ging es um das Messen mehrerer unterschiedlicher (Betriebs-) Spannungen am Gleichstrommotor [24] mit dem Ziel eine entsprechende Spannungsmessreihe mit I_Motor = f (U_Motor) aufzunehmen und in einer Wertetabelle zu erfassen. Dabei wurden die Spannungsmesswerte der Reihe nach mit dem Digital-Voltmeter-Programm des „Calliope mini“-Rechners gemessen, während die zu den Spannungsmesswerten zugehörigen Stromstärken mit einem Multimeter als Strommessgerät gemessen wurden.

Diesbezüglich verhält es sich so, dass sich mit einem Voltmeter (= Spannungsmessgerät) auch Ströme in Form der Stromstärke messen lassen! Aber nur indirekt über den Spannungsabfall U_{R Mess} an einem in den Stromkreis geschalteten Messwiderstand. Dabei wird der Messwiderstand R_Mess in Reihe mit dem zu messenden Lastwiderstand R_Motor (= Gleichstrommotor [24]) geschaltet mit der Folge, dass sich durch das Einbringen des Messwiderstandes der Laststrom I_Motor entsprechend verringert!

Beispiel:

Wenn der in den Schaltkreis eingebrachte Messwiderstand R_Mess = 1 Ω beträgt, dann berechnet sich der neue, verringerte Laststrom I_Motor des Gleichstrommotors [24] wie folgt:

R_{Last, ges} = R_Mess + R_Last = R_Mess + U_Motor / I_Motor

= 1 Ω + 1 V / 130 mA = 1 Ω + 0,00769 KΩ = 1 Ω + 7,69 Ω = 8,69 Ω ≈ 8,7 Ω

I_{Last, neu} = U_Motor / R_{Last, ges} = 1 V / 8,7 Ω = 0,1149 A = 114,9 mA (= - 11,6 %)

Wie man sieht, ergibt sich durch das Hinzuschalten des Messwiderstandes R_Mess = 1 Ω ein Messfehler von - 11,6 %, was schon ganz ordentlich und demzufolge nicht zu vernachlässigen ist!

Demzufolge gilt: Je kleiner der Messwiderstand in Reihe zum Lastwiderstand ist, umso kleiner ist der Messfehler beim Messen des Laststroms!

Frage:

Wie klein muss der Messwiderstand sein bzw. welchen Widerstandswert muss der Messwiderstand haben, damit sich ein Messfehler von nur - 1,5 % einstellt?

100,0 % → 7,69 Ω

1,5 % → x Ω

x = 7,69 Ω / 100 % * 1,5 % = 0,11535 Ω ≈ 0,115 Ω

Mit dem kleineren Messwiderstand ergibt sich nun auch ein insgesamt kleinerer Gesamtwiderstand, der sich wie folgt berechnet:

R_{ges, neu} = R_{Mess, neu} + R_Last = R_{Mess, neu} + U_Motor / I_Motor

= 0,115 Ω + 1 V / 130 mA = 0,115 Ω + 0,00769 KΩ = 0,115 Ω + 7,69 Ω = 7,805 Ω ≈ 7,8 Ω

I_{Last, neu} = U_Motor / R_{Last, ges} = 1 V / 7,8 Ω = 0,1282 A = 128,2 mA (= - 1,385 %)

Mit einem Messfehler von ± 1,5 % würde es sich bei der Strommessung bereits um eine Präzisionsmessung handeln, die es ansonsten nur bei entsprechend teuren analogen Drehspulmessgeräten mit einer hochempfindlichen Drehanker-Messspule (I_Spule = 50 µA), Messerzeiger und Spiegelskala gibt.

Berechnen wir abschließend noch den Spannungsabfall U_{Mess, neu} am neuen Messwiderstand R_{Mess, neu} wie folgt:

U_{Mess, neu} = I_{Motor, neu} * R_{Mess, neu} = 128,2 mA * 7,8 Ω = 999,96 mV = 0,99996 V ≈ 1 V

Bevor wir uns mit dem nachfolgenden Sachverhalt auseinandersetzen, stellt sich die Frage nach dem Unterschied zwischen den beiden Dezimalzahlen 1023 und 1024.

Wandelt man die Dezimalzahl 1023 zur Basis 10 in eine Binärzahl zur Basis 2 um, so folgt:

1023₁₀ = 11 1111 1111₂

Addiert man zu der Binärzahl 11 1111 1111₂ eine binäre +1₂, so folgt: 100 0000 0000₂

Wandelt man die Binärzahl 100 0000 0000₂ wieder in eine Dezimalzahl zurück, so folgt:

100 0000 0000₂ = 1024₁₀

Dabei verhält es sich so, dass die Binärzahl 100 0000 0000₂ genau eine Stelle mehr hat als die die nächst kleinere Binärzahl 11 1111 1111₂

Wenn man die beiden Binärzahlen untereinander schreibt, dann sieht man den Unterschied auch mathematisch

binär	11 1111 1111	dezimal	1023
	+1		+1
	100 0000 0000		1024

Wenn man zu der Binärzahl 11 1111 1111₂ eine binäre +1₂ addiert, dann gibt es im Binärsystem bei dem wir immer nur mit zwei Zahlen von 0 bis 1 zählen einen binären Überlauf auf die nächst höhere Binärzahl 100 0000 0000₂, weil die binäre Addition

1₂ +1₂ = 01₂ +01₂ = 10₂ ergibt usw.

Im Dezimalsystem wäre das vergleichbar mit 99 999 999₁₀ + 1₁₀ = 100 000 000₁₀, das einem dezimalen Überlauf auf die nächst höhere Dekade entspricht, nämlich der 100sten Million.

Beim Vergleich der beiden Dezimalzahlen 1023₁₀ und 1024₁₀ sieht man es der Dezimalzahl 1024₁₀ sozusagen von außen aus der Sicht des Dezimalzahlensystems nicht an, dass diese bereits zur nächst höheren binären Dekade 100 0000 0000₂ gehört.

Beim „Calliope mini“ mit den integrierten Analog-/Digital-Wandlern bei den Ports „Pin P1“ und „Pin P2“ werden also immer Dezimalwerte aus dem Bereich [ 0, …, 1023 ] eingelesen und intern binär weiter verarbeitet, weil die ALU, engl. „Arithmatic Logic Unit“ (= arithmetisch-logische Einheit) in Form der internen Recheneinheit nur mit zwei binären Fingern von 0 bis 1 rechnet.

Während wir also mit den A/D-Wandlern stets Dezimalwerte aus dem Bereich [ 0, …, 1023 ] erfassen, haben wir es demzufolge immer mit insgesamt 1024 unterschiedlichen Werten zu tun, da die Null mathematisch auch eine Zahl ist.

Trotzdem gilt es zu beachten, dass wir es bei der Messwerterfassung mit den A/D-Wandlern stets nur mit Dezimalwerten bis maximal 1023 zu tun haben, da der nächst höhere Wert von 1024 bereits einen Überlauf in die nächst höhere Binärdekade zur Folge hat!

Diesbezüglich stellt sich dann auch gleich noch die Frage, welcher maximalen Spannung der maximale Binärwert 1023₂ zugeordnet wird. Nämlich der maximalen Spannung +3,3 V, die auch mit „U_3v3“ bezeichnet wird.

Frage:

Weshalb ist es wichtig zu wissen, wie groß bzw. klein der Spannungsabfall U_{Mess, neu} am neuen Messwiderstand R_Mess, neu ist?

1023 Messwerte → 3,3 V

1 Messwert → x V

x = 3,3 V / 1023 * 1 = 0,003226 V = 3,226 mV ≈ 3,23 mV pro einzelnem Bit = 3,23 mV/Bit = 3,23 mV Bit^-1

Demzufolge beginnt der Messbereich der A/D-Wandler bei 3,3 V / 1023 Bit im Bereich [ 0, …, 1023 ] = 3,23 mV / 1 Bit

Gegenprobe:

3,23 mV/Bit * 1023 Bit = 3 304,29 mV = 3,3043 V ≈ 3,3 V

Umgekehrt entspricht der Spannungsabfall U_{Mess, neu} am neuen Messwiderstand R_Mess, neu = 0,115 Ω einem Bitwert von:

3,3 V → 1023 Bit

1,0 V → x Bit

x = 1023 Bit / 3,3 V * 1,0 V = 310 Bit

Dabei entspräche ein noch kleinerer Spannungsabfall von z.B. U_Mess = 0,1 V einem noch kleineren Bitwert:

3,3 V → 1023 Bit

0,1 V → x Bit

x = 1023 Bit / 3,3 V * 0,1 V = 31 Bit

Dass der analoge Eingang am Port „Pin P1” des „Calliope mini“ so empfindlich ist und man mit diesem bereits mit wenigen Bit Spannungen im Millivoltbereich messen kann, ist dem Umstand geschuldet, dass sich 1023 Bit auf einen Spannungsbereich von bis zu 3,3 V verteilen.

Würden sich die 1023 Bit auf einen Spannungsbereich von bis zu 300 V verteilen, dann sähe das Ganze schon anders aus:

1023 Messwerte → 300 V

1 Messwert → x V

x = 300 V / 1023 * 1 = 0,293255132 V = 0,29326 V = 293,26 mV pro einzelnem Bit ≈ 293 mV/Bit

Rund 293 mV/Bit ist angesichts der max. Spannung von bis zu 300 V trotzdem ein sehr guter Wert, der die hohe Eingangsempfindlichkeit des analogen Eingangs am Port „Pin P1” bestätigt.

Wenn es also darum geht, dass wir parallel zum sehr kleinen Messwiderstand gemäß dem ohmschen Gesetz auch sehr kleine Spannungen messen, dann spielen plötzlich kleine Bitwerte von z.B. 14 Bit (= 293 mV/Bit * 14 Bit = 4,102 V) eine große Rolle, weil sich mit diesen kleinen Werten dicke, d.h. große Ströme bzw. Stromstärken berechnen lassen:

I_Mess = I_Last = I_Motor = U_Mess / R_Mess = 4102 mV / 205,30 mΩ = 19,98 A ≈ 20 A

Unglücklicherweise verhält es sich bei unserem „Digitalvoltmeter“-Programm „mini-programm_03_19.py“ leider so, dass die am analogen Eingang vom Port „Pin P1“ gemessenen Bitwerte nicht angezeigt werden, da wir diesen zum damaligen Zeitpunkt aus der Anwendersicht heraus keine Bedeutung beigemessen haben. Schließlich sieht man es den kleinen Bitwerten nicht an, dass sich mit diesen auch dicke Stromstärken des Gleichstrommotors [24] berechnen und im 9 x 9 großen LED-Matrix-Display des „Calliope mini“ als Laufschrift anzeigen lassen. Demzufolge kommen wir nicht umhin das bisherige „Digitalvoltmeter“-Programm entsprechend umzuprogrammieren und zu erweitern.

Batterie-Tester mit Bit-Anzeige [ programmieren ]

[ electronic 159 ] [ Seitenanfang ] [ Programmieren ] [ Versuch 3 ]