[ electronic 159 ] [ Seitenende ] [ zurück ]

electronic 159 – Programmieren 4

Der analoge/digitale Batterie-Tester mit Bit-Anzeige

Damit sich mit dem bisherigen „Python“-Programm „mini-programm_03_19.py“ auch die am Port „Pin P1“ gemessene Bitwerte anzeigen lassen, ersetzen wir im Quellprogramm als erstes die Variable „digital_pin_p1“ durch die neue Variable „volt_pin_p1“, um auf diese Weise zum Ausdruck zu bringen, dass es sich bei der neuen Variablen um eine solche handelt, die jetzt umgerechnete Spannungswerte bearbeitet und speichert.

Dabei erfolgt das Ersetzen der bisherigen Variable „digital_pin_p1“ mittels der Funktion „Suchen & Ersetzen“. 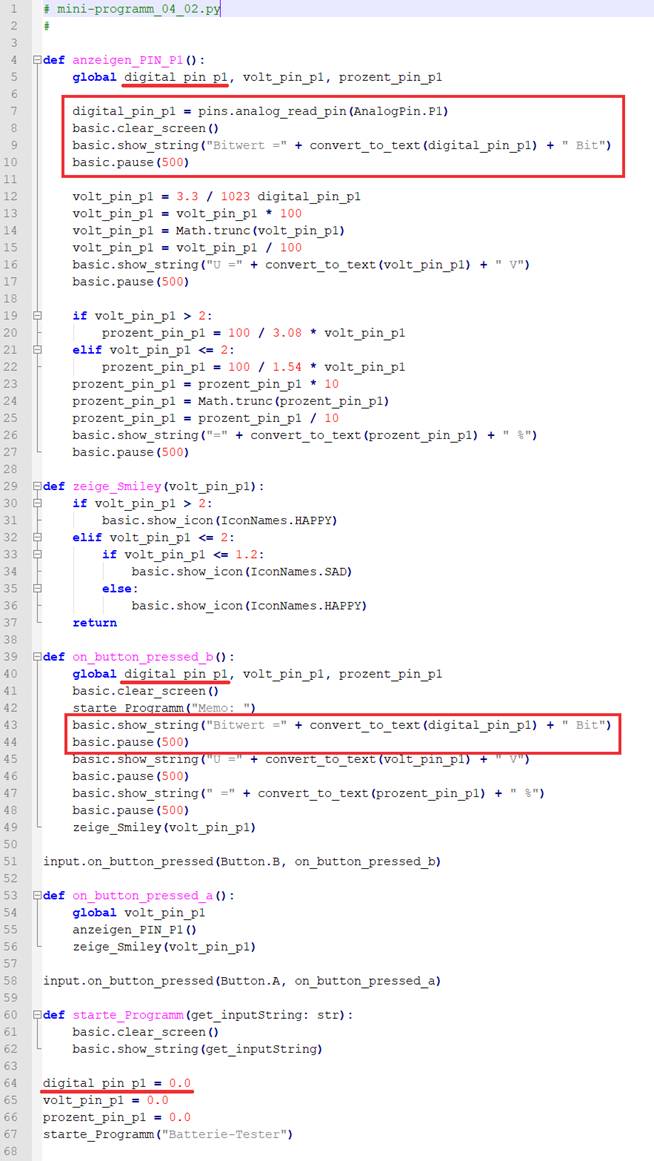Da es in der Entwicklungsumgebung des „Calliope mini“ keine „Suchen & Ersetzen“-Funktion gibt, laden wir uns das bisherige „Python“-Programm „mini-programm_03_19.py“ in einen eigenen, externen (Windows-) Programmier-Editor namens „Notepad++“, führen dort die entsprechenden Änderungen mittels der Funktion „Suchen & Ersetzen“ durch und speichern den neuen Quellkode im „Python“-Programm „mini-programm_04_01.py“ ab.

Jetzt wo die Variable „digital_pin_p1“ umbenannt wurde, steht sie wieder für das Programmieren zur Verfügung. Und zwar für das Einlesen und die Anzeige der Bitwerte (siehe roter Kasten):

(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_02.py)

Als nächstes führen wir mit dem Batterietester eine Spannungsmessung an einem ganz kleinen Messwiderstand R_Mess durch, messen dabei den Bitwert = 14 Bit und rechnen diesen mittels Dreisatz in den Spannungsabfall U_Mess wie folgt um:

1023 Bit → 3,3 V

14 Bit → x V

x = 3,3 V / 1023 Bit * 14 Bit = 0,041 V = 41 mV

Bei der Spannungsmessung beträgt dabei der Motorstrom I_Motor = 220 mA, wobei es zu beachten gilt, dass dieser wegen der Reihenschaltung auch durch den sehr kleinen Messwiderstand R_Mess fließt, sodass sich dessen Widerstandswert wie folgt berechnet:

R_Mess = U_Mess / I_Motor

= 41 mV / 220 mA = 0,1864 Ω = 186,4 mΩ

Jetzt ist es auch an der Zeit, die Frage zu beantworten, wie man an einen solch kleinen Widerstand gelangt! Kann man den kaufen und wenn ja, wo? Da der kleine Messwiderstand ja auch vom großen Motorstrom I_Motor = 220 mA durchflossen wird, stellt sich noch die Frage über wie viel Leistung dieser verfügen muss, damit er nicht durchbrennt:

P_Mess = U_Mess * I_Mess

= 41 mV * 220 mA = 9 020 * 10^-6 W = 9,020 * 10³ * 10^-6 W = 9,020 * 10^-3 W = 9,020 mW ≈ 9 mW

Zum Glück ist wegen des sehr kleinen Spannungsabfalls U_Mess = 41 mV am Messwiderstand R_Mess auch die Wärmeverlustleistung P_Mess = 9 mW sehr klein, sodass man sich keine Sorgen machen muss, dass der Messwiderstand eventuell durchschmoren könnte.

Hier beim Elektronik-Versender „Conrad“ aus Hirschau/Bayern kann man sich z.B. einen Messwiderstand der Größe 0,1 Ω = 100 mΩ mit einer Verlustleistung von 1 Watt zum Preis von 4,15 € bestellen. Bei zwei in Reihe zu schaltenden Messwiderständen wären das dann schon 8,30 € zzgl. Versandkosten! -

Aber es geht natürlich auch wesentlich preiswerter! Ganze 0,15595 €, also rund 16 Eurocent zzgl. Versandkosten kostet unserer Spezial-Messwiderstand mit folgenden Nennwertangaben: U = 250 V, I = 2 A vom Typ „F“, d.h. „flink“ für eine schnelle Reaktion im Sinne des schnellen Durchschmelzens im Falle, dass die Stromstärke von I = 2 A überschritten wird!

Und, man höre und staune! Der „Spezial“-Messwiderstand der Größe R_Mess = 186,4 mΩ (siehe oben) befindet sich sogar in unserem Elektronik-Baukasten „electronic 159“ und zwar in Form einer Feinsicherung, die sich in der Batteriehalterung [19] befindet und das Batteriepack gegen einen Kurzschluss absichert! Und das Schöne daran ist, dass es im Elektronik-Baukasten bis zu zwei (Ersatz-) Sicherungen gibt, sodass wir eine davon als unseren Messwiderstand nehmen können, den wir ja weiter oben ausführlich berechnet haben! -

Jetzt, wo wir die Größe des Messwiderstandes R_Mess = 0,1864 Ω (siehe oben) kennen, können wir diesen ins obenstehende „Python“-Programm „mini-programm_04_02.py“ aufnehmen und mit diesem den Messtrom I_Mess ( = I_Sicherung = I_Motor) wie folgt berechnen:

R = U / I = U_Mess / I_Mess →

I_Mess = U_Mess / R_Mess = 0,041 V / 0,1864 Ω = 0,041 V / 0,1864 V/A = 0,219957 A ≈ 220 mA þ

Das Messen und Bestimmen von sehr kleinen Widerständen und dessen Widerstandswerten kann sehr schwierig sein, weil man nicht ausschließen kann, dass die kleinen Widerstände der Messleitungen je nach Leiterquerschnitt und Länge auf dem vom Messobjekt zum Ohmmeter in die Messung mit einfließen und diese gegebenenfalls verfälschen.

Im vorliegenden Fall kommt erschwerend noch hinzu, dass der Gleichstrommotor [24] verhältnismäßig viel Motorstrom I_Motor = 220 mA zieht, sodass sich die beiden in Serie geschalteten 1,5 Volt Batterien vom Typ „Mignon AA“ relativ schnell entladen mit der unangenehmen Folge, dass sich die Batteriespannung, der Laststrom und damit auch der Messtrom I_Mess ( = I_Sicherung = I_Motor ) durch den Messwiderstand R_Mess = 0,1864 Ω fortwährend verkleinern!

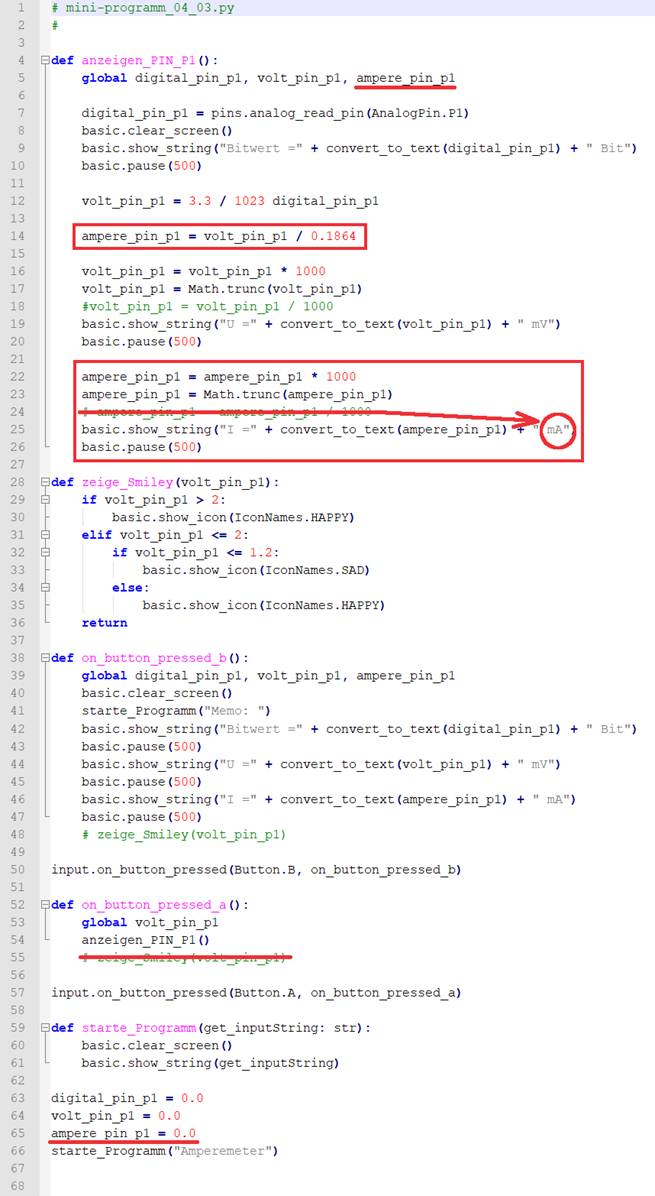
Deshalb wird der nicht mit konstanter Drehzahl laufende Gleichstrommotor [24] durch die Glühlampe [18] ersetzt.

Außerdem wird das „Python“-Programm „mini-programm_04_02.py“ zum Strommessprogramm „mini-programm_04_03.py“ weiter entwickelt, indem die indirekt zu messende und anzuzeigende Stromstärke mit der Variablen „ampere_pin_p1“ einfach aus dem kleinen Spannungsabfall U_Mess = 0,041 V = 41 mV berechnet wird:

(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_03.py)

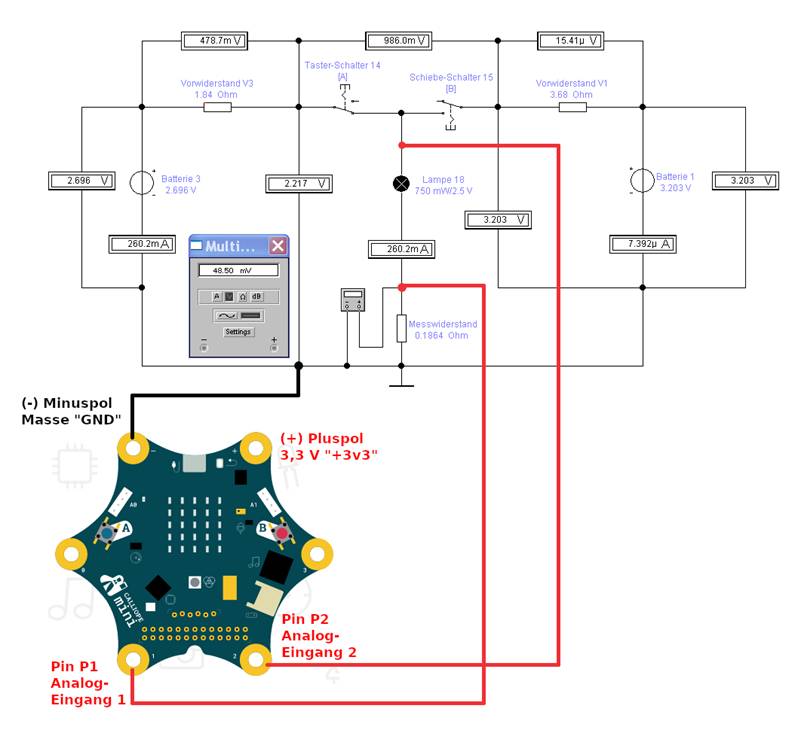
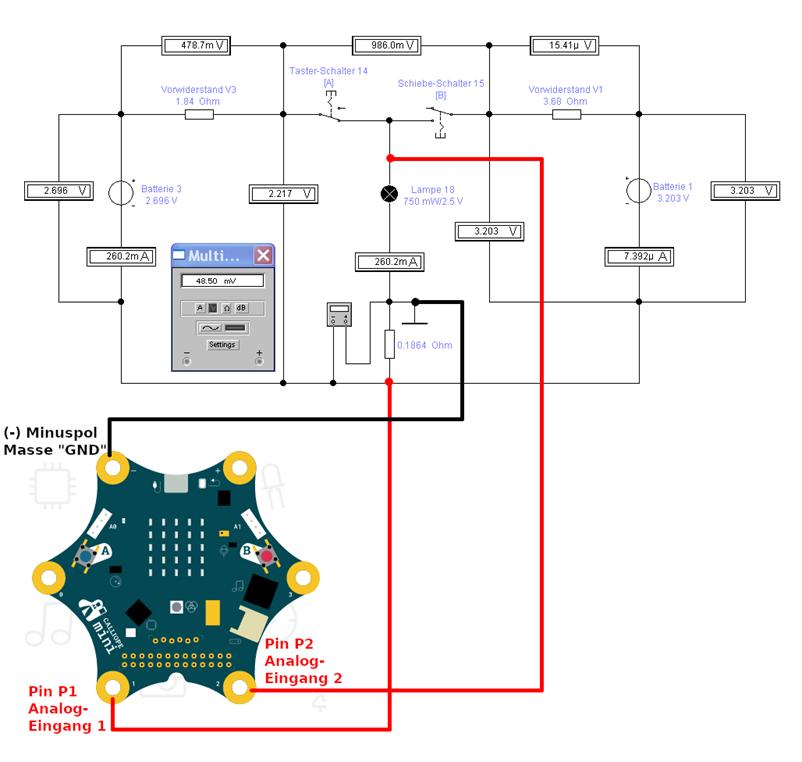
Bevor es daran geht, das obenstehende „Python“-Programm weiter zu entwickeln, geht es nachfolgend noch darum zu klären, wie denn die Hardware des „Calliope mini“, d.h. die Anschlüsse „Masse „GND“, „Pin P1“ und „Pin P2“ mit der nachfolgenden Schaltung „schaltung_04-01.ewb“ der Elektronik-Simulation „Electronics Workbench“ verbunden werden müssen, um

· den Spannungsabfall U_Mess = 48,5 mV am Messwiderstand R_Mess = 0,1864 Ω sowie

· den Spannungsabfall U_Lampe = 2,1685 V am Lastwiderstand R_Lampe = 8,333 Ω

messen zu können.

Dabei gilt es zu beachten, dass der Spannungsabfall U_{R Mess} = 48,5 mV am Messwiderstand R_Mess = 0,1864 Ω als auch der Spannungsabfall U_Lampe = 2,217 V am Lastwiderstand R_Lampe = 8,52 Ω gegen Masse („┴“) gemessen wurden, sodass im Spannungsabfall der Glühlampe [18] der Spannungsabfall des Messwiderstandes bereits enthalten ist (siehe weiter unten in der Schaltung „schaltung_04-01.ewb“ von „Electronics Workbench“)!

1. Demzufolge würde die Spannungsteilerformel R_Mess / R_Lampe = U_{R Mess} / U_Lampe zu falschen Ergebnissen führen:

R_Lampe = R_Mess / ( U_{R Mess} / U_Lampe )

= 0,1864 Ω / ( 48,5 mV / 2,1685 V ) = 0,1864 Ω / ( 0,0485 V / 2,1685 V )

= 0,1864 Ω / ( 0,0224 ) = 8,3214 Ω FALSCH!

2. Rechnet man den Spannungsabfall der Messspannung U_Mess = 48,5 mV aus dem Spannungsabfall der Glühlampe [18] heraus, so folgt mit der Spannungsteileformel:

R_Lampe = R_Mess / [ U_{R Mess} / ( U_Lampe - U_{R Mess} ) ]

= R_Mess / [ U_{R Mess} / ( 2,217 V - 0,0485 V ) ] = R_Mess / [ U_{R Mess} / ( 2,1685 V ) ] → Siehe oben!

= R_Mess / [ 1 / ( ( U_Lampe / U_{R Mess} ) - 1 ) ]

= 0,1864 Ω / [ 1 / ( ( 2,217 V / 0,0485 V ) - 1 ) ]

= 0,1864 Ω / [ 1 / ( 45,71134 - 1 ) ]

= 0,1864 Ω / [ 1 / 44,71134 ] = 0,1864 Ω / [ 0,02237 ] = 8,333 Ω

Zum Vergleich:

Betriebsdaten der Glühlampe [18]

U_Nenn = 2,5 V

I_Nenn = 0,3 A

Für die Berechnung des ohmschen Widerstandes der Glühlampe [18] folgt dann:

R = U / I →

R_Glühlampe = U_Nenn / I_Nenn

= 2,5 V / 0,3 A = 8,33 Ω

Wie man weiter oben bei der Spannungsteilerformel gemäß Punkt 1.) sieht, muss man schon höllisch aufpassen, dass man nicht versehentlich mit verketteten Spannungen rechnet!

Nachfolgend also die Schaltung „schaltung_04-01.ewb“ der Elektronik-Simulation „Electronics Workbench“ als Vorstufe zu einer kombinierten Spannungs- und Strommessung sowohl am Messwiderstand als auch an der Glühlampe [18]:

(Bild vergrößern: auf Bild klicken! Webverzeichnis schaltung_04-01.ewb)

Wie aber konnte es dazu kommen, dass wir im Punkt 1.) bei der Spannungsteilerformel versehentlich mit der verketteten Spannung der Glühlampe [18] gerechnet haben?

Ganz einfach:

Alle analogen oder digitalen Ein- und Ausgänge des „Calliope mini“-Rechners beziehen sich stets auf nur eine einzige Masse und zwar den Port Pin „GND“, engl. „ground“ (siehe obenstehende Schaltung).

Und, da die Masse bei der Schaltung „schaltung_04-01.ewb“ von „Electronics Workbench“ bereits vorgegeben war, war es naheliegend den Masseanschluss von Port Pin „GND“ (= Masse) des „Calliope mini“ mit dem der elektronischen Schaltung („┴“) bzw. mit dem Versuchsaufbau des Elektronik-Baukasten „electronic 159“ zu verbinden. -

Eine elektrische/elektronische Schaltung ist dann potentialfrei, wenn z.B. deren Stromversorgung (= Netzteil) auf der Netzseite mit 230 V~ Netzwechselspannung des Energieversorgers galvanisch von der Niederspannungsseite (= Brückengleichrichter, Siebkondensatoren und ggf. Längsregler für die Spannungsregelung) getrennt ist.

Üblicherweise erfolgt dabei die galvanische Trennung durch einen Transformator mit je einer Primärwicklung (= Spule mit vielen Windungen) auf der 230 V~ Wechselspannungsseite des Energieversorgers und einer Sekundärwicklung (= Spule mit weniger als halb so vielen Windungen) auf der Niedervoltseite mit nachgeschalteter Gleichrichtung und ggf. Stabilisierung.

Dabei bedeutet „galvanisch“, dass es zwischen der Primär- und Sekundärseite keine elektrische Verbindung gibt. Also auch keine gemeinsame Masse („┴“)!

Beim Netztransformator sind zwar Primär- und Sekundärspule elektrisch voneinander getrennt, aber nicht elektromagnetisch, da sich beide Spulen in einem gemeinsamen, geschlossenen magnetischen Kreis nebst (Wechselstrom-) Magnetfeld befinden. Das hat zur Folge, dass sich ein Kurzschluss auf der Sekundärseite auch auf die Primärseite z.B. durch einen größeren Strom durch die Primärspule auswirkt. Deshalb wird die Primärspule des Transformators durch eine entsprechende Schmelzsicherung abgesichert, die unter gar keinen Umständen geflickt, d.h. durch Silberpapier, Alufolie oder ähnliches ersetzt werden darf!

Sogenannte „Klingeltransformatoren“ sind wegen ihrer losen magnetischen Kopplung durch einen entsprechenden Luftspalt im magnetischen Kreis kurzschlussfest! Dies ist das besondere Merkmal, das aber gleichzeitig durch einen entsprechenden Nachteil, nämlich dass die sekundär induzierte Wechselspannung nicht stabil ist, d.h. bei einer größeren Belastung „in die Knie geht“, sich maßgeblich verringert, erkauft werden.

Personal-Computer (PCs), Desktop-PCs, Mini-Tower-PCs usw. verfügen alle über ein entsprechend dimensioniertes, teils auch großes PC-Netzteil, das als Schaltnetzteil ausgelegt ist. Demzufolge ist der Netztransformator ziemlich klein, da er nur für die galvanische Trennung und die Potentialfreiheit gegenüber der Netzwechselspannung von 230 V~ zuständig ist. Die eigentliche Regelung der ausgangsseitigen Gleichspannung zwecks Stromversorgung des Motherboards sowie der Festplatte, des CD-ROM und/oder DVD-Laufwerks erfolgt dann in der nachgeschalteten Spannungsstabilisierung mittels Leistungselektronik.

Die netzseitige Stromversorgung mittels 230 V~ Wechselspannung auf der Primärseite erfolgt über ein sogenanntes dreipoliges (Euro-) Kaltgeräte-Anschlusskabel vom Typ „C14“. Eines der drei Litzenkabel ist für den gelbgrünen Schutzleiter vorgesehen, um im Falle eines Kurzschlusses den Kurzschlussstrom über den Schutzleiter zum Erdpotential hin der Schukosteckdose abzuleiten. Gleiches gilt, falls durch einen Defekt die lebensgefährliche Netzwechselspannung von 230 V~ am PC-Blechgehäuse anliegen sollte. Um einen lebensgefährlichen Stromschlag zu verhindern, wird deshalb die Fremdspannung über den gelbgrünen Schutzleiter zum Erdpotential hin abgeleitet, d.h. „vernichtet“.

Sollte es wider Erwarten im Haushalt elektrische Geräte geben, die eine kleine, teils ungefährliche Fremdspannung (= Brummspannung, fehlerhafte Abschirmung bei NF-Verstärkern der Stereoanlage, Fehlspannung z.B. aufgrund nicht ausreichender Isolierung einer Herdplatte von bis zu 80 V~) ins das Haushaltsnetz einspeisen, dann liegt diese Fehl- oder auch Kriechspannung mit geringer Stromstärke auch am Schutzleiter des PCs und damit auch am PC-Gehäuse an.

Feststellen lässt sich eine Fehlspannung u.a. mittels eines Spannungsprüfers oder durch einen kleinen Kontaktfunken, wenn man ein geerdetes Elektrogerät oder Zusatzgerät an ein anderes anschließt. Dabei kommt es zu einer kleinen Funkenentladung, sobald man den Stecker einsteckt.

Zu Fehlspannungen kommt es gelegentlich, wenn verschiedene NF-Verstärker und Lautsprecherverstärker an teils unterschiedliche Phasen des Energieversorgers bei Drehstrom angeschlossen werden und über keine eigene, d.h. gemeinsame durchgeschleifte Erdung (= gelbgrüne Schutzkontaktleitung) verfügen. Dies hat dann zur Folge, dass die Mikrofon-Verstärkeranlage aufgrund der Fehlspannung quasi unter Strom steht. Sobald der Redner oder Sänger mit dem Mund die per Drahtgeflecht abgeschirmte Mikrofonkapsel berührt, bekommt er einen leichten, aber nicht tödlichen Stromschlag.

Gefährlich wird es aber, wenn die Verstärkeranlage oder Teile davon bei einem Open-Air-Festival in einer heftigen Regenschauer feucht werden oder sogar in einer kleinen Wasserpfütze stehen. Dann vergrößert sich die Fehl- und Fremdspannung wegen der „verbesserten“ Leitfähigkeit maßgeblich, sodass ein Stromschlag beim Berühren der unter (Fremd-) Spannung stehenden Verstärkeranlage tödlich sein kann.

Spätestens wenn es beim Anschließen der USB-Stromversorgung des „Calliope mini“-Rechners an die USB-Buchse des PCs ein kleinen Funkenüberschlag gibt, sollten die Alarmglocken schrillen, scheint der PC nicht wirklich potentialfrei zu sein, sodass man mit zerstörerischen Ausgleichsströmen zwischen unterschiedlichen Geräten rechnen muss.

Wenn man von wegen der Potentialfreiheit im Zweifelsfall ganz auf Nummer sicher gehen will, dann verzichtet man beim „Calliope mini“ auf die USB-Stromversorgung und verwendet stattdessen das mitgelieferte ansteckbare Batteriefach mit den zwei 1,5 Volt Batterien vom Typ „Micro AAA“.

Doch nun wieder zurück zu den beiden Spannungsmessungen am Port „Pin P1“ (= parallel dem Messwiderstand) und „PinP2“ (= parallel zum Lastwiderstand der Glühlampe [18]).

Da wir jetzt aber die Glühlampe [18] als Lastwiderstand verwenden und diese mit der Batteriespannung von zwei in Serie geschalteten 1,5 V Batterien versorgen, messen wir den Messwiderstand in Form der Schmelzsicherung neu aus, indem wir über den Port „Pin P1“ den Spannungsabfall parallel zur Schmelzsicherung messen

1023 Bit → 3,3 V

33 Bit → x V

x = 3,3 V / 1023 Bit * 33 Bit = 0,0967 V ≈ 97 mV

und mittels des mit einem Multimeter gemessenen Laststromes von I_Last = I_Mess = 260 mA den Messwiderstand R_Mess wie folgt berechnen:

R_Mess = U_Mess / I_Mess = 97 mV / 260 mA = 0,3731 Ω

Im Vergleich zum bisher gemessenen und berechneten Messwiderstand R_Mess = 0,1864 Ω stellt sich die Frage, weshalb dieser ungefähr nur halb so groß ist (siehe weiter oben!).

Der Grund dafür ist der, dass das zur Laststrommessung verwendete Digital-Multimeter für die Strommessung nur drei Strommessbereiche für Gleichstrom hat, und zwar:

· Strommessbereich 1: → 2 mA,

Strommessbereich 1.1 → 20 mA fehlt,

· Strommessbereich 2: → 200 mA

Strommessbereich 2.1: → 2 A fehlt,

· Strommessbereich 3: → 20 A

Wie man sieht, liegen die drei Strommessbereiche zu weit auseinander, sind die Sprünge zwischen den Messbereichen mit je dem 100-fachen Abstand zueinander eindeutig zu groß, sodass die Messgenauigkeit leidet!

Schließlich sollen Spannungs-, Strom- oder Widerstandsmessungen stets im oberen Drittel der Messskala vorgenommen werden, jedenfalls bei analogen Drehspul-Messinstrumenten!

Man braucht halt immer, entsprechend dem Messbereich bzw. der Messskala, eine möglichst große Messspannung, sodass dementsprechend auch ein möglichst großer Messtrom entsteht.

Aber es gibt natürlich noch weitere Gründe, weshalb der bisher gemessene und berechnete Messwiderstand nur halb so groß war als der neue berechnete.

Bei der Messung und Berechnung des bisherigen, zu kleinen Messwiderstandes kam eine Stromversorgung

· mit nur einer 1,5 Volt Batterie in der Batteriehalterung [19] zum Einsatz,

· die zudem auch noch mit U_Batterie < 1 V ziemlich „verbraucht“, d.h. entladen war und demzufolge den Laststrom von bis zu I_Last = 220 mA überhaupt nicht zur Verfügung stellen konnte und,

· dass es sich bei dem Laststrom I_Last = 220 mA in Wirklichkeit um keinen gemessenen, sondern um den zweiten Messwert aus der aufgenommenen Wertetabelle handelt.

Wenn wir, wie in der bisherigen Schaltung „schaltung_04-01.ewb“ zu sehen ist, den Port „Pin P2“ an der Rundbuchse „2“ des „Calliope mini“ verwenden, um die Spannung U_Lampe parallel am Lastwiderstand R_Lampe zu messen, dann beinhaltet diese wegen des Masseanschlusses („┴“) auch den kleinen Spannungsabfall U_Mess = 97 mV am Messwiderstand R_Mess, sodass vom Port „Pin P2“ aus gegen Masse („┴“) beide Spannungsabfälle am Lastwiderstand R_Lampe und am Messwiderstand R_Mess (= Schmelzsicherung) erfasst werden (siehe weiter oben)!

Wenn man aber nur den Spannungsabfall parallel zum Lastwiderstand R_Lampe haben möchte, dann muss man den kleinen Spannungsabfall parallel zum Messwiderstand R_Mess wie folgt herausrechnen:

U_Lampe = U_{Pin_P2} - U_{R Mess} = 2,026 V - 90 mV = 2,026 V - 0,090 V = 1,936 V

Da der Laststrom I_Last = I_{R Mess} = I_Lampe überall gleich groß ist, lässt sich nun der Lastwiderstand R_Lampe gemäß dem Ohmschen Gesetz wie folgt berechnen:

R_Lampe = U_Last / I_Last = U_Lampe / I_{R Mess} = 1,936 V / 243 mA = 1,936 V / 0,243 A = 7,9671 Ω

Die ins Ohmsche Gesetz eingesetzten Werte für die Spannung U_Lampe sowie den Strom I_{R Mess} wurden alle mit dem „Python“-Prgramm „mini-programm_04_04.py“ an den Ports „Pin P1“ (= Messwiderstand) und „Pin P2“ (= Lampenwiderstadt) des „Calliope mini“ gemessen:

(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_04.py)

Bezüglich des obenstehenden „Python“-Programms muss noch geklärt werden, wie der Wert „7.9467“ ermittelt wurde und was es mit diesem auf sich hat (siehe grüner Kasten).

Wir messen am Port „Pin P2“ gegen Masse die Gesamtspannung U_ges = U_Batterie = U_Lampe + U_{R Mess} und zwar in Form des Bitwertes mit der Variablen „digital_pin_p2“ von dem wir allerdings noch den Spannungsabfall am Messwiderstand U_R Mess wie folgt bitmäßig(!) subtrahieren müssen:

· Statement ampere_pin_p2 = 3.3 / 1023 * (digital_pin_p2 - digital_pin_p1)

Durch die Umrechnung liegt der Variableninhalt der Variablen „ampere_pin_p2“ bereits als Wert der Stromstärke vor, sodass wir mittels des Ohmschen Gesetzes I_Lampe = U_Lampe / R_Lampe den Lampenwiderstand (= Lastwiderstand) wie folgt berechnen können:

· Statement ampere_pin_p2 = ampere_pin_p2 / 7.9467 # Ohm; Glühlampe, 2 * 1,5 V Batterien

Dabei handelt es bei der Variablen „ampere_pin_p2“ und deren Inhalt bereits um den Wert des Spannungsabfalls an der Glühlampe [18] und bei dem Wert „7.9467“ [Ω] um den ohmschen Widerstand der Glühlampe R_Lampe.

Bildet man von beiden Werten den Quotienten „ampere_pin_p2 / 7.9467“, so erhält man gemäß dem Ohmschen Gesetz I_Lampe = U_Lampe / R_Lampe bereits als Ergebnis die Stromstärke des Lampenstromes I_Lampe = 0,243 A.

Wegen der besseren Lesbarkeit in der Laufschrift, wird die Stromstärke des Lampenstromes I_Lampe = 0,243 A noch in Milliampere [mA] umgerechnet: I_Lampe = 243 mA (siehe grüner Kasten oben).

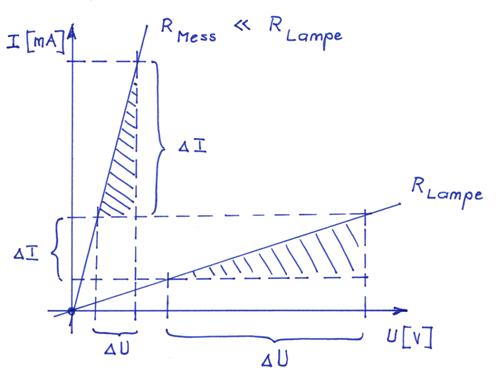
Bei der Berechnung des Skalierungsfaktors in Form des Lastwiderstandes R_Lampe = 7.9467 Ω … 7.9625 Ω lässt sich beobachten und feststellen,

· dass kleine Spannungsänderungen am kleinen Messwiderstand R_Mess

zu großen Laststromänderungen ∆I_Lampe führen und

· dass große Spannungsänderungen am größeren Lampenwiderstand R_Lampe

zu kleinen Laststromänderungen ∆I_Lampe führen.

(Zum Vergrößern bitte auf das Bild klicken!)

Und da beide Widerstände als Spannungsteiler in Reihe geschaltet sind, beeinflussen sich diese fortwährend wechselseitig. Dabei lassen sich beide Widerstände auch als Balkenwaage mit sehr unterschiedlichen Balkenlängen links und rechts der Drehachse und sehr unterschiedlichen Hebelarmkräften vergleichen.

Demzufolge ist die Balkenlänge des Lampenwiderstandes R_Lampe um ein Vielfaches länger und gegenüber Änderungen der eingeleiteten Kraft sensibler als die kurze Balkenlänge des Messwiderstandes R_Mess, sodass der Lampenwiderstand R_Lampe mit der vielfachen Balkenlänge über einen sehr großen Hebelarm nebst Hebelarmkräften verfügt:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man anhand der nachfolgenden Tabelle sieht, ist das Ermitteln des richtigen Skalierungsfaktors in Form des Lastwiderstandes R_Lampe = 7,9467 Ω … 7,9625 Ω sehr mühselig und zeitaufwendig, sodass es sich anbietet, die Skalierung zwischen dem Messwiderstand R_Mess und dem Lastwiderstand R_Last der Glühlampe [18] zukünftig automatisch, d.h. programmgesteuert, vorzunehmen (siehe weiter oben grüner Kasten im Programmkode):

Port „Pin P1“ Messwiderstand				Port „Pin P2“ Lastwiderstand (Lampe)		Lastwiderstand, berechnet
Bitwert	Spannung	Stromstärke	Widerstand	Spannung	Stromstärke	Widerstandswert
31 Bit	90 mV	243 mA	370,4 mΩ	1,936 V	243 mA	7,9671 Ω
30 Bit	87 mV	235 mA	370,2 mΩ	1,954 V	245 mA	7,9755 Ω
31 Bit	90 mV	243 mA	370,4 mΩ	1,921 V	241 mA	7,9709 Ω
31 Bit	90 mV	243 mA	370,4 mΩ	1,942 V	244 mA	7,9590 Ω
30 Bit	87 mV	235 mA	370,2 mΩ	1,939 V	244 mA	7,9467 Ω
30 Bit	87 mV	235 mA	370,2 mΩ	1,927 V	249 mA	7,7390 Ω
31 Bit	90 mV	243 mA	370,2 mΩ	1,924 V	249 mA	7,7270 Ω
32 Bit	93 mV	251 mA	370,5 mΩ	1.936 V	232 mA	7,7130 Ω

Um das Auftreten der Kettenspannung U_Lampe gegen Masse („┴“) mit

U_Lampe = U_{Pin_P2} - U_{R Mess} = 2,026 V - 90 mV = 2,026 V - 0,090 V = 1,936 V

in der Schaltung „schaltung_04-01.ewb“ zu vermeiden, muss man den Masseanschluss („┴“) wie folgt auf den Mittelpunkt des Spannungsteilers legen:

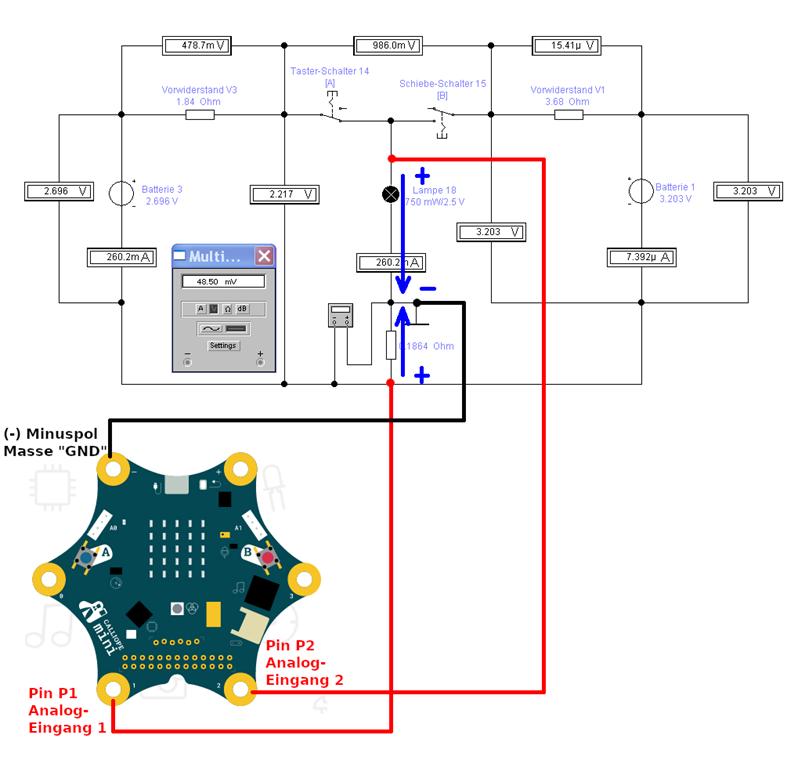
(Bild vergrößern: auf Bild klicken! Webverzeichnis schaltung_04-02.ewb)

Wie man in der obenstehenden Schaltung sieht, liegt der Masseanschluss („┴“) jetzt auf dem Mittelpunkt des Spannungsteilers, sodass es aus der Sicht des Ports „Pin Pin P2“ keine Kettenspannung mehr gibt, weil die beiden Teilspannungen U_Lampe und U_{R Mess} einander entgegengesetzt gepolt sind:

(Bild vergrößern: auf Bild klicken! Webverzeichnis schaltung_04-02.ewb)

Obwohl man den Port „Pin GND“, d.h. den Minuspol des „Calliope mini“ elektrotechnisch und potentialmäßig sehr wohl auf Masse („┴“) legen kann, stört das die Eingänge der A/D-Wandler an den Ports „Pin P1“ oder „Pin P2“ in keinster Weise mit der Folge, dass wir am Eingang des A/D-Wandlers am Port „Pin P1“ wider Erwarten keine analoge Spannung mehr messen können und demzufolge auch keinen Bitwert mehr als Ergebnis der A/D-Umwandlung mehr angezeigt bekommen!

Was aber ist der Grund dafür, dass der A/D-Wandler am Port „Pin P1“ nicht mehr funktioniert, während der A/D-Wandler am Port „Pin P2“ sehr wohl (noch) funktioniert?

Wenn man sich die beiden blauen Spannungspfeile in der obenstehenden Schaltung anschaut, dann fällt auf, wie bereits erwähnt, dass beide Spannungspfeile und damit auch die Spannungen entgegengesetzt gepolt sind. Der Knackpunkt dabei ist aber der, dass wir es waren, die die Masse („┴“) auf die Mittelanzapfung des Spannungsteilers R_Lampe und R_Mess gelegt haben, während sich gleichzeitig die Eingänge Port „Pin P1“ und „Pin P2“ der A/D-Wandler des „Calliope mini“ nicht daran stören bzw. im Falle des Port „Pin P1“ sogar die Zusammenarbeit verweigern!

Der Grund dafür ist ein ganz einfacher, nämlich der, dass die Eingänge Port „Pin P1“ und „Pin P2“ der A/D-Wandler des „Calliope mini“ stets nur analoge (Eingangs-) Spannungen in einen digitalen Bitwert umwandeln, wenn die Eingänge Port „Pin P1“ und „Pin P2“ auf positivem Potential („+“) liegen!

Und, diese Bedingung ist bei der obenstehenden Schaltung „schaltung_04-02.ewb“ nur für den Eingang am Port „Pin P2“ erfüllt, nicht aber für den Port „Pin P1“ (siehe entgegengesetzt gerichteter blauer Spannungspfeil)!

Jetzt sind wir zwar schlauer und auch sensibler bezüglich der richtungsabhängigen Spannungsbepfeilung, aber zugleich auch etwas ratlos, da die Eingänge an den Ports „Pin P1“ und „Pin P2“ nur funktionieren, wenn diese auf positivem Potential („+“) liegen: U_{Pin P1, P2} ≥ 0 V

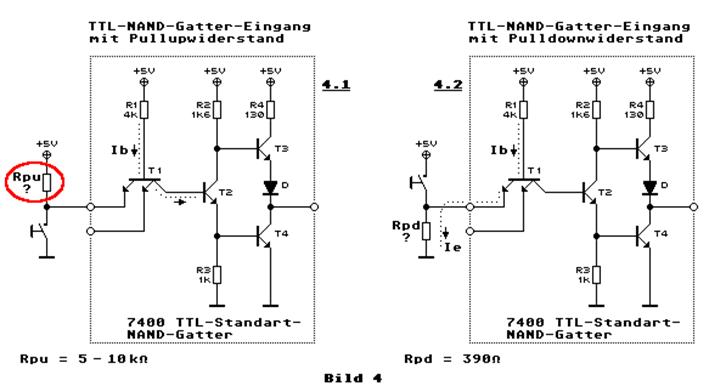
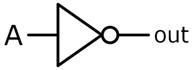
Was wir also bräuchten wäre ein sogenannter Inverter. In der Digitaltechnik gibt es (digitale) Inverter und zwar in Form eines sogenannten „NICHT“-Gatters. Wir brauchen aber keinen digitalen, sondern einen analogen Inverter!

Wie man anhand des Schaltsymbols gemäß „US ANSI 91-1984“-Norm sieht,

(Zum Vergrößern bitte auf das Bild klicken! Quelle: Wikipedia)

besteht der digitale Inverter hardwaremäßig aus einem sogenannten Operationsverstärker (siehe „Dreieck“), dem ein invertierender, analoger Wandler (siehe kleiner „Kreis“) nachgeschaltet ist. In Wirklichkeit lässt sich aber der Operationsverstärker (OPV) von vorn herein von außen so beschalten, dass der Ausgang „out“ ein invertiertes, analoges Ausgangssignal, d.h. mit umgekehrter Polarität gegenüber Masse („┴“) liefert. Dazu braucht der OPV aber zwei Versorgungsspannungen mit je einer „+5 Volt“- und einer „-5 Volt“-Versorgungsspannung.

Aber da wir in dem Elektronik-Baukasten „electronic 159“, der ja für Anfänger und Einsteiger in die Elektrotechnik/Elektronik ab 8 Jahren gedacht ist, keinen OPV haben, müssen wir uns etwas anderes einfallen lassen!

Beispielsweise könnten wir einen sogenannten „Brückengleichrichter“ verwenden, der normalerweise dafür gedacht ist, um eine Wechselspannung („~“) mittels seiner vier (Gleichrichter-) Dioden (= Halbleiter) in eine pulsierende Gleichspannung („=“) umzuwandeln.

Zwar gibt es im Elektronik-Baukasten „electronic 159“ eine spezielle Diode, nämlich die rote Leuchtdiode [17], die zwar rot leuchtet, aber wegen des dazu erforderlichen Vorwiderstandes (siehe Rückseite) nur Ströme von z.B. I_{LED, rot} = 20 mA durchlässt. Da aber der (Gleichstrom-) Motor [24] oder die (Glüh-) Lampe [18] einen Nennstrom vom mehr als dem Zehnfachen aufnehmen, scheidet die Möglichkeit eines Brückengleichrichters, der aus vier roten Leuchtdioden (LEDs) besteht, von vornherein aus. Demzufolge bräuchten wir also tatsächlich vier Dioden, die sich für den Gleichrichterbetrieb eignen oder noch besser einen entsprechenden Gleichrichter, in dem intern vier Gleichrichterdioden verbaut sind.

Das Problem beim Brückengleichrichter, der intern aus 2 x 2 Gleichrichterdioden besteht, wäre aber, dass dieser erst aber einer eingangsseitigen Spannung von mehr als 2 x 0,7 V Durchlassspannung einer einzelnen Diode, insgesamt also größer 1,4 V, arbeiten würde. Zur Erinnerung: die Eingangsspannung des analogen A/D-Wandlers am Port „Pin P1“ des „Calliope mini“ beträgt gerade mal U_{Pin P1} = 90 mV, d.h. neunzig Tausendstel (= „Milli“ = 0,001 = 10^-3) Volt!

Wir müssen uns also noch etwas Drittes als Lösung des Problems „Falsche Polarität am A/D-Wandler Port ‚Pin P1’“ einfallen lassen!

Wie wäre es z.B., wenn wir uns einen Spannungs-Inverter selbst bauen bzw. programmieren, indem wir den die Spannung bzw. den Spannungsabfall ganz einfach zwischen den beiden Ports „Pin P1“ und „Pin P2“ messen und dabei die Masse („┴“) des Ports „Pin GND“ einfach weglassen?!

Doch bevor wir loslegen, sollten wir uns noch überlegen, welche Spannung bzw. welchen Spannungsabfall wir zwischen den beiden Ports „Pin P1“ und „Pin P2“ messen wollen bzw. sollten. Sollten wir den Spannungsabfall parallel zur (Glüh‑) Lampe [18] oder besser zum Messwiderstand (= Schmelzsicherung) messen?

Prinzipiell sollte es am analogen Eingang des Inverters, d.h. zwischen den beiden Ports „Pin P1“ und „Pin P2“ eine möglichst große Eingangsspannung geben, sodass sich der Bitbereich von [ 0 … 1023 ] mit 1024 verschiedenen Bitwerten voll ausschöpfen lässt. Und, da wir eine Eingangsspannung in Form des anliegenden Spannungsabfalls erfassen, sollten wir den Spannungsabfall an der (Glüh‑) Lampe [18] messen, da deren Lastwiderstand R_Lampe um ein Vielfaches größer ist als der Messwiderstand R_Mess für die Strommessung:

(Bild vergrößern: auf Bild klicken! Webverzeichnis schaltung_04-03.ewb)

Wir führen gleich eine Spannungsmessung parallel zum Lastwiderstand R_Lampe durch, indem wir den Spannungsabfall, wie in der obenstehenden Schaltung zu sehen, an die beiden Ports „Pin P1“ und „Pin P2“ des „Calliope mini“ heranführen.

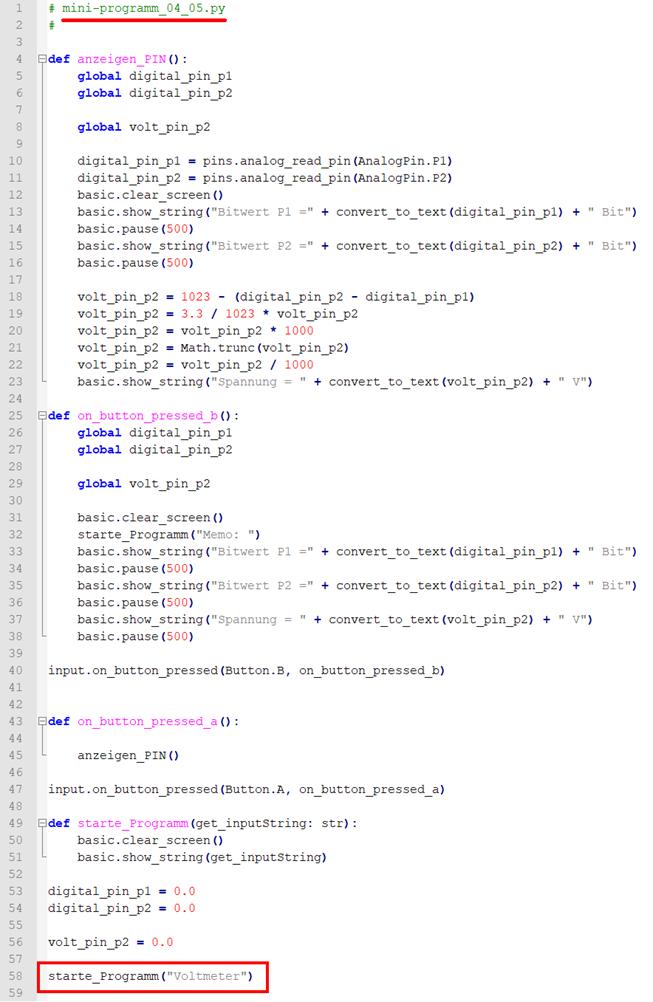
Dabei messen wir mit dem neuen „Python“-Programm „mini-programm_04_05.py“

(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_05.py)

Wie exakt der Spannungsabfall U_Lampe in Form der anliegenden Eingangsspannung an den beiden Ports „Pin P1“ und „Pin P2“ des „Calliope mini“ gemessen wird, wird anhand der nachfolgenden Berechnung deutlich:

U_Lampe = 3,3 V / 1023 Bit * [ 1023 Bit - ( Bitwert Pin P2 - Bitwert Pin P1 ) ]

= 3,3 V / 1023 Bit * [ 1023 Bit - Bitwert Pin P2 + Bitwert Pin P1 ]

= 3,3 V / 1023 Bit * [ 1023 Bit - 639 Bit + 318 Bit ] = 3,3 V / 1023 Bit * [ 703 Bit ]

= 3,3 V / 1023 * 703 = 2,2677 V ≈ 2,29 V

→ Messfehler gegenüber Multimeter-Anzeige von 2,03 V ≈ +12,8 %

Dass wir unsere Messspannung, d.h. den Spannungsabfall an der Glühlampe [18] als Lastwiderstand, jetzt als Differenzspannung ∆U_Mess = U_{Port P2} - U_{Port P1} ohne Masseanschluss („┴“) messen, ist schon eine feine Sache, da wir es demzufolge beim Spannungsabfall an der Glühlampe nicht mehr mit einer Kettenspannung zu tun haben und uns über den Masseanschluss („┴“) des „Calliope mini“ keine Gedanken mehr machen müssen, d.h. 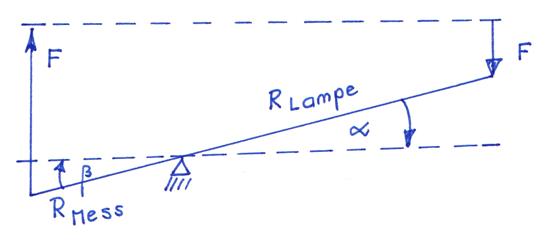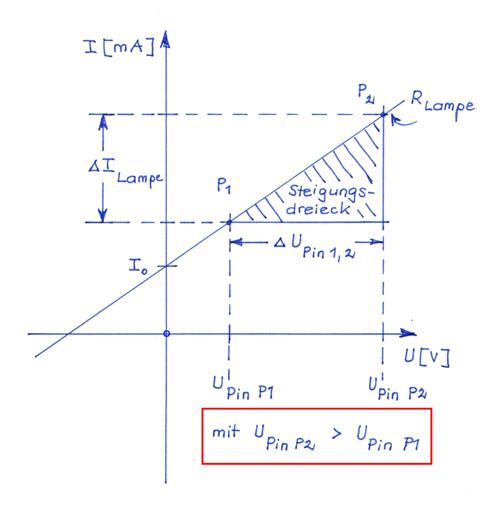diesen nicht mehr anschließen müssen!

Insgesamt kann man sagen, dass wir wegen der Differenzspannung ∆U_Mess = U_{Port P2} - U_{Port P1} ohne Massean-schluss („┴“) quasi das Steigungsdreieck der Widerstandsgeraden der Glühlampe als Lastwiderstand nebst Zwei-Punkte-Form anwenden, sodass eine eventuell in der Schaltung vorhandene Konstantstromquelle I₀ mit I₀ ≠ 0 die für die Parallelverschiebung der Widerstandsgeraden aus dem Ursprung des Koordinatenkreuzes heraus verantwortlich wäre, folgenlos bleibt und nicht zu falschen Messergebnissen führt:

(Zum Vergrößern bitte auf das Bild klicken!)

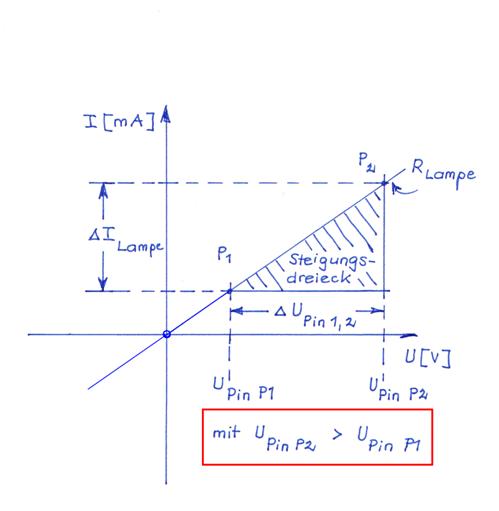
Um herauszufinden, ob sich unser neues Digitalvoltmeter auch universell verwenden lässt, entfernen wir den bisherigen Messwiderstand R_Mess ohne den Port „Pin P1“ selbst auf null Volt, d.h. auf Masse („┴“) des Ports „Pin „GND“ zu legen, sodass wir ab sofort den Spannungsabfall ∆U_{Pin 1, 2} am Lastwiderstand R_Lampe völlig potentialfrei messen!

Wenn wir dann außerdem in der obenstehenden Schaltung die Konstantstromquelle mit dem Konstantstrom I₀ entfernen, dann bedeutet dies praktisch, dass sich das Steigungsdreieck parallel nach unten verschiebt, aber eben nicht zwangsläufig bis in den Koordinatenursprung:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden Bild sieht, führt das Entfernen der Konstantstromquelle I₀ wider Erwarten nicht dazu, dass die Spannung im Punkt P₁ bzw. dem Port „Pin P1“ auf null Volt sinkt!

Auch das Entfernen des bisherigen Messwiderstandes R_Mess (= Schmelzsicherung) führt wider Erwarten nicht dazu, dass die Spannung im Punkt P₁ bzw. dem Port „Pin P1“ auf null Volt sinkt!

Der Grund dafür ist der, dass das Spannungspotential am Port „Pin P2“ in Form der Batteriespannung der beiden in Serie geschalteten 1,5 V Batterien unverändert bleibt bzw. durch dieses auf dem Spannungspotential der Batteriespannung U_Batt gehalten wird! -

Was aber bedeutet dies praktisch?

Praktisch bedeutet dies, dass die Schaltung mit den beiden 1,5 Volt in Serie geschalteten Batterien in der Batteriehalterung [19] zusammen mit der in Reihe geschalteten Glühlampe [18] ihr eigenes Massepotential mit null Volt hat, nämlich aufgrund unserer persönlichen, individuellen, d.h. auch willkürlichen Festlegung! Dabei macht es aber aus der Sicht der Elektrotechnik absolut Sinn, dass wir die Masse entsprechend der Schaltung festlegen!

Im vorliegenden Fall legen wir die Masse („┴“) auf den Minuspol („-“) der Batteriehalterung [19], aber nicht wegen der Stromversorgung mit der beiden 1,5 Volt Batterien, sondern wegen der Elektronik-Simulation „Electroncis Worbench“, die wir von Fall zu Fall bemühen und die im Falle einer nicht festgelegten, definierten Masse wider Erwarten nicht funktioniert bzw. sich nicht starten lässt!

Dazu muss man wissen, dass die Elektronik-Simulation einen Bezugspunkt im Sinne eines spannungsmäßigen Bezugspunktes, eines klar definierten Spannungspotentials als Startpunkt für das weitere Berechnen des Maschennetzes (= interne Maschenumläufe, Stromknoten, Superposition zweier Maschen usw.) benötigt!

Und, da ist es natürlich am einfachsten und naheliegendsten, wenn man den elektrischen Bezugspunkt, d.h. die Masse („┴“) auf null Volt legt.

Vergleichen lässt sich das Ganze, wenn wir mit mehreren mathematischen Funktionen, elektrotechnisch Widerstandsgeraden nebst (Konstant-) Spannungs- oder Stromquellen oder Arbeitspunkten, arbeiten, die den Ursprung des Koordinatensystems mit den Nullpunkt-Koordinaten (x₀ = 0, y₀ = 0) = (0 / 0) als gemeinsamen Bezugspunkt haben!

Da schon seit einigen Jahrzehnten bei den Computer- und Elektronik-Chips überwiegend nur Silizium-Transistoren vom Typ „NPN“ (= Anordnung der Sperrschichten) oder (Silizium-) MOS-FET-Transistoren verwendet werden, legt man die Masse („┴“) nicht nur auf null Volt, sondern gerade eben deswegen auf den Minuspol („-“) der Stromversorgung. -

Doch zurück zur Schaltung mit dem Spannungsteiler, bestehend aus den beiden Widerständen R_Lampe und R_Mess und dem „Python“-Programm „mini-programm_04_05.py“.

Durch das Verwenden der beiden eingangsseitigen Ports „Pin P1“ und „Pin P2“ mit den A/D-Wandlern des „Calliope mini“ arbeiten wir, d.h. messen wir zwar den Spannungsabfall parallel zum Laststandwiderstand R_Lampe völlig potentialfrei, d.h. ohne den Masseanschluss („┴“) am Port „GND“, benötigen dafür aber immer einen entsprechenden Spannungsteiler, der z.B. aus den beiden in Serie geschalteten Widerständen R_Lampe und R_Mess besteht!

Mit anderen Worten: Wenn wir mittels des Spannungsteilers der Widerstände R_Lampe und R_Mess arbeiten und den Spannungsabfall parallel zum Laststandwiderstand R_Lampe völlig potentialfrei messen, haben wir es elektrotechnisch mit dem Steigungsdreieck der Widerstandsgeraden nebst ∆R_Lampe = ∆U_Lampe / ∆I_Lampe zu tun, sodass die potentialfreie Spannungsmessung immer mit dem zweiten Widerstand, d.h. dem Messwiderstand R_Mess des Spannungsteilers durchgeführt werden muss!

Dabei gibt es den entscheidenden Nachteil, dass wir zwecks potentialfreier Spannungsmessung am Laststandwiderstand R_Lampe stets die Schaltung am Lastwiderstand auftrennen und den Messwiderstand R_Mess einfügen müssen!

Aber es gibt noch einen weiteren Grund, weshalb wir den Messwiderstand R_Mess benötigen!

Da wir es bei der vorliegenden potentialfreien Spannungsmessung mit den beiden eingangsseitigen Ports „Pin P1“ und „Pin P2“ zu tun haben, sind die beiden Eingänge wegen des sehr großen Eingangswiderstandes R_{Pull up} = 10 MΩ sehr hochohmig und demzufolge sehr empfindlich, sodass bereits kleine (Körper-) Spannungen ausreichen, um einen Schaltvorgang wie z.B. das Einschalten einer LED auszulösen (siehe „Python“-Programm „mini-programm_04_06.py“ im Webverzeichnis).

Wegen des hochohmigen Eingangs an einem beiden eingangsseitigen Ports „Pin P1“ und „Pin P2“ mit dem hochohmigen Eingangswiderstand R_{Pull up} = 10 MΩ und dem gleichzeitig sehr niedrigen Eingangsstrom I_{Pull up} = 0,24 µA ( → sehr hohe Eingangsempfindlichkeit),

Leerlauf-Eingangsspannung U_Leer = 2,41 V

I_{Pin P1} = U_Leer / R_{Pull up} = 2,41 V / 10 MΩ = 0,241 µA

sollte man bei Spannungsmessungen die hochempfindlichen Eingänge niemals mit undefinierten Spannungspotentialen „frei schwebend in der Luft hängen lassen“, sondern diese vielmehr durch einen definierten hochohmigen Eingangswiderstand R_{Pull up} = 10 MΩ „absichern“ bzw. auf ein klar definiertes, eingangsseitiges Spannungspotential anheben, engl. „pull up“.

>> Pull-up bezeichnet in der Elektrotechnik einen (relativ hochohmigen) Widerstand, der eine Signalleitung mit dem höheren Spannungs-Potential verbindet. Durch ihn wird die Leitung auf das höhere Potential gebracht, für den Fall, dass kein Ausgang die Leitung aktiv auf ein niedrigeres Potential bringt. Übliche Werte liegen im Bereich von 1 kΩ bis rund 10 kΩ. << (Quelle: Wikipedia)

(Zum Vergrößern bitte auf das Bild klicken!)

In der linken Schaltung des TTL-NAND-Gatter-Eingangs (= negierendes UND-Gatter) würde der Eingang am Emitter 1 des Transistors T1 ohne Pull-Up-Widerstand spannungsmäßig undefiniert „in der Luft hängen“, sodass die erste Transistorstufe mit dem Transistor T1 beim Anliegen einer eingangsseitigen kleinen Fremdspannung gegen Masse elektrisch leitend werden und so zu unkontrolliertem Ein-/Aus- oder Umschalten neigen würde.

Durch den „Klimmzug“-Widerstand „R_pu“, engl. „pull up“, d.h. Hochziehen, wird das Spannungspotential bei geöffnetem Schalter am Emitter 1 des Transistors T1 auf +5 V der Spannungsversorgung hochgezogen, sodass der Transistor T1 absolut sicher sperrt und das unkontrollierte Ein-/Aus- oder Umschalten aufgrund einer externen Fremd- oder. Schmutzspannung unmöglich wird (siehe auch „Standard-TTL und die Pullup- und Pulldown-Widerstände“ des „Elektronik-Kompendiums“).

Wenn wir also mit den beiden Spannungseingängen Port „Pin P1“ und „Pin P2“ eine potentialfreie Spannungsmessung am Laststandwiderstand R_Lampe vornehmen, sodass das Steigungsdreieck der Widerstandsgeraden mit der Zwei-Punkte-Form zugrunde gelegt wird, dann darf der Spannungseingang Port „Pin P1“ nicht „in der Luft hängen“, sondern muss stets mit dem Messwiderstand R_Mess (= Schmelzsicherung) beschaltet sein! -

Im Zusammenhang mit der Masse („┴“) und dem positiven oder negativen Massepotential werfen wir noch einen Blick in die Vergangenheit, in die Historie der Elektrizität und deren Entwicklung. Und zwar zu der Zeit, wo die Straßenbahnen noch von Pferden gezogen wurden. Das war am 26. November 1832 als in New York die erste Pferdebahn eröffnet wurde. Wenn man wissen wollte, wo die Pferdebahn fuhr und welche Strecke sie befuhr, dann musste man nur der Spur der Pferdeäpfel zwischen den Gleisen folgen. Kritische Zeitgeister befürchteten dann auch, dass New York mit dem wachsenden Streckennetz der Pferdebahnen eines Tages im Pferdemist ersticken würde. Doch bevor es dazu kam, wurde die Pferdebahn im Mai 1881, also rund 50 Jahre später, von der elektrisch betriebenen Straßenbahn abgelöst. Und zwar in Lichterfelde in Berlin. Dabei fuhren die von Werner von Siemens gebauten Wagen auf einer 2,5 km langen Strecke mit einer Geschwindigkeit von maximal 20 km/h, wobei die Stromversorgung des 3,7 kW (5 PS) starken Motors über beide Fahrschienen, die als Hin- und Rückleiter dienten, erfolgte. Wegen der 180 V Gleichspannung wurden die Gleise über eine vom übrigen Verkehr getrennte Trasse geführt, wobei das Betreten der Gleise verboten war. Zwecks Isolation der beiden Leiter wurden Holzschwellen verwendet. Ob und falls ja, welche der beiden Stromschienen dabei als Masse („┴“) herangezogen wurde, ist nicht bekannt.

>> Am 15. Mai 1881 fanden erste Fahrten für den Publikumsverkehr statt. Der Andrang war vormittags noch mäßig, stieg aber zum Nachmittag hin an, sodass der einzige Triebwagen mehrfach voll belegt war. „Dabei ward von den Zurückgebliebenen vielfach die Gelegenheit benutzt, um sich durch Betasten der beiden Schienen mit nassen Fingerspitzen gratis elektrisieren zu lassen. Auch eine neue Errungenschaft der Verkehrsmethode.“^[10] Der fahrplanmäßige Verkehr auf der Elektrischen Eisenbahn in Lichterfelde, wie die Bahn seinerzeit genannt wurde, begann am Folgetag. Der Abschnitt vom Bahnhof bis zur Wilhelmstraße war zu diesem Zeitpunkt noch nicht in Betrieb. In den ersten Tagen nach der Eröffnung kam es zu einzelnen Vorfällen, bei denen Pferde die Leitungen durch gleichzeitiges Betreten beider Schienenköpfe überbrückten und mehr oder weniger heftige Schläge erlitten.^[11] Um dem zu begegnen, wurden an den Wegeübergängen isolierte Schienenstücke eingebaut und die Leitungen unterirdisch miteinander verbunden. Der Wagen befuhr die Übergänge mit Schwung. Später wurden Schütze installiert, die beim Befahren der Übergänge eingeschaltet wurden, sodass die besagten Gleisabschnitte kurzzeitig unter Spannung standen.^[3] << (Quelle: Wikipedia)

1890 wurde dann die Stromversorgung mittels einer Oberleitung vorgenommen, sodass die Stromrückführung über beide Schienen mit Erdpotential erfolgte. 1893 wurde dann die Betriebsspannung der Bahn von 180 auf 500 Volt Gleichspannung angehoben mit der Folge, dass die Schienen wegen der höheren Gleichspannung geerdet, d.h. auf Erdpotential gelegt werden mussten, das dann dem Minuspol der Stromrückführung entsprach. Demzufolge lagen also die Schienen auf negativem („-“) Massepotential („┴“).

Diesbezüglich muss man wissen, dass das an sich neutrale Erdpotential sowohl dem Ausgleich positiv als auch negativ geladener Potentiale zur Verfügung steht, je nachdem um welche Art von Ladungen es sich handelt. Das sieht man auch bei Gewittern bei dem es nicht nur Blitze gibt, die von einer Wolke aus in die Erde einschlagen, sondern auch umgekehrt, von der Erde aus in eine Wolke, je nachdem, ob sich in einer Gewitterwolke positive oder negative Ladungen gebildet haben!

Bei der ersten großen Funkausstellung wurden 1924 in Berlin die ersten deutschen Rundfunk-Röhrenempfänger vorgestellt, die die sogenannten Detektorempfänger bis Ende der 1920er Jahre ablösten. Ab den 1960er Jahren wurden wiederum die Röhrenradios durch die mit Dioden und Transistoren (= Halbleiter) bestückten Radios abgelöst. Bei den Dioden und Transistoren handelte es sich um solche aus dem Halbleitermaterial Germanium (Ge), sodass die Gerätemasse („┴“) wegen der Emitteranschlüsse der PNP-Transistoren mit dem Pluspol stets auf positivem Spannungspotential lagen.

Als dann ab Mitte der 1960er Jahre die PNP-Transistoren aus Germanium durch NPN-Transistoren aus Silizium ersetzt wurden, wechselte die Gerätemasse („┴“) wegen der Emitteranschlüsse der NPN-Transistoren mit dem Minuspol auf negatives Spannungspotential.

Dabei ist es mir dann auch passiert, dass mein erstes Transistor-Kofferradio, das noch aus PNP-Germanium-Transitoren aufgebaut war, und an das ich Jahre später einen externen UKW-Stereo-Dekoder, der dann schon aus NPN-Silizium-Transistoren bestand, anschloss, wegen der unterschiedlichen Massepotentiale (Germanium = „+“ und Silizium = „-“) und der fehlenden galvanischen Trennung einen heftigen Kurzschluss auslöste, der aber zum Glück nur die Schmelzsicherung im externen Stromversorgungsnetzteil zerfetzte.

Also immer dann, wenn man es mit zwei mit teils unterschiedlicher Elektronik ausgerüsteten Geräten oder Schaltungen und deren Stromversorgung zu tun hat, sollte man sich vorab darüber informieren, ob und welche positiven oder negativen Spannungspotentiale auf die Gerätemasse („┴“) oder das neutrale Erdpotential (= gelb-grüner Schutzleiter „PE“ am Gehäuse) gelegt wurden.

Im Zweifelsfall sollte man deshalb bei Spannungs- oder Strommessungen stets ein (digitales) Multimeter im Kunststoffgehäuse mit eigener Stromversorgung ohne Schutzleiter oder (Schutz-) Erdung verwenden, die meistens intern mit einer 9 Volt Blockbatterie betrieben werden.

Mal ganz davon abgesehen, dass wir prinzipiell aus Gründen der Sicherheit, und weil wir keine ausgebildeten (Starkstrom-) Elektriker sind, keine Messungen an lebensgefährlichen Spannungen ab 50 V~ Wechselspannung oder 120 V= Gleichspannung durchführen! -

Für unseren „Calliope mini“-Rechner bedeutet dies, dass wir diesen im Zweifelsfall, wenn wir nicht wissen wie die Gerätemasse („┴“) oder der Anschluss des gelb-grünen Schutzleiters ausgeführt ist, mit dem Strom aus dem mitgelieferten Batteriepack versorgen.

Früher oder später kann es dabei aber vorkommen, dass die beiden 1,5 Volt Batterien vom Typ „Micro AAA“ im Batteriepack bereits mehr oder weniger stark entladen sind, sodass die Versorgungsspannung „3v3“ von U_Batterie = +3,3 V, die sich übrigens an der großen Rundbuchse „+“ (oben rechts neben der kleinen Micro-USB-Buchse) messen lässt, nicht mehr ausreicht, um den „Calliope mini“ mit Energie, d.h. Spannung und Strom, zu versorgen, sodass es dadurch dann auch unbemerkt zu fehlerhaften Spannungs- oder Strommessungen kommen kann, weil der kleine Rechner nicht mehr richtig rechnet!

Diesem Umstand sollte man besondere Beachtung schenken, falls man in das Batteriepack zwei 1,5 Volt NiMH-Akkus mit nur 2 * 1,2 V Zellenspannung = 2,4 V Klemmenspannung einsetzt!

Wenn man also sicherstellen will, dass man möglichst fehlerfreie Spannungs- oder Strommessungen durchführt, dann sollte man im Zweifelsfall verbrauchte Batterien oder entladene NiMH-Akkus wegen der zu geringen Klemmenspannung durch zwei fabrikneue 1,5 Volt Batterien ersetzen!

Nichtsdestotrotz werden wir das bisherige „Python“-Programm „mini-programm_04_05.py“ um eine Testfunktion zum Testen der Versorgungsspannung am Port Pin „+“, d.h. an der großen Rundbuchse mit der „+3v3“-Stromversorgung, wie folgt erweitern:

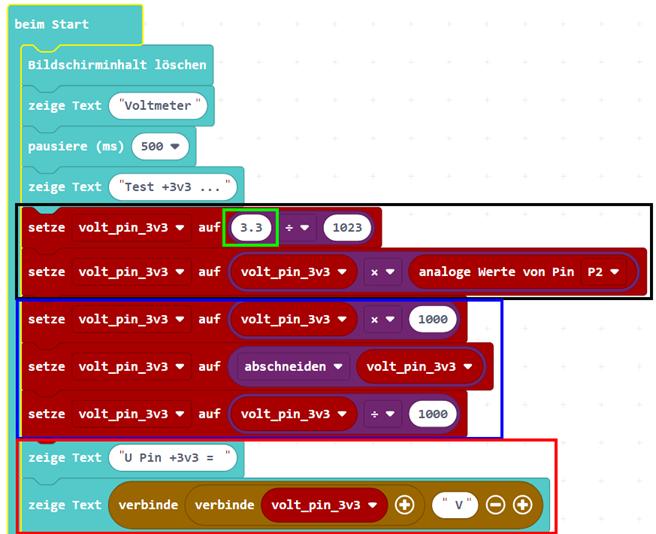
(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_06.py)

Wie man im obenstehenden Screenshot sieht, wird das Testprogramm zum Testen der „+3v3“-Versorgungsspannung an der großen Rundbuchse „+“ gleich zu Beginn im Programmblock „beim Start“ programmiert und später beim Programmstart ausgeführt.

Zu diesem Zweck messen wir am Port „Pin P2“ mit dem integrierten A/D-Wandler die (Gleich-) Spannung an der großen Rundbuchse „+“. Und zwar mittels der beiden Statements im schwarzen Kasten (siehe obenstehendes Bild).

Da die vom A/D-Wandler am Port „Pin P2“ eingelesene Spannung sofort in einen äquivalenten Binärwert umgewandelt wird, rechnen wir diese zwecks Laufschriftanzeige im LED-Display ebenfalls sofort in einen entsprechenden Dezimalwert mittels Dreisatz wie folgt um:

1023 Bit → 3,3 V

1021 Bit → x V

x = 3,3 V / 1023 Bit * 1021 Bit = 3,293 V

Dabei entspricht 1 Bit der Spannung U_{1 Bit} = 3,3 V / 1023 Bit * 1 Bit = 0,00322581 V ≈ 3,226 V und 1021 Bit entsprechen dann der Spannung U_{1021 Bit} = 3,3 V / 1023 Bit * 1021 Bit = 3,2936 V ≈ 3,29 V

Da der vom A/D-Wandler eingelesene und automatisch in Bit umgerechnete Bitwert 1021₂ vom obenstehenden „Block“-Programm „mini-programm_04_06.py“ nicht angezeigt wird, wurde dieser rückwärts aus der angezeigten Spannung von U_{1021 Bit} = 3,29 V errechnet!

Frage:

Was passiert, wenn wir im obenstehenden Programm anstelle des Dezimalwertes „3.3“ (siehe grüner Kasten) den Dezimalwert „3.29 V“ der an der großen Rundbuchse „+“ tatsächlich gemessenen „+3v3“-Versorgungsspannung ins Programm einpflegen?

Antwort:

Dann würden wir im Programm den Quotienten von vormals 3.3 / 1023 = 0,0032258 V/Bit auf nunmehr 3.29 / 1023 = 0,0032160 V/Bit entsprechend verringern, sodass das Programm nicht mehr richtig rechnet, weil sich der interne A/D-Wandler „an die interne Abmachung 3.3 V = 1023 Bit“ der Umrechnung hält! -

Im blauen Kasten wird dann der eingelesene und bereits umgewandelte Dezimalwert der gemessenen „+3v3“-Versorgungsspannung auf drei Nachkommastellen abgeschnitten!

Anstelle des

· Statements „abschneiden“

lässt sich aber auch das

· Statements „runden“

einsetzen, wobei dann z.B. der Wert 3,296 kaufmännisch auf 3,3 aufgerundet werden würde! –

Im roten Kasten des obenstehenden „Block“-Programms „mini-programm_04_06.py“ wird die an der großen Rundbuchse „+“ gemessene und zwischenzeitlich berechnete „+3v3“-Versorgungsspannung U_+3v3 in einen Textstring umgewandelt und zusammen mit dem Anzeigetext „U Pin +3v3 = “ als Laufschrift im 9 x 9 Matrix großen LED-Display angezeigt.

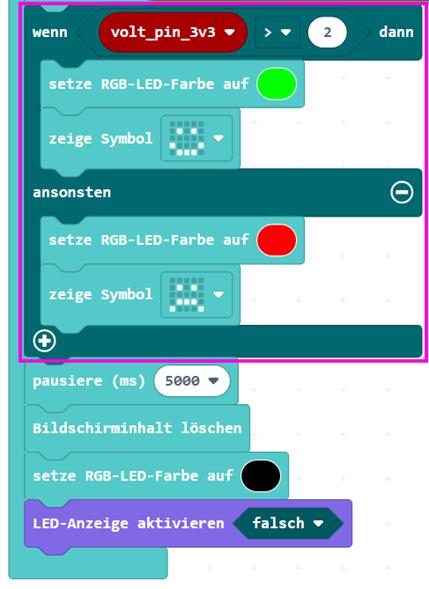
(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_06.py)

Im pinkfarbenen Kasten wird in der engl. „If then … else“, d.h. “Wenn dann … ansonsten”-Abfrage der berechnete und bis auf drei Nachkommastellen abgeschnittene Messwert, der in der Variablen „volt_pin_3v3“ gespeichert ist, mittels Vergleich „volt_pin_3v3 > 2“ ausgewertet und durch Aufleuchten der grünen J oder roten L (Kombi-) RGB-LED (R = Rot, G = Grün, B = Blau) nebst Smiley angezeigt.

Nur wenn der Wert der Variablen „volt_pin_3v3“ > 2 Volt ist, leuchtet die RGB-LED grün J, um anzuzeigen, dass die Versorgungsspannung an der großen Rundbuchse „+“ bzw. „+3v3“ ausreichend groß ist, um möglichst fehlerfrei zu rechnen zu können.

Die Smiley-Anzeige sowie das Aufleuchten der RGB-LED dauern dabei insgesamt bis zu 5000 ms = 5 * 1000 ms = 5 * 1000 * 1/100 s = 5 s an und erlischt dann wieder.

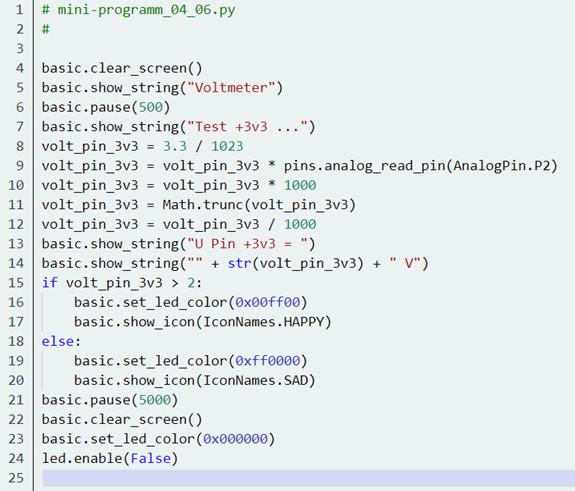
Setzt man abschließend im Programm die Farbe der RGB-LED mit der hexadezimalen Farbaufteilung „RRGGBB“ = „000000₁₆“ auf schwarz, so erlischt diese wieder.

Mit der hexadezimalen Farbaufteilung „RRGGBB“ = „FFFFFF₁₆“ würde die RGB-LED hellweiß leuchten.

Wandelt man in der Programmierumgebung des „Calliope mini“ den obenstehenden „Block“-Programmkode in die „Python“-Programmiersprache um, dann sieht der „Python“-Sourcecode folgendermaßen aus:

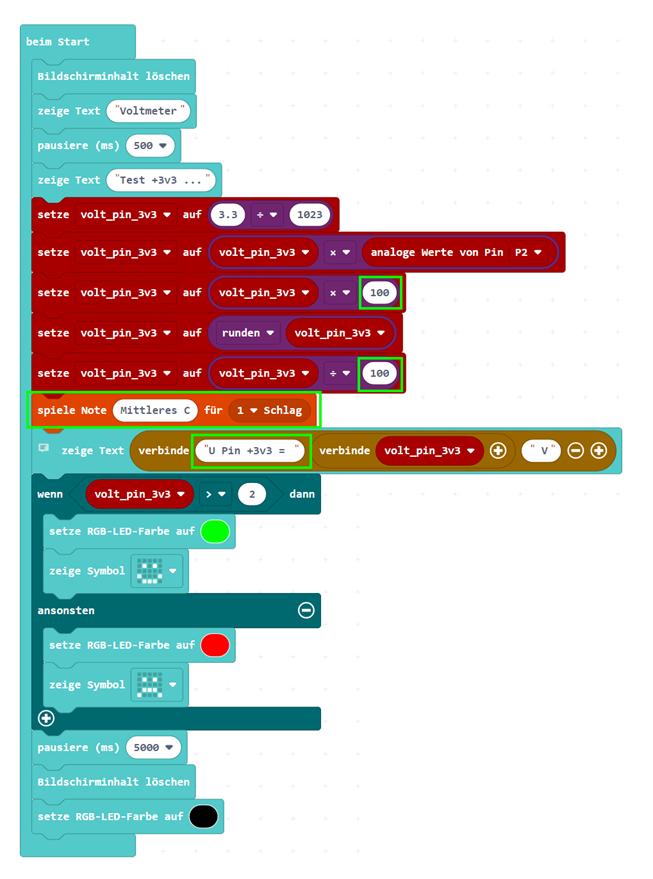
(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_06.py)

Bevor wir aber das bisherige Programm erweitern, nehmen wir noch ein paar Verbesserungen vor (siehe grüne Kärsten), als da sind:

· Für das Anzeigen der gemessenen Spannung genügt uns eine Genauigkeit von zwei Nachkommastellen. Demzufolge wird der Skalierungsfaktor für die Anzahl der Nachkommastellen von bisher 1000 auf nur noch 100 abgeändert. Außerdem wird die gemessene und berechnete Spannung mit der Variablen „volt_pin_3v3“ nicht mehr abgeschnitten, sondern bei den zwei Nachkommastellen kaufmännisch auf- oder abgerundet.

· Da die anfangs vorangestellten Laufschriften „Voltmeter“ und „Test +3v3“ zwecks Information des Anwenders bei der Anzeige doch einiges an Zeit erfordern und den Anwender auf eine kleine Geduldsprobe stellen, wurde vor der Anzeige des gemessenen Spannungswertes mit dem

Statement zeige Text verbinde „U Pin +3v3 = “ verbinde volt_pin_3v3 + „ V“

ein weiteres

Statement spiele Note Mittleres C für 1 Schlag

in den Sourcecode eingefügt.

Zu guter Letzt wurde das

· Statement LED-Anzeige aktivieren <falsch>

entfernt, da mit diesem die 9 x 9 Matrix LED-Anzeige deaktiviert wurde, sodass die Laufschriftanzeige bei der nächsten Anzeige dunkel blieb!

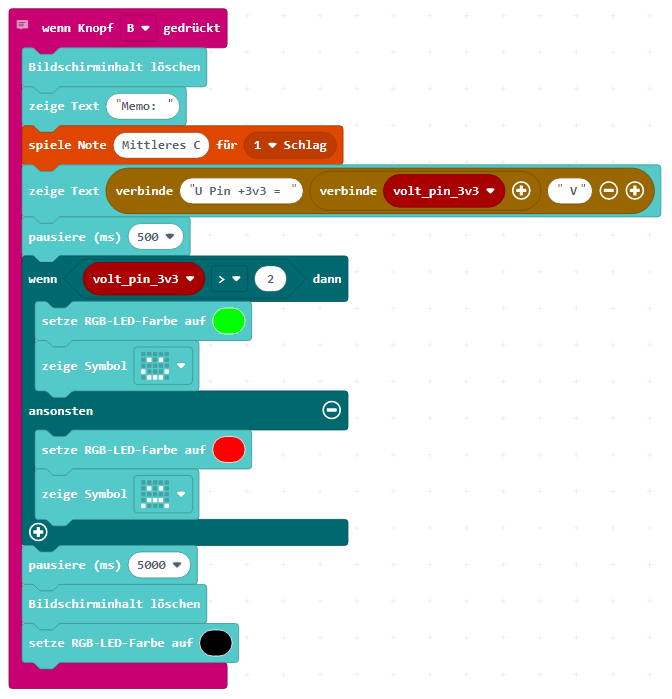
(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_07.py)

Mit dem eigenständigen Programmblock „wenn Knopf B gedrückt“, der permanent im Hintergrund läuft, lässt sich der Taster „B“ jederzeit drücken, um sich den eingelesen Spannungswert der Variablen „volt_pin_3v3“ wiederholt anzeigen lassen zu können:

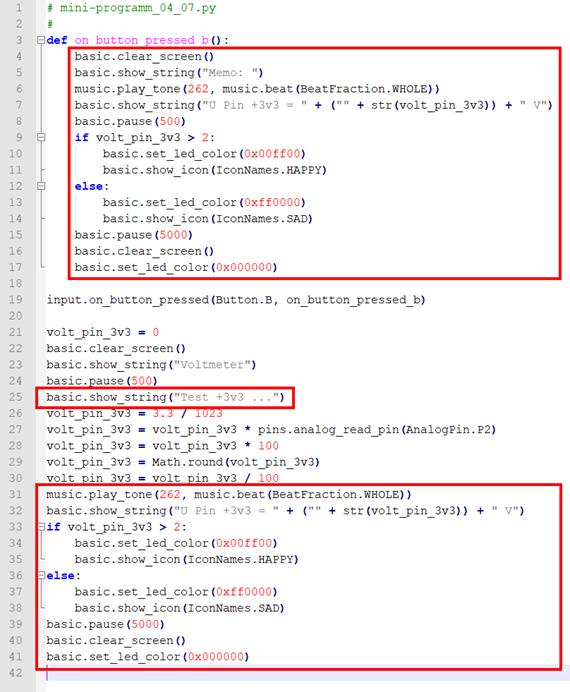
(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_07.py)

Wenn man sich das obenstehende „Block“-Programm im „Python“-Sourcecode anschaut, dann fällt auf, dass sich die Laufschriftanzeige an mehreren Stellen wie z.B. im Programmblock „on_button_pressed_b()“ wiederholt (siehe rote Kästen):

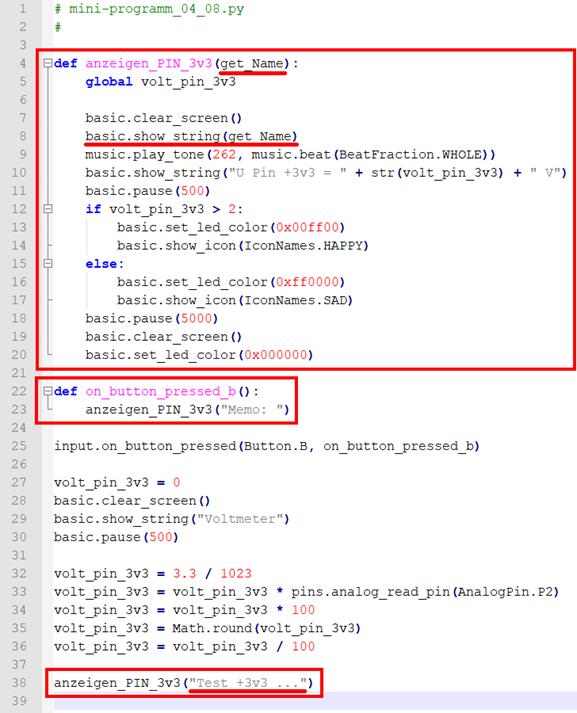
(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_07.py)

Als nächstes lagern wir den Programmkode aus den roten Kästen aus (siehe oben), indem wir diesen quasi in die

· Funktion „def anzeigen_PIN_3v3(get_Name)“

verschieben.

Dabei fällt sofort auf, dass der Funktion im Funktionskopf der Textstring „Test +3v3 …“ beim Funktionsaufruf

· anzeigen_PIN_3v3("Test +3v3 ...")

mit auf den Weg gegeben wird, der wiederum von der Variablen „get_Name“ entgegengenommen und innerhalb der Funktion zwecks weiterer Verarbeitung und Nutzung zur Verfügung gestellt wird:

· basic.show_string(get_Name)

Durch das Auslagern von Programmkode in die Funktion „def anzeigen_PIN_3v3(get_Name)“ sieht das neue „Python“-Programm „mini-programm_04_08.py“ recht übersichtlich aus:

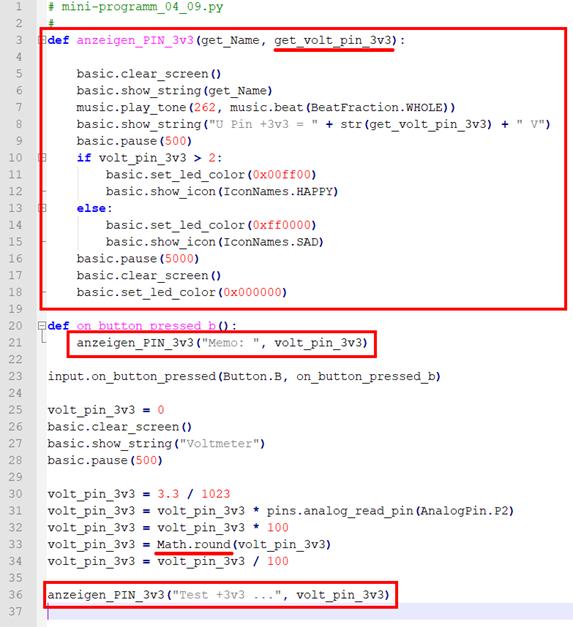
(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_08.py)

Wie man sich anhand des „Python“-Programms „mini-programm_04_09.py“ selbst überzeugen kann, lässt sich das obenstehende „Python“-Vorgängerprogramm noch dahingehend optimieren, indem man die Variable „volt_pin_3v3“ mit in den Funktionskopf der

· Funktion „def anzeigen_PIN_3v3(get_Name, get_volt_pin_3v3)“

aufnimmt.

Dabei muss der Funktionsaufruf selbst auch noch entsprechend angepasst werden (siehe rote Kästen):

· anzeigen_PIN_3v3("Test +3v3 ...", volt_pin_3v3)

(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_09.py)

Um die Stromversorgung des „Calliope mini“ am großen Rundloch („+“), d.h. am Port „Pin +3v3“ überprüfen zu können, mussten wir den Port „Pin +3v3“ mit dem Anschluss am großen Rundloch („2“), d.h. dem Port „Pin P2“, verbinden und nach dem erfolgreichen Test mit der Versorgungsspannung U_+3v3 > 2 V wieder von dieser trennen.

Damit sich die dann nachfolgende Messung der Lastspannung U_Last = U_Glühlampe nebst dem Messwiderstand R_Mess der Schmelzsicherung fehlerfrei durchführen lässt, muss zuvor überprüft und sichergestellt werden, dass die Verbindung am großen Rundloch („+“) mit dem Port „Pin +3v3“ und am großen Rundloch („2“) mit dem Port „Pin P2“ definitiv aufgehoben wurde.

Zu diesem Zweck müssten die beiden Ports „Pin +3v3“ und „Pin P2“ abgefragt werden, was aber so nicht geht, weil es sich eben beim großen Rundloch („+“) mit dem Port „Pin +3v3“ um die Stromversorgung externer Schaltungskomponenten handelt.

Demzufolge lässt sich am Port „Pin P2“ ( = großes Rundloch („2“) ) nur das Spannungspotential abfragen.

Liegt es auf dem Potential des Ports „Pin +3v3“ ( = großes Rundloch („+“) ), dann besteht eine elektrische Verbindung von diesem zum Port „Pin P2“ ( = großes Rundloch („2“) ), sodass gilt: U_{Pin P2} = U_{Pin +3v3}

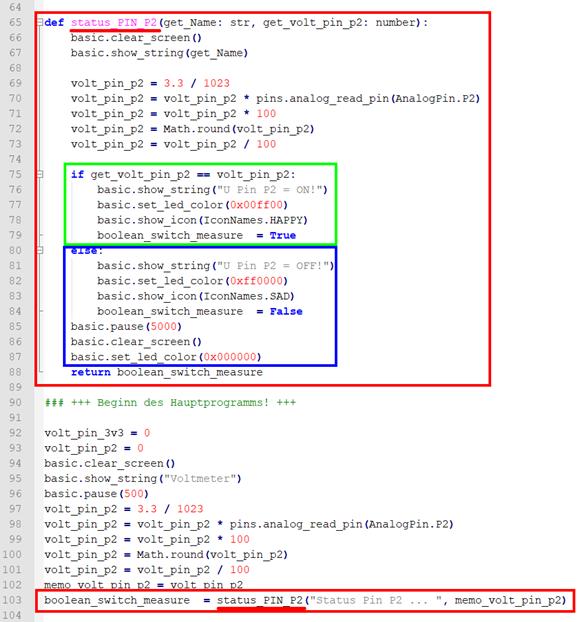
Ist diese Bedingung erfüllt, so wird dies durch die Laufschrift „U Pin P2 = ON!", durch grünes Aufleuchten der RGB-LED und durch die Anzeige eines lächelnden Smileys J im 9 x 9 Matrix großen LED-Display angezeigt (siehe grüner Kasten in der Funktion „status_PIN_P2(…)“ ):

(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_10.py)

Ist die Bedingung im

· Statement if get_volt_pin_p2 == volt_pin_p2:

wider Erwarten nicht erfüllt, so wird dies durch die Laufschrift „U Pin P2 = OFF!", durch rotes Aufleuchten der RGB-LED und durch die Anzeige eines schmollenden Smileys L im 9 x 9 Matrix großen LED-Display angezeigt (siehe blauer Kasten im obenstehenden Quellkode).

Interessant ist übrigens auch noch der Funktionsaufruf „status_PIN_P2(…)“ (siehe roter Kasten in Zeile 103 im obenstehenden Quellkode):

· Statement boolean_switch_measure = status_PIN_P2("Status Pin P2 ... ", memo_volt_pin_p2)

Wie man sieht, werden beim Funktionsaufruf „status_PIN_P2(…)“ zwei Werte, und zwar der als Laufschrift anzuzeigende Textstring „Status Pin P2 ...“ sowie die am Port „Pin P2“ ( = großes Rundloch („2“) ) gemessene Spannung U_{Pin P2} = U_{Pin +3v3}, an die Funktion selbst übergeben.

Wie wir ja bereits wissen, wird die Funktion „status_PIN_P2(…)“ ohne Rückgabewert ganz einfach mit dem

· Statement status_PIN_P2("Status Pin P2 ... ", memo_volt_pin_p2)

aufgerufen.

Da aber unsere Funktion „status_PIN_P2(…)“ im vorliegenden Fall auch noch den booleschen Rückgabewert

· Statement return boolean_switch_measure

nach dem Funktionsaufruf an den aufrufenden Programmblock des Hauptprogramms zurückliefert, muss dieser noch wie folgt erweitert werden:

· Statement boolean_switch_measure = status_PIN_P2("Status Pin P2 ... ", memo_volt_pin_p2)

Jetzt wissen wir nicht nur, wie sich eine Funktion aufrufen lässt, sondern auch, wie sich mittels des Funktionsaufrufs ein Variablenwert aus der Funktion selbst an das aufrufende Hauptprogramm zurückgeben lässt!

Bei dem

· Statement boolean_switch_measure = status_PIN_P2("Status Pin P2 ... ", memo_volt_pin_p2)

wird also zunächst die Funktion „status_PIN_P2(…)“ aufgerufen und nachdem diese abgearbeitet wurde, wird dann wieder ins Hauptprogramm zurückgekehrt und dabei der Rückgabewert der Funktion „status_PIN_P2(…)“ ans Hauptprogramm, d.h. der boolesche Variablen boolean_switch_measure, übergeben. -

Nachdem die Stromversorgung des „Calliope mini“ am großen Rundloch („+“), d.h. am Port „Pin +3v3“ überprüft wurde, kann mit der eigentlichen Spannungsmessung U_Lampe an der Glühlampe [18] als Lastwiderstand fortgefahren werden, wobei diese extra durch Tastendruck auf den Taster „A“ veranlasst werden muss.

Dabei gilt es zu beachten, dass die eigentliche Spannungsmessung U_Lampe an der Glühlampe [18] als Lastwiderstand nur dann erfolgen darf, wenn zuvor die Stromverbindung am großen Rundloch („+“) mit dem Port „Pin +3v3“ und am großen Rundloch („2“) mit dem Port „Pin P2“ definitiv aufgehoben wurde:

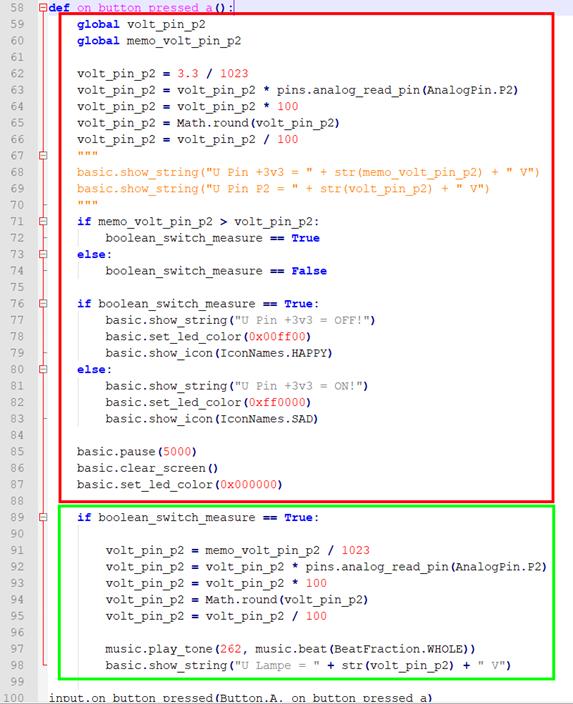
(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_10.py)

Aus diesem Grund wird in der Funktion „on_button_pressed_a()“ als erstes die Spannung am Port „Pin P2“ ( = großes Rundloch („2“) ) gemessen und mit dem gespeicherten Wert der beim Programmstart gemessenen Spannung am Port „Pin +3v3“ ( = großes Rundloch („+“) ) wie folgt verglichen (siehe roter Kasten):

· Statement „if memo_volt_pin_p2 > volt_pin_p2:”

Sobald die Bedingung im Statement erfüllt ist, wird der diesbezügliche boolesche Schalter „boolean_switch_measure“

auf den Wert „True“ gesetzt, werden

· der Textstring „U Pin +3v3 = OFF!“ als Laufschrift und

· das Smiley J im 9 x 9 großen LED-Matrix-Display

angezeigt, um auf diese Weise mittels

· des Aufleuchten der grünen RGB-LED

zu signalisieren, dass die ursprüngliche Verbindung zwischen dem großen Rundloch („+“) mit dem Port „Pin +3v3“ und dem großen Rundloch („2“) mit dem Port „Pin P2“ definitiv aufgehoben wurde.

Abschließend wird dann die eigentlichen Spannungsmessung U_Lampe an der Glühlampe [18] als Lastwiderstand durchgeführt und der Textstring "U Lampe = 1.65 V" als Laufschrift angezeigt (siehe grüner Kasten).

Achtung: Der tatsächliche Spannungsabfall an der Glühlampe [18] als Lastwiderstand beträgt aber ∆U_Lampe = 1,87 V (je nach verbleibender Kapazität der beiden in Serie geschalteten 1,5 Volt Batterien vom Typ „Mignon AA“).

Die Spannungsdifferenz von ∆U_Lampe - U_Lampe = 1,87 V – 1,65 V = 0,22 V ist darauf zurückzuführen, dass wir bis jetzt am Port „Pin P2“ ( = großes Rundloch („2“) ) nur die Spannung im Punkt P₂ des Steigungsdreiecks messen (siehe Bild weiter oben).

Mit dem „Python“-Programm „mini-programm_04_11.py“ wird nun auch die die Spannung am Port „Pin P1“ ( = großes Rundloch („1“) ) gemessen, die der Spannung im Punkt P₁ des Steigungsdreiecks entspricht (siehe Bild weiter oben).

Wenn wir jetzt mit einem herkömmlichen Multimeter die Stromstärke ∆I_Lampe = 260 mA durch die Glühlampe [18] messen, dann lassen sich erste Berechnungen, die aber noch trivial (= einfach) sind, durchführen:

R_Steig = ∆U / ∆I = ( U₂ - U₁ ) / ∆I þ

= ( U_{Pin P2} - U_{Pin P1} ) / ∆I_Lampe → FALSCH!

= ( 2,37 V – 1,51 V ) / 260 mA → … (Die Stromstärke der Glühlampe [18] wurde gemessen!)

= ( 0,86 V ) / 260 mA

= 0,00330769 KΩ ≈ 3,308 Ω → FALSCH!

R_Steig = ∆U / ∆I = ( U₂ - U₁ ) / ∆I þ

= ( U_{Pin P2} - U_{Pin P1} ) / ∆I_Steig → RICHTIG!

= ( 0,86 V ) / 103,2 mA

= 0,00833 KΩ = 8,33 Ω → RICHTIG (siehe weiter unten!)

Hier an dieser Stelle muss man aufpassen, gilt es zu klären, ob der Steigungswiderstand R_Steig identisch ist mit dem Lastwiderstand der Glühlampe [18] oder nicht.

Da das Steigungsdreieck wegen I₀ aus dem Koordinatenursprung heraus verschoben sein kann, wir aber den Konstantstrom I₀ noch nicht berechnet haben bzw. noch nicht berechnen können, muss man zunächst davon ausgehen, dass der Steigungswiderstand R_Steig nicht identisch ist mit dem Lastwiderstand R_Lampe, sodass ∆I_Steig ≠ ∆I_Lampe ist!

Schließlich handelt es sich bei dem Lastwiderstand R_Lampe um einen tatsächlich vorhandenen, d.h. physischen ( = greifbar körperlichen) und physikalischen Widerstand, der z.B. bei Überlastung (= zu hohe Spannung) abrauchen oder abfackeln kann!

Beim Steigungswiderstand R_Steig handelt es sich hingegen, wegen des Steigungsdreiecks sowie des Anwendens der Geradengleichung, zunächst um einen rechnerischen, fiktiven (= nicht real vorhandenen) Widerstand. Deshalb ist ∆I_Steig ≠ ∆I_Lampe, darf man ∆I_Steig nicht durch ∆I_Lampe = 260 mA ersetzen!

Dabei gilt es insbesondere zu beachten, dass das Steigungsdreieck durch den rechten Winkel sowie die beiden Messpunkte P₂ ( U₂, I₂ ) und P₁ ( U₁, I₁ ) geometrisch bzw. koordinatenmäßig definiert ist. Und bisher kennen wir aufgrund der Messung durch das Programm „mini-programm_04_11.py“ (siehe Webverzeichnis) nur die beiden Spannungen U_{Pin P2} = 2,37 V und U_{Pin P1} = 1,51 V (siehe oben).

Da aber die beiden Spannungen U_{Pin P2} = 2,37 V und U_{Pin P1} = 1,51 V parallel zur Glühlampe [18] gemessen wurden und wir die

Betriebsdaten der Glühlampe [18]

U_Nenn = 2,5 V

I_Nenn = 0,3 A

kennen, sodass sich der ohmsche Widerstand R_Lampe der Glühlampe [18] wie folgt berechnet,

R = U / I →

R_Lampe = U_Nenn / I_Nenn

= 2,5 V / 0,3 A = 8,33 Ω

lassen sich mit diesem auch die beiden Ströme I₂ und I₁ durch die Glühlampe [18] wie folgt berechnen:

I₂ = U_{Pin P2} / R_Lampe = 2,37 V / 8,33 Ω = 2,37 V / 8,33 V/A = 0,2845 A = 284,5 mA

I₁ = U_{Pin P1} / R_Lampe = 1,51 V / 8,33 Ω = 1,51 V / 8,33 V/A = 0,1813 A = 181,3 mA

Bildet man nun den Differenzenquotienten, so folgt:

R_Steig = ∆U / ∆I = ( U₂ - U₁ ) / ( I₂ - I₁ )

= ( U_{Pin P2} - U_{Pin P1} ) / ( I₂ - I₁ )

= ( 2,37 V - 1,51 V ) / ( 284,5 mA - 181,3 mA )

= 0,86 V / 103,2 mA = 0,00833 KΩ ≈ 8,33 Ω

Dadurch, dass wir zu beiden Spannungen U_{Pin P2} und U_{Pin P2} auch die Ströme I₂ und I₁ durch die Glühlampe [18] berechnet haben, verhält es sich jetzt so, dass der Steigungswiderstand R_Steig tatsächlich identisch ist mit dem Lastwiderstand R_Lampe der Glühlampe [18]!

Mittels der Geradengleichung ∆I_Steig = 1 / R_Steig * ∆U_Steig + I₀ lässt sich der Konstantstrom I₀ wie folgt berechnen:

∆I_Steig = 1 / R_Steig * ∆U_Steig + I₀ →

I₀ = ∆I_Steig – ( 1 / R_Steig * ∆U_Steig )

= 103,2 mA - ( 1 / 8,33 Ω * 0,86 V ) = 103,2 mA - ( 0,12005 A/V * 0,86 V )

= 103,2 mA - ( 120,05 mA * 0,86 ) = 103,2 mA - 103,24 mA ≈ 103,2 mA - 103,2 mA

= 0 mA →

∆I_Steig = 1 / R_Steig * ∆U_Steig

= 1 / 8,33 Ω * 0,86 V = 0,12005 A/V * 0,86 V = 0,103243 A

= 103,2 mA

Probe 1:

∆I_Steig = 1 / R_Steig * ∆U_Steig →

R_Steig = ∆U_Steig / ∆I_Steig = ∆U_Steig / ∆I_Steig

= 0,86 V / 103,2 mA = 0,00833 KΩ = 8,33 Ω

Probe 2:

I₂ = 1 / R_Steig * U_{Pin P2}

= 1 / 8,33 Ω * 2,37 V = 0,120048 A/V * 2,37 V = 0,2845 A = 284,5 mA

Wie bereits weiter oben ausgeführt, beträgt die mit einem herkömmlichen Multimeter gemessene Stromstärke ∆I_Lampe = 260 mA durch die Glühlampe [18].

Diesbezüglich gilt es die Frage zu klären, weshalb die gemessene Stromstärke I_Lampe = 260 mA geringer ist als die im Punkt P₂ ( U_{Pin P2}, I₂ ) berechnete Stromstärke mit I₂ = 284,5 mA:

U_Lampe = I_Lampe * R_Lampe = 260 mA * 8,33 Ω ≈ 2,17 V

Logisch! Wenn die Spannung bzw. der Spannungsabfall an der Glühlampe [18] mit U_Lampe = 2,17 V niedriger ist als die im Messpunkt P₂ ( U_{Pin P2}, I₂ ) digital mit dem Programm „mini-programm_04_11.py“ gemessene Spannung, dann ist auch die Stromstärke I_Lampe = 260 mA entsprechend geringer!

Tabula Rasa – alles zurück auf Anfang

Wenn man sich zulange mit ein und derselben Sache befasst, sich in diese verrannt hat, die aus irgendwelchen Gründen nicht so wie gedacht, wie gewünscht funktioniert, dann sollte man eine mehrtägige Pause machen. Nach der mehrtägigen Pause sollte man sich wieder auf das Altbewährte besinnen, die Dinge quasi bei Null, d.h. von vorn beginnen und streng systematisch vorgehen und sich Schritt für Schritt vom bereits bekannten Sachstand bzw. vom dem was mit Sicherheit funktioniert nach vorn bewegen.

Was wir bereits wissen und was auch einwandfrei funktioniert, ist, dass sich an den Ports „Pin P1“ (= große Rundbuchse „1“) und „Pin P2“ (= große Rundbuchse „2“) gegen Masse „┴“ am Port „Pin „-“ analoge (Gleich-) Spannungen messen, in digitale, d.h. binäre Bitwerte umwandeln und als dezimale Spannungswerte in Volt [V] umrechnen und in dem 9 x 9 großen LED-Diesplay als Laufschrift anzeigen lassen:

3,3 V → 1023 Bit

0,1 V → x Bit

x = 1023 Bit / 3,3 V * 0,1 V = 3,1 Bit ≈ 3 Bit

oder

1023 Bit → 3,3 V

1 Bit → x V

x = 3,3 V / 1023 Bit * 1 Bit = 0,00323 V = 3,23 mV ≈ 3 mV

Was wir ferner wissen, ist, dass das digitale Multimeter immer wieder und wieder andere Spannungswerte angezeigt hat als das von uns programmierte Digitalvoltmeter.

Dafür kann es verschiedene Gründe geben wie z.B. die unterschiedliche Messempfindlichkeit von z.B. 50 mV bei einem analogen Drehspulmessgerät oder die Auflösung von [ 0 … 1023 ] = 1024 Bit mit 3,23 mV / 1 Bit bei einem analogen/digitalen A/D-Wandler.

Da wir selbst keinen Eingriff in das Digitalvoltmeter vornehmen können, weil intern alles exakt aufeinander abgestimmt und miteinander fest verbaut ist, gleichen wir beide Geräte miteinander ab, indem wir unser programmiertes Digitalvoltmeter an das Multimeter (= Spannungsmessgerät) anpassen.

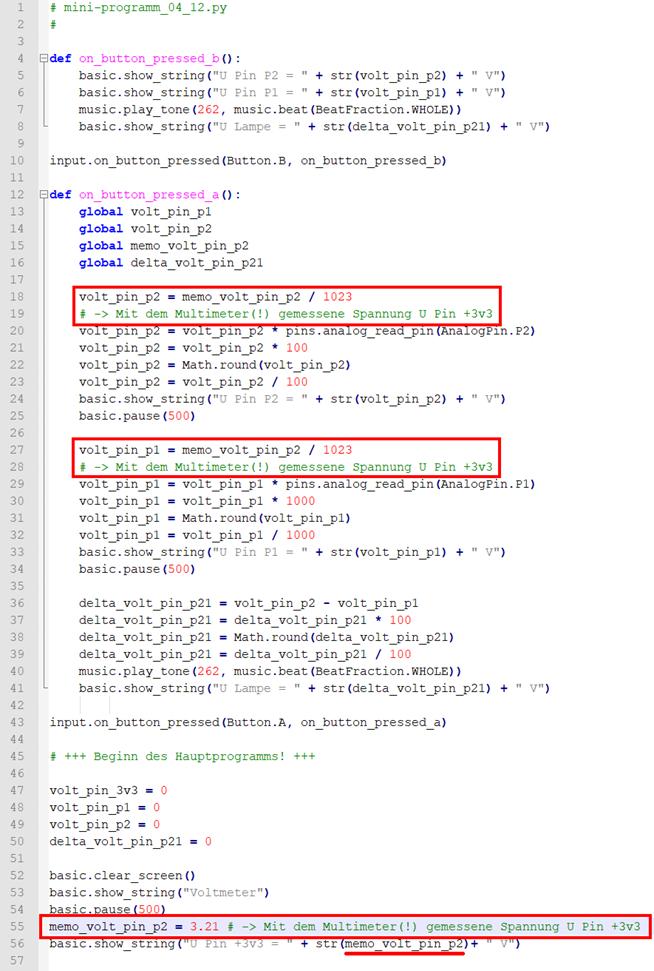
Zu diesem Zweck messen wir mit dem Multimeter die intern stabilisierte 3,3 Volt Betriebsspannung des „Calliope mini“-Rechners am Port „Pin 3v3“ (= großes Rundloch „+“) gegen Masse „┴“ am Port „Pin -“ (= großes Rundloch „-“) mit der Spannung U_3v3 = 3,22 V und übernehmen diesen Wert in das Programm „mini-programm_04_12.py“:

· Statement „memo_volt_pin_p2 = 3.22” (siehe Hauptprogramm)

Dabei gilt es zu beachten, dass wir die mit dem Multimeter gemessene 3,3 Volt Betriebsspannung auf die Spannung U_3v3 = 3,22 V angleichen und nicht auf einen Bitwert:

3,3 V → 1023 Bit

3,22 V → x Bit

x = 1023 Bit / 3,3 V * 3,22 V = 998,2 Bit ≈ 998 Bit → Im Vergleich zum Bitwert 1023 ist das schon ein Unterschied!

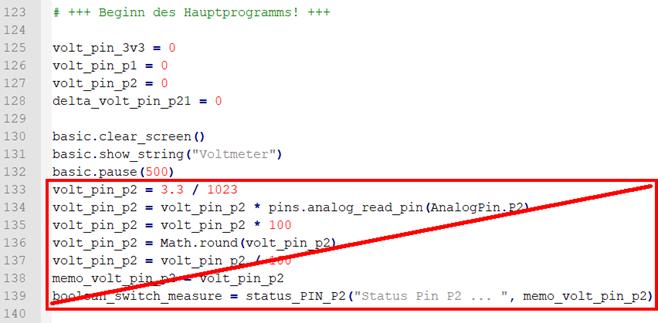
Da wir im Programm „mini-programm_04_12.py“ (siehe Webverzeichnis) nicht mehr die externe Spannung U_3v3 direkt am Port „Pin +3v3“ (= großes Rundloch „+“) referenzieren, d.h. einlesen und abspeichern, sondern vielmehr den Spannungswert U_3v3 = 3,22 V, den wir mit dem externen Multimeter zwischen dem Port „Pin 3v3“ (= großes Rundloch „+“) gegen Masse „┴“ am Port „Pin -“ (= großes Rundloch „-“) gemessen haben, entfällt der entsprechende Programmblock im Hauptprogramm komplett:

(Zum Vergrößern bitte auf das Bild klicken!)

Des Weiteren entfallen die Funktionen

· status_PIN_P2(get_Name: str, get_volt_pin_p2: number),

· measure_PIN_P1(get_Name: str, get_volt_pin_p1: number),

· measure_PIN_P2(get_Name: str, get_volt_pin_p2: number) und

· anzeigen_PIN_PX(get_Name: str, get_volt_pin_px: number),

sodass das Programm „mini-programm_04_12.py“ (siehe Webverzeichnis) ziemlich abgespeckt und damit gut überschaubar ist.

Übrig bleiben neben dem Hauptprogramm die bisherigen Funktionen

· on_button_pressed_a() und

· on_button_pressed_b()

Dabei dient die Funktion on_button_pressed_a() dazu, sozusagen auf Tastendruck auf den Taster „A“, die Spannungsmessungen an den Ports „U_{Pin P2}“ (= großes Rundloch „2“) sowie „U_{Pin P1}“ (= großes Rundloch „1“) auszulösen und abzuspeichern.

Mit der Funktion on_button_pressed_b() lassen sich dann die gespeicherten Spannungswerte U_{Pin P2} und U_{Pin P1} wieder abrufen und im 9 x 9 Matrix LED-Display als Laufschrift anzeigen:

(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_12.py)

(Zum Vergrößern bitte auf das Bild klicken!)

Wir starten das Digitalvoltmeter-Messprogramm „mini-programm_04_12.py“ (siehe Webverzeichnis) und warten bis die Laufschrift-Anzeige „Voltmeter" komplett durchgelaufen ist.

Als nächsten drücken wir den Taster [14], halten diesen gedrückt, drücken den Taster „A“ auf dem „Calliope mini“, um den Messvorgang an den beiden Ports „Pin P2“ und „Pin P1“ auszulösen.

Sobald die zuerst gemessene Spannung U_{Pin 2} = 2,04 V als Laufschrift im 9 x 9 Matrix LED-Display des „Calliope mini“ angezeigt wird, können wir den Taster [14] wieder loslassen.

Durch Drücken auf den Taster „B“ auf dem „Calliope mini“ lassen wir uns dann die gemessenen und gespeicherten Messwerte wie z.B. die als Zweites gemessene Spannung U_{Pin 1} = 0,003 V sowie die Lampenspannung U_Lampe = 2,04 V als Laufschrift im 9 x 9 Matrix LED-Display des „Calliope mini“ anzeigen.

Dabei gilt es zu beachten, dass die beiden Spannungen U_{Pin 2} = 2,04 V und Spannung U_{Pin 1} = 0,003 V stets gegen Masse „┴“ ( = großes Rundloch „-“) gemessen werden!

Demzufolge ist also bei der Spannung U_{Pin 2} = 2,04 V die am Messwiderstand R_Mess anliegende Spannung U_{Pin 1} = 0,003 V bereits enthalten!

Demzufolge berechnet sich der Spannungsabfall parallel zur Glühlampe [18] mit U_Lampe = 2,037 V ≈ 2,04 V aus der Differenz der an den beiden Ports „Pin P2“ und „Pin P1“ anliegenden Spannungen:

U_Lampe = U_{Pin P2} – U_{Pin P1} = 2,04 V – 0,003 V = 2,037 V ≈ 2,04 V

Dabei beträgt die mit dem Multimeter gegen Masse „┴“ gemessene Spannung U_{Pin 2} = 2,02 V (= - 1 %).

Diesbezüglich müssen wir aber noch der Frage nachgehen, was der Spannungswert U_{Pin P1} = 0,003 V der zweiten Spannungsmessung parallel zum Messwiderstand R_Mess praktisch bedeutet:

3,3 V → 1023 Bit

0,003 V → x Bit

x = 1023 Bit / 3,3 V * 0,003 V = 0,93 Bit ≈ 1 Bit →

Der Spannungswert U_{Pin P1} = 0,003 V der zweiten Spannungsmessung parallel zum Messwiderstand R_Mess bedeutet praktisch, dass wir mit der Messempfindlichkeit (= Bitauflösung) des A/D-Wandlers am Anschlag sind bzw. die Messempfindlichkeit des A/D-Wandlers nicht ausreicht, um den winzig kleinen Spannungsabfall von U_{Pin P1} = 0,003 V wirklich ausreichend genau messen zu können!

Wenn man die als Messwiderstand R_Mess zusätzlich eingefügte Schmelzsicherung (250 V, 2 A) mit dem Widerstandsmessgerät, volkstümlich auch „Ohmmeter“ genannt, des Multimeters misst, so kommt man auf den Wert R_Mess = 0,2 Ω, sodass sich der Spannungsabfall am Messwiderstand R_Mess bei einem Laststrom von I_Last = I_Lampe = I_Mess = 260 mA wie folgt berechnet:

I_Mess = U_Mess / R_Mess →

U_Mess = I_Mess * R_Mess

= 260 mA * 0,2 Ω = 52 mV = 0,052 V

Da die Schmelzsicherung (250 V, 2 A) als Messwiderstand R_Mess mit dem Wert R_Mess = 0,2 Ω doch extrem klein ist und der resultierende Spannungsabfall mit U_Mess = 0,052 V ebenfalls sehr klein ist, verwenden wir als nächstes ein größeren Messwiderstand mit R_Mess = 1,5 Ω, betätigen oben auf der Experimentierplatte den Taster [14], um den Stromkreis zu schließen, halten den Taster [14] einige Sekunden lang gedrückt und messen mit dem Amperemeter des Multimeters die Stromstärke I_Mess = 250 mA, sodass sich der Spannungsabfall am Messwiderstand R_Mess wie folgt berechnet:

U_Mess = I_Mess * R_Mess

= 250 mA * 1,5 Ω = 375 mV = 0,375 V

Des Weiteren messen wir die Versorgungsspannung U_Batt = 2,1 V bei Belastung, d.h. beim Einschalten der Glühlampe [18], die an den beiden Batterieanschlüssen, d.h. zwischen Plus- und Minuspol der Batteriehalterung [19] mit den beiden in Serie geschalteten 1,5 Volt Batterien vom Typ „Mignon AA“ anliegt und berechnen den Widerstand R_Last = R_Lampe der Glühlampe [18] wie folgt:

U_Lampe = U_Batt - U_Mess

= 2,1 V - 0,375 V = 1,725 V

R_Lampe = U_Lampe / I_Lampe = U_Lampe / I_Mess = 2,1 V / 250 mA = 2,1 V / 0,250 A = 8,4 Ω ≈ 8,33 Ω

Achtung:

Wenn man die Spannung an der Glühlampe gegen Masse „┴“ misst, dann handelt es sich bei dieser um eine Kettenspannung, sodass in dieser bereits der Spannungsabfall U_Mess am Messwiderstand R_Mess enthalten ist!

Wenn man den alleinigen Spannungsabfall U_Lampe am Lastwiderstand R_Last = Lampenwiderstand R_Lampe der Glühlampe [18] berechnen will, dann gilt: U_Lampe = U_Batt - U_Mess (siehe oben).

Und damit sind wir wieder bei der Messschaltung zur Messung des Spannungsabfall U_Lampe parallel zur Glühlampe [18] gegen Masse „┴“ und der Kettenspannung angelangt!

Denn auch bei den beiden Messspannungen an den Ports „Pin P2“ (= großes Rundloch „2“) und „Pin P1“ (= großes Rundloch „1“) gegen Masse „┴“ handelt es sich um eine Kettenspannung!

Der kleine Mikrorechner „Calliope mini“ aber ist so „intelligent“, dass er die Kettenspannung „erkennt“ und als Messwert für die gemessene Spannung U_{Pin P1} = 0,003 V = 3 mV ausgibt (siehe weiter oben)!

Nur unser „dummes“ Digitalvoltmeter-Messprogramm „mini-programm_04_12.py“ bekommt von der Kettenspannung am Port „Pin P1“ (= großes Rundloch „1“) gegen Masse „┴“ nichts mit:

· Statement volt_pin_p1 = volt_pin_p1 * pins.analog_read_pin(AnalogPin.P1)

Demzufolge kommt man gemäß dem derzeitigen Sachstand nicht umhin, entweder auf den Masseanschluss „┴“ des “Calliope mini”-Rechners oder den zweiten A/D-Wandler-Anschluss am Port „Pin P1“ (= großes Rundloch „1“) oder „Pin P2“ (= großes Rundloch „2“) verzichten zu müssen!

Jetzt wo wir wissen, dass sich die Spannung U_Lampe an der Glühlampe [18] und die Spannung U_Mess am Messwiderstand R_Mess wegen der verketteten Spannungen gegen Masse „┴“ an den beiden Ports „Pin P2“ und „Pin P1“ nicht gleichzeitig messen lassen, können wir einen „Trick“ anwenden und die Spannung U_Mess am Messwiderstand R_Mess berechnen, vorausgesetzt, dass die beiden Widerstände R_Lampe und R_Mess wertmäßig bereits bekannt sind (siehe oben):

Berechnung der Lampenspannung U_Lampe mittels Spannungsteilerformel

U_Lampe / U_Batt = R_Lampe / ( R_Lampe + R_Mess )

= 1 / [ 1 + ( R_Mess / R_Lampe ) ]

U_Lampe = 1 / [ 1 + ( R_Mess / R_Lampe ) ] * U_Batt

= U_Batt / [ 1 + ( R_Mess / R_Lampe ) ]

= 2,1 V / [ 1 + ( 1,5 Ω / 8,33 Ω ) ] = 2,1 V / [ 1 + 0,1800720288115246 ] = 2,1 V / [ 1,180072 ]

= 2,1 V / [ 1,180 ] = 1,7797 V ≈ 1,78 V

Berechnung der Messspannung U_Mess mittels Spannungsteilerformel

U_Mess / U_Lampe = R_Mess / R_Lampe →

U_Mess = R_Mess / R_Lampe * U_Lampe

= 1,5 Ω / 8,33 Ω * 1,78 V = 0,320 V

Berechnung des Lampenstroms I_Lampe

I_Lampe = U_Lampe / R_Lampe

= 1,78 V / 8,33 Ω = 1,78 V / 8,33 V/A = 0,2137 A = 213,7 mA

Da es im Experimentierkasten „elektronik 159“ keinen Messwiderstand R_Mess 1,5 Ω gibt, verwenden wir alternativ den kleinen Lautsprecher [20], dessen (Gleichstrom-) Spulenwiderstand, meistens 4 Ω oder 8 Ω, leider nicht bekannt ist und deshalb explizit berechnet werden muss.

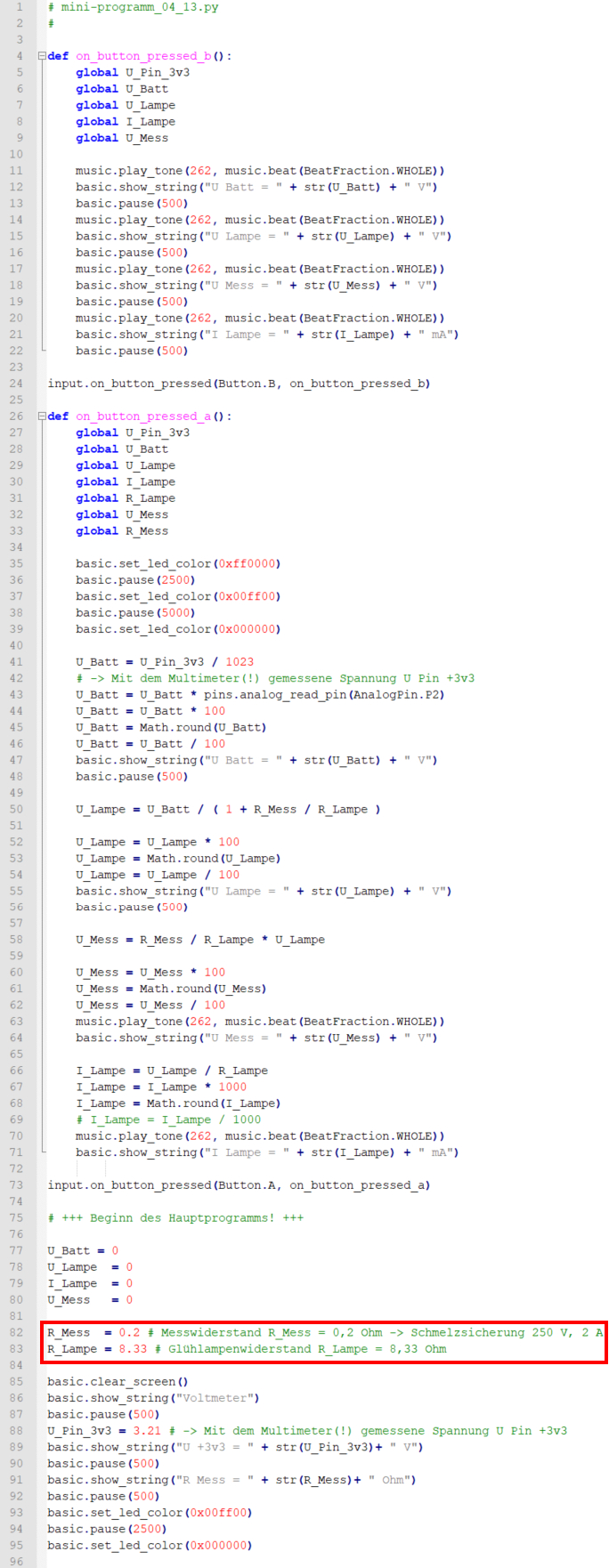
Zu diesem Zweck tauschen wir den bisherigen Messwiderstand R_Mess 1,5 Ω gegen den kleinen Lautsprecher [20] aus dem Experimentierkasten aus, starten das neue Digitalvoltmeter-Messprogramm „mini-programm_04_13.py“ (siehe Webverzeichnis) mit nur einer Messspannung am Port „Pin P2“ (= großes Rundloch „2“) und nehmen folgende Messwerte auf:

U_Batt = 2,17 V, U_Lampe = 1,84 V →

U_Mess = U_Batt - U_Lampe = 2,17 V - 1,84 V = 0,33 V þ

I_Lampe = 221 mA →

U_Lampe / U_Batt = R_Lampe / ( R_Lampe + R_Mess ) →

R_Lampe / ( R_Lampe + R_Mess ) = U_Lampe / U_Batt →

1 / ( 1 + R_Mess / R_Lampe ) = U_Lampe / U_Batt →

1 + R_Mess / R_Lampe = U_Batt / U_Lampe →

R_Mess / R_Lampe = ( U_Batt / U_Lampe ) - 1 →

R_Mess = [ ( U_Batt / U_Lampe ) - 1 ] * R_Lampe

= [ ( 2,17 V / 1,84 V ) - 1 ] * 8,33 Ω = [ ( 1,17935 ) - 1 ] * 8,33 Ω

= [ ( 0,17935 ) ] * 8,33 Ω = 1,4939855 Ω = 1,494 Ω ≈ 1,5 Ω

Das ist jetzt richtig interessant! Da staunt der Laie und der Fachmann wundert sich! Schließlich hat der kleine Lautsprecher [20] aus dem Experimentierkasten definitiv einen (Gleichstrom-) Spulenwiderstand von 4 Ω oder 8 Ω, sodass der größere (Mess-) Widerstand schon jetzt bewirkt, dass die Glühlampe [18] nicht mehr hell leuchtet, sondern nur noch schwach glimmt!

Was sich also durch das Verwenden des Lautsprechers [20] als größerer Messwiderstand R_Mess ändert, sind die äußeren elektrischen Umstände, während sich aber an dem (Berechnungs-) Programm selbst intern nichts geändert hat, sodass sich bei der Berechnung wieder der alte Messwiderstand R_Mess = 1,5 Ω einstellt!

Wenn wir also den Lautsprecher [20] als größeren Messwiderstand R_Mess einsetzen, dann müssen wir diesen gleichzeitig auch im (Berechnungs-) Programm ändern! Aber wir wissen ja noch nicht, welchen Widerstandswert der Lautsprechers [20] tatsächlich hat!

Erst wenn wir die Stromstärke I_Lampe durch die Glühlampe [18] mit einem externen Multimeter messen, lässt sich der neu in die Schaltung eingebrachte Messwiderstand R_Mess in Form des kleinen Lautsprechers [20] wie folgt berechnen:

I_Lampe = 137 mA →

U_Lampe = I_Lampe * R_Lampe

= 137 mA * 8,33 Ω = 0,137 A * 8,33 V/A = 1,14 V

R_Mess = U_Mess / I_Mess

= ( U_Batt - U_Lampe ) / I_Lampe

= ( 2,18 V - 1,14 V ) / 137 mA = ( 1,04 V ) / 0,137 A = 7,59 Ω ≈ 7,6 Ω

Da die Glühlampe [18] bei der Verwendung des kleinen Lautsprechers [20] als Messwiderstand R_Mess = 7,6 Ω nur noch ganz schwach glimmt, setzen wir wieder die Schmelzsicherung ( 250 V, 2 A ) als Messwiderstand R_Mess = 0,2 Ω ein! Und zwar auch im (Berechnungs-) Programm „mini-programm_04_13.py“ (siehe Webverzeichnis)

(Bild vergrößern: auf Bild klicken! Webverzeichnis mini-programm_04_13.py)

Werfen wir abschließend noch einen Blick auf die Schaltung mit nur einem Messeingang und zwar am Port „Pin P2“ (= großes Rundloch „2“) und der Schmelzsicherung ( 250 V, 2 A ) als Messwiderstand R_Mess = 0,2 Ω:

(Zum Vergrößern bitte auf das Bild klicken!)

Wenn man sich die obenstehende Schaltung mit dem Messeingang am Port „Pin P2“ (= großes Rundloch „2“) anschaut, dann könnte man auf den ersten Blick meinen, dass der Spannungsabfall der Glühlampe [18] gegen Masse „┴“ gemessen wird, obwohl bei der Spannungsmessung die Batteriespannung U_Batt als Versorgungsspannung gemessen wird, sodass gilt: U_Lampe = U_Batt - U_Mess

Wenn man sich dann noch die Berechnung des Spannungsabfalls der Glühlampe [18] im obenstehenden Quellkode mit dem

· Statement U_Lampe = U_Batt / ( 1 + R_Mess / R_Lampe )

anschaut, dann wird deutlich, dass es sich beim Spannungsabfall der Glühlampe [18] um keine Kettenspannung handelt in der der Spannungsabfall am Messwiderstand bereits enthalten ist, da wir die Lampenspannung mittels der Spannungsteilerformel berechnen:

U_Lampe / U_Batt = R_Lampe / ( R_Lampe + R_Mess ) → Zähler und Nenner durch R_Lampe dividieren!

U_Lampe / U_Batt = 1 / ( R_Lampe / R_Lampe + R_Mess / R_Lampe )

U_Lampe / U_Batt = 1 / [ ( R_Lampe + R_Mess ) / R_Lampe ]

U_Lampe / U_Batt = 1 / ( 1 + R_Mess / R_Lampe )

U_Lampe = U_Batt / ( 1 + R_Mess / R_Lampe )

U_Lampe = U_Batt / ( 1 + R_Mess / R_Lampe ) → Siehe Statement oben!

U_Lampe = U_Batt / ( R_Mess / R_Lampe + 1 )

Probe:

U_Lampe = U_Batt / ( R_Mess / R_Lampe + 1 )

= 2,11 V / ( 0,2 Ω / 8,33 Ω + 1 ) = 2,11 V / ( 0,02401 + 1 )

= 2,11 V / ( 1,02401 ) = 2,06 V þ

Achtung:

Auch wenn wir den Spannungsabfall U_Lampe an der Glühlampe [18] im (Computer-) Messprogramm mittels der Spannungsteilerformel ohne den direkten Einfluss der verketteten Spannung U_Mess am Messwiderstand R_Mess berechnen, heißt das nicht zwangsläufig, dass sich nicht doch klammheimlich eine verkettete Spannung ins System, d.h. in den „Calliope mini“-Rechner, einschleicht!

Diesbezüglich gibt es im vorliegenden Fall einen eklatanten Widerspruch! Und zwar wird die Lampenspannung U_Lampe = 2,06 V vom Computerprogramm richtig, d.h. verkettungsfrei, wie folgt berechnet:

U_Batt = U_Lampe + U_Mess = 2,06 V + 0,05 V = 2,11 V

Aber die Lampenspannung U_Lampe = 2,06 V selbst wird am Port „Pin P2“ gegen Masse „┴“ gemessen und enthält deshalb den Spannungsanteil U_Mess = 0,05 V des Messwiderstandes R_Mess! Demzufolge ist der tatsächliche Spannungsabfall parallel zur Glühlampe [18] um den Spannungsanteil des Messwiderstand R_Mess niedriger:

U_Lampe = U_Batt - U_Mess

= 2,11 V - 0,05 V = 2,06 V

Der Knackpunkt ist also der, dass wir im (Computer-) Messprogramm anders rechnen, nämlich wegen der Spannungsteilerformel ohne die verkettete Spannung U_Mess = 0,05 V des Messwiderstand R_Mess, während wir direkt in der Schaltung die Spannung an der Glühlampe [18] gegen Masse „┴“ am Port „Pin P2“ zusammen mit der verketteten Spannung U_Mess = 0,05 V des Messwiderstand R_Mess messen! -

Was also tun?

Wenn wir im Berechnungsprogramm mit der Spannungsteilerformel arbeiten, sodass verkettete Spannungen in der Berechnung nicht vorkommen, dann sollten wir das auch bei der Spannungsmessung am Port „Pin P2“ gegen Masse „┴“ tun und auf die Verwendung eines Messwiderstandes R_Mess mit verketteter Spannung verzichten!

Und, da das Steigungsdreieck wegen I₀ aus dem Koordinatenursprung heraus verschoben sein kann, setzt sich der Gesamtstrom durch die Glühlampe [18] wie folgt zusammen: ∆I_Lampe = ∆I_Steig + I₀, sodass folgt:

R_Steig = ∆U / ∆I = ( U_{Pin P2} - U_{Pin P1} ) / ∆I_Steig = ( U_{Pin P2} - U_{Pin P1} ) / ( ∆I_Lampe - I₀ ) →

R_Steig * ( ∆I_Lampe - I₀ ) = ( U_{Pin P2} - U_{Pin P1} )

( ∆I_Steig - I₀ ) = 1 / R_Steig * ( U_{Pin P2} - U_{Pin P1} ) →

- I₀ = 1 / R_Steig * ( U_{Pin P2} - U_{Pin P1} ) - ∆I_Steig →

I₀ = - 1 / R_Steig * ( U_{Pin P2} - U_{Pin P1} ) + ∆I_Steig →

I₀ = ∆I_Steig - 1 / R_Steig * ( U_{Pin P2} - U_{Pin P1} )

Für ∆U_Steig = ( U_{Pin P2} - U_{Pin P1} ) = 0 V folgt:

I₀ = ∆I_Steig

Für die Geradengleichung ∆I_Steig = 1 / R_Steig * ∆U_Steig + I₀ folgt:

∆I_Steig = 1 / R_Steig * ∆U_Steig + I₀ = 1 / R_Steig * ∆U_Steig + I_Steig = 2 * I_Steig = 260 mA →

I_Steig = ½ * ∆I_Lampe = ½ * 260 mA = 130 mA

Berechnet man den Lampenwiderstand R_Lampe anhand der Betriebsdaten, so stellt sich heraus, dass dieser größer ist als der oben berechnete Steigungswiderstand R_Steig:

Betriebsdaten der Glühlampe [18]

U_Nenn = 2,5 V

I_Nenn = 0,3 A

Für die Berechnung des ohmschen Widerstandes der Glühlampe [18] folgt dann:

R = U / I →

R_Glühlampe = U_Nenn / I_Nenn

= 2,5 V / 0,3 A = 8,33 Ω

Dafür, dass Lampenwiderstand R_Lampe größer ist als der oben berechnete Steigungswiderstand R_Steig, gibt es hauptsächlich nachfolgenden Grund:

· die Spannungsmessung parallel zum Lampenwiderstand R_Lampe erfolgt zwischen der beiden analogen Eingängen an den Ports „Pin P1“ und „Pin P2“ ( = große Rundlöcher „1“ und „2“) ohne Masseanschluss („┴“), sodass es sich um eine relative Spannungsmessung handelt.

R_Mess = 186,4 mΩ → siehe weiter oben im Abschnitt „Der analoge/digitale Batterie-Tester mit Bit-Anzeige“

U_Mess = I_Mess * R_Mess = 260 mA * 186,4 mΩ = 48 464 * 10^-3 mV = 48,46 mV

Wendet man die Spannungsteilerformel auf die beiden Widerstände R_Steig und R_Mess an, so folgt:

R_Steig / R_Mess = U_Steig / U_Mess →

R_Steig = ( U_Steig / U_Mess ) * R_Mess

= ( 0,86 V / 0,04846 V ) * 186,4 mΩ = 3 307,96 mΩ = 3,30796 Ω ≈ 3,308 Ω

Hier geht’s dann weiter!

R_Lampe = U_Lampe / I_Lampe →

U_Lampe = R_Lampe * I_Lampe

Schauen wir uns als nächstes die Geradengleichung ∆I_Lampe = 1 / R_Steig * ∆U_Steig + I₀ an:

I₀ = ∆I_Lampe - 1 / R_Steig * ∆U_Steig

= 260 mA - 1 / 3,308 Ω * 0,86 V = 0,260 A - 0,25998 A = 0

Berechnung des Lampenwiderstandes R_Lampe mittels der Geradengleichung:

I_Lampe = 1 / R_Lampe * U_Lampe + I₀ → mit I₀ = 0 →

U_Lampe = I_Lampe * R_Lampe

= 260 mA * 3,308 Ω = 0,260 A * 3,308 V/A = 0,86008 V ≈ 0,860 V

→ Steigungswiderstand R_Steig = ∆U_Lampe / ∆I_Lampe = 0,86 V / 260 mA = 0,0033077 KΩ = 3,308 Ω

= 1 / ( 0,86 V / 260 mA ) * U_Lampe + 260 mA

= 1 / ( 3,308 V/A ) * 0,86 V + 260 mA = 0,259976 A + 0,260 A

= 0,1696 A - 0,0396 A = 0,13 A = 130 mA þ

I_Motor = 1 / R_Steig * U_Motor + I₀

I_Motor - I₀ = ( 1 / R_Steig ) * U_Motor

( I_Motor - I₀ ) / U_Motor = 1 / R_Steig

U_Motor / ( I_Motor - I₀ ) = R_Steig þ

U_Motor = R_Steig * ( I_Motor - I₀ )

R_Motor = U_Motor / I_Motor

= R_Steig * ( I_Motor - I₀ ) / I_Motor

R_Motor = R_Steig * ( 1 - I₀ / I_Motor )

= 5,895 Ω * ( 1 + 39,6 mA / 130 mA ) = 5,895 Ω * 1,305 = 7,693 Ω þ

per Festlegung am Minuspol („-“) der Batteriehalterung, während gleichzeitig der „Calliope mini“ ebenfalls über seine eigenes Massepotential von null Volt am Port „Pin GND“ verfügt!

Der Grund dafür ist eben der, dass beide, d.h. der „Calliope mini“ und die Glühlampen-Schaltung über ihre eigene, potentialfreie Spannungsversorgung verfügen! -

Aber es gibt noch eine weitere, praktische Bedeutung des Ganzen! Nämlich den, dass sich die beiden Ports „Pin P1“ und „Pin P2“ auch als Ausgang, d.h. abgehende, einstellbare Spannungsquellen programmieren lassen!

Da aber nur ein sehr kleiner Ausgangsstrom I_{Pin 1,2, out} ≤ 15 mA zur Verfügung steht, lassen sich weder die Glühlampe [18] noch der Gleichstrommotor [24] an den beiden Ports „Pin P1“ und „Pin P2“ betreiben, da diese einen wesentlich größeren Laststrom I_Last ≥ 200 mA ziehen! Aber dies ist kein Grund zur Verzweiflung, da es im Elektronikbaukasten ja noch die rote Leuchtdiode [17] gibt, die sich über die beiden Ports „Pin P1“ und „Pin P2“ ansteuern lässt. Dazu aber später mehr (siehe Versuch 14: Der Gebrauch einer Leuchtdiode auf Seite 13 des Handbuchs).

Trotzdem stellt sich natürlich die Frage, wie man herausfinden kann, welche maximale Stromstärke die beiden Ports „Pin P1“ und „Pin P2“ zur Verfügung stellen können. Wenn man den Innenwiderstand R_Innen der beiden Ports „Pin P1“ und „Pin P2“ kennen würde, dann ließe sich die max. Stromstärke in Form des Kurzschlussstroms und der Leerlaufspannung an den Ports wie folgt berechnen:

I_Kurz = U_Leer / R_Innen →

R_Innen = U_Leer / I_Kurz = 3,3 V / 15 mA = 0,22 KΩ = 220 Ω

Da die Ausgangsspannung U_{Pin P1} bei einer Belastung von I _{Pin P1} = 15 mA aber bereits „in die Knie geht“, d.h. auf U_Pin P1 = 1,5 V absinkt, folgt für den Innenwiderstand R_Innen am Port „Pin P1“:

R_Innen = U_{Pin P1} / I_{Pin P1} = 1,5 V / 15 mA = 0,10 KΩ = 100 Ω

Was aber, wenn wir einen der beiden Ports „Pin P1“ und „Pin P2“ tatsächlich gegen Masse, d.h. Port „Pin GND“ kurzschließen und mit einem Amperemeter die Stromstärke des Kurzschlussstroms messen würden, löst sich dann der „Calliope mini“ in einer Rauchwolke auf?

Da der „Calliope mini“ hardwaremäßig mit dem „micro:bit“-Rechner der BBC London kompatibel ist, müssen wir selbst keinen Kurzschlusstest durchführen, da dies schon andere für uns getan haben:

>> Einige haben sich ja schon Sorgen gemacht, ob die vielen englischen Schüler nicht laufend Kurzschlüsse an den Ports verursachen und damit alles in Rauch aufgehen lassen. Aber bisher wurden noch keine schwarzen Wolken über den britischen Inseln gesichtet. Und das hat einen Grund, den ich ganz zufällig entdeckt habe: Die Entwickler des Micro:bit unter der Federführung der BBC haben nämlich einen Kurzschluss-Sicherung für die Ports eingebaut!

Das ganze habe ich ganz zufällig gefunden, als ich die Belastbarkeit und den On-Widerstand der Ports untersuchen wollte. Wenn ich den Ausgang hochohmig mit 10 kOhm belaste, ist noch alles normal. Es kommen ca. 3,3 V raus. Eine Belastung mit nur 100 Ohm ging manchmal gerade noch. Die Spannung am Port war dann schon auf ca. 1,5 V zusammengebrochen. Das bedeutet 15 mA, und mehr geht nicht! Wenn ich nämlich die Belastung noch etwas erhöhe, schaltet der Port ab! Beim ersten Mal dachte ich, Schreck lass nach, alles durchgebrannt. Aber nach einem Reset ist alles wieder wie neu. << (Quelle: Elektronik-Labor von Burkhard Kainka)

Interessant ist bei dem Belastungstest, dass der Autor von einer Versorgungsspannung U_{Rundloch +} = U_+3v3 = 3,3 V gegenüber der Masse („┴“) = Rundloch („-“) ausgeht, was aber nicht unbedingt immer so sein muss.

Wenn wir den „Calliope mini“ mittels des Micro-USB-Kabels über die USB 2.0-Buchse am Personal Computer (PC) mit Strom versorgen, dann haben wir es gemäß dem USB-Standard mit einer Nennsspannung U_{USB, Nenn} = 5 V zu tun, wobei die USB-Spannung am USB 2.0 (High-Powered-Port) auch niedrigere oder höhere Werte im Bereich [ 4,75 V, …, 5,25 V ] annehmen kann. Dabei darf die Stromstärke durch ein angeschlossenes Gerät bis zu I_{USB 2.0} ≤ 0,5 A betragen. Allerdings erst nach Freigabe durch den Host-Controller (engl. „host“, d.h. Gast gebender Controller). Bis dahin gilt eine maximale Stromstärke von „nur“ 0,1 A; das entspricht bei einer Spannung von 5 Volt gleich der Leistung P mit

P_{USB 2.0, min} = U * I = U_{USB, Nenn} * I_{USB, min} = 5 V * 0,1 A = 0,5 W

Der Stromverbrauch des „Calliope mini“ sollte übrigens ebenfalls nicht mehr als 100 mA betragen!

Wegen des zulässigen „USB 2.0“-Spannungsbereichs von [ 4,75 V, …, 5,25 V ] müssen wir also sehr wohl damit rechnen, dass die USB-Spannungsversorgung des „Calliope mini“ durchaus vom Mittelwert 5 V abweichen kann und damit dann auch die Versorgungsspannung von +3,3 V an der Rundbuchse („+“) bzw. („+3v3“). So beträgt z.B. die („+“) Spannung an der Rundbuchse („+“) gerade mal 3,12 V im Leerlauf!

Wenn man den „Calliope mini“ früher oder später auch mobil einsetzt, d.h. die mitgelieferte Batteriehalterung mit den zwei 1,5 Volt Batterien vom Typ „Micro AAA“ verwendet, dann werden die Batterien je nach Nutzung eher früher als später entladen sein, sodass die Batteriespannung dann auf weniger als 3 Volt absinkt mit der unangenehmen Folge, dass sich unsere Messungen mit dem digitalen Voltmeter verfälschen. Im ungünstigsten Fall auch noch ohne dass wir es merken!

Wenn wir z.B. die mit dem „Calliope mini“ mitgelieferte Batteriehalterung mit den zwei 1,5 Volt Batterien vom Typ „Micro AAA“ verwenden, dann beträgt die Batteriespannung U_Batterie = 3,03 V bei fabrikneuen Batterien! Ersetzen wir diese z.B. gegen wieder aufladbare 1,5 V NiMH-Batterien mit einer Batteriespannung U_Batterie = 2,48 V (= - -18,15 % ), dann verfälscht sich die Spannungsmessung mit dem „Python“-Programm „mini-programm_04_05.py“ parallel zur Glühlampe [18] auf nur noch 0,805 V (1,315 V

2,48 V Spannung des Batteriepacks (= 100 % / 3,03 V * 2,48 V = -18,15 % !!!)

1,391 V Messung mit USB-Spannungsversorgung

0,805 V Messung mit dem Batteriepack (= 100 % / 1,391 V * 0,805 V = -42,128 % !!!)

Wir führen wieder eine Spannungsmessung aus und messen den Spannungsabfall U_Lampe in Form der anliegenden Eingangsspannung an den beiden Ports „Pin P1“ und „Pin P2“ des „Calliope mini“, wobei es aus der Sicht des „Calliope mini“ zu beachten gilt, dass der Port „Pin P1“ nicht auf Masse des Ports „Pin GND“ liegt:

U_Lampe = 3,0 V / 1024 Bit * [ 1024 Bit - ( Bitwert Pin P2 - Bitwert Pin P1 ) ]

= 3,0 V / 1024 Bit * [ 1024 Bit - Bitwert Pin P2 + Bitwert Pin P1 ]

= 3,0 V / 1024 Bit * [ 1024 Bit - 719 Bit + 404 Bit ] = 3,0 V / 1024 Bit * [709 Bit ]

= 3,0 V / 1024 * 709 = 2,077 V

→ Messfehler gegenüber Multimeter-Anzeige von 2,07 V ≈ +0,338 %

[ electronic 159 ] [ Seitenanfang ] [ zurück ]