[ Home ] [ zurück ] [ Seitenende ]

Die smarte LED im Internet of Electronics

Wie aber steuert und regelt man eine LED?

Eine LED lässt sich nicht nur programmiert steuern und regeln, sondern auch programmiert ein- und ausschalten. Bevor man sich daran macht und eine LED steuert und regelt, sollte man den Unterschied zwischen einer Steuerung und einer Regelung kennen. Das „60 Grad Buntwäsche“-Programm einer Waschmaschine wurde z.B. früher, d.h. vor der Jahrtausendwende, mittels eines elektrisch-mechanischen Schaltwerks in Form mehrerer Steuerscheiben nebst Kontakten gesteuert, während die Temperatur von 60 Grad der Buntwäsche mittels eines Temperaturfühlers und Thermostaten geregelt wurde.

Da sich eine LED mittels eines elektrischen bzw. elektronischen Schalters ein- und ausschalten lässt und sich die Einschaltdauer mittels eines Tasters oder einer entsprechenden Elektronik praktisch beliebig vornehmen und kombinieren lässt, lässt sich über das variable (Tast-) Verhältnis von Einschalt- und Ausschaltdauer und dessen (Tast-) Frequenz auch die Helligkeit der LED steuern bzw. „pulsen“.

Damit aber die LED beim langsamen Pulsen, d.h. bei einer gleichzeitig kurzen Einschaltdauer und langen Ausschaltdauer nicht flackert, muss die Pulsfrequenz stets über 50 Hz liegen, sodass das menschliche Auge wegen seiner Trägheit das kurze Ein- und lange Ausschalten nebst Frequenz nicht als störend empfindet. Zu diesem Zweck bedient man sich der sogenannten „Pulsweitenmodulation (PWM)“ bei der sich sowohl die Pulsfrequenz als auch das Tastverhältnis von Ein- zu Ausschaltdauer einstellen lassen. Der Vorteil des kleinen „micro:bit“-Rechners besteht nun darin, dass dieser nicht nur über eine integrierte PWM verfügt, sondern dass sich diese auch programmieren lässt.

Wie lässt sich eine LED von außen steuern und regeln

ohne die Schaltung der LED aufzutrennen? Wie lässt sich eine LED von außen ein- oder ausschalten ohne einen Ein-/Ausschalter zu betätigen? Kann man mit Strom eine bereits eingeschaltete und leuchtende LED ausschalten? Ja! Dazu muss man wissen, dass eine LED ein Halbleiter ist und im Prinzip wie eine (Halbleiter-) Diode arbeitet, die den Strom durch den PN-Übergang in Durchlassrichtung hindurchfließen lässt oder in umgekehrter Richtung, d.h. beim Betrieb in Sperrrichtung, sperrt. Bildlich gesprochen arbeitet eine Halbleiterdiode wie die LED quasi als ein elektrisches Ventil.

Da eine LED nur dann leuchtet, wenn sie in Durchlassrichtung betrieben wird und sich dabei elektrisch auch noch sehr niederohmig verhält, lässt sich der Durchlasswiderstand der roten LED anhand des linearen Bereichs der Kennlinie gemäß des Ohmschen Gesetzes berechnen:

R = U / I → konstant!

= ∆U / ∆I = U₂ - U₁ / I₂ – I₁ → konstant!

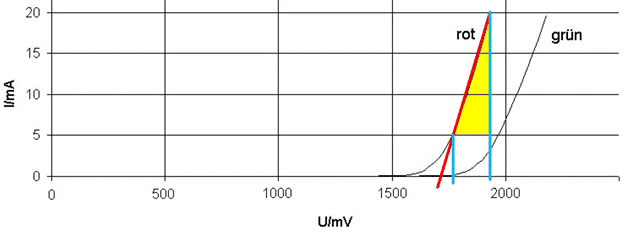
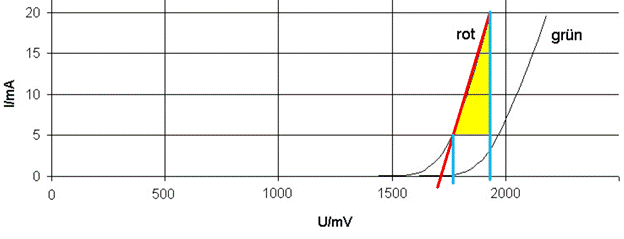
Dabei verhält es sich so, dass sich der Widerstand R nicht nur als Quotient U / I von Spannung U und Strom I, sondern auch als Differenzquotient ∆U / ∆I mit ∆U = U₂ - U₁ mit U₂ > U₁ und ∆I = I₂ - I₁ mit I₂ > I₁ berechnen lässt.

Für den Arbeitspunkt AP2 lassen sich aus dem linearen Bereich der Kennlinie das Wertepaar AP2 = ( U₂, I₂ ) = ( 1900 mV, 20 mA ) und AP1 = ( U₁, I₁ ) = ( 1800 mV, 5 mA ) ablesen:

(Zum Vergrößern bitte auf das Bild klicken!)

Der abschnittsweise, lineare Widerstand r_LED der roten LED berechnet sich dann wie folgt:

r_LED = ∆U / ∆I = U₂ - U₁ / I₂ - I₁

= 1900 mV - 1800 mV / 20 mA - 5 mA = 100 mV / 15 mA = 6,667 Ω

Gegenprobe:

R = U / I → I = U / R →

∆i_LED = ∆u_LED / r_LED

= 1900 mV - 1800 mV / 6,667 Ω = 100 mV / 6,667 Ω = 14,99 mA ≈ 15 mA

Wie aber berechnet man den ohmschen Widerstand der roten LED im Arbeitspunkt AP2 = ( U₂, I₂ ) = ( 1900 mV, 20 mA )?

r_{LED, AP2} = U₂ / I₂ = 1900 mV / 20 mA = 95 Ω

Für den Arbeitspunkt AP1 = ( U₁, I₁ ) = ( 1800 mV, 5 mA ) folgt:

r_{LED, AP1} = U₁ / I₁ = 1800 mV / 5 mA = 360 Ω

Diesbezüglich stellen die beiden unterschiedlichen Widerstandwerte r_{LED, AP2} und r_{LED, AP1} keinen Widerspruch!

Schließlich besagt das Ohmsche Gesetz, dass bei

· einem kleinen Widerstand ein entsprechend großer und bei

· einem großen Widerstand ein entsprechend kleiner Strom

fließt!

Nun stellt sich die Frage, wozu der differentielle Widerstand r_LED = 6,667 Ω gut sein soll.

Von der Widerstandsgeraden zur Geradengleichung

Den im obenstehenden Bild zu sehenden linearen Bereich der roten LED, der dem gelben Steigungsdreieck zuzuordnen ist, nennt man Widerstandsgerade, die sich wegen des Ohmschen Gesetzes aus der Geradengleichung ableitet:

y = ax + b a = Steigung der Geraden

b = Parallelverschiebung der Geraden in y-Richtung,

d.h. im Koordinatenkreuz nach oben oder unten

Entsprechend der ersten Ableitung y’ folgt dann für die Steigung a:

y’ = ax → a = y’ / x = ( dy / dx ) / x → dy = a x dx

Wendet man die Mathematik auf die Elektrotechnik und das Ohmsche Gesetz an, so folgt:

y’ = dy / dx = ∆y / ∆x → ∆I / ∆U = 1 / ∆U / ∆I = 1 / R = G → elektrischer Leitwert G

y = ax + b → I = 1 / R * U + I₀ → I₀ = Konstantstrom (Parallelverschiebung)

Geradengleichung

Da wir von der roten LED die Kennlinie, das Steigungsdreieck und die zwei Arbeitspunkte AP1 und AP2 kennen, lassen sich deren Werte in die Geradengleichung einsetzen und der Konstantstrom I₀ (= Parallelverschiebung) wie folgt berechnen:

i_LED = 1 / r_{LED, AP} * u_{LED, AP} + I₀ → … mit Parallelverschiebung I₀ ≠ 0

Zwei-Punkte-Form

y – y₁ / x – x₁ = y₂ – y₁ / x₂ – x₁

y = ( y₂ – y₁ ) / ( x₂ – x₁ ) * ( x – x₁ ) + y₁

i_LED = ( i_{LED, AP2} – i_{LED, AP1} ) / ( u_{LED, AP2} – u_{LED, AP1} ) * ( u_LED – u_{LED, AP1} ) + i_{LED, AP1}

= ( 20 mA – 5 mA ) / ( 1900 mV – 1800 mV ) * ( u_LED – 1800 mV ) + 5 mA

= (15 mA ) / ( 100 mV ) * ( u_LED – 1800 mV ) + 5 mA

= 0,15 A/V * ( u_LED – 1800 mV ) + 5 mA

Für den AP1 mit u_LED = u_{LED, AP1} = 1800 mV folgt:

= 0,15 A/V * ( 1,8 V – 1,8 V ) + 5 mA = 5 mA

Für den AP2 mit u_LED = u_{LED, AP2} = 1900 mV folgt:

= 0,15 A/V * ( 1,9 V – 1,8 V ) + 5 mA = 0,15 A * ( 0,1 ) + 5 mA

= 0,15 A/V * ( 1,9 V – 1,8 V ) + 5 mA = 0,015 A + 5 mA = 20 mA

Zwei-Punkte-Form

u.a. auch zur Ermittlung des Konstantstroms I₀ (= Parallelverschiebung der W.geraden)

i_LED = ∆i_{LED, AP} / ∆u_{LED, AP} * ( u_LED – u_{LED, AP1} ) + i_{LED, AP1}

= 1 / r_{LED, AP} * ( u_LED – u_{LED, AP1} ) + i_{LED, AP1}

Mit u_LED = 0 (= Schnittpunkt mit der Stromachse) wird i_LED zum Konstantstrom I₀:

I₀ = – 1 / r_{LED, AP} * u_{LED, AP1} + i_{LED, AP1}

Die obenstehende Zwei-Punkte-Form lässt sich verkürzt auch wie folgt schreiben:

i_LED = ∆i_{LED, AP} / ∆u_{LED, AP} * ( u_LED – u_{LED, AP1} ) + i_{LED, AP1}

= 1 / r_{LED, AP} * ( u_LED – u_{LED, AP1} ) + i_{LED, AP1}

= 1 / r_{LED, AP} * u_LED – ( 1 / r_{LED, AP} * u_{LED, AP1} ) + i_{LED, AP1}

Nebenrechnung für den Term 1 / r_{LED, AP} (= Steigung der Geradengleichung)

1 / r_{LED, AP} = ∆i_{LED, AP} / ∆u_{LED, AP} = 15 mA / 100 mV = 0,15 A/V = 0,15 1/Ω = 0,15 S

→ r_{LED, AP} = ∆u_{LED, AP} / ∆i_{LED, AP} = 100 mV / 15 mA = 6,667 Ω

i_LED = 1 / r_{LED, AP} * u_LED – ( 1 / r_{LED, AP} * u_{LED, AP1} ) + i_{LED, AP1}

Einsetzen liefert:

= 0,15 S * u_LED – (0,15 A/V * 1800 mV ) + 5 mA

= 0,15 1/Ω * u_LED – 270 mA + 5 mA

= 1 / 6,667 Ω * u_LED + ( – 265 mA )

Um den Konstantstrom I₀ (= Parallelverschiebung der Widerstandsgeraden) berechnen zu können, muss man die Geradengleichung am Schnittpunkt S = ( u_LED, i_LED ) = ( u_LED = 0, i_LED = I₀ ) = ( 0, I₀ ) mit der Stromachse betrachten:

i_LED = I₀ = 1 / 6,667 Ω * 0 V + ( – 265 mA )

I₀ = – 265 mA → Konstantstrom (= Parallelverschiebung der Widerstandsgeraden)

Allgemein folgt für die Geradengleichung der abschnittsweise linearen Widerstandsgeraden der roten LED:

i_LED = 1 / r_{LED, AP1,2} * u_LED + I₀

→ r_{LED, AP1,2} = 6,667 Ω (= differentieller Widerstand)

→ I₀ = - 265 mA (= Parallelverschiebung der Geraden)

Die Geradengleichung zur Berechnung des Durchlassstromes i_LED durch die rote LED lässt sich auch nach der Durchlassspannung u_LED wie folgt umstellen:

i_LED = 1 / r_{LED, AP1,2} * u_LED + I₀ →

i_LED - I₀ = 1 / r_{LED, AP1,2} * u_LED

Wenn von der Schaltung mit der rotten LED nur der bereits vorgegebene Durchlassstrom i_LED bekannt ist, dann lässt sich die dazugehörige Durchlassspannung u_LED mittels der umgestellten Geradengleichung wie folgt berechnen:

u_LED = r_{LED, AP1,2} * ( i_LED - I₀ )

→ r_{LED, AP1,2} = 6,667 Ω (= differentieller Widerstand)

→ I₀ = - 265 mA (= Parallelverschiebung der Geraden)

Beispiele

1.) Der Durchlassstrom i_LED durch die rote LED soll i_LED = 15 mA betragen. Berechne die dazu erforderliche Durchlassspannung u_LED!

u_LED = r_{LED, AP1,2} * ( i_LED - I₀ )

= 6,667 Ω * ( 15 mA – ( - 265 mA ) )

= 6,667 Ω * ( 15 mA + 265 mA )

= 100,005 mV + 1766,755 mV = 1866,76 mV ≈ 1867 mV þ

2.) Der Durchlassstrom i_LED durch die rote LED soll i_LED = 20 mA betragen. Berechne die dazu erforderliche Durchlassspannung u_LED!

u_LED = r_{LED, AP1,2} * ( i_LED - I₀ )

= 6,667 Ω * ( 20 mA – ( - 265 mA ) )

= 6,667 Ω * ( 20 mA + 265 mA )

= 133,34 mV + 1766,755 mV = 1900,095 mV ≈ 1900 mV þ

3.) Der Durchlassstrom i_LED durch die rote LED soll i_LED = 5 mA betragen. Berechne die dazu erforderliche Durchlassspannung u_LED!

u_LED = r_{LED, AP1,2} * ( i_LED - I₀ )

= 6,667 Ω * ( 5 mA – ( - 265 mA ) )

= 6,667 Ω * ( 5 mA + 265 mA )

= 33,335 mV + 1766,755 mV = 1800,09 mV ≈ 1800 mV þ

Punktsteigungsform

Wenn man anstelle zweier Wertepaare für die Arbeitspunkte AP1 = ( U₁, I₁ ) = ( 1800 mV, 5 mA ) und AP2 = ( U₂, I₂ ) = ( 1900 mV, 20 mA ) nur ein Wertepaar für den Arbeitspunkt AP1 oder AP2 dafür aber noch die Steigung a der Widerstandsgeraden y = a x + b kennt, dann lässt sich die auch die sogenannte „Punktsteigungsform“ anwenden, um darüber zur Geradengleichung zu gelangen:

y – y₁ = a ( x – x₁ )

y = a ( x – x₁ ) + y₁ = → mit Steigung a = ∆y / ∆x = ( y₂ – y₁ ) / ( x₂ – x₁ )

i_LED = 1 / r_{LED, AP} * ( u_LED – u_{LED, AP1} ) + i_{LED, AP1}

→ Punktsteigungsform

1 / r_{LED, AP} = ( i_LED - i_{LED, AP1} ) / ( u_LED – u_{LED, AP1} )

→ Steigung a der Geradengleichung

Die Umkehrung der Steigung 1 / r_{LED, AP} führt zum differentiellen Widerstand r_{LED, AP}:

r_{LED, AP} = ( u_LED - u_{LED, AP1} ) / ( i_LED – i_{LED, AP1} )

→ differentieller Widerstand

Setzt man z.B. der Werte der beiden Arbeitspunkte AP1 und AP2 ein, so folgt:

r_{LED, AP} = ( u_LED – u_{LED, AP1} ) / ( i_LED - i_{LED, AP1} )

= ( u_{LED, AP2} – u_{LED, AP1} ) / ( i_{LED, AP2} - i_{LED, AP1} )

= ( 1900 mV – 1800 mV ) / ( 20 mA – 5 mA )

= 100 mV / 15 mA = 6,667 Ω (siehe weiter oben!)

Einsetzen von r_{LED, AP} = 6,667 Ω in die Punktsteigungsform führt zu:

i_LED = 1 / r_{LED, AP} * ( u_LED – u_{LED, AP1} ) + i_{LED, AP1}

= 1 / r_{LED, AP} * ( u_{LED, AP2} – u_{LED, AP1} ) + i_{LED, AP1}

= 1 / 6,667 Ω * (1900 mV – 1800 mV ) + 5 mA

= 0,14999 A/V * 100 mV + 5 mA = 14,999 mA + 5 mA ≈ 20 mA (siehe oben!)

Wie man unschwer sieht, lässt sich aus der Punktsteigungsform

i_LED = 1 / r_{LED, AP} * ( u_LED – u_{LED, AP1} ) + i_{LED, AP1}

oder dem differentiellen Widerstand r_{LED, AP}

r_{LED, AP} = ( u_LED - u_{LED, AP1} ) / ( i_LED – i_{LED, AP1} )

die Parallelverschiebung I₀ der Widerstandsgeraden nicht direkt bestimmen.

Da aber die Punktsteigungsform auch für den Schnittpunkt S = ( u_LED, i_LED ) = ( 0, I₀ ) der Widerstandsgeraden mit der y-Achse gilt, muss man für diese nur den Wert u_LED = 0 V und die Werte des Arbeitspunktes AP1 einsetzen, um den Konstantstrom I₀ wie folgt berechnen zu können:

i_LED = 1 / r_{LED, AP} * ( u_LED – u_{LED, AP1} ) + i_{LED, AP1}

Mit u_LED = 0 V wird i_LED zum Konstantstrom I₀ (= Parallelverschiebung):

I₀ = i_{LED, AP1} - 1 / r_{LED, AP} * u_{LED, AP1}

→ Konstantstrom I₀ (= Parallelverschiebung)

I₀ = i_{LED, AP1} - 1 / r_{LED, AP} * u_{LED, AP1}

= 5 mA - 1 / 6,667 Ω * 1800 mV

= 5 mA - 0,14999 A/V * 1800 mV

= 5 mA - 269,982 mA= -264,982 mA ≈ - 265 mA (siehe weiter oben!)

So lange sich die eingesetzten Wertepaare (u_LED, i_LED) allesamt auf der Geradengleichung bzw. der Widerstandsgeraden befinden, lässt sich die Formel zur Berechnung des Konstantstroms I₀ auch auf andere Werte, wie z.B. dem Arbeitspunkt AP2 anwenden:

I₀ = i_{LED, AP2} - 1 / r_{LED, AP} * u_{LED, AP2}

= 20 mA - 1 / 6,667 Ω * 1900 mV

= 20 mA - 0,14999 A/V * 1900 mV

= 20 mA - 284,986 mA= -264,986 mA ≈ - 265 mA (siehe weiter oben!)

Selbstverständlich lässt sich die Geradengleichung bzw. die Widerstandsgerade mit

i_LED = 1 / r_{LED, AP1,2} * u_LED + I₀

u_LED = r_{LED, AP1,2} * ( i_LED - I₀ )

auch auf das Steigungsdreieck und den differentiellen Widerstand r_{LED, diff} anwenden!

Die Widerstandsgerade mit dem differentiellen Widerstand r_{LED, diff} liefert eine Aussage darüber, welcher Strom sich als Folge einer kleinen Spannungsänderung von [ 0 … 100 ] mV als Spannungsabfall ∆u_LED an der roten LED einstellt!

Da die Widerstandsgerade, d.h. der lineare Teil der Kennlinie (= gelbes Steigungsdreieck) im Arbeitspunkt AP1 beginnt, können wir beide wie folgt zusammen bringen und somit den resultierenden Ausgangsstrom i_{LED, res} als Funktion der Spannungsänderung ∆u_LED wie folgt berechnen:

i_LED = 1 / r_{LED, AP1,2} * u_LED + I₀ Geradengleichung mit Parallelverschiebung!

i_LED = f(u_LED) → di_LED / du_LED = ( 1 / r_{LED, AP1,2} * u_LED + I₀ )’ →

di_LED = 1 / r_{LED, AP1,2} * du_LED erste Ableitung der Funktion: I₀ entfällt!

Für die Stromänderung als Funktion der Spannungsänderung am Steigungsdreieck folgt:

∆i_LED = f (∆u_LED) = 1 / r_{LED, AP1,2} * ∆u_LED

Für die Spannungsänderung als Funktion der Stromänderung am Steigungsdreieck folgt:

∆u_LED = f (∆i_LED) = r_{LED, AP1,2} * ∆i_LED

Für die Stromänderung als Funktion der Spannungsänderung am Steigungsdreieck folgt dann:

∆i_LED = 1 / r_{LED, AP1,2} * ∆u_LED

= 1 / 6,667 Ω * 100 mV

= 14,999 mA ≈ 15 mA

Für die Spannungsänderung als Funktion der Stromänderung am Steigungsdreieck folgt dann:

∆u_LED = r_{LED, AP1,2} * ∆i_LED

= 6,667 Ω * 15 mA

= 100,005 mA ≈ 100 mV

Wenn man den Mittelwert der Widerstandsgeraden mit ∆u_LED = 50 mV als Arbeitspunkt wählt, dann stellt sich nachfolgender Durchlassstrom ∆i_LED durch die rote LED ein:

∆i_LED = 1 / r_{LED, AP1,2} * ∆u_LED

= 1 / 6,667 Ω * 50 mV = 7,4996 mA ≈ 7,5 mA

Umgekehrt lässt sich auch die erforderliche Spannung u_LED an der roten LED errechnen, die man einstellen muss, damit sich der geforderte Durchlassstrom i_LED = 7,5 mA einstellt:

∆u_LED = r_{LED, AP1,2} * ∆i_LED

= 6,667 Ω * 7,5 mA

= 50,0025 mA ≈ 50 mV

Anhand der obenstehenden Berechnungen bestätigt sich, dass sich die Geradengleichung bzw. die Widerstandsgerade im Bereich von u_LED = [ 1800 mV … 1900 mV ] und i_LED = [ 5 mA … 20 mA ] tatsächlich linear verhält (siehe Bild unten).

Weshalb Leuchtdioden (LEDs) nur mit Vorwiderstand betrieben werden dürfen

Würde man die rote LED ohne Vorwiderstand direkt an der Versorgungsspannung von U_Batt = 9 V betreiben, so würde diese von einem Durchlassstrom (= Kurzschlussstrom) I_max = U_Batt / r_LED = 9 V / 6,667 Ω = 1,35 A durchflossen und dabei auch noch die (Wärme-) Leistung von P_Verlust = U_Batt / I_max = 9 V / 1,35 A = 12,15 W umsetzen!

In Wirklichkeit darf aber die elektrische (Licht- und Leucht-) Leistung der roten LED nur P_LED = U_Durchfluss * I_Durchlass ≈ 2 V * 15 mA = 30 mW (Milliwatt!) betragen, damit diese nicht gleich beim Einschalten durchbrennt! Demzufolge darf die rote LED stets nur mit einem entsprechend großen Vorwiderstand R_Vor = (U_Batt - U_Durchfluss) / I_Durchlass = (9 V – 2 V) / 15 mA = 7 V / 15 mA = 0,47 KΩ = 470 Ω betrieben werden!

Was aber macht eine smarte, quasi „intelligente“ LED, wenn sie vom zu geringen Vorwiderstand eine zu hohe Spannung zugeteilt bekommt, sodass die LED eventuell Schaden nimmt?

Ganz einfach, sie meldet sich beim Netzteil mit der Spannungsversorgung und teilt diesem mit, dass die Betriebsspannung beim eingeschalteten Zustand der LED zu hoch ist! Und, wie macht sie das? Schließlich ist die LED nicht wirklich intelligent und der Vorwiderstand ist es auch nicht! Wie aber lassen sich diese quasi intelligent machen?

Ganz einfach durch entsprechende Werkzeuge wie z.B. einem hinzu geschalteten Sensor und einem „Taschenrechner“. Dabei überprüft der Spannungssensor permanent den Spannungsabfall ∆u_LED der LED gegen Masse und meldet diesen an den „Taschenrechner“. Der „Taschenrechner“ wiederum berechnet permanent den optimalen Widerstandswert des Vorwiderstandes R_Vor sowie die maximale Versorgungsspannung U_Batt der Schaltung. Schließlich ist die Durchlassspannung u_Durchlass der LED eine Funktion der Versorgungsspannung U_Batt und des Spannungsabfalls ∆U_Vor am Vorwiderstand R_Vor mit u_LED = f(U_Batt, U_Vor).

Kleine, quasi „intelligente“ Helferlein

In diesem Zusammenhang stellt sich nun die Frage nach den kleinen, quasi „intelligenten“ Helferlein, die erfolgreich verhindern, dass die rote LED vorzeitig den Hitzetod stirbt für den Fall, dass sie wider Erwarten längere Zeit mit einer zu hohen Durchlassspannung u_Durchlass > 2 V betrieben wird, weil entweder die Versorgungsspannung U_Batt und/oder der Spannungsabfalls ∆U_Vor am Vorwiderstand R_Vor zu groß sind („YouTube“-Video zur Berechnung des Vorwiderstandes).

Als Sensor für das Überwachen der an der roten LED anliegenden Durchlassspannung u_Durchlass im Bereich [ 1,764 V … 1,925 V ] kommt der kleine „micro:bit“-Rechner zum Einsatz. Und zwar einer der analogen Eingänge wie z.B. der am Port mit dem Pin „P0“, der die anliegende Durchlassspannung misst und dabei in Echtzeit mittels eines kleinen Computerprogramms berechnet und ggf. korrigiert. Dabei erfolgt die Korrektur der evtl. zu hohen Durchlassspannung an der roten LED mittels eines erzwungenen Spannungsabfalls ∆u_LED wider Erwarten nicht durch das Parallelschalten einer bezüglich der Abgabespannung programmierbaren Spannungsquelle am analogen Ausgang des „micro:bit“-Rechners, sondern vielmehr durch das Parallelschalten einer programmierbaren analogen (Konstant-) Stromquelle des „micro:bit“-Rechners, die dafür sorgt, dass sich der Spannungsabfall ∆u_LED parallel zur roten LED verringert:

(Zum Vergrößern bitte auf das Bild klicken!)

Tatsächlich sorgt aber die am Mittelpunkt M des Spannungsteilers hinzugeschaltete regel- und programmierbare (Konstant-) Stromquelle dafür, dass sich der Arbeitspunkt der roten LED in der Mitte der Arbeitsgeraden (siehe gelbes Steigungsdreieck) entsprechend verschiebt.

Da der Durchlasswiderstand der roten LED mit r_LED = 6,667 Ω sehr klein ist, führt bereits eine kleine Spannungsänderung ∆u_LED = 1,925 V - 1,764 V = 161 mV zu einer großen Stromänderung ∆i_LED = 15 mA im Stromstärkebereich von [ 5 mA … 20 mA ], sodass sich der Arbeitspunkt der LED am besten mittels einer regel- und programmierbare (Konstant-) Stromquelle des „micro:bit“-Rechners einstellen lässt:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man sieht, beschreibt das gelbe Steigungsdreieck das lineare Verhalten der roten LED, indem man zu einer beliebigen Spannung u_LED im Bereich von [ 1,764 V … 1,925 V ] den sich ergebenden Strom i_Durchlass durch die LED abliest.

Für den linearen Bereich der roten LED (= gelbes Steigungsdreieck) gilt übrigens das Ohmsche Gesetz mit

r_LED = u_Durchlass / i_Durchlass = ∆u_Durchlass / ∆i_Durchlass →

i_Durchlass = u_Durchlass / r_LED = 161 mV / 6,667 Ω = 24,14 mA ≈ 24 mA

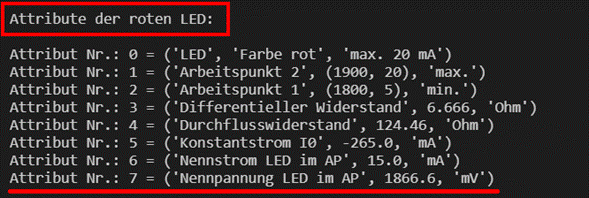
Der im roten Kasten beschriebene Sachverhalt bedeutet praktisch, dass die rote LED vom Arbeitspunkt AP1 aus mit der u_{LED, AP1} = 1,764 V startet. Dabei führt jede noch so kleine Spannungserhöhung um wenige Millivolt im Bereich von [ 0 mV … 161 mV ] bis zu

u_{LED, AP2} = u_{LED, AP1} + ∆U_LED = 1,764 V + 0,161 V = 1,925 V im Arbeitspunkt AP2

zu einer, quasi wegen der „elektrischen Übersetzung“ (= gelbes Steigungsdreieck) maßgeblich höheren Stromstärke i_{LED, AP2} = i_{LED, AP1} + ∆I_LED ≈ 24 mA.

Dabei bedeutet aber der Startwert der Spannung u_{LED, AP1} = 1,764 V im Arbeitspunkt AP1 des Steigungsdreiecks, dass die rote LED in Wirklichkeit mit einem entsprechend großen Vorwiderstand R_Vor = 470 Ω zum Schutz der LED gegen Durchbrennen betrieben wird! Demzufolge muss bei der weiteren Berechnung ohne Steigungsdreieck die entsprechenden Geradengleichung zur Strom- und Spannungsberechnung verwendet werden:

i_LED = 1 / r_{LED, AP1,2} * u_LED + I₀ Geradengleichung mit Parallelverschiebung!

u_LED = r_{LED, AP1,2} * ( i_LED - I₀ ) r_{LED, AP1,2} = 6,667 Ω (= differentieller Widerstand)

I₀ = - 265 mA (= Parallelverschiebung der Geraden)

Für den Arbeitspunkt AP1 = (1,764 V , 5 mA) folgt:

u_LED = r_{LED, AP1,2} * ( i_LED - I₀ ) = 6,667 Ω * [ 5 mA - ( - 265 mA ) ] = 1800,1 mV

Für den Arbeitspunkt AP2 = (1,925 V , 20 mA) folgt:

u_LED = r_{LED, AP1,2} * ( i_LED - I₀ ) = 6,667 Ω * [ 20 mA - ( - 265 mA ) ] = 1900,1 mV

Für den praktischen Betrieb der roten LED mit dem Nennstrom i_{LED, nenn} = 15 mA folgt:

u_LED = r_{LED, AP1,2} * ( i_LED - I₀ ) = 6,667 Ω * [ 15 mA - ( - 265 mA ) ] = 1866,76 mV

(Zum Vergrößern bitte auf das Bild klicken!)

Die im obenstehenden Bild angezeigte Nennspannung u_{LED, nenn} = 1866,6 mV der roten LED lässt sich auch im „Python“-Programm batterie_oop_03.py berechnen. Dabei kann man sich den Quelltext direkt im Browser anzeigen lassen.

Selbstverständlich lässt sich das Programm auch auf den heimischen Rechner herunterladen. Und zwar indem man den Mauszeiger auf den blau markierten Hyperlink positioniert und mittels der rechten Maustaste „Ziel speichern unter …“ herunterlädt. -

[ Home ] [ zurück ] [ Seitenanfang ]