[ Home ] [ zurück ] [ Seitenende ]

IoE - Arbeitsteilung ist das A&O

Vorwiderstand und rote LED arbeiten zusammen (… Fortsetzung)

Wegen des Spannungsteilers, d.h. der Reihenschaltung von Vorwiderstand und roter LED und der überall gleich großen Stromstärke I = I_ges = I_{R Vor} = i_{LED AP} = 15 mA muss man im Arbeitspunkt AP = (1866,76 mV, 15 mA) nur beide Geradengleichungen wie folgt einander gleich setzen (= Gleichsetzungverfahren):

i_{LED AP} = 1 / r_{LED, AP1,2} * u_LED + I₀

= 1 / 6,667 V/A * 1866,76 mV + ( - 265 mA )

= 280,0 mA - 265 mA= 15 mA

i_{R Vor} = 1 / R_Vor * U_{R Vor} = 1 / R_Vor * ( U_Klemme - u_{LED AP} )

= 1 / 470 V/A * ( 9 V – 1,867 V ) = 0,0152 A = 15,2 mA

Gleichsetzungsverfahren:

i_{LED AP} = 1 / r_{LED, AP1,2} * u_LED + I₀

i_{R Vor} = 1 / R_Vor * U_{R Vor} = 1 / R_Vor * ( U_Klemme - u_{LED AP} )

Wegen I = I_ges = I_{R Vor} = i_{LED AP} folgt:

1 / R_Vor * U_{R Vor} = 1 / r_{LED, AP1,2} * u_LED + I₀ →

U_{R Vor} = R_Vor / r_{LED, AP1,2} * u_LED + I₀ * R_Vor

= R_Vor * ( 1 / r_{LED, AP1,2} * u_LED + I₀ )

U_{R Vor} = 470 Ω * ( 1 / 6,667 Ω * 1866,76 mV + (- 265 mA ) )

= 470 V/A * ( 280 V/A * mV+ (- 265 mA ) )

= 470 V/A * ( 15 mA ) = 7,05 V

Selbstverständlich lässt sich der Spannungsabfall U_RVor auch direkt und kürzer berechnen,

U_RVor = I_RVor * R_Vor = 15 mA * 470 Ω = 7050 mV = 7,05 V

aber uns geht es ja genau darum, die Spannung bzw. den Spannungsabfall am Vorwiderstand R_Vor im Arbeitspunkt AP = (1866,76 mV, 15 mA) zu berechnen! Und zwar unabhängig von der Stromstärke I = I_ges = I_{R Vor} = i_{LED AP} = 15 mA!

Und, mit der obenstehenden Gleichsetzungsverfahren klappt das hervorragend, auch wenn es etwas aufwendig zu sein scheint, da die Berechnungsmethode (= Algorithmus) nicht so oft verwendet wird und deshalb ungewohnt ist.

Zu jeder Gleichung y = f(x) mit einer oder mehreren Unbekannten gibt es in der Mathematik auch jeweils eine grafische Lösung.

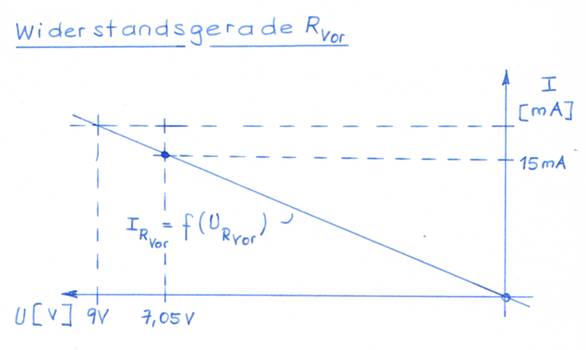
So auch zu der Geradengleichung y = f(x) = ax + b mit a = Steigung der Geraden und b = Parallelverschiebung aus dem Ursprung. Dabei lässt sich die Geradengleichung in der Elektrotechnik selbstverständlich auch auf die Widerstandgerade eines konstanten, d.h. linearen, ohmschen Widerstand wie folgt anwenden:

y = f(x) = ax + b → I_{R Vor} = 1 / R_Vor * U_{R Vor} + I₀ = 1 / R_Vor * U_RVor wegen I₀ = 0

Einsetzen der Werte in die Geradengleichung der Widerstandsgeraden R_Vor liefert:

I_{R Vor} = 1 / R_Vor * U_{R Vor}

= 1 / 470 V/A * 7,05 V = 0,015 A = 15 mA

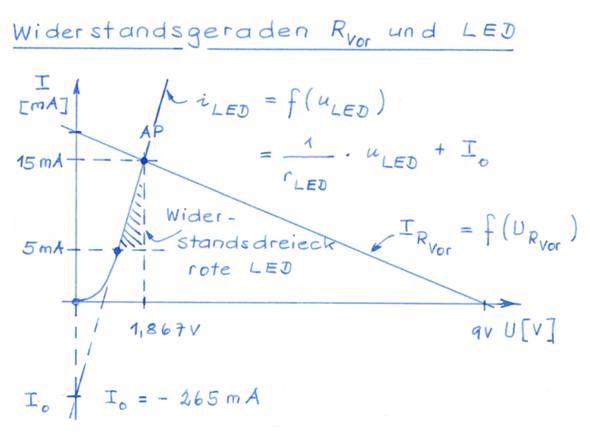
(Zum Vergrößern bitte auf das Bild klicken!)

Um den Schnittpunkt (= Arbeitspunkt AP) der Widerstandgeraden R_Vor mit der Kennlinie der roten LED grafisch bestimmen zu können, muss man die Widerstandgeraden R_Vor zuvor horizontal spiegeln:

(Zum Vergrößern bitte auf das Bild klicken!)

Wenn man beide Kennlinien und deren Koordinatensystem, d.h. die gespiegelte Widerstandsgerade R_Vor und die Kennlinie der roten LED übereinander legt, dann schneiden sich diese im gemeinsamen Arbeitspunkt AP:

(Zum Vergrößern bitte auf das Bild klicken!)

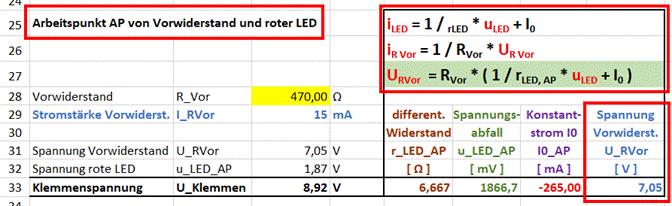
Damit sich die obenstehende Berechnung der Spannung bzw. des Spannungsabfalls am Vorwiderstand U_RVor = 7,05 V besser nachvollziehen und nachberechnen lässt, erweitern wir die bisherige Tabellenkalkulation um den Teil „Arbeitspunkt AP von Vorwiderstand und roter LED“:

(Zum Vergrößern bitte auf das Bild klicken!)

Neben der Tabellenkalkulation gibt es natürlich noch das entsprechende „Python“-Programm batterie_oop_03.py, dessen Quelltext man sich direkt im Browser anzeigen lassen kann.

Selbstverständlich lässt sich das Programm auch auf den heimischen Rechner herunterladen. Und zwar indem man den Mauszeiger auf den blau markierten Hyperlink positioniert und mittels der rechten Maustaste „Ziel speichern unter …“ herunterlädt. -

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man sich anhand des obenstehendes Screenshots selbst überzeugen kann, wurde der Spannungsabfall U_{RVor, nenn} = 7,04 V am Vorwiderstand R_Vor = 470 Ω sowohl vom „Python“-Programm batterie_oop_03.py als auch von der Tabellenkalkulation bis auf 1/100 genau berechnet (siehe Bild weiter oben). -

[ Home ] [ zurück ] [ Seitenanfang ]