[ easy electronik 200 ] [ Seitenende ] [ Versuch 1 ] [ Versuch 8 ]

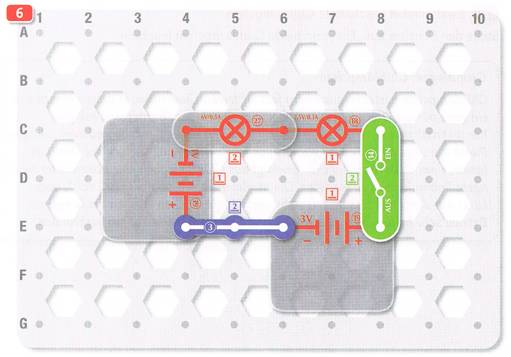
easy electronic 200 - Versuch 6

Zwei in Reihe geschaltete Glühlämpchen

Bei dem sechsten Versuch geht es um einen einfachen Stromkreis: bei dem sowohl zwei Batteriefächer 19 als auch zwei Glühlämpchen, und zwar ein Glühlämpchen 18 und ein Glühlämpchen 27, hintereinander, d.h. in Reihe geschaltet sind:

(Vergrößern: auf Bild klicken! | KOSMOS easy electronic, Seite 11)

Wie man anhand des obenstehenden Stromkreises sieht, besteht dieser aus

1. der Spannungsquelle

in Form des Batteriefaches 19 mit den beiden in Reihe geschalteten Batterien vom Typ „AA“, wobei jede Batterie über eine (Klemmen-) Spannung U_Batt von 1,2 V bis 1,5 V verfügt, zusammen also über eine (Gesamt-) Spannung U_{Batt, ges} von 2,4 V bis 3,0 V,

2. dem (Schiebe-) Schalter 14

mit dem sich die Stromzufuhr der Batterie innerhalb des Stromkreises ein- oder ausschalten lässt,

3. dem Glühlämpchen 18,

das sich mittels einer (Nenn-) Spannung von U_{Glüh 18} = 2,5 V bei einer (Nenn-) Stromstärke I_{Glüh 18} = 0,3 A betreiben lässt, ohne dass dieses dabei durchbrennt,

4. dem Glühlämpchen 27,

das sich mittels einer (Nenn-) Spannung von U_{Glüh 27} = 6,0 V bei einer (Nenn-) Stromstärke I_{Glüh 27} = 0,5 A betreiben lässt, ohne dass dieses dabei durchbrennt,

5. der Spannungsquelle

in Form des Batteriefaches 19 mit den beiden in Reihe geschalteten Batterien vom Typ „AA“, wobei jede Batterie über eine (Klemmen-) Spannung U_Batt von 1,2 V bis 1,5 V verfügt, zusammen also über eine (Gesamt-) Spannung U_{Batt, ges} von 2,4 V bis 3,0 V sowie

6. den Verbindungsleitungen,

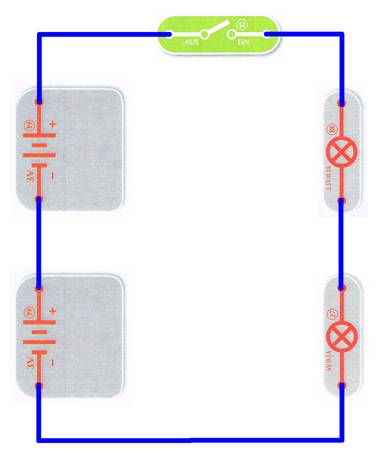
die alle einzelnen Bauelemente der Schaltung zu einem Stromkreis miteinander verbinden.

Wir ordnen die Bauelemente des Stromkreises neu an, sodass sich die Schaltung wie gewohnt von links nach rechts im Uhrzeigersinn lesen lässt:

(Zum Vergrößern bitte auf das Bild klicken!)

Aus Gründen der elektrischen Sicherheit gewöhnen wir es uns weiterhin an, Magnetschalter 12, Schalter 14 oder Taster 15 zum Ein- und Ausschalten der Stromzufuhr möglichst nahe, d.h. in direkter Folge nach der Stromversorgung - im vorliegenden Fall direkt hinter dem Batteriefach 19 - im Stromkreis anzuordnen!

Dies hat den sicherheitstechnischen Vorteil, dass bei geöffnetem Schalter 14 alle nach dem Ein- und Ausschalter angeschlossenen Bauelemente wie z.B. das Glühlämpchen 18, aber auch der gesamte restliche Stromkreis bis zum Minuspol des Batteriefaches 19 spannungs- und stromlos sind (siehe nachfolgendes Bild!)

Bei der Analyse und der Erläuterung der obenstehenden Schaltung beginnen wir auf der linken Seite, wo sich die beiden Batteriefächer 19 befinden, die elektrisch hintereinander, d.h. in Reihe zusammengeschaltet sind, sodass sich insgesamt eine Batterie-Gesamtspannung U_{Batt, ges} von

U_{Batt, ges} = U_{Batt, 1} + U_{Batt, 2} → mit U_{Batt, 1} = U_{Batt, 2} = 3,0 V →

= U_{Batt, 2} + U_{Batt, 2} = 2 * U_{Batt, 2} = 2 * 3,0 V = 6,0 V

einstellt.

Hinter dem Schalter 14 befinden sich in der obenstehenden Schaltung rechts die beiden in Reihe geschalteten Glühlämpchen 18 und 27 mit den nachfolgenden Nennbetriebsdaten:

Glühlämpchen 18: (Nenn-) Spannung von U_{Glüh 18} = 2,5 V mit einer (Nenn-) Stromstärke I_{Glüh 18} = 0,3 A sowie

Glühlämpchen 27: (Nenn-) Spannung von U_{Glüh 27} = 6,0 V mit einer (Nenn-) Stromstärke I_{Glüh 27} = 0,5 A.

Da die beiden Glühlämpchen 18 und 27 über unterschiedliche (Nenn-) Spannungen von U_{Glüh 18} = 2,5 V und U_{Glüh 27} = 6,0 V verfügen, stellen sich auch unterschiedliche Stromstärken I_{Glüh 18} = 0,3 A und I_{Glüh 27} = 0,5 A ein. Aber eben nur für jedes einzelne Glühlämpchen!

Diesbezüglich stellt sich die Frage, welche Stromstärke I_Glüh stellt sich ein, wenn man die beiden Glühlämpchen 18 und 27 hintereinander in Reihe schaltet (siehe Schaltung weiter oben)? Beläuft sich die Stromstärke dabei dann auf I_{Glüh 18} = 0,3 A oder auf I_{Glüh 27} = 0,5 A?

Oder vielleicht sogar auf I_Glüh = 0,3 A + 0,5 A = 0,8 A?

Oder vielleicht auf den Mittelwert (= Durchschnittswert) von ( I_{Glüh 18} + I_{Glüh 27} ) / 2 = ( 0,3 A + 0,5 ) / 2 = 0,4 A?

Wie wir bereits wissen, ist die Stromstärke I in einem einfachen Stromkreis wie in Versuch 1 oder hier im Versuch 6 überall, d.h. an jeder Stelle im Stromkreis gleich groß, sodass folgt: I_Glüh = 0,3 A + 0,5 A = 0,8 A " FALSCH!

Das mit dem Durchschnittswert von ( I_{Glüh 18} + I_{Glüh 27} ) / 2 = ( 0,3 A + 0,5 ) / 2 = 0,4 A wäre mathematisch richtig, wenn wir es mathematisch auch mit der Durchschnittsspannung von ( U_{Glüh 18} + U_{Glüh 27} ) / 2 = ( 2,5 V + 6,0 V ) / 2 = 8,5 V / 2 = 4,25 V zu tun hätten! Haben wir aber nicht! Physikalisch und elektrotechnisch gibt es aber in der obenstehenden Reihenschaltung der Glühlämpchen keine Durchschnittsspannung!

Nehmen wir mal an, es gäbe eine Durchschnittsspannung von U_Mittel = 4,25 V, dann würde an jedem Glühlämpchen eine Durchschnittsspannung von U_Mittel = 4,25 V anliegen! Also auch am Glühlämpchen 18 mit der maximal zulässigen (Nenn-) Spannung von U_{Glüh 18} = 2,5 V, sodass dieses sofort durchbrennen würde! Außerdem müsste sich bei einer Durchschnittsspannung von U_Mittel = 4,25 V die erforderliche Gesamtspannung des Batteriefachs 19 auf U_{Batt, ges} = U_Mittel * 2= 4,25 V * 2 = 8,5 V belaufen, was aber nicht der Fall ist!

Wenn sich aber die erforderliche Gesamtspannung des Batteriefachs 19 tatsächlich auf U_{Batt, ges} = U_{Glüh 18} + U_{Glüh 27} = 2,5 V + 6,0 V = 8,5 V belaufen würde, würden dann beide Glühlämpchen gleich hell leuchten? Nein!

Aber weshalb würden beide Glühlämpchen nicht gleich hell leuchten? Ganz einfach, weil das Glühlämpchen 18 nur von einer Stromstärke von I_{Glüh 18} = 0,3 A durchflossen werden darf und es bei einer größeren Stromstärke von I_{Glüh 18} > 0,3 A sofort durchbrennen würde! Und außerdem darf das Glühlämpchen 18 nur mit einer maximal zulässigen (Nenn-) Spannung von U_{Glüh 18} = 2,5 V betrieben werden, da es bei einer höheren Betriebsspannung von U_{Glüh 18} > 2,5 V sofort durchbrenn würde:

(Vergrößern: auf das Bild klicken! | Quelle: KOSMOS „Easy Electronic 200“, Seite 9)

Damit wir uns jetzt nicht im Kreis drehen und irgendwann wie das Glühlämpchen „durchbrennen“, brauchen wir eine Idee, ob und wie sich die Glühlämpchen doch noch physikalisch und elektrotechnisch richtig berechnen lassen! [ Video ]

Wenn man sich im obenstehenden Bild die rote Beschriftung „2,5V/0,3A“ des Glühlämpchens 18 anschaut (siehe auch im roten Kasten), dann fällt einem auf, dass es zwischen 2,5 V und 0,3 A einen Schrägstrich / gibt, der sinngemäß ausdrücken soll, dass sich die Spannung von U_{Glüh 18} = 2,5 V auf die Stromstärke I_{Glüh 18} = 0,3 A bezieht, sodass sich die Spannung von U_{Glüh 18} = 2,5 V nicht nur auf die Stromstärke I_{Glüh 18} = 0,3 A bezieht, sondern auch aufteilt:

U_{Glüh 18} / I_{Glüh 18} = 2,5 V / 0,3 A = 8,333333333333333 V/A ≈ 8,33 V/A = 8,33 W " [ V/A ] = [ W ] für die Maßeinheiten!

U_{Glüh 27} / I_{Glüh 27} = 6,0 V / 0,5 A = 12 V/A ≈ 12 V/A = 12 W

Da die beiden Glühlämpchen hintereinander in Reihe geschaltet sind, lassen sich nicht nur die jeweiligen Teilspannungen U_{Glüh 18} und U_{Glüh 27} addieren, sondern auch deren Widerstände wie folgt addieren:

R_ges = R_{Glüh 18} + R_{Glüh 27} = 8,33 W + 12 W = 20,33 W

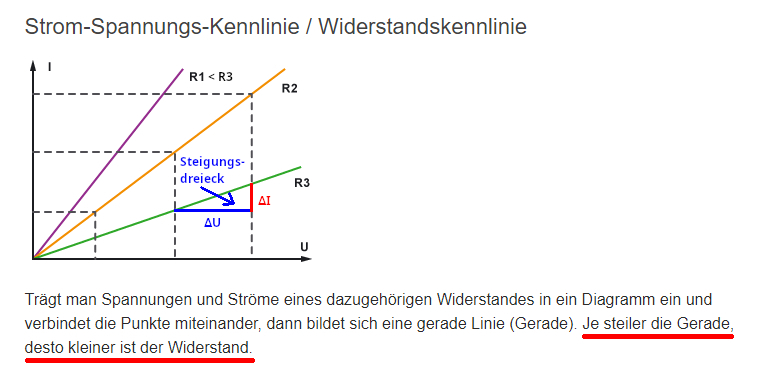
Aus der Maßeinheit [ V/A ] = [ W ] lässt sich übrigens die Formel R = U / I ableiten und nach dem Strom I umstellen:

I = U / R = 1 / R * U " Strom-Spannungs-Kennline mit I = f(U) = 1/R + U und der Geradensteigung 1/R

Und bei der Formel R = U / I handelt es sich um das sogenannte Ohmsche Gesetz.

Das Ohmsche Gesetz legt fest, wie sich Spannung U und Strom I im Verhältnis U / I zueinander verhalten. Dabei spricht man beim Verhältnis U / I auch von dem Quotienten U / I mit

Widerstand R = U / I = ∆U / ∆I = U₂ – U₁ / ( I₂ – I₁ ) " Strom- und Stromdifferenz

(Vergrößern: auf das Bild klicken! | Quelle: Elektronik-Kompendium)

So, jetzt wo wir wissen, dass das Verhältnis (= Quotient) von Spannung U zu Stromstärke I, d.h. U / I, gleich dem Widerstand R mit R = U / I entspricht (siehe Beschriftung auf den beiden Glühlämpchen 18 und 27), hindert uns niemand daran, den zuvor berechneten arithmetischen Mittelwert (= Durchschnittswert)

>> Das mit dem Durchschnittswert von ( I_{Glüh 18} + I_{Glüh 27} ) / 2 = ( 0,3 A + 0,5 ) / 2 = 0,4 A wäre mathematisch richtig, wenn wir es mathematisch auch mit der Durchschnittsspannung von ( U_{Glüh 18} + U_{Glüh 27} ) / 2 = ( 2,5 V + 6,0 V ) / 2 = 8,5 V / 2 = 4,25 V zu tun hätten! << (Siehe weiter oben!)

mit ( U_{Glüh 18} + U_{Glüh 27} ) / 2 = ( 2,5 V + 6,0 V ) / 2 = 8,5 V / 2 = 4,25 V und ( I_{Glüh 18} + I_{Glüh 27} ) / 2 = ( 0,3 A + 0,5 ) / 2 = 0,4 A wie folgt in die Formel des Ohmschen Gesetzes einzusetzen:

R = U / I = 4,25 V / 0,4 A = 10,625 V/A = 10,625 W " elektrotechnisch FALSCH, da der Durchschnittswert des Widerstandes R = U / I = 10,625 W eben NICHT dem Gesamtwiderstandes R_ges entspricht:

R_ges = R_{Glüh 18} + R_{Glüh 27}

= ( U_{Glüh 18} / I_{Glüh 18} ) + ( U_{Glüh 27} / I_{Glüh 27} )

= ( 2,5 V / 0,3 A ) + ( 6,0 V / 0,5 A ) ≈ 8,33 W + 12 W = 20,33 W

R_ges = U_ges / I_ges

= ( U_{Glüh 18} + U_{Glüh 27} ) / I_ges "

I_ges = ( U_{Glüh 18} + U_{Glüh 27} ) / R_ges

= ( 2,5 V + 6,0 V ) / 20,33 W = 8,5 V / 20,33 V/A = 0,418101328 A ≈ 0,418 A = 418 mA

" bei einer Gesamtspannung von U_ges = 2,5 V + 6,0 V = 8,5 V 7

Würde man die Reihenschaltung der beiden Glühlämpchen 18 und 27 jeweils mit der Nenn-Spannung von zusammen U_{Glüh 18} + U_{Glüh 27} = 2,5 V + 6,0 V = 8,5 V 7 betreiben, dann würde das Glühlämpchen 18 wegen des größeren Gesamtstroms von I_ges = 0,418 A anstelle der erlaubten I_{Glüh 18} = 0,3 A durchbrennen!

Aber zum Glück lässt sich mit den beiden in Reihe zusammengeschalteten Batteriehalterungen nur eine Gesamtspannung U_{Batt, ges} = U_{Batt 1} + U_{Batt 2} = 2 * 1,5 V + 2 * 1,5 V = 4 * 1,5 V = 6,0 V realisieren, sodass sich der Gesamtstrom I_ges entsprechend verkleinert:

I_ges = U_ges / R_ges

= 6,0 V / 20,33 W = 6,0 V / 20,33 V/A = 0,29513 A ≈ 0,295 A = 295 mA

" bei einer Gesamtspannung von U_ges = 6,0 V 7

Mit I_ges ≈ 0,295 A ≈ 0,3 A ist also die Welt des Glühlämpchens 18 wieder in Ordnung, brennt dieses nicht mehr durch!

Im nachfolgenden Abschnitt lernen wir, wie man die Teilspannungen beiden Glühlämpchen 18 und 27 berechnet. [ Video ]

Reihenschaltung der Glühlämpchen 18 und 27

Da beide Glühlämpchen hintereinander, d.h. in Reihe geschaltet sind, ließen sich diese entsprechend der jeweiligen (Nenn-) Spannungsangaben an einer Gesamtspannung U_{Glüh, ges} von

U_{Glüh, ges} = U_{Glüh 18} + U_{Glüh 27}

= 2,5 V + 6,0 V = 8,5 V

betreiben!

Da aber die Batterie-Gesamtspannung U_{Batt, ges} nur U_{Batt, ges} = 6,0 V beträgt, fehlen insgesamt noch

∆U = U_{Glüh, ges} - U_{Batt, ges} = 8,5 V – 6,0 V = 2,5 V,

damit alle Glühlämpchen maximal hell leuchten!

Wie wir bereits im Versuch 1 gelernt haben, gehören Spannung U und Strom I immer zusammen.

Nehmen wir deshalb einmal an, dass uns bei der Reihenschaltung der beiden Glühlämpchen die Gesamtspannung U_{Glüh, ges} = 8,5 V zur Verfügung steht. Wie groß ist dann die Stromstärke I_Batt = I_Glüh durch alle Glühlämpchen?

Um die Stromstärke I_Batt = I_Glüh durch alle Glühlämpchen berechnen zu können, müssen wir wissen, wie groß die einzelnen Widerstände der Glühlämpchen sind:

Glühlämpchen 18:

(Nenn-) Spannung von U_{Glüh 18} = 2,5 V mit einer (Nenn-) Stromstärke I_{Glüh 18} = 0,3 A →

R_{Glüh 18} = U_{Glüh 18} / I_{Glüh 18} = 2,5 V / 0,3 A = 8,33 Ω

Glühlämpchen 27:

(Nenn-) Spannung von U_{Glüh 27} = 6,0 V mit einer (Nenn-) Stromstärke I_{Glüh 27} = 0,5 A →

R_{Glüh 27} = U_{Glüh 27} / I_{Glüh 27} = 6,0 V / 0,5 A = 12 Ω

Da die beiden Glühlämpchen 18 und 27 hintereinander, d.h. in Reihe, geschaltet sind, addieren sich deren (Teil-) Widerstände R_{Glüh 18} und R_{Glüh 27} wie folgt zum Gesamtwiderstand R_{Glüh, ges}:

R_{Glüh, ges} = R_{Glüh 18} + R_{Glüh 27} = 8,33 Ω + 12 Ω = 20,33 Ω

Gemäß dem Ohmschen Gesetz R = U / I folgt mit I = U / R:

I = U / R →

I_Glüh = U_{Glüh, ges} / R_{Glüh, ges} = 8,5 V / 20,33 Ω = 0,418 A

Jetzt wissen wir, dass die Stromstärke I_Glüh = 0,418 A kleiner ist als die (Nenn-) Stromstärke I_{Glüh 27} = 0,5 A des Glühlämpchens 27, sodass dieses eben nicht maximal hell leuchten kann!

Als nächstes berechnen wir Stromstärke I_Glüh, wenn bei der Reihenschaltung der beiden Glühlämpchen nur die Gesamtspannung U_{Glüh, ges} = 6,0 V zur Verfügung steht. Wie groß ist dann die Stromstärke I_Batt = I_Glüh durch alle Glühlämpchen?

I_Glüh = U_{Glüh, ges} / R_{Glüh, ges} = 6,0 V / 20,33 Ω = 0,295 A (siehe auch weiter oben!)

Jetzt wissen wir, dass die Stromstärke I_Glüh = 0,295 A ungefähr gleich groß ist wie die (Nenn-) Stromstärke I_{Glüh 18} = 0,3 A des Glühlämpchens 18, sodass dieses maximal hell leuchten kann!

Wenn wir wissen wollen, ob das Glühlämpchen 18 wirklich mit maximaler Helligkeit leuchten kann, dann müssen wir noch die Spannung bzw. den Spannungsabfall U_{Glüh 18} am Glühlämpchen wie folgt berechnen:

U_{Glüh 18} = = I_Glüh * R_{Glüh 18} = 0,295 A * 8,33 Ω = 2,46 V → das Glühlämpchen 18 leuchtet fast mit maximaler Helligkeit!

Für das Glühlämpchen 27 berechnet sich der Spannungsabfall U_{Glüh 27} am Glühlämpchen wie folgt:

U_{Glüh 27} = = I_Glüh * R_{Glüh 27} = 0,295 A * 12 Ω = 3,54 V → das Glühlämpchen 27 leuchtet nicht mit maximaler Helligkeit!

Und tatsächlich, das dicke, untere Glühlämpchen 27 leuchtet deutlich erkennbar nicht mit maximaler Helligkeit:

(Zum Vergrößern bitte auf das Bild klicken!)

Von der Reihenschaltung zum unbelasteten Spannungsteiler

Wenn man wie in diesem Versuch zwei ohmsche Verbraucher in Form der beiden Glühlämpchen 18 und 27 hintereinander, d.h. in Reihe schaltet, dann addieren sich deren Teilspannungen U_{Glüh 18} = 2,46 V und U_{Glüh 27} = 3,54 V zur Gesamtspannung U_{Glüh, ges} = 2,46 V + 3,54 V = 6,0 V, sodass man von einer Reihenschaltung spricht.

Bei einer Reihenschaltung addieren sich aber nicht nur die beiden Teilspannungen zur Gesamtspannung, sondern auch deren Einzel- bzw. Teilwiderstände zum Gesamtwiderstand:

R_{Glüh, ges} = R_{Glüh 18} + R_{Glüh 27} = 8,33 Ω + 12 Ω = 20,33 Ω

Dabei gilt es zu beachten, dass der Stromfluss und die Stromstärke durch alle Verbraucher (= Glühlämpchen) und an jeder Stelle im Stromkreis gleich groß ist: I_{Batt, ges} = I_{Glüh 18} = I_{Glüh 27} = 0,295 A. Das gilt übrigens auch für die 1,5 Volt Batterien in den Batteriefächern 19.

Wenn man wie in diesem Versuch nur zwei ohmsche Verbraucher in Form der beiden Glühlämpchen 18 und 27 hintereinander, d.h. in Reihe schaltet, dann spricht man auch von einem unbelasteten Spannungsteiler. Unbelastet deswegen, weil sich parallel zum Glühlämpchen 27 kein weiterer ohmscher Verbraucher als sogenannter Lastwiderstand befindet!

Vom unbelasteten Spannungsteiler zur Spannungsteilerformel

Um die einzelnen Teilspannungen U_{Glüh 18} = 2,46 V und U_{Glüh 27} = 3,54 V berechnen zu können, mussten wir zunächst die beiden Lämpchen-Widerstände R_{Glüh 18} = 8,33 Ω und R_{Glüh 27} = 12 Ω, den Gesamtwiderstand R_{Glüh, ges} = 20,33 Ω der Reihenschaltung und den Strom I_Glüh = 0,295 A für die anliegende Spannung U_Batt = U_{Glüh, ges} = 6,0 V berechnen, was natürlich etwas umständlich ist, da es auch noch einfacher und schneller geht. Und zwar mit der sogenannten

Spannungsteilerformel

Ein Spannungsteiler besteht im Regelfall aus zwei Widerständen, an denen sich die Gesamtspannung U_ges in zwei Teilspannungen aufteilt. Die Grundform ist der unbelastete Spannungsteiler, der einer Reihenschaltung aus zwei Widerständen entspricht.

Spannungsteiler werden verwendet, um Arbeitspunkte (Spannungsverhältnisse) an aktiven Bauelementen einzustellen. Zum Beispiel bei einer Transistor-Verstärkerschaltung. Dabei wird nur ein kleiner Stromfluss erzeugt. Hauptsächlich werden mit einem Spannungsteiler Spannungspotentiale erzeugt, die geringer sind als die Gesamtspannung.

(Quelle: Elektronik-Kompendium)

Spannungsteilerformel:

UGlüh 18 / UGlüh, ges UGlüh 18 UGlüh 27 / UGlüh, ges UGlüh 27

= RGlüh 18 / RGlüh, ges → = ( RGlüh 18 / RGlüh, ges ) * UGlüh, ges = ( 8,33 Ω / 20,33 Ω ) * 6,0 V = 0,4097 * 6,0 V = 2,458 V ≈ 2,46 V = RGlüh 27 / RGlüh, ges → = ( RGlüh 27 / RGlüh, ges ) * UGlüh, ges = ( 12 Ω / 20,33 Ω ) * 6,0 V = 0,59026 * 6,0 V = 3,542 V ≈ 3,54 V

Wie man sieht, geht es mit der Spannungsteilerformel deutlich schneller, muss man nicht zuvor den (Quer-) Strom I_Glüh = 0,295 A berechnen! [ Video ]

(Vergrößern: auf Bild klicken! │Quelle: Wikipedia)

Um die Spannungsteilerformel

U_{Glüh 18} / U_{Glüh, ges} = R_{Glüh 18} / R_{Glüh, ges}

besser verstehen zu können, sollte man sich die Mühe machen und diese wie folgt herleiten:

I_{Glüh 18} = I_{Glüh, ges} "

U_{Glüh 18} / R_{Glüh 18} = U_{Glüh, gest} / R_{Glüh, ges}

U_{Glüh 18} / U_{Glüh, ges} = R_{Glüh 18} / R_{Glüh, ges} oder

I_{Glüh 27} = I_Glüh,ges "

U_{Glüh 27} / U_{Glüh, ges} = R_{Glüh 27} / R_{Glüh, ges} oder

I_{Glüh 18} = I_{Glüh 27} "

U_{Glüh 18} / U_{Glüh 27} = R_{Glüh 18} / R_{Glüh 27}

Arbeitsteilung durch Stromteilung

Wenn die Beleuchtungskörper wie die beiden Glühlämpchen 18 und 27 unterschiedlich hell leuchten, obwohl das nicht zwingend so sein muss, wie wir gleich sehen werden, kann unter Umständen schon ziemlich nervig und störend sein, weil sich das maximal helle Glühlämpchen 18 oder 27 meistens genau an der falschen Stelle im Raum befindet. Aber das muss nicht so sein!

Man muss nämlich nur dafür sorgen, dass jedes Glühlämpchen mit der entsprechenden Nennbetriebsspannung von U_{Glüh 18, Nenn} = 2,5 V und dem entsprechenden Nennbetriebsstrom I_{Glüh 18, Nenn} = 0,3 A oder U_{Glüh 27, Nenn} = 6,0 V und I_{Glüh 27, Nenn} = 0,5 A betrieben wird!

Wie wir aber inzwischen gelernt haben, ist das mit der Reihenschaltung der beiden Glühlämpchen nicht zu machen!

Wie aber wäre es mit einer Arbeitsteilung durch Stromteilung? Und ja, wie müsste diese elektro- und schaltungstechnisch aussehen?

Fakt ist, sozusagen als Bedingung und Voraussetzung, dass beide Glühlämpchen optimal und effizient sowohl mit der Nennbetriebsspannung als auch dem Nennbetriebsstrom versorgt werden!

Da trifft es sich gut, dass sich mit den beiden Batteriefächern 19 sowohl die Nennbetriebsspannung U_{Glüh 18, Nenn} = 2,5 V ( ≈ 3.0 V) als auch U_{Glüh 27, Nenn} = 6,0 V realisieren lassen.

Erfreulich ist dabei auch, dass man dazu die beiden Batteriefächer 19 mit je einer Batteriespannung von U_{Batt, Glüh 18} = U_{Batt, Glüh 27} = 3,0 V nur in Reihe, d.h. hintereinander schalten muss, sodass das erste Batteriefach 19 mit der Batteriespannung von U_{Batt, Glüh 18} = 3,0 V das Glühlämpchen 18 mit Energie versorgt, während beide Batteriefächer 19 in Reihenschaltung mit der Batteriespannung von U_{Batt, Glüh 27} = 6,0 V das Glühlämpchen 27 mit Energie versorgen:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden Bild sieht, leuchten beide Glühlämpchen maximal hell, vorausgesetzt natürlich, dass beide Batteriefächer 19 mit den in Reihe geschalteten Batterien vom Typ „AA“ allesamt über die gleich große Batteriekapazität (= Aufladung) verfügen, d.h. vollständig aufgeladen sind.

Trotzdem verhält es sich natürlich so, dass die Energieentnahme der beiden Glühlämpchen 18 und 27 aus den beiden Batteriefächern 19 unterschiedlich ist!

Demzufolge beträgt die Energieentnahme des Glühlämpchens 18 nur

P_{Glüh 18} = U_{Glüh 18, Nenn} * I_{Glüh 18, Nenn} = 2,5 V * 0,3 A = 0,75 W,

während die Energieentnahme des Glühlämpchens 27 u.a. wegen der größeren Nennbetriebsspannung mit U_{Glüh 27, Nenn} = 6,0 V exakt doppelt so groß ausfällt:

P_{Glüh 27} = U_{Glüh 27, Nenn} * I_{Glüh 27, Nenn} = 6,0 V * 0,5 A = 3,0 W

Dabei gilt es aber noch zu beachten, dass sich die doppelt so große Energieentnahme des Glühlämpchens 27 wegen der Reihenschaltung der beiden Batteriefächer 19 auf diese jeweils zur Hälfte aufteilt!

Demzufolge belastet die doppelt so große Energieentnahme des Glühlämpchens 27 die beiden Batteriefächer 19 tatsächlich nur zur Hälfte, während die Energieentnahme des Glühlämpchens 18 als Ganzes nur die Batterien im unteren Batteriefach 19 belasten! Deshalb werden sich also die Batterien im unteren Batteriefach 19 doppelt so schnell entladen als die im oberen Batteriefach 19. – [ Video ]

Weiter geht’s mit [ Versuch 8 ].

[easy electronik 200 ] [ Seitenanfang ] [ Versuch 1 ] [ Versuch 8 ]