|
|
[ easy electronik 200 ] [ Seitenende ] [ Versuch 6 ] [ Versuch 10 ] |
|
||||
|
|
easy electronic 200 -
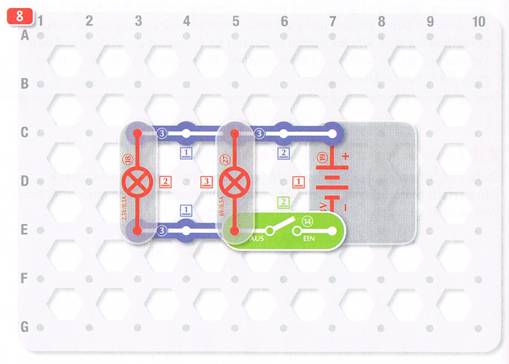
Versuch 8 Zwei parallel geschaltete Glühlämpchen Bei dem achten Versuch geht es um einen
einfachen Stromkreis: bei dem
nur ein Batteriefach
19
mit zwei Glühlämpchen, und zwar ein Glühlämpchen 18 und ein Glühlämpchen 27, nebeneinander, d.h. parallel geschaltet sind: (Vergrößern: auf Bild
klicken! | KOSMOS easy electronic,
Seite 12) Wie man anhand des obenstehenden Stromkreises sieht, besteht dieser
aus 1.
der Spannungsquelle in Form des Batteriefaches 19 mit den beiden in Reihe geschalteten Batterien vom Typ „AA“,
wobei jede Batterie über eine (Klemmen-) Spannung UBatt von 1,2 V bis 1,5 V
verfügt, zusammen also über eine (Gesamt-) Spannung UBatt, ges von 2,4 V bis 3,0 V,
2.
dem (Schiebe-) Schalter 14 mit dem sich die Stromzufuhr der Batterie innerhalb des Stromkreises
ein- oder ausschalten lässt, 3.
dem Glühlämpchen
18, das sich mittels einer
(Nenn-) Spannung von UGlüh 18 = 2,5 V bei einer (Nenn-) Stromstärke IGlüh 18
= 4.
dem Glühlämpchen
27, das sich mittels einer
(Nenn-) Spannung von UGlüh 27 = 6,0 V
bei einer (Nenn-) Stromstärke IGlüh 27 = 5.
den Verbindungsleitungen,
die alle einzelnen Bauelemente der Schaltung
zu einem Stromkreis miteinander
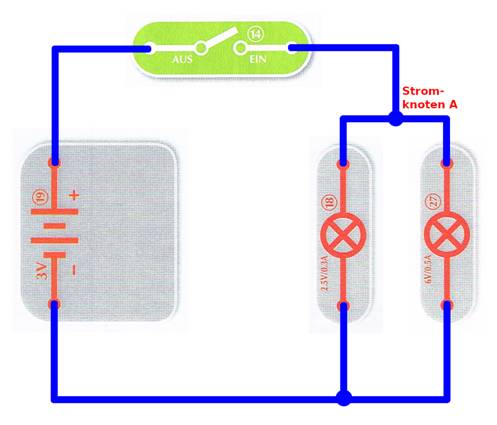
verbinden. Wir ordnen die Bauelemente des Stromkreises neu an, sodass sich
die Schaltung wie gewohnt von links nach rechts im Uhrzeigersinn lesen lässt:
(Zum Vergrößern bitte
auf das Bild klicken!)
Bei der Analyse und der Erläuterung der
obenstehenden Schaltung beginnen
wir auf der linken Seite, wo sich das Batteriefach 19 befindet, das über zwei in Reihe geschaltete 1,5 V „Mignon“-Batterien vom Typ „AA“
verfügt, sodass sich insgesamt eine Batteriespannung UBatt von UBatt = 2 * 1,5 V = 3,0
V
einstellt. Auf der rechten Seite der Schaltung bzw. des Stromkreises haben wir es mit einem sogenannten Stromteiler zu tun,
bei dem die beiden Glühlämpchen
18
und 27 zueinander parallel geschaltet sind. Dabei stellt sich gleich die Frage, ob die
geringe Batteriespannung von UBatt = 3,0 V ausreicht, um das Glühlämpchen 27 mit der Nenn-Betriebsspannung von UGlüh 27 = 6,0 V
zum Leuchten zu bringen. Ob das Glühlämpchen 27 auch bei einer Betriebsspannung von UGlüh 27 = 3,0 V leuchtet, ist aber nicht nur eine Frage der Spannung, sondern auch des Stromes.
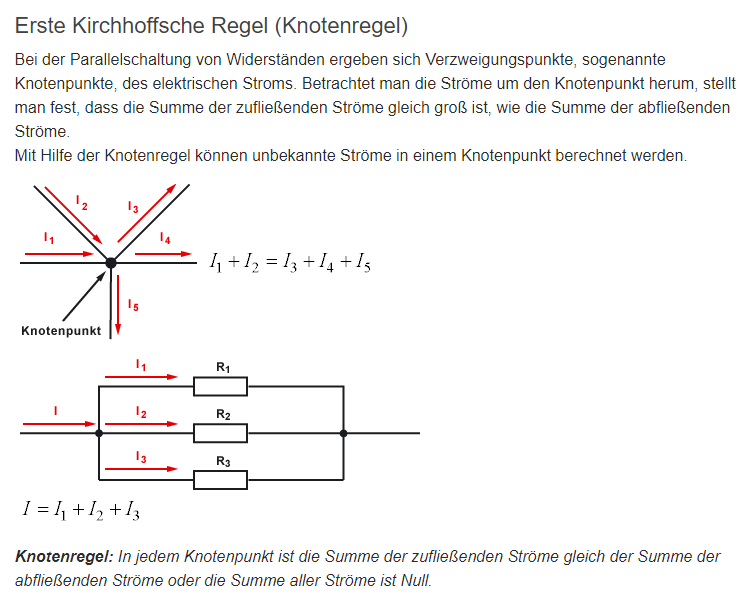
Kirchhoffsche
Regeln beim Stromknoten >> Die Kirchhoffschen Regeln sind
Formeln, die in der Praxis nicht so häufig angewendet werden. Sie wurden 1845
von Gustav Robert Kirchhoff formuliert. Die Kirchhoffschen Regeln basieren
hauptsächlich auf theoretischen Überlegungen. Zur Berechnung von Strömen und
Spannungen wird eher das Ohmsche Gesetz angewendet. << (Quelle: Elektronik-Kompendium)
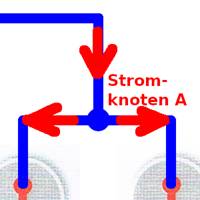
Wie man im obenstehenden Bild mit dem Stromkreis sieht, gibt es dort wo die beiden parallel geschalteten Glühlämpchen 18 und 27 miteinander verbunden sind, einen sogenannten
Stromknoten.
(Vergrößern: auf Bild
klicken! ⌡ Quelle: Elektronik-Kompendium) Bezüglich des Stromteilers ist es falsch zu sagen, dass in den beiden Glühlämpchen elektrischer Strom „verbraucht“ wird. Im Sinne von „vernichtet“.
Vielmehr
verhält es sich so, dass es sich bei den beiden Glühlämpchen um Energiewandler
handelt, die den in die Glühlämpchen
hinein fließenden elektrischen Strom in heraus fließendes sichtbares Licht (= Lichtstrahlung) und heraus
fließendes unsichtbares Licht
(= Wärmestrahlung) umwandeln, wobei kein bisschen Energie verloren
geht!
Bei einem Holzofen im Flur der Wohnung, der
alle rundum liegenden Zimmer mit Wärme versorgt, kann man die Wärmestrahlung auf
der Haut fühlen und das Feuer als sichtbares Licht sehen. Der Elektromotor 24 im Experimentierkasten z.B. wandelt
zugeführte elektrische Energie in mechanische
Energie in Form des Antriebs und der Drehbewegung um. Aber nicht nur! Durch Reibung der Motorwelle
in den Kugellagern entsteht auch geringe Reibungswärme (= Strahlungsenergie), die sich nicht nutzen lässt und
nach außen abgeführt werden muss. Im Inneren des Motors wird die zugeführte elektrische
Energie in den Kupferwicklungen der Magnetspulen in magnetische Energie und darüber hinaus in mechanische Bewegungsenergie (= Antrieb)
umgewandelt. Und da der Motor auch
Krach macht, entsteht auch noch akustische Schwingungsenergie (= Schall), die logischer Weise unerwünscht
ist. Ein Photovoltaik-Modul
z.B. wandelt das eintreffende Sonnenlicht
(= Strahlungsenergie) nebst UV- und
Infrarot-Licht um in elektrische Energie
(= Gleichstrom) und in etwas Wärmenergie (= Wärmestrahlung). Ein Mikrofon z.B. wandelt
den eintreffenden Schall (= Strahlungsenergie) mittels einer kleinen und sehr
dünnen Membrane nebst Magnetspule in elektrische Energie (= schwankende und oszillierende
Wechselspannung von wenigen Millivolt) um, die sich mittels eines
elektronischen Verstärkers so kräftig „verstärken“, d.h. in noch mehr
elektrische Energie, umwandeln lässt, sodass der Lautsprecher
als elektrischer, magnetischer und mechanischer Energiewandler arbeitet und die ganz kleine Mikrofonspannung ganz laut
über die Lautsprechermembrane nach
außen wiedergibt. Demzufolge arbeitet ein Lautsprecher quasi als umgekehrtes Mikrofon! So, nun wird es wieder Zeit, dass wir uns den
beiden parallel geschalteten Glühlämpchen zuwenden. Dass das Glühlämpchen 18 mit der (Nenn-) Spannung von UGlüh 18 = 2,5 V bei einer (Nenn-) Stromstärke von IGlüh 18 = Wie aber sieht es bei dem Glühlämpchen 27 mit der (Nenn-) Spannung von UGlüh 27 = 6,0 V
bei einer (Nenn-) Stromstärke von IGlüh 27 = Berechnung der Stromstärke IGlüh
27
des Glühlämpchen 27 bei einer Batteriespannung von UBatt = 3,0 V: Es gilt das Ohmsche
Gesetz mit R = U / I →
I = U / R IGlüh 27 = UGlüh 27 / RGlüh 27 →
RGlüh 27 = UGlüh 27 / IGlüh 27 = 6,0 V / = UBatt / RGlüh 27 = 3,0 V / 12 Ω = 3,0 Jetzt bestätigt es sich, dass das Glühlämpchen 27 bei der hälftigen
Betriebsspannung von UGlüh 27 = UBatt = 3,0 V auch nur den hälftigen Strom mit IGlüh 27 = Berechnung der Stromstärke IGlüh
18
des Glühlämpchen 18 bei einer Batteriespannung von UBatt = 3,0 V: Es gilt das Ohmsche
Gesetz mit R = U / I →
I = U / R IGlüh 18 = UGlüh 18 / RGlüh 18 →
RGlüh 18 = UGlüh 18 / IGlüh 18 = 2,5 V / = UBatt / RGlüh 18 = 3,0 V / 8,33 Ω = 3,0 Wie man unschwer sieht, „zieht“ das Glühlämpchen 18 (links) wegen der höheren
Betriebsspannung von UGlüh 18 = UBatt = 3,0 V
einen größeren Strom von IGlüh 18 = (Zum Vergrößern bitte
auf das Bild klicken!) So wie Strom und Spannung zusammen gehören, gehört der Stromknoten zum Stromteiler, d.h. der Parallelschaltung zweier oder mehrerer ohmscher Verbraucher (= Widerstände,
Glühlampen), aber auch Spannungsquellen (= Batterien, Akkus)
oder Stromquellen (=
Konstantstromquelle, Labornetzteil mit getrennter Spannungs- und
Stromregelung). [ Video ] Demzufolge lässt sich der Stromteiler in Form der beiden parallel geschalteten Glühlämpchen 18 und 27 nicht nur herkömmlich mittels des Ohmschen
Gesetzes berechnen, sondern auch mittels der sogenannten Stromteilerformel: (Vergrößern: auf Bild
klicken! ⌡ Quelle: Elektronik-Kompendium) >>
Der Stromteiler ist eine Parallelschaltung aus passiven elektrischen
oder magnetischen Zweipolen, durch die ein elektrischer Strom bzw. ein magnetischer Fluss in mehrere
Teilströme/-flüsse aufgeteilt wird. Stromteiler für Wechselstrom
können auch mit Transformatoren realisiert werden, sie heißen dann Stromwandler.
(…) Allgemeine
Stromteilerregel Zur einfachen Berechnung der Teilströme bietet sich die Stromteilerregel an. Diese Regel gilt nur, wenn alle Zweige, auf die sich
der Gesamtstrom aufteilt, passiv sind. Bei Gleichstrom sind dies ohmsche Widerstände. Bei Wechselstrom wären zusätzlich Kondensatoren (kapazitiver Stromteiler) und Spulen (induktiver Stromteiler) möglich. In magnetischen Schaltungen gibt es
nur magnetische Widerstände. Sobald aktive Bauelemente wie Quellen vorkommen, muss auf
das Maschenstromverfahren zurückgegriffen werden. Anwendung findet die
Stromteilerregel auch bei Berechnung eines Netzwerkes mit Hilfe des
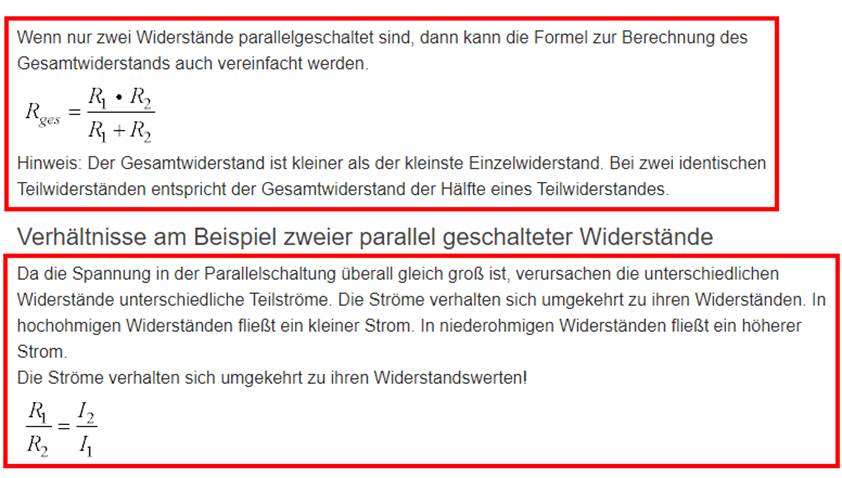
Überlagerungsverfahrens. << (Quelle: Wikipedia) Die Stromteilerformel kann man sich
am besten merken, wenn man sich die Mühe macht und diese mittels des Ohmsches Gesetzes mit
R = U / I → I = U / R " U = I * R wie folgt herleitet: Das
Charakteristische, d.h. das besondere Merkmal, der Stromteilerformel ist, dass die Spannung U und der Spannungsabfall an allen parallel geschalteten Widerständen
R gleich
groß ist: UR1 = UR2 = UR3 = … = URn. Auch und obwohl alle Glühlämpchen 18 und 27 über unterschiedliche
Nenn-Betriebsdaten UGlüh 18, Nenn, IGlüh 18, Nenn und UGlüh 27, Nenn, IGlüh 27, Nenn verfügen Glühlämpchen 18: Nennspannung UGlüh 18, Nenn = 2,5 V, Nennstromstärke IGlüh 18 = Glühlämpchen 27: Nennspannung UGlüh 27, Nenn = 6,0 V, Nennstromstärke IGlüh 27 = so lassen sich dennoch mit diesen die
Einzelwiderstände RGlüh
18 und
RGlüh 27 wie folgt berechnen: RGlüh 18 = UGlüh 18, Nenn / IGlüh 18, Nenn =
2,5 V / RGlüh 27 = UGlüh 27, Nenn / IGlüh 27, Nenn =
6,0 V /
Da
der Stromteiler
mit den beiden parallel
geschalteten Glühlämpchen an der Batteriespannung UBatt = 3,0 V
betrieben wird, fließt durch das Glühlämpchen 27 nur die hälftige
Nennstromstärke mit IGlüh 27 = IGlüh 18 / IGlüh 27 = RGlüh 27 / RGlüh 18 IGlüh 18 = ( RGlüh 27 / RGlüh 18 ) * IGlüh 27 → IGlüh 27 = UGlüh 27 / RGlüh 27 = ( UGlüh 27 /
2 )
/ RGlüh 27 = 3,0 V / 12 Ω = = ( 12 Ω / 8,33 Ω ) * Jetzt, wo wir wissen, wie
groß der Gesamtstrom IGlüh, ges
= IBatt = IGlüh 18 / IGlüh, ges = RGlüh, ges / RGlüh 18 RGlüh, ges = ( IGlüh 18 / IGlüh, ges ) * RGlüh 18 →
IGlüh, ges = IGlüh 18 + IGlüh 27 = = (
Weiter geht’s mit [ Versuch 10 ]. |
|
||||
|
|
[easy electronik 200 ] [ Seitenanfang ] [Versuch 6 ] [ Versuch 10 ] |
|