[ easy electronik 200 ] [ Seitenende ] [ Versuch 8 ] [ Versuch 10 ] [ Versuch 17 ]

easy electronic 200 - Wissenserweiterung 10-1

Vom Ohmschen Gesetz I zum Ohmschen Gesetz II

Wenn man sich das elektronische Simulationsprogramm „Circuit Simulator 2.8.1js“ von der Homepage „Paul Falstadt“ aus dem Internet herunterlädt, auf dem Windowsrechner installiert und anschließend startet, dann stößt man früher oder später in der Menüauswahl auf den Menüpunkt <Schaltungen> mit einer Sammlung von verschiedenen passiven und aktiven Bauelementen usw.

Mittels der Menüauswahl <Schaltungen>, <Weitere passive Schaltungen> und <Stromquelle> lässt sich die interessante Schaltung „Stromquelle“ in die Simulation laden:

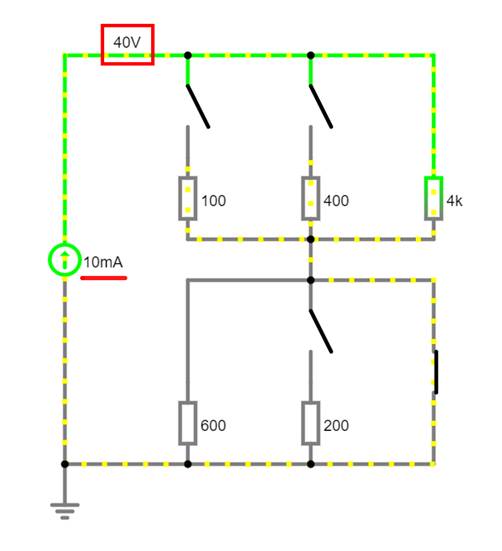
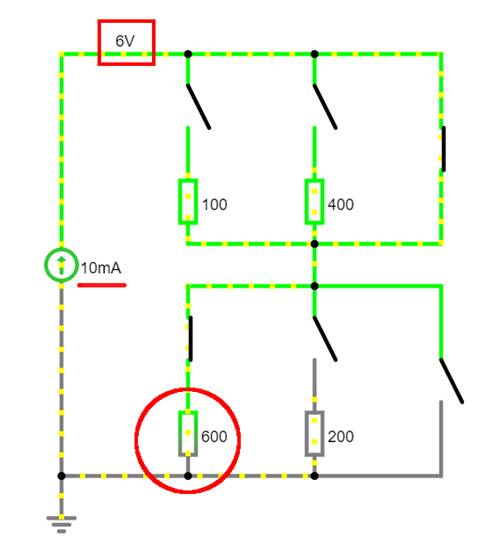
(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-01.js)

Wie man in der obenstehenden Schaltung sieht, lassen sich mittels verschiedener Schalter unterschiedliche Widerstände einstellen, d.h. zur Schaltung hinzuschalten oder abschalten. Im vorliegenden Fall ist in der Schaltung aber nur der Widerstande R_4k wirksam:

U₀ = R_4k * I₀

= 4 kW * 10 mA = 4 kV/A * 10 mA = 40 V (siehe roter Kasten im obenstehenden Bild)

Wie wir wissen, richtet sich die (Ursprungs-) Spannung U₀ einer idealen Stromquelle I₀ (= ohne Innenwiderstand R_i) stets nach dem Widerstandswert des angeschlossenen (Last-) Widerstandes R_4k als Verbraucher mit R_4k = 4 kW.

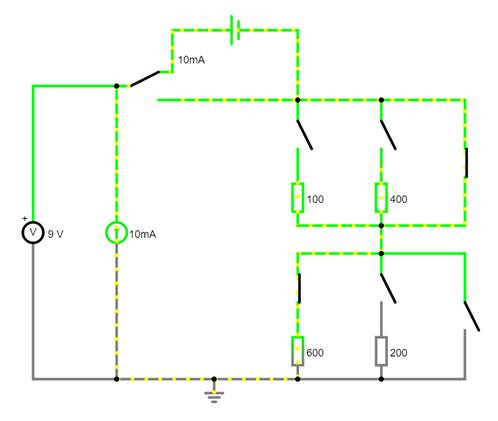
Da die resultierende Spannung U₀ mit U₀ = 40 V ziemlich groß ist und auch im Alltag eines Elektronikers eher selten vorzufinden ist, weil die meisten elektrischen Geräte wie z.B. ein Smartphone, DECT-Telefon, DAB+ Radio usw. mittels wesentlich kleineren Batteriespannungen von z.B. 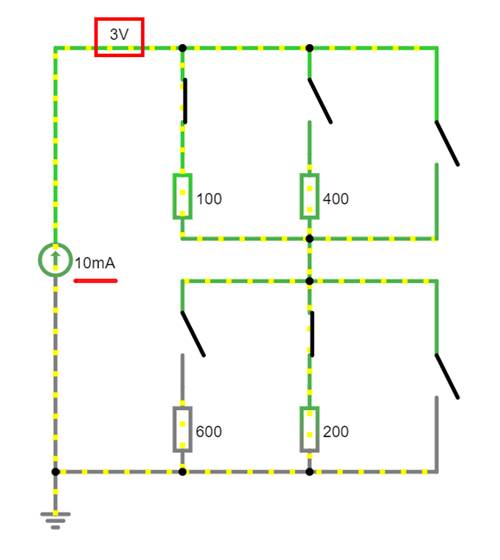3 V, 5 V, 6 V oder 9 V betrieben werden, ändern wir die vorherige Schaltung dahingehend ab, sodass diese wie folgt nur noch mit der Spannung U = 3 V betrieben wird:

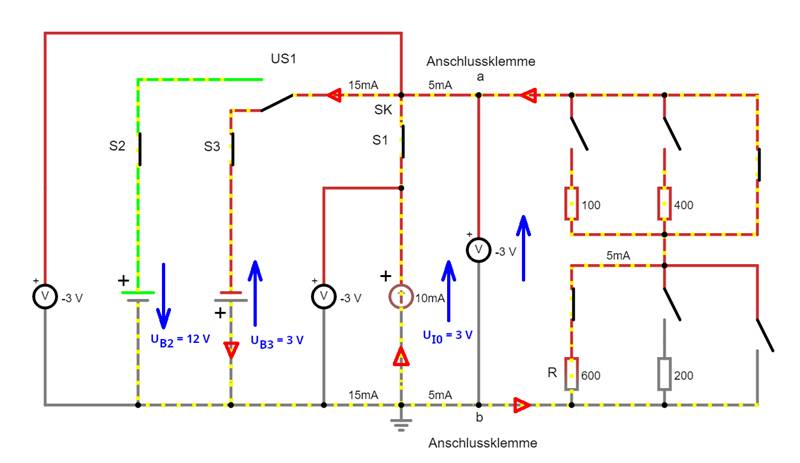
(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-02.js)

Wie man unschwer sieht, beträgt jetzt der Gesamtwiderstand R_ges:

R_ges = R₁₀₀ + R₂₀₀

= 100 W + 200 W = 300 W

U = R_ges * I₀

= 300 W * 10 mA = 300 V/A * 10 mA = 3000 mV = 3 V (siehe roter Kasten im obenstehenden Bild)

Als nächstes gehen wir der Frage nach, ob sich auf die obenstehende Schaltung mit der Stromquelle I₀ das Ohmsche Gesetz I und/oder II anwenden lässt:

R = U / I " Ohmsches Gesetz I

R_ges = U_ges / I_ges

= U_{10 mA} / I₀

= 3 V / 10 mA = 0,3 kW = 300 W þ

Da es in der obenstehenden Schaltung mit dem 300 W Gesamtwiderstand von außen keine treibende Spannungsversorgung z.B. in Form einer Batterie oder Spannungsquelle gibt, gibt es außer dem eingeprägten Konstantstrom I₀ mit I₀ = 10 mA keinen weiteren Strom I_R mit dem sich mittels eines Widerstandes R ein weitere Spannung U_R erzeugen ließe, sodass das Ohmsches Gesetz I angewendet werden darf bzw. 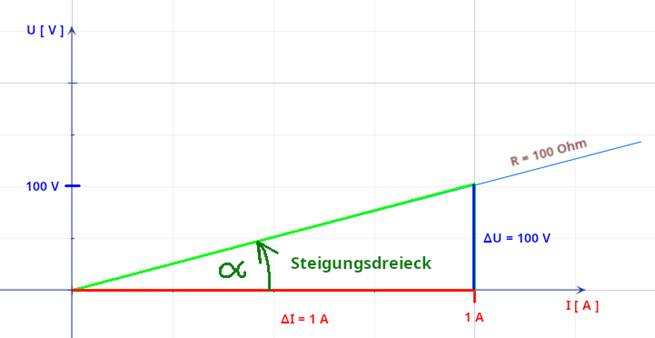zu keiner fehlerhaften Berechnung führt!

R = ∆U / ∆I " Ohmsches Gesetz II

= 6 V / 20 mA " Siehe Steigungsdreieck in der nachfolgenden Kennlinie!

= 6 V / 0,020 A = 300 V/A = 300 W þ

= ∆U / ∆I = ( U₂ – U₁ ) / ( I₂ – I₁ )

= ( U – U₀ ) / ( I – I₀ ) " In der obenstehenden Schaltung gibt es keine Spannungsquelle U₀.

= U / ( I – I₀ ) "

I – I₀ = 1 / R * U

I = 1 / R * U + I₀ " Widerstandsgerade (= Kennlinie) der obenstehenden Schaltung!

= 1/300 W * 3 V + 10 mA = 1/300 V/A * 3 V + 10 mA

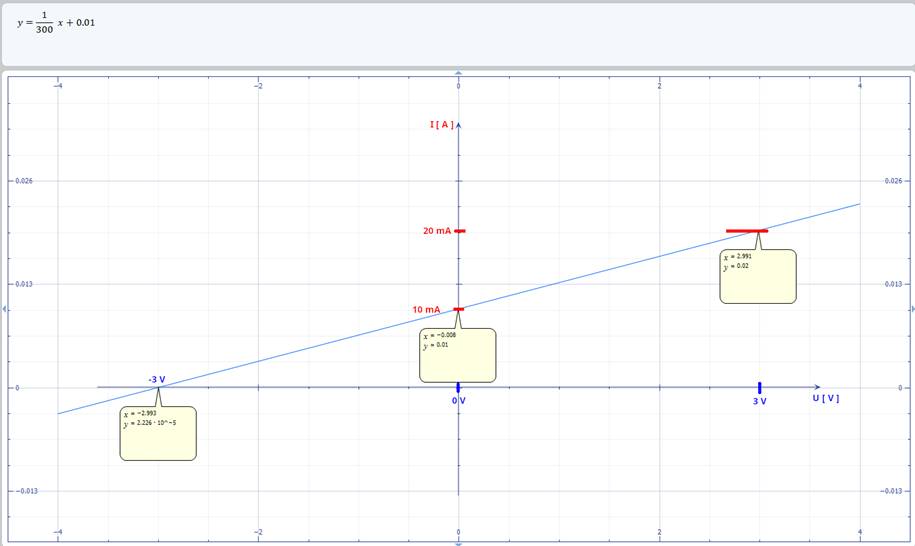
= 1/100 A + 10 mA = 0,010 A + 10 mA = 20 mA þ " Siehe nachfolgende Kennlinie!

(Vergrößern: auf Bild klicken! | MS Mathematics, easy-electronic_200, W-10-02.gcw)

Betrachtet man die obige Widerstandsgerade an der Stelle mit der Spannung U = 0 V, so lässt sich anhand des Graphen der Funktion trotzdem der Konstantstrom I₀ mit I₀ = 10 mA feststellen. Und genau das ist das typische Verhalten einer (Konstant-) Stromquelle I₀.

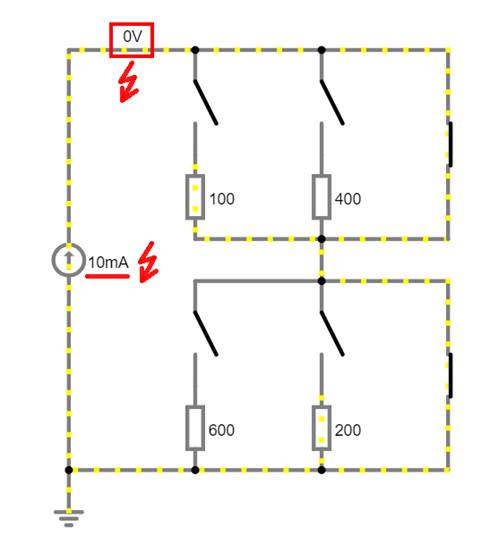
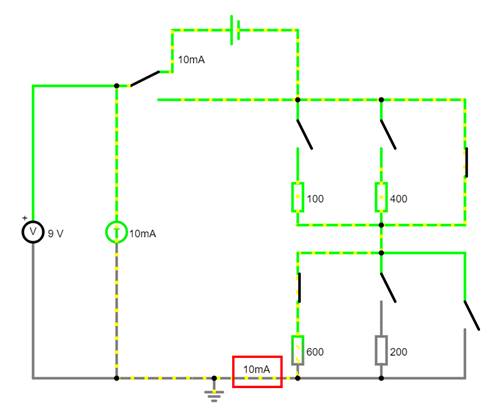
Demzufolge liefert auch die elektronische Schaltungssimulation bei einer Spannung von U = 0 V einen Stromfluss der Stromstärke I = 10 mA, wie man sich augenscheinlich überzeugen kann:

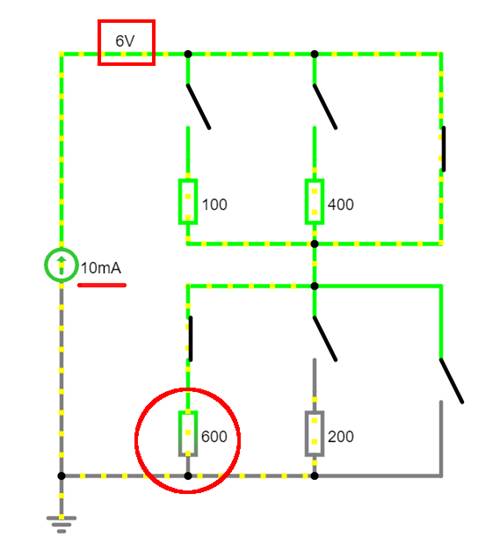
(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-03.js)

Nachfolgend soll die Spannung U bzw. der Spannungsabfall U_{R, ges} am Gesamtwiderstand R_ges auf U_{R, ges} = 6 V vergrößert werden. Dabei soll aber die Stromstärke der (Konstant-) Stromquelle I₀ mit I₀ = 10 mA unverändert bleiben! Wie groß muss der Gesamtwiderstand R_ges werden, damit sich ein Spannungsabfall U_{R, ges} von U_{R, ges} = 6 V einstellt?

Wie wir bereits wissen und gelernt haben, ist das Charakteristische einer (Konstant-) Stromquelle I₀, dass sich die Spannung U bzw. der Spannungsabfall am Widerstand R stets nach dessen Widerstandswert richtet. Und zwar im vorliegenden Fall bei unverändertem (Konstant-) Strom mit I₀ = 10 mA.

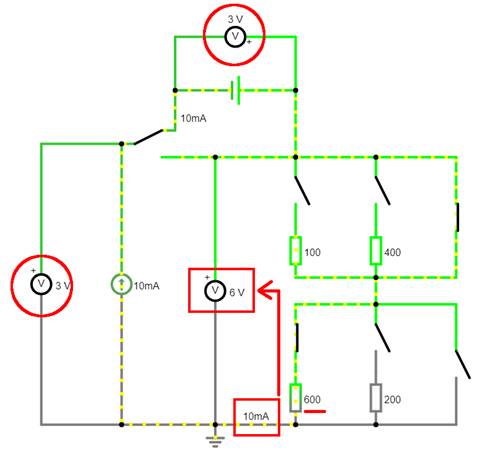
Demzufolge muss man den Widerstand R_ges von vormals R_ges = 300 W auf nunmehr R₆₀₀ = 600 W vergrößern (siehe roter Kreis unten im Bild), damit sich die Spannung U bzw. der Spannungsabfall am neuen Widerstand R₆₀₀ auf dann U_R = 6 V vergrößert:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-04.js)

Der Vorteil der Elektroniksimulation ist der, dass man die Spannungsvergrößerung auf jetzt U = U_3V + ∆U = 3 V + 3 V = 6 V einfach durch Ausprobieren und Umschalten auf den 600 W Widerstand (siehe roter Kreis) vornehmen kann.

Selbstverständlich lässt sich der erforderliche Widerstand R, um die Vergrößerung der Spannung U bzw. des Spannungsabfalls auf U_R = 6 V vorzunehmen, auch wie folgt berechnen:

R = U / I " Ohmsches Gesetz I

= ( U_3V + ∆U ) / ( I₀ + ∆I ) " … das ist neu!

= ( 3 V + 3 V ) / ( 10 mA + 0 mA )

= 6 V / 10 mA = 0,6 kW = 600 W þ

Dabei gilt es zu beachten, dass sich eine um 3 Volt vergrößerte Spannung U auch in der Form U = U_3V + ∆U und ein um 0 mA „vergrößerter“ Strom I in der Form I = I₀ + ∆I ausdrücken und berechnen lässt!

R = ∆U / ∆I " Ohmsches Gesetz II

= ( U₂ – U₁ ) / ( I₂ – I₁ )

= ( U – U₀ ) / ( I – I₀ ) " In der obenstehenden Schaltung gibt es keine Spannungsquelle U₀. "

= U / ( I – I₀ ) " In der obenstehenden Schaltung gibt es auch keine (Konstant-) Stromquelle I₀. "

I = 1 / R * U "

= 1 / R * U " Widerstandsgerade (= Kennlinie) der obenstehenden Schaltung!

= 1 / R * ( U_3V + ∆U )

= 1 / 600 W * ( 3 V + 3V )

= 0,00167 A/V * 6 V

= 1,67 mA * 6

= 10,02 mA ≈ 10 mA þ

Der vergrößerte Widerstand R = 600 W lässt selbstverständlich auch mit dem Ohmschen Gesetz II wie folgt berechnen:

R_ges = ( U – U₀ ) / ( I – I₀ ) " Im vorliegenden Fall gibt es keine (Konstant-) Spannung U₀ "

= U / I " … und auch keine (Konstant-) Stromquelle I₀

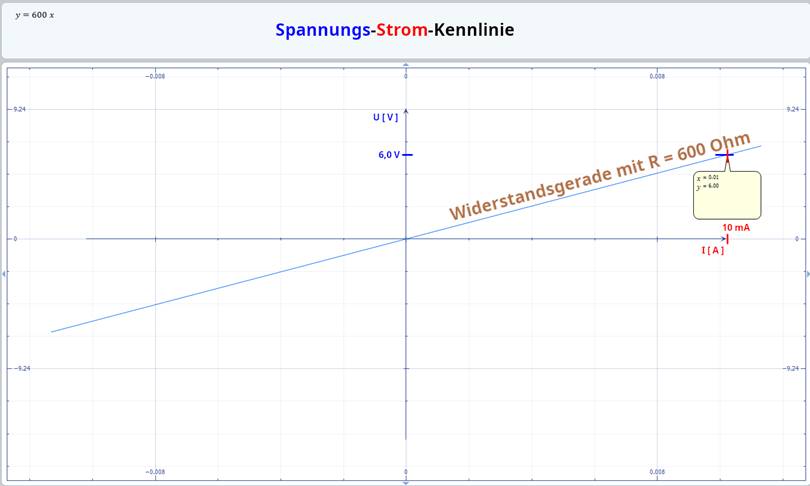
= 6 V / 10 mA = 0,6 kW = 600 W þ (Siehe weiter oben!)

U = R_ges * I " y = 600 * x " mathematische Geradengleichung

Obwohl die Stromstärke der (Konstant-) Stromquelle I₀ mit I₀ = 10 mA unverändert bleibt, ändert sich wegen des größeren Gesamtwiderstandes R_ges und des größeren Spannungsabfalls U_R, ges mit U_R, ges = 6 V die Steigung m der Widerstandskennlinie mit

m = 1 / R_ges

= 1 / ( ∆U / ∆I )

= ∆I / ∆U þ

= 10 mA / 6 V = 1,667 mS

= 0,001667 S = ( 1 / 0,001667 S )^-1= ( 599,88 W )^-1 ≈ 1 / ( 600 W ) = 1 / R_ges þ

Berechnung des Steigungswinkels a und der Steigung m im Steigungsdreieck:

Wenn man im Physikunterricht der Realschule oder in der Mittelstufe des Gymnasiums einen Blick in das Physikbuch wirft, dann stellt man anhand des Inhaltsverzeichnisses fest, dass sich die Physik in verschiedene Disziplinen wie z.B.

· Materie,

· Maße und Gewichte,

· Mechanik,

· Kinematik,

· Wärmelehre,

· Elektrizitätslehre,

· Atomphysik usw.

unterteilt.

Bei der Elektrizitätslehre geht es dann nicht nur um elektrische Potentiale, Spannungen und Ströme, sondern auch um das Ohmsche Gesetz, das Spannung U und Strom I zueinander in Beziehung bzw. ins Verhältnis setzt.

So ist der Quotient q (= das Verhältnis zweier Größen) von U und I immer konstant, d.h. unveränderlich: q = U / I = konstant.

Das Verdienst von Georg Simon Ohm war es dabei, dass dieser herausgefunden hat, dass der konstante Quotient q = U / I dem elektrischen Widerstand R entspricht: R = U / I.

Und weil viele Menschen, die nicht Elektrotechnik/Elektronik studiert haben, sich das Ohmsche Gesetz auf Dauer nicht merken können, weil sie keine Beziehung zu diesem haben und nicht mit dem Ohmsche Gesetz leben, prägen sie sich die Gedächtnisstütze „URI“ ein, weil das so ähnlich klingt wie „urig“ (= urwüchsig, urtümlich, sonderbar, originell, seltsam) oder wie Uri Geller, der Gabeln mit angeblich magischen Kräften verbogen hat.

Tatsächlich ist die Gedächtnisstütze „URI“ gar nicht so schlecht und sogar noch besser als das Ohmsche Gesetz R = U / I selbst, weil in „URI“ die Gleichung bzw. Funktion U = f(I) mit U = R * I steckt.

Dabei ist der Widerstand R die Unveränderliche, die Konstante, die sich nicht ändert, außer wenn man den Widerstand R überlastet, sodass dieser stark erhitzt und durchschmort.

Da der Strom I auf der rechten Seite der Gleichung steht, handelt es sich bei diesem mathematisch um die unabhängige Variable I. Der Strom I als unabhängige Variable, ist sozusagen frei, vogelfrei im Sinne von ungebunden, unabhängig. Der Strom I als unabhängige Variable ist sozusagen das Rädchen, die Stellschraube an der man dreht bzw. „Gas geben kann“, pardon „Strom geben kann“.

In der Praxis aber wird der unabhängige Strom I vom Widerstand R ausgebremst bzw. auf ein bestimmtes Maß begrenzt, man könnte auch sagen reduziert. Im Stromkreis wird nämlich vom Widerstand R über die Zeit t immer nur eine bestimmte Menge, lateinisch „Quantum Q“ mit Q = I * t an elektrischem Strom „durchgelassen“, das aber gleichmäßig und konstant.

Auf der linken Seite der Gleichung steht die Spannung U als abhängige Variable, die das Ergebnis der Berechnung anhand der Formel (= Rechenvorschrift, Rechenanweisung) U = R * I enthält. Diesbezüglich spricht man auch von der Ergebnisvariablen (auf der linken Seite der Gleichung).

In der Mathematik gibt es zu jeder rechnerischen Lösung bzw. zu jedem Lösungsweg auch eine grafische Veranschaulichung und grafische Lösung z.B. in Form des Graphen einer Funktion (= Kennlinie, Diagramm) im Koordinatensystem:

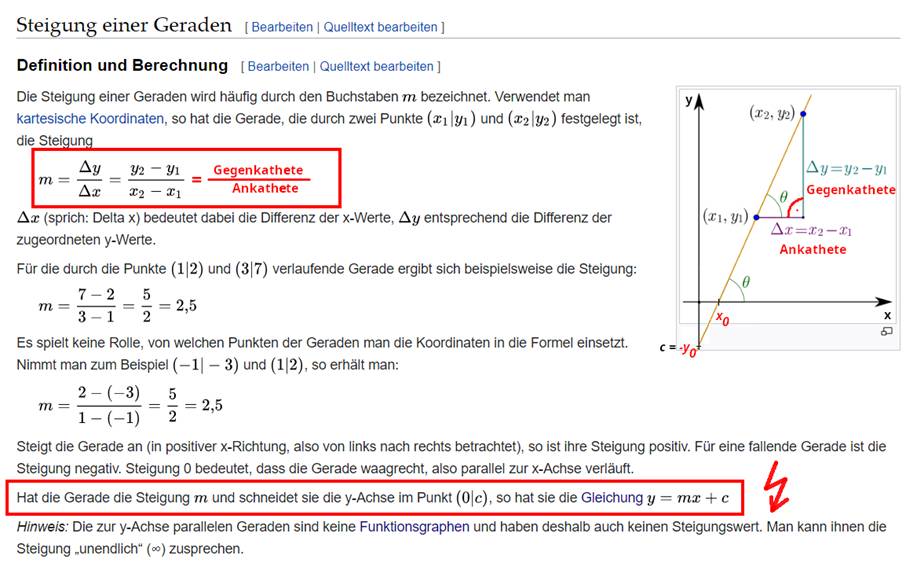
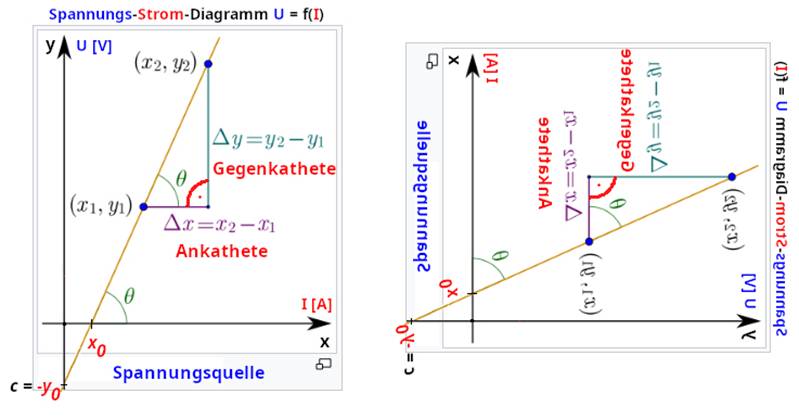
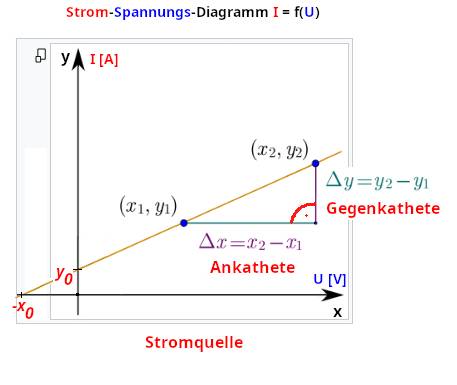
(Zum Vergrößern bitte auf das Bild klicken!)

Mathematische Berechnung der Steigung m für die Geradengleichung

y = m x + b " m = Steigung, b = Parallelverschiebung aus dem Koordinatenursprung

m = ∆y / ∆x

tan a = Gegenkathete / Ankathete = ∆y / ∆x

a = arctan(m)

(Vergrößern: auf Bild klicken! | Wikipedia, Definition und Berechnung der Steigung)

Elektrotechnische Berechnung der Steigung m mit dem Widerstand R

m = R " Geradengleichung y = m x + b " Widerstandsgerade I = 1 / R * U + I₀

R = ∆U / ∆I

= ( U₂ – U₁ ) / ( I₂ – I₁ ) mit U₂ > U₁ und I₂ > I₁

= ( 100 V – 0 V ) / ( 1 A – 0 A ) = 100 V / 1 A = 100 V/A = 100 W þ

R * ( I₂ – I₁ ) = ( U₂ – U₁ ) … linke und rechte Seite vertauschen!

( U₂ – U₁ ) = R * ( I₂ – I₁ ) "

( U – U₀ ) = R * ( I – I₀ ) "

Allgemeine Form der Widerstandsgeraden:

U = R * ( I – I₀ ) + U₀ " Widerstandsgerade mit U₀ und I₀ als Parallelverschiebung aus dem Koordinatenursprung!

Widerstandsgerade nur mit U₀ als Parallelverschiebung nach oben oder unten:

U = R * I + U₀

Widerstandsgerade nur mit Widerstand R:

U = R * I " das berüchtigte „URI“

= ∆U / ∆I * I

= Gegenkathete ∆U / Ankathete ∆I * I

= tan a * I "

tan a = U / I = R 7

= 100 V / 1 A = 100 W þ …siehe weiter oben!

tan a = 100 "

a = arctan ( 100 )

= 89,427^o

Wegen des unterschiedlichen Maßstabes bei der Bemaßung der Achsen des Koordinatensystems im Programm „Mathematics“ von Microsoft, lässt sich der Winkel a des Steigungsdreiecks nicht maßstabsgerecht bzw. im 1:1 Seitenverhältnis darstellen. -

Die Aussage, dass der tan a gleich dem Widerstand R und dessen Steigung m im Steigungsdreieck ist, findet sich in jedem guten Fachbuch der Elektrotechnik.

Dabei wird aber oftmals verschwiegen bzw. unterschlagen, dass diese Aussage nur für die „Allgemeine Form der Widerstandsgeraden mit der Geradengleichung“

U = R * ( I – I₀ ) + U₀ " Ohmsches Gesetz II " für Spannungsquelle U₀

oder U = R * I " Ohmsches Gesetz I

gilt! Und zwar mit den Koordinatenachsen x " I in der Waagrechten und y " U in der Senkrechten!

Mal sehen, ob der Steigungswinkel a dem Tangens von tan(a) = R entspricht:

U = R * ( I – I₀ ) + U₀ " U = f(I)

U = R * I

= 100 W * 1 A =

= 100 V/A * 1 A = 1 V þ

tan(a) = Gegenkathete ∆U / Ankathete ∆I

= ∆U / ∆I

= R

= 100 W = 100

a = arctan( 100 ) = 89,427^o ≈ 89,4^o

Selbstverständlich lässt sich die „Allgemeine Form der Widerstandsgeraden mit der Geradengleichung“

U = R * ( I – I₀ ) + U₀ " U = f(I)

auch wie folgt nach I = f(U) umstellen:

U = R * ( I – I₀ ) + U₀

( U - U₀ ) = R * ( I – I₀ )

1 / R * ( U - U₀ ) = ( I – I₀ )

( I – I₀ ) = 1 / R * ( U - U₀ )

I = 1 / R * ( U - U₀ ) + I₀ " Ohmsches Gesetz II " für Stromquelle I₀

oder I = 1 / R * U " Ohmsches Gesetz I

Und zwar mit den Koordinatenachsen x " U in der Waagrechten und y " I in der Senkrechten!

Mal sehen, ob der Steigungswinkel a dem Tangens von tan(a) = 1 / R entspricht:

I = 1 / R * ( U - U₀ ) + I₀ " I = f(U)

I = 1 / R * U

= 1 / 100 W * 100 V

= 1 / ( 100 V/A ) * 100 V = 1 A þ

tan(a) = Gegenkathete ∆I / Ankathete ∆U

= ∆I / ∆U

= 1 / R

= 1 / 100 W = 0,01

a = arctan( 0,01 ) = 0,57294^o ≈ 0,57^o

Wie man anhand des sehr kleinen Steigungswinkels a sieht, verläuft die Widerstandsgerade jetzt ganz flach in Richtung der Spannungsachse (= x-Achse im Koordinatensystem), während die Stromachse (= y-Achse im Koordinatensystem) senkrecht nach oben verläuft (Bild rechts):

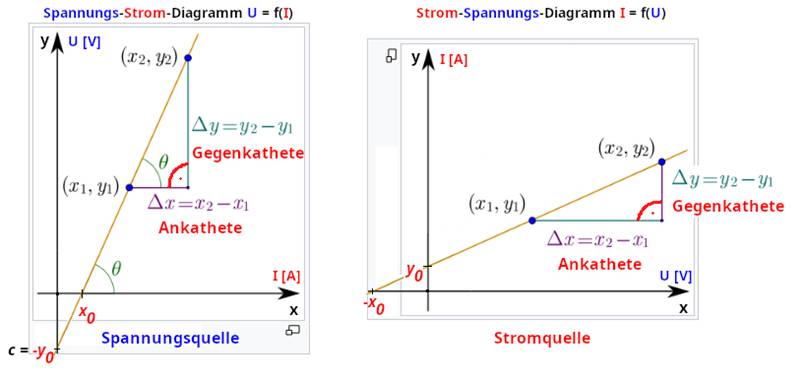
(Vergrößern: auf Bild klicken! | Wikipedia, Definition und Berechnung der Steigung)

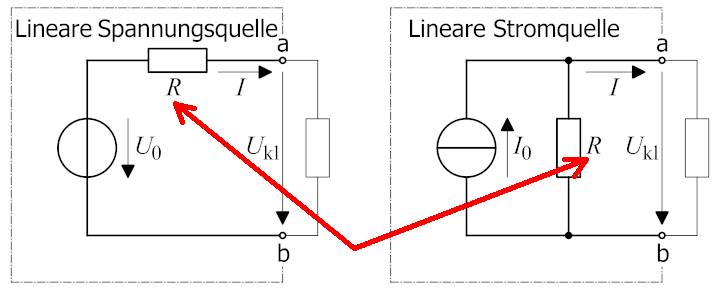
Noch einmal zur Verdeutlichung (siehe im Bild oben): das linke Diagramm bezieht sich mit der Widerstandgeraden auf das Ohmsche Gesetz II mit der Gleichung U = R * ( I – I₀ ) + U₀, während sich das rechte Diagramm auf die Gleichung I = 1 / R * ( U - U₀ ) + I₀ bezieht.

Da sich das Ohmsche Gesetz II mit der Gleichung U = R * ( I – I₀ ) + U₀ in die Gleichung I = 1 / R * ( U - U₀ ) + I₀ umrechnen lässt, verhalten sich beide zugrundeliegenden Schaltungen mit der Spannungsquelle einerseits und der Stromquelle andererseits äquivalent, d.h. gleichwertig zueinander! Demzufolge müssen die Steigungen beider Widerstandsgeraden (= Kennlinie) ebenfalls gleich sein:

Steigungswinkel a der Spannungsquelle (siehe oben links im Bild)

tan(a) = Gegenkathete / Ankathete = ∆y / ∆x

= Gegenkathete / Ankathete = ∆U / ∆I

= R = ∆U / ∆I

Steigungswinkel a der Stromquelle (siehe oben rechts im Bild)

tan(a) = Gegenkathete / Ankathete = ∆y / ∆x

= Gegenkathete / Ankathete = ∆I / ∆U

= G = 1 / R " elektrischer Leitwert G mit der Maßeinheit „Siemens“ [S]

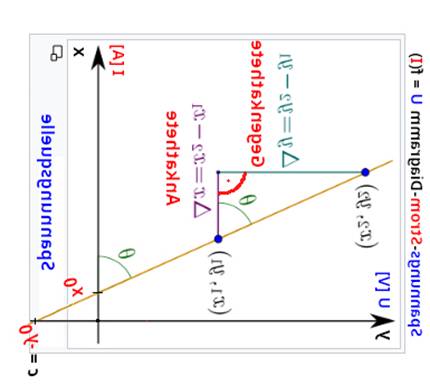
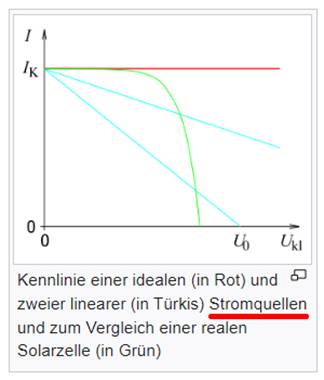
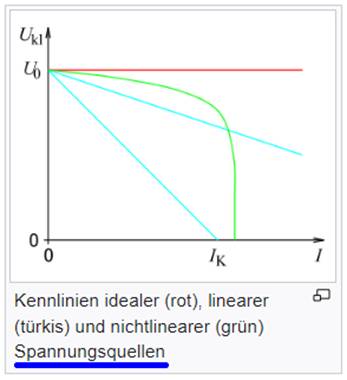
Nun ist also durch die Formel G = 1 / R eindeutig bewiesen, dass beide Schaltungen über ein und denselben Steigungswinkel a verfügen und demzufolge tatsächlich zueinander äquivalent sind!

Demzufolge ist das rechte Diagramm mit der Stromquelle und der Gleichung I = 1 / R * ( U - U₀ ) + I₀ falsch (siehe im Bild oben rechts)! 7

Nimmt man nämlich das linke Diagramm mit der Spannungsquelle, dreht das Ganze um 90^o nach links, spiegelt das nach links gedrehte Bild um die Vertikalachse

(Vergrößern: auf Bild klicken! | Wikipedia, Definition und Berechnung der Steigung)

und vertauscht abschließend noch die y- mit der x-Achse, dann entsteht das falsche(!) rechte Diagramm mit der Stromquelle:

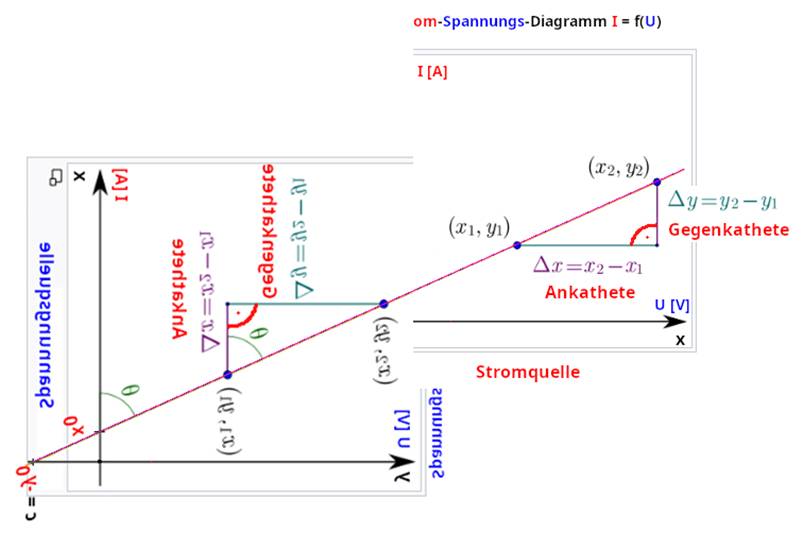
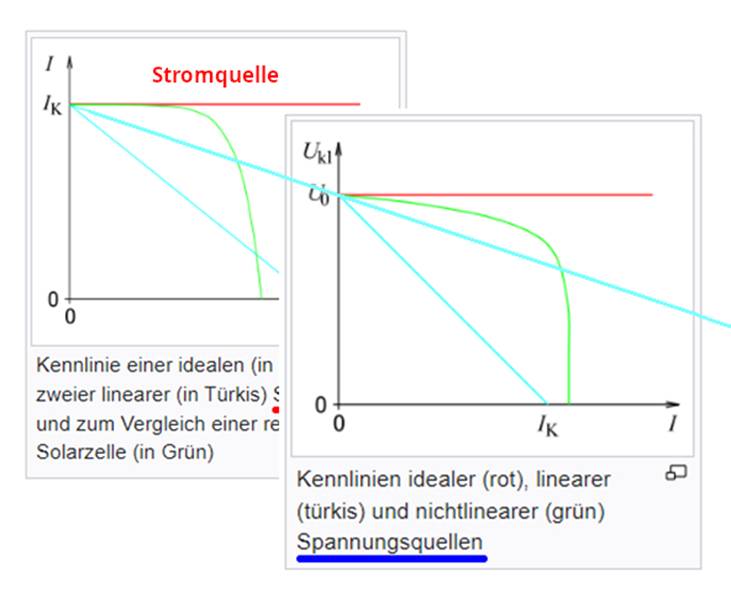
Während das Drehen und Spiegeln des Spannungs-Strom-Diagramms U = f(I) noch in Ordnung ist, geht das willkürliche Vertauschen der y- mit der x-Achse überhaupt nicht!

Aber wenn man die beiden Kennlinien jetzt nebeneinander legt und etwas ineinander verschiebt, dann sieht man sehr gut, dass der Steigungswinkel a bei der Spannungs- und der Stromquelle gleich groß ist, gleich groß sein muss:

(Zum Vergrößern bitte auf das Bild klicken!)

Und den Grund dafür, dass der Steigungswinkel a bei der Spannungs- und der Stromquelle gleich groß ist, kennen wir ja bereits, weil sich die Gleichung U = R * ( I – I₀ ) + U₀ mit der Spannungsquelle U₀ aus der Gleichung I = 1 / R * ( U - U₀ ) + I₀ mit der Stromquelle I₀ ableiten lässt und umgekehrt!

Ohmsches Gesetz II mit zusätzlicher Spannungsquelle U₀ und/oder Stromquelle I₀

Wir wenden uns wieder der Schaltung „easy-electronic_200, W-10-04.js“ mit der Stromquelle I₀ = 10 mA und dem Widerstand R = 600 W zu

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-04.js)

und berechnen diese mit dem Ohmschen Gesetz II und der Gleichung

I = 1 / R * ( U - U₀ ) + I₀ " U₀ = 0 und I₀ = 0, da in der Schaltung nicht vorhanden!

= 1 / R * U

= 1 / ( 600 W ) * 6 V

= 1 / ( 600 V/A ) * 6 V = 6 / 600 A = 10 mA

Als nächstes geht es darum, dass wir die Versorgungsspannung der Schaltung von vormals U_6V = 6 V auf U_9V = U_6V + ∆U = 9 V erhöhen. Und zwar durch Hinzuschalten der (Konstant-) Spannungsquelle U₀.

Demzufolge muss die Versorgungsspannung der Schaltung um ∆U = 3 V vergrößert werden. Diesbezüglich liegt es nahe, dass man die (Konstant-) Spannungsquelle U₀ mit U₀ = ∆U = 3 V in Reihe zur (Konstant-) Stromquelle I₀ hinzu schaltet:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-06.js)

Dabei lässt sich mittels des Umschalters zwischen der Versorgungsspannung von U_6V = 6 V auf U_9V = 9 V beliebig hin- und herschalten.

In diesem Zusammenhang stellt sich nun die Frage, wie sich die um die (Konstant-) Spannungsquelle erweiterte Schaltung berechnen lässt:

U = R * ( I – I₀ ) + U₀ " Ohmsches Gesetz II " für Spannungsquelle U_3V mit U₀ = U_3v = 3 V

U - U₀ = R * ( I – I₀ )

( U - U₀ ) / R = ( I – I₀ )

I = ( U - U₀ ) / R + I₀

= ( 9 V – 3 V ) / 600 W + 10 mA = 1 V / ( 100 V/A ) + 10 mA = 20 mA " FALSCH!

Wie man aber anhand der nächsten Schaltung und des nachfolgenden Screenshots sieht, beläuft sich die Stromstärke I auf nur I = 10 mA (siehe im roten Kasten). Diesbezüglich stellt sich die Frage, weshalb sich die Stromstärke I auf nur I = 10 mA beläuft!

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-07.js)

Die Frage aber, weshalb sich die Stromstärke I auf nur I = 10 mA beläuft, lässt sich ganz einfach beantworten! Und zwar deshalb, weil die Stromquelle I₀ in der gesamten(!) Schaltung einen eingeprägten Strom I₀ = 10 mA „auf’s Auge drückt!“, wobei der eingeprägte Strom I₀ = 10 mA selbstverständlich auch durch die hinzu geschaltete Batterie mit U₀ = 3 V fließt! Und zwar unabhängig davon, wie die 3 Volt Batterie gepolt ist!

Außerdem gilt es zu beachten, dass die Stromquelle mit dem eingeprägten Strom I₀ = 10 mA immer nur zusammen mit einem Widerstand einen Spannungsabfall (am Widerstand selbst) aufzubauen vermag (siehe rote Kästen)!

Deshalb ändert auch die hinzu geschaltete und falsch gepolte Batterie mit U₀ = 3 V nichts am Spannungsabfall des Widerstandes R (siehe vorherige Schaltung „easy-electronic_200, W-10-07.js“ und die Voltmeter nebst Polung in den roten Kreisen der nachfolgenden Schaltung):

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-08.js)

Nach den Fehlerkorrekturen stellt sich die Berechnung des Stromes I jetzt wie folgt dar:

U = R * ( I – I₀ ) + U₀ " Ohmsches Gesetz II " für Spannungsquelle U_3V mit U₀ = U_3v = 3 V

U - U₀ = R * ( I – I₀ )

( U - U₀ ) / R = ( I – I₀ )

I = ( U - U₀ ) / R + I₀

= ( 3 V – 3 V ) / 600 W + 10 mA = 0 V / ( 100 V/A ) + 10 mA = 10 mA þ

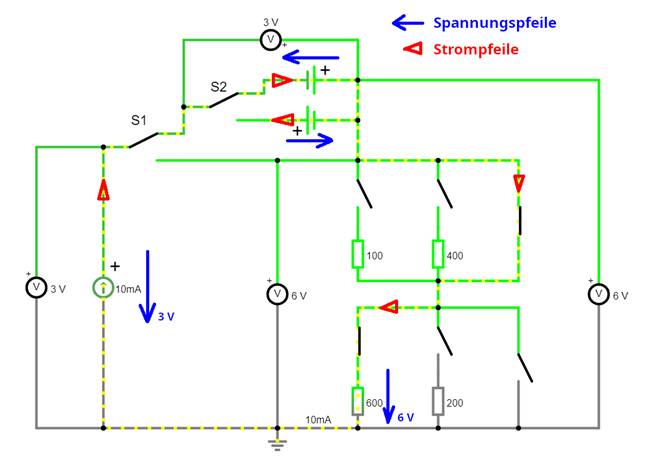
Um das mit dem eingeprägten Strom I₀ = 10 mA noch besser zu verstehen, setzen wir noch einen drauf und erweitern die obenstehende Schaltung dahingehend, indem wir noch eine zweite 3 Volt Batterie mit entgegengesetzter Polung nebst Umschalter wie folgt hinzufügen:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-09.js)

Wie gesagt, richtet sich der Spannungsabfall U_R = 6 V am Widerstand R = 600 W stets nach dem eingeprägten Strom I₀ = 10 mA der (Konstant-) Stromquelle I₀, sodass sich die (Konstant-) Stromquelle I₀ und die 3 Volt Spannungsquelle den Spannungsabfall von U_R = U_I0 + U_3V = 6 V miteinander als Spannungsteiler aufteilen müssen:

U_I0 = U_R - U_3V = 6 V – 3 V = 3 V " durch Umschalten des Schalters S2 folgt "

U_I0 = U_R - U_3V = 6 V – ( -3 V ) = 9 V

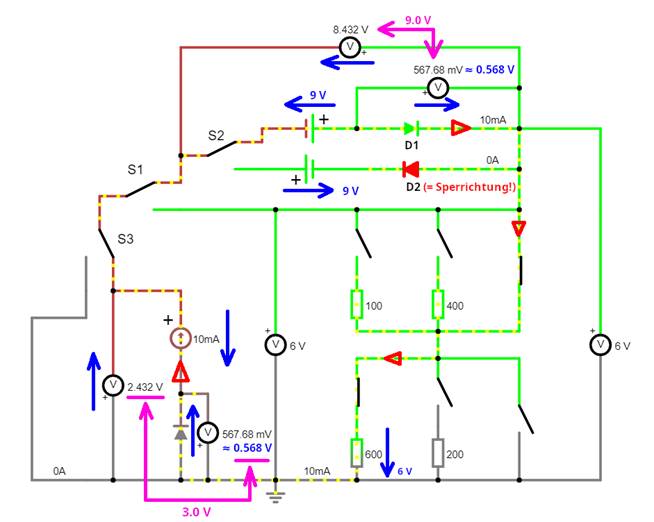
Wenn man sich nicht sicher ist, in welche Richtung der eingeprägte (Konstant-) Strom der Stromquelle I₀ = 10 mA fließt, dann kann man hinter den beiden Spannungsquellen jeweils eine Diode, sozusagen als elektrisches Ventil, einfügen, sodass der elektrische Strom immer nur in eine Richtung fließen kann:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-10.js)

Dabei hat jede Diode in Durchlassrichtung eine Durchlassspannung von U_F ≈ 0,568 V. Der Index „F“ steht dabei für den engl. Ausdruck „forward“, d.h. vorwärts (in Durchlassrichtung).

Diesbezüglich gilt es zu beachten, dass die Durchlassspannung U_F ≈ 0,568 V von dem Spannungsabfall (= 3 V) an der Stromquelle I₀ oder den beiden Batterien (= 9 V) subtrahiert werden muss (siehe pinkfarbene Doppelpfeile), da die jeweilige Diode ein elektrischer Verbraucher ist!

In diesem Zusammenhang gilt es ferner zu beachten, dass der Spannungspfeil einer Strom- oder Spannungsquelle, da diese zu den Energieerzeugern zählen, zu den anderen Spannungspfeilen der angeschlossenen Verbraucher stets entgegengesetzt gerichtet ist! Der Grund dafür ist der, dass ein Volt- und Amperemeter ebenfalls ein Verbraucher ist, wenn auch mit einem sehr, sehr geringem Energieverbrauch!

Zur Erinnerung sei nochmals gesagt, dass sich der eingeprägte Strom der Stromquelle I₀ in der obenstehenden Schaltung „easy-electronic_200, W-10-10.js“ überall „durchsetzt!“

Demzufolge fließt der eingeprägte Strom der Stromquelle I₀ über die Wechselschalter S3, S1 und S2 in die 9 Volt Batterie hinein, dann wieder aus der 9 Volt Batterie heraus, über die Diode D1 in Durchlassrichtung hin zum 600 W Widerstand als Verbraucher und von dort wieder zurück zur Stromquelle I₀.

Der Unterschied zwischen einer Batterie und einem Akku(mulator) ist der, dass sich ein entladener Akku jederzeit wieder aufladen lässt. Im Gegensatz zu einem Akku lässt sich eine leere, d.h. entladene Batterie nicht wieder aufladen, da sich der chemische Umwandlungs- und Zersetzungsprozess bei der Entladung der Batterie nicht wieder rückgängig machen lässt. Trotzdem handelt es sich bei beiden um einen elektrischen Leiter, der elektrischen Strom leitet. Dabei entstammt dieser bei einer neuen, sozusagen chemisch aufgeladenen Batterie dem Elektrolyten zwischen den Elektroden (= Anode und Kathode). Dabei haben die Begriffe Anode und Kathode aber nichts mit dem Vorzeichen der Polung der Batterie zu tun!

Bei einer altersschwachen, d.h. größtenteils bereits entladenen Batterie vergrößert sich mit zunehmender Entladung der Innenwiderstand R_{i, Batt} der Batterie, sodass sich gleichzeitig die an den Batterieklemmen zur Verfügung stehende Batteriespannung als auch Stromstärke mehr und mehr verringern: U_Batt = R_{i, Batt} * I_Entlade mit R_{i, Batt} " ¥ und I_Entlade "0 bis schließlich das angeschlossene Elektrogerät oder der Motor keinen Mucks mehr von sich geben.

Dabei verhält es sich so, dass man einer entladenen Batterie wieder etwas „auf die Sprünge helfen kann“, indem man diese bildlich gesprochen „ins Kreuz oder den Allerwertesten tritt.“ Ähnlich wie im vorliegenden Fall in der obenstehenden Schaltung „easy-electronic_200, W-10-10.js“ mit den Wechselschaltern S3, S1 und S2. Dort wird nämlich der entladenen 9 Volt Batterie der eingeprägte (Konstant-) Strom der Stromquelle I₀ = 10 mA von links kommend zugeführt, der wiederum mit dem Innenwiderstand R_{i, Batt} der Batterie zu dem Spannungsabfall von z.B. U_10mA = R_{i, Batt} * I₀ = 920 W * 10 mA = 9200 mV = 9,2 V mit U_10mA > U_Batt führen kann. Da dabei der Spannungsabfall U_10mA an der Batterie zwangsweise auf mehr als U_{Batt, Nenn} = 9,0 V ansteigen kann, erwärmt sich der Elektrolyt im Inneren der Batterie entsprechend, dehnt sich dabei aus und sprengt das Batteriegehäuse auf, sodass der auslaufende Elektrolyt das Batteriefach und die Batteriekontakte verätzt! Es versteht sich also von selbst, dass man es niemals so weit kommen lassen sollte!

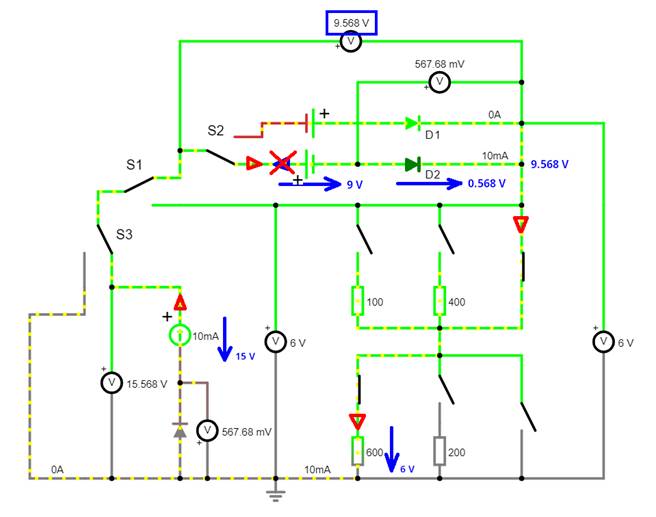
Aber es ist eben trotzdem gut zu wissen, dass ein von außen zugeführter Konstantstrom eine Batterie den Hitzetod sterben lassen kann! Insbesondere dann, wenn der eingeprägte (Konstant-) Strom der Stromquelle I₀ = 10 mA von links kommend - also ganz entgegengesetzt zur Stromflussrichtung der 9 Volt Batterie - zugeführt wird:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-11.js)

Gegenüber der vorherigen Schaltung wird jetzt die Diode D2 nicht mehr in Sperrrichtung, sondern durch Umpolen in Durchlassrichtung betrieben, sodass diese nun den eingeprägte (Konstant-) Strom der Stromquelle I₀ = 10 mA hindurch lässt! Dabei entsteht an der Diode D2 ein Spannungsabfall von U_F ≈ 0,568 V. Der Index „F“ steht für den engl. Ausdruck „forward“, d.h. vorwärts (in Durchlassrichtung).

Da aber jetzt die 9 Volt Batterie wegen der entsprechenden Polung nicht mehr bestimmungsgemäß als Energielieferant arbeitet, sondern durch den aufgezwungenen (Konstant-) Strom von I₀ = 10 mA geringfügig „aufgeladen“, d.h. aufgefrischt wird, verläuft der Spannungspfeil an der Batterie in die selbe Richtung wie der Spannungspfeil am 600 W Widerstand, sodass sich beide Spannungen wie folgt addieren:

U_ges = U_Batt + U_D2 + U_R600

= 9 V + 0,568 V + 6 V = 15,568 V

Der eingangsseitige Spannungsabfall U_{10 mA} + U_F an der (Konstant-) Stromquelle I₀ berechnet sich gemäß dem Maschenumlauf im Uhrzeigersinn wie folgt:

U_Batt + U_D2 + U_R600 + ( - U_F ) + ( - U_{10 mA} ) = 0 "

U_Batt + U_D2 + U_R600 = U_F + U_{10 mA}

U_{10 mA} = U_Batt + U_D2 + U_R600 - U_F " U_D2 = U_F

= U_Batt + U_R600

= 9 V + 6 V = 15 V " Siehe Spannungspfeil an der (Konstant-) Stromquelle I₀ in der obenstehenden Schaltung!

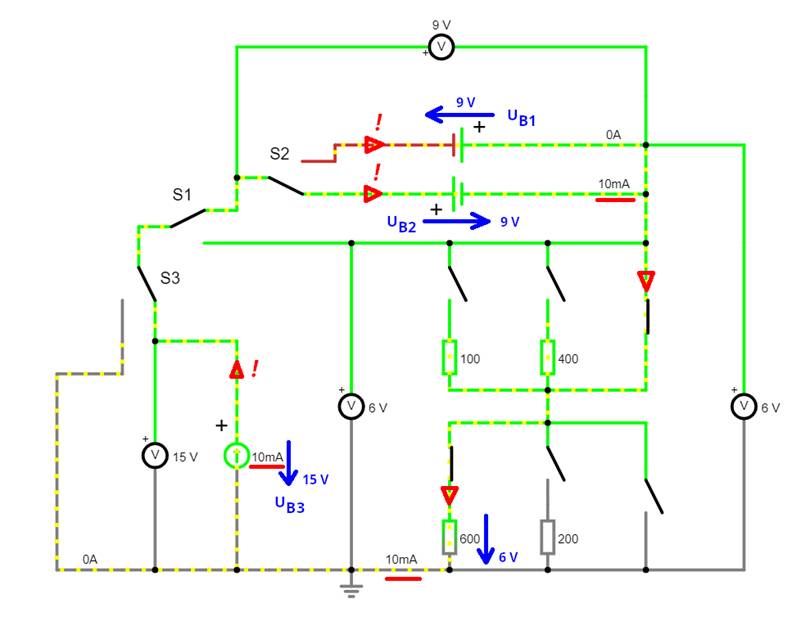
Jetzt wo wir wissen, was es mit den beiden entgegengesetzt gepolten 9 Volt Batterien auf sich hat und wie diese arbeitsteilig bezüglich (Batterie-) Spannung und (Konstant-) Strom mit der (Konstant-) Stromquelle I₀ zusammenarbeiten, können wir die obenstehende Schaltung wieder vereinfachen und die „Stromfluß“-Dioden entfernen:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-12.js)

So wie sich eine lineare Spannungsquelle U₀ (unten links) problemlos in eine lineare Stromquelle I₀ (unten rechts) umrechnen lässt,

(Wikipedia: Von Saure, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=12632634 )

lässt sich auch eine lineare Stromquelle I₀ jederzeit in eine lineare Spannungsquelle U₀ umrechnen.

Dabei verfügt sowohl die lineare Spannungsquelle U₀ als auch die lineare Stromquelle I₀ wegen der äquivalenten Umrechnung jeweils über den gleich großen Widerstand R mit der gleichen Steigung m (= R) bei der linearen Spannungsquelle U₀ mit

U = R * ( I – I₀ ) + U₀ " Ohmsches Gesetz II " zur Berechnung der Spannung am Widerstand R

sowie über den gleich großen Widerstand R mit der gleichen Steigung m (= 1 / R) bei der linearen Stromquelle I₀ mit

I = 1 / R * ( U - U₀ ) + I₀ " Ohmsches Gesetz II " zur Berechnung der Stromstärke am Widerstand R

Obwohl beide Energiequellen U₀ und I₀ über ein und denselben Widerstand R mit jeweils der gleichen Steigung m und den gleichen Steigungswinkel a verfügen, verlaufen deren Kennlinien innerhalb des Koordinatensystems zwar deckungsgleich, trotzdem aber an verschiedenen Positionen:

(Vergrößern: auf Bild klicken! | Wikipedia (links), Wikipedia (rechts))

(Zum Vergrößern bitte auf das Bild klicken!)

Demzufolge sorgt nur die Stromquelle I₀ mit ihrem eingeprägten Strom I₀ = 10 mA am Widerstand R = 600 W für den entsprechenden Spannungsabfall U_R,

U = R * ( I – I₀ ) + U₀ " Ohmsches Gesetz II

U_R = R * I " Ohmsches Gesetz I wegen I = I₀ und U₀ = 0 " Kennlinie nur für den Widerstand allein!

= 600 W * 10 mA = 6 V þ

(Zum Vergrößern bitte auf das Bild klicken!)

Das Ohmsche Gesetz II sollte eigentlich nur dann eingesetzt werden, wenn es in der Schaltung wegen einer Stromquelle I₀ und/oder einer Spannungsquelle U₀ zu einer Parallelverschiebung der Widerstandsgeraden aus dem Ursprung des Koordinatensystems kommt.

Mit dem Ohmschen Gesetz II lässt sich die Spannung U aber auch direkt am Widerstand R berechnen. Allerdings sollte es vor oder nach dem Widerstand R keinen Stromknoten geben, bei dem ein (Konstant-) Strom I₀ abzweigt (oder hinzugefügt) wird, sodass es weder eine Stromdifferenz (I – I₀ ) noch eine Stromänderung ∆I gibt: I = I₀. Außerdem sollte parallel zum Widerstand R keine Spannungsquelle mit einer aufgeprägten Spannung U₀ zugeschaltet sein: U₀ = 0. Kurz gesagt: Wenn es allein nur um die Kennlinie und die Berechnung des Widerstandes R geht, dann lässt sich das Ohmsche Gesetz I direkt anwenden, was natürlich einfacher ist, weil es kein I₀ oder U₀ gibt.

Wenn es hingegen um die Kennlinie und die Berechnung einer Strom- und/oder Spannungsquelle geht, die auch noch mit einem Widerstand R beschaltet ist, der als Innenwiderstand R_i in die Berechnung eingeht, dann kommt man um das Ohmschen Gesetz II nicht umhin!

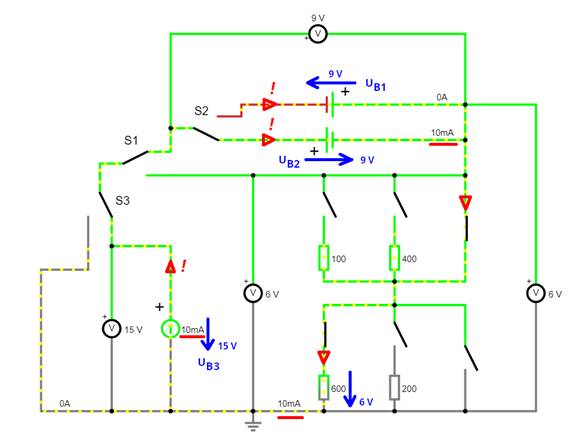
Die obenstehende Schaltung „easy-electronic_200, W-10-12.js“ (siehe Bild oben) besteht im Wesentlichen aus drei Teilen. Und zwar aus der (Konstant-) Stromquelle I₀, über die Schalter S3, S1 und S2 in Reihe geschaltete Spannungsquelle U_B2 und dem gemeinsamen Widerstand R, der sowohl dem Innenwiderstand R_i der (Konstant-) Stromquelle I₀ als auch der Spannungsquelle U_B2 zugeordnet werden kann.

Für den äußeren Maschenumlauf im Uhrzeigersinn folgt:

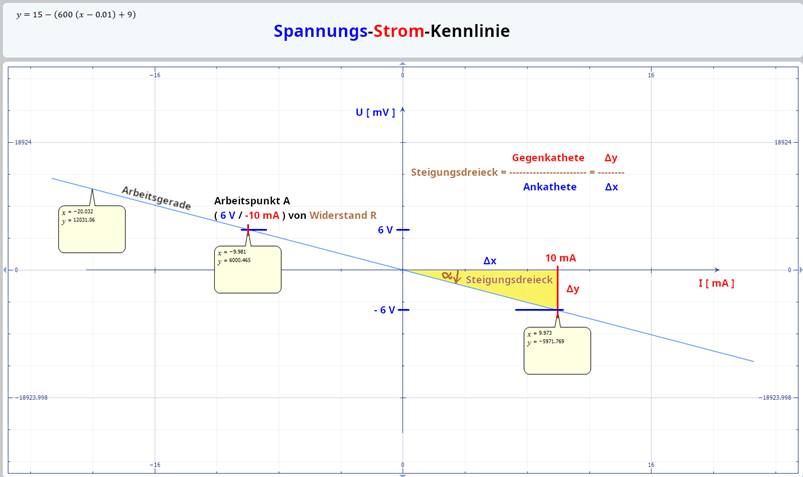
( - U_B3 ) + U_B2 + U_R = 0 " … wie man sieht, sind die Spannungen U_B3 und U_B2 entgegengesetzt gepolt!

U_B3 = U_B2 + U_R = 0

= 9 V + 6 V = 15 V

Berechnung der Spannungs-Strom-Kennlinie

U = R * ( I – I₀ ) + U₀ " Ohmsches Gesetz II

U_B2 = R * ( I_B2 – I₀ ) + U₀ " Der Strom I₀ gehört zur Stromquelle I_B3 und die Spannung U₀ zur Spannungsquelle U_B2.

= 600 W * ( 10 mA – 10 mA ) + 9 V

= 600 W * ( 0 mA ) + 9 V = 9 V þ

Berechnung mit Maschenumlauf und Ohmsches Gesetz II

( - U_B3 ) + U_B2 + U_R = 0

U_B2 = U_B3 - U_R

= R * ( I_B3 – I₀ ) + U₀ – U_R " Bei der Spannungsquelle U_B3 gibt es keine Ursprungsspannung U₀.

= R * I_B3 + R * I₀ + 0 – ( I_B3 * R )

= U₀ = 9 V þ

( - U_B3 ) + U_B2 + U_R = 0

U_R = U_B3 – U_B2

= U_B3 – [ R * ( I_B2 – I₀ ) + U₀ ] " Geradengleichung y = 15 – ( 600 * ( x – 0.010 ) + 9 )

= U_B3 – [ R * ( 0 ) + U₀ ] " Wegen I_B2 = I₀ ist I_B2 – I₀ = 0

= 15 V – 9 V = 6 V þ

Überraschung! Die Widerstandsgerade vom Widerstand R verläuft mit negativer Steigung im 4. Quadranten des Koordinatensystems von links oben nach rechts unten im 2. Quadranten. Demzufolge ist auch der Steigungswinkel a negativ. Was aber bedeutet es, wenn sowohl der Steigungswinkel a als auch die Steigung negativ sind? Wenn die Stromstärke I_R = I₀ mit I_R = -10 mA im Arbeitspunkt A ebenfalls negativ ist?

In der Elektrotechnik, Elektronik hat man es bei den Elektro- und Elektronikgeräten und deren Schaltungen überwiegend mit passiven Bauteilen zu tun, wie z.B. mit Widerständen, die sich als elektrische (Energie-) „Verbraucher“ verhalten, wobei sie sich gelegentlich auch erwärmen. Dabei wird aber keine Energie „verbraucht“, sondern lediglich in eine andere Energieform wie z.B. Wärme, Antriebsenergie eines Motors oder in Lichtenergie (= Lumen) umgewandelt!

Und so, wie es massenhaft (Energie-) Verbraucher gibt, muss es auf der anderen Seite, d.h. auf der (Energie-) Erzeugerseite auch „negative Verbraucher“, d.h. Energieerzeuger z.B. in Form von Gleichstrom- und/oder Wechselstrom-Generatoren, Photovoltaik-Panels, Wasser- oder Gas-Kraftwerke zwecks Stromerzeugung usw. geben.

Wie aber unterscheidet sich ein Energieerzeuger von einem Energieverbraucher? Und zwar innerhalb eines Schaltplans, einer Schaltung oder in einem Diagramm?

Beim Diagramm erkennt man einen Energieerzeuger (= Energiewandler) an der negativen Steigung der Kennlinie und innerhalb der Schaltung an der negativen Stromflussrichtung!

(Vergrößern: auf Bild klicken! | MS Mathematics, easy-electronic_200, W-10-12.gcw)

Während also der Strom bei einem ohmschen (Last-) Widerstand als Verbraucher in den Widerstand hinein fließt, fließt er beim Energieerzeuger (Generator, Dynamo, Batterie, USB-Netzteil, Netzgerät, Konstant-Stromquelle, Spannungsquelle usw.) aus der Quelle heraus! Ganz so wie im richtigen Leben, wo das Wasser aus dem Wasserrohr einer eingefassten Quelle herausläuft bzw. abfließt.

Demzufolge zählt man in einen Stromknoten hinein fließende Ströme positiv und aus dem Stromknoten heraus fließende Ströme negativ!

Wenn z.B. ein Akkumulator (= Auto„batterie“) aufgeladen wird, dann stellt dieser elektrisch einen (Energie-) Verbraucher dar, dessen Strompfeil vom Erzeuger bzw. vom Ausgang des Ladegeräts in Richtung des Akkus als Verbraucher zeigt, eben so, als ob der Strom in den Verbraucher (= Akku) hinein fließt!

Wird hingegen der Akku(mulator) entladen, dann liefert dieser den gespeicherten Strom nach außen hin zum angeschlossenen Verbraucher, sodass der Strompfeil vom Akku nach außen weg zeigt!

Der Spannungspfeil an den Anschlussklemmen eines Akkus zeigt aber beim Aufladen als auch beim Entladen stets in die gleiche Richtung, d.h. vom Pluspol zum Minuspol des Akkus!

Siehe auch „Zählpfeilsystem für Erzeuger und Verbraucher“

Um die Arbeitsweise der Schaltung insbesondere im Zusammenspiel mit dem Kennliniendiagramm besser zu verstehen, wird als nächstes der Umschalter S2 umgelegt, sodass jetzt die Spannungsquelle U_B1 wirksam wird, deren Polarität, im Gegensatz zur Spannungsquelle U_B2, umgekehrt gepolt ist, sodass der Spannungspfeil ebenfalls in die umgekehrte Richtung zeigt.

Bei der (Konstant-) Stromquelle U_B3 verhält es sich ebenso so. Auch bei dieser verläuft jetzt der Spannungspfeil in umgekehrte Richtung. Dabei verläuft aber der Strompfeil weiterhin in derselben Richtung wie bisher, nämlich von unten nach oben. Das Besondere bei der (Konstant-) Stromquelle U_B3 ist aber jetzt, dass diese nicht mehr als Energieerzeuger bzw. Energielieferant im Sinne der Stromquelle arbeitet, sondern als Verbraucher im Sinne eines Widerstandes bei dem der Strom stets durch das Bauelement hindurchfließt!

Aber ist dem wirklich so? Kann eine (Konstant-) Stromquelle U_B3 tatsächlich plötzlich als elektrischer Verbraucher im Sinne eines Widerstandes arbeiten?

Wie wir bereits wissen, kann man sich eine (Konstant-) Stromquelle nicht als Stromerzeuger ähnlich wie eine 1,5 Volt Batterie vom Typ AA (= Spannungserzeuger) im Elektronikmarkt oder im Supermarkt kaufen. Und zwar deshalb nicht, weil es sich bei dieser stets um eine elektronische Schaltung, bestehend aus Widerständen, Potentiometer, Kleinsignal-Transistoren oder einem Operationsverstärker (OPV) und einem Leistungstransistor oder MOSFET-Transistor handelt, die noch dazu in einem Gehäuse verbaut sind, das um ein Vielfaches größer ist als eine kleine 1,5 Volt Batterie!

Je nach der Art und Weise wie eine elektronische (Konstant-) Stromquelle schaltungstechnisch aufgebaut ist, wird sie auch im Falle der externen und entgegengesetzt gepolten Spannungszufuhr weiterhin den eingestellten bzw. berechneten Konstantstrom I_konst nach außen abgeben. Wenn aber die von außen zugeführte Spannung mit entgegengesetzter Polung gleich groß wird wie der bisherige Spannungsabfall am (Last-) Widerstand R bzw. den angeschlossenen Verbrauchern, dann wird die (Konstant-) Stromquelle mehr und mehr belastet und am Ende kurzgeschlossen! -

Entscheidend ist also, dass eine (Konstant-) Stromquelle stets unabhängig von der Betriebsspannung den entsprechend berechneten und eingestellten Konstantstrom nach außen an den Lastwiderstand liefert. Dabei richtet sich dann die resultierende Ausgangsspannung nach dem angeschlossenen Lastwiderstand und nach der von extern zugeführten, entgegengesetzt gepolten Spannung, die letztlich eine Stromumleitung gegen Masse („^“) bis hin zum Kurzschluss zur Folge haben kann.

Doch zurück zur Frage, ob eine (Konstant-) Stromquelle, hier die (Konstant-) Stromquelle U_B3, tatsächlich als elektrischer Verbraucher im Sinne eines Widerstandes arbeiten kann.

Gemäß der roten und blauen Strom- und Spannungspfeile der (Konstant-) Stromquelle U_B3 sieht es ganz danach aus, als ob diese als Verbraucher, aber nicht zwingend als ohmscher Widerstand arbeitet.

Solange man also das Innenleben einer (elektronischen) Konstantstromquelle nicht kennt, müsste man diese als engl. „Black Box“, d.h. „Schwarze Kiste“, bezeichnen. Von dieser wissen wir aber bereits, dass sich unsere Black Box nach außen hin als Konstantstromquelle verhält, indem ein eingangsseitiger Strom I_e an den zweipoligen Eingangsklemmen in einen, oftmals auch einstellbaren, Konstantstrom I_const an den ebenfalls zweipoligen Ausgangsklemmen umgewandelt wird.

Da Ein- und Ausgang der Black Box elektrisch voneinander unabhängig, aber nicht galvanisch voneinander getrennt, sind, beeinflusst die eingangsseitige Spannung U_e weder den abgegebenen Konstantstrom I_const, noch dessen Ausgangsspannung U_a.

Dabei kann man eine elektronische Konstantstromquelle auch so entwickeln, dass deren Eingangspannung U_a im Verhältnis 1:1 an die Ausgangsspannung U_a, aber elektrisch voneinander getrennt, weitergegeben wird. Und zwar unabhängig von der Polarität der Eingangspannung U_e (= Richtung des Spannungspfeils).

Dies hätte dann zur Folge, dass die eingangsseitige Polarität der Eingangspannung U_e und deren Spannungshöhe von z.B. U_e = 3 V im Verhältnis 1:1 an die Polarität und Höhe der Ausgangsspannung U_a mit U_a = U_e = 3 V weitergegeben wird. Und zwar völlig unabhängig vom abgegebenen Konstantstrom I_const, aber mit der Folge, dass sich die Polarität der Eingangspannung U_e (= Richtung des Spannungspfeils) nach der übrigen Beschaltung richtet (siehe Batterie U_B1):

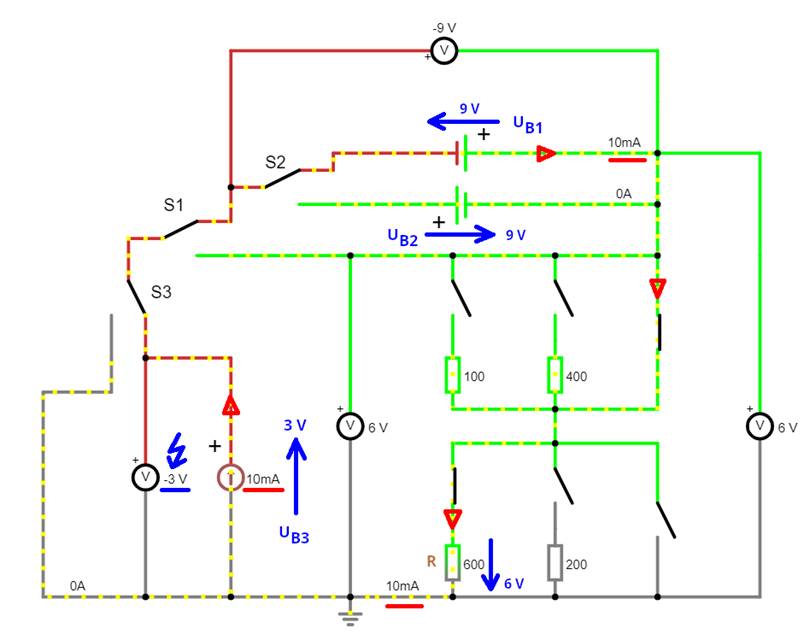
(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-12.js)

Zu der obenstehenden Schaltung lässt sich wie gewohnt ein äußerer Maschenumlauf im Uhrzeigersinn wie folgt durchführen:

U_B3 + ( - U_B1 ) + U_R = 0

U_R = U_B1 – U_B3

= U_B1 – [ R * ( I_B2 – I₀ ) + U₀ ] " Geradengleichung y = –3 – ( 600 * ( x – 0.010 ) - 9 )

= U_B1 – [ R * ( 0 ) + U₀ ] " Wegen I_B2 = I₀ ist I_B2 – I₀ = 0

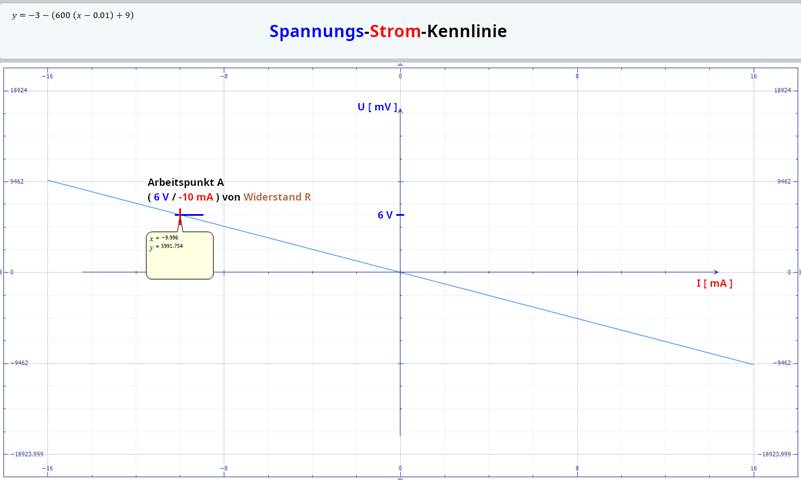
= - 3 V – 9 V = 6 V þ " Siehe Arbeitspunkt A im Spannungs-Strom-Diagramm

Wenn man die nachfolgende Spannungs-Strom-Kennlinie vom Widerstand R mit der vorherigen Kennlinie (siehe Bild) miteinander vergleicht, dann fällt auf, dass die beiden Kennlinien die gleiche Steigung und den gleichen Steigungswinkel a haben. Dies ist dann auch nicht verwunderlich, da beide Kennlinien mit ein und demselben Widerstand R aufgenommen wurden. Dies lässt sich auch anhand des gleichen Arbeitspunktes A mit den Koordinaten ( 6 V / -10 mA ) feststellen:

(Vergrößern: auf Bild klicken! | MS Mathematics, easy-electronic_200, W-10-13.gcw)

Abschließend vergleich wir noch die beiden bisherigen Geradengleichungen:

1. y = 15 – ( 600 * ( x – 0.010 ) + 9 ) ó U_R = U_B3 – [ R * ( I_B2 – I₀ ) + U₀ ]

Bei dem Wert 15 handelt es sich um die Spannung U_B3 an der Konstantstromquelle I_{10 mA} (siehe Bild).

Der Wert 600 ist der Widerstandswert des Widerstandes R.

Bei der Angabe 0.010 handelt es sich um den Konstantstrom I₀ der Konstantstromquelle I_{10 mA} und

beim Wert 9 um die Spannung U_B2 = U₀ an der gleichnamigen Batterie.

Vergleicht man die Werte 15 und 9, dann fällt auf, dass beide Werte positiv sind, sodass die Spannungspfeile der Batterien U_B3 und U_B1 beim Maschenumlauf im Uhrzeigersinn in die gleiche Richtung zeigen und demzufolge nicht entgegengesetzt gepolt sind.

2. y = –3 – ( 600 * ( x – 0.010 ) - 9 ) ó U_R = U_B1 – [ R * ( I_B2 – I₀ ) + U₀ ]

Bei dem Wert -3 handelt es sich um die Spannung U_B3 an der Konstantstromquelle I_{10 mA} (siehe Bild).

Der Wert 600 ist wieder der Widerstandswert des Widerstandes R.

Bei der Angabe 0.010 handelt es sich ebenfalls wieder um den Konstantstrom I₀ der Konstantstromquelle I_{10 mA} und

beim Wert -9 um die Spannung U_B1 an der gleichnamigen Batterie.

Vergleicht man die Werte -3 und -9, dann fällt auf, dass beide Werte negativ sind und die Spannungspfeile der Batterien U_B3 und U_B1 beim Maschenumlauf im Uhrzeigersinn in entgegengesetzte Richtung zeigen und demzufolge entgegengesetzt gepolt sind.

Fazit

Es ist absolut faszinierend, dass die Konstantstromquelle I_{10 mA} ihren Konstantstrom I₀ in die Schaltung drückt, sodass dieser auch durch Batterien hindurchfließt, egal wie herum diese spannungsmäßig gepolt sind! Dabei wird der Konstantstrom I₀ erst „sichtbar“, wenn dieser auf den Widerstand R trifft, der den Konstantstrom I₀ gemäß dem Ohmschen Gesetz in einen entsprechenden Spannungsabfall umwandelt!

Interessant ist auch, dass die zwei Spannungsquellen U_B1 und U_B3, die entgegengesetzt gepolt sind und demzufolge spannungsmäßig gegeneinander arbeiten, die resultierende Spannungsdifferenz ∆U = U_B1 - U_B3 von 9 V – 3 V = 6 V unter sich „aushandeln“ müssen, da der Spannungsabfall von U_R = 6 V am Widerstand R bereits wegen des Konstantstroms von I₀ = 10 mA und dessen Spannungsabfalls „vergeben“ ist. Und zwar mit der Folge, dass sich der Spannungsabfall an der Konstantstromquelle I_{10 mA} von vormals U_B3 = 6 V auf aktuell nur U_B3 = - 3 V reduziert, wobei der Widerstand R am verringerten Spannungsabfall von U_B3 = - 3 V vollkommen unschuldig ist, da dieser wegen des durch den Widerstand R hindurch fließenden Konstantstroms mit I₀ = 10 mA nicht am Geschehen beteiligt ist!

Wenn die Konstantstromquelle I_{10 mA} mit der Spannungsquelle U_B2 in Reihe geschaltet ist und der Spannungspfeil von U_B3 dem Spannungspfeil von U_B2 entgegengesetzt gerichtet ist (siehe Bild), dann drückt die Konstantstromquelle I_{10 mA} ihren Konstantstroms mit I₀ = 10 mA in den Pluspol der Spannungsquelle U_B2 hinein, sodass diese mit dem kleinen Ladestrom aufgefrischt wird:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-13.js)

Und da der kleine Ladestrom I_{10 mA} der Konstantstromstromquelle I_{10 mA} auch über den Innenwiderstand R_i - hier der Widerstand R - der Spannungsquelle U_B2 fließt, wird diese beim mehrstündigen Auffrischen über Nacht auch entsprechend erwärmt. Aber solange die Batterie U_B2 nur mit dem kleinen Ladestrom I_{10 mA} von I_{10 mA} = 10 mA aufgefrischt wird, hält sich die Erwärmung der Batterie in Grenzen, sodass sich diese nicht ausdehnt, keinen Schaden nimmt und am nächsten Morgen über eine um ca. 10% gestiegene Ladungsträgermenge Q nebst elektrischer Energie W_el verfügt.

Berechnung der in einer 9 Volt Blockbatterie gespeicherten, elektrischen Energie W_el:

Q = I * t

= 0,010 A * 6 h = 0,060 Ah = 60 mAh

W_el = P_el * t_Lade

= U_B2 * I * t_Lade = U_B2 * I * t_Lade = U_B2 * Q_Lade

= 9 V * 60 mAh = 540 mVAh = 540 mWh

Bei einer 9 V Blockbatterie aus Alkali-Mangan mit einer Akku-Kapazität von bis zu 600 mAh entspricht die über Nacht hinzugefügte Ladungsträgermenge Q = 60 mAh insgesamt einer Kapazitätsauffrischung von

600 mAh " 100 %

60 mAh " x %

_________________

x = 100 % / 600 mAh * 60 mAh = 10 %

Die Berechnung mit der Kapazitätsberechnung bestätigt, dass der kleine Ladestrom von I_{10 mA} = 10 mA durchaus geeignet ist, eine 9 Volt Alkali-Mangan Blockbatterie aufzufrischen, ohne dass sich diese übermäßig erwärmt.

Dabei verhält es sich so, dass das Auffrischen der 9 V Blockbatterie am besten funktioniert, wenn man es sich angewöhnt, diese gleich von Anfang an, wenn die Batterie nur zu einem geringen Teil entladen wurde, aufzufrischen. Und zwar deshalb, weil dann der fortschreitende Zersetzungsprozess der Zellchemie und der Elektroden noch nicht so weit fortgeschritten ist.

Erfahrungsgemäß lässt sich eine bis dahin nicht so stark entladene Batterie bis zu zwölf Mal und mehr auffrischen und so die Lebensdauer um etliche Wochen verlängern. Entscheidend ist dabei aber, dass die 9 V Blockbatterie zuvor nicht mit einem zu hohen Entladestrom (= Laststrom des Verbrauchers) belastet und auch nicht länger als z.B. 90 Minuten am Stück entladen wurde. Wenn sich der Laststrom des entsprechenden Gerätes so um die 50 mA bis max. 100 mA bewegt, im Mittel also 75 mAh, dann berechnet sich die Nutzungsdauer der 9 V Blockbatterie wie folgt:

Q = I * t "

t_Ent = Q / I

= 600 mAh / 75 mA = 8 h Ges.nutzungsdauer

Berechnung der Batterie-Laufzeit in Wochen:

Durchschnittliche, wöchentliche Nutzungsdauer (= Einschaltzeit) t_Ein = 30 Min. pro Wochentag an jedem zweiten Tag pro Woche führt zu …

8 h Ges.nutzungsdauer / ( 0,5 h * 3 Tage/Wo. ) = 8 h / ( 1,5 h/Wo. ) = 5,33 Wo. ≈ 5,3 Wochen Batterielaufzeit

Verlängerte Batterie-Laufzeit in Wochen:

0,5 h * 3 Tage/Wo. * ( 60 mAh / h ) = 1,5 Tage/Wo. * 60 mAh = 90 mAh

90 mAh / Wo. * 5,3 Wo. = 477 mAh zusätzlicher Akku-Kapazität durch das laufende Auffrischen

Berechnung der zusätzlichen Batterie-Laufzeit in Wochen:

t_Ent = Q / I

= 477 mAh / 75 mA = 6,36 h zusätzliche Nutzungsdauer

6,36 h zusätzliche Nutzungsdauer / ( 0,5 h * 3 Tage/Wo. ) = 6,36 h / ( 1,5 h/Wo. ) = 4,24 Wo. zus. Wo. Batterielaufzeit

Berechnung der gesamten Batterie-Laufzeit in Wochen:

t_ges = 5,3 Wo. Batterielaufzeit + 4,24 Wo. zus. Wo. Batterielaufzeit

= 9,54 Wo. Gesamt-Batterielaufzeit durch Auffrischen der 9 V Blockbatterie über die gesamte Nutzungsdauer!

Aber was nutzt das Auffrischen der 9 V Blockbatterie oder z.B. von vier 1,5 Volt „Mignon“-Batterien von Typ „AA“ für eine Nennspannung von 6 Volt, wenn man diese jedes Mal beim Auffrischen händisch aus dem Batteriefach entnehmen und anschließend wieder ins Ladegerät zum Auffrischen einlegen muss?

Aber keine Sorge, man muss die Batterie oder die Batterien keineswegs aus dem Batteriefach entnehmen, um sie aufzufrischen!

Praktisch jedes „Taschen-“, „Koffer-“ oder „Transistor“-Radio - heute meist digitale „DAB+“-Radios - verfügt über einen entsprechenden Stromversorgungsanschluss für den Anschluss eines externen Netzstecker-Netzteils mit Hohlstecker und teils unterschiedlicher „+/-“ Polung(7 ) für unterschiedliche Betriebsspannungen, meistens für 6 Volt (= 4 x 1,5 Volt Batterien) oder 9 Volt (= 9 V Blockbatterie), um diese Batterie sparend am 230 V Wechselstromnetz (= Haushaltsstrom) betreiben zu können.

Wenn man also ein externes (Stecker-) Netzteil mittels des Hohlsteckers an die Stromversorgungsbuchse des portablen Radios anschließt, dann sorgt ein kleiner Umschalter an der Stromversorgungsbuchse dafür, dass die Stromzufuhr von Batteriebetrieb auf Netzbetrieb (und umgekehrt) umgeschaltet wird.

Und damit man die Batterien zum Auffrischen nicht aus dem Batteriefach nehmen muss, um diese extern aufzufrischen, wird der kleine Umschalter an der Stromversorgungsbuchse mit einem Widerstand von R = 600 W (bei der Stromversorgung mit 6 V) oder mit einem Widerstand von R = 1 kW (bei der Stromversorgung mit 9 V) überbrückt, sodass ein kleiner Ladestrom von um die 10 mA bei angeschlossenem (Stecker-) Netzteil und beim Netzbetrieb in die teilentladenen Batterien fließen und diese auffrischen kann.

Demzufolge werden die Batterien im Batteriefach immer nur dann aufgefrischt, wenn das externe (Stecker-) Netzteil angeschlossenen ist. Dabei spielt es dann keine Rolle, ob das Radio eingeschaltet ist oder nicht!

Wenn man aber nicht will, dass die Batterien über einen längeren Zeitraum von Tagen, Wochen und Monaten aufgefrischt werden, dann muss man den Hohlstecker vom Netzteil abziehen!

Trotz der Auffrischung verhält es sich natürlich so, dass die Batterien je nach intensiver Nutzung des Radios früher oder später komplett entladen sind, sodass sich diese auch nicht mehr auffrischen lassen, weil sich der Elektrolyt und die in ihm gespeicherten, elektrischen Ladungsträger aufgebraucht haben und der sich dabei veränderte chemische Zersetzungsprozess nicht mehr rückgängig machen lässt. Volkstümlich könnte man auch sagen: „Von nichts kommt nichts (mehr)!“ Schließlich ist die Batterie kein Endlosspeicher, lassen sich die an den Elektroden voneinander getrennten Ladungsträger in Form von Anionen und Kationen und die im Elektrolyten gespeicherte elektro-chemische Energie nicht mehr in elektrischen Strom umwandeln! Spätestens dann sollte man die Batterien gegen neue austauschen, um zu vermeiden, dass der ätzende Elektrolyt der leeren Batterien früher oder später wegen dessen Ausdehnung z.B. durch Erwärmung auszulaufen droht!

Wenn man die leeren Batterien gegen fabrikneue ersetzt hat, dann weisen diese wegen der vollen Aufladung vorübergehend eine teils höhere Klemmenspannung auf, meist aber nur im Leerlauf (ohne Last), als die Nennspannung im Normalbetrieb, wenn die Batterien nicht mehr ganz taufrisch sind: U_Batt > U_Netzteil.

Der Spannungsüberschuss der fabrikneuen Batterien von z.B. U_Kl = U_Nenn + 0,5 V = 6,0 V + 0,5 V = 6,5 V kann dann dazu führen, dass die Batterie wegen des höheren Spannungspotentials einen kleinen bis größeren Strom in das extern angeschlossene Netzteil mit geringerer Versorgungsspannung von z.B. U_Netzteil = 5,5 V drückt! Je nachdem wie klein dann der Ausgangswiderstand im Inneren des (elektronischen) Netzteils ist, kann dabei ein mehr oder weniger großer Ausgleichsstrom von den Batterien in das angeschlossene Netzteil fließen. Bei einem inneren Ausgangswiderstand R_out = 50 W des Netzteils würde sich dann folgender Ausgleichsstrom I_Aus einstellen:

I_Aus = ( U_{Kl, Batt} – U_Netzteil ) / R_out

= ( 6,5 V – 5,5 V ) / 50 W = 1 V / 50 V/A = 0,020 A = 20 mA " Ausgleichsstrom von der Batterie zum Netzteil

Bei einem noch kleineren Ausgangswiderstand im Inneren des elektronischen Netzteils von R_out = 5 W wäre der Ausgleichsstrom schon um das 10fache größer:

I_Aus = ( U_{Kl, Batt} – U_Netzteil ) / R_out

= ( 6,5 V – 5,5 V ) / 5 W = 1 V / 5 V/A = 0,200 A = 200 mA 7 " Ausgleichsstrom von der Batterie zum Netzteil

Das wäre jetzt aber schon der GAU (= Größter, Anzunehmender Unfall), der aber nie eintreten wird, weil wir es nicht nur mit dem kleineren Ausgangswiderstand im Inneren des elektronischen Netzteils von R_out = 5 W zu tun haben, sondern vielmehr auch mit dem in Reihe geschalteten Vorwiderstand für die Batterie-Auffrischung von R_Vor = 53,4 W bei jetzt einer Batteriespannung von U_{Kl, Batt} = 6,032 V:

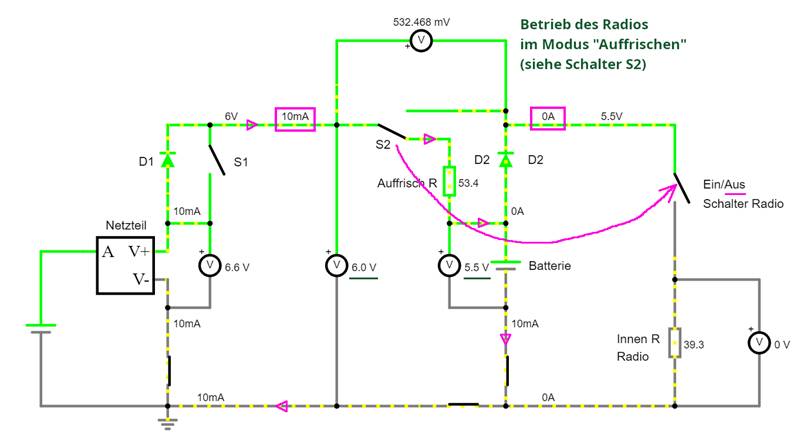
I_Aus = ( U_{Kl, Batt} – U_Netzteil ) / R_Vor

= ( 6,032 V – 5,5 V ) / 53,4 W = 0,532 V / 53,4 V/A = 0,00996 A ≈ 10 mA " Stromstärke des Auffrischstroms!

Nachfolgend zum besseren Verständnis noch die Schaltung mit dem Umschalter S2 in der Hohlsteckerbuchse für den Anschluss eines Netzteils mit Hohlstecker zwecks Auffrischung von 4 x 1,5 V Mignon Batterien vom Typ „AA“.

Wie man anhand des pinkfarbenen Hinweispfeils sieht, muss das Radio am Ein-/Ausschalter ausgeschaltet sein, damit es über den Umschalter S2 in den Modus „Batterien auffrischen“ geschaltet wird:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-14.js)

Eigentlich müsste der Umschalter S2 mit dem Ein-/Ausschalter mechanisch oder elektronisch gekoppelt sein, sodass der Umschalter S2 und der Ein-/Ausschalter nicht mehr allein betätigen lassen.

In der obenstehenden Elektronik-Simulation „Circuit Simulator version 2.8.1js“ von Paul Falstad lassen sich jedenfalls keine Taster, Schalter oder Umschalter miteinander koppeln, sodass man diese händisch in der richtigen Abfolge bzw. logischen Folge bedienen muss.

Demzufolge lässt sich die obenstehende Schaltung mit dem Umschalter S2 in den Modus „Batterien auffrischen“ umschalten, gleichzeitig aber lässt sich auch das Radio mit dem Ein-/Ausschalter einschalten, obwohl es sich ja im Modus „Batterien auffrischen“ befindet. Und zwar mit der Folge, dass das Radio keinen Ton von sich gibt, weil es nur mit dem Strom zum Auffrischen von I_Aus = 10 mA betrieben wird, obwohl das Radio für den laufenden, ordnungsgemäßen Betrieb einen Nennstrom von I_Nenn = 150 mA benötigt (siehe Modus „Radio hören“):

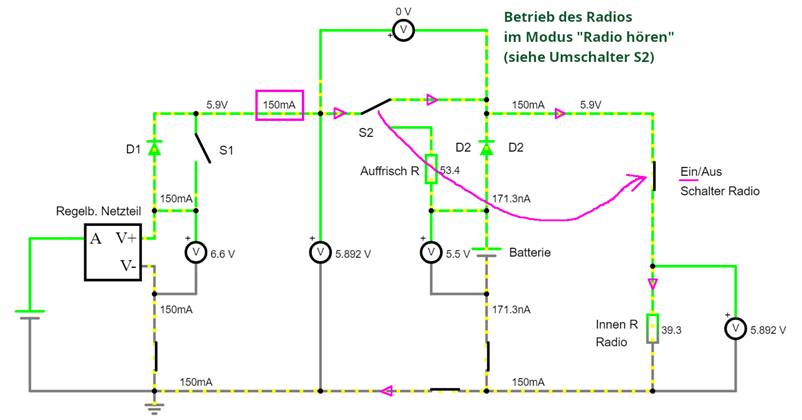
(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-15.js)

Wie man in der obenstehenden Schaltung sieht, wird diese mit dem Umschalter S2 und dem Ein-/Ausschalter jetzt im Modus „Radio hören“ betrieben. Und zwar mit dem Nennstrom von I_Nenn = 150 mA und einer Betriebsspannung von U_Radio = 5,9 V die sich auf den Innenwiderstand R = 39,3 W des Radios bezieht.

Abschließend noch ein Hinweis darauf, dass das Auffrischen von Batterien tatsächlich funktioniert und in Form eines entsprechendes Batterie-Ladegerätes des chinesischen Herstellers „Rictron“ mit der Bezeichnung „Intelligent controlled universal fast battery charger RC999“ hergestellt wird. Auf dem Online-Portal von „Weltbild“ wird das Batterie-Ladegerät derzeit für 39,99 Euro abverkauft. Bei dem Online-Portal „Pearl“ gibt es das Batterie-Ladegerät bereits für 35,99 Euro.

Auf der Hersteller-Webseite von Rictron findet sich weiter unten die Tabelle „Charging time“ der zufolge das Auffrischen einer 9 V Blockbatterie mit einer Kapazität von Q = 200 mAh bis zu 7 Stunden dauert. Demzufolge berechnet sich der Ladestrom zum Auffrischen der 9 V Blockbatterie wie folgt:

Q = I * t "

I = Q / t

= 200 mAh / 7 h = 28,57 mA ≈ 29 mA

Da die heutigen 9 V Blockbatterien mit Alkali-Mangan aber über eine Kapazität von bis zu 600 mAh besitzen, müsste die Aufladung mit einem Ladestrom von I_Laden = 29 mA bis zu

Q = I * t "

t = Q / I

= 600 mAh / 29 mA = 17,4 h dauern.

Dabei ist aber die lange Ladezeit dem Umstand geschuldet, dass die 9 V Blockbatterie mit Alkali-Mangan, gegenüber der Kapazität von 200 mAh, eben diese um das Dreifache höhere Kapazität hat!

Bei den weiteren Recherchen hat sich aber soeben herausgestellt, dass es sich bei der 9 V Blockbatterie mit Alkali und der Kapazität von Q = 200 mAh um einen wieder aufladbaren Akku handelt und nicht um die bisher berechnete 9 V Blockbatterie mit Alkali-Mangan zum wieder Auffrischen! –

Aber immerhin bestätigt sich, dass wir mit dem dauerhaften Ladestrom von I_Laden = 10 mA zwecks Auffrischen der 6 V und 9 V Alkali-Mangan-Batterien im grünen Bereich liegen, sodass sich diese eben nicht zu stark erwärmen, ausdehnen, das Batteriegehäuse aufdrücken und den Elektrolyten heraus fließen lassen!

Deshalb sollte man gerade aus den genannten Gründen heraus niemals nicht wieder aufladbare Batterien in ein Akku-Ladegerät stecken und aufladen!

Interessant ist in diesem Zusammenhang noch, dass es inzwischen 9 V Lithium-Ionen Blockakkus mit integriertem Batterie-Management-System (BMS) gibt, die sich über eine „USB 3.0“-Buchse mehrfach wieder aufladen lassen (siehe „ENEGON 2-Pack 9V Blockbatterie-Wiederaufladbar mit 1000mAh“ bei Amazon). -

Spannungsquelle und Stromquelle arbeiten parallel zusammen

Wenn man die Kapitelüberschrift liest, dann fällt sofort auf, dass das Adjektiv „parallel“ kursiv geschrieben ist. Das deutet darauf hin, dass die Spannungs- und die Stromquelle parallel geschaltet sind. 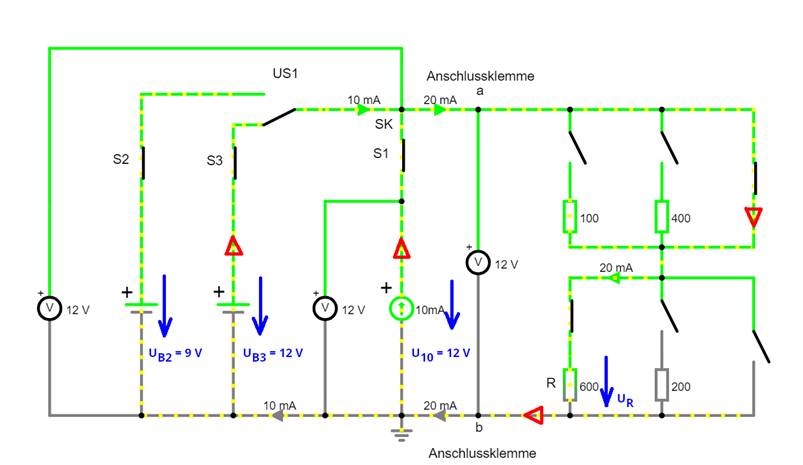Und, da eine reale Spannungs- oder Stromquelle auch jeweils über einen Innenwiderstand R_i verfügt, der sich wegen der Parallelschaltung beider Energielieferanten auch als gemeinsamer (Last-) Widerstand R quasi auslagern und nach außen hinter die gemeinsamen Anschlussklemmen a, b führen lässt, drängt sich ein weiterer Gedanke auf. Und zwar der eines Stromknotens (SK),der alle Ströme von Spannungs-, Stromquelle und Widerstand R zusammen führt (siehe roter Kreis):

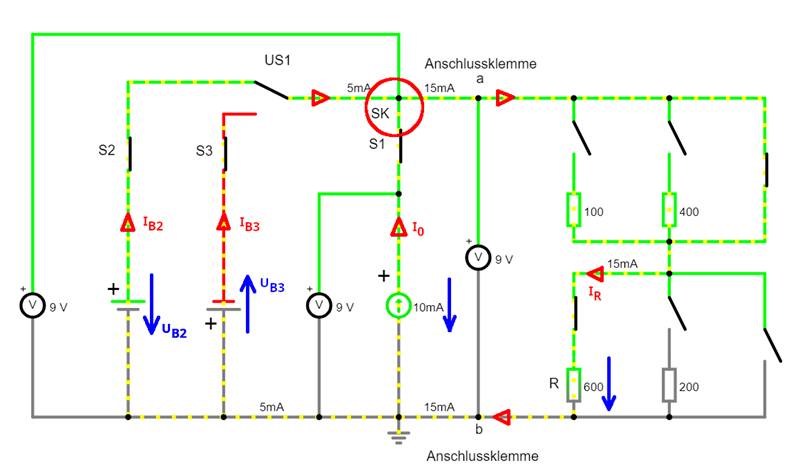
(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-17.js)

Da in der obenstehenden Schaltung beide Spannungsquellen U_B2 und U_B3 jetzt parallel zur Konstantstromquelle I₀ geschaltet sind, hat dies den Vorteil, dass der Konstantstrom I₀ = 10 mA nicht mehr durch eine der beiden Spannungsquellen U_B2 und U_B3 zum Lastwiderstand R, der zugleich auch der Innenwiderstand R_i der Strom- und Spannungsquellen ist, hindurchfließen muss und dabei den Innenwiderstand R_i mehr oder weniger stark erwärmt!

Wie man anhand der obenstehenden Schaltung sieht, liegt am Widerstand R = 600 W die Spannung U_R = 9 V an, sodass der Widerstand von einem Strom I_R = 15 mA durchflossen wird. Dabei setzt sich der Strom I_R im Stromknoten SK aus den beiden Teilströmen I_B2 = 5 mA und I₀ = 10 mA zusammen, wobei der Konstantstrom I₀ im Widerstand R zu einen Spannungsabfall von

U_RI0 = R * I₀

= 600 W * 10 mA = 6000 mV = 6 V führt.

Tatsächlich beträgt der Spannungsabfall am Widerstand R aber U_R = 9 V:

U_R = R * I_R

= 600 W * 15 mA = 9000 mV = 9 V

U_R = R * I₀ + R * I_B2

= R * ( I₀ + I_B2 )

= 600 W * ( 10 mA + 5 mA ) = 600 W * 15 mA = 9000 mV = 9 V

Dass der Konstantstrom I₀ im Widerstand R zwingend zu einem Spannungsabfall von U_RI0 = 6 V führt, dürfte unbestritten sein, sodass sich jetzt die Frage stellt, ob die Spannungsquelle U_B2 am Stromknoten SK mit der Parallelschaltung U_B2 // U_RI0 nur die Spannungsdifferenz

∆U_B2 = U_R - U_RI0

= 9 V – 6 V = 3 V hinzufügt.

Rechnerisch sieht es ganz danach aus. Aber so wie die Konstantstromquelle I₀ den Konstantstrom I₀ = 10 mA in den Widerstand R drückt, drückt die Spannungsquelle U_B2 dem Widerstand R die Spannung U_R = 9 V „auf’s Auge“, was dazu führt, dass nun der Widerstand R vom Strom I_R = 15 mA durchströmt wird. Dabei gilt es aber zu beachten, dass der Gesamstrom I_R = 15 mA nicht mehr als Ganzes konstant ist, sondern nur mit dem Konstantstrom I₀ = 10 mA.

Folgerichtig handelt es sich bei der Spannungsquelle U_B2 nur noch teilweise um eine Konstant-Spannungsquelle:

U_B2 = U_RI0 + ∆U_B2

= R * I₀ + ∆U_B2

= U₀ + ∆U_B2

= 6 V + 3 V = 9 V

Jetzt wissen wir, dass die Ursprungsspannung U₀ der Spannungsquelle U_B2 nur U₀ = 6 V beträgt!

Wir überprüfen das Ganze, indem wir das Ohmsche Gesetz II wie folgt anwenden:

I = 1 / R * ( U – U₀ ) + I₀ " Ohmsches Gesetz II " zur Berechnung der Stromstärke am Widerstand R

I_R = 1 / R * ( U – U₀ ) + I₀

= 1 / 600 W * ( 9 V – 6 V ) + 10 mA

= 1 / 600 W * ( 3 V ) = 5 mA + 10 mA = 15 mA þ

Wie wir ferner wissen, leitet sich das Ohmsches Gesetz II aus dem differentiellen Widerstand R und der Zweipunkteform wie folgt ab:

R = ∆U / ∆I " ( y- y₁ ) / ( x – x₁ ) = ( y₂- y₁ ) / ( x₂ – x₁ ) "

= ( U – U₁ ) / ( I – I₁ ) /

= ( U – U₀ ) / ( I – I₀ )

R * ( I – I₀ ) = ( U – U₀ )

( I – I₀ ) = 1 / R * ( U – U₀ )

I = 1 / R * ( U – U₀ ) + I₀

= 1 / 600 W * ( 9 V – 6 V ) + 10 mA

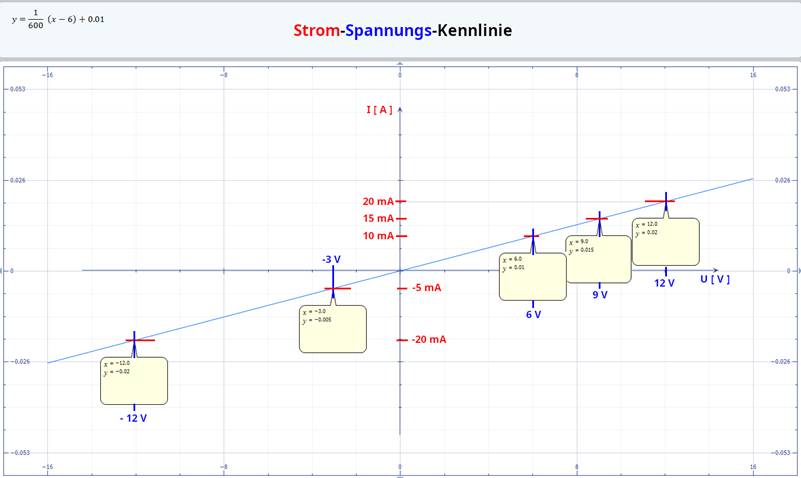
= 1 / 600 W * ( 3 V ) + 10 mA = 5 mA + 10 mA = 15 mA þ " Strom-Spannungs-Kennlinie

y = 1 / 600 * ( x – 6 ) + 0.010 " Geradengleichung für das Zeichnen der Widerstandskennlinie I = f(U)

Um die Richtigkeit der Geradengleichung zu überprüfen, wenden wir noch ein weiteres Verfahren an. Und zwar das der Zweipunkteform direkt. Da braucht es dann aber zwei Messpunkte P₁ und P₂ von denen der Messpunkte P₂ koordinatenmäßig der größere sein soll: P₂ > P₁.

Da wir den ersten, d.h. kleineren Messpunkt P₁ mit den Koordinaten ( x / y ) = ( U_B2 / I_B2 ) = ( 9 V / 15 mA ) brauchen wir als nächstes noch einen zweiten, größeren Messpunkt P₂.

Dabei wäre es naheliegend, dass wir in der obenstehenden Schaltung „easy-electronic_200, W-10-17.js“ einfach den Umschalter US1 umlegen und die Spannungsquelle U_B3 mit der umgekehrten Polung und der Spannung ( - U_B3 ) = 9 V und dem Strom ( - I_B3 ) = 15 mA verwenden. Dabei besteht aber die Gefahr, dass sich die Schaltung wegen der umgekehrt gepolten Spannungsquelle U_B3 nicht nur anders verhält, sondern dass es sich bei dieser auch um eine komplett andere Schaltung handelt!

Dass man eine Schaltung einfach auch mal mit einer niedrigeren oder höheren Versorgungsspannung betreibt, ist in Ordnung, solange es sich um dieselbe Schaltung handelt bei der eine oder alle zwei Spannungsquellen U_B2 und U_B3 nicht umgepolt werden!

Um diesem Risiko aus dem Weg zu gehen, ändern wir die obenstehende Schaltung dahingehend ab, dass wir die Spannungsquelle U_B3 mit der gleichen Polung betreiben wie die Spannungsquelle U_B2, wenn auch mit einer höheren Spannung von U_B3 = 12 V, sodass wir auf diese Weise zu unseren zweiten, größeren Messpunkt P₂ mit den Koordinaten ( x / y ) = ( U_B3 / I_B3 ) = ( 12 V / 20 mA ) kommen:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-18.js)

Wenn man nun die zwei Messpunkte

· P₁ = ( U_B2 | I_R ) = ( 9 V | 15 mA ) und

· P₂ = ( U_B3 | I_R ) = ( 12 V | 20 mA ) mit

· P₂ > P₁

in die Zweipunkteform einsetzt,

( y- y₁ ) / ( x – x₁ ) = ( y₂ – y₁ ) / ( x₂ – x₁ ) " mathematisch!

( U- U₁ ) / ( I – I₁ ) = ( U₂ – U₁ ) / ( I₂ – I₁ ) " elektrotechnisch!

dann lässt sich mit der Zweipunkteform später die Strom-Spannungs-Kennlinie wie folgt erstellen:

( U- U_B2 ) / ( I – I_B2 ) = ( U_B3 – U_B2 ) / ( I_B3 – I_B2 ) | Zähler und Nenner vertauschen

( I – I_B2 ) / ( U – U_B2 ) = ( I_B3 – I_B2 ) / ( U_B3 – U_B2 ) | mit ( U – U_B2 ) multiplizieren

( I – I_B2 ) = [ (I_B3 – I_B2 ) / ( U_B3 – U_B2 ) ] * ( U – U_B2 ) | I_B2 addieren

I = [ ( I_B3 – I_B2 ) / ( U_B3 – U_B2 ) ] * ( U – U_B2 ) + I_B2 | Hier stellt sich die Frage, wie man von U_B2 und I_B2 …

= [ ( I_B3 – I_B2 ) / ( U_B3 – U_B2 ) ] * ( U – U₀ ) + I₀ | auf U₀ und I₀ kommt! Siehe weiter unten!

= [ ( 10 mA – 5 mA ) ) / ( 12 V – 6 V ) ] * ( U – 6 V ) + 10 mA

= [ ( 5 mA ) / ( 3 V ) ] * ( U – 6 V ) + 10 mA

= [ 5 mA / 3 V ] * ( U – 6 V ) + 10 mA | Kehrwert bilden

= [ 1 / ( 3 V / 5 mA ) ] * ( U – 6 V ) + 10 mA

= [ 1 / ( 0,6 kW ) ] * ( U – 6 V ) + 10 mA

= [ 1 / ( 600 W ) ] * ( U – 6 V ) + 10 mA

= [ 1 / R ] * ( U – U₀ ) + I₀ | Widerstandskennlinie, abgeleitet aus der Zweipunkteform

Wichtige Erläuterung zur Zweipunkteform:

Wie der Name bereits sagt, lässt sich aus der Zweipunkteform die mathematische Geradengleichung y = mx + b ableiten, vorausgesetzt, dass zwei Punkte P₁ und P₂ mit P₂ > P₁ bekannt sind. Dabei lässt sich mit der Zweipunkteform auch elektrotechnisch die Geradengleichung für die Widerstandskennlinie aufstellen.

Der Knackpunkt dabei ist aber der, dass man die einzelnen Koordinaten der beiden Punkte P₁ und P₂ in die Zweipunkteform einpflegen muss, was schnell unübersichtlich wird, sodass sich Fehler einschleichen können:

( y- y₁ ) / ( x – x₁ ) = ( y₂ – y₁ ) / ( x₂ – x₁ ) " mathematisch!

( U- U₁ ) / ( I – I₁ ) = ( U₂ – U₁ ) / ( I₂ – I₁ ) " elektrotechnisch!

( U- U_B2 ) / ( I – I_B2 ) = ( U_B3 – U_B2 ) / ( I_B3 – I_B2 )

Der erfahrene Mathematiker oder Elektrotechniker weiß aber, dass sich in dem Term ( U_B3 – U_B2 ) / ( I_B3 – I_B2 ) der Differenzenquotient R = ∆U / ∆I versteckt, sodass sich der differentielle Widerstand r = dU / dI sofort wie folgt berechnen lässt:

R = ∆U / ∆I

= ( U_B3 – U_B2 ) / ( I_B3 – I_B2 )

= ( 12 V – 9 V ) / ( 20 mA – 15 mA )

= ( 3 V ) / ( 5 mA ) = 0,6 kW = 600 W þ

Wenn man also für den Term ( U_B3 – U_B2 ) / ( I_B3 – I_B2 ) den ohmschen Widerstand R einsetzt, dann wird die Zweipunkteform auf einmal wesentlich übersichtlicher:

( U – U_B2 ) / ( I – I_B2 ) = ( U_B3 – U_B2 ) / ( I_B3 – I_B2 ) "

( U – U_B2 ) / ( I – I_B2 ) = R " An dieser Stelle wird die Zweipunkteform zur Punksteigungsform!

( I – I_B2 ) / ( U – U_B2 ) = 1 / R

( I – I_B2 ) = 1 / R * ( U – U_B2 )

I = 1 / R * ( U – U_B2 ) + I_B2 "

Da die Spannung U_B2 wegen der Parallelschaltung der Spannungsquelle zum Widerstand R gleich groß ist, gilt: U_B2 = U₀ mit:

I = 1 / R * ( U – U₀ ) + I₀ " Alle Spannungsquellen in der Schaltung ausschalten führt zu: U₀ = 6 V, I₀ = 10 mA

In die Punktsteigungsform lassen sich jetzt verschiedene Werte von Wertepaaren, deren Punkte alle auf der Widerstandsgeraden (= Kennlinie) liegen müssen, für die Spannung U einsetzen.

Setzt man die Ursprungswerte U₀ = 6 V, I₀ = 10 mA in die Formel für das Ohmsches Gesetz II

I = 1 / R * ( U – U₀ ) + I₀ " zur Berechnung der Stromstärke am Widerstand R

ein, so lässt sich mit der mathematischen Geradengleichung

y = 1 / 600 * ( x – 6 ) + 0.010 " Alles ohne Maßeinheiten!

der Graph der Funktion I = f(U) der Strom-Spannungs-Kennlinie wie folgt zeichnen:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-19.js)

Wie man im obenstehenden Diagramm mit der Widerstandskennlinie R = 600 W sieht, gibt es jetzt erstmals auch Messpunkte im dritten Quadranten des Koordinatensystems bei denen sowohl die Spannungen U als auch die Ströme I negativ sind.

Was aber hat das zu bedeuten? Ist jetzt der Widerstand R negativ? Hat jetzt der Widerstand R einen negativen Widerstandswert?

Nein, der Widerstand R ist weder negativ, noch hat dieser einen negativen Widerstandswert!

Bei Widerständen im Gleichstromschaltungen, d.h. Schaltungen die mit einer Gleichspannung oder einem Gleichstrom (= Konstantstromquelle) als Versorgungsspannung betrieben werden, handelt es sich bei rein ohmschen Widerständen (= keine Spulen, keine Kondensatoren oder ähnliches) stets um passive Bauelemente (= ohne aktive Verstärkung) im Sinne von Verbrauchern, die elektrische Energie z.B. in Wärme und/oder in sichtbares Licht umwandeln (= Glühlampen, Halogenlampen, LEDs, Infrarotlampen, Infrarotstrahler, Rotlicht, Heizdecke, herkömmliche Kochplatten, Backofen usw.).

Schließlich verhält es sich bei den beiden Messpunkten im dritten Quadranten des Koordinatensystems um negative Spannungen und (7 ) Ströme, deren Vorzeichen sich beim Ohmschen Gesetz R = U / I, aber auch beim Differenzenquotienten r = dU / dI bzw. R = ∆U / ∆I mit ∆U, ∆I > 0 gegenseitig aufheben:

R = U / I = ( -12 V ) / ( - 20 mA ) = 12 V / 20 mA = 0,6 kW = 600 W

Wenn also an dem Widerstand R eine negative Spannung ( –U ) anliegt und (7 ) ein negativer Strom (–I) fließt, dann haben ganz einfach Spannung und (7 ) Strom ihre Polarität gewechselt! Nichts weiter!

Schauen wir uns zur obenstehenden Strom-Spannungs-Kennlinie noch die zugehörige Schaltung an, dann sieht man anhand der roten Strompfeile sehr deutlich, dass diese zusammen mit den Spannungspfeilen ihre Richtung geändert haben:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-20.js)

Wer’s nicht glaubt oder sich unsicher ist, der muss in der obenstehenden Schaltung nur den Umschalter US1 umlegen, um zu sehen wie die Spannungen und Ströme jeweils ihre Richtung ändern!

Zur Erinnerung: Eine Batterie ist nur umgangssprachlich ausgedrückt eine Stromquelle; physikalisch/elektrotechnisch aber in Wirklichkeit ein voltaisches, elektro-chemisches (Spannungs-) Element im Sinne der Voltaschen Säule, die im Leerlauf (= ohne Lastwiderstand R) über eine Ursprungsspannung U₀ im Sinne der Leerlaufspannung U₀ = U_leer verfügt.

Wenn man eine Batterie als elektro-chemischen Energiewandler und Energielieferant an einen Stromkreis mit einem Lastwiderstand R_Last anschließt, dann fließt der Strom I_Batt = I_Last stets aus dem Pluspol („+“) der Batterie heraus und quasi auf dem Rückweg wieder in den Minuspol („-“) der Batterie hinein (= technische Stromrichtung!). Dabei zeigt der Spannungspfeil an den Anschlussklemmen der Batterie stets vom Pluspol („+“) zum Minuspol („-“) der Batterie, sodass der Spannungspfeil stets entgegengesetzt zum Strompfeil der Batterie gerichtet verläuft, woran genau man einen Energieerzeuger erkennt! Dabei gilt die entgegengesetzte Bepfeilung auch für (Konstant-) Stromquellen (siehe in der obenstehenden Schaltung!).

In diesem Zusammenhang stellt sich nun noch die interessante Frage, ob die Konstantstromquelle I₀ in der obenstehenden Schaltung noch wirklich als Konstantstromquelle arbeitet?!

Das ist jetzt natürlich eine rhetorische Frage, die sich deswegen selbst beantwortet: Nein! Fragt sich nur weshalb?

So wie eine Konstantstromquelle den Stromfluss und die Stromstärke in einer Schaltung mit einem Widerstand R beherrscht, indem diese am Widerstand R einen entsprechenden Spannungsabfall U_R erzwingt, dominiert nun die Spannungsquelle mit U_B3 = 3 V wegen der entgegengesetzten Polung das elektrische Verhalten der Schaltung, indem diese an der Konstantstromquelle einen umgekehrten, entgegengesetzten Stromfluss der Stromstärke I₁₀ = 10 mA erzwingt, sodass die Konstantstromquelle jetzt als ohmscher Verbraucher R₁₀ arbeitet:

R₁₀ = U₁₀ / I₁₀

= 3 V / 10 mA = 0,3 kW = 300 W

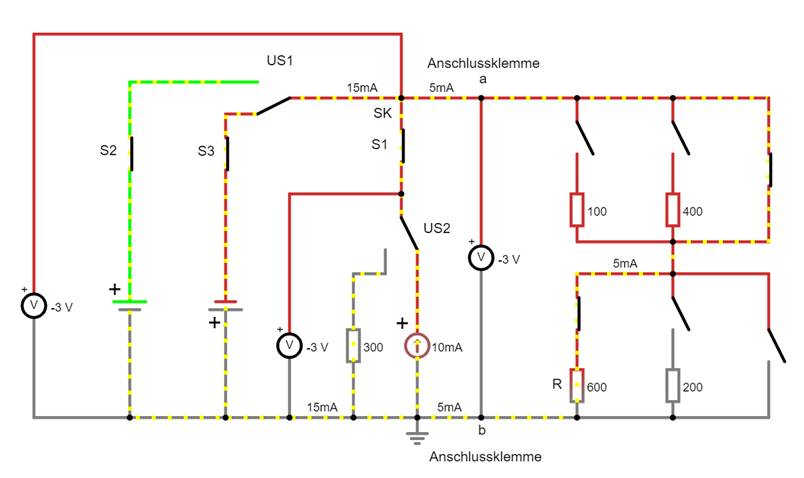
Und wer’s nicht glaubt, kann sich selbst besser belehren, indem er in der obenstehenden Schaltung die Konstantstromquelle I₁₀ durch den Widerstand R₁₀ = 300 W ersetzt bzw. beide mittels Umschalter US2 umschaltbar macht:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-21.js)

Tja, wer hätte das gedacht, dass die Konstantstromquelle I₁₀ jetzt ihren Konstantstrom von I₁₀ = 10 mA nicht mehr an den Widerstand R liefert, sondern vielmehr an die Spannungsquelle U_B3.

Wirklich? Könnte es nicht auch sein, dass der Konstantstrom von I₁₀ = 10 mA von der Spannungsquelle U_B3 aufgebracht wird? Wie lässt sich so etwas überprüfen?

Beim Parallelwiderstand R₃₀₀ mit R₃₀₀ = 300 W und der Konstantstromquelle I₁₀ mit I₁₀ = 10 mA handelt es sich um eine Parallelschaltung. Wenn man nun den Widerstand R₃₀₀ von R₃₀₀ = 300 W auf R₃₀₀ = 3 W um das Hundertfache verkleinert, dann fließt durch diesen ab sofort ein entsprechend dicker Strom von

I_R300 = U_R300 / R₃₀₀

= 3 V / 3 W = 1 A

Wenn man im nächsten Schritt die treibende Spannungsquelle U_B3 von U_B3 = 3 V auf U_B3 = 21 V vergrößert und gleichzeitig den Widerstand R₃₀₀ von R₃₀₀ = 3 W auf R₃₀₀ = 1 W verkleinert, dann wird der entsprechende Strom noch dicker:

I_R300 = U_R300 / R₃₀₀

= 21 V / 1 W = 21 A

Setzt man den Parallelwiderstand R₃₀₀ mit R₃₀₀ = 1 W ins Verhältnis zum Widerstand R₁₀ der Konstantstromquelle I₁₀, so folgt für das Widerstandsverhältnis ü:

ü = R₁₀ / R₃₀₀

= ( U₁₀ / I₁₀ ) / R₃₀₀

= ( 21 V / 10 mA ) / 1 W = 2,1 kW / 1 W = 2100 / 1

Mit der unterschiedlichen Stromstärke gerechnet folgt für das Stromstärkeverhältnis ü:

ü = I₁₀ / I₃₀₀

= 10 mA / 21 A = 0,010 A / 21 A = 4,7619 * 10^-4 ≈ 0,00048 = 48 / 100 000

Mit anderen Worten: Der Widerstand R₁₀ der Konstantstromquelle I₁₀ ist im Verhältnis, d.h. im Vergleich zum Parallelwiderstand R₃₀₀ mit R₃₀₀ = 1 W so riesengroß und gleichzeitig ist dessen Stromstärke I₁₀ der Konstantstromquelle I₁₀ so winzig klein gegenüber dem Strom von I_R300 = 21 A des Parallelwiderstand R₃₀₀, dass man den Widerstand R₁₀ der Konstantstromquelle I₁₀ vernachlässigen kann:

R_ers = ( R₁₀ * R₃₀₀ ) / (R₁₀ + R₃₀₀ )

= ( 2,1 kW * 1 W ) / ( 2,1 kW + 1 W )

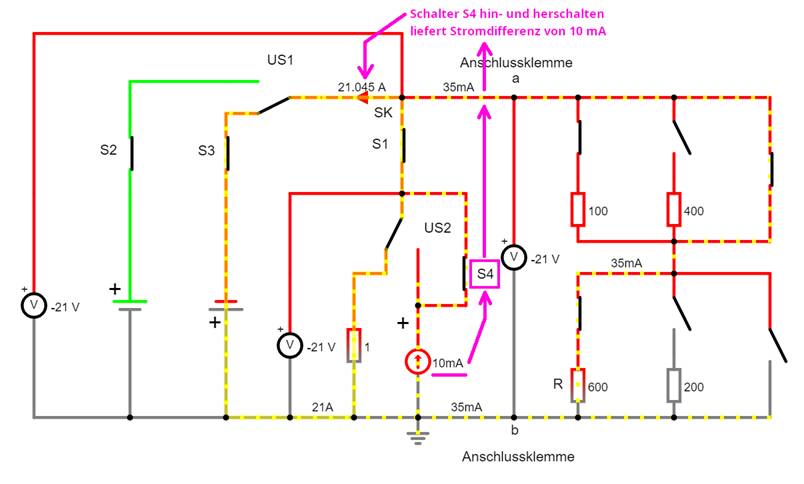
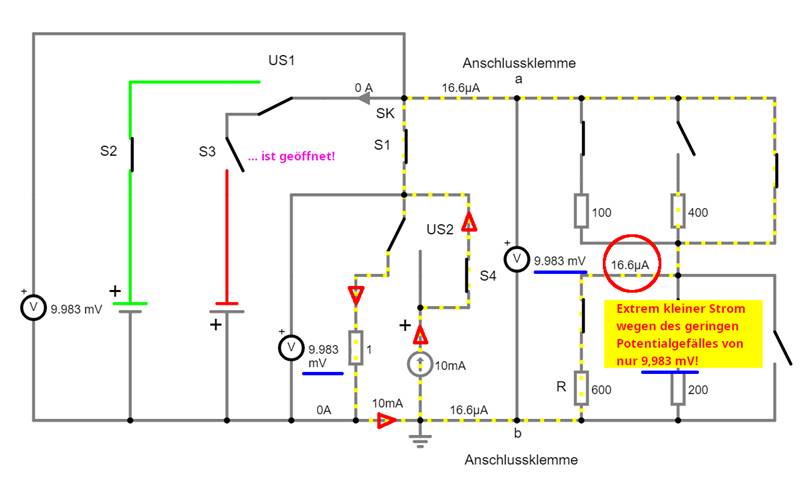
= 2100 W² / 2101 W = ( 2100 / 2101 ) W = 0,999524 W ≈ 1 W " Widerstand R₁₀ darf vernachlässigt werden!

Die nachfolgende Schaltung bestätigt durch Hin- und Herschalten des Schalters S4, dass man den Widerstand R₁₀ = 2,1 kW der Konstantstromquelle I₁₀ vernachlässigen darf:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-22.js)

Die obenstehende Schaltung mit dem Schalter S4 bestätigt ein weiteres Mal, dass sich die Konstantstromquelle I₁₀ mit dem Konstantstrom von I₁₀ = 10 mA nicht von außen durch Anlegen einer höheren Spannung von U_B3 = 21 V beeinflussen lässt. Die Konstantstromquelle I₁₀ liefert unabhängig vom anliegenden Spannungsabfall und vom sehr kleinen Parallelwiderstand R₃₀₀ mit R₃₀₀ = 1 W stets den Konstantstrom von I₁₀ = 10 mA.

In der Physik (Kapitel „Elektrizitätslehre“) und der Elektrotechnik/Elektronik gilt stets der Erfahrungsgrundsatz, dass sich der Strom stets den Weg des geringsten Widerstandes sucht. Dabei wird der Weg des geringsten Widerstandes aber auch von der Größe der anliegenden (Versorgungs-) Spannung von wegen des Potentialunterschieds und des vorherrschenden Potentialgefälles maßgeblich beeinflusst!

Wenn beispielsweise die Batterie B3 mit vormals U_B3 = 21 V erschöpft und vollständig entladen ist, dann gibt es an den beiden Batterieanschlüssen das Potentialgefälle von U_B3 = 21 V nicht mehr, sodass die Batterie B3 auch keinen (Batterie-) Strom mehr liefert (= Schalter S3 geöffnet) und sich der noch verbleibende Konstantstrom von I₁₀ = 10 mA der Konstantstromquelle I₁₀ den Weg des geringsten Widerstandes über den Parallelwiderstand R₃₀₀ mit R₃₀₀ = 1 W sucht:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, W-10-23.js)

Fragen wir abschließend noch die Künstliche Intelligenz (KI) von Google mit dem „Bard“-Chatbot.

1. Worum handelt es sich bei der Formel I = 1 / R * ( U - U₀ ) + I₀ ?

Die Formel I = 1 / R * ( U - U₀ ) + I₀ ist eine erweiterte Form des ohmschen Gesetzes. Sie beschreibt den Stromfluss durch einen Widerstand R, wenn an den Widerstand eine Spannung U angelegt wird.

Beschreibung der Formel

· I ist der Stromfluss durch den Widerstand, in Ampere (A)

· R ist der Widerstand, in Ohm (Ω)

· U ist die angelegte Spannung, in Volt (V)

· U₀ ist die Leerlaufspannung der Spannungsquelle, in V

· I₀ ist der Urstrom der Stromquelle, in A

Erklärung der Formel

Der erste Teil der Formel, I = 1 / R * ( U - U₀ ), entspricht dem ohmschen Gesetz. Er beschreibt den Stromfluss als proportional zur Spannung und umgekehrt proportional zum Widerstand.

Der zweite Teil der Formel, I₀, entspricht dem Urstrom der Stromquelle. Er beschreibt den Stromfluss, der durch die Stromquelle fließt, wenn die Spannungsquelle kurzgeschlossen wird.

Beispiel

An einen Widerstand von 10 Ω wird eine Spannung von 10 V angelegt. Die Leerlaufspannung der Spannungsquelle beträgt 5 V. Der Urstrom der Stromquelle beträgt 2 A.

Nach der Formel ergibt sich folgender Stromfluss:

I = 1/10 * (10 - 5) + 2

I = 1 * 5 + 2

I = 7 A

[ Anmerkung des Autors:

Es sieht so aus, als ob sich hier die KI von Google verrechnet hat, weil die sprachorientierte KI von Haus aus nicht richtig rechnen kann:

I = 1 / R * ( U - U₀ ) + I₀

= 1 / ( 10 W ) * ( 10 V – 5 V ) + 2 A

= 1 / ( 10 V/A ) * ( 5 V ) + 2 A = 5 / 10 A + 2 A = 2,5 A 7

/ Anmerkung ]

Anwendung

Die Formel kann verwendet werden, um den Stromfluss durch einen Widerstand zu berechnen, wenn an den Widerstand eine Spannung angelegt wird. Sie kann auch verwendet werden, um den Widerstand eines Bauteils zu berechnen, wenn der Stromfluss und die angelegte Spannung bekannt sind.

Weitere Informationen

· Ohmsches Gesetz

· Stromquelle

· Widerstand

· Leerlaufspannung

· Urstrom

2. Handelt es sich bei Formel U = R * ( I – I₀ ) + U₀ um die Umrechnung der Formel I = 1 / R * ( U - U₀ ) + I₀ ?

Ja, die Formel U = R * ( I – I₀ ) + U₀ ist die Umrechnung der Formel I = 1 / R * ( U - U₀ ) + I₀.

(…)

Erklärung der Umrechnung

Die Umrechnung basiert auf der Tatsache, dass die Leerlaufspannung U₀ auch als konstanter Stromfluss I₀ durch einen Widerstand R mit unendlichem Widerstand verstanden werden kann.

Wenn an einen Widerstand R mit unendlichem Widerstand eine Spannung U angelegt wird, dann fließt ein Stromfluss I₀ durch den Widerstand. Dieser Stromfluss ist unabhängig von der Spannung U.

Die Leerlaufspannung U₀ kann daher auch als Gleichung U = R * I₀ geschrieben werden.

Wenn diese Gleichung in die erste Formel eingesetzt wird, dann ergibt sich die Umrechnung U = R * ( I - I₀ ) + U₀.

Anwendung der Umrechnung

Die Umrechnung kann verwendet werden, um die Formel I = 1 / R * ( U - U₀ ) + I₀ in eine Form zu bringen, die für bestimmte Anwendungen besser geeignet ist.

Zum Beispiel kann die Umrechnung verwendet werden, um die Formel für den Fall zu vereinfachen, dass die Leerlaufspannung U₀ vernachlässigbar ist.

In diesem Fall ist die Leerlaufspannung U₀ sehr klein und kann daher vernachlässigt werden. Die Umrechnung ergibt dann folgende Formel:

U = R * I

Diese Formel ist eine einfache Gleichung für den ohmschen Widerstand. -

3. Wie ist die Geradengleichung für eine reale Spannungsquelle mit Innenwiderstand R, Leerlaufspannung U₀ und Kurzschlussstrom I₀?

Die Geradengleichung für eine reale Spannungsquelle mit Innenwiderstand R, Leerlaufspannung U₀ und Kurzschlussstrom I₀ ist:

U = R * I + U₀ " Bei dieser realen Spannungsquelle gibt es keinen Kurzschlussstrom I₀.

Diese Gleichung beschreibt den Zusammenhang zwischen der Spannung U, dem Strom I und dem Innenwiderstand R einer realen Spannungsquelle.

Die Leerlaufspannung U₀ und der Kurzschlussstrom I₀ sind Konstanten, die die Eigenschaften der Spannungsquelle bestimmen.

Erklärung der Geradengleichung

Die Geradengleichung besteht aus zwei Teilen:

· Der erste Teil, R * I, beschreibt den ohmschen Widerstand der Spannungsquelle. Er ist proportional zum Strom I.

· Der zweite Teil, U₀, beschreibt die Leerlaufspannung der Spannungsquelle. Sie ist unabhängig vom Strom I.

Die Geradengleichung kann auch als Darstellung einer Geraden in einem Koordinatensystem verstanden werden. Die x-Achse stellt den Strom I dar, die y-Achse stellt die Spannung U dar.

Die Steigung der Geraden entspricht dem Innenwiderstand R der Spannungsquelle. Der y-Achsenabschnitt entspricht der Leerlaufspannung U₀ der Spannungsquelle.

Beispiel

Eine Spannungsquelle hat einen Innenwiderstand von 10 Ω, eine Leerlaufspannung von 5 V und einen Kurzschlussstrom von 2 A.

Die Geradengleichung für diese Spannungsquelle lautet:

U = 10 * I + 5

Wenn an diese Spannungsquelle ein Strom von 1 A fließt, dann beträgt die Spannung:

U = 10 * 1 + 5

U = 15 V

Wenn an diese Spannungsquelle ein Kurzschlussstrom von 2 A fließt, dann beträgt die Spannung:

U = 10 * 2 + 5

U = 25 V

Anwendung der Geradengleichung

Die Geradengleichung kann verwendet werden, um die Spannung an einer realen Spannungsquelle zu berechnen, wenn der Strom I oder der Innenwiderstand R bekannt sind.

Die Gleichung kann auch verwendet werden, um den Innenwiderstand R einer Spannungsquelle zu bestimmen, wenn die Spannung U und der Strom I bekannt sind. -

[ easy electronik 200 ] [ Seitenanfang ] [ Versuch 8 ] [ Versuch 10 ] [ Versuch 17 ]