[ easy electronik 200 ] [ Seitenende ] [ Versuch 8 ] [ Versuch 17 ]

easy electronic 200 - Versuch 10

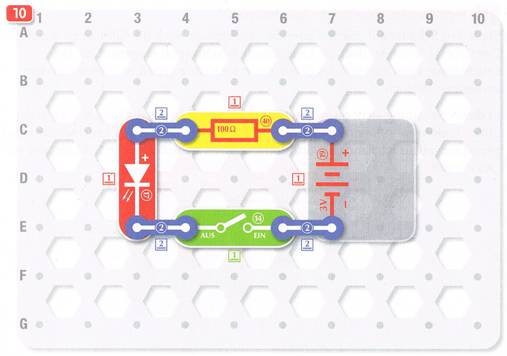
Einfache Schaltung mit einer Leuchtdiode

Beim zehnten Versuch geht es um einen einfachen Stromkreis, in dem erstmals eine Leuchtdiode (LED) und zwar die rote Leuchtdiode 17 zusammen mit dem in Reihe geschalteten Widerstand 40 wie folgt eingesetzt wird:

(Vergrößern: auf Bild klicken! | KOSMOS easy electronic, Seite 13)

Wie man anhand des obenstehenden Stromkreises sieht, besteht dieser aus

1. der Spannungsquelle

in Form des Batteriefaches 19 mit den beiden in Reihe geschalteten Batterien vom Typ „AA“, wobei jede Batterie über eine (Klemmen-) Spannung U_Batt von 1,2 V bis 1,5 V verfügt, zusammen also über eine (Gesamt-) Spannung U_{Batt, ges} von 2,4 V bis 3,0 V,

2. dem Widerstand

mit dem Widerstandswert R₄₀ = 100 Ω, der dazu dient, dass dieser den Stromfluss durch die rote Leuchtdiode 17 begrenzt, damit diese nicht überlastet wird und durchbrennt!

3. der Leuchtdiode (LED)

mit der roten Leuchtdiode 17, die bei einer Durchlassspannung U_F = 1,6 V und einem Durchlassstrom I_F von I_F = 8 mA bis I_F = 12 mA, hell leuchtet.

4. dem (Schiebe-) Schalter 14

mit dem sich die Stromzufuhr der Batterie innerhalb des Stromkreises ein- oder ausschalten lässt und

5. den Verbindungsleitungen,

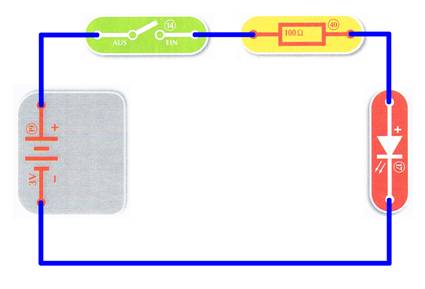
die alle einzelnen Bauelemente der Schaltung zu einem Stromkreis miteinander verbinden.

Wir ordnen die Bauelemente des Stromkreises neu an, sodass sich die Schaltung wie gewohnt von links nach rechts im Uhrzeigersinn lesen lässt:

(Zum Vergrößern bitte auf das Bild klicken!)

Aus Gründen der elektrischen Sicherheit handhaben wir es weiterhin so, den Magnetschalter 12, Schalter 14 oder Taster 15 zum Ein- und Ausschalten der Stromzufuhr möglichst nahe, d.h. in direkter Folge nach der Stromversorgung - im vorliegenden Fall direkt hinter dem Batteriefach 19 - im Stromkreis anzuordnen!

Dies hat den sicherheitstechnischen Vorteil, dass bei geöffnetem Schalter 14 alle nach dem Ein- und Ausschalter angeschlossenen Bauelemente wie z.B. das Glühlämpchen 18, aber auch der gesamte restliche Stromkreis bis zum Minuspol des Batteriefaches 19 spannungs- und stromlos sind.

Glühlämpchen kontra Leuchtdiode (LED)

Das Glühlämpchen 18 glüht und die Leuchtdiode 17 leuchtet rot. Was aber ist der wirkliche Unterschied zwischen dem Glühlämpchen und der Leuchtdiode? [ Video ]

Bei einer Glühlampe bzw. Glühfadenlampe glüht die Glühwendel, die bei herkömmlichen Glühlampen aus dem Edelmetall Wolfram besteht. Dabei kann man Glühen und Leuchten der Glühlampe durchaus wörtlich nehmen, da diese wegen des Glühens der Wolfram-Glühwendel hauptsächlich Wärme durch Wärmestrahlung produziert und nur zu einem geringen Teil Helligkeit in Form von Licht!

Wenn aber eine Glühlampe mehr Wärme als Licht produziert, dann handelt es sich bei dieser eher um einen elektrischen Heizofen mit Glüheffekt als um eine Energie sparende LED-Lampe.

Demzufolge verbraucht eine LED-Lampe mit der Helligkeit einer 100 Watt Glühlampe nur 11 Watt an elektrischer Leistung. Das sind gerade mal 11 % der Leistung einer 100 Watt Glühlampe!

Da also herkömmliche Glühlampen wegen der hohen Wärmeentwicklung und des hohen Energieverbrauchs richtige Energieverschwender sind, wurden diese in Europa ab 2009 verboten! [ Video ]

Elektrische Leistung des Glühlämpchens und der roten LED

U_{Glüh, Nenn} = 2,5 V → Nennspannung der Glühlampe 18

I_{Glüh, Nenn} = 0,3 A → Nennstromstärke der Glühlampe 18

P_{el, Glüh} = U_{Glüh, Nenn} * I_{Glüh, Nenn} → Elektrische Leistung der Glühlampe 18

= 2,5 V * 0,3 A = 0,75 W

U_{LED, Nenn} = 1,6 V → Nennspannung der Leuchtdiode 17

I_{Glüh, Nenn} = 10 mA → Nennstromstärke der Leuchtdiode 17

P_{el, LED} = U_{LED, Nenn} * I_{LED, Nenn} → Elektrische Leistung der Leuchtdiode 17

= 1,6 V * 10 mA = 16 mW = 0,016 W → 2,13 %

Demzufolge beträgt die Leistungsaufnahme der Leuchtdiode 17 nur 2,13 % der Leistung der Glühlampe 18!

Arbeitsteilung zwischen Widerstand und roter Leuchtdiode

>> Eine Leuchtdiode erzeugt Licht beim Betrieb in der richtigen Polung (du musst „Plus" und „Minus" beachten). Somit musst du bei Versuchen mit Leuchtdioden darauf achten, sie genau wie in der Aufbauzeichnung einzubauen. Leuchtdioden gibt es in verschiedenen Farben, Größen und Bauformen. In deinem Kasten findest du zwei unterschiedliche Leuchtdioden. Achtung: Es muss immer ein Widerstand im Stromkreis der Leuchtdiode vorhanden sein, denn sonst würde zu viel Strom fließen, der dann die Leuchtdiode zerstört! << (Quelle: Handbuch „KOSMOS easy electronic 200“, Seite 8, Leuchtdioden)

>> Eine Diode ist ein Bauteil, das wie ein Ventil den Strom nur in einer Richtung durchlässt. Eine Leuchtdiode (abgekürzt „LED" von der englischen Bezeichnung Light Emitting Diode = Licht aussendende Diode) kann aber mehr als eine normale Diode: Sie erzeugt beim Betrieb in der richtigen Polung (du musst „Plus" und „Minus" beachten) Licht. Aber Achtung: Es muss immer ein Widerstand im Stromkreis der Leuchtdiode vorhanden sein, denn sonst würde zu viel Strom fließen, der die Leuchtdiode zerstört! << (Quelle: Handbuch „KOSMOS easy electronic 200“, Seite 13, Versuch 10)

Bei einer Diode (sendet kein Licht), einer Leuchtdiode (sendet Licht), einer Photodiode (empfängt Licht) und einer Zenerdiode (stabilisiert die Spannung) handelt es sich um sogenannte Halbleiter. Halbleiter bestehen hauptsächlich aus Selen (= Gleichrichterdiode), Germanium oder Silizium.

Ein Halbleiter kann den elektrischen Strom in eine Richtung vom Plus- zum Minuspol durchlassen, während dieser in umgekehrter Richtung vom Minus- zum Pluspol gesperrt wird.

Halbleiter wie z.B. Leuchtdioden haben in Durchlassrichtung einen sehr geringen Widerstand, sodass diese mittels eines Vorwiderstandes unbedingt vor zu großen Stromstärken geschützt werden müssen!

>> Eine Diode ist ein elektronisches Bauelement, das Strom in einer Richtung passieren lässt und in der anderen Richtung den Stromfluss sperrt. Daher wird von Durchlassrichtung und Sperrrichtung gesprochen. Entdeckt wurde das Verhalten 1874 von Ferdinand Braun an Punktkontakten auf Bleisulfid (Galenit).

Die Bezeichnung Diode wird üblicherweise für Halbleiterdioden verwendet, die mit einem p-n-Übergang oder einem gleichrichtenden Metall-Halbleiter-Übergang (Schottky-Kontakt) arbeiten. In der Halbleitertechnik bezieht sich der Begriff Diode nur auf Siliziumdioden mit p-n-Übergang, während andere Varianten durch Namenszusätze gekennzeichnet werden, beispielsweise Schottky-Diode oder Germaniumdiode. Veraltet sind Bezeichnungen wie Ventilzellen, die bis Mitte des 20. Jahrhunderts in der damals neu entstandenen Halbleitertechnik für Dioden gebraucht wurden und auf die analoge Funktion eines mechanischen Ventils zurückgehen.

Dioden werden unter anderem zur Gleichrichtung, der Umwandlung von Wechselspannung zu Gleichspannung, eingesetzt. Daneben zeigt der Halbleiterübergang weitere nutzbare Eigenschaften, die z. B. in Zener-, Photo-, Leuchtdioden und Halbleiterdetektoren ausgenutzt werden. << (Quelle: Wikipedia)

Da die Leuchtdiode 17 (= LED) bei richtiger Polung von Plus („+“) nach Minus („-“) im Durchlassbetrieb hell leuchtet und der Halbleiterwiderstand der LED dabei sehr klein ist (siehe Berechnung weiter unten), würde durch diese ein sehr großer Strom fließen, der die LED sofort zerstört!

Um dies von vornherein zu verhindern, muss man den Vorwiderstand 40 zur Strombegrenzung vor (oder hinter) die Leuchtdiode 17 schalten.

Dabei gilt es zu beachten, dass bei einer Reihenschaltung von Vorwiderstand 40 und Leuchtdiode 17 beide Bauteile vom gleich großen Strom I = I_R40 = I_{LED, Nenn} = 10 mA durchflossen werden! [ Video ]

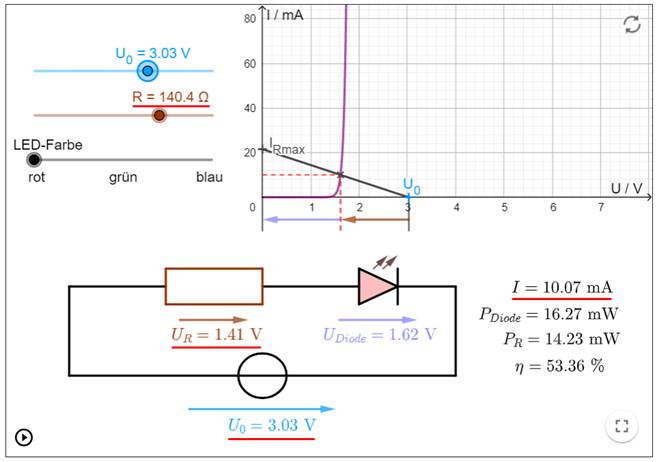
Berechnung des Vorwiderstandes

Da wir die gesamte Batterie-Spannung U_{Batt, ges} mit 2,4 V bis 3,0 V, den Spannungsabfall U_{LED, Nenn} = 1,6 V und den Strom I_{LED, Nenn} = 10 mA, der durch die Leuchtdiode 17 fließt, kennen, lässt sich der Vorwiderstand 40 wie folgt berechnen:

U_R40 + U_{LED, Nenn} + ( - U_{Batt, ges} ) = 0 " Spannungsumlauf im Uhrzeigersinn!

U_R40 + U_{LED, Nenn} - U_{Batt, ges} = 0

U_R40 + U_{LED, Nenn} = U_{Batt, ges} "

U_R40 = U_{Batt, ges} – U_{LED, Nenn}

= 3,0 V – 1,6 V = 1,4 V

Wie man sieht, berechnet sich die verbleibende, d.h. restliche Spannung U_R40 am Vorwiderstand 40 aus der Differenz von Batteriespannung U_{Batt, ges} minus LED-Spannung U_{LED, Nenn} = 3,0 V – 1,6 V = 1,4 V:

Der Vorwiderstand 40 wiederum berechnet sich nach dem Ohmschen Gesetz entsprechend der Formel R = U / I:

R₄₀ = U_R40 / I_R40 = U_R40 / I_{LED, Nenn}

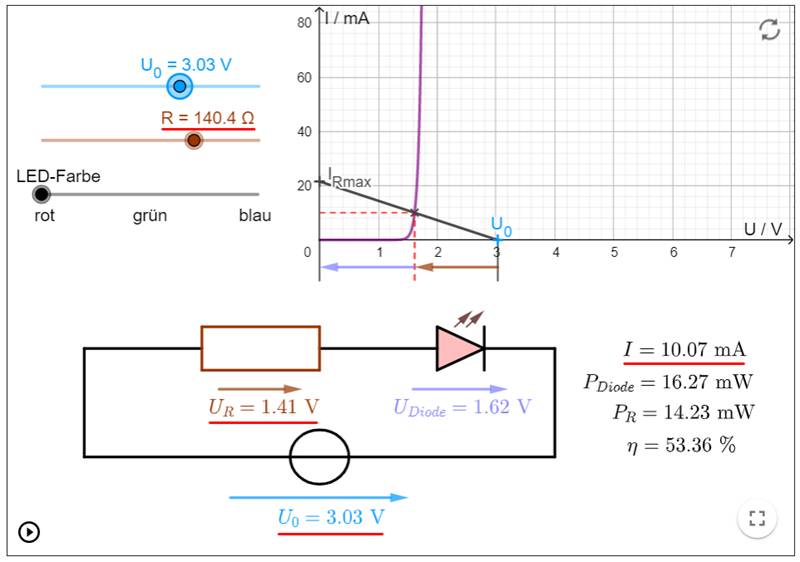
= 1,4 V / 10 mA = 1,4 V / 0,01 A = 140 Ω [ Video ]

Mit der nachfolgenden Web-App zwecks Berechnung des Vorwiderstandes R_Vor = R₄₀ = 140 Ω lässt sich nicht nur der Vorwiderstand R₄₀ berechnen, sondern auch dessen Widerstandsgerade zeichnen und berechnen:

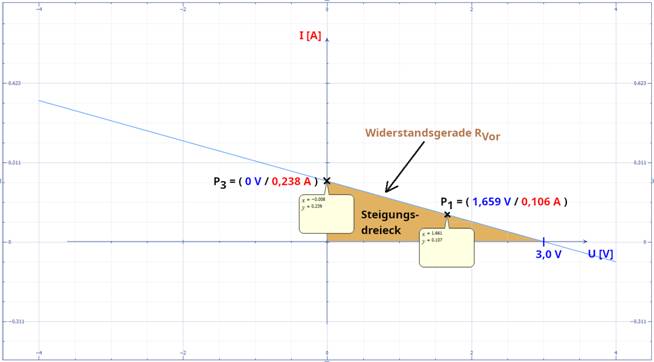
(Vergrößern: auf Bild klicken! | Quelle: GeoGebra)

Und wie man im obenstehenden Screenshot sieht, verläuft die Widerstandsgerade des Vorwiderstandes R_Vor = R₄₀ von links oben nach rechts unten und eben nicht wie bei der allgemeinen Geradengleichung y = f(x) = a x + b (siehe weiter unten im Abschnitt „Berechnung des Arbeitspunktes A der roten Leuchtdiode 17“) von links unten nach rechts oben!

Diesbezüglich stellt sich jetzt also die Frage, wie die Geradengleichung der Widerstandsgerade des Vorwiderstandes R_Vor = R₄₀ aussieht, nämlich:

y = f(x) = a (x₀ - x ) + b " mathematisch " a = Steigung der Geraden, b = Parallelverschiebung der Geraden

I = f(U) = 1 / R₄₀ ( U₀ - U ) " elektrotechnisch " Steigung der Geraden 1 / R₄₀ = 1 / (U_R40 / I_R40 ) = I_R40 / U_R40 = ∆I / ∆U

Einsetzen der obenstehenden Werte in die elektrotechnische Geradengleichung liefert:

I = 1 / R₄₀ ( U₀ - U )

= 1 / 140 W * ( 3,0 V – 1,6 V ) = 0,00714 A/V * 1,4 V = 0,009996 A ≈ 0,010 A = 10 mA þ [ Video ]

Da es sich bei der Schaltung von Vorwiderstand 40 und Leuchtdiode 17 um eine Reihenschaltung handelt, werden alle in Reihe geschalteten Bauelemente vom gleich großen Strom I = I_R40 = I_{LED, Nenn} = 10 mA durchflossen! -

Frage:

Wie groß muss der Vorwiderstand 40 bei gleich großer Stromstärke I_R40 = I_{LED, Nenn} = 10 mA sein, wenn die gesamte Batterie-Spannung U_{Batt, ges} = 2,4 V groß ist?

Antwort:

U_R40 + U_{LED, Nenn} + ( - U_{Batt, ges} ) = 0 " Spannungsumlauf im Uhrzeigersinn!

U_R40 + U_{LED, Nenn} - U_{Batt, ges} = 0

U_R40 + U_{LED, Nenn} = U_{Batt, ges} "

U_R40 = U_{Batt, ges} – U_{LED, Nenn}

= 2,4 V – 1,6 V = 0,8 V

R₄₀ = U_R40 / I_R40 = U_R40 / I_{LED, Nenn}

= 0,8 V / 10 mA = 0,8 V / 0,01 A = 80 Ω

Alternative Berechnung mittels der gespiegelten Geradengleichung:

I = 1 / R₄₀ ( U₀ - U ) "

1 / R₄₀ = I / ( U₀ - U ) "

R₄₀ = ( U₀ - U ) / I

= ( 2,4 V – 1,6 V ) / 10 mA = 0,8 V / 10 mA = 0,08 KW = 80 W

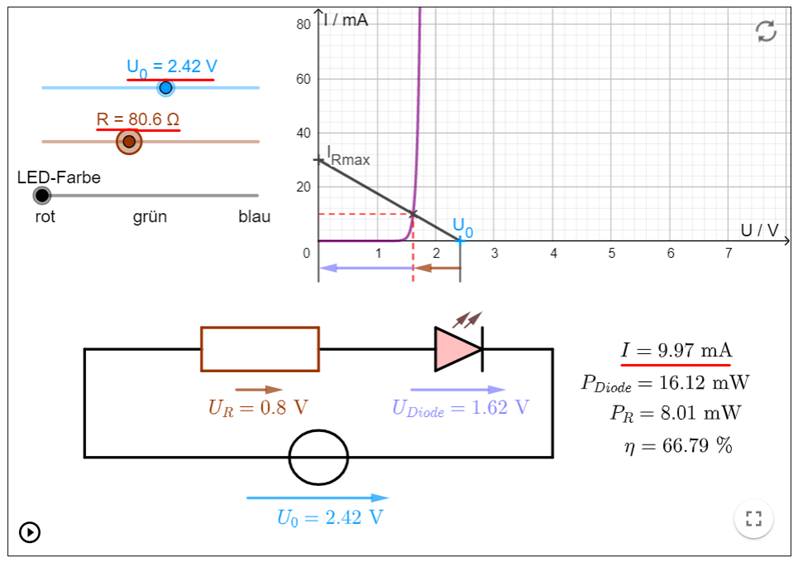
Da sich die Batteriespannung je nach Nutzungsdauer und -häufigkeit im Laufe der Zeit verringert, weil sich die Batterie mehr und mehr entlädt, müsste man, damit die Leuchtdiode 17 auch bei schwacher Batterie noch leuchtet, den Vorwiderstand 40 von vormals R₄₀ = 140 Ω im Laufe der Zeit auf nur noch R₄₀ = 80 Ω verringern:

(Vergrößern: auf Bild klicken! | Quelle: GeoGebra)

Wie man im obenstehenden Screenshot sieht, besitzt die Widerstandsgerade von R₄₀ = 80 Ω mit der neuen Geradengleichung I = 1 / R₄₀ ( U₀ - U ) insgesamt zwei Schnittstellen. Und zwar eine an der U-Achse mit S₁ = ( U / I ) = ( 2,4 V / 0 mA ) sowie an der I-Achse mit S₂ = ( U / I ) = ( 0 V / 30 mA ).

Mit I = 0 folgt für die neue Geradengleichung I = 1 / R₄₀ ( U₀ - U ):

I = 1 / R₄₀ ( U₀ - U ) "

0 = 1 / 80 Ω * ( 2,4 V – U )

= 1 / 80 Ω * 2,4 V – 1 / 80 Ω * U )

1 / 80 Ω * U = 1 / 80 Ω * 2,4 V

U = 1 / 80 Ω * 2,4 V / 1 / 80 Ω = 2,4 V

Mit U = 0 folgt für die neue Geradengleichung I = 1 / R₄₀ ( U₀ - U ):

I = 1 / R₄₀ U₀ "

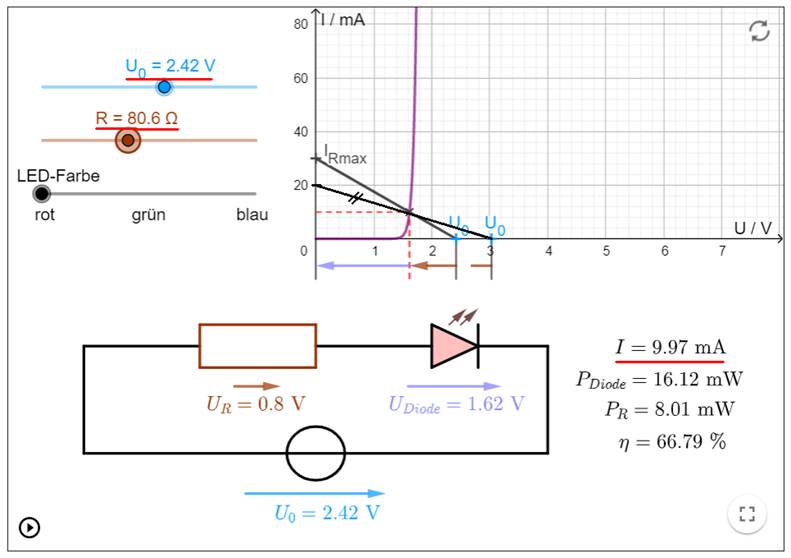
U₀ = I * R₄₀

= 30 mA * 80 W = 2 400 mV = 2,4 V

Legt man beide Widerstandsgeraden als Funktion von U₀ = 3,0 V (vormals, jetzt durchgestrichen // ) und U₀ = 2,4 V übereinander, so fällt sofort auf, dass die neue Widerstandsgerade mit R₄₀ = 80 Ω wesentlich steiler verläuft, da diese jetzt die verringerte Batteriespannung von U₀ = 2,4 V strommäßig kompensieren muss:

(Vergrößern: auf Bild klicken! | Quelle: GeoGebra)

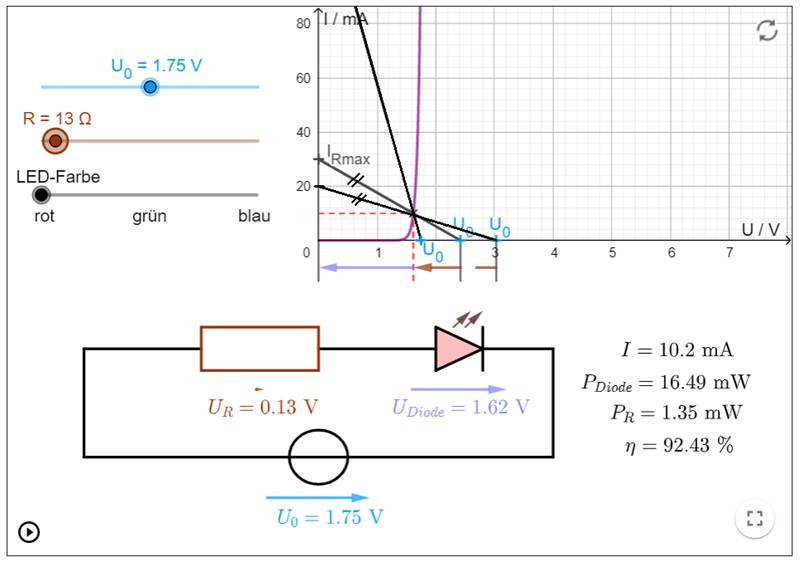
Wenn die rote Leuchtdiode 17 in der obenstehenden Schaltung bei einer abgesunkenen Batteriespannung von U₀ = 2,4 V noch hell leuchten soll, dann muss man den Vorwiderstand von vormals R_Vor = R₄₀ = 140 W auf nur noch R₄₀ = 80 W verringern!

Wenn die rote Leuchtdiode 17 in der nachfolgenden Schaltung bei einer abgesunkenen Batteriespannung von U₀ = 1,75 V noch hell leuchten soll, dann muss man den Vorwiderstand von vormals R_Vor = R₄₀ = 80 W auf nur noch R₄₀ = 13 W verringern:

(Vergrößern: auf Bild klicken! | Quelle: GeoGebra)

Wie man im obenstehenden Screenshot sieht, verläuft die neue Widerstandsgerade mit R₄₀ = 13 Ω wesentlich steiler als bisher. Und zwar so steil, sodass sich der Strom I_Rmax > 80 mA nicht mehr ablesen lässt.

Allerdings lässt sich dieser mittels der neuen Geradengleichung I = 1 / R₄₀ ( U₀ - U ) wie folgt berechnen:

I_Rmax = 1 / R₄₀ ( U₀ - U ) "

= 1 / 13 W * ( 1,75 V – 0 V )

= 1 / 13 W * 1,75 V = 1,75 V / 13 V/A = 0,1346 A ≈ 135 mA

Frage:

Was bedeutet es elektrotechnisch, wenn der Strom durch den Vorwiderstand R₄₀ bis zu I_Rmax = 135 mA groß werden kann?

Antwort:

Wie wir bereits gelernt haben, gehört zu einem großen Strom stets auch eine entsprechend große Spannung, da die Spannung die treibende Kraft ist und eine entsprechend große Stromstärke die Folge davon ist. Aber ist gibt noch einen Dritten im Bunde. Und das ist der ohmsche Widerstand, der entsprechend klein sein muss, damit ein größerer Strom fließen kann.

R_Vor = R₄₀ = 13 W, I_R40 = I_LED = 10 mA "

U_Vor = R_Vor * I_Vor = 13 W * 10 mA = 130 mV = 0,130 V = 0,13 V

R_Vor = R₄₀ = 13 W, I_Rmax = 135 mA "

Wenn man den Vorwiderstand R_Vor = R₄₀ = 13 W direkt an der Versorgungsspannung U₀ betreibt, dann folgt:

U₀ = R_Vor * I_Rmax = 13 W * 135 mA = 1 755 mV = 1,755 V ≈ 1,75 V

Der Vorwiderstand wurde mit R₄₀ = 13 Ω deshalb so klein gewählt, damit bei einem kleinen Spannungsabfall von U_Vor = 0,13 V der Strom der Stromstärke I_Vor fließen kann:

I_Vor = 1/R_Vor * U_Vor = 1 / ( 13 W ) * 0,130 V = 0,0769 W^-1 * 0,130 V = 0,0769 A/V * 0,130 V = 0,009997 A ≈ 10 mA

Doch zurück zur Frage, ob und wann der Strom durch den Vorwiderstand R₄₀ bis zu I_Rmax = 135 mA groß werden kann.

Der Strom durch den einzelnen Vorwiderstand R₄₀ = 13 Ω kann nur dann bis zu I_Rmax = 135 mA groß werden, wenn der Spannungsabfall an diesem

U_Rmax = R₄₀ * I_Rmax

= 13 Ω * 135 mA = 13 V/A * 0,135 A = 1,755 V ≈ 1,76 V beträgt!

Da aber der Spannungsabfall an der roten Leuchtdiode 17 mit U_LED = 1,62 V betragen muss, damit diese hell leuchtet, müsste die Batteriespannung

U_{0, max} = U_Rmax + U_LED

= 1,76 V + 1,62 V = 3,38 V betragen! [ Video ]

Dabei gilt es allerdings zu beachten, dass die Batteriespannung U_{0, max} bei zwei in Reihe geschalteten Batterien vom Typ „AA“ im fabrikneuen, d.h. im voll aufgeladenen Zustand (Alkali-Mangan, IEC-Norm „LR6“), nur bis zu U_{0, max} = 2 * 1,51 V = 3,02 V beträgt (mit Multimeter gemessen).

Da sich also die rechnerische Maximal-Batteriespannung von U_{0, max} = 3,38 V mit den beiden in Reihe geschalteten Batterien vom Typ „AA“ im Batteriefaches 19 wider Erwarten nicht erreichen lässt, lässt sich auch die maximal mögliche

Stromstärke von I_Rmax = 135 mA durch den einzelnen Vorwiderstand R₄₀ = 13 Ω nicht bewerkstelligen!

Auch wenn man die beiden in Reihe geschalteten Batterien vom Typ „AA“ energiemäßig „bis auf den letzten Tropfen“ ausquetschen will, so gelingt das nur bedingt, weil die dazu erforderliche Batteriespannung von

U_Batt = U₀

= U_Vor + U_LED

= 0,13 V + 1,62 V = 1,75 V (siehe Screenshot!)

niemals unter den Wert von U_Batt = 1,75 V absinken darf, weil ansonsten die rote Leuchtdiode 17 in den Sperrbereich wechseln und ausgehen würde!

Wenn man aber den kleinen Vorwiderstand mit R₄₀ = 13 Ω verwendet, um möglichst viele Elektronen aus den beiden in Reihe geschalteten Batterien vom Typ „AA“ herauszuholen, dann sollte man die Schaltung früher oder später nicht einfach so, d.h. ungeprüft, mit einer höheren Batteriespannung von U_Batt = U₀ = U_R40 + U_{LED, Nenn} = 3,0 V beaufschlagen, indem man auf’s Geradewohl fabrikneue, voll aufgeladene Batterien in das Batteriefach 19 einsetzt! Dabei könnte es nämlich passieren, dass die rote Leuchtdiode 17 mit einer zu großen Durchlassspannung mit U_F >> 1,62 V betrieben wird.

Frage:

a) Wie groß ist der Spannungsabfall U_Vor am Vorwiderstand R₄₀, wenn die Schaltung mit dem kleinen Vorwiderstand mit R₄₀ = 13 Ω und der Batteriespannung von U_Batt = 3,0 V betrieben wird?

b) Berechne die Stromstärke I_Rmax = I_{LED. Nenn} durch die Schaltung.

Antwort:

a) Der Spannungsabfall U_Vor = U_R40 am Vorwiderstand R₄₀ mit R₄₀ = 13 Ω berechnet sich jetzt wie folgt:

U_Batt = U₀

= U_R40 + U_{LED, Nenn} "

U_R40 = U_Batt - U_{LED, Nenn}

= 3,0 V – 1,62 V = 1,38 V

b) Die Stromstärke I_Rmax = I_{LED. Nenn} durch die Schaltung berechnet sich wie folgt:

I = U / R "

I_R40 = 1 / R₄₀ * U_R40

= 1 / 13 Ω * 1,38 V ≈ 0,076923 A/V * 1,38 V = 0,10615374 A ≈ 0,106 A = 106 mA 7 " LED brennt durch!

Berechnung des LED-Widerstandes im Durchlassbetrieb

Wenn die Leuchtdiode 17 (= LED) bei richtiger Polung von Plus („+“) nach Minus („-“) im Durchlassbetrieb hell leuchtet und der Halbleiterwiderstand der LED dabei sehr klein ist, darf die Spannung bzw. der Spannungsabfall an der LED nicht viel größer werden als U_{LED, Nenn} = 1,6 V und die Stromstärke durch die LED nicht viel größer als I_{LED, Nenn} = 10 mA damit die LED nicht durchbrennt!

Demzufolge berechnet sich der Bahnwiderstand R_LED durch den Halbleiter der LED gemäß dem Ohmschen Gesetz wie folgt:

R = U / I →

R_LED = U_{LED, Nenn} / I_{LED, Nenn}

= 1,6 V / 10 mA = 1,6 V / 0,010 A = 160 Ω

Berechnung des Batterie-Innenwiderstandes

Eine Batterie wie z.B. die beiden in Reihe geschalteten 1,5 V Mignon-Batterien vom Typ „AA“ mit einer gesamten Batterie-Spannung U_{Batt, ges} von 2,4 V bis 3,0 V ist quasi eine kleine Chemiefabrik, deren chemisches Innenleben mit dem Elektrolyten und den beiden Elektroden (Anode und Kathode) sich mit fortschreitender Entladung laufend verändert bis sich die Anode („+“) aufgezehrt hat.

Dabei wird der elektro-chemische Innenwiderstand R_i der Batterie als Spannungsquelle mit zunehmender Entladung immer größer und zwar mit der unangenehmen Folge, dass die Klemmenspannung U_Klemmen = U_{Batt, ges} immer kleiner wird!

Wenn die gesamte Klemmenspannung U_Klemmen = U_{Batt, ges} der beiden in Reihe geschalteten 1,5 V Mignon-Batterien vom Typ „AA“ nur noch U_{Batt, ges} = 2 * U₀ = 2 * 1,0 V = 2,0 V beträgt, sind die beiden „Alkali-Mangan“-Batterien vollständig entladen, sollte man diese umgehend gegen fabrikneue Batterien auswechseln, damit diese nicht aufplatzen und der chemisch aggressive Elektrolyt ausläuft und das Batteriefach beschädigt!

Dabei handelt es sich bei der einzelnen Batteriespannung von U₀ = 1,0 V um die sogenannte Entladeschlussspannung. Wie der Name bereits sagt, handelt es sich bei dieser um diejenige Spannung, bei der sich aus der Batterie praktisch keine Energie mehr entnehmen lässt. Demzufolge ist eine 1,5 Volt „Alkali-Mangan“-Batterie bereits nach 2/3 der Nennkapazität (Q_Nenn = 3000 mAh) erschöpft (siehe Wikipedia).

Frage:

Wie groß ist der Innenwiderstand R_i der beiden in Reihe geschalteten 1,5 V Mignon-Batterien vom Typ „AA“, wenn diese fabrikneu sind, die gesamte Klemmenspannung U_Klemmen = U_{Batt, ges} = 3,0 V und der Kurzschlussstrom I_Kurz = 3 A betragen!

Antwort:

Es gilt wieder das Ohmsche Gesetz zur Berechnung des Innenwiderstand R_i:

R = U / I →

R_i = U₀ / I_Kurz → U₀ = Leerlaufspannung der Batterien

I_Kurz = Kurzschlussstrom der Batterien

= 3,0 V / 3 A = 1 Ω

Tatsächlich soll aber der Innenwiderstand R_i einer 1,5 Volt „Alkali-Mangan“-Batterie nur R_i = 0,15 W betragen (siehe Wikipedia), sodass sich der Kurzschlussstrom I_Kurz wie folgt berechnen würde:

I_Kurz = U₀ / R_i

= 2 * 1,5 V / 2 * 0,15 W " Reihenschaltung der beiden 1,5 Volt Batterien!

= ( 2 * 1,5 V ) / ( 2 * 0,15 W ) = 1,5 V / 0,15 V/A = 10 A

Frage:

Wie groß ist der Innenwiderstand R_i der beiden in Reihe geschalteten 1,5 V Mignon-Batterien vom Typ „AA“, wenn diese teilentladen sind und die gesamte Klemmenspannung U_Klemmen = U_{Batt, ges} = 1,6 V und der Kurzschlussstrom I_Kurz = 80 mA betragen?

Antwort:

Es gilt wieder das Ohmsche Gesetz zur Berechnung des Innenwiderstandes R_i:

R = U / I →

R_i = U₀ / I_Kurz → U₀ = Leerlaufspannung der Batterien

I_Kurz = Kurzschlussstrom der Batterien

= 1,6 V / 80 mA = 1,6 V / 0,080 A = 20 Ω

Da die rote Leuchtdiode 17 bei der (Nenn-) Spannung von U_{LED, Nenn} = 1,6 V und dem (Nenn-) Strom I_{LED, Nenn} = 10 mA hell leuchtet, ließe sich diese auch direkt an der teilentladenen(!) Batterie mit den zwei in Reihe geschalteten 1,5 V Mignon-Batterien vom Typ „AA“ betreiben. Dazu müsste man allerdings den Vorwiderstand 40 mit R₄₀ = 100 Ω stufenweise bis auf R₄₀ = 0 Ω verringern, was für die rote Leuchtdiode 17 in dem Moment tödlich wäre, wenn man früher oder später die verbrauchten Batterien durch fabrikneue ohne Verwendung des Vorwiderstandes ersetzt! [ Video ]

>> LED-Kennlinie (Dezember 2003, März 2004)

Auch wenn man inzwischen mit LEDs schon kräftig Licht machen kann, verhalten sich LEDs elektrisch völlig anders als Glühlampen, denn sie bestehen nicht aus einer Glühwendel sondern aus einem Halbleiterchip, das die Kennlinie einer Halbleiterdiode hat, nämlich eine nichtlineare (exponentielle) I = f(U)-Kennlinie mit einem ausgeprägten Knick bei einer farbspezifischen Spannung (einige typischen Werte siehe Tabelle in der Rubrik Vorwiderstand).

Die "Knickspannung" wird oft als Schnittpunkt einer Tangente (blau gestrichelt) im Nennarbeitspunkt (hier 2,1V/50mA) an der LED-Kennlinie und der waagrechten Achse definiert.

Im gezeigten Beispiel einer roten LED würde sich eine Knickspannung von ca. 1,85 V ergeben.

Tatsächlich beginnt der LED-Strom bei dieser roten LED aber schon ab ca. 1,7 V nennenswert zu fließen (ist alles eine Frage des Maßstabes!).

Hier gibt es neuerdings (25.10.2016) eine per Scope aufgezeichnete Kennlinie einer weißen Golden Dragon von Osram, die zum Schutz sogar eine kleine rote LED anti-parallel geschaltet hat.

Und das heißt, auf einen Nenner gebracht, dass man direkt an eine LED nicht irgend eine Spannung anlegt und dann ein Strom nach dem ohmschen Gesetz^[1] fließt, sondern dass man den gewünschten LED-Strom fließen lässt (wie das geht, steht auf dieser Website) und sich dann die LED-Spannung zwangsläufig laut LED-Kennlinie ergibt.

Das ohmsche Gesetz ist bei LEDs aufgrund deren nichtlinearen Kennlinie also nicht anwendbar, wohl aber für LED-Vorwiderstände. << (Quelle: www.LED-treiber.de) [ Video ]

Berechnung des Arbeitspunktes A der roten Leuchtdiode 17

Wie bereits wissen, gibt es zu jeder mathematischen Gleichung auch eine grafische Lösung. Dabei ist die grafische, d.h. zeichnerische Lösung einer Geradengleichung 1. Grades mit y = f(x) = a x + b oder y = f(x) = m x + b besonders einfach.

Dabei handelt es sich bei den Koeffizienten a und m um die Steigung der Geraden mit

a = m = ∆y / ∆x = ( y₂ – y₁ ) / ( x₂ – x₁ ) mit y₂ > y₁ und x₂ > x₁ " mathematisch!

a = m = ∆I / ∆U = 1/R = ( I₂ – I₁ ) / ( u₂ – u₁ ) mit I₂ > I₁ und U₂ > U₁ " elektrotechnisch!

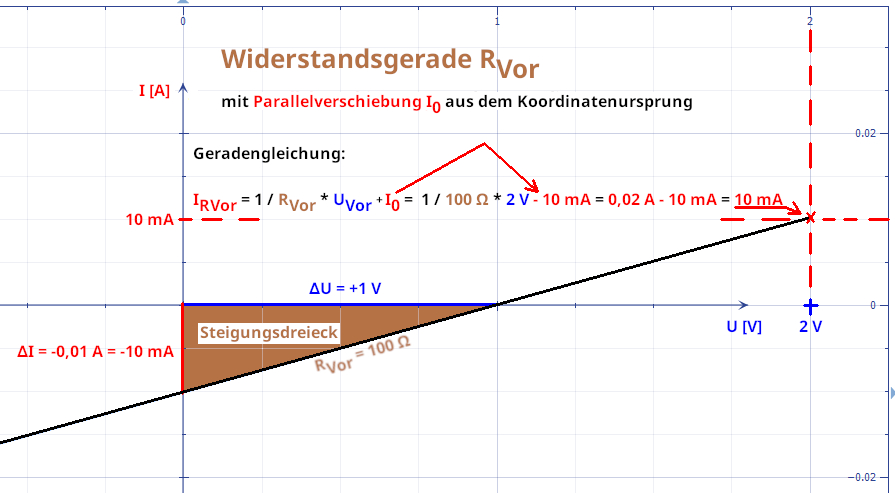
und bei dem Koeffizienten b um die Parallelverschiebung der Geraden aus dem Koordinatenursprung heraus:

Geradengleichung mit y = f(x) = a x + b oder y = f(x) = m x + b " mathematisch!

Widerstandsgerade mit I = f(U) = 1 / R_Vor U_Vor + I₀ " elektrotechnisch " mit grafische Darstellung:

(Vergrößern: auf Bild klicken! | Quelle: Microsoft „Mathematics“)

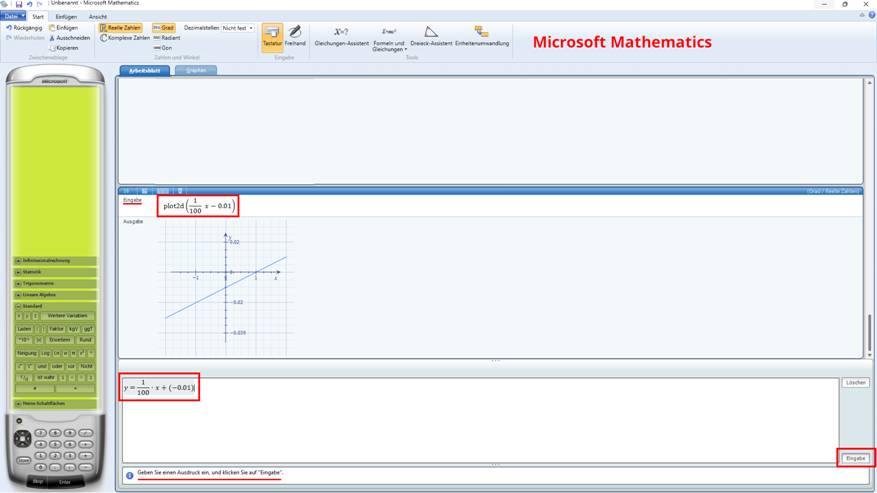
Wie man im obenstehenden Screenshot sieht, ist die Widerstandsgerade des Vorwiderstandes R_Vor = 100 W um I₀ = ‑10 mA aus dem Koordinatenursprung heraus nach unten verschoben! Demzufolge fließt bei der Spannung U₀ = 0 V im Koordinatenursprung bereits ein Strom der Stromstärke I₀ = -10 mA, der von einer sogenannten Konstantstromquelle generiert wird! -

Die obenstehende Grafik wurde übrigens mit dem Microsoft-Programm „Mathematics“ für Windows erstellt:

(Vergrößern: auf Bild klicken! | Quelle: „Mathematics“) [ Video ]

Selbstverständlich lässt sich die Widerstandsgerade mit y = f(x) = 1/100 x auch ohne das Vorhandensein einer Konstantstromquelle I₀ wie folgt darstellen, sodass diese durch den Koordinatenursprung verläuft:

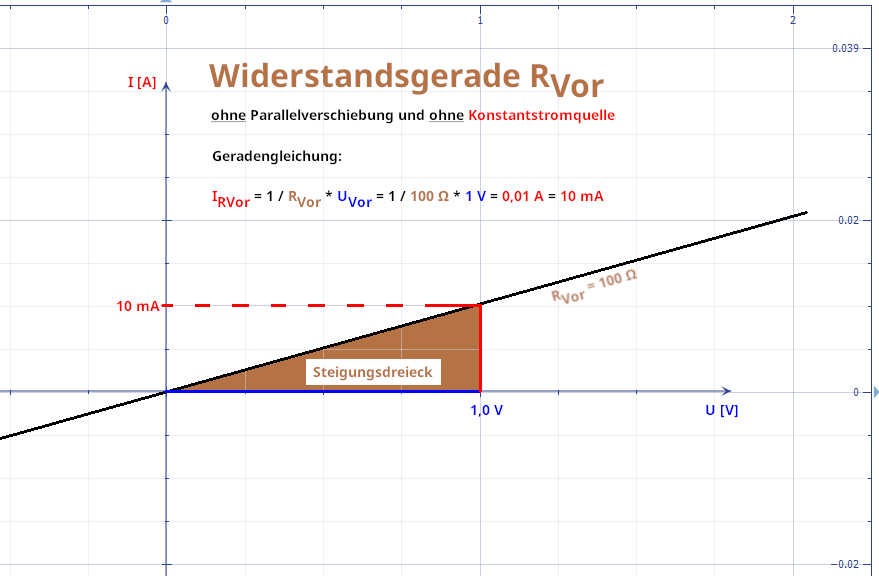
(Vergrößern: auf Bild klicken! | Quelle: „Mathematics“)

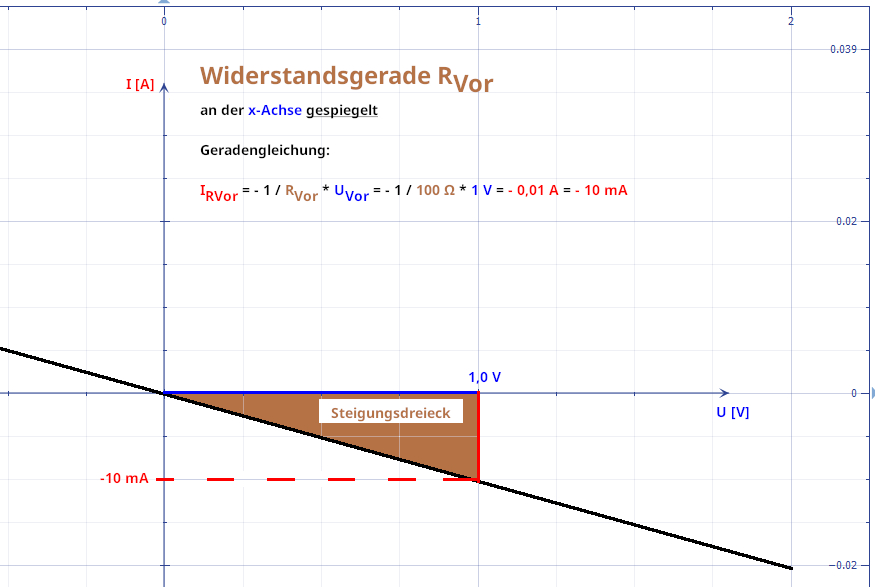
Ebenso lässt sich die obenstehende Widerstandsgerade I_RVor = 1 / R_Vor * U_Vor ganz einfach wie folgt an der x-Achse spiegeln:

(Vergrößern: auf Bild klicken! | Quelle: „Mathematics“)

Das im obenstehenden Screenshot zu sehende Steigungsdreieck mit der Geradengleichung

I_RVor = - 1 / R_Vor * U_Vor

= - 1 / 100 W * 1 V = - 0,01 A = - 10 mA

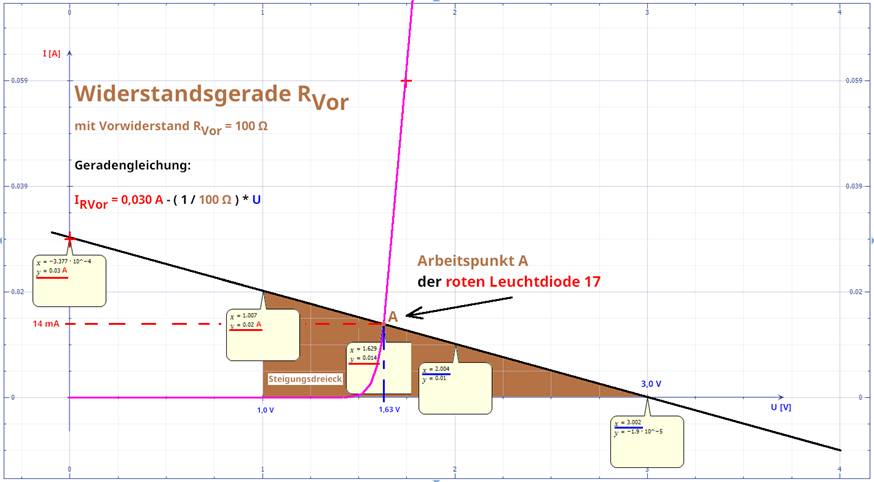
lässt sich selbstverständlich auch nach oben wie folgt verschieben:

I_RVor = I₀ - 1 / R_Vor * U_Vor = - 1 / R_Vor * U_Vor + I₀

= 0,030 A - 1 / 100 W * 1,63 V

= 0,030 A - 0,01 V/A * 1,63 V

= 0,030 A - 0,0163 A = 0,0137 A = 13,7 mA ≈ 14 mA " siehe Arbeitspunkt A!

(Vergrößern: auf Bild klicken! | Quelle: „Mathematics“)

In diesem Zusammenhang gilt es noch zu klären, wie man auf den Konstantstrom-Anteil von I₀ = 0,030 A in der Geradengleichung I_RVor = I₀ - 1 / R_Vor * U_Vor bzw. I_RVor = - 1 / R_Vor * U_Vor + I₀ kommt.

Wenn man den Vorwiderstand R_Vor = R₄₀ = 100 W für sich allein nimmt und diesen mit der Batteriespannung U₀ = 3,0 V beaufschlagt, dann stellt sich der Strom I₀ wie folgt ein:

I₀ = 1 / R₄₀ * U₀ " Diese Widerstandsgerade verläuft vom Koordinatenursprung aus diagonal nach rechts oben!

= 1 / 100 W * 3,0 V

= 0,01 V/A * 3,0 V = 0,03 A

Wenn man die Widerstandsgerade an der Spannungsachse U (= x-Achse) spiegelt, dann verläuft diese mit einer negativen Steigung vom Koordinatenursprung aus diagonal nach rechts unten:

I₀ = - 1 / R₄₀ * U₀ " Diese Widerstandsgerade verläuft vom Koordinatenursprung aus diagonal nach rechts unten!

= - 1 / 100 W * 3,0 V

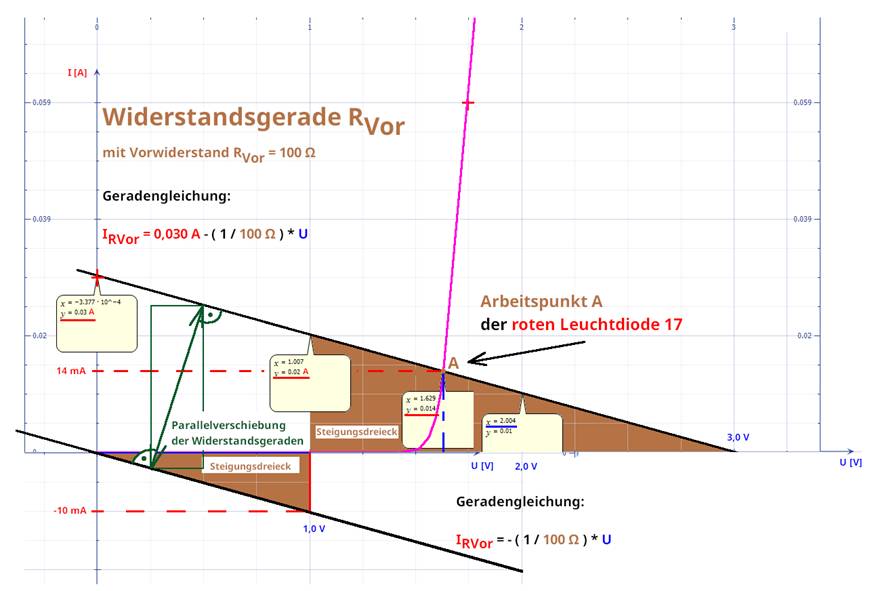
= - 0,01 V/A * 3,0 V = - 0,03 A

Nun muss man die Widerstandsgerade mit der negativen Steigung I₀ = - 1 / R₄₀ * U₀ nur noch nach oben in Richtung der Stromstärke-Achse (= y-Achse) bis zur Stromstärke I = 0,03 A verschieben (siehe grüner Doppelpfeil mit 90^o Winkel):

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden Bild sieht, muss man zu der Geradengleichung I_RVor = - ( 1 / 100 W ) * U nur den Stromstärkewert ∆I_RVor = 0,030 A = 30 mA addieren, um auf die Widerstandgerade, die durch den Arbeitspunkt A verläuft, zu kommen, sodass für die Geradengleichung folgt:

I_RVor = - ( 1 / 100 W ) * U + 0,030 A

= 0,030 A - ( 1 / 100 W ) * U

Um die Widerstandgerade durch den Arbeitspunkt A zeichnen zu können, muss man sich nur eine Wertetabelle wie folgt anlegen:

U [V]	0	1	2	3
I [mA]	30	20	10	0

Die Naturkonstanten PI „p“ und die Eulersche Zahl „e“

In der Mathematik und Physik gibt es im Wesentlichen zwei wichtige Naturkonstanten. Und zwar die Kreiszahl p ≈ 3,14 zwecks Berechnung des Kreisumfangs U = 2p r, der Kreisfläche A = p r², der Kugeloberfläche A_O = 4 p r² oder des Kugelvolumens V = 4/3 p r³.

Während sich praktisch alle Schüler und Schülerinnen, die eine Realschule, die Fachoberschule, das Berufliche Gymnasium. die Sekundarstufe II der Gesamtschule oder das Gymnasium besuchen, nicht vor der Kreiszahl p drücken können, sieht es bei der Eulerschen Zahl e ≈ 2,718 schon anders aus, die erst in der Oberstufe der Klassen 12 bis 13 der Sekundarstufe II zum Zuge kommt. Und zwar meistens in der Mathematik, d.h. bei der Differential- und Integralrechnung.

Aber auch in der Wirtschaft, d.h. der Betriebs- und Volkswirtschaft, spielt die Eulersche Zahl e ≈ 2,718 eine bedeutende Rolle. Und zwar immer dann, wenn es um das exponentielle Wachstum bei Wachstumsprozessen geht.

Dabei bedeutet „exponentiell“, dass sich das Wachstum nicht von Mal zu Mal verdoppelt, verdreifacht, vervierfacht, …, ver-x-facht, sondern eben exponentiell wie z.B. 10⁰, 10¹, 10², 10³, …, 10^x = 1, 10, 100, 1000, …, d.h. jeweils um den Faktor 10 vervielfacht bzw. multipliziert. Dabei gilt es zu beachten, dass sich das Wachstum exponentiell in 10er Potenzen vollzieht und wir uns im Dezimalsystem, auch Zehnersystem oder dekadisches System genannt, bewegen. Demzufolge rechnen wir im Dezimalsystem mit den zehn Fingern des Menschen, d.h. mathematisch zur Basis 10: 10⁰, 10¹, 10², 10³, …, 10^x.

Neben dem Dezimalsystem bei dem zur Basis 10 gerechnet wird, gibt es aber auch noch andere Zahlensysteme wie z.B. das Dualsystem zur Basis 2, weshalb dieses auch Zweiersystem oder Binärsystem genannt wird. Mikrocontroller und Computer rechnen beispielsweise in diesem, so als ob Computer nur zwei Finger zum Zählen hätten:

1₂ + 1₂ = 10₂ = 1 * 2¹ + 0 * 2⁰ = 1 * 2 + 0 * 1 = 2 + 0 = 2₁₀.

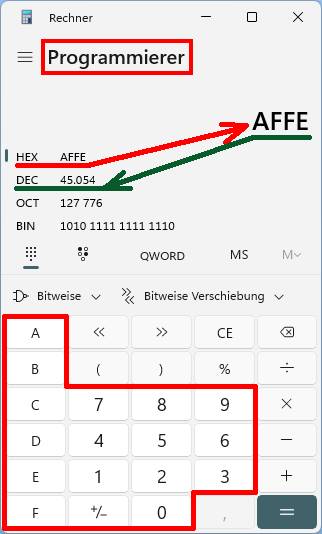
Obwohl sich bei den Computern das Binärsystem durchgesetzt hat, können diese auch oktal zur Basis 8 und hexadezimal zur Basis 16 rechnen:

AFFE₁₆ = A * 16³ + F * 16² + F * 16¹ + E * 16⁰

= A * 4096 + F * 256 + F * 16 + E * 1

= 10 * 4096 + 15 * 256 + 15 * 16 + 14 * 1

= 40960 + 3840 + 240 + 14 = 45054₁₀

Die ungewohnte und teils umständliche Umrechnung kann man sich sparen, wenn man den Taschenrechner von Microsoft Windows von der Standard-Ansicht auf die Programmierer-Ansicht umschaltet:

(Zum Vergrößern bitte auf das Bild klicken!)

Wenn man jemanden beleidigen will ohne sich strafbar zu machen, dann muss man nur sagen: „Du dummer, hexdezimaler 45 0 54!“ Was natürlich nichts anderes bedeutet als „Du dummer hexadezimaler Affe!“. [ Video ]

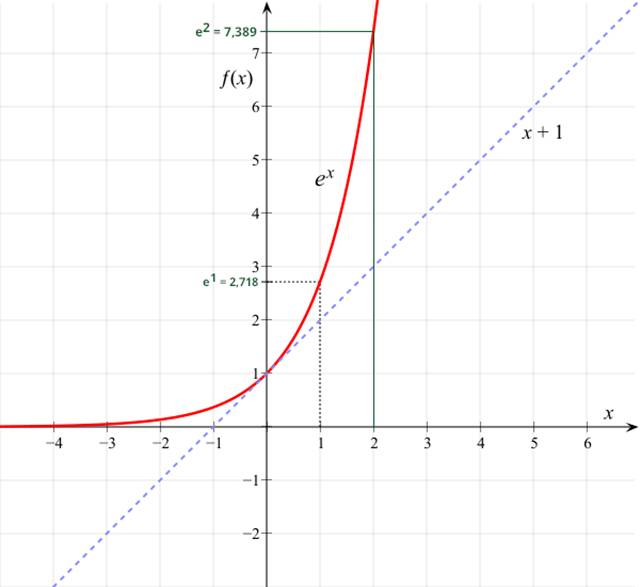
So wie es neben dem Dezimalsystem zur Basis 10 noch weitere Zahlensysteme gibt, gibt es auch noch das Eulersche Zahlensystem zur Basis e ≈ 2,718

Beispiel:

4 * e³ + 3 * e² + 2 * e¹ + 1 * e⁰ ≈ 4 * 20,086 + 3 * 7,389 + 2 * 2,718 + 1 * 1 = 80,344 + 22,167 + 5,436 + 1 = 108,947₁₀ dezimal!

Wie man anhand der aufsteigenden Wertigkeiten 1, 2.718, 7.389, 20.086 sieht, wachsen die Wertigkeiten der Eulerschen Zahl exponentiell an (siehe rote Kennlinie der e-Funktion):

(Vergrößern: auf Bild klicken! | Quelle: „Wikipedia“)

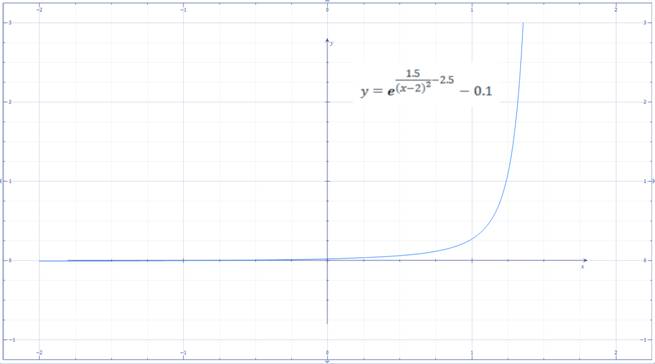
Das Charakteristische einer e-Funktion wie z.B. y = f(x) = e^x ist der exponentielle Anstieg des Graphen (= rote Kennlinie) der Funktion (siehe Bild oben). Dabei lässt sich der steile Anstieg des Graphen der e-Funktion noch steigern, wenn man entsprechende Koeffizienten (= Beiwerte) im Exponenten wie folgt verändert (siehe Bild unten):

(Vergrößern: auf Bild klicken! | Quelle: „Mathematics“)

Wenn man nun im obenstehenden Bild den Graphen der Funktion y = e^{1,5 / (x-2)^2 - 2,5} - 0,1 (= blaue Kennlinie) mit dem Graphen der Funktion (= violette Kennlinie) im nachfolgenden Bild vergleicht, dann bestätigt sich, dass es in beiden Kennlinien einen steilen Anstieg mit U_F > 1 V (= Durchflussspannung) als Indiz für den exponentiellen Werteanstieg der Durchflussstromstärke I_F > 10 mA und das Vorhandensein der e-Funktion gibt:

(Vergrößern: auf Bild klicken! | Quelle: GeoGebra)

Auf dem Webportal „PHYSIK compact“, Kapitel „Basiswissen 7“ wird im Abschnitt „17 Halbleiter“ die „Ideale Halbleiter-Diode“ mathematisch wie folgt beschrieben:

>> Die mathematische Beschreibung der idealen Halbleiter-Diode

Lernziele

Mit der Funktion I_D = I_S * ( e^{( U}_D^{/ (n * U}_T^{) )} - 1 ) kann die Kennlinie einer idealen Halbleiterdiode beschrieben werden. Dabei hängt die Durchlassstromstärke I_D von der Sättigungsstromstärke I_S von der angelegten Durchlassspannung U_D und vom Produkt n·U_T (Emissionskoeffizient n · Temperaturspannung U_T = (k · T) / q ≈ 26 mV) ab. << (Quelle: PHYSIK compact - Basiswissen 7)

Dabei geht es bei der Funktion I_D = I_S * ( e^{( U}_D ^{/ (n U}_T^{) )} – 1 ) darum, die Durchlassstromstärke I_D als Funktion der Sättigungsstromstärke I_S sowie der e-Funktion einer idealen Halbleiter-Diode (nicht der roten Leuchtdiode) zu berechnen:

I_D = I_S * ( e^(U_D^{/(n * U}_T^{) )} - 1 )

I_D / I_S = e^(U_D^{/(n * U}_T^{) )} - 1

Mit der Temperaturspannung U_T = (k · T) / q ≈ 26 mV folgt:

I_D / I_S = e^(U_D^{/(n * U}_T^{) )} - 1

I_D / I_S = e^(U_D^{/(n * 26 mV) )} - 1

Gemäß Wikipedia

(Vergrößern: auf Bild klicken! | Quelle: Wikipedia)

handelt es sich bei der obenstehenden Sättigungsstromstärke I_S um die Sättigungssperrstromstärke I_S (kurz: Sperrstrom) I_S ≈ 10^-12 … 10^-6 A " [ pA ] = „Pikoampere“ … [ µA ] = „Mikroampere“.

Wie man sieht, sind Sperrströme naturgemäß sehr klein:

I_D / I_S = e^(U_D^{/(n * U}_T^{) )} - 1

= e^{( 0,7 V / ( 1,5 * 26 mV ) )} - 1 = e^{( 700 mV / 39 mV )} - 1 ≈ e^{17,94871794871795} - 1 ≈ e^17,95 - 1 ≈ e^17,95 - 1

= 62 457 694,655237545391745485019513 – 1 ≈ 62.457.693,65524 ≈ 62,46 * 10⁶

I_D = 62,46 * 10⁶ * I_S "

I_S = I_D / ( 62,46 * 10⁶ )

≈ 10 mA / 62,5 10⁶ = 10 * 10^-3 A / ( 62,5 10⁶ )

= 10 / 62,5 * 10^-3 A * 10^-6 = 0,16 * 10^-9 A = 0,16 nA = 160 pA

Wie man anhand des Ergebnisses sieht, liegt der (Sättigungs-) Sperrstrom I_S tatsächlich im Bereich von I_S ≈ 10^-12 … 10^-6 A = [ pA ] … [ µA ].

Während sich die winzig kleinen Sperrströme I_S im Bereich von einigen Picoampere [ pA ] (= Billionstel Ampere = 10^-12 A) oder Nanoampere [ nA ] ( = Milliardstel Ampere = 10^-9) nicht messen lassen, lassen sich hingegen kleine Sperrströme I_S im Bereich von einigen Mikroampere [ µA ] (= Millionstel Ampere = 10^-6 A) sehr wohl mit einem sehr empfindlichen analogen Drehspulmessgerät oder digitalem Strommessgerät messen. [ Video ]

Frage:

Ein analoges Multimeter trägt auf der Skala die Beschriftung „20 KW/V DC“. Lässt sich mit diesem der kleine Sperrstrom I_S von I_S ≈ 152,2 µA messen?

Antwort:

Um die Frage beantworten zu können, muss man den Innenwiderstand R_i des Drehspulmesswerks wie folgt berechnen:

Aus der Beschriftung „20 KW/V DC“ folgt für die Maßeinheiten [ KW ] und [ V ] gemäß dem Ohmschen Gesetz die Formel

R / U = 1 / I "

I_Mess = U_Mess / R_i

= 1 V / 20 KW = 1 V / 20 * 10³ V/A = 0,05 * 10^-3 A = 0,05 * mA = 50 µA

Jetzt wissen wir, dass die Messempfindlichkeit des Drehspulmesswerks tatsächlich groß genug ist. Um den berechneten Sperrstrom I_S von I_S ≈ 152,2 µA messen zu können, müsste man sogar den Messbereich von 50 µA auf 500 µA umschalten! -

Wenden wir uns wieder der obenstehenden Formel I_D / I_S = e^(U_D^{/(n * U}_T⁾ - 1 zu und stellen diese wie folgt um:

I_D / I_S = e^{( U}_D ^{/ ( n * U}_T ^{) )} - 1 "

I_D = [ e^{( U}_D ^{/ ( n * U}_T ^{) )} - 1 ] * I_S

= [ e^{( U}_D ^{/ 250 mV )} - 1 ] * 152,2 µA

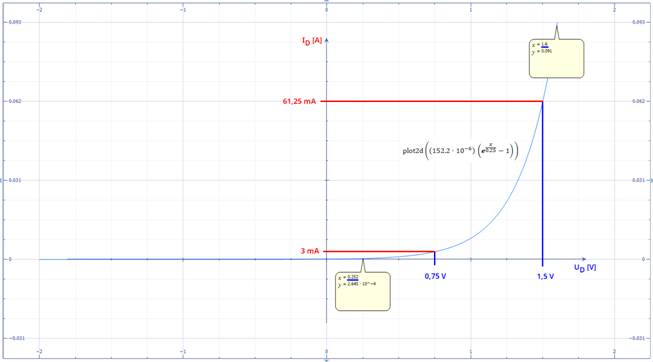
= [ e^{( U}_D ^{/ 0,25 V )} - 1 ] * 152,2 * 10^-6 A

Einsetzen von U_D = 1,5 V liefert:

I_D = [ e^{( 1,5 V / 0,25 V )} - 1 ] * 152,2 * 10^-6 A

= [ e⁶ - 1 ] * 152,2 * 10^-6 A ≈ [ 402,43 ] * 0,1522 * 10^-3 A = 0,06125 A ≈ 61,25 mA

Mit dem Microsoft-Programm „Mathematics“ für Windows lässt sich die Funktion

y_D = f(x_D) "

I_D = ( e^{( U}_D ^{/ n * U}_T ⁾ -1 ) * I_S

= ( e^{( U}_D ^{/ 0,25 V )} -1 ) * 152,2 * 10^-6 A

Wegen des Exponenten ( x_D / n * U_T ) der e-Funktion inkl. der runden Klammern mit ( e^{( x}_D ^{/ 0,25 V )} -1 ) muss man im Microsoft-Programm „Mathematics“ die Reihenfolge der Multiplikanden vertauschen:

y_D = f(x_D) "

I_D = ( e^{( U}_D ^{/ n * U}_T ⁾ -1 ) * I_S

= I_S * ( e^{( U}_D ^{/ n * U}_T ⁾ -1 )

= ( 152,2 * 10^-6 A ) * ( e^{( U}_D ^{/ 0,25 V )} -1 )

(Vergrößern: auf Bild 19 klicken! | Quelle: „Mathematics“)

Bei dem obenstehenden Diagramm mit der Berechnung des Durchlassstromes I_D als Funktion der (Sättigungs-) Stromstärke I_S, der Temperaturspannung U_T ≈ n * 25 mV und mit dem Emissionskoeffizienten n ≈ 1 … 2 gilt es zu beachten, dass bei dieser mit dem Emissionskoeffizienten n = 10 7 wie folgt gerechnet wurde:

I_D = I_S * [ e^{( U}_D ^{/ ( n * U}_T ^{) )} - 1 ]

= 152,2 * 10^-6 A * [ e^{( U}_D ^{/ ( 10 * 25 mV ) )} - 1 ]

= 152,2 * 10^-6 A * [ e^{( U}_D ^{/ ( 0,25 V ) )} - 1 ]

Selbstverständlich lässt sich der Emissionskoeffizient n = 10 jederzeit abändern, d.h. variieren! Wie man aber sieht, wirken sich kleinste Änderungen des Quotienten 1 / ( n * U_T ) wegen der e-Funktion und des exponentiellen Wachstums äußerst dramatisch, d.h. exponentiell wie folgt aus:

1 / 0,125 = 1 / ( 125/1000 ) = 8_e " e⁸ ≈ 2 980,96₁₀

1 / 0,25 = 1 / ( 25/100 ) = 4_e " e⁴ ≈ 54,60₁₀

1 / 0,50 = 1 / ( 50/100 ) = 2_e " e² ≈ 7,39₁₀

Bei dem Quotienten 1 / ( n * U_T ) handelt es sich bildlich gesprochen um eine „kleines Schräubchen“, dessen achtel Umdrehung bereits zu einer Steigerung des Durchflussstromes I_D um rund das Dreitausendfache führt!

Bildlich gesprochen könnte man sich das exponentielle Wachstum der e-Funktion auch mit einer Balkenwaage oder einer Wippe für zwei Personen auf dem Kinderspielplatz vorstellen. Wenn sich auf diese zwei Personen sehr unterschiedlichen Gewichtes setzen, wie z.B. ein Erwachsener und ein Kind, dann kann der Erwachsene mit seinem größeren Körpergewicht das Kind auf der anderen Seite der „Waage“ quasi in der Luft verhungern lassen. Ließe sich ein Ausleger der Wippe nebst dem Sitz um etliche Meter verlängern, dann könnte das Kind wegen des größeren Hebelarms den Erwachsenen in der Luft verhungern lassen!

Würde sich eine Balkenwaage gewichtsmäßig nicht wie üblich symmetrisch verhalten, sondern exponentiell, dann könnte man auf der linken Waagschale ein Gewicht von rund 2 981 kg ≈ 3 Tonnen anheben und ins Gleichgewicht bringen, indem man auf der rechten Seite ein Gegengewicht von nur etwas mehr als 1 kg in die rechte Waagschale legt! Wahnsinn!

./Anfang Der nachfolgende Abschnitt ist nur für Schüler:innen ab der 12. Klasse der Fachoberschule oder der 12. bis 13. Klasse einer Gesamtschule (Sekundarstufe II) oder des (Technischen) Gymnasiums von Bedeutung!

Frage:

Auf welcher Rechen- bzw. Zahlenbasis, wie z.B. 2, …, 8, 10, 16, beruht das gewichtsmäßige Übersetzungsverhältnis der asymmetrischen, exponentiellen Balkenwaage?

Antwort:

Um die Rechen- bzw. Zahlenbasis, wie z.B. 2, …, 8, 10, 16, der asymmetrischen, exponentiellen Balkenwaage herauszufinden, muss man die achte Wurzel von 2 981 kg, exakt von 2.980,96 kg (siehe oben), bilden:

y = f(x)

= e^x " x = Exponent, abgekürzt „exp“ " für die Ergebnisgröße y = 2.980,96

e^x = 2.980,96

ln e^x = ln 2.980,96

exp = x

x = 8_e

Probe:

e⁸ = e^{2 * 4} = ( e² ) ⁴ = e^{2 * 2 * 2}

= 2.980,96₁₀

Achtung:

Um die obenstehende Berechnung durchführen zu können, muss man bereits wissen, dass der (Dezimal-) Wert 2.980,96₁₀ dem Eulerschen Zahlensystem zur Basis e¹ = 2,718 entstammt! [ Video ]

Frage:

Wie lässt sich herausfinden, ob eine beliebige Zahl n dem Eulerschen Zahlensystem (= e-Funktion) entstammt?

Antwort:

Indem man aus der betreffenden Zahl n = 2.980,96 die Quadratwurzel (= zweite Wurzel = „\/¯“) zieht mit:

x = \/¯ n

= \/¯ 2.980,96

= 2.980,96^1/2

≈ 54,598 " 1. Zwischenergebnis

Aus dem 1. Zwischenergebnis zieht man dann wieder die Quadratwurzel:

x = \/¯ n

= \/¯ 54,598

= 54,598^1/2

≈ 7,389 " 2. Zwischenergebnis

Und aus dem 2. Zwischenergebnis zieht wieder die Quadratwurzel:

x = \/¯ n

= \/¯ 7,389

= 7,389^1/2

≈ 2,718 " 3. Zwischenergebnis = Endergebnis!

= Eulersche Zahl e¹ = 2,718

Demzufolge muss man erstens aus der Zahl n = 2.980,96 die Quadratwurzel ziehen, zweitens aus dem 1. Zwischenergebnis ein weiteres Mal die Quadratwurzel ziehen und drittens aus dem 2. Zwischenergebnis ein letztes Mal die Quadratwurzel ziehen.

Oder anders ausgedrückt: Man muss aus sich selbst, d.h. aus dem Anfangswert n = 2.980,96 und aus den weiteren Zwischenergebnissen insgesamt drei Mal die Quadratwurzel ziehen, bis sich das gewünschte Ergebnis in Form der Eulerschen Zahl e¹ = 2,718 einstellt!

Probe:

n = { [ ( 2,718 )² ]² }²

= ( 2,718 )⁸

= e⁸

= 2.980,96

Selbstverständlich lässt sich alternativ auch mit dem Logarithmus naturalis „ln“ (= Umkehrung der e-Funktion) wie folgt rechnen:

ln 2.980,96 = 8

Allgemein:

y = f(x)

= e^x " mit exp x = 8 folgt …

= e⁸

= 2.980,96 " mit tausender Punkt zwecks Übernahme in den Windows Taschenrechner (Modus „Wissenschaftlich“)

Oder mit der Umkehrung der e-Funktion zwecks Kontrolle:

y = f(x)

ln y = ln f(x)

= ln e^x mit exp x = 8 folgt …

= ln e⁸

= ln 2.980,96

num = exp 8 " Beim Logarithmieren bezeichnet man den Numerus (= Anzahl) abgekürzt mit „num“.

e^{ln y} = e^{ln 2.980,96}

= e⁸ = 2.980,96

Mit der Umkehrung der e-Funktion folgt auch:

y = f(x)

= e^x " mit exp x = 8 und y = 2.980,96 folgt …

= e⁸

= 2.980,96

ln y = ln e^x

num = x

x = ln 2.980,96

= exp 8

Frage:

Weshalb muss man von der Zahl n = 2.980,96 insgesamt drei Mal die Quadratwurzel \/¯ ziehen

" 2.980,96 " Zahlenfolge { ( \/¯ 2.980,96 ) , ( \/¯ 54,598 ), ( \/¯ 7,389 ), 2,718 },

um auf die Eulersche Zahl e¹ = 2,718 zu kommen?

Antwort:

Wenn man zu Recht vermutet, dass es sich bei der Zahl n = 2.980,96 wegen des exponentiellen Wachstums (siehe weiter oben) um ein exponentielles Vielfaches exp x der Eulerschen Zahl e^x = 2,178^x handelt,

2.980,96 " umgekehrte Zahlenfolge { 2,718¹ , 2,718², 7,389², 54,598² } = 2.980,96

{ 2,718¹ , 2,718², 2,718⁴, 2,718⁸ } = 2.980,96

dann bietet es sich an, dass man die Umkehrung der e-Funktion in Form des Logarithmus naturalis (= natürlicher Logarithmus auf Basis der Eulerschen Zahl) wie folgt anwendet:

e⁸ ≈ 2.980,96 ó ln 2.980,96 ≈ exp 8 "

Der Exponent mit exp = 8 = 2 * 2 * 2 gibt an, wie oft das Zwischenergebnis(!) des ursprünglichen Quadrats der Eulerschen Zahl wiederum ins Quadrat erhoben werden muss, um auf den Ergebniswert = 2.980,96 zu kommen:

( 2,718 )² " ( 2,718² )² " ( 2,718⁴ )² " 2,718⁸ = e⁸ ≈ 2.980,96

( 2,718 )² " ( 7,389 )² " ( 54,598 )² " 2.980,96 = e⁸ = e^{2 * 2 * 2}

Wie man unschwer sieht, muss das Zwischenergebnis(!) drei Mal ins Quadrat erhoben werden, um auf den Ergebniswert = 2.980,96 zu kommen!

Probe:

8. Wurzel aus 2.980,96 = 2.980,96^1/8 ≈ 2,718

So, das soll es denn erst Mal gewesen sein mit der e-Funktion, dem exponentiellen Wachstum und dem Logarithmus naturalis als Umkehrfunktion. [ Video ]

./Ende des vorausgegangenen Abschnitts für Schüler:innen ab der 12. Klasse der Fachoberschule oder der 12. bis 13. Klasse einer Gesamtschule (Sekundarstufe II) oder des (Technischen) Gymnasiums von Bedeutung!

Wenn man sich den Graphen der e-Funktion mit dem runden Bauch im Bild 19 so anschaut, dann könnte man schon daran zweifeln, ob die Kennlinie einer idealen Diode tatsächlich so ausschaut, weil man aus den Lehr- und Fachbüchern eher den nachfolgenden Kennlinienverlauf gewohnt ist (siehe dünne blaue Linie):

(Vergrößern: auf Bild 20 klicken! | Quelle: „Mathematics“)

Aber es verhält sich tatsächlich so, dass Bild 19 und Bild 20 bis auf den Maßstab identisch sind und auf der gleichen e-Funktion beruhen. Es ist halt wie im richtigen Leben, wo es immer wieder auf die Sichtweise ankommt und darauf, diese auch mal zu ändern, um Neues zu entdecken oder die Vorteile einer anderen Betrachtungs- und Argumentationsweise!

Bei der obenstehenden blauen Diodenkennlinie geht es nachfolgend darum, den Arbeitspunkt AP und den dazugehörigen Vorwiderstand R_{Vor, AP} auf der grünen Arbeitsgeraden zu berechnen.

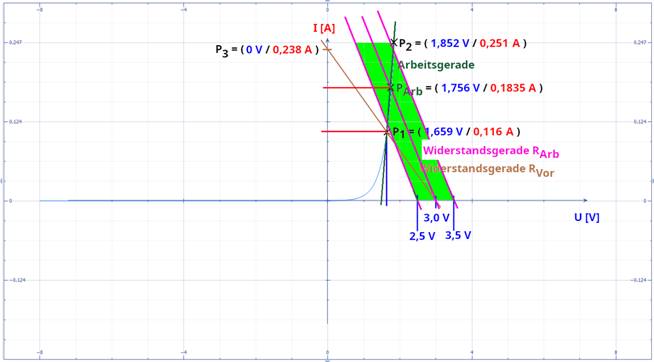
Dabei gilt es zu beachten, dass die blaue Diodenkennlinie zwischen den Punkten P₁ und P₂ linear, d.h. geradlinig mit konstanter Steigung a = m = ∆y / ∆x verläuft, sodass sich diese u.a. mit dem Ohmschen Gesetz R = U / I und auch mit dem differentiellen Widerstand r = ∆R = ∆U / ∆I " Steigung 1 / R = ∆I / ∆U = dI / dU wie folgt berechnen lässt:

Mathematisch mit der

Geradengleichung y = f(x) = a x + b " a = Steigung, b = Parallelverschiebung aus dem Koordinatenursprung

Elektrotechnisch mit dem

differentiellen Widerstand r_Arb für die Steigung a_Arb der grünen Arbeitsgeraden

1 / r_Arb = ∆I / ∆U

= ( I₂ – I₁ ) / ( U₂ – U₁ ) " mit I₂ > I₁ und U₂ > U₁

= ( 251 mA – 116 mA ) / ( 1,852 V – 1,659 V )

= ( 135 mA ) / ( 193 mV )

= 0,69948 A/V ≈ 0,7 1/W = 0,7 W^-1 " Steigung der grünen Arbeitsgeraden im Punkt P₁

r_Arb = ∆U / ∆I

= 1 / 0,7 W^-1

= ( 1 / 0,7 ) W = 1 / ( 7/10 ) W = 10/7 W = 1,42857 W ≈ 1,43 W

Wie man sieht, ist der differentielle Widerstand r_Arb der grünen Arbeitsgeraden zwischen P₁, P₂ mit r_Arb = 1,43 W sehr klein!

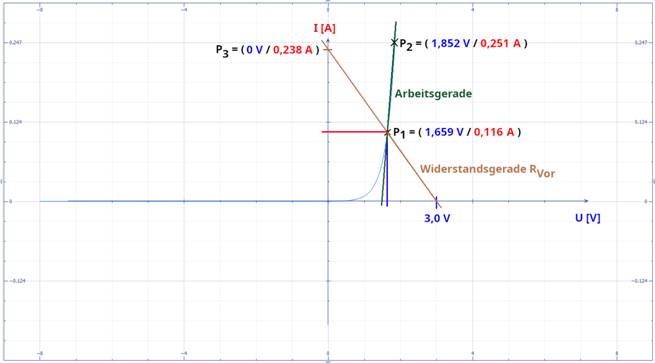
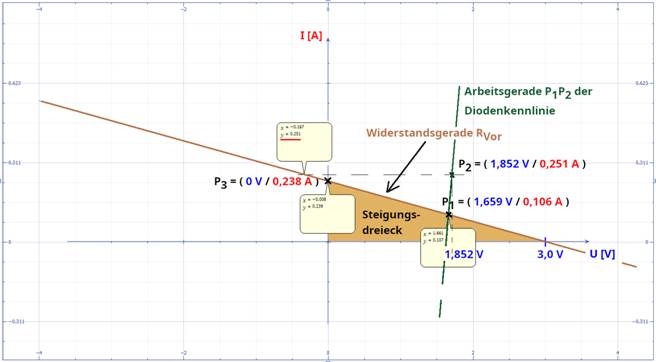
Dies ist weiter nicht verwunderlich, da die e-Funktion mit dem linearen Teil der blauen Diodenkennlinie zwischen den Punkten P₁ und P₂ sehr steil mit exponentiellem Wachstum verläuft.

Da die zwei Punkte P₂ = ( U₂ / I₂ ) = ( 251 mA / 1,852 V ) und P₁ = ( U₁ / I₁ ) = ( 116 mA / 1,659 V ) auf der grünen Arbeitsgeraden bereits bekannt sind, lässt sich die Geradengleichung zu dieser am einfachsten mittels der sogenannten

Zwei-Punkte-Form

( y – y₁ ) / ( x – x₁ ) = ( y₂ – y₁ ) / ( x₂ – x₁ )

wie folgt bestimmen:

( I – 0,116 A ) / ( U – 1,659 V ) = ( 0,251 A – 0,116 A ) / ( 1,852 V – 1,659 V )

= ( 0,135 A ) / ( 0,193 V ) = 0,69948 A/V ≈ 0,7 W^-1

( I – 0,116 A ) = 0,7 W^-1 * ( U – 1,659 V )

I = 0,7 W^-1 * ( U – 1,659 V ) + 0,116 A

= 0,7 W^-1 * U – 0,7 A/V * 1,659 V + 0,116 A

= 0,7 W^-1 * U – 1,1613 A + 0,116 A

= 0,7 W^-1 * U - 1,0453 A "

Geradengleichung (mathematisch):

y = a_Arb x + b_Arb

= 0,7 x + ( - 1,0453) ≈ 0,7 x - 1,045 "

Geradengleichung (elektrotechnisch):

I = 1 / R_Arb U + I₀ ≈ 0,7 W^-1 U - 1,045 A [ Video ]

Schnittpunkt S_x = (x₀ / y₀) mit der x-Achse:

y = f(x) "

y₀ = f(x₀) "

y₀ = a_Arb x₀ + b_Arb

= 0,7 x + ( - 1,0453) ≈ 0,7 x - 1,045 "

0 = 0,7 x₀ - 1,045 "

x₀ = 1,045 / 0,7

= 1,492857 ≈ 1,49 "

Elektrotechnisch:

I = 1 / R_Arb * U + I₀ "

Für I = f(U₀) mit I = I(U₀) = 0 folgt dann:

I(U₀) = 1 / R_Arb * U₀ + I₀ "

0 = 0,7 W^-1 * U₀ - 1,045 A "

U₀ = ( I(U₀) + 1,045 A ) / 0,7 W^-1

= ( 0 + 1,045 A ) / 0,7 W^-1

= 1,045 A / 0,7 A/V = ( 1,045 / 0,7 ) V

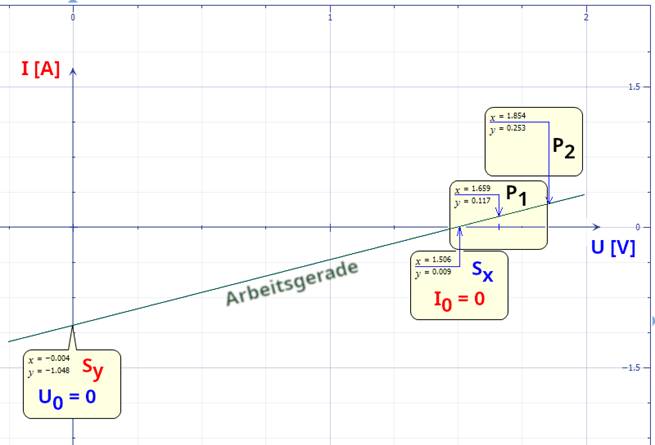
= 1,492857 V ≈ 1,493 V ≈ 1,5 V " im mathematischen Schnittpunkt S_x = (x₀ / y₀) mit der x-Achse

Wie man im nachfolgenden Diagramm sieht, verläuft die grüne Arbeitsgerade (von links unten nach rechts oben) ziemlich flach, ist der Abschnitt P₁P₂ der grünen Arbeitsgeraden im Vergleich zum Bild 20 ziemlich gestaucht:

(Vergrößern: auf Bild 21 klicken! | Quelle: „Mathematics“)

Der Grund dafür ist der, dass die grüne Arbeitsgerade im obenfolgenden Bild mit einer linearen Skalierung bzw. im linearen Maßstab (= nicht eponentiell!) abgetragen wurde, weil es sich bei der grünen Arbeitsgeraden um eine lineare Gleichung 1. Grades (= Hochzahl exp 1 mit x¹ = x, y = f(x) = a x¹ + b = a x +b) handelt!

Was jetzt noch fehlt, ist die Parallelverschiebung b des linearen Teils der grünen Arbeitsgeraden aus dem Koordinatenursprung heraus, die sich berechnen lässt, wenn man die Geradengleichung und die verlängerte grüne Arbeitsgerade an der Schnittstelle mit der y-Achse und der Stelle x₀ = 0 untersucht:

y = f(x) "

y₀ = f(x₀) = a x₀ + b " mit x₀ = 0

= a * 0 + b

= b

b = y – a x

= y₂ – a x₂ " siehe Punkt P₂ ( 1,852 V / 0,251 A ) im Bild 20

Elektrotechnisch:

I₀ = 0,251 A – 0,7 W^-1 * 1,852 V

= 0,251 A – 0,7 A/V * 1,852 V

= 0,251 A – 1,2964 A = -1,0454 A ≈ -1,05 A " siehe Schnittpunkt S_y = ( 1,852 V / - 1,05 A ) im Bild 21

Die Geradengleichung der Widerstandsgeraden R_Vor 7 (siehe Bild 20) lässt sich entweder mittels der Zwei-Punkte-Form oder der

Punkt-Steigungs-Form

( y – y₁ ) = a_Vor * ( x – x₁ ) " mit a_Vor = m = ∆I / ∆U

wie folgt berechnen:

a_Vor " 1 / R_Vor = ∆I / ∆U " Steigung der Widerstandsgeraden R_Vor zwischen den Punkten P₃P₄

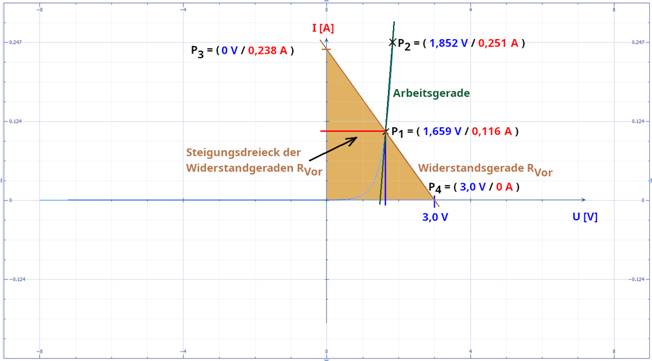
1 / R_Vor = ( I₃ – I₄ ) / ( U₃ – U₄ ) " mit I₃ > I₄ und U₃ > U₄

= ( 0,238 A - 0 A) / ( 0 V - 3,0 V ) " Beachte: 0 V > - 3,0 V

= 0,238 A / ( - 3,0 V )

= - 0,07933 W^-1

= - 0,079333 W^-1 ≈ - 0,079 W^-1 " siehe großes Steigungsdreieck im Bild 22

R_Vor = 1 / a_Vor

= 1 / - 0,079333 W^-1 ≈ - 12,605 W

Frage:

Was bedeutet es normalerweise, wenn ein Widerstand R negativ ist bzw. einen negativen Wert aufweist?

Antwort:

Wenn ein Widerstand R negativ ist bzw. einen negativen Wert aufweist, dann handelt es sich bei diesem nicht um einen ohmschen Verbraucher mit Wärmeverlusten wie bei der Glühlampe, sondern um einen elektrischen Generator, d.h. Stromerzeuger, z.B. im Sinne einer Konstantstromquelle, der in seinem Inneren wegen des (Innen-) Widerstandes R_i auch etwas Wärme produziert.

Weil aber ein Generator als Stromerzeuger elektrische Energie nach außen in das Stromnetz bzw. einen Stromkreis abgibt, wird der heraus fließende Strom I_Gen negativ gezählt.

Achtung:

Im vorliegenden Fall aber verhält es sich so, dass die Widerstandsgerade des Vorwiderstandes R_Vor gespiegelt und parallel aus dem Koordinatenursprung nach oben verschoben wurde, um den gemeinsamen Schnittpunkt P₁ mit der grünen Arbeitsgeraden und auch der blauen Diodenkennlinie ermitteln und berechnen zu können!

Aus diesem Grund ist die Steigung der Widerstandsgeraden R_Vor zwischen den Punkten P₃P₄ negativ, d.h. fallend (siehe nachfolgendes Bild). Bei dem Vorwiderstand R_Vor handelt es sich aber weiterhin um einen rein ohmschen Widerstand, der Energie „konsumiert“, den Stromfluss und die Stromstärke begrenzt und einen entsprechenden Spannungsabfall U_Vor am Vorwiderstand R_Vor zur Folge hat!

Bezüglich der Geradengleichung der Widerstandsgeraden R_Vor

I_Vor = - 1 / R_Vor * U_Vor + I_{0, Vor}

bedeutet dies, dass die Widerstandsgerade R_Vor mit negativer Steigung von links oben nach rechts unten verläuft (siehe nachfolgendes Bild):

(Vergrößern: auf Bild 22 klicken! | Quelle: „Mathematics“) [ Video ]

Jetzt lässt sich auch der Strom I_Vor an der Stelle U_Vor = 0 V wie folgt berechnen:

I_Vor(0 V) = 1 / R_Vor * U_Vor + I_{0, Vor}

= 1 / - 12,605 W * 0 V + 0,238 A

I_{0, Vor} = 0,238 A " entspricht mathematisch der Parallelverschiebung b aus dem Koordinatenursprung.

Zu Kontrollzwecken lassen sich in die Geradengleichung der Widerstandsgeraden R_Vor

I_Vor = - 1 / R_Vor * U_Vor + I_{0, Vor}

u.a. die Werte vom Punkt P₁ = ( 1,659 V / 0,116 A ) einsetzen:

= - 1 / 12,605 W * 1,659 V + 0,238 A

≈ - 0,079334 W^-1 * 1,659 V + 0,238 A

≈ - -0,1316 A + 0,238 A

≈ - 0,132 A + 0,238 A = 0,106 A

(Vergrößern: auf Bild 23 klicken! | Quelle: „Mathematics“)

Wenn man im Microsoft-Programm „Mathematics“ den Player zwecks Anzeige der Graphenwerte startet und diesen mittels der „||“-Pausetaste anhält, dann lässt sich dieser mittels der Maus manuell entlang dem Graphen beliebig verschieben:

(Zum Vergrößern bitte auf das Bild klicken!)

Wenn man den Punkt P₂ der grünen Arbeitsgeraden P₁P₂ ermitteln und nachfolgend in das Diagramm eintragen will, dann muss man die Werte vom Punkt P₂ = ( 1,852 V / 0,251 A ) einzeln mittels des Graphen-Players anfahren und für die einzelne Spannung U = 1,852 V die Senkrechte in das Diagramm eintragen. An der Stelle der Stromstärke I = 0,251 A muss man die Waagrechte in das Diagramm eintragen. Der Schnittpunkt der Senkrechten mit der Waagrechten (siehe dünne gestrichelte schwarze Linien) ist dann der Punkt P₂ = ( 1,852 V / 0,251 A ):

(Vergrößern: auf Bild 25 klicken! | Quelle: „Mathematics“)

Mit der grünen Arbeitsgeraden P₁P₂ und der Widerstandsgeraden R_Vor verfügen wir jetzt über zwei Geradengleichungen und zwar a) I = 1 / R_Arb * U + I₀ mit R_Arb ≈ 1,43 W und b) I = - 1 / R_Vor * U + I_{0, Vor} mit R_Vor ≈ 12,61 W.

Gemäß dem Gleichsetzungsverfahren lassen sich beide Gleichungen a) und b) wie folgt gleichsetzen:

1 / R_Arb * U + I_{0. Arb} = - 1 / R_Vor * U + I_{0, Vor} "

( 1 / R_Arb + 1 / R_Vor ) * U = I_{0, Vor} - I_{0. Arb} "

U = ( I_{0, Vor} - I_{0. Arb} ) / ( 1 / R_Arb + 1 / R_Vor )

= [ 0,238 A – ( - 1,045 A ) ] / ( 1 / 1,43 W + 1 / 12,61 W )

= [ 0,238 A + 1,045 A ] / ( 1 / 1,43 W + 1 / 12,61 W )

≈ [ 1,282 A ] / ( 0,6993 A/V + 0,0793 A/V )

= [ 1,282 ] / ( 0,7786 V ) ≈ 1,6466 V ≈ 1,65 V " Schnittpunkt P₁ = ( U_P1 / … ) = ( 1,65 V / … )

Um den zweiten Wert für die Stromstärke I im Schnittpunkt P₁ = ( U_P1 / I_P1 ) zu berechnen, muss man nur die Spannung U_P1 = 1,65 V in eine der beiden Gleichungen a) oder b) wie folgt einsetzen:

a)

I = 1 / R_Arb * U + I₀

= 1 / 1,43 W * 1,65 V + ( - 1,045 A )

= 1,65 V / ( 1,43 V/A ) - 1,045 A

= 1,153846 A - 1,045 A ≈ 1,154 A - 1,045 A

= 0,109 A " Schnittpunkt P₁ = ( U_P1 / I_P1 ) = ( 1,65 V / 0,109 A )

b)

I = - 1 / R_Vor * U + I_{0, Vor}

= - 1 / ( 12,61 W ) * 1,65 V + 0,238 A

= - 1,65 V / ( 12,61 V/A ) + 0,238 A

= 0,238 A - 0,1308485 A ≈ 0,238 A - 0,131 A

= 0,107 A " Schnittpunkt P₁ = ( U_P1 / I_P1 ) = ( 1,65 V / 0,107 A )

Wie man unschwer sieht, weichen die berechneten Stromstärken im Schnittpunkt P₁ geringfügig voneinander ab, wobei die Ungenauigkeit mit

0,109 A ó 100 %

0,107 A ó x %

________________

x = 100 % / 0,109 A * 0,107 A = 98,165 % ≈ 98,2 % " 100 % - 98,2 % = 1,8 % absolut akzeptabel ist.

Auch die Ungenauigkeit in Bezug auf die Stromstärke von I_P1 = 0,116 A (siehe im Bild 20) mit

0,116 A ó 100 %

0,107 A ó x %

________________

ist mit x = 100 % / 0,116 A * 0,107 A = 92,24 % ≈ 92,2 % " 100 % - 92,2 % = 7,8 % ebenfalls noch akzeptabel!

Was aber ist die Ursache für die Ungenauigkeiten?

Wenn man im Microsoft-Programm „Mathematics“ den Player zwecks Anzeige der Graphenwerte startet und diesen mittels der „||“-Pausetaste anhält, dann lässt sich dieser mittels der Maus manuell entlang dem Graphen beliebig verschieben, lassen sich zwar die x- und y-Werte an der betreffenden Messstelle anhand der gelben Sprechblase ablesen, aber wider Erwarten nicht ganz exakt bis auf die 3. Nachkommastelle auf dem Graphen einstellen, sodass es beim Ablesen mehrerer x- und y-Werte immer wieder zu kleinen Ungenauigkeiten bei der 3. Nachkommastelle kommt.

Unterschiedliche Arbeitspunkte P₁, P₂ und P_Arb für verschiedene Zwecke

Insgesamt gibt es bei jeder Diodenkennlinie, also auch bei der Kennlinie der roten Leuchtdiode 17, prinzipiell drei unterschiedliche Arbeitspunkte P₁, P₂ und P_Arb (siehe Bild 20).

Arbeitspunkt P₁

Dabei befindet sich der Arbeitspunkte P₁ sozusagen am unteren Ende des linearen Kennlinienverlaufs von P₁ bis P₂ (siehe grüne Arbeitsgerade). Nämlich dort, wo die Diode gerade anfängt, richtig elektrisch leitend zu werden. Dabei bietet der Arbeitspunkt P₁ den Vorteil, dass die Diode bzw. Leuchtdiode 17 schon bei einer geringen Versorgungsspannung mit gleichzeitig geringer Stromstärke zu leuchten beginnt. Der Vorteil des Arbeitspunktes P₁ ist aber gleichzeitig sein Nachteil. Zwar lässt sich die Diode bzw. Leuchtdiode 17 schon bei einer geringen Versorgungsspannung zum Leuchten bringen, erlischt aber gleichzeitig auch wieder sofort, sobald sich die Versorgungsspannung geringfügig verringert. Demzufolge ist die Diode bzw. Leuchtdiode 17 besonders spannungsempfindlich!

Arbeitspunkt P₂

Befindet sich der Arbeitspunkt P₂ sozusagen am oberen Ende des linearen Kennlinienverlaufs von P₁ bis P₂ (siehe grüne Arbeitsgerade), dann wird die Diode bzw. Leuchtdiode 17 wegen der höheren Versorgungsspannung von einem größeren Strom durchflossen, sodass sie deutlich heller leuchtet! Gleichzeitig ist die Diode bzw. Leuchtdiode 17 weitestgehend spannungsunempfindlicher gegenüber einer geringeren Versorgungsspannung, da der Arbeitsbereich auf der grünen Arbeitsgerade insgesamt größer, d.h. länger ist.

Wenn man beispielsweise erreichen will, dass sich Diode bzw. Leuchtdiode 17 mit einer Batterieladung möglichst lange im Sinne der Ergonomie und gleichzeitig intensiv betreiben lässt, dann muss man sich für den Betrieb der Schaltung mit dem Arbeitspunkt P₂ entscheiden, damit sich später, wenn die Batterieladung zur Neige geht und sich die Versorgungsspannung verringert, die Schaltung bis zum Arbeitspunkt P₁ noch betreiben lässt.

Wenn man sich für den Arbeitspunkt P₂ entscheidet, dann sollte man gleichzeitig dafür sorgen, dass die Versorgungsspannung keine größeren Werte als z.B. U_Batt = 3,0 V annehmen kann, weil jede - und sei es auch noch so kleine - Spannungserhöhung der Versorgungsspannung wegen des exponentiellen Anstiegs der Diodenkennlinie sofort zu einer „explosionsartigen“ Zunahme der Stromstärke führt und die Diode bzw. Leuchtdiode 17 zerstört!

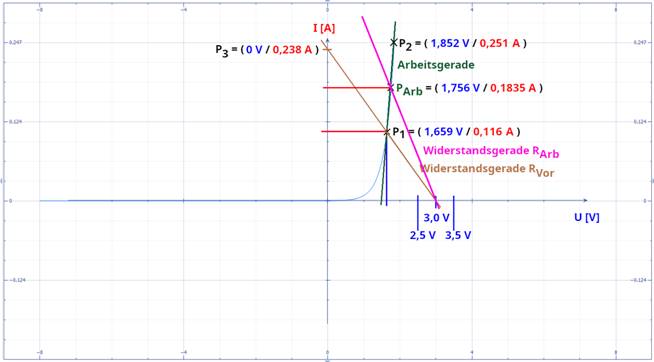
Arbeitspunkt P_Arb

Wenn man aber auf Nummer sicher gehen will, dann muss man einen Kompromiss zwischen den beiden Arbeitspunkten P₁ und P₂ eingehen und sich für den Arbeitspunkt P_Arb entscheiden, der genau in der Mitte zwischen P₁ und P₂ der grünen Arbeitsgeraden liegt:

(Vergrößern: auf Bild 26 klicken! | Quelle: „Mathematics“)

Dabei bietet der Arbeitspunkt P_Arb in der Mitte der grünen Arbeitsgeraden den Vorteil, dass sich die Versorgungsspannung U_Batt = 3,0 V durchaus um +/- 0,5 V (= +/- 16,7 % ) auf U_{Batt, max} = 3,5 V nach oben oder auf U_{Batt, min} = 2,5 V nach unten verändern kann, ohne dass die Diode durchbrennt oder in den Sperrbereich übergeht.

Frage:

Was passiert mit der pinkfarbenen Widerstandsgeraden R_Arb, wenn sich die Versorgungsspannung U_Batt = 3,0 V um +/-0,5 V (= +/- 16,7 % ) auf U_{Batt, max} = 3,5 V nach oben oder auf U_{Batt, min} = 2,5 V nach unten verändert?

(Vergrößern: auf Bild 27 klicken! | Quelle: „Mathematics“)

Antwort:

Wenn sich die Versorgungsspannung U_Batt = 3,0 V um +/-0,5 V (= +/- 16,7 % ) auf U_{Batt, max} = 3,5 V nach oben oder auf U_Batt, min = 2,5 V nach unten verändert,

(Vergrößern: auf Bild 28 klicken! | Quelle: „Mathematics“)

dann verschiebt sich die pinkfarbenen Widerstandsgeraden R_Arb ausgehend vom dunkelgrünen Arbeitspunkt P_Arb parallel 7 nach rechts bzw. links!

Frage:

Weshalb muss sich die pinkfarbene Widerstandsgerade R_Arb ausgehend vom dunkelgrünen Arbeitspunkt P_Arb parallel 7 nach rechts bzw. links verschieben? Oder anders gefragt: Weshalb ändert sich nicht die Steigung der pinkfarbenen Widerstandsgeraden R_Arb, wenn sich die Versorgungsspannung U_Batt = 3,0 V um +/-0,5 V (= +/- 16,7 % ) auf U_{Batt, max} = 3,5 V nach oben oder auf U_Batt, min = 2,5 V nach unten verändert?

Antwort:

Trotz der Änderung der Versorgungsspannung U_Batt = 3,0 V um +/-0,5 V (= +/- 16,7 % ) auf U_{Batt, max} = 3,5 V nach oben oder auf U_Batt, min = 2,5 V nach unten, ändert sich an der Schaltung, bestehend aus der Spannungsversorgung U_Batt, dem Vor- bzw. Arbeitswiderstand R_Arb und der Diode selbst, nichts(!), bleibt der Widerstand des Arbeitswiderstandes R_Arb wertmäßig unverändert! Demzufolge bleibt mit dem unveränderten Arbeitswiderstand R_Arb auch die Steigung der pinkfarbenen Widerstandsgeraden R_Arb unverändert, kann sich diese nur parallel 7 nach rechts bzw. links verschieben! –

[ Video ]

Von der Spannungsquelle zur Stromquelle

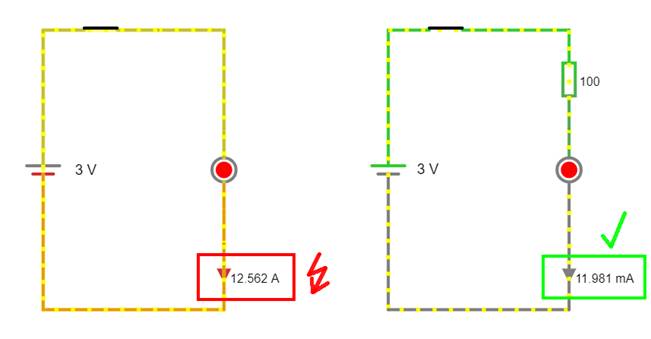
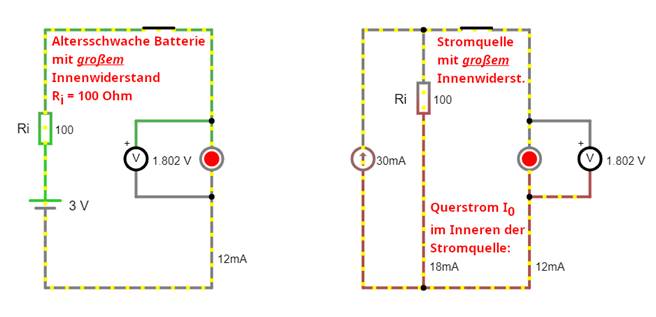
Nachfolgend benutzen wir das Elektronik-Simulationsprogramm „Circuit Simulator 2.8.1js“ des Anbieters „Paul Falstad“, das sich sowohl online im Browser als auch offline unter Windows nutzen lässt! -

Wie wir inzwischen wissen, dürfen Leuchtdioden (LEDs) niemals direkt an einer Spannungsquelle, wie z.B. dem KOSMOS Batteriefach 19 mit den zwei in Reihe geschalteten Batterien vom Typ „AA“ mit der Gesamtspannung von U_{Batt, ges} = 3,0 V, angeschlossen und betrieben werden (siehe linke Schaltung):

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, S-10-01.js1)

Wird nämlich eine Leuchtdiode direkt an eine Spannung von U_LED > 1,6 V angeschlossen, dann wird der PN-Übergang der LED elektrisch leitend und damit niederohmig mit einem Bahnwiderstand R_PN von:

R_PN = U_LED / I_Kurz

= U_Batt / I_Kurz

= 3,0 V / 12,562 A ≈ 0,2388 W = 238,8 mW

Wie man in der linken, obenstehenden Schaltung sieht, entspricht der Durchlassstrom der LED mit I_LED = 12,562 A praktisch dem Kurzschlussstrom I_Kurz der Batterien, sodass die LED sofort durchbrennt! Dabei ist der Lichtblitz zeitlich so kurz, dass man ihn mit bloßen Augen nicht sieht!

Um die LED vor dem Durchbrennen zu bewahren, muss diese stets mit einem Vorwiderstand R zwecks Reduzierung der Spannung U_LED als auch der Stromstärke auf I_LED = I_R = 11,98 mA betrieben werden!

Dabei berechnen sich der Spannungsabfall U_R am Vorwiderstand R als auch der Spannungsabfall U_LED an der LED wie folgt:

Maschenumlauf in der rechten, obenstehenden Schaltung

U_R + U_LED + ( - U_Batt) = 0 "

U_R = U_Batt – U_LED

= I_R * R

= 11,98 mA * 100 W = 11,98 mA * 100 V/A = 1198 mV = 1,198 V ≈ 1,2 V

U_LED = U_Batt – U_R

= 3 V – 1,2 V = 1,8 V

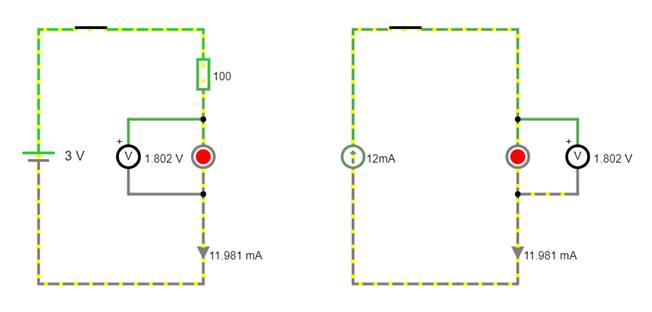
Was aber tun, wenn man keinen passenden Vorwiderstand mit R = 100 W zur Verfügung hat? Dafür aber anstelle der Spannungsquelle mit U_Batt = 3 V eine entsprechende Stromquelle mit I_Batt = 11,981 mA.

Wie man anhand der Simulation sieht, lässt sich praktisch jede Spannungsquelle durch eine entsprechende Stromquelle wie folgt ersetzen:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, S-10-02.js1)

Wenn man sich in dem obenstehenden Bild beide Schaltungen links und rechts anschaut und miteinander vergleicht, dann fällt einem früher oder später auf, dass in der rechten Schaltung mit der Stromquelle I_12mA = 11,981 mA der Widerstand R = 100 W fehlt, was beweist, dass sich eine LED auch ohne Vorwiderstand R, dafür aber nur mit einer passenden Stromquelle betreiben lässt. 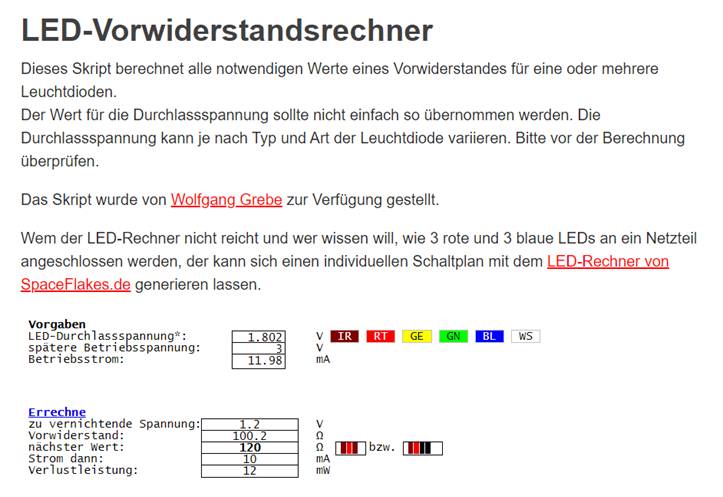Dabei darf im vorliegenden Fall die Stromstärke mit I_LED = I_Batt nicht viel größer als I_LED = I_Batt = 11,98 mA werden!

Bei dem Webportal „Elektronik-Kompendium“ gibt es einen sogenannten LED-Vorwiderstandsrechner mit dem sich der jeweilige Vorwiderstand R_Vor passend zu der jeweilig verwendeten LED wie folgt berechnen lässt:

(Zum Vergrößern bitte auf das Bild klicken!)

Im Zusammenhang und im Vergleich der beiden obenstehenden Schaltungen links und rechts (siehe Bild) stellt sich die Frage, ob sich die linke Schaltung mit der 3 Volt Spannungsquelle ebenfalls ohne Vorwiderstand R = 100 W betreiben lässt.

Ja, und zwar unter der Voraussetzung, dass wir bei der 3 Volt Spannungsquelle eine absolut altersschwache, d.h. größtenteils bereits entladene Batterie verwenden, deren gesamter Innenwiderstand R_i insgesamt exakt R_i = 100 W groß ist, sodass nur ein maximaler Strom von I_LED = I_Batt = 11,981 mA durch die LED fließen kann:

(Vergrößern: auf Bild klicken! | Circuit JS1, easy-electronic_200, S-10-03.js1)

Selbstverständlich dürfte es in der Praxis schwerfallen, eine größtenteils entladene Batterie mit exakt dem Innenwiderstand R_i von R_i = 100 W zu finden. Zumal sich bei der altersschwachen Batterie die restliche Ladungsmenge sehr schnell aufbrauchen und demzufolge die LED nur kurzzeitig leuchten dürfte.

In diesem Zusammenhang ist noch interessant und wichtig, dass der Querstrom I₀ mit I₀ = 18 mA durch den Innenwiderstand R_i der realen Stromquelle stets größer ist als der eigentliche Laststrom mit I_LED = 12 mA durch die LED (siehe rechte Schaltung im obenstehenden Bild).

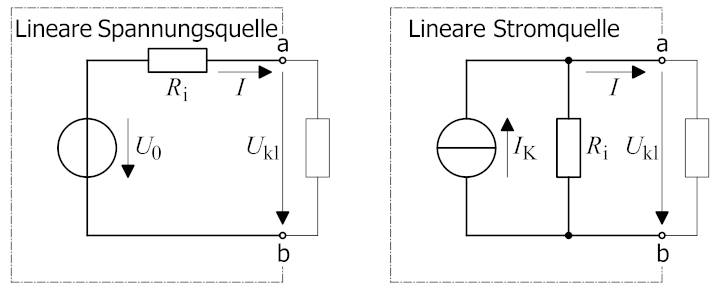
Jetzt kennen wir auch den Unterschied zwischen einer idealen Spannungs- und Stromquelle (= ohne Innenwiderstand R_i) und einer realen Spannungs- und Stromquellen (= mit Innenwiderstand R_i):

(Wikipedia: Von Saure, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=12632634 )

Wie man im obenstehenden Bild unschwer sieht, lässt sich eine reale Spannungsquelle (links) problemlos in eine reale Stromquelle (rechts) umwandeln! Dabei verhält es sich so, dass der Innenwiderstand R_i in beiden Schaltungen gleich groß ist bzw. auch gleich groß sein muss!

Mit der nachfolgenden Aufgabe 10-1 zur Berechnung des Widerstandes R einer einfachen Schaltung soll das Wissen um die Widerstandsgeraden ( = Widerstandskennlinie) maßgeblich ausgebaut und erweitert werden.

Falls sich die Aufgabe 10-1 nicht auf Anhieb lösen lässt, dann könnte es sein, dass noch weiteres profundes Wissen fehlt!

Auf der Webseite „easy electronic 200 - Wissenserweiterung 10-1“ kann man sich das zur Lösung der Aufgabe 10-1 erforderliche Wissen noch nachträglich aneignen! -

Weiter geht’s mit [ Versuch 17 ].

[ easy electronik 200 ] [ Seitenanfang ] [ Versuch 8 ] [ Versuch 17 ]