[ Home ] [ zurück ] [ Seitenende ]

Das IoE mit OOP programmieren

Vom dummen, statischen Widerstand … (Fortsetzung)

Allerdings gibt es ein Problem dabei. Und zwar die gemeinsame Masse, engl. „Ground (GND)“. Wenn man den kleinen „micro:bit“-Rechner mittels des USB-Kabels mit Strom versorgt, dann lässt sich der Rechner nicht potentialfrei betreiben, lässt sich der analoge Ausgang „Pin P0“ eben nicht einfach so zum Vorwiderstand R_Vor parallel schalten.

Zum Glück lässt sich aber der kleine „micro:bit“-Rechner auch unabhängig von der USB-Stromversorgung betreiben. Und zwar mittels eines kleinen Batteriepacks mit 2 x 1,5 Volt Batterien der Größe „AAA“, das mittels eines zweiadrigen Kabels nebst Steckkontakt an den „micro:bit“-Rechner angeschlossen wird. Aber trotz der potentialfreien Stromversorgung mittels Batteriepack gilt es zu beachten, dass die Klemmenspannung z.B. am analogen Ausgang „Pin P0“ niemals größer als 3,3 Volt werden darf, damit dieser nicht zerstört wird!

Wie wir aber gleich noch sehen und berechnen werden, beläuft sich der Spannungsabfall am Vorwiderstand R_Vor auf U_RVor ≈ 7 V, sodass sich das direkte gegenpolige(!) Parallelschalten der analogen Spannungsquelle am Port „Pin P0“ verbietet! Es sei denn, man würde die analoge, programmierbare Spannungsquelle am Port „Pin P0“ mit einem entsprechend großen Vorwiderstand R_{Pin P0} in Reihe schalten!

Mit Strom den Strom ausschalten

Kann man wirklich mittels eines Stromes einen anderen Strom ausschalten? Ja, man kann mit einem bestimmten Strom einen anderen Strom ausschalten. Aber nur quasi ausschalten und nicht wirklich abschalten im Sinne von elektrisch stromlos machen! Strom fließt nämlich immer nur dann, wenn es zwischen zwei Klemmen A und B einen Potentialunterschied gibt, wobei sich dieser durch einen Spannungsmesser (= Voltmeter) messen und in Volt [V] messen lässt.

Hebt man den Potentialunterschied auf, d.h. kompensiert man diesen, indem man eine gleich große, aber mit umgekehrter Polarität betriebene Spannungsquelle an die Klemmen A und B anschließt, dann kann wegen des fehlenden Potentialgefälles kein Strom mehr fließen.

Alternativ lässt sich ein Potentialunterschied aber auch zunichte machen, indem man die Klemme A mit dem positiven Potential (= +2 V) im Sinne der technischen Stromrichtung von + nach - ganz einfach gegen Masse (= 0 V, Klemme B) kurzschließt. Dabei gilt es allerdings zu beachten, dass der Kurzschlussstrom um ein Vielfaches höher sein kann als der ursprüngliche Nennstrom durch den angeschlossenen Verbraucher.

Würde man also die rote LED mit dem Spannungsabfall von u_LED = 1,98 V im Stromkreis außer Funktion setzen, indem man deren Kontakte wie bei einem Kurzschluss überbrückt, dann würde die volle Klemmenspannung der Batterie U_{Batt, Last} = U_{R Vor} + u_LED = 7 V + 1,98 V = 8,98 V betragen und nur noch am Vorwiderstand R_Vor anliegen, sodass sich ein Strom I_{Batt, Last} = I_{R Vor} = U_{Batt, Last} / R_Vor = 8,98 V / 470 Ω = 0,019 A = 19 mA einstellen würde.

Jetzt wissen wir, dass Spannung und Strom wegen des Vorwiderstandes R_Vor tatsächlich maßgeblich begrenzt werden, sodass sich Vorwiderstand R_Vor und rote LED problemlos durch die nachfolgende Schaltung, ebenfalls mit roter LED und Vorwiderstand, ersetzen lassen. Dabei lässt sich der neue Vorwiderstand R_Vor = 1 KΩ später wieder durch den vorherigen R_Vor = 470 Ω ersetzen (siehe auch Kapitel „2. 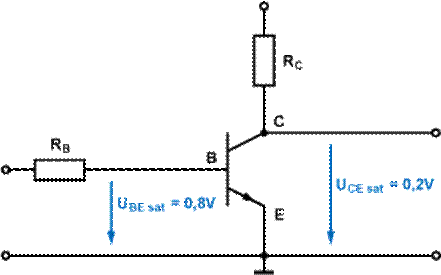Stromversorgung beim „micro:bit“-Rechner“).

Bei der nachfolgenden invertierenden Transistorschaltung mit dem NPN-Transistor BC547 lässt sich der durch die rote LED fließende Durchlassstrom i_LED = 15 mA im leitenden Zustand über die sehr niederohmige Kollektor-Emitter-Strecke des NPN-Transistors umleiten, d.h. gegen Masse (= 0 V) ableiten, sodass die LED erlischt, weil das Spannungspotential am Mittelpunkt M in Höhe von u_LED = 1,98 V gegen Masse auf u_LED = 0,132 V ( ≈ 0 V) reduziert wird:

(Zum Vergrößern bitte auf das Bild klicken!)

(Quelle: Das Franzis Lernpaket Elektronik mit Burkhard Kainka)

Dabei gilt es zu beachten, dass der NPN-Transistor BC547 in der sogenannten Sättigung betrieben wird! Bei einer Kollektor-Emitter-Spannung von U_{CE satt} = 0,132 V mit u_LED = U_CE satt ist dies aber genau der Fall!

>> Sättigung

Sättigung bedeutet, dass der Transistor "ganz auf" bzw. "voll leitend" ist. Gerne wird auch die unförmige Bezeichnung "voll durchgesteuert" verwendet. An diesem Punkt kann man den Basisstrom I_B erhöhen wie man will. In der Kollektor-Emitter-Strecke fließt deshalb nicht mehr Strom. Physikalisch liegt die Kollektor-Emitter-Spannung bei "voll leitend" nicht bei 0 V, sondern je nach Transistor eher bei 0,05...0,2 V.

Der Sättigungszustand ist erreicht, wenn die Kollektor-Emitter-Strecke des Transistors ihren niederohmigsten Zustand erreicht hat. Das passiert dann, wenn die Basisspannung U_BE und der Basisstrom I_B vergrößert wird und der Transistorkristall mit Ladungsträgern überschwemmt ist. Dann unterschreitet die Kollektor-Emitter-Spannung U_CE den Wert der Basis-Emitter-Spannung U_BE.

Bei der Sättigungsspannung U_CEsat knicken die Kennlinien im Ausgangskennlinienfeld scharf ab und verlaufen näherungsweise durch den Ursprung des Kennlinienfeldes.

Im Sättigungszustand wird auch die Basis-Kollektor-Diode leitend. Das bedeutet, ein Teil des Basis-Steuerstroms fließt über den Kollektor zum Emitter ab. Das bedeutet, man braucht im Sättigungsbereich einen immer größeren Basisstrom, um einen bestimmten Kollektorstrom bei kleiner werdender Kollektor-Emitter-Spannung zu erhalten. Außerhalb des Sättigungsbereichs ist der Kollektorstrom fast unabhängig von der Kollektor-Emitter-Spannung. << (Quelle: Elektronik-Kompendium)

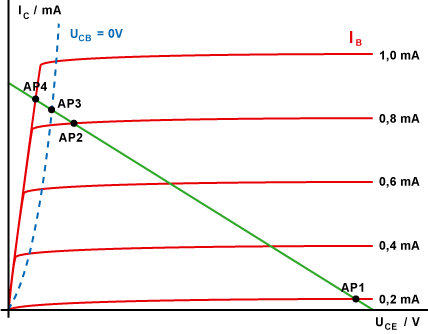
>> Zustände einer Transistor-Schalterstufe

Insgesamt gibt es 4 Zustände, die eine Transistor-Schalterstufe (Transistor als Schalter) einnehmen kann. Die meisten Elektroniker kennen zwei. Den sperrenden und den leitenden Zustand. Denkbar wäre auch EIN und AUS. Bei den insgesamt 4 Zuständen handelt es sich um Arbeitspunkte (AP).

• AP1: Im Sperrzustand der Schalterstufe liegt der Arbeitspunkt bei AP1.
  
  
• AP2: Beim Wechsel in den leitenden Zustand wandert der Arbeitspunkt von AP1 nach AP2.
  
  
• AP3: Wird die Basisspannung und der Basisstrom weiter erhöht, erreicht der Arbeitspunkt AP3, den Bereich der Übersteuerung. Der Übersteuerungsbereich eines Transistors liegt zwischen AP3 und AP4. Hier kann der Transistor einen beliebigen Arbeitspunkt einnehmen.
  
  
• AP4: Der Sättigungszustand beim Arbeitspunkt AP4 ist dann erreicht, wenn trotz Erhöhung des Basisstromes I_B die Kollektor-Emitter-Spannung U_CE nicht mehr weiter sinkt. << (Quelle: Elektronik-Kompendium)

Die obenstehende invertierende Transistorschaltung aus dem Franzis Lernpaket Elektronik, Kapitel „4.4 Umgekehrt“ (Abb. 4.10: Ein Transistor als Invertierer), werden wir später dahingehend abändern, indem wir die BE-Spannung U_BE zum Ansteuern und Schalten des NPN-Transistors BC547 direkt mittels des analogen Spannungsausgangs am Port „Pin P0“ des „micro:bit“-Rechners einspeisen, da sich diese entsprechend programmieren lässt, sodass unsere LED-Schaltung mit der roten LED im Sinne des „Inter of Electronics (IoE)“ quasi intelligent wird. -

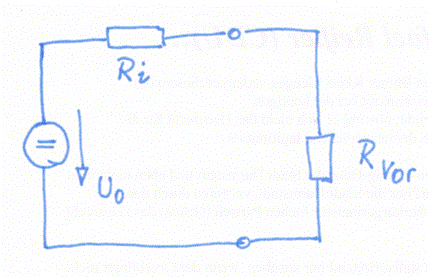
Den Vorwiderstand R_Vor als Objekt berechnen und programmieren

Wenn wir die bisherige Schaltung mit der roten LED, die ja im Moment nur aus der 9 Volt Blockbatterie als Objekt besteht, mit einem Vorwiderstand R_Vor = 470 Ω erweitern, indem wir diesen an die Batterieklemmen, quasi als Lastwiderstand, anschließen, dann verhält es sich aus Sicht der Batterie, d.h. der Quellenspannung U₀ = 9,76 V so, dass sowohl der (Batterie-) Innenwiderstand R_i = 340 Ω als auch der Vorwiderstand R_Vor = 470 Ω in Reihe geschaltet sind:

(Zum Vergrößern bitte auf das Bild klicken!)

Diesbezüglich gilt es daran zu erinnern, dass es sich bei der 9 Volt Blockbatterie umgangssprachlich um eine „Stromquelle“ handelt, bei der es sich aber in Wirklichkeit um eine reale Spannungsquelle mit der Ursprungsspannung U₀ = 9,76 V (= Leerlaufspannung im unbelasteten Zustand mit U_Klemme = U₀ und I_Batt = 0) handelt.

Ferner sei daran erinnert, dass eine reale, d.h. verlustbehaftete Spannungsquelle mit der Ursprungsspannung U₀ = U_leer = 9,76 V in ihrem Inneren auch noch über einen entsprechenden Innenwiderstand R_i verfügt, der in Reihe zur Spannungsquelle geschaltet ist (siehe obenstehendes Bild) und den es bei den weiteren Berechnungen zu berücksichtigen gilt.

Da es sich bei der 9-Volt-Blockbatterie um eine Zink-Kohle-Batterie handelt, deren Zink-Elektroden sich im Laufe der Zeit bei entsprechender Stromentnahme zersetzen, verhält es sich so, dass sich der elektro-chemische Innenwiderstand R_i mit zunehmender Entladung vergrößert, sodass die Batterie immer weniger Stromstärke zu liefern vermag.

>> 9-V-Blöcke werden mit verschiedenen elektrochemischen Systemen hergestellt, die sich in Leerlaufspannung, Kapazität und Belastbarkeit deutlich unterscheiden können.

Üblich sind 9-V-Blöcke als nicht wiederaufladbare Primärzellen mit sechs Zellen als Alkali-Mangan-Batterie, früher auch mit nicht auslaufsicheren sechs Zink-Kohle-Zellen. Weiters werden 9-V-Blöcke auf Basis der Lithium-Mangandioxid-Batterie Li-MnO₂^[1] mit drei Zellen zu 3,5 V (Leerlaufspannung 10,5 V) angeboten. Alternativ sind sie mit einer etwas höheren Leerlaufspannung von 11,1 V auch als Lithium-Thionylchlorid-Batterie Li-SOCl₂ mit drei Zellen zu je 3,7 V erhältlich. << (Quelle: Wikipedia)

Neben der 9-Volt-Blockbatterie als Spannungsquelle gibt es aber tatsächlich auch noch eine sogenannte Stromquelle, die es aber so nicht zu kaufen gibt, sondern nur als elektronische Schaltung z.B. in einem Labornetzgerät mit einstellbarem, d.h. begrenzten und deshalb kurzschlussfestem Laststrom. Bei einer solchen Stromquelle im Labornetzgerät handelt es sich deshalb um eine elektronisch geregelte und verstärkte Konstantstromquelle, die in ihrem Inneren oftmals aus einem oder mehreren Operationsverstärkern besteht.

Bei der 9-Volt-Blockbatterie als Spannungsquelle hilft uns der reale Innenwiderstand R_i = 340 Ω dabei, die Batterie als Objekt mit entsprechenden Eigenschaften (Leerlaufspannung U₀, Klemmenspannung U_Klemme, Ladungsmenge Q_ges = 330 mAh) besser zu verstehen und zu berechnen:

(Zum Vergrößern bitte auf das Bild klicken!)

Bezüglich des zugrunde gelegten Innenwiderstandes R_i = 340 Ω stellt sich noch die rechnerische Frage, wie der Widerstandswert R_i zustande gekommen ist.

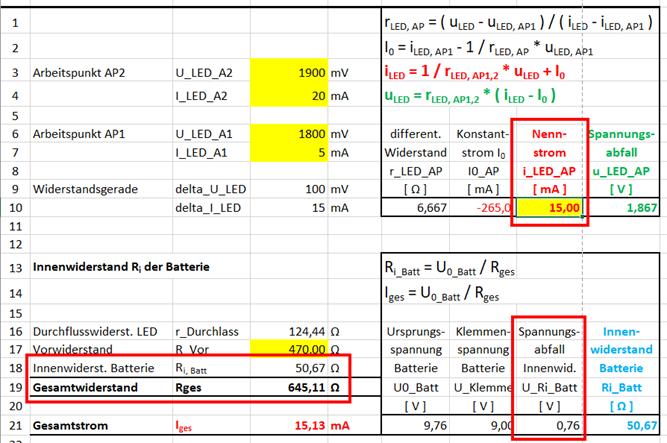
Wenn man von einer Ursprungsspannung U₀ = 9,76 V im Inneren der Batterie und einem maximalen Gesamtstrom I_ges = I_max = I_{LED, max} = 25 mA ausgeht, dann berechnet sich der Gesamtwiderstand R_ges wie folgt:

R_ges = U_ges / I_ges = U₀ / I_ges = 9,76 V / 25 mA = 0,3904 KΩ = 360,4 Ω

U₀ = 9,76 V mit I_{LED, max} = 25 mA lässt sich der Gesamtwiderstand R_ges der Schaltung mit dem Vorwiderstand R_Vor = 470 Ω (siehe weiter oben), aber (noch) ohne Durchgangswiderstand r_LED der roten LED selbst, wie folgt berechnen:

R_ges = U₀ / I_{LED, max} = 9,76 V / 25 mA = 0,3904 KΩ = 390,4 Ω ≈ 390 Ω

Da aber die Ursprungsspannung U₀ = 9,76 V wegen des Batterie-Innenwiderstandes R_i, Batt nicht bis nach außen, d.h. an die Batterie-Anschlussklemmen gelangt, stehen uns als Spannungsversorgung für die LED-Schaltung mit Vorwiderstand nur die Klemmenspannung U_Klemme = 9 V zur Verfügung, sodass sich der Gesamtwiderstand’ R’_Klemme an den Batterieklemmen der äußeren Beschaltung nun wie folgt berechnet:

R’_Klemme = U_Klemme / I_{LED, max} = 9 V / 25 mA = 0,36 KΩ = 360 Ω

Bei einem geringeren (Gesamt-) Strom von nur I_{LED, nenn} = 15 mA berechnet sich der Gesamtwiderstand“ R“_Klemme an den Batterieklemmen jetzt wie folgt:

R“_Klemme = U_Klemme / I_{LED, nenn} = 9 V / 15 mA = 0,6 KΩ = 600 Ω

(Zum Vergrößern bitte auf das Bild klicken!)

Die bisherigen als auch die nachfolgenden Berechnungen zur Reihenschaltung der roten LED mit dem Vorwiderstand lassen sich am besten mittels Tabellenkalkulation anstellen, da sich diese sehr flexibel gestalten lässt.

An dieser Stelle bestätigt sich wieder der Erfahrungsgrundsatz aus dem Ohmschen Gesetz:

· „Kleiner Widerstand → große Stromstärke!“ und

· „Großer Widerstand → kleine Stromstärke!“

Berücksichtigt man den Batterie-Innenwiderstand R_i, Batt = 50,67 Ω bei der Berechnung des Gesamtwiderstandes R_ges, dann vergrößert sich dieser entsprechend:

(Zum Vergrößern bitte auf das Bild klicken!)

Berechnung des Innenwiderstandes R_i, Batt der Batterie:

R_{i, Batt} = ( U₀ - U_Klemm ) / I_ges → I_ges = I_{LED, nenn}

= ( U_{Ri, Batt} ) / I_{LED, nenn}

Die Ursprungsspannung U₀ im Inneren der Batterie misst man, indem man an den Batterieklemmen die Batteriespannung ohne Belastung, d.h. ohne Entnahme-/Laststrom bzw. ohne Lastwiderstand, misst (I_ges = I_{LED, nenn} = 0 mA)!

Die Klemmenspannung U_Klemm misst man mit Belastung, d.h. mit einem Lastwiderstand wie z.B. dem Betrieb der roten LED mit Vorwiderstand (I_ges = I_{LED, nenn} = 15 mA).

Bei dem Innenwiderstand der Batterie handelt es sich um einen elektro-chemischen Widerstand, der sich mit zunehmender Entladung vergrößert! -

Wenn wir formelmäßig alles richtig gemacht und berechnet haben, dann müsste sich der Batterie-Innenwiderstand R_i, Batt = 50,67 Ω auch folgerichtig aus dem Spannungsabfall am Innenwiderstand selbst wie folgt berechnen lassen:

R_{i, Batt} = ( U₀ - U_Klemm ) / I_ges = ( U_{Ri, Batt} ) / I_{LED, nenn}

= ( 9,76 V – 9 V ) / 15 mA = 0,76 V / 15 mA

= 0,05067 KΩ = 50,67 Ω

Wenn weiß wie es geht, ist alles einfach. Aber dazu muss man wissen, dass sich ein Widerstand eben ganz einfach berechnen lässt, wenn man den Quotienten von Spannungsabfall ( U₀ - U_Klemm ) zu Stromstärke I_{LED, nenn} bildet.

Apropos „Quotient“, bei der Spannungsteilerformel handelt es sich auch um einen Quotienten. Und zwar auf beiden Seiten der Gleichung bzw. Formel. Mittels dieser lässt ebenfalls der (Gesamt-) Strom durch die Schaltung bzw. den Vorwiderstand R_Vor wie folgt berechnen:

U_RVor / U₀ = R_Vor / R_ges = R_Vor / ( R_i + R_Vor+ r_Durchfluss )

I_RVor * R_Vor * 1 / U₀ = R_Vor / ( R_i + R_Vor+ r_Durchfluss )

I_RVor = U₀ / ( R_i + R_Vor+ r_Durchfluss ) = U₀ / ( R_i + R_Vor+ u_{LED AP} / i_{LED AP} )

= 9,76 V / ( 50,67 Ω + 470 Ω + 1,867 V / 15 mA )

= 9,76 V / ( 50,67 Ω + 470 Ω + 124,47 Ω )

= 9,76 V / ( 645,14 Ω ) = 0,015128 A ≈ 15,13 mA

Wichtig bei der Berechnung ist, dass wir den Durchflusswiderstand r_Durchfluss = 124,47 Ω der roten LED nehmen müssen und nicht den differentiellen Widerstand r_LED, diff, da dieser nur für das Steigungsdreieck, z.B. im Arbeitspunkt AP1, zuständig ist!

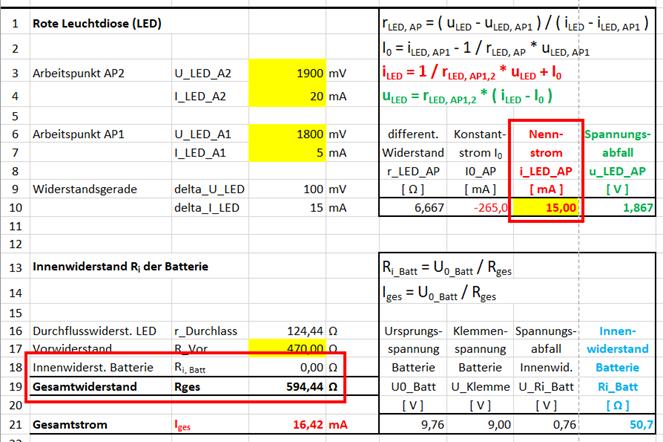
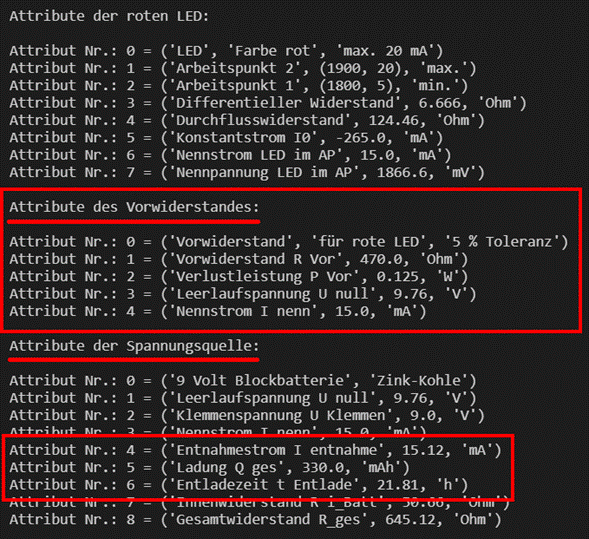
Berechnung des Gesamtwiderstandes anhand der Batterie-Kapazität

Da uns von der 9-Volt-Blockbatterie mit den Zink-Kohle-Elementen auch die im Elektrolyten gespeicherte Ladungsmenge Q_ges = 330 mAh bekannt ist (siehe obenstehendes Bild), lässt sich darüber auch noch der Innenwiderstand R_i der Batterie berechnen.

(Batterie-) Kapazität C_Batt (siehe Kondensator)

C_Batt = Q_Batt / U_Batt = I_Batt * t_Entlade / U_Batt → [ As / V ] = [ 1 s / ( V/A ) ] = [ 1 s / Ω ]

Q_Batt = I_Batt * t_Entlade →

t_Entlade = Q_Batt / I_Batt = 330 mAh / 15,13 mA = 21,8 h

= I_Batt * t_Entlade / U_Batt

= 15,13 mA * 21,8 h / 9,76 V = 329,8 mAh / 9,76 V = 33,79 mAh / V

= I_Batt / U_Batt * t_Entlade = 1 / ( U_Batt / I_Batt ) * t_Entlade

= 1 / R_ges * t_Entlade [ As / V ] →

R_ges = t_Entlade / C_Batt

= t_Entlade / ( Q_Batt / U_Batt ) = 1 * t_Entlade / ( I_Batt * t_Entlade / U_Batt ) = U_Batt / I_Batt

= 21,8 h / ( 33,79 mAh / V ) = 0,64516 V/mA = 645,16 V/A

= 645,16 Ω

Siehe auch Berechnung in der Tabellenkalkulation!

Damit wäre dann rechnerisch bewiesen, dass der Gesamtwiderstand R_ges der Schaltung, letztlich also auch als Funktion des Innenwiderstandes der Batterie, definitiv von der noch gespeicherten, restlichen Ladungsmenge Q_Batt bzw. (Rest-) Kapazität C_Batt abhängt! -

Gemäß der Berechnungsformel wird also der Innenwiderstand R_{i Batt} der Batterie umso größer, je größer die Entladedauer t_Entlade, d.h. die Nutzungsdauer der Batterie, ist. Und diese wird umso größer, je geringer der Entladestrom (= Laststrom) ist!

Da aber mit zunehmender Entladung der Batterie auch deren Kapazität (= Energiedichte, d.h. der Quotient Ladungsmenge Q_Batt pro Volt Batteriespannung) gemäß der sogenannten e-Funktion abnimmt, vergrößert sich zunehmend, d.h. kontraproduktiv, der Innenwiderstand R_{i Batt}.

Ob und inwieweit der Innenwiderstand R_{i Batt} bei der Berechnung und der Programmierung der Objekte (Innenwiderstand, Vorwiderstand, nichtlinearer Widerstand r_LED der Leuchtdiode) eine unverzichtbare Rolle spielt, muss sich noch zeigen. Spätestens dann, wenn sich alle Objekte untereinander vernetzen und sich zu einer Schaltung zusammenfügen. -

Speicherkapazität C_Batt als Funktion der gespeicherten elektrischen Energie W_el

Die als Antriebsenergie vorhandene oder als gespeicherte, verfügbare elektrische Energie W_el wird auch als elektrisch verrichtete Arbeit A_el, wie z.B. bei einem Elektromotor, bezeichnet. Je länger der Elektromotor mit seiner Antriebsleistung P_el läuft, umso mehr Arbeit A_el verrichtet er: W_el = A_el = P_el * t_Dauer .

W_el = P_el * t_Dauer = U * I * t_Dauer = I * R * I * t_Dauer = I² * R * t_Dauer = Q * I * R

R_ges = W_el / ( Q * I ) = P_el * t_Dauer / ( Q * I ) → C = Q / U → Q = C * U

= U * I * t_Dauer / ( C * U * I ) = t_Dauer / C_Batt →

R_ges = ( 1 / C_Batt ) * t_Dauer

C_Batt = ( 1 / R_ges ) * t_Dauer

Jetzt haben wir den formelmäßigen Beweis, dass die Batteriekapazität C_Batt tatsächlich eine Funktion des Gesamtwiderstandes R_ges mit R_ges = R_i + R_Vor + r_{LED, AP} ist! –

Zwecks Bestätigung, dass die Formel im roten Kasten auch wirklich funktioniert, wenden wir diese an, indem wir entsprechende Werte einsetzen:

C_Batt = ( 1 / R_ges ) * t_Dauer

= ( 1 / 645,16 Ω ) * 21,8 h = 0,03379 A/V h = 33,79 mAh/V (siehe weiter oben!)

Nachfolgend lässt sich der Vorwiderstand R_Vor hinreichend als Objekt mit den Eigenschaften (Attributen) wie folgt definieren:

· Name des Bauelements: Vorwiderstand

Toleranz des Bauelements: +/- 5 %

· Widerstandswert: 470 Ω

· (Wärmeverlust-) Leistung: 1/8 Watt = 0,125 W = 125 mW

Beispiel:

P_{R Vor} = U_{R Vor} * I_Last = 7,05 V * 15 mA = 105,75 mW

Die nachfolgenden elektrischen Werte müssen von der 9 Volt Blockbatterie geholt, d.h. ausgelesen werden:

· Leerlaufspannung der Batterie U_{Batt, leer} = 9,76 V

· Nennstrom (= Entladestrom auf Dauer) I_Nenn = 15 mA

· Maximale Ladungsmenge bei voller Batterie Q_{Batt, voll} = 330 mAh

Maximale Betriebsdauer bei I_ges = i_{LED, AP} = 15,12 mA: = 21,8 h

Da sich die max. Betriebsdauer direkt aus Q_{Batt, voll} berechnen lässt, muss dieser Wert nicht explizit als Attribut in das Objekt aufgenommen werden!

(Zum Vergrößern bitte auf das Bild klicken!)

Die obenstehende Anzeige zu den Attribute der Objekten „Rote LED“, „Vorwiderstand“ und „Spannungsquelle“ werden im „Python“-Programm batterie_oop_03.py berechnet und programmiert, das man sich auch direkt im Browser anzeigen lassen kann.

Selbstverständlich lässt sich das Programm auch auf den heimischen Rechner herunterladen. Und zwar indem man den Mauszeiger auf den blau markierten Hyperlink positioniert und mittels der rechten Maustaste „Ziel speichern unter …“ herunterlädt. -

[ Home ] [ zurück ] [ Seitenanfang ]