[ Home ] [ zurück ] [ Seitenende ] [ Teil 2 ] [ Teil 4 ]

micro:bit-Programmieren, Teil 3

1. Einleitung

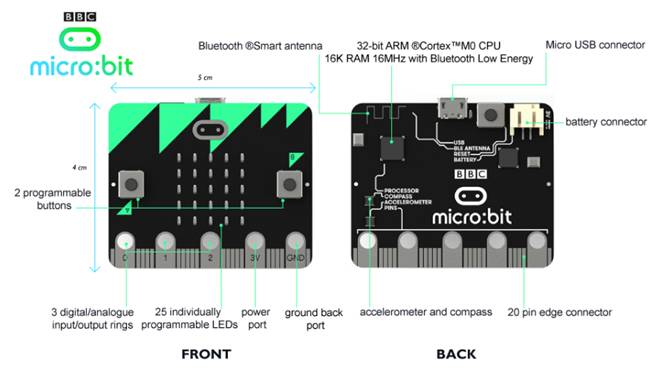
Nachdem wir uns im Teil 1 und Teil 2 bereits intensiv mit der Programmierung des „micro:bit“-Rechners befasst haben, haben wir uns eine kleine Abwechselung verdient, indem wir uns nachfolgend mit der Hardware des kleinen Rechners beschäftigen:

(Bild 01 von der „micro:bit“-Homepage, Hardware)

Wie man links im obenstehenden Screenshot sieht, gibt es bei auf der Vorderseite, engl. „front“, des „micro:bit“-Rechners insgesamt fünf große Ringanschlüsse zum Einstecken von sogenannten „Bananen“-Steckern mit der Beschriftung (von links nach rechts): „0“, „1“, „2“, „3V“ und „GND“.

Bei den beiden Ringanschlüssen „3V“ und „GND“ handelt es sich um die nach außen geführte Stromversorgung mit U_3V = +3,3 V und U_GND = 0 V. Dabei steht die englischsprachige Abkürzung „GND“ für engl. „ground“, d.h. Masse mit 0 V neutralem Spannungspotential.

Bezüglich der positiv gepolten Spannung U_3V = U_VCC = +3,3 V stellt sich gleich die Frage, weshalb sich die Ausgangsspanung U_3V = U_VCC auf +3,3 V beläuft und nicht auf z.B. 5 V.

Denn eigentlich würde man eher eine Ausgangsspanung von U = 5 V erwarten, wenn wir den „micro:bit“-Rechner z.B. mittels eines entsprechenden USB-Kabels an den heimischen PC anschließen. Dabei wird der kleine „USB-2.0-Micro-B-Stecker“ des USB-Kabels direkt an den „micro:bit“-Rechner angeschlossen und der größere „USB-2.0-Typ-A-Stecker“ am anderen Ende des Kabels an die USB-2.0-Buchse des heimischen Windows-PCs zwecks Stromversorgung über USB und zum Datenaustausch angesteckt.

Sobald das USB-Kabel mit dem Windows-PC verbunden wird, erkennt Windows von sich aus, dass ein USB-Gerät angeschlossen wurde, lädt im Hintergrund die entsprechenden Treiber und bindet das USB-Gerät automatisch in das Windows-Dateisystem ein, sodass man ab sofort auf dieses zugreifen kann.

Der Grund für die etwas krumme Ausgangsspannung von U_3V = U_VCC auf +3,3 V liefert uns die Angabe „V_CC“ im Index. Dabei steht der Buchstabe „V“ für engl. „voltage“, d.h. Spannung und die beiden anderen Buchstaben „cc“ für engl. „common collector“, d.h. gemeinsamer Kollektor.

Dazu muss man wissen, dass es zu Zeiten der Erfindung des Transistors um 1948 herum nur Germanium als Ausgangsmaterial für Halbleiter, Dioden und Transistoren mit der Sperrschichtfolge „pnp“ als sogenannte Bipolartransistoren gab.

Ab 1954 gab es dann auch Silizium-Transistoren mit der Sperrschichtfolge „npn“, die die Germanium-Transistoren schnell verdrängten.

Ab 1960 gab es die ersten „Feldeffekt-Transistoren“ (FET) und „Metall-Oxid-Halbleiter-Feldeffekttransistoren“ (MOS-FET) aus Silizium. Die Wirkungsweise von MOS-FETs wird u.a. auch im Elektronik-Kompendium anschaulich beschrieben.

Dioden, Transistoren, FET- und MOS-FET-Transistoren wurden dann in sogenannten „Integrierten Schaltkreisen“ (ICs) wie z.B. Verstärkerschaltungen, Schmitt-Trigger (= Schwellwert-Schalter), UND-, ODER-, RS-Flip-Flops, JK-Flipflops, Gatterschaltungen der Digitaltechnik, Operationsverstärker (NF-Verstärker, Komperatoren, Konstantstromquellen, Spannungskonstanter usw.), AC-/DC- und DC-/DC-Wandler, Schaltnetzteile, Mikrocontroller (Arduino), Einplatinencomputer (8080, 8085, 6502, Z80, micro:bit, Raspberry Pi) zusammen gefasst und verdichtet.

Operationsverstärker, Mikrocontroller und Einplatinencomputer verfügen über teils programmierbare analoge oder digitale Ein- und Ausgänge, integrierte Strom- und Spannungsquellen wie z.B. in Form von Spannungsreglern, Stromkonstantern (= Konstantstromquelle) usw., die meistens kurzschlussfest ausgelegt sind.

2. Stromversorgung beim „micro:bit“-Rechner

Beim „micro:bit“-Rechner gibt es zwei Möglichkeiten der externen Stromversorgung. Und zwar mittels

a) Micro-USB-Kabel und USB-2.0-Micro-B-Stecker

Siehe Beschriftung „Micro USB connector“ im Bild oben!

Für den Elektronik-Einsteiger empfiehlt es sich, die Stromversorgung des „micro:bit“-Rechners mittels Micro-USB-Kabel vorzunehmen, weil die Stromstärke bei einem

· „USB 1.0/1.1“-Anschluß auf 100 mA bei 4,40 V - 5,50 V
und bei einem

· „USB 2.0“-Anschluß auf 500 mA bei 4,75 V - 5,50 V
begrenzt ist.

Dabei beträgt die Nennspannung bei beiden USB-Anschlüsse 5 Volt, sodass der „USB 2.0“-Anschluß insgesamt eine Leistung von bis zu P = U * I = 5 V * 0,5 A = 2,5 W zur Verfügung stellt. -

Wie man oben im Bild sieht, verfügt der „micro:bit“-Rechner auf der Vorderseite über insgesamt fünf große Ringanschlüsse zum Einstecken von sogenannten „Bananen“-Steckern mit der Beschriftung (von links nach rechts): „0“, „1“, „2“, „3V“ und „GND“.

Dabei beziehen sich die ersten drei Ringanschlüsse mit der Beschriftung (von links nach rechts): „0“, „1“, „2“ auf die programmieren Ports „P0“ bis „P2“, die über eine interne, elektronische Sicherung verfügen, so dass die Ports ab einem Laststrom I_Last > 15 mA automatisch abgeschaltet werden!

Die interne, elektronische Sicherung für die Ports P0 bis P2 steht aber nur zur Verfügung, wenn man den „micro:bit“-Rechners mittels Micro-USB-Kabel mit Strom versorgt!

Da aber die Ausgangsspanung bei einem Laststrom I_Last > 15 mA bereits auf U_Last ≈ 0,9 V zusammengebrochen ist, berechnet sich der Innenwiderstand R_i wie folgt: R_i = U_Last / I_Last = 0,9 V / 15 mA = 900 mV / 15 mA = 60 Ω.

Was wir jetzt also schon wissen, ist, dass die nach außen verfügbare (Ausgangs-) Leistung an den Ports P0 bis P2 in Form des Produktes von Spannung und Strom so gering ist, dass man an diese im Prinzip nur eine Leuchtdiode (LED) anschließen kann: P_out = U_out * I _Last ≈ 1 V * 15 mA = 15 mW.

Demzufolge wird es später notwendig sein, dass man an die leistungsschwachen Ausgänge des „micro:bit“-Rechners einen nachgeschalteten FET- oder MOS-FET-Transistor als „Stromverstärker“ anschließt.

Dabei scheiden herkömmliche Silizium NPN- (oder PNP-Komplementär-) Transistoren aus, da sich diese nur mittels eines Basisstroms von I_B = 5 mA bis 50 mA ansteuern lassen, was aber mit den Ports P0 bis P2 nicht möglich ist!

Die beiden weiter rechts befindlichen Ringanschlüsse mit der Beschriftung „3V“ und „GND“ dienen der ausgangsseitigen, abgehenden Stromversorgung mit einer Ausgangsspanung von U_3V = +3,3 V gegenüber dem Masseanschluss „GND“.

Dabei gilt es zu beachten, dass die nach außen geführte Stromversorgung nicht elektronisch abgesichert ist, der maximale Laststrom aber auf I_max = 500 mA entsprechend dem „USB 2.0“-Anschluß begrenzt ist (siehe weiter oben).

b) Batterie-Anschlussbuchse nebst zweiadrigem Kabel

Siehe Beschriftung „battery connector“ im Bild oben!

Wenn man die Stromversorgung des „micro:bit“-Rechners mittels des externen Batterieanschlusses herstellt, dann wird diese einfach nur „durch das System geschleust“, d.h. an der internen Elektronik vorbei geführt, sodass es für die Ports P0 bis P2 keine interne elektronische Sicherung gibt!

Wegen der sehr dünnen Leiterbahnen auf dem Board des „micro:bit“-Rechners kann es im Falle eines Kurzschlusses dazu kommen, dass ein größerer Kurzschlussstrom von ein bis zwei Ampere diese verschmoren!

Die im Kurzschlussfall auftretenden großen Ströme nebst Batteriespannung bewirken dabei eine elektrische Wärmeleistung von bis zu 3,0 V * 2 A = 6 Watt.

Zum Vergleich: Die Lötspitze eines kleinen „Nadel“-Lötkolbens entwickelt bei einer Löt-Wärmeleistung von „nur“ 15 Watt eine Temperatur von bis zu 420 Grad.

3. Es werde Licht - mit einer LED

Jetzt wo wir also wissen, was es mit der Stromversorgung auf sich hat und wie diese funktioniert, haben wir uns ein kleines Erfolgserlebnis verdient, wird es Zeit, dass wir z.B. den Port „P0“ programmieren und eine Leuchtdiode (LED) zum Leuchten bringen.

Doch vorab berechnen wir noch schnell den Vorwiderstand R_V mittels der die rote LED in Reihenschaltung betrieben wird, um die max. zulässige Stromaufnahme von I_LED = 20 mA für Standard-LEDs nicht zu überschreiten.

Bezüglich der Flussspannung der roten LED in Durchlassrichtung von U_LED = 1,6 V - 2,2 V ≈ ( 2,2 V - 1,6 V ) / 2 + 1,6 V = 0,3 V + 1,6 V = 1,9 V (= Mittelwert) und der Versorgungsspannung U_P0 = 3,3 V am Port mit dem Pin „P0“ folgt, dass man die Spannungsdifferenz von ∆U_RV = U_P0 - U_LED = 3,3 V – 1,9 V = 1,4 V am Vorwiderstand R_V „vernichten“ muss.

Zusammen mit dem Durchlassstrom der roten LED von I_LED = 20 mA folgt dann für den Vorwiderstand R_V:

R_V = ∆U_RV / ∆I = ( U_P0 - U_LED ) / I_LED = 1,9 V / 20 mA = 0,095 KΩ = 95 Ω

Auf der Homepage vom „Elektronik-Kompendium“ gibt es übrigens einen sogenannten LED-Vorwiderstandsrechner für verschieden farbige LEDs.

Die Ports mit den Pins „P0“ bis „P2“ des „micro:bit“-Rechners lassen sich nicht nur programmieren, sondern durch Programmierung auch für unterschiedliche Zwecke einrichten. Dabei lassen sich diese sowohl für analoge als auch digitale Anwendungen programmieren.

Da es sich bei der roten LED nebst Vorwiderstand R_V um analoge Bauelemente handelt,

programmieren wir den Port mit dem Pin „P0“ als analogen Ausgang, sodass sich mit diesem mittels der einstellbaren, programmierbaren Ausgangsspannung später auch die Helligkeit der LED in gewissen Grenzen verändern lässt.

Obwohl es sich bei der Ausgangsspannung am Pin „P0“ also um eine analoge Gleichspannung handelt, lässt sich diese wegen der Programmierung und des intern verwendeten Digital-/Analog-Wandlers, kurz D/A-Wandler, intern nur digital einrichten und steuern, wobei wir als Anwender und Programmierer davon fast nichts mitbekommen.

Wenn wir aber am Ausgang vom Pin „P0“ die intern von digital nach analog umgewandelte Gleichspannung auf einen bestimmten Wert einstellen wollen, dann müssen wir wissen, mit welchen digitalen, d.h. binären Werten sich diese einstellen und programmieren lässt.

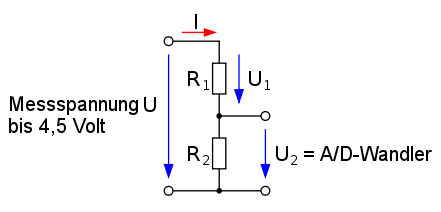
Wenn man also z.B. mit einem A/D-Wandler eine eingangsseitig anliegende bis zu einem Maximalwert schwankende Gleichspannung einlesen, d.h. „samplen“ (= abtasten) will, dann muss ich vom A/D-Wandler wissen, in wie vielen „Treppenstufen förmigen Säulen“ dieser das anliegende Signal abtasten kann.

Wie man dem Datenblatt zum Controller „nRF51822“ mit dem 2.4 GHz Hochfrequenz-Chip-System für das Bluetooth LE, engl. „low energy“ (= Niedrig-Energieverbrauch), entnehmen kann, verfügt dieser u.a. auch über einen „8/9/10 bit ADC - 8 configurable channels“, d.h. 8/9/10 Bit Analog-/Digital-Konverter mit 8 konfigurierbaren Kanälen.

Was aber bedeutet es, wenn der A/D-Wandler das Eingangssignal mit 10 Bit einliest, d.h. abtastet und auflöst? 10 Bit = 11 1111 1111₂ = 2⁹ + 2⁸ + 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2¹ + 2⁰ = 1023₁₀ → U_P0 = +3,3 V → 3,3 V / 1024₂ = 0,003227 V = 3,227 mV/Bit ≈ 3,23 V/Bit

Probe:

3,227 mV/Bit * 1024 Bit = 3304,448 V ≈ 3,3 V

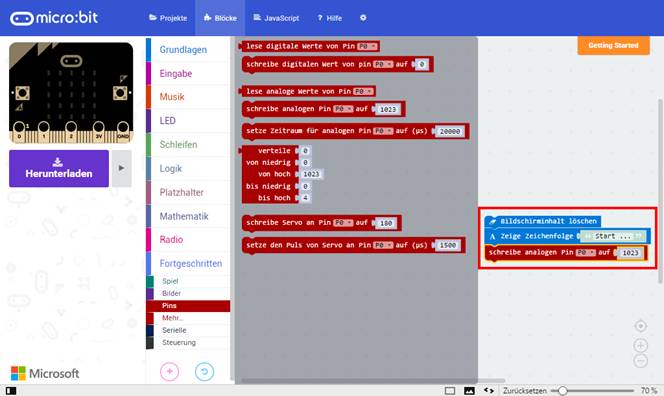
Wenn also unsere rote LED später mit maximaler Helligkeit leuchten soll, dann müssen wir dafür sorgen, dass der „Pin P0“-Port eine Ausgangsspannung von 3,3 Volt liefert, was einem Dezimalwert von 1023₁₀ entspricht (siehe roter Kasten rechts unten im Bild):

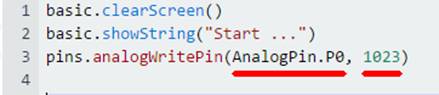
(Bild 02 zur Schaltung „microbit_teil_03_prog_01“)

In JavaScript sieht das Programm „microbit_teil_03_prog_01.hex“ mit dem Quelltext „microbit_teil_03_prog_01.js“ dann folgendermaßen aus:

(Bild 03 zum Programm „microbit_teil_03_prog_01“)

Wenn man Dinge in Betrieb nimmt, d.h. einschaltet, dann sollte man sich auch gleich damit befassen und sich schlau machen, wie man diese wieder ausschaltet. Das klingt zwar trivial, ist es aber nicht immer, da das Abschalten eines Gerätes gänzlich anders verlaufen kann als das Einschalten. So lässt sich z.B. eine Waschmaschine nach dem letzten Spül- und Schleudergang problemlos ausschalten, aber noch lange nicht die Bullaugentür öffnen, um die Wäsche entnehmen zu können. 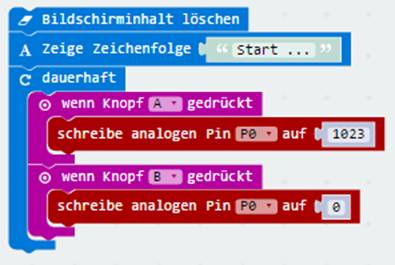Die Bullaugentür lässt sich nämlich erst nach einer gewissen Wartezeit von ein, zwei Minuten öffnen, um auf diese Weise sicherzustellen, dass sich die Trommel vom letzten Schleudergang nicht mehr dreht und den Anwender verletzt, wenn er nach dem Öffnen der Bullaugentür sofort in die Trommel greift, um die Wäsche zu enthemen

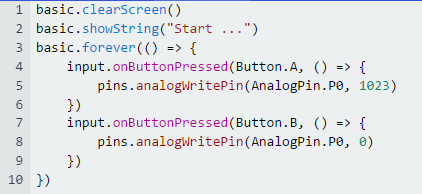
Wenn wir also die rote LED nach dem Einschalten mittels Taster A auch wieder ausschalten wollen, dann müssen wir nur dafür sorgen, dass ein Tastendruck auf den Taster B den binären Wert des Ports „Pin P0“ auf null setzt:

(Bild 04 zur Schaltung „microbit_teil_03_prog_02“)

Der Quelltext „microbit_teil_03_prog_02.js“ zum Programm „microbit_teil_03_prog_02.hex“ sieht dabei natürlich noch recht übersichtlich und unspektakulär aus:

(Bild 05 zur Schaltung „microbit_teil_03_prog_02“)

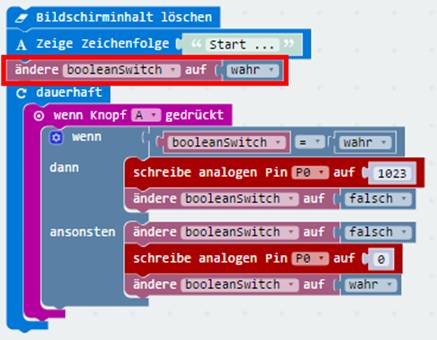
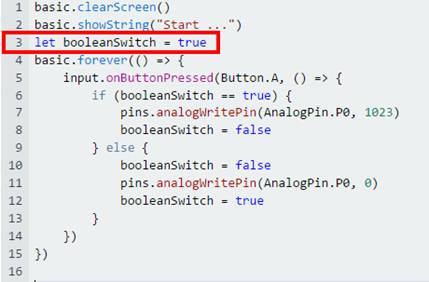
Nachdem wir jetzt wissen, wie sich die rote LED ein- und ausschalten lässt, nämlich mit den Tastern A und B, können wir uns daran machen und das System optimieren, indem wir ganz einfach auf den Taster B verzichten und die LED nur noch mit einem Taster, dem Taster A, ein- und ausschalten, sodass dieser als Wechseltaster arbeitet:

(Bild 06 zur Schaltung „microbit_teil_03_prog_03“)

Im Quelltext „microbit_teil_03_prog_03.js“ zum Programm „microbit_teil_03_prog_03.hex“ sieht man auf einen Blick, dass jetzt der Taster A bei der „wenn … dann“-Abfrage mit dem Statement

if (booleanSwitch == true) {

pins.analogWritePin(AnalogPin.P0, 1023)

booleanSwitch = false

} else {

booleanSwitch = false

pins.analogWritePin(AnalogPin.P0, 0)

booleanSwitch = true

}

zwei Schaltfunktionen, nämlich „ein“ (= 1023) und „aus“ (= 0) übernimmt:

(Bild 07 zur Schaltung „microbit_teil_03_prog_03“)

Haben Sie schon mal als „Strippenleger“, d.h. als Elektroinstallateur, gearbeitet oder diesem über die Schulter geschaut? Falls Sie mal einem begegnen, dann fragen Sie ihn mal, ob er Ihnen erklären kann, wie eine sogenannte „Wechselschaltung“ im langen Wohnungsflur funktioniert! Und zwar mit zwei Wechselschaltern und nicht Wechseltastern!

Das Besondere an einer Wechselschaltung mit zwei herkömmlichen Kippschaltern ist nämlich, dass diese ohne ein Umschaltrelais im Sicherungskasten auskommt! Deshalb hört man beim Umschalten auch kein Klackgeräusch im Sicherungskasten!

Eine weitere Besonderheit liegt darin begründet, dass man das Flurlicht am Ort A mit dem Schalter A einschaltet und am anderen Ort B mit dem Schalter B ausschaltet, was ja logisch ist und genau so sein soll, da man zum Ausschalten des Lichts ja nicht wieder zum Schalter A zurücklaufen will (siehe Bilder bei Wikipedia)!

Eine dritte Besonderheit liegt darin begründet, dass die Umschalt-Kippschalter A und B je nach Umschaltung des Flurlichts eine unterschiedliche Kippstellung haben!

Normalerweise ist es nämlich so, dass man einen Kippschalter zum Einschalten des Lichts nach unten und zum Ausschalten wieder nach oben kippen muss, sodass man allein an der Kippstellung des Schalters erkennen kann, ob das Licht ein- oder ausgeschaltet ist!

Bei einer Wechselschaltung haben aber die Kippschalter A und B eine teils abweichende Kippstellung, sodass man diesen nicht mehr von außen ansieht, ob das Flurlicht ein- oder ausgeschaltet ist!

Im Falle eines Defektes an der Wechselschaltung kann man sich also auf keinen Fall darauf verlassen, dass einer der Wechselschalter mit Kippstellung nach oben auch tatsächlich die Stromzufuhr zur Glühlampe unterbricht! Deshalb muss man auf jeden Fall mittels der Sicherung im Sicherungskasten die Stromzufuhr unterbrechen! Alles andere wäre lebensgefährlich! -

Falls Sie sich bei Gelegenheit mal langweilen sollten, so machen Sie sich mal die Mühe, und programmieren Sie eine herkömmliche Wechselschaltung. Dazu müssten Sie sich aber zuvor noch zwei kleine Druckschalter (nicht „Reset“-Taster vom PC) besorgen! Dabei werden Sie wahrscheinlich nicht umhin kommen, sich eine sogenannte boolesche Wahrheitstabelle anlegen zu müssen. -

Bei dem obenstehenden Programm „microbit_teil_03_prog_03.hex“ mit dem Quelltext „microbit_teil_03_prog_03.js“ gibt es noch einen kleinen Schönheitsfehler in Form einer überflüssigen, redundanten (= doppelten) Programmzeile.

Finden Sie den Schönheitsfehler heraus oder schauen Sie sich einfach das korrigierte Programm „microbit_teil_03_prog_04.hex“ mit dem Quelltext „microbit_teil_03_prog_04.js“ an.

3.1 Vom Dauerlicht zum Blinklicht

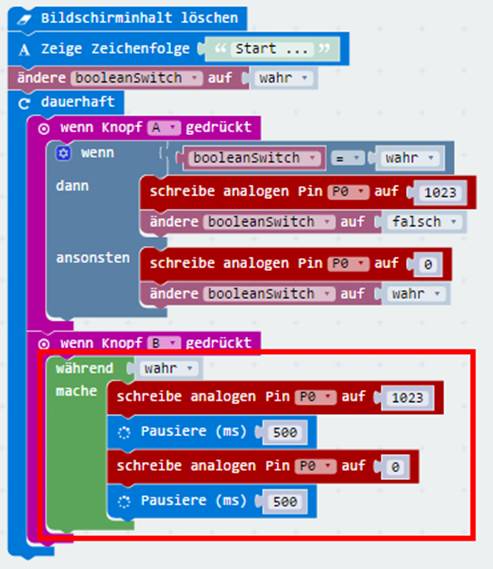
Da jetzt der Taster B frei geworden ist und beim Tastendruck ins Leere führt, programmieren wir diesen als nächstes als Blinklicht:

(Bild 08 zur Schaltung „microbit_teil_03_prog_05“)

Wie aber funktioniert ein Blinklicht? Ganz einfach, werden Sie sagen, indem man die Glühlampe vom Blinklicht ständig ein- und ausschaltet. Das ist sicherlich richtig.

Wenn es sich aber um ein Blinklicht einer Autobahnbaustelle handelt, dann soll dieses, d.h. die Glühlampe möglichst lange halten und die Glühwendel nicht wegen des erhöhten Verschleißes vorzeitig durchbrennen.

Da aber gerade das Einschalten einer Glühlampe, deren Heizwendel kalt ist, besonders verschleißbehaftet ist, muss man die Glühlampe vorheizen, damit die Heizwendel beim Einschalten aufgrund der Vorwärmung bereits einen höheren Widerstand hat, der den Einschaltstromstoß entsprechend verringert.

Praktisch realisiert man das, indem man das Blinklicht in der Blinkpause nicht komplett abschaltet, sondern nur abdunkelt. Zu diesem Zweck verwendet man einen entsprechenden Vorwiderstand, der die Heizwendel der Glühlampe stets etwas glimmen lässt, sodass diese in der Blinkpause nicht vollständig abkühlt und beim nächsten Einschalten bereits vorgewärmt ist.

Da wir aber als Blinklicht eine LED verwenden, die wegen der fehlenden Heizwendel praktisch keine Wärme produziert, brauchen wir auch keinen Vorwiderstand zum Vorheizen derselben, sodass eine LED als Halbleiter eine deutlich höhere Lebens- und Betriebsdauer hat, praktisch also nie kaputt geht.

Aber vielleicht ist Ihnen trotzdem schon einmal aufgefallen, dass die kreisrunden LED-Bremsleuchten bei einigen VW-Modellen nicht nur sehr schnell blinken, wenn der Fahrer den Blinker zum Abbiegen eingeschaltet hat, sondern das Blinken auch als besonders aggressiv wahrgenommen wird, weil das Einschalten sehr schnell und abrupt erfolgt, also nicht so weich wie bei einem herkömmlichen Blinklicht mit Glühlampe, wo die Heizwendel einige Millisekunden braucht um auf die volle Lichtleistung zu kommen.

Diesbezüglich werden wir später noch eine Methode, ein Verfahren kennenlernen, bei der man das Blinklicht ganz weich ein- und ausschalten kann. Im Moment aber wollen wir die Dinge nicht komplizierter gestalten und verzichten deshalb auf den weichen Ein- und Ausschalteffekt des Blinklichtes.

Wenn man im obenstehenden Programm „microbit_teil_03_prog_05.hex“ mit dem Quelltext „microbit_teil_03_prog_05.js“ das Ein- und Ausschalten der LED mittels Taster A mit dem Blinken der LED mit dem Tasters B vergleicht, dann fällt sofort auf, dass sich beide Programmteile gleichen. Bis auf einen wesentlichen Unterschied: beim fortwährenden Blinken, d.h. Ein- und Ausschalten der LED, brauchen wir noch eine entsprechende Endlosschleife mit dem Statement „while (true) { do … }“, d.h. auf deutsch „während (wahr) { mache … }“ (siehe weiter oben).

Aber so bequem die Endlosschleife auch für den Programmier-Einsteiger sein mag, so hat diese natürlich auch eine Schattenseite. Nämlich die, dass man wegen der Schleifenbedingung „wahr“, engl. „true“, praktisch keine Abbruchmöglichkeit der Endlosschleife hat, weil es keine konkrete Abbruchbedingung gibt! Außer der Strom fällt aus oder man drückt die rückseitige „Reset“-Taste am „micro:bit“-Rechner.

Aber zum Glück gibt es beim „micro:bit“-Rechner auch noch eine besondere Endlosschleife, die still und leise im Hintergrund werkelt. Es ist die Ereignis gesteuerte Endlosschleife „dauerhaft“, engl. „forever“, die sich z.B. durch Drücken eines der Taster A oder B problemlos verlassen lässt:

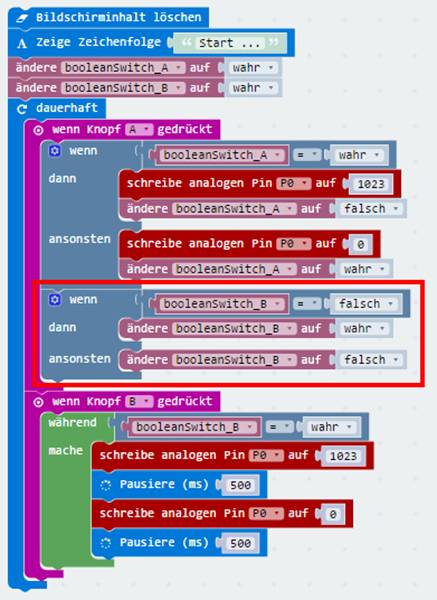
(Bild 09 zur Schaltung „microbit_teil_03_prog_06“)

Wie man im obenstehenden Programm „microbit_teil_03_prog_06.hex“ mit dem Quelltext „microbit_teil_03_prog_06.js“ sieht, wurde die Abbruchmöglichkeit des Blink-Programms, das sich mit dem Taster B starten lässt, mittels des logischen Schalters „booleanSwitch_B“ in der Endlosschleife mit dem Statement „while (true) { do … }“, d.h. auf deutsch „während (wahr) { mache … }“ programmiert (siehe im Bild oben).

Das Abbrechen/Beenden des Blink-Programms wird aber durch Druck auf den Taster A veranlasst, wobei der logische Schalter „booleanSwitch_B“ von vormals „wahr“ auf nunmehr „falsch“ umgeschaltet wird (siehe roter Kasten im obenstehenden Bild).

Das Blinklicht lässt sich übrigens auch als Alarmgeber einsetzen. Zum Beispiel wenn eine bestimmte Temperatur, Helligkeit oder ein Messwert über- oder unterschritten wird. Der Alarmgeber lässt sich auch als Diebstahlsicherung einsetzen, da ja der „micro:bit“-Rechner über einen integrierten Bewegungsmelder in Form eines Beschleunigungssensors verfügt.

Bei vielen elektrischen oder elektronischen Geräten zeigt eine kleine Leuchtdiode an, wenn das Geräte eingeschaltet und in Betrieb ist. Dabei wird der laufende Betrieb durch Dauerleuchten z.B. einer roten LED signalisiert, wobei diese im Falle einer Störung auf Blinken umgeschaltet wird.

In der Praxis kommt es aber auch vor, dass man sich die Betriebsanzeige „Gerät eingeschaltet“ (= Dauerleuchten) oder „Störung“ (= Blinken) getrennt, d.h. mittels zweier, teils verschieden farbiger LEDs anzeigen lassen möchte.

Wie man im Programm „microbit_teil_03_prog_07.hex“ mit dem Quelltext „microbit_teil_03_prog_07.js“ sieht, ist das gar nicht so schwer in die Praxis umzusetzen. Diesbezüglich benötigt man eine zweite LED, wobei beide LEDs über zwei voneinander getrennte Ports, hier Port „Pin P0“ und „PinP1“ angesteuert werden. Da die beiden LEDs niemals gleichzeitig leuchten, sondern immer nur abwechselnd geschaltet werden, können sich diese den Vorwiderstand zu den beiden LEDs miteinander teilen!

Beim Programm „microbit_teil_03_prog_08.hex“ mit dem Quelltext „microbit_teil_03_prog_08.js“ wurde der Taster B durch den Schüttel-/Bewegungs-Sensor ersetzt, sodass der Alarm immer dann ausgelöst wird, wenn man den kleinen „mirco:bit“-Rechner schüttelt oder schnell um die eigene Achse dreht.

Da sich der Alarm- oder die Störungsmeldung nicht wieder von allein abschalten soll, muss dieser mittels des Tasters A wieder zurückgesetzt werden!

Beim Programm „microbit_teil_03_prog_09.hex“ mit dem Quelltext „microbit_teil_03_prog_09.js“ wurde der Schüttel-/Bewegungs-Sensor parallel zum Taster B programmiert, sodass sich der Alarm nun auf zweifache Art und Weise auslösen lässt:

(Bild 10 zur Schaltung „microbit_teil_03_prog_09“)

Bedienungsanleitung

zum Programm „microbit_teil_03_prog_7.hex“ und dem Quelltext „microbit_teil_03_prog_7.js“

1. Starten und Ausführen des Programms

Das in den Arbeitsspeicher des „micro:bit“-Rechners geflashte Programm wird vom System automatisch gestartet und ausgeführt!

Wenn bei dem in den Arbeitsspeicher geladenen Programm nichts anderweitiges programmiert wurde, wie z.B. ein kleiner Begrüßungstext als Laufschrift auf dem „5 x 5 LED-Matrix“-Display, dann bleibt das Display dunkel, sieht man nicht, dass das geladene Programm gestartet wurde! Dies ist auch der Fall, wenn die Laufschrift durchgelaufen ist!

Im vorliegenden Fall, d.h. beim Programm „microbit_teil_03_prog_7.hex“, verhält es sich so, dass sich das herunter geladene und in den Arbeitsspeicher geflashte Programm nach etwa 20 Sekunden von allein meldet und im Display die programmierte Laufschrift „Start ...“ anzeigt.

Nachdem die Laufschrift durchgelaufen ist, bleibt das Display zwar dunkel, aber das Programm mit den zwei Tastern A und B weiterhin aktiv.

4. Taster A zum Aufrufen des Dauerlichts

Nach dem selbständigen Programmstart befindet sich das Programm im Grundmodus bei dem die beiden Taster A und B fortwährend auf einen eventuellen Tastendruck hin abgefragt werden.

Drückt man nun auf den Taster A, so wird die rote LED 1 für die Dauerbeleuchtung eingeschaltet.

Nachmaliges Drücken auf den Taster A schaltet die Dauerbeleuchtung der roten LED 1 wieder aus.

5. Taster B zum Aufrufen des Blinklichts

Nach dem selbständigen Programmstart befindet sich das Programm im Grundmodus bei dem die beiden Taster A und B fortwährend auf einen eventuellen Tastendruck hin abgefragt werden.

Drückt man nun auf den Taster B, so wird die rote LED 2 für das Blinklicht eingeschaltet.

Nachmaliges Drücken auf den Taster B schaltet das Blinklicht der roten LED 2 wieder Erwarten nicht aus!

Will man das Blinklicht der roten LED 2 wieder ausschalten, so muss man den Taster A drücken!

Als Folge dessen geht die rote LED 2 aus und die rote LED 1 für das Dauerlicht wieder an. Die rote LED 1 mit dem Dauerlicht lässt sich aber, wie in Punkt 4.) beschrieben, wieder ausschalten.

Die rote LED 2 für das Blinklicht lässt sich erst wieder oder erneut mit dem Taster B einschalten, wenn zuvor die rote LED 1 für das Dauerlicht mit dem Taster A ausgeschaltet wurde!

6. Mit dem „Reset“-Taster alles wieder auf Anfang setzen

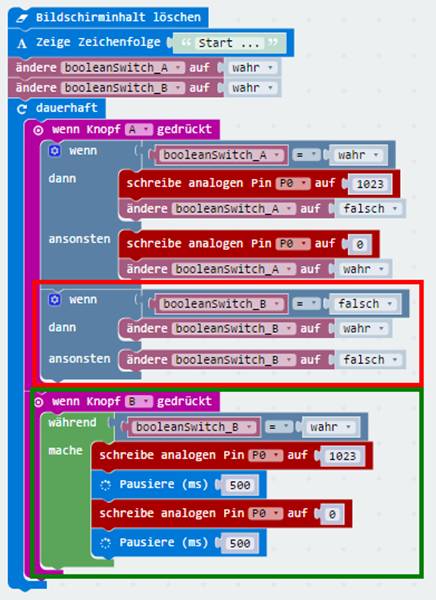
Auf der Rückseite des „micro:bit“-Rechners befindet sich ein sogenannter „Reset“-Taster mit dem sich der Rechner neu starten lässt. Dabei wird auch das zuvor in den Arbeitsspeicher geflashte Programm wieder neu gestartet, sodass sich dieses wieder im zuvor beschriebenen Grundmodus befindet! -

Wie man unten im nachfolgenden Screenshot zum Programm „microbit_teil_03_prog_09.hex“ mit dem Quelltext „microbit_teil_03_prog_09.js“ sieht, ist die

· Abbruchmöglichkeit des Blink-Programms
im Programmteil „wenn Knopf B gedrückt“ (siehe grüner Kasten)

· nur von außen
im Programmteil „wenn Knopf A gedrückt“ (siehe roter Kasten)

gegeben. Demzufolge muss man sich im Programmteil „wenn Knopf A gedrückt“ (siehe roter Kasten) befinden, um das Blink-Programm im im Programmteil „wenn Knopf B gedrückt“ (siehe grüner Kasten) beenden zu können. Das mag zwar programmiertechnisch noch angehen, aber dem Anwender ist das so nicht vermittel- und zumutbar! Und das alles noch dazu, weil man mit dem derzeitigen Programmierwissen über keine Möglichkeit verfügt, um das „während (Bedingung erfüllt ist) mache { … }“-Programmteil wieder verlassen zu können:

(Bild 11 zur Schaltung „microbit_teil_03_prog_09“)

Deshalb wenden wir uns wieder der objektorientierten Programmierung zu. Und das, obwohl wir ja bisher nur zwei Objektvariablen nebst Klassen programmiert haben und noch nicht wirklich wissen, was es mit einem Objekt auf sich hat. Aber eines sei an dieser Stelle schon verraten, nämlich dass sich Objekte vererben und auch erweitern lassen, ohne dass man sie neu programmieren muss!

3.2 Klasse statt Masse

Nachfolgend greifen wir das Programm microbit_teil_02_prog_34.hex mit dem Quellkode microbit_teil_02_prog_34.js, das hier in Kopie als Programm „microbit_teil_03_prog_10.hex“ mit dem Quelltext „microbit_teil_03_prog_10.js“ abgespeichert wurde, wieder auf und fügen den Programmkode zum Ein- und Ausschalten der roten LED 1 wie folgt ein:

(Bild 12 zur Schaltung „microbit_teil_03_prog_11“)

Wie man im Quellkode des obenstehenden Screenshots sieht, wurden nur zwei Statements eingefügt, um die rote LED 1 mittels der Taster A und B ein- und ausschalten zu können.

Dabei gilt es zu beachten, dass man sich nach dem Aufspielen und des Programmstarts mit der Anzeige „Start …“ zunächst auf der obersten Menüebene befindet, sodass man mit dem Taster A und B erst im nächsten Schritt in die nächst tiefere, darunter befindliche Menüebene gelangt.

Dabei führt das erstmalige Betätigen des Tasters A aber nicht nur auf die nächste, tiefere Menüebene, sondern schaltet in dieser auch bereits die rote LED 1 ein, sodass diese sofort dauerhaft aufleuchtet! Da wir uns jetzt schon in der nächsten, tieferen Menüebene befinden, lässt sich die rote LED 1 mittels der Taster A und B ein- und ausschalten!

Wenn man die untere, tiefere Menüebene wieder verlassen will, um in die obere Menüebene des Hauptprogramms mit dem Programmblock basic.forever(() => { … } gelanden will,

(Bild 13 zur Schaltung „microbit_teil_03_prog_11“)

dann muss man die beiden Taster A & B so lange „gleichzeitig“, d.h. zusammen, gedrückt halten bis die Anzeige „exit …“ im „5 x 5 LED-Matrix“-Display erscheint.

Das Interessante am erweiterten Programm „microbit_teil_03_prog_11.hex“ mit dem Quelltext „microbit_teil_03_prog_11.js“ ist weiterhin, dass sich die Funktionen „LED1 on!“ und „LED1 off!“ der Taster A und B zwar beide in der Klasse „starteKlasse_1 { … }“ abspielen, diese aber wiederum einzeln und voneinander getrennt in der Funktion „starteFunktion_1( … )“ und in der Methode „objektvar_starteMethode_1“ abgearbeitet werden!

Diese funktionale und programmiertechnische Trennung hat dabei den Vorteil, dass sich die beiden Taster A und B, obwohl sie innerhalb einer Klasse abgefragt werden, dann bei Tastendruck aber in unterschiedlichen Programmteilen, nämlich der Funktion und der Methode aufgerufen werden.

Alternativ hätte man auch zwei Funktionen, Funktion_1 und Funktion_2 oder zwei Methoden, Methode_1 und Methode_2, programmieren können. Aber es sollte ja demonstrativ gezeigt werden, dass sich das Ein- und Ausschalten der LED 1 mittels zweier unterschiedlicher Varianten, nämlich Funktion und Methode, programmieren lässt! Und zwar mit dem Ergebnis, dass es Sinn macht und tatsächlich funktioniert.

Frage: Lässt sich eine defekte, durchgebrannte LED ein- und ausschalten? Ja und nein! Physikalisch und physisch (= körperlich, stofflich, gegenständlich) lässt sich eine durchgebrannte LED natürlich nicht einschalten! Schließlich ist sie ja defekt! Deshalb lässt sie sich physikalisch auch nicht ausschalten! Elektrisch aber lässt auch eine defekte LED ausschalten! Nämlich am Lichtschalter! Ob dann die LED wirklich ausgeht und nicht mehr leuchtet, interessiert den Lichtschalter dabei nicht. Ebenso interessiert es den Lichtschalter nicht, ob die LED defekt ist oder nicht. Der Grund dafür ist der, dass der Lichtschalter eben nicht intelligent ist und deshalb nicht wissen kann, ob die LED im eingeschalteten Zustand auch wirklich leuchtet oder nicht.

Ebenso verhält es sich mit den von uns programmierten Tastern A und B und dem Ein- und Ausschalten der roten LED 1. Auch die beiden Taster sind dumm und wissen nicht, ob die LED 1 durchgebrannt ist oder nicht! Mit dem kleinen „micro:bit“-Rechner aber haben wir die Möglichkeit, den betreffenden Port „Pin P0“ abzufragen, ob an diesem nach dem Einschalten der LED 1 auch tatsächlich eine Spannung anliegt oder nicht. Das Problem dabei ist dann aber, dass auch im Falle einer defekten LED 1 am Port „Pin P0“ eine elektrische Spannung anliegt! Nämlich in Form der sogenannte Leerlaufspannung! Demzufolge müsste man zusätzlich die Spannung an der LED 1 messen! Noch einfacher und noch besser wäre es, wenn man den Stromfluss in Form der Stromstärke misst. Dazu bräuchte man dann aber ein sogenanntes Amperementer (= Strommessgerät).

Da es aber bei dem kleinen „micro:bit“-Rechner nur ein Voltmeter (= Spannungsmessgerät) gibt, müssen wir mit diesem Vorlieb nehmen und mit diesem die Stromstärke indirekt messen, d.h. den Spannungsabfall an der LED 1 messen und in die entsprechende Stromstärke umrechnen! Außerdem gilt es zu beachten, dass es sich bei dem Voltmeter des kleinen „micro:bit“-Rechners in Wirklichkeit um einen A/D-Wandler handelt, der eine analoge Eingangsspanung bis max. +3,3 V in einen digitalen Wert bis 1023 umwandelt. Aber das hatten wir ja bereits (siehe weiter oben). -

Wenden wir uns wieder der objektorientierten Programmierung und der Programmerweitung „Blinklicht mit roter LED 2“.

Nachfolgend greifen wir das Programm „microbit_teil_03_prog_11.hex“ mit dem Quelltext „microbit_teil_03_prog_11.js“ auf, und fügen den nachfolgenden Programmkode zum Ein- und Ausschalten der roten LED 2 in Form des Blinklichts wie folgt ein:

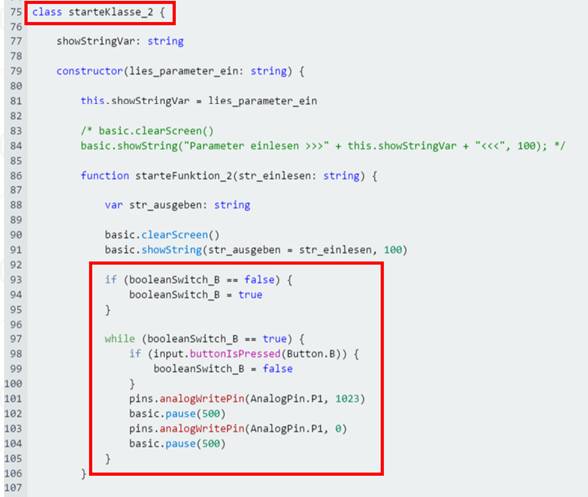
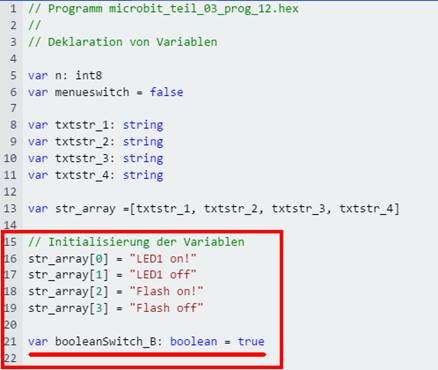
(Bild 14 zur Schaltung „microbit_teil_03_prog_12“)

Neben dem Quellkode im obenstehenden Screenshot muss man noch die Deklaration und Initialisierung der booleschen Variablen „booleanSwitch_B“ vornehmen und die Displayanzeige „Flash …“ entsprechend anpassen:

(Bild 15 zur Schaltung „microbit_teil_03_prog_12“)

Wie man im Programm „microbit_teil_03_prog_12.hex“ mit dem Quelltext „microbit_teil_03_prog_12.js“ sieht, plagen wir uns noch immer mit der Endlosschleife „while (booleanSwitch_B == true) { … }“ herum, stellt sich die Frage, wie man diese wieder mittels Tastendruck auf den Taster B verlassen kann.

Aber das Problem wurde dahingehend gelöst, dass in die Endlosschleife der Einfachheit halber eine weitere Tastendruckabfrage des Taster B eingefügt wurde (siehe Bild 14).

Der Nachteil dabei ist aber, dass der Anwender die Taster B nun zweimal hintereinander drücken muss, um das Blinklicht wieder ausschalten zu können. Praktisch muss man aber nur den Taster B etwas länger, d.h. ein bis zwei Sekunden lang gedrückt halten.

Bedienungsanleitung

Zum Programm „microbit_teil_03_prog_12.hex“ und dem Quelltext „microbit_teil_03_prog_12.js“

1. Starten und Ausführen des Programms

Das in den Arbeitsspeichers des „micro:bit“-Rechners geflashte Programm wird vom System automatisch gestartet und ausgeführt!

Wenn bei dem in den Arbeitsspeicher geladenen Programm nichts anderweitiges programmiert wurde, wie z.B. ein kleiner Begrüßungstext als Laufschrift auf dem „5 x 5 LED-Matrix“-Display, dann bleibt das Display dunkel, sieht man nicht, dass das geladene Programm gestartet wurde! Dies ist auch der Fall, wenn die Laufschrift durchgelaufen ist!

Im vorliegenden Fall, d.h. beim Programm „microbit_teil_03_prog_12.hex“, verhält es sich so, dass sich das herunter geladene und in den Arbeitsspeicher geflashte Programm nach etwa 20 Sekunden von allein meldet und im Display die programmierte Laufschrift „Start ...“ anzeigt.

Nachdem die Laufschrift durchgelaufen ist, bleibt das Display zwar dunkel, aber das Programm mit den zwei Tastern A und B weiterhin aktiv.

4. Taster A zum Aufrufen des Dauerlichts

Nach dem selbständigen Programmstart befindet sich das Programm im Grundmodus bei dem die beiden Taster A und B fortwährend auf einen eventuellen Tastendruck hin abgefragt werden.

Drückt man nun auf den Taster A, so wird die rote LED 1 für die Dauerbeleuchtung eingeschaltet.

Drücken auf den Taster B schaltet die Dauerbeleuchtung der roten LED 1 wieder aus.

5. Taster B zum Aufrufen des Blinklichts

Nach dem selbständigen Programmstart befindet sich das Programm im Grundmodus bei dem die beiden Taster A und B fortwährend auf einen eventuellen Tastendruck hin abgefragt werden.

Um das Blinklicht mit der LED 2 einschalten zu können, muss man zunächst in das entsprechende Untermenü 2 wechseln!

Drücken Sie zu diesem Zweck auf den Taster B, sodass in das Untermenü 2 für den Blinklichtmodus umgeschaltet wird. Dabei erscheint im „5 x 5 LED-Matrix“-Display die Laufschrift „Flash off!“

Durch Tastendruck auf den Taster A lässt sich nun das Blinklicht mit der LED 2 einschalten.

Will man das Blinklicht der roten LED 2 wieder ausschalten, so muss man den Taster B etwa für zwei bis drei Sekunden lang gedrückt halten!

6. Mit dem Kombi-Tastendruck das Untermenü 1 oder 2 verlassen

Wenn man das Dauerlicht mit der LED 1 aufgerufen hat und diese aufleuchtet, dann befindet man sich im Untermenü 1.

Wenn man das Blinklicht mit der LED 2 aufgerufen hat und diese aufleuchtet, dann befindet man sich im Untermenü 2.

Ob man sich aktuell im Untermenü 1 oder Untermenü 2 befindet, erkennt man also daran, dass entweder die LED 1 oder LED 2 leuchtet!

Wenn beide LEDs ausgeschaltet sind, dann drücken Sie auf den Taster A, sodass Sie anhand der Laufschrift im Display erkennen, ob Sie sich im Untermenü 1 oder Untermenü 2 befinden. Außerdem wird dann auch die LED 1 oder LED 2 eingeschaltet.

Durch den kombinierten Tastendruck auf die beiden Taster A&B für die Zeitdauer von bis zu 5 Sekunden lässt sich das Untermenü 1 oder Untermenü 2 wieder verlassen. Dabei erscheint im Display die Laufschrift „exit …“, sodass man sich anschließend wieder im Grundmodus befindet.

7. Mit dem „Reset“-Taster alles wieder auf Anfang setzen

Auf der Rückseite des „micro:bit“-Rechners befindet sich ein sogenannter „Reset“-Taster mit dem sich der Rechner neu starten lässt. Dabei wird auch das zuvor in den Arbeitsspeicher geflashte Programm wieder neu gestartet, sodass sich dieses wieder im zuvor beschriebenen Grundmodus befindet! -

Wir befassen uns weiterhin mit der Endlosschleife „while (booleanSwitch_B == true) { … }“ und stellen uns ein weiteres Mal die Frage, wie man diese in verbesserter Form mittels Tastendruck auf den Taster B verlassen kann (siehe roter Kasten im Bild 14).

Diesbezüglich mussten wir ja bisher die schmerzliche Erfahrung machen, dass sich eine einmal gestartete Endlosschleife nicht wieder so einfach verlassen lässt. Vielleicht liegt es ja auch daran, dass die Endlosschleife immer erst dann mittels Tastendruck wieder verlassen werden soll, nachdem diese schon gestartet und mehrfach durchlaufen wurde.

Vielleicht ist es ja besser, wenn die Endlosschleife immer erst dann durchlaufen wird, wenn kein Taster B gedrückt wurde:

(Bild 16 zur Schaltung „microbit_teil_03_prog_13“)

Es ist sicherlich besser, wenn man erst dann in die Endlosschleife geht, wenn der Taster B zum Abbrechen des Blink-Programms nicht gedrückt wurde (siehe roter Kasten im Bild 16). Aber eine spürbare Verbesserung bei der Bedienung des Programms „microbit_teil_03_prog_13.hex“ mit dem Quelltext „microbit_teil_03_prog_13.js“ stellt sich trotzdem nicht ein, weil sich an der Menüstruktur mit den gestaffelten Menüebenen mit den Untermenüs eben doch nichts ändert! -

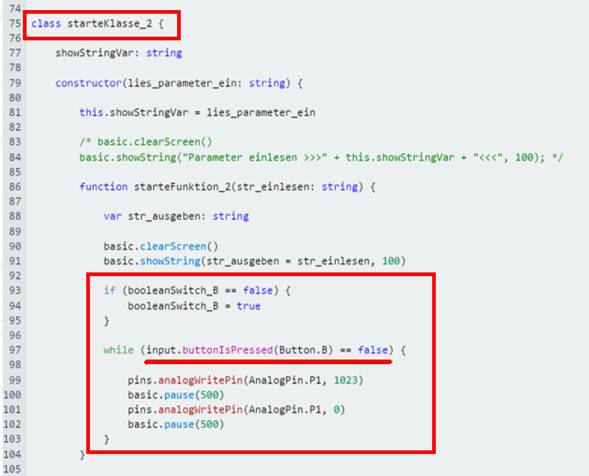
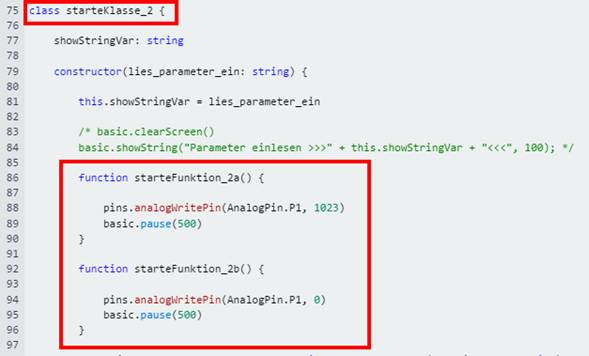
Beim nächsten Programm „microbit_teil_03_prog_14.hex“ mit dem Quelltext „microbit_teil_03_prog_14.js“ gehen wir in der Klasse „starteKlasse_2“, die für das Blinklicht zuständig ist, arbeitsteilig vor. Dazu „klonen“ wir die Funktion „starteFunktion_2(str_einlesen: string)“, indem wir diese einfach kopieren und entsprechend in „starteFunktion_2a()“ und „starteFunktion_2b()“ umbenennen. Außerdem verzichten wir auf die Übergabe eines Parameters im Kopf der Funktion, da wir diese Option im Moment nicht brauchen. Bezüglich der Arbeitsteilung gehen wir so vor, dass man mit der Funktion „starteFunktion_2a()“ die rote LED 2 einschaltet und diese wieder mit der Funktion „starteFunktion_2b()“ ausschaltet:

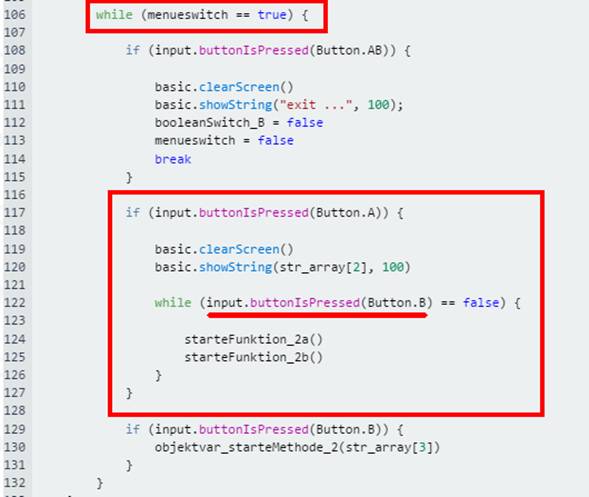
(Bild 17 zur Schaltung „microbit_teil_03_prog_14“)

Gestartet wird das Blinklicht mittels Funktionsaufruf der beiden Funktionen „starteFunktion_2a()“ und „starteFunktion_2b()“ in der Untermenü-Schleife „while (menueswitch == true) { … }“.

Wie man per Tastendruck auf die Taster A und B in das Untermenü zum Starten des Blinklichts gelangt, ist in der

· Bedienungsanleitung im
Punkt „5. Taster B zum Aufrufen des Blinklichts“ beschrieben.

Beim Statement „while (input.buttonIsPressed(Button.B) == false) { … }“ verhält es sich so, dass der Taster B abgefragt wird, der für das Ausschalten der roten LED 2 zuständig ist. Demzufolge lässt sich die rote LED 2 immer nur dann einschalten, solange der Taster B nicht gedrückt wird:

(Bild 18 zur Schaltung „microbit_teil_03_prog_14“)

Dass das Statement „while (input.buttonIsPressed(Button.B) == false) { … }”, d.h. die bisher problematische „while ()”-Endlosschleife, nun endlich so funktioniert, wie man das erwartet, liegt u.a. daran, dass diese immer nur dann aufgerufen wird, solange der Taster B nicht gedrückt wird!

Die bessere Bedienung ist aber auch eine Folge der konsequenten Trennung beim Ein- und Ausschalten des Blinklichts in Form der beiden Funktionen „starteFunktion_2a()“ und „starteFunktion_2b()“ in der Untermenü-Schleife „while (menueswitch == true) { … }“ (siehe im Bild oben).

3.3 Auf dem Weg zur Eintastenbedienung

Wie ja nun schon mehrmals erwähnt, liegt die Herausforderung beim kleinen „micro:bit“-Rechner wegen des fehlenden LCD-Displays und der Tastatur u.a. darin, die beiden Taster A und B möglichst so zu verwenden, dass sich auch umfangreichere Programme möglichst intuitiv bedienen lassen. Deshalb machen wir uns an die Arbeit und verändern das bisherige Programm „microbit_teil_03_prog_14“ dahingehend, sodass sich das Dauerlicht mit der roten LED 1 mit dem Taster A ein- und ausschalten lässt und das Blinklicht mit der roten LED 2 mit dem Taster B.

(Bild 19 zur Schaltung „microbit_teil_03_prog_15“)

Wie man im obenstehenden Screenshot im roten Kasten sieht, wurde das Dauerlicht mit der roten LED 1 nebst des Ein- und Ausschaltens mit dem Taster A in nur einer Funktion und zwar in der Funktion „starteFunktion_1()“ programmiert. Dabei leuchtet die rote LED 1 am Port „Pin P0“. Da wir es jetzt bei dem Taster A mit einem Wechseltaster für das Ein- und Ausschalten zu tun haben, braucht es die boolesche Variable „booleanSwitch_A“ als Schalter, um den jeweiligen Schaltzustand „ein“ oder „aus“ speichern und übermitteln zu können.

Die Methode „starteMethode_1(str_einlesen: string)“ (siehe grüner Kasten im obenstehenden Bild 19) ist noch ein Überbleibsel, um die rote LED 1 mittels des Tasters B vom Untermenü 1 aus ausschalten zu können.

Im Hauptprogramm aber, in dem man sich automatisch nach dem Programmstart befindet, dient der Tasters B im Moment immer noch dazu ins Untermenü 2 umzuschalten.

Mit dem Programm „microbit_teil_03_prog_15.hex“ und dem Quelltext „microbit_teil_03_prog_15.js“ lässt sich nicht nur das Dauerlicht der roten LED 1 mittels des Tasters A ein- und ausschalten, sondern auch das Blinklicht der roten LED 2. Dazu muss man aber zuvor mittels des Tasters B ins Untermenü 2 umgeschaltet haben. -

Bei der Eintastenbedienung im Programm „microbit_teil_03_prog_16.hex“ und dem Quelltext „microbit_teil_03_prog_16.js“ geht es darum, dass sich das Dauerlicht mit der roten LED 1 mit dem Taster A ein- und ausschalten lässt und das Blinklicht mit der roten LED 2 mit dem Taster B. 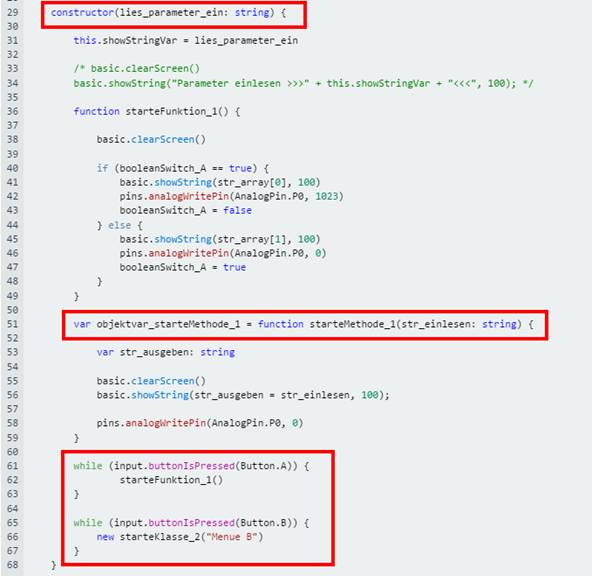Und zwar so, dass man nicht mehr mittels des Tasters B ins Untermenü 2 umschalten muss, um das Blinklicht mit der roten LED 2 einschalten zu können!

Demzufolge wird die boolesche Variable „var menueswitch = false“ für die Menüumschaltung nicht mehr benötig! Damit es aber nicht zu kompliziert wird und wir den Überblick verlieren, entfernen wir diese zunächst nur in der Klasse „starteKlasse_1“ bzw. im dazugehörigen Konstruktor „constructor(lies_parameter_ein: string)“:

(Bild 20 zur Schaltung „microbit_teil_03_prog_16“)

Wie man im obenstehenden Screenshot sieht, vereinfachen sich jetzt die Dinge plötzlich drastisch (siehe großer roter Kasten)! -

Etwas aufwendiger und komplexer wird es, wenn man die boolesche Variable „var menueswitch = false“ aus der Klasse „starteKlasse_2“ bzw. im dazugehörigen Konstruktor „constructor(lies_parameter_ein: string)“ entfernt:

(Bild 21 zur Schaltung „microbit_teil_03_prog_16“)

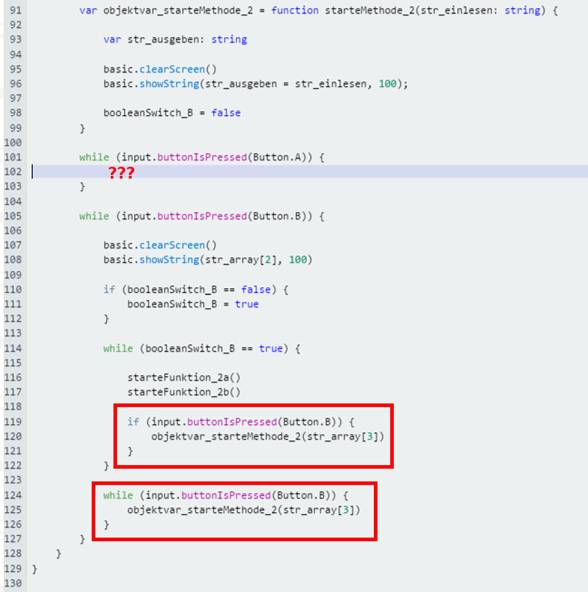
Wie man im obenstehenden Screenshot sieht, müssen noch weitere Programmänderungen vorgenommen werden (siehe die beiden roten Kästen). Außerdem muss auch noch der Taster A (siehe „???“) programmiert werden, damit sich das Dauerlicht wieder ein- oder ausschalten lässt. Aber insgesamt funktioniert das Programm „microbit_teil_03_prog_16.hex“ und dem Quelltext „microbit_teil_03_prog_16.js“ schon recht gut.

Besonders interessant ist, dass sich nun mit beiden Taster A und B sowohl das Dauerlicht (Taster A) als auch das Blinklicht (Taster B) ein- und ausschalten lassen, sodass sich jetzt beide Lichter auch zusammen einschalten lassen.

Das Programm „microbit_teil_03_prog_17.hex“ und dem Quelltext „microbit_teil_03_prog_17.js“ ist nun ausgereift, übersichtlich, kompakt und lässt sich intuitiv bedienen.

Interessant ist in diesem Zusammenhang, dass sich aus einer Klasse heraus eine andere Klasse aufrufen lässt. Selbstverständlich lässt sich dabei auch die eigene Klasse ein weiteres Mal aufrufen:

(Bild 22 zur Schaltung „microbit_teil_03_prog_17“)

Wenn man beide LEDs einschaltet, wobei die rote LED2 blinkt, dann lässt sich beobachten, dass die rote LED 1 ebenfalls leicht im Takt, d.h. synchron zur LED 2 blinkt. Finden Sie heraus, woran das liegt und erklären Sie das Phänomen! -

3.4 Vertrauen ist gut, Kontrolle besser

Wie allgemein bekannt sein dürfte, machen Glühlampen ihrem Namen alle Ehre. Soll heißen, dass diese mehr glühen, d.h. Wärme produzieren als Licht. Demzufolge haben Glühlampen wegen der Hitze des Glühfadens und dessen Verschleiß nur eine begrenzte Lebensdauer. Hinzu kommt, dass Glühlampen immer dann kaputt gehen, wenn man nicht damit rechnet oder wenn man es garantiert nicht gebrauchten kann, weil man genau in dem Moment auf das Licht, die Beleuchtung, die Helligkeit angewiesen ist, wenn der Glühfaden durchbrennt.

Wenn in der Praxis Signalgeber und Leuchtmittel weiter auseinander liegen, dann ist es wahrscheinlich, dass man das Leuchtmittel selbst nicht mehr sieht, weil es zu weit weg entfernt ist oder sich hinter einer Ecke befindet. Spätestens dann wünscht man sich eine Kontrollleuchte direkt beim Ein- und Ausschalter, um kontrollieren zu können, ob das Leuchtmittel in Form der Lampe auch wirklich leuchtet oder nicht. Zu diesem Zweck darf die Kontrollleuchte aber nicht anzeigen, dass der Strom zur Lampe eingeschaltet wurde, sondern sie sollte tatsächlich signalisieren, dass die Lampe brennt, also hell erleuchtet ist. Zu diesem Zweck müsste man streng genommen die Helligkeit direkt an der Lampe messen, z.B. mittels eines Fotowiderstandes, einer Fotodiode oder die Temperatur, d.h. die Hitze an der Glühlampe.

Da wir im Moment weder über einen Fotowiderstand, eine Fotodiode noch über einen externen Temperatursensor verfügen, müssen wir uns etwas anderes einfallen lassen, um kontrollieren zu können, ob das Leuchtmittel eingeschaltet wurde und leuchtet oder nicht.

Da unser „micro:bit“-Rechner über ein integriertes Voltmeter (= Spannungsmesser) in Form eines A/D-Wandlers verfügt, messen wir zur Kontrolle, ob das Leuchtmittel, d.h. unsere LED, leuchtet oder nicht, den Spannungsabfall an der LED. Dabei stellt sich dann gleich die Frage, wie groß der Spannungsabfall an der LED werden kann. Dieser richtet sich nach der Art der LED, d.h. nach deren Farbe. Wegen der Kennlinie einer LED, deren Temperaturempfindlichkeit und der Größe des Vorwiderstandes kann die Flussspannung bei der roten LED im einen oder anderen Fall etwas von 1,6 V abweichen. Dies kann dann auch von der angeschlossenen Gleichspannungsquelle und deren Versorgungsspanung abhängen.

Wie wir bereits wissen, handelt es sich bei dem integrierten A/D-Wandler um einen 10-Bit-Wandler, sodass sich mit diesem dezimale Werte von 0 … 1023₁₀ erfassen lassen (siehe weiter oben): 10 Bit = 11 1111 1111₂ = 2⁹ + 2⁸ + 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2¹ + 2⁰ = 1023₁₀ → U_P0 = +3,3 V → 3,3 V / 1024₂ Bit = 0,0032227 V/Bit = 3,227 mV/Bit ≈ 3,23 mV/Bit.

Dabei gilt es zwischen dem dezimalen Wertebereich von 0 … 1023 mit 1023 als Maximalwert zum weiteren dezimalen Rechnen mit den angezeigten Messwerten des Millivoltmeters (A/D-Wandler) und den binären Bitwerten 1023 + 1 = 1024₂ als interne, binäre Messsignale und -werte des A/D-Wandlers zu unterscheiden!

In der Praxis kann es z.B. bei der externen Spannungsversorgung über das Micro-USB-Kabel und die interne Strombegrenzung im Sinne einer elektronischen Sicherung bei den Ports „Pin P0“ bis „Pin P2“ und auch „Pin 3V“ dazu kommen, dass die an den Ports zur Verfügung stehende Spannung etwas höher oder niedriger ausfällt.

Im vorliegenden Fall beträgt die extern verfügbare Spannung am Ringanschluss „3V“ gegen „GND“ (= Masse) nur U_3V = +3,24 V. Dabei wurde die Spannung mittels eines Multimeters gemessen, wobei keinerlei Verbraucher z.B. in Form einer roten LED 1 angeschlossen waren. Demzufolge handelt es sich bei der gemessenen Spannung U_3V = +3,24 V um eine sogenannte Leerlaufspannung, die sich bei einer entsprechenden Belastung durch einen „stromfressenden“ Verbraucher entsprechend verringern kann.

Deshalb empfiehlt es sich, die Spannung am Ringanschluss „3V“ von Fall zu Fall neu zu messen, um auf diese Weise zu prüfen, ob die Spannungsquelle am Port U_3V nicht versehentlich überlastet wird.

Diesbezüglich sei nochmals daran erinnert, dass die externe Spannungsquelle am Ringanschluss „3V“ nicht gegen Überlastung abgesichert ist. Dies gilt es insbesondere dann zu beachten, wenn anstelle der Stromversorgung über USB-Kabel ein externes Batteriepack mit zwei 1,5 Volt Batterien der Größe „AA“ oder „AAA“ verwendet wird! -

Übrigens: Bei der kleinen Anschlussbuchse für das Anschließen einer externen Stromversorgung bis U_Batterie = +3,3 V (siehe engl. Beschriftung „battery connector“ im Bild 01) scheint es sich um ein spezielles Exemplar vom Typ „JST X2B-PH-SM4-TB“ zu handeln, da man dieses im einschlägigen Elektronik-Fachgeschäft nicht bekommt, dieses dort auch nicht bekannt zu sein scheint.

Diesbezüglich verhält es sich aber so, dass man das externe und wegen der Exportsteuer aus England extrem teure Batterieanschlusskabel nebst Batteriepack (siehe eBay „Power Up your BBC Micro:Bit -Battery Power Supply Box - 2 AAA Switched“) gar nicht braucht, da sich auch ein herkömmliches Batteriepack nebst „Ein/Aus“-Schiebeschalter für 2 x 1,5 Volt AA-Batterien direkt an die Ringanschlüsse „3V“ (= Pluspol „+“) und „GND“ (= Minuspol „-“) mittels „Bananen“-Stecker anschließen lässt! -

Das Messen der sogenannten Leerlaufspannung ohne Anschalten eines Lastwiderstandes im Sinne eines Verbrauchers ist bei Niedervolt-Netzteilen ohne elektronische Sicherung, Strombegrenzung oder Spannungsstabilisierung mittels Leistungselektronik unkritisch, da diese ziemlich konstant ist. Ähnlich verhält es sich bei Batterien, die zur Stromversorgung eingesetzt werden. Zwar verringert sich die Batteriespannung mit zunehmender Entladung der Batterien, bleibt aber trotzdem halbwegs konstant. Es sei denn, dass die Batterien total leer sind und keinen Strom mehr liefern.

Bei elektronischen Netzteilen zur Stromversorgung, die intern mittels Operationsverstärker, Komparatoren (= Spannungsvergleicher), DC/DC-Wandlern sowie FET- und MOS-FET-Transistoren ausgerüstet sind, kann es wie bei unserem „micro:bit“-Rechner vorkommen, dass die Leerlaufspannung quasi „undefiniert in der Luft hängt“ und von Messung zu Messung „spinnt“. Diesbezüglich spricht man dann von einem „offenen Eingang“.

Im vorliegenden Fall benutzen wir als externe Spannungsquelle den Port „Pin P2“, der im Leerlauf ohne Last betrieben wird. Die dabei mit dem einfachen Programm microbit_teil_03_prog_18.hex und dem Quelltext microbit_teil_03_prog_18.js gemessene Leerlaufspannung bewegt sich im Bereich von 1,61 V bis 1,63 V, im Mittel also um die (1,61 V + 1,63 V) / 2 = 3,24 V / 2 = 1,62 V.

Demzufolge müsste der A/D-Wandler einen umgerechneten, dezimalen Wert von 1024₂ Bit / 3,24 V * 1,62 V = 512 Bit anzeigen. Dabei handelt es sich beim dem Quotienten 1024₂ Bit / 3,24 V um den Kehrwert ( = 1 / … ) der sogenannten Bereichsbreite des 10-Bit-A/D-Wandlers (siehe weiter unten).

Angezeigt werden aber Werte von 389, 546, 253, 255, 440, 510 usw., d.h. im Mittel also (389 + 546 + 253 + 255 + 440 + 510) Bit / 6 Messwerte = 2393 Bit / 6 Messungen ≈ 399 Bit, was einer Spannung von 399 Bit * 3,24 V / 1024 Bit ≈ 1,26 V entspräche. Das wären dann 100 % / 3,24 V * 1,26 V = 38,9 %. Da dieser Wert inakzeptabel niedrig ist, ist diese Art der Messung der Leerlaufspannung ungeeignet, da sich so der Innenwiderstand R_i der Spannungsquelle nicht zuverlässig berechnen lässt.

Als Nächstes schließen wir nun eine rote LED zusammen mit einem Vorwiderstand R_Vor = 100 Ω in Reihe an den Port „Pin P2“ an, wobei dieser immer noch im Leerlauf betrieben, da die rote LED erst ab einer Flussspannung von U_Fluss = 1,6 V elektrisch leitend wird! Mit dem Multimeter messen wir nun eine Leerlaufspannung von 1,07 V bis 1,08 V, im Mittel also (1,07 V + 1,08 V) / 2 = 2,15 V / 2 = 1,075 V. Dabei zeigt das Messprogramm in der Laufschrift folgende Messwerte an: 269, 279, 266, 281, 356, 251, d.h. im Mittel also (269 + 279 + 266 + 281 + 356 + 251) Bit / 6 Messungen= 1702 Bit / 6 Messungen = 283,7 Bit ≈ 284 Bit, was einer Spannung von 3,24 V / 1024 Bit * 284 Bit ≈ 0,899 V entspräche. Das wären dann 100 % / 3,24 V * 0,899 V = 27,75 %. Da dieser Wert ebenfalls inakzeptabel niedrig ist, ist auch diese Art der Messung der Leerlaufspannung ungeeignet!

Was wir also nach wie vor bräuchten, wäre ein definierter, stabiler und verlässlicher Systemzustand am Ausgang der externen Spannungsversorgung am Port „Pin P2“.

Diesbezüglich greifen wir nun zu einem Trick und erzwingen eine stabile und verlässliche Leerlaufspannung, indem wir den Ausgang am Port „Pin P2“ mit einem „Lastwiderstand“ von R_Last = 9,97 KΩ „belasten“, den wir parallel zur roten LED nebst Vorwiderstand schalten, sodass wir eine halbwegs stabile Leerlaufspannung erhalten.

Mit dem Multimeter messen wir nun eine konstante Leerlaufspannung von 0,003 V. Dabei zeigt das Messprogramm in der Laufschrift folgende Messwerte an: 6, 9, 9, 7, 6, 6, 4, 6, 9, 6, d.h. im Mittel also (6 + 9 + 9 + 7 + 6 + 6 + 4 + 6 + 9 + 6) Bit / 10 Messungen = 68 Bit / 10 Messungen = 6,8 Bit ≈ 7 Bit, was einer Spannung von 3,24 V / 1024 Bit * 7 Bit ≈ 0,022 mV entspräche. Das wären dann 100 % / 3,24 V * 0,022 V = 0,679 %, sodass man nun mit dieser marginalen Ungenauigkeit leben kann.

Spätestens jetzt wird also deutlich, dass es absolut sinnvoll ist, eine hochohmige Spannungsquelle wie sie der Port „Pin P2“ darstellt, durch einen zugeschalteten, d.h. parallelen Belastungswiderstand niederohmig zu machen, d.h. zu belasten, um auf diese Weise zu verlässlichen, stabilen Messwerten im Falle des Leerlaufs zu gelangen.

Das zuvor beschriebene Verhalten der externen Spannungsquelle am Port „Pin P2“, die im Leerlauf ohne Last betrieben wird, entspricht in etwa dem einer total leer gesaugten, d.h. entladenen Batterie.

>> Eine elektrische Zelle ist ein elektrochemischer Energiespeicher und ein Energiewandler. Bei der Entladung wird gespeicherte chemische Energie durch die elektrochemische Redoxreaktion in elektrische Energie umgewandelt. Diese kann von einem vom Stromnetz unabhängigen elektrischen Verbraucher genutzt werden. Alternativ kann sie auch in einem vom Stromnetz abhängigen Verbraucher eingesetzt werden, um kurzzeitige Ausfälle im Stromversorgungsnetz zu überbrücken und so eine unterbrechungsfreie Stromversorgung sicherstellen.

Primärzellen können nur einmal entladen und nicht wieder aufgeladen werden. In diesen Zellen sind die Reaktionen bei der Entladung teilweise umkehrbar, das führt jedoch nicht zur Wiederherstellung eines dem Neuzustand ähnlichen Energieinhalts. Dagegen sind die wiederaufladbaren Sekundärbatterien (Akkumulatoren) weitgehend in den Ladezustand ähnlich dem Neuzustand zu bringen, so dass eine mehrfache Umwandlung von chemischer in elektrische Energie und zurück möglich ist. (…)

Die schwächste Zelle bestimmt die Qualität einer Batterie. In Parallelschaltung kommt es durch Ausgleichsströme zu größeren Verlusten, wenn die Zelle mit geringerer Kapazität früher entladen ist. In Reihenschaltung bricht die Spannung unter Last eher zusammen, weil stärkere, noch geladene Zellen Strom durch schwächere, schon entladene Zellen treiben. Deren Innenwiderstand führt nach dem Ohmschen Gesetz zu einer Zellerwärmung, ohne dass die elektrische Energie nutzbar ist. << (Quelle: Wikipedia)

Eine Batterie, auch Primärelement genannt, ist ein chemisches Element mit einem Elektrolyten zwischen den Elektroden, in dem die chemische Energie gespeichert ist, die bei der Entladung in elektrische Energie umgewandelt wird.

Im Gegensatz zu einem Akku, der auch Sekundärelement genannt wird, bei dem der chemische Prozess bei der Entladung als auch beim Aufladen wieder umkehrbar sind, lässt sich eine Batterie, bei der die internen chemischen Zersetzungsprozesse unwiderruflich also nicht umkehrbar sind, nicht wieder aufladen.

Vielleicht kennen Sie ja noch die alten Zink-Kohle-Batterien mit 3 Volt Nennspannung, die von der Größe her zwei in Reihe geschalteten 1,5 Volt Batterien entsprachen und z.B. in Taschenlampen verwendet wurden. Die genaue Bezeichnung lautet „Duplex Stabbatterie“. Wenn diese Batterien zur Neige gingen, weil sich die Elektrode durch den chemischen Umwandlungsprozess zersetzte, dann konnte man ihnen noch etwas Leben einhauchen, indem man sie auf den Heizkörper, nicht aber auf die heiße Ofenplatte(!), legte. Durch die handwarme Erwärmung wurden die frei beweglichen Elektronen in den Elektroden zu Schwingungen angeregt, sodass man noch den letzten Funken Energie aus der Batterie ausquetschen konnte. Aber länger als 5 bis 10 Minuten konnte man damit die Taschenlampe dann auch nicht mehr leuchten lassen, weil der Innenwiderstand einfach schon zu groß war, um größere Ströme entnehmen zu können. Einer Batterie sieht man es von außen also nicht an, ob sie schon leer ist, d.h. einen hohen Innenwiderstand hat, oder nicht!

Ähnlich verhält es sich bei einer hochohmigen Spannungsquelle mit großem Innenwiderstand wie z.B. die externe Spannungsquelle am Port „Pin P2“. Auch dieser sieht man es nicht an, wie groß der Innenwiderstand ist und welche maximale Stromstärke sich entnehmen lässt! Aber wir haben ja eine Methode gefunden, wie man herausfinden kann, wie groß die verfügbare Stromstärke einer hochohmigen Spannungsquelle sein kann, indem wir nämlich den Lastwiderstand am Port „Pin P2“ schrittweise verringert haben! Und zwar so lange, bis die in der Laufschrift angezeigte Ausgangsspannung der tatsächlich mit dem Voltmeter gemessenen entsprach! Dabei zeigte es sich, dass die vom A/D-Wandler angezeigte Spannung von U_Last = 0,022 V bei einem Lastwiderstand von R_Last = 9,97 KΩ ziemlich stabil war.

Nach dem Ohmschen Gesetz berechnet sich dann der im Lastwiderstand fließende Strom wie folgt: I_Last = U_Last / R_Last = 0,022 V / 9,97 KΩ = 22 mV / 9,97 KΩ = 22 * 10^-3 V / 9,97 * 10³ Ω = 22 / 9,97 * 10^-6 A ≈ 2,21 µA. Das ist eine sehr, sehr kleine Stromstärke, die sich nur mit teueren Messgeräten messen lässt. -

3.5 Black Box - das unbekannte Wesen?

Wir wissen jetzt, dass es bei elektronischen Schaltungen und Geräten in denen FET-, MOS-FET-Transistoren, Operationsverstärker, Spannungs-Frequenzwandler, Komperatoren, A/D-Wandler, Konstantstromquellen, Leistungselektronik zur Spannungsstabilisierung oder Strombegrenzung auch hochohmige Spannungsquellen gibt, die sich durch einen hohen Innenwiderstand und sehr kleine Ströme auszeichnen.

Da hochohmige Spannungsquellen nur sehr kleine Ströme liefern und das auch noch dazu bei stark einknickenden Ausgangsspannungen, gibt es für diese quasi nur eine praktische Anwendung. Und zwar die, einen niederohmigen Ausgang hochohmig zu machen, sodass dieser „kurzschlussfest“ ist und zwar dadurch, dass keine größeren Ströme fließen können. So lassen sich z.B. mit einer hochohmigen Spannungsquelle ganz gut FET- und MOS-FET-Transistoren ansteuern, da sich das Gate, so heißt der Basisanschluss bei diesen, im Gegensatz zu Transistoren, leistungslos ansteuern lässt, sodass eben kein Strom in das Gate fließt.

Wie man mit einer hochohmigen Spannungsquelle umgeht und dieser „Manieren“ beibringt, sodass sich stabile Spannungen und Ströme, wenn auch sehr kleine, einstellen, haben wir ja schon beim A/D-Wandler am Port „Pin P2“ kennengelernt. Und zwar für den Betriebssystemzustand bei dem am Spannungsausgang des A/D-Wandlers keine Spannung anliegt, sodass dessen Ausgang nahezu auf Massepotential mit null Volt liegt. Der Grund dafür ist dabei der, dass der A/D-Wandler noch nicht mittels „JavaScript“-Programm programmiert, d.h. initialisiert wurde, sodass sich dieser im Leerlauf befindet und keine Aufgabe zu bewerkstelligen hat.

Der A/D-Wandler war also für uns von außen gesehen, d.h. dem Ausgang am Port „Pin P2“ eine sogenannte „Black Box“ mit einem bisher nicht exakt definierten Nullpotential von ≈ 0 Volt am Ausgang.

Nachfolgend befassen wir uns mit einem hochohmigen Spannungseingang eines sogenannten „Berührungssensors“. In großen Warenhäusern, neudeutsch „Shopping Mall“, gibt es an mehreren Stellen Fahrstühle, die anstelle von Bedientastern über Berührungssensoren verfügen, sodass eine leichte Berührung ausreicht, um über den Sensor das gewünschte Stockwerk auszuwählen.

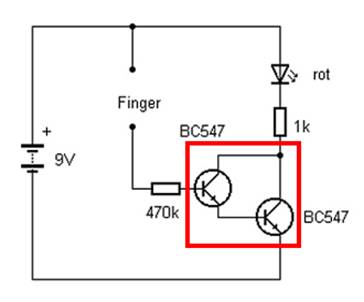
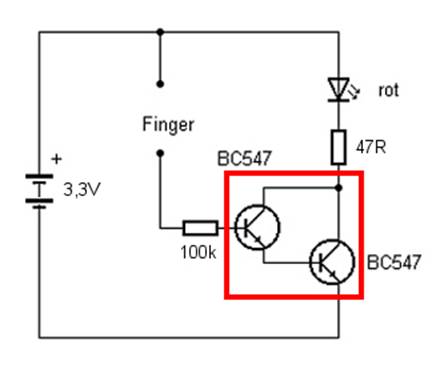
Vielleicht haben Sie ja zu Hause im Schlafzimmer auf dem Beistelltischchen eine elektronisch gedimmte Nachtischlampe, deren Helligkeit sich durch Berühren in drei Stufen von dunkel bis hell leuchtend einstellen lässt. Wie ein solcher Berührungssensor funktioniert, lässt sich anhand der nachfolgenden Schaltung ausprobieren:

(Bild 23: Berührungssensor mittels Darlington-Schaltung)

Wie man in der obenstehenden Schaltung anhand des roten Kastens sieht, wurden zwei NPN-Transistoren quasi in Reihe, d.h. hintereinander, geschaltet. Diese Art des Zusammenschaltens zweier Transistoren als Emitterfolger nennt man „Darlington-Schaltung“ bei der sich die resultierende (Großsignal-) Stromverstärkung B = B₁ * B₂ beider Transistoren im Bereich von ≈ 500 … 10⁴ bewegt. (siehe Wikipedia).

Eine rote LED benötigt zum hellen Leuchten eine Flussspannung von U_Fluss = 1,6 V. Dabei fließt beim hellen Leuchten ein Durchlassstrom von I_Fluss = 20 mA, sodass sich am Kollektorwiderstand R_C = 1 KΩ rein rechnerisch ein Spannungsabfall von U_RC = I_Fluss * R_C = 20 mA * 1 KΩ = 20 V einstellen würde. Da wir aber nur über eine Gesamtspannung von U_Batterie = 9 V verfügen, bleibt für den Spannungsabfall am Kollektorwiderstand R_C nur eine entsprechend kleinere Spannung übrig:

U_Batt. = U_Fluss + U_RC + ( U_CE1 + U_BE2 ) = U_Fluss + U_RC + U_CE2 →

U_RC = U_Batterie - ( U_Fluss + U_CE2 ) = 9 V - ( 1,6 V + 0,4 V ) = 9 V - 2,0 V = 7,0 V

= 9,3 V - ( 1,95 V + 0,69 V ) = 9,3 V - 2,64 = 6,6 V gemessen!

Wenn man die beiden Anschlüsse beim Fingerkontakt mittels Drahtbrücke miteinander verbindet, dann folgt für den Spannungsumlauf am Basiswiderstand R_Basis:

U_Batt. ≈ U_{R Basis} + 2 * U_BE →

U_{R Basis} ≈ U_Batterie - ( 2 * U_BE ) ≈ 9,3 V - ( 2 * 0,69 V ) = 9,3 V - 1,38 V = 7,92 V

Der Basisstrom I_Basis beider Transistoren durch den Basiswiderstand R_Basis berechnet sich dann zu:

I_Basis = U_{R Basis} / R_Basis = 7,92 V / 470 KΩ = 7,92 V * 10³ / ( 470 * 10³ Ω * 10³)

= 7920 V / 470 Ω * 10^-6 = 16,85 µA ≈ 17 µA

Wie man sieht, ist der Basisstrom durch beide Transistoren wegen der hohen Verstärkung extrem klein, lässt sich dieser nur mit teueren Multimetern messen. Dabei muss aber der Basisstrom so klein sein, damit man bei Berührung mit den Fingern den geringen Körperstrom einleiten und nutzen kann, um die rote LED zum Leuchten zu bringen!

Der oben im Bild 23 zu sehende Berührungssensor mittels Darlington-Schaltung wird an einer 9-Volt-Blockbatterie betrieben und darf deshalb nicht mit dem „micro:bit“-Rechners verbunden werden, da dessen Ports „Pin P0“ bis „Pin P2“ nur mit einer Spannung von bis zu U_3V = 3,3 V betrieben werden dürfen!

Aber das Umgekehrte ist natürlich erlaubt, dürfen wir die Schaltung des Berührungssensors ohne 9-Volt-Blockbatterie direkt an die Spannungsversorgung unseres „micro:bit“-Rechners , d.h. an dessen Ports „Pin P0“ bis „Pin P2“ oder an dem Pin U_3V = 3,3 V anschließen. Dabei wird natürlich die rote LED des Berührungssensors wegen der geringeren Versorgungsspanung nicht mehr so hell leuchten wie zuvor.

Da wir trotzdem möchten, dass die rote LED wieder hell leuchtet und rote Bäckchen bekommt, kommen wir nicht umhin, den Vorwiderstand in Form des Kollektorwiderstandes R_C = 1 KΩ neu zu berechnen und entsprechend zu verringern, damit die rote LED wieder hell leuchtet!

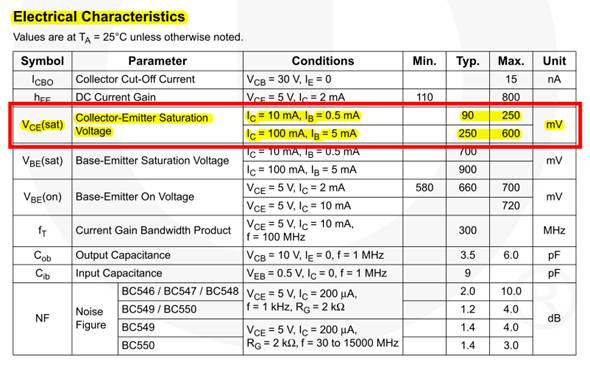
Demzufolge darf sich die Flussspannung von U_Fluss = 1,6 V nicht ändern! Die zum hellen Leuchten der roten LED erforderliche Fluss- bzw. Durchlassspannung wird sich aber nur einstellen, wenn sich beide NPN-Transistoren „BC 547“ im Durchlass-, übersteuerten Bereich oder Sättigungsbereich betreiben lassen:

(Bild 24: maximale Werte bei der Sättigung des BC 547)

Erinnern wir uns bezüglich der Reihenschaltung an die Regel „Großer Widerstand = großer Spannungsabfall und kleiner Widerstand = kleiner Spannungsabfall am jeweiligen Widerstand!“

Wenn also der Transistor bei einem Kollektorstrom I_C = 100 mA im Sättigungsbereich betrieben wird, dann ist der dynamische Durchgangswiderstand der CE-Strecke sehr niedrig, sodass der Spannungsabfall maximal nur U_{CE sat} < 0,6 V groß sein darf:

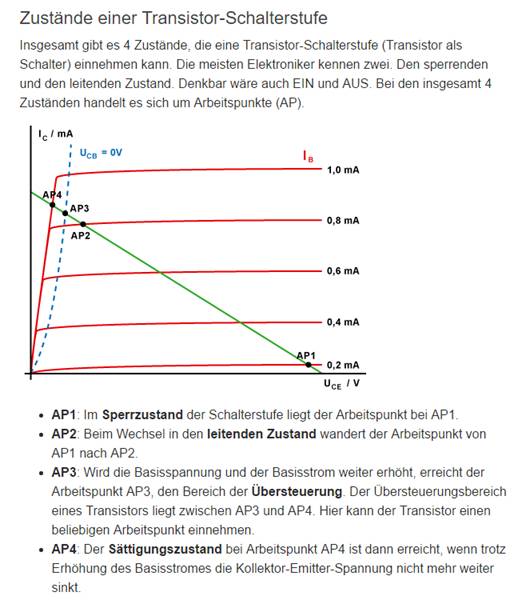
(Bild 25: Kennlinienfeld eines Transistors mit Sättigung im AP4)

Werfen wir also nochmals einen Blick auf die Berechnung des Spannungsabfalls am Kollektorwiderstand R_C (= Vorwiderstand der roten LED):

U_Batt. = U_Fluss + U_RC + ( U_CE1 + U_BE2 ) = U_Fluss + U_RC + U_CE2 →

U_RC = U_Batterie - ( U_Fluss + U_CE2 ) = 9 V - ( 1,6 V + 0,4 V ) = 9 V - 2,0 V = 7,0 V

= 9,3 V - ( 1,95 V + 0,69 V ) = 9,3 V - 2,64 = 6,6 V gemessen!

Damit die rote LED wirklich hell leuchtet, darf die Flussspannung U_Fluss = 1,6 V bei einer verringerten Versorgungsspannung von U_3V = 3,3 V nicht unterschritten werden:

U_3V = U_Fluss + U_RC + ( U_CE1 + U_BE2 ) = U_Fluss + U_RC + U_CE2 →

U_RC = U_3V - ( U_Fluss + U_CE2 ) = 3,3 V - ( 1,6 V + 0,4 V ) = 3,3 V - 2,0 V = 1,3 V

= 3,3 V - ( 1,97 V + 0,72 V ) = 3,3 V - 2,69 V = 0,61 V → Mittelwert = 0,955 V

= 0,45 V gemessen!

U_CE = U_3V - U_Fluss - U_RC = 3,3 V - 1,97 V - 0,61 V = 0,72 V

= 0,71 V gemessen!

Wie bereits oben gezeigt, befinden sich die beiden Transistoren mit U_CE = 0,71 V im übersteuerten Bereich, d.h. kurz vor der Sättigung, sodass wir nun den Kollektorwiderstand R_C (= Vorwiderstand der roten LED) wie folgt berechnen können:

R_C = U_RC / I_LED = 0,955 V / 20 mA = 0,955 * 10³ V / ( 20 * 10^-3 A * 10³ )

= 995 / 20 Ω = 49,75 Ω

Da wir wegen der geringeren Versorgungsspannung von U_3V = 3,3 V mittels des „micro:bit“-Rechners den Kollektorwiderstand R_C (= Vorwiderstand der roten LED) neu berechnet und damit auch einen neuen Arbeitspunkt eingestellt haben (siehe AP2 bis AP4 im obenstehenden Bild 24), müssen wir nachfolgend auch noch den Basiswiderstand R_Basis zum Ansteuern der Darlington-Transistoren neu berechnen, damit unser Berührungssensor wieder empfindlich genug ist und einwandfrei arbeitet.

Zu diesem Zweck führen wir wieder ein eingangsseitigen Spannungsumlauf im Basis-Emitter-Bereich der Schaltung wie folgt durch:

U_3V ≈ U_{R Basis} + 2 * U_BE →

U_{R Basis} ≈ U_3V - ( 2 * U_BE ) = 3,3 V - 1,27 V = 3,3 V - 1,27 V ≈ 2,0 V

Der Basiswiderstand R_Basis berechnet sich dann zu:

R_Basis = U_{R Basis} / I_Basis

= 2,0 V / 17 µA = 2,0 V / ( 17 * 10^-6 A ) = 2,0 V / 17 * 10⁶ A

= 2000 V / 17 * 10³ A = 117,65 10³ Ω ≈ 118 KΩ

Der Basisstrom I_Basis beider Transistoren durch den Basiswiderstand R_Basis berechnet sich dann zu:

I_Basis = U_{R Basis} / R_Basis = 2,0 V / 118 KΩ = 2,0 V * 10³ / ( 118 * 10³ Ω * 10³ )

= 2000 V / 118 * 10^-6 Ω = 16,95 µA ≈ 17 µA (siehe auch weiter oben!)

Abschließend berechnen wir noch die Stromverstärkung B beider Transistoren, indem wir den Kollektorstrom I_C = I_LED = 20 mA ins Verhältnis setzen zum Basisstrom I_Basis = 17 µA:

B = I_C / I_Basis = 20 mA / 17 µA = 20 * 10^-3 A / ( 17 * 10^-6 A )

= 20 * 10^-3 A / 17 * 10⁶ A = 20 A / 17 * 10³ A

= 1,1765 * 10³ = 1176,5

Da sich die Stromverstärkungen der beiden Transistoren wegen der Darlington-Schaltung multiplizieren, müssen wir die Wurzel ziehen, um die Verstärkung eines einzelnen Transistors näherungsweise berechnen zu können: B_T = √ B = √ 1176,5 ≈ 34,30.

Genau genommen müssten wir aber die Stromverstärkungsfaktor B für jeden Transistor einzeln berechnen, da die beiden Transistoren, obwohl vom Typ her gleichartig, gerade wegen der Darlington-Beschaltung unterschiedliche Stromverstärkungsfaktoren aufweisen. Der Grund dafür ist der, dass der zweite Transistor (rechts) den dicksten Kollektorstrom I_C2 führt, während der erste Transistor (links) wegen der nachgeschalteten BE-Diode des zweiten Transistors nebst Spannungsabfall U_BE2 einen etwas geringeren Kollektorstrom I_C1 führt. Der Grund dafür ist also der Spannungsteiler der beiden in Reihe geschalteten BE-Dioden der Transistoren T₁ und T₂. (von links nach rechts).

(Bild 26: Berührungssensor mit U_3V = +3,3 V Stromversorgung)

Der resultierende Stromverstärkungsfaktor B_res = B₁ * B₂ = 1176,5 mit B₁ = B₂ ≈ 34,30 für einen einzelnen Darlington-Transistor ist im Vergleich zu dem eines einzelnen Kleinleistungstransistors im Bereich von B = 100 … 500 eher klein als groß.

Nach Aussage von Wikipedia beträgt der (Großsignal-) Stromverstärkungsfaktor B von Darlington-Transistoren aber „nur“ B ≈ 500 … 10⁴, d.h. bis zu 10 000 und eben nicht bis zu 90.000 wie im nachfolgenden Zitat beschrieben:

>> Wenn man von einem Verstärkungsfaktor von 300 für jeden der Transistoren ausgeht, hat die Darlington-Schaltung eine Verstärkung von 90.000. Nun leitet bereits ein Basiswiderstand von 10 MΩ genügend, um die LED einzuschalten. Im realen Versuch kann man statt des extrem hochohmigen Widerstands einen Berührungskontakt verwenden. Wegen der großen Verstärkung reicht bereits eine leichte Berührung mit trockenem Finger. Der zusätzliche Schutzwiderstand in der Zuleitung zur Batterie schützt die Transistoren für den Fall, dass die Berührungskontakte versehentlich direkt verbunden werden. << (Quelle: „Lernpaket Conrad Components Basic Elektronik 3964“, PDF-Datei, Versuch „5. Berührungssensor“, Seite 16)

Der Grund dafür, weshalb Darlington-Transistoren bei dem einzelnen Stromverstärkungsfaktor B₁ oder B₂ geringere Werte aufweisen als herkömmliche Kleinleistungstransistoren, ist der, dass diese, wie im vorliegenden Fall, im übersteuerten Bereich „AP3“ bis hin zum Sättigungsbereich „AP4“ betrieben werden (siehe Bild 25).

Aber nichtsdestotrotz ist der resultierende Stromverstärkungsfaktor B_res = B₁ * B₂ = 1176,5 und die damit verbundene Eingangsempfindlichkeit am Basiswiderstand R_B1 = 100 KΩ schon beachtlich!

Aber was soll man sich konkret unter der Eingangsempfindlichkeit vorstellen? Vielleicht helfen uns ein paar Beispiele bzw. Anwendungen weiter. Kennen Sie noch die älteren Rundfunkempfänger aus den 50er Jahren bei denen man nach dem Einschalten gut eine Minute warten musste bis ein Ton zu hören war? Der Grund dafür war der, dass diese Geräte zu der Zeit ausschließlich mit Röhren betrieben wurden, die nach dem Einschalten erst noch aufheizen mussten. Gute Röhrenradios zeichnen sich dadurch aus, dass sich mit diesen ohne externe Antenne praktisch keine Sender empfangen ließen, weil die Empfangsempfindlichkeit im HF-Empfangsteil mit Schwingkreis, bestehend aus Spule und Kondensator und HF-Röhrenverstärker, zu wünschen übrig ließ. Und das war beabsichtigt und gut so. Gute Empfangsgeräte sollen nämlich nur bei angeschlossener, externer Dachantenne Radiosender empfangen, weil sich nur durch eine entsprechende Hochantenne eine Antennenspannung am Eingang der HF-Empfangsstufe von einigen Millivolt [mV] einstellte. Wegen des starken HF-Eingangssignals war dann der Störabstand, gemessen in Dezibel [dB], also der spannungsmäßige Abstand zwischen Nutzen- und Störsignal (Rauschen) besonders groß und so der Hörgenuss gewährleistet.

Anfang der 60er gab es dann bereits die ersten Transistorradios. Zunächst nur mit Mittelwellenempfang (MW bzw. „AM“ für engl. „amplitude modulation“, d.h. „Amplitudenmodulation“) und später auch mit UKW-Empfang („FM“ für engl. „frequency modulation“, d.h. Frequenzmodulation). Dabei ließ der UKW-Empfang sehr zu wünschen übrig, weil die HF-Empfangsempfindlichkeit der meist einstufigen HF-Verstärkung mittels HF-Transistor zu gering war.

Mit der Einführung des FM-Stereo-Rundfunks Mitte der 70er Jahre wiederholte sich das Dilemma mit der zu geringen HF-Empfangsempfindlichkeit bei den Stereo-FM-Empfangsteilen, da man für einen störungs- und rauschfreien UKW-Stereo-Empfang ein um das Zehnfache stärkeres Empfangssignal gegenüber dem Monoempfang brauchte. -

Wie der Name „Eingangsempfindlichkeit“ schon sagt, bezieht sich diese auf den Eingang einer Schaltung; In unserer Fall der Darlington-Schaltung. Dabei kann ein Eingang hoch- oder niederohmig sein, d.h. einen großen oder kleinen Eingangswiderstand haben. Diesbezüglich reden wir von einem Eingang bei dem eingangsseitig eine mehr oder weniger kleine Gleichspannung eingespeist wird. Dabei kann die an den Eingang angelegte Gleichspannung auch von einer kleinen Wechselspannung, einem NF-Signal, einem Störsignal oder einer Brummschleife überlagert sein. Um das ggf. feststellen zu können, bräuchte man allerdings ein Oszilloskop, das ggf. auch höherfrequente Spannungen anzeigen kann.

Wenn man das eventuelle Vorhandensein von Fremd-, Stör- oder Brummspannungen am Eingang ausschließen will, dann müsste man die Schaltung nebst Stromversorgung potentialfrei betreiben, d.h. z.B. ohne ein Steckernetzteil das an die 230 Volt Steckdosenleiste in der Wohnung angeschlossen ist oder die Stromversorgung mittels USB-Kabel, das an den PC angeschlossen ist. Heutzutage wäre das gar nicht so schwer zu realisieren und auch nicht teuer, da es inzwischen sogenannte „Powerpacks“ gibt, die sich mittels Micro-USB-Kabel an das Smartphone anschließen lassen, um dieses mit Strom zu versorgen, wenn der Akku leer ist. Diesbezüglich müsste man dann auch dafür sorgen, dass die Datenübertragung auf den „micro:bit“-Rechner potentialfrei, d.h. ohne USB-Kabel erfolgt wie z.B. über Bluethooth LE.

Doch zurück zur Eingangsempfindlichkeit der Darlington-Schaltung. Wie wir inzwischen wissen besteht einer der Unterschiede zwischen einem Transistor und einem Feldeffekt-Transistor (FET) u.a. darin, dass sich FETs weitestgehend leistungs- bzw. verlustlos schalten lassen! Demzufolge lässt sich die Basis eines Transistors nur dann ansteuern, wenn an der BE-Diode eine Spannung von U_BE > 0,7 V anliegt. Da bei unserer Darlington-Schaltung die beiden BE-Dioden in Reihe geschaltet sind, müsste die resultierende BE-Spannung U_BE1,2 nahezu doppelt so groß sein: U_BE1,2 ≈ 2 * 0,7 V = 1,4 V.

Um die BE-Spannung U_BE2 des zweiten Darlington-Transistors (rechts) messen zu können, müssen beide Transistoren aufgesteuert, d.h. mit einer entsprechend großen BE-Spannung beaufschlagt werden, sodass die rote LED hell aufleuchtet. Dazu müssen wir die Darlington-Schaltung in einen verlässlichen, stabilen und später wieder nachvollziehbaren Systemzustand bringen. Deshalb reicht es nicht, wenn wir den Kontakt am Basiswiderstand R_100k mit dem Finger berühren, um die Darlington-Transistoren mittels unserer Körperspannung aufzusteuern. Zu diesem Zweck überbrücken wir die beiden Fingerkontakte, sodass über den Basiswiderstand R_100k = 100k der weiter oben berechnete Basisstrom von I_Basis = 17 µA fließen kann.

Mit dem Programm microbit_teil_03_prog_19.hex und dem Quelltext microbit_teil_03_prog_19.js, das auf dem Programm „microbit_teil_03_prog_17.hex“ und dem Quelltext „microbit_teil_03_prog_17.js“ aufbaut und das um die Spannungsmessung bis 3,3 V mittels des integrierten A/D-Wandlers am Pin „P2“ erweitert wurde:

(Bild 27: Millivoltmeter mit dem A/D-Wandler am Pin „P2“)

Wie bereits gesagt wurde, handelt es sich bei dem integrierten A/D-Wandler des „micro:bit“-Rechners um einen 10-Bit-Wandler, sodass sich mit diesem und der Binärzahl 1111111111₂ verschiedene Dezimalzahlen im Bereich 0 … 1023₁₀ darstellen lassen und zwar 1024 verschiedene Werte einschließlich null!

Da der „micro:bit“-Rechner intern mit der Betriebsspannung von 3,3 Volt arbeitet, lassen sich mit dem 10-Bit-A/D-Wandler rechnerisch Spannungswerte bis 3,3 * 1023 ≈ 3376 mV = 3,376 V messen.

Wenn aber bei der Spannungsversorgung mit dem Micro-USB-Kabel die „USB-2.0“-Versorgungsspannung am USB-Steckernetzteil im Bereich 4,75 V - 5,50 V etwas geringer ausfällt, dann liegt am Ringanschluss „3V“ und „GND“ eben keine Spannung von 3,3 V an, sondern nur eine verringerte von z.B. 3,18 V = 3180,8 mV (siehe oben im Bild 27).

Wenn dann später das Millivoltmeter des „micro:bit“-Rechners trotz einer geringeren Versorgungsspannung exakte Messwerte liefern soll, dann muss es von Fall zu Fall neu justiert werden, indem man den Maximalwert der in der Laufschrift anzuzeigenden Millivolt im „JavaScript“-Programm vorab entsprechend anpasst!

Dabei stellt es sich dann plötzlich und völlig überraschend heraus, dass der „micro:bit“-Rechner wider Erwarten keine Dezimalzahlen beherrscht, sodass sich nicht mit Kommazahlen rechnen lässt.

Ob es dabei nur an dem absichtlich eingeschränkten „Basic“-Befehlsvorrat liegt oder am Rechenwerk, engl. „Arithmatic Logic Unit“ (ALU) des „micro:bit“-Rechners lässt sich von außen nicht feststellen. Es kann aber auch sein, dass sich nur beim Programmieren des A/D-Wandlers keine Dezimalzahlen verwenden lassen, da diese aus der Sicht des Wandlers, der ja nur mit binären Werten arbeitet, keine Rolle spielen, weil diese in seinem „Innenleben“ nicht vorkommen.

Sei es wie es ist, mit einem kleinen Trick lassen sich Dezimalzahlen umgehen bzw. in ganzzahlige Integerwerte umrechnen. Im vorliegenden Fall muss man also den Maximalwert von 3,18 V bzw. 3180,8 mV nur mit dem Faktor 10 multiplizieren, um einen ganzzahligen Wert mit 31808 mV zu erhalten. Auch und obwohl sich dieser Wert überhaupt nicht messen lässt. Deshalb muss man nach der Berechnung und der Justierung den in der Laufschrift anzuzeigenden Millivolt-Wert abschließend wieder durch den Faktor 10 teilen (siehe roter Kasten oben im Bild 27)! Dabei entsteht dann natürlich wieder eine Dezimalzahl, wobei die Nachkommastellen bei der Zuweisung an die (Integer-) Variable „u_analog“ einfach abgeschnitten werden! Das muss man wissen, da beim Abschneiden der Nachkommastellen und der fehlenden Rundung eventuelle Ungenauigkeiten entstehen können!

3.6 Mehr Genauigkeit durch Referenzieren?

Da die Energieversorgung mittels eines Micro-USB-Kabels an den „USB 2.0“-Anschluss eines PCs oder USB-Steckernetzteils mit einer Nennspannung von 5 V und einem Strom von bis zu 0,5 A endlich ist, verfügt auch unser „micro:bit“-Rechner auch nur über endliche Ressourcen mit dem Vorteil, dass im Falle eines Kurzschlusses die USB-Stromversorgung am PC abgeriegelt wird.

Anders verhält es sich bei einem 12-Volt-Adapter mit USB-Buchse zum Aufladen des Smartphones oder Tablet-PCs während der Fahrt. Diesbezüglich gibt es nämlich auch USB-Ladeadapter für den Anschluss zweier USB-Geräte bzw. eines USB-Gerätes mit 1 A Ladestrom und einen weiteren für 3 A Ladestrom.

Während also die „USB 2.0“-Buchse am PC bezüglich der Leistungsabgabe deutlich begrenzt ist, ist das bei dem USB-Ladeadapter im PKW mit 3 A Entnahmestrom keineswegs der Fall, sodass das Smartphone während der Fahrt im PKW bei voller Displayhelligkeit, eingeschaltetem Navi mit GPS und Internetzugang für die Online-Navigation mit Google Maps wegen der hohen Stromstärke dann schon mal richtig heiß werden kann. Ähnlich verhält es sich, wenn Sie Ihr Smartphone an einem Powerpack oder einer Powerbank schnell aufladen, weil dort auch größere Ladeströme bis 3 A fließen können.

Wenn Sie also die Energieversorgung des „micro:bit“-Rechners an einem limitierten „USB 2.0“-Anschluß am PC oder einem leistungsschwachen, weil billigen USB-Steckernetzteil betreiben, dann wirkt sich jede am Rechner leuchtende LED und deren Energieverbrauch hinsichtlich der Versorgungsspannung an einem der Ringanschlussbuchsen mit den Ports „Pin P0“ bis „Pin P2“ dahingehend nachteilig aus, dass diese in die Knie geht, d.h. mehr und mehr reduziert. Aus der ursprünglichen 3,3 Volt Versorgungsspannung wird dann schnell eine mit nur noch 3,1 Volt mit der unangenehmen Folge, dass unser Digitalvoltmeter am Port „Pin P2“ mit dem A/D-Wandler ungenau wird!

Um diese Ungenauigkeit des Digitalvoltmeters weitestgehend zu vermeiden, sollten Sie am „micro:bit“-Rechner stets nur ganz wenige Energieverbraucher wie z.B. LEDs während des Betriebs als Digitalvoltmeter angeschlossen haben! Dies betrifft dann auch die Laufschriftanzeige des „5 x 5 LED-Matrix“-Displays, dessen Stromverbrauch je nach angezeigter Schrift schwankt! Praktisch bedeutet dies, dass das Digitalvoltmeter bei jeder sich ändernden Betriebssituation nebst Energieverbrauch neu justiert und abgeglichen werden müsste!

Da sich unser Digitalvoltmeter in Form des A/D-Wandlers leider nicht mittels einer eigenen, extra stabilisierten Stromversorgung betreiben lässt, müssen wir uns etwas anderes einfallen lassen, um das Digitalvoltmeter bei jeder Messung automatisch justieren zu können!

Zu diesem Zweck werden wir als nächstes eine stabile Referenz-Spannungsquelle in Form eines externen Batteriepacks mit zwei 1,5 Volt AA-Batterien verwenden, mit dem „micro:bit“-Rechner über einen Port verbinden und den automatischen Abgleich für das Digitalvoltmeter programmieren! Wer will, kann aber auch einen kleinen Batterieclip mit einer 3 Volt Knopfzelle als Pufferbatterie verwenden, die weniger Platz beansprucht, dafür aber deutlich teurer ist.

Da die eingesetzten 1,5 Volt Batterien im Neuzustand eine höhere Nennspannung als 1,5 Volt haben, muss man davon ausgehen, dass die Gesamtspannung zweier 1,5 Volt Batterien, die in Reihe geschaltet werden, deutlich höher ist als die 3,2 Volt des A/D-Wandlers für das Digitalvoltmeter. Demzufolge müssten wir noch einen Spannungsteiler, bestehend aus zwei Widerständen, die ebenfalls in Reihe geschaltet werden, einsetzen. Das Problem dabei wäre dann aber, dass durch den Spannungsteiler stets ein entsprechend großer Querstrom fließen würde, der die Batterien im Dauerbetrieb fortwährend entleert! Dazu muss man wissen, dass der Querstrom mindestens doppelt (besser fünfmal) so groß sein muss als der Entnahmestrom an einem der beiden Teilwiderstände!

Um dieses Problem zu umgehen, wäre es also einfacher, wenn wir nur eine 1,5-Volt-AA-Batterie als Referenzspannung verwenden! Dies hätte dann auch den Vorteil, dass sich die Referenzspannung von 1,5 Volt stets in der Mitte des Spannungsbereichs des A/D-Wandlers befindet!

Was aber nutzt eine Referenzspannung von 1,5 Volt, wenn das Messen dieser Referenzspannung mit unserem Digitalvoltmeter (= A/D-Wandler) des „micro:bit“-Rechners wegen der schwankenden Versorgungsspannung an den Ports „Pin P0“ bis „Pin P2“ ständig zu sich verändernden Messwerten führt? Nichts! Demzufolge bleibt uns nichts anderes übrig, als die Referenzspannung extern mit einem Multimeter zu erfassen, in das Messprogramm des Digitalvoltmeters aufzunehmen, um diesen dann zur Justierung unseres Digitalvoltmeters fortwährend heranzuziehen!

Die Messung der Klemmenspannung an der externen 1,5-Volt-AA-Batterie mit einem empfindlichen Multimeter liefert die Referenzspannung U_Ref = 1,484 V = 1484 mV.

Mit dem einfachen Programm microbit_teil_03_prog_18.hex und dem Quelltext microbit_teil_03_prog_18.js messen wir am Port „Pin P2“ die Leerlaufspannung ohne jegliche Belastung der externen 1,5-Volt-AA-Batterie und bekommen dabei den Bitwert U_{1,5V leer} = 480₂ angezeigt, der sich dem Referenzwert von U_Ref = 1484 mV₁₀ zuweisen lässt.

Da der binäre Messbereich des 10-Bit-A/D-Wandlers von 0 bis 1023₂ reicht, würde sich gemäß Dreisatz die maximal anzuzeigende Spannung auf = 1484₁₀ mV / 480₂ * 1023₂ = 3162,775 ≈ 3163₂ mV belaufen.

Dabei setzt die Berechnung mit dem Dreisatz stillschweigend voraus, dass die Umrechnung des A/D-Wandlers über den gesamten Bereich von 0 bis 1023 linear verläuft!

Elektronisch verlaufen Dinge aber nur dann linear, wenn man es im Inneren, d.h. bei der Umwandlung mittels A/D-Wandler ebenfalls mit z.B. linear verlaufenden Spannungen usw. zu tun hat. Demzufolge dürfen Kondensatoren nicht herkömmlich mittels Spannungs- und Stromverlauf einer e-Funktion aufgeladen werden, sondern ausschließlich linear so wie bei einer Widerstandsgeraden. Dazu braucht man dann aber eine möglichst präzise Konstantstromquelle, die sich z.B. mittels eines Operationsverstärkers realisieren ließe.

Dabei kann eine Konstantstromquelle aber immer nur so stabil sein und einen festen, konstanten Strom liefern, wie es letztlich die externe Spannungsversorgung von außen zulässt. Und die darf bei einem „USB 2.0“-Anschluß zwischen 4,75 V und 5,50 V betragen und kann evtl. auch schwanken!

Wenn Sie z.B. Ihren Desktop-PC oder Tower-PC nachträglich mit einer schnellen und hochauflösenden Grafikkarte ausgerüstet haben, um auch Spiele mit aufwendiger Grafik spielen zu können, dann muss man damit rechnen, dass die Grafikkarte allein bis zu 200 Watt in Form von Rechnenleistung verbraucht. Dabei verfügen solche Grafikkarten auch über ein eigenes, umschlossenes Kühlsystem inklusive Heatpipe mit Ventilator und können auch schon mal bis 250,- Euro und mehr kosten! Wenn Sie dann bei der Verwendung einer solchen Hochleistungs-Grafikkarte nebst Energieverbrauch das intern verbaute Standard-Netzteil wider Erwarten nicht gegen eine Hochleistungs-Netzteil von bis zu 450 Watt Leistung ausgewechselt haben, ist es um eine stabile Spannungsversorgung, auch und gerade der USB-Schnittstellen mit USB-Buchsen, nicht gut bestellt.

Immer dann, wenn bei einem Computerspiel eine Action reiche Szene auftaucht, die besonders viel Grafikleistung erfordert, müssen Sie damit rechnen, dass die Spannung einer „USB 2.0“-Buchse von 5,5 V auf nur noch 4,75 V absinkt und nach der Actionszene wieder auf bis zu 5,5 Volt ansteigt. Diese schnellen Spannungsschwankungen übertragen sich so gar auf die 230 Volt Haushaltsstromversorgung und lassen sich mit einem sogenannten Smart Meter (= „intelligenter“ Strom- bzw. Energieverbrauchszähler) erfassen und auswerten. Mit dem über ein entsprechendes Zeitfenster erfassten Energieverbrauchs-Fingerabdruck ließe sich dann so gar ermitteln, welches grafikintensive Computerspiel zuvor gespielt wurde!

Da wir nicht wissen, welcher schaltungstechnischer Aufwand bei der internen Konstantstromquelle und der Spannungsstabilisierung bei der Stromversorgung des A/D-Wandlers getrieben wurde, machen wir uns von der externen „USB 2.0“-Stromversorgung mittels Micro-USB-Kabel unabhängig, indem wir stattdessen ein externes Batteriepack mit zwei neuen 1,5 Volt AA-Batterien (in Reihenschaltung) an die Ringanschlussbuchsen mit den Ports „3V“ (= Pluspol!) „GND“ (= Minuspol, Masse) anschließen.

Dabei messen wir mit dem Mulitmeter eine Batteriespannung von U_Batt = 3,24 V, wobei aber der „micro:bit“-Rechner bereits angeschlossen und im Leerlauf, d.h. ohne leuchtende LEDs oder Laufschriftanzeige, bereits einen Strom von 1,7 mA zieht.

Da der intern verbaute „nRF51822 Bluetooth LE“-Chip nebst integriertem A/D-Wandler in einem Spannungsbereich von 1,8 V bis 3,6 V arbeitet und der „micro:bit“-Rechner selbst mit einer externen USB-Versorgungsspannung von 4,5 V bis 5,25 V betrieben werden darf, befinden wir uns mit der externen Batterie-Stromversorgung und der Batteriespannung von U_Batt = 3,24 V im grünen Bereich!

Bezüglich der externen Stromversorgung mittels Batterie-Pack gilt es nochmals ausdrücklich darauf hinzuweisen, dass wir dabei über keine Kurzschlußstromsicherung mehr verfügen!

>> This device also performs the voltage regulation from the USB supply (4.5-5.25V) down to the nominal 3.3 volts used by the rest of the PCB. When running on batteries this regulator is not used. << (Quelle: englischsprachige Wikipedia)

Da wir uns mit der externen Stromversorgung mittels Batteriepack und der Batteriespannung von U_Batt = 3,24 V unterhalb der zulässigen 3,3 V bewegen, stellt sich nun die interessante Frage, welchen Wert der A/D-Wandler anzeigt.

Wenn wir dabei den zuvor am Port „Pin P2“ ermittelten Bitwert U_{1,5V leer} = 480₂ der Leerlaufspannung ohne jegliche Belastung der externen 1,5-Volt-AA-Batterie zugrunde legen und diesen auf den max. Bitwert 1023₂ hochrechnen, dann dürfte die am Port „Pin P2“ des A/D-Wandlers eine Messspannung von U_{A/D, max} = 1484₁₀ mV / 480₂ * 1023₂ = 3162,775₁₀ mV ≈ 3162,8₁₀ mV nicht überschreiten! Tut es aber mit U_Batt = 3,24 V doch!

Jetzt stellt sich die spannende Frage, was der A/D-Wandler anzeigt! Signalisiert uns dieser, dass die max. zulässige Eingangsspanung von U_{A/D, max} = 3162,8₁₀ mV nicht überschritten werden darf, weil sich der A/D-Wandler bereits am Anschlag der Messskala befindet und sich der „Digitalzeiger“ bereits um den Pin des Endanschlags (wie bei einem analogen Voltmeter) wickelt?

Wir benutzen wieder das einfache Programm microbit_teil_03_prog_18.hex mit dem Quelltext microbit_teil_03_prog_18.js, messen am Port „Pin P2“ die externe Batteriespannung und bekommen dabei den Bitwert U_Batt = 1023₂ angezeigt!

Wahnsinn! Jetzt haben wir es schwarz auf weiß, dass uns der A/D-Wandler wider Erwarten keine Messwertüberschreitung der max. zulässigen Messspannung anzeigt!

Wir machen die Gegenprobe und präzisieren unsere Messung in der Weise, dass wir den Eingang des A/D-Wandlers mit einem Spannungsteiler „belasten“. Schließlich kennen wir den Eingangswiderstand des A/D-Wandlers und den des Multimeters nicht. Auch wenn der Eingangswiderstand des Multimeters ziemlich hoch sein und im zweistelligen MΩ liegen dürfte, da sich mit dem diesem auch Widerstände bis 20 MΩ messen lassen.

Der Knackpunkt dabei ist aber nicht der, dass wir eine kleine Spannung einer hochohmigen, nicht belastungsfähigen Spannungsquelle messen wollen, sondern eine kleine Spannung an dem hochohmigen Spannungseingang des A/D-Wandlers, dessen Eingang wegen der relativ hohen Empfindlichkeit und des großen Eingangswiderstands des A/D-Wandlers quasi in der Luft hängt.

Damit aber keine Gefahr besteht, dass wir am Eingang des A/D-Wandlers irgendeine Schmutzspannung messen, „belasten“ wir diesen mit einem einfachen Spannungsteiler, der aus zwei Widerständen besteht, die in Reihe geschaltet werden. Dabei ist der Widerstand R₂ des Spannungsteilers, der übrigens parallel zum Eingang des A/D-Wandlers geschaltet ist, sehr groß, nämlich R₂ = 3,3 MΩ.

Bei dem Widerstand R₁ = 1,5 KΩ des Spannungsteilers verhält es sich so, dass dieser im Vergleich zum R₂ recht niederohmig ist und als Vorwiderstand dient, um die anliegende Messspannung ganz geringfügig zu verringern, sodass sich am Mittelpunkt des Spannungsteilers (= Eingang des A/D-Wandlers) eine Spannung von U₂ = 3,22₁₀ V einstellt, die dem Binärwert = 1022₂ entspricht.

Wenn man den Binärwert = 1022₂ auf den max. messbaren Binärwert = 1023₂ hoch rechnet, dann ergibt dies eine max. messbare, dezimale Meßspannung von U_{A/D max} = 3,22₁₀ V / 1022₂ * 1023₂ = 3,22315₁₀ V = 3223,15₁₀ mV.

Wenn wir nun wieder die Leerlaufspannung ohne jegliche Belastung der externen 1,5-Volt-AA-Batterie als Referenzspannung messen, dann stellt sich am Port „Pin P2“ des A/D-Wandlers eine Messspannung von U_{A/D, max} = 1484₁₀ mV / 479₂ * 1023₂ = 3169,38 mV ≈ 3169,4 mV ein (vormals 3162,775₁₀ mV ≈ 3162,8₁₀ mV).

Wir stellen wieder die Stromversorgung des „micro:bit“-Rechners mit dem Micro-USB-Kabel her, messen eine Versorgungsspannung von U_USB = 3,24 V, klemmen das Batteriepack mit zwei etwas altersschwachen „1,5 Volt AA“-Batterien an, um deren Leerlaufspannung U_Batt = 2,86 V mit dem A/D-Wandler am Port „Pin P2“ zu messen.

Mit dem zuletzt ermittelten Umrechnungsfaktor von 1022₂ / 3,22₁₀ V = 317,39 Binärwert / Volt müsste für die Leerlaufspannung U_Batt = 2,86 V des Batteriepacks ein Binärwert von 317,39 Binärwert / Volt * 2,86 V = 908 angezeigt werden. Tatsächlich sind es aber 915 als Binärwert, was einer Spannung von 3,22₁₀ V / 1022₂ * 915₂ ≈ 2,88 V entspricht!

Wie man sieht, bringt uns die Rechnerei mit der Umrechnung usw. nicht weiter. Auch wenn es sich anfangs ganz toll anhört, dass sich mit dem „micro:bit“-Rechner auch ein Millivoltmeter programmieren lässt, so zeigen sich doch jetzt einige Dinge, die uns das Leben schwer machen:

· Eine Batterie verhält sich nicht wirklich wie eine Konstantstromquelle, die über einen längeren Zeitraum selbst bei einem kleinen, konstanten Entnahmestrom eine konstante Klemmenspannung bereit stellt. Solange man die Klemmenspannung nur bis auf eine Stelle nach dem Komma misst und anzeigt, ist die Welt noch in Ordnung, könnte man von außen gesehen tatsächlich den Eindruck gewinnen, dass die Klemmenspannung konstant ist.

· Sobald man aber eine Lupe mit entsprechendem Vergrößerungsfaktor zur Hand nimmt und die Klemmenspannung mit dem Millivoltmeter misst, dann werden aus 1,5 Volt vermeintlich exakte 1,484 V = 1484 mV, gibt es drei Nachkommastellen, die eine Genauigkeit im Bereich von einigen Hundertstel vorgaukeln!

· Wenn dann noch aus den 1,484 V durch „Umschalten“ der Anzeige 1484 mV werden, dann haben wir zwar einen um den Faktor 1000 höher aufgelösten Anzeigewert, der aber in Wirklichkeit die fehlende Genauigkeit in Form der fehlenden Messwerterauflösung jetzt erst recht verschleiert! Wir lernen daraus, dass eine vierstellige Millivoltanzeige keineswegs genau sein muss, weil man ihr es nicht ansieht, dass sie mit einer zu geringen Messwertauflösung gemessen wurde!

· Wenn dann noch die Millivoltanzeige im zweistelligen Bereich, um bis zu 20, 30, 40 oder mehr Millivolt schwankt, weil die Klemmenspannung des Batteriepacks selbst bei kleinen Lastströmen nicht konstant ist, dann stellt sich die Frage, wie man damit umgehen soll und wie man eine Messwertkorrektur bei der Messwerterfassung mit dem A/D-Wandler umsetzen soll. Mal ganz abgesehen davon, dass sich Schwankungen im Bereich von z.B. 50 mV = 0,050 V bei einer Spannung von 1,5 V in der Praxis nicht nachteilig bemerkbar machen.

· Ein Millivoltmeter ist, auf den ersten Blick gesehen, sicherlich ein tolle Sache. Bei genauerem Hinsehen aber nicht mehr! Insbesondere dann, wenn nur die Anzeige auf bis zu vier Stellen aufgebläht wurde ohne aber gleichzeitig die Messwertauflösung maßgeblich zu verbessern!

So wie es im Moment aussieht, muss man vor jeder Messung mit dem Millivoltmeter eine Meßwertkorrektur vornehmen, da weder die Klemmenspannung des Batteriepacks noch die USB-Spannungsversorgung mittels Micro-USB-Kabel alles andere als konstant sind, obwohl uns das bisher noch nie negativ aufgefallen ist, sondern erst seit dem es die vierstellige Anzeige mit dem Millivoltmeter gibt.

Bevor wir nun weiter machen, sollten wir unbedingt noch das Problem lösen, nämlich dass beim Überschreiten des Messbereichs mit dem Bitwert 1023 kein Alarm ausgelöst, kein Hinweis angezeigt werden und z.B. beim Erfassen einer Spannung von 3,3 V vom A/D-Wandler stets der maximale Bitwert 1023 angezeigt wird, obwohl doch eigentlich ein Überlauf in Form des Springens auf das Inkrement 0 erfolgen müsste.

Wenn man nämlich binär nur bis 1023 zählen kann, weil eben nur eine Auflösung von 10 Bit zur Verfügung steht, dann beläuft sich der nächst höhere Bitwert eben nicht auf 1024, sondern wieder auf 0, fängt der Bitzähler wieder von vorn an zu zählen.

Um aber genau den binären Überlauf von Bit 1023 auf das inkrementelle Bit 0 und eben nicht 1024 erfassen zu können, bleibt uns nichts anderes übrig als den Messbereich zu erweitern! Da aber genau das hardwaremäßig nicht geht, weil der A/D-Wandler nur über einen digitalen, binären Messbereich von 10 Bit = 2¹⁰ = 11 1111 1111₂ = 1023₁₀ verfügt, müssen wir diesen analog in Form eines eingangsseitigen, einfachen Spannungsteilers vornehmen!

Dazu muss man wissen, dass sich die Messgenauigkeit von analogen Spannungs- oder Strommessgeräten ab dem oberen Drittel des Messbereichs bis hin zum Maximalwert (= Endanschlag) zunehmend verschlechtert!

Wenn man also beim Messen von z.B. Spannungen oder Stromstärken eine hohe Messgenauigkeit erreichen will, dann sollte man bei einem analogen Vielfachmessinstrument (= Multimeter) einen Messbereich wählen, bei dem der anzuzeigende Messwert im Bereich der hälftigen Skala bis hin zum oberen Drittel liegt. Aber eben nicht darüber!

In diesem Zusammenhang gilt es noch zu beachten, dass es sich bei vielen, insbesondere preiswerten Multimetern mit Digitalanzeige in Wirklichkeit um analoge Messgeräte handelt, bei denen der analoge Messwert in einen digital anzuzeigenden umgewandelt und auf dem LCD-Display angezeigt wird. Es ist nämlich nicht alles wirklich digital nur weil man über eine Digitalanzeige verfügt! Deshalb müssen im LCD-Display digital angezeigte Messwerte nicht zwangsläufig genauer sein! Es ist eben nicht alles Gold was glänzt!

3.7 Messbereich mittels Spannungsteiler vergrößern

Damit sich Messwerte um die 3 Volt später im oberen Drittel der „Messskala“ anzeigen lassen, wählen wir einen anzuzeigenden Messbereich bis 4,5 Volt. Damit der A/D-Wandler bei Spannungswerten von mehr als 3 Volt nicht übersteuert wird und stets einen Binärwert von 1023 anzeigt, obwohl dieser längst überschritten wurde, müssen wir die überschüssige Spannung in Form eines Spannungsabfalls von ∆U = 4,5 V - 3,0 V = 1,5 V „vernichten“ bzw. vom Eingang des A/D-Wandlers fernhalten. Dazu verwenden wir einen einfachen Spannungsteiler am Eingang des A/D-Wandlers, der aus den beiden Widerständen R₁ und R₂ besteht:

(Bild 29: Millivoltmeter mit Spannungsteiler)

Dabei dient der Widerstand R₁ des Spannungsteilers als Vorwiderstand des A/D-Wandlers, damit dieser wegen des Spannungsabfalls nicht mit mehr als 3 Volt Eingangsspannung beaufschlagt wird.

Diesbezüglich gilt die Spannungsteiler-Regel, dass am kleinen Widerstand R₁ die kleine (= 1,5 V) und am großen Widerstand R₂ die große Spannung (= 3,0 V) abfällt!

Damit der Widerstand R₂, der sich ja parallel zum Eingang des A/D-Wandlers befindet, diesen mit seinem Querstrom nicht unnötig belastet, muss dieser mit R₂ = 100 KΩ hochohmig sein (siehe weiter oben)!

Für den Spannungsteiler gilt die Spannungsteilerformel

R₁ / R₂ = U₁ / U₂ →

R₁ = U₁ / U₂ * R₂ = 1,5 V / 3,0 V * 100 KΩ = 0,5 * 100 KΩ = 50 KΩ

Soweit zu den rechnerischen Widerstandswerten des Spannungsteilers.

Bei der Verwendung des Widerstandes R₁ kommt ein Widerstand mit vier Farbringen gelb, gelb, orange, silber = 4 4 1000 = 44 * 1000 = 44 * 10³ = 44 KΩ +/- 10 % Abweichung mit R₁ = 44 KΩ zum Einsatz.

Bei der Verwendung des Widerstandes R₂ kommt ebenfalls ein Widerstand mit vier Farbringen braun, schwarz, gelb, silber = 1 0 10000 = 10 * 10000 = 10 * 10⁴ = 100 * 10³ = 100 KΩ *+/- 10 % Abweichung mit R₂ = 100 KΩ zum Einsatz (siehe Widerstandsbestimmung mit 4 Ringen bei Kohleschichtwiderständen).

Demzufolge berechnet sich die Messspannung U₂ am Eingang des A/D-Wandlers bei einer Gesamtspannung von U_ges = 2,86 V wie folgt:

U₂ / U_ges = R₂ / R_ges →

U₂ = R₂ / R_ges * U_ges

= 100 KΩ / (100 KΩ + 44 KΩ) * 2,86 V

= 100 KΩ / 144 KΩ * 2,86 V = 1,986 V ≈ 1,99 V

= 2,02 V mit dem Multimeter gemessen!

Dabei zeigt der A/D-Wandler am Widerstand R₂ einen Bitwert von 616 an, der einer gemessenen Spannung von U₂ = 2,02 V entspricht.

Demzufolge ergibt sich ein Volt pro 1 Bit Wert von 2,02 V / 616 Bit = 0,003279 V/Bit. Rechnet man diesen Wert auf den 10 Bit Wert von 1023 Bit hoch, dann folgt für die max. mögliche Messspannung des A/D-Wandlers = 0,003279 V/Bit * 1023 = 3,3544 V ≈ 3,35 V.

Wir führen eine weitere Berechnung für ein nahezu voll geladenes, neues Batteriepack mit der Batteriespannung U_Batt = 3,22 V wie folgt durch:

Demzufolge berechnet sich die Messspannung U₂ am Eingang des A/D-Wandlers bei einer Gesamtspannung von U_ges = 3,22 V wie folgt:

U₂ / U_ges = R₂ / R_ges →

U₂ = R₂ / R_ges * U_ges

= 100 KΩ / (100 KΩ + 44 KΩ) * 3,22 V

= 100 KΩ / 144 KΩ * 3,22 V = 2,236 V ≈ 2,24 V

= 2,27 V mit dem Multimeter gemessen!

Dabei zeigt der A/D-Wandler am Widerstand R₂ einen Bitwert von 688 an, der einer gemessenen Spannung von U₂ = 2,27 V entspricht.

Demzufolge ergibt sich ein Volt pro 1 Bit Wert von 2,27 V / 688 Bit = 0,003299 V/Bit. Rechnet man diesen Wert auf den 10 Bit Wert von 1023 Bit hoch, dann folgt für die max. mögliche Messspannung des A/D-Wandlers = 0,003299 V/Bit * 1023 = 3,375 V ≈ 3,37 V.

Da wir schon zwei Volt pro 1 Bit Werte berechnet haben, bilden wir den Mittelwert:

0,003279 V/Bit + 0,003299 V/Bit = 0,006578 / 2 = 0,003289 V/Bit

Gegenprobe:

0,003289 V/Bit * 1023 Bit = 3,365 V

3.8 Vom Millivoltmeter zum Multimeter

Worin unterscheidet sich ein Millivoltmeter von einem Multimeter? Durch den auswählbaren bzw. einstellbaren und deshalb variablen Spannungsteiler. Ein Millivoltmeter zeichnet sich dadurch aus, dass sich mit diesem tausendstel Volt [ mV ] messen lassen. Dazu muss es entsprechend empfindlich sein und ganz kleine Ströme wie z.B. bis zu 50 µA messen können. Das sind 50 Millionstel Ampere [ µA = 10^-6 A ]. Das ist verdammt wenig. Dabei ist ein Millivoltmeter in Form eines analogen Drehspulmessinstruments umso empfindlicher, je mehr dünner Kupferdraht sich auf der Magnetspule des Drehspulrahmens befindet.

Wie groß ist der Innenwiderstand R_i eines Millivoltmeters mit dem sich eine Spannung bis 1000 mV = 1 V messen lässt, wenn in diesem ein Mikroamperemeter verbaut ist, mit dem sich ganz kleine Ströme bis zu 50 µA messen lassen? Mit dem Ohmschen Gesetz R = U / I = ∆U / ∆I folgt:

R_i = U / I = ∆U / ∆I = 1 V / 50 µA

= 1 V / ( 50 10^-6 A ) = 1 / 50 * 10⁶ Ω = 0,02 MΩ = 20 MΩ

Da sich mit einem Multimeter auch ohmsche Widerstände messen lassen, sollten Sie mal einen Blick auf den Messbereichsschalter (= Drehschalter) werfen. Wenn es dort einen Widerstandsmessbereich mit der Beschriftung „20 MΩ“ gibt, dann können Sie bei einem Multimeter mit Drehspulmessinstrument davon ausgehen, dass im Innersten ein Mikroamperemeter („µA“) verbaut ist, das zugleich auch ein Millivoltmeter („mV“)ist! Beim kleinsten Messbereich von z.B. 1 V handelt es sich beim Millivoltmeter gleichzeitig auch um ein Mikroamperemeter mit dem sich z.B. bei 1 V auch kleine Ströme von 50 µA messen lassen!

Bei dem Multimeter mit dem hier Messungen durchgeführt werden, lassen sich mit dem kleinsten Strommessbereich Stromstärken bis 2 mA messen. Gleichzeitig gibt es einen Widerstandsmessbereich bis 20 MΩ. Berechne die dazu erforderliche (Mess-) Spannung!

U_Mess = I_Mess * R_i = 2 mA * 20 MΩ = 2 * 10^-3 A * 20 * 10^-6 Ω = 2 * 20 * 10^-9 V

= 40 * 10^-3 10^-6 V = 40 * 10^-3 µV = 0,04 µV

Diese Messspannung ist so winzig, dass sie sich mit keinem herkömmlichen, analogen Millivoltmeter mehr messen lassen dürfte. Demzufolge muss sich im Multimeter ein kleiner, hochohmiger Messverstärker u.a. mit einem Operationsverstärker befinden. Wenn man mit dem digitalen Multimeter auch Wechselspannungen messen will, dann bräuchte man noch einen (Mess-) Gleichrichter z.B. aus empfindlichen Siliziumdioden sowie einen A/D-Wandler. Da eine Si-Diode erst ab einer Spannung U_S > 0,6 V elektrisch leitend wird, beläuft sich bei preiswerten Multimetern der kleinste Spannungsmessbereich auf 1 oder 2 V, sofern kein Messverstärker zum Einsatz kommt. -

In der Bastelkiste hat sich noch eine sogenannte 9-Volt-Blockbatterie gefunden, deren Leerlaufspannung U_leer nachfolgend mit dem A/D-Wandler gemessen werden soll. Wie groß muss der Vorwiderstand bzw. der Widerstand R₁ des vorgeschalteten Spannungsteilers sein, wenn der Messbereich bis 12 V gehen soll?

Für den Spannungsteiler gilt die Spannungsteilerformel

R₁ / R₂ = U₁ / U₂ →

R₁ = U₁ / U₂ * R₂ = ( U_ges - U₂ ) / U₂ * R₂

= ( 12 V - 3 V ) / 3 V * 100 KΩ = 9 V / 3 V * 100 KΩ = 3 * 100 KΩ = 300 KΩ

Soweit zu den rechnerischen Widerstandswerten des Spannungsteilers.

Da wir in der Bastelkiste nur einen Widerstand mit R₁ = 240 KΩ finden, lässt sich mit diesem nur eine Spannung

R₁ / R₂ = U₁ / U₂ →

U₁ = R₁ / R₂ * U₂ = 240 KΩ / 100 KΩ * 3 V = 2,4 * 3 V = 7,2 V

Hier zeigt sich wieder, dass am großen Widerstand R₁ die große Spannung U₁ und am kleinen Widerstand R₂ die kleine Spannung U₂ abfällt.

U_ges = U₁ + U₂ = 7,2 V + 3 V = 10,2 V

Bevor wir aber nun die 9-Volt-Blockbatterie an den Vorwiderstand R₁ = 240 KΩ des A/D-Wandlers anklemmen, messen wir sicherheitshalber noch die Leerlaufspannung U_Leer = U_Batt = 9,415 V der Blockbatterie, um sicherzustellen, dass die max. zulässige Gesamtspannung U_ges = 10,2 V an unserem Spannungsteiler nicht überschritten wird!

3.8.1 Funktionsprüfung des Spannungsteilers

Wir führen noch eine weitere Überprüfung durch. Und zwar die, um die richtige Funktionsweise des Spannungsteilers in Verbindung mit dem A/D-Wandler zu testen.

Zu diesem Zweck verwenden wir wieder das Batteriepack mit den zwei nahezu neuen und unverbrauchten „1,5 Volt AA“-Batterien in Reihenschaltung und messen mit dem Multimeter eine Klemmen-/Leerlaufspannung von U_Klemme = U_Leer = 3,22 V.

Dann verbinden wir das Batteriepack mit dem Spannungsteiler des A/D-Wandlers, indem wir den Pluspol (+) an den Vorwiderstand R₁ des Spannungsteiler klemmen und den Minuspol (-) an die Masse des „micro:bit“-Rechners mit dem Rundanschluss „GND“.

Die Gesamtspannung am Spannungsteiler entspricht jetzt der Klemmen-/Leerlaufspannung von U_Klemme = U_Leer = 3,22 V des Batteriepacks. Wie groß ist nun der Spannungsabfall U₂ (= Eingangsspannung am A/D-Wandler) am Widerstand R₂ des Spannungsteilers (siehe Bild 29 weiter oben)?

U₂ / U_ges = R₂ / R_ges →

U₂ = R₂ / R_ges * U_ges

= 100 KΩ / (100 KΩ + 240 KΩ) * 3,22 V

= 100 KΩ / 340 KΩ * 3,22 V

= Spannungsteilerquotient * U_Batterie → (… siehe unten!)

= 0,294117647 * 3,22 V = 0,9470588 V ≈ 0,947 V

= 1,006 V mit dem Multimeter gemessen!

Dabei zeigt der A/D-Wandler am Widerstand R₂ einen Bitwert von 305 an, der einer gemessenen Spannung von U₂ = 1,006 V entspricht.

Demzufolge ergibt sich ein Volt pro 1 Bit Wert von 1,006 V / 305 Bit = 0,003298361 ≈ 0,003298 V/Bit. Zum Vergleich: Der zuletzt ermittelte Mittelwert betrug 0,003289 V/Bit.

Mit dem soeben ermittelten Volt pro 1 Bit Wert lässt sich nun ein weiterer, neuer Mittelwert von 0,003298 V/Bit + 0,003289 V/Bit = 0,006587 V/Bit / 2 = 0,003294 V/Bit errechnen!

Rechnet man diesen Wert auf den 10 Bit Wert von 1023 Bit hoch, dann folgt für die max. mögliche Messspannung des A/D-Wandlers = 0,003294 V/Bit * 1023 = 3,369762 V ≈ 3,37 V.

3.8.2 Die 9-Volt-Blockbatterie am Spannungsteiler

Nun berechnen wir noch den zukünftigen, zu erwartenden Spannungsabfall (= Eingangsspanung am A/D-Wandler), wenn wir gleich die 9-Volt-Blockbatterie mit der Leerlaufspannung U_Leer = U_Batt = 9,41 V an den Vorwiderstand R₁ des Spannungsteilers anklemmen:

U₂ / U_ges = R₂ / R_ges →

U₂ = R₂ / R_ges * U_ges

= 100 KΩ / (100 KΩ + 240 KΩ) * 9,41 V

= 100 KΩ / 340 KΩ * 9,41 V = 2,7676 V ≈ 2,77 V

= 2,90 V mit dem Multimeter gemessen!

Dabei zeigt der A/D-Wandler am Widerstand R₂ einen Bitwert von 815 an, der einer gemessenen Spannung von U₂ = 2,90 V entspricht. Das entspricht einem Plus von 4,7 % gegenüber dem berechneten Wert von U₂ = 2,77 V.

Was jetzt noch fehlt, ist die Berechnung des Quotienten (= Unterteilungsverhältnis) für den Spannungsteiler. Schließlich wird ja durch diesen die Batteriespannung der 9-Volt-Blockbatterie von U_Batt = 9,41 V auf nur noch U₂ = 2,77 V herabgesetzt:

U₂ / U_ges = R₂ / R_ges = R₂ / ( R₁ + R₂ ) →

U₂ = R₂ / ( R₁ + R₂ ) * U_ges

= 100 KΩ / ( 100 KΩ + 240 KΩ ) * 9,41 V

= 100 KΩ / 340 KΩ * 9,41 V = 0,294117647 * 9,41 V

= 0,29412 * 9,41 V = 2,768 V

Der Untersetzungsfaktor, sprich Koeffizient oder Quotient unseres Spannungsteilers hat also den Wert 0,29412.

Wie man sieht, lässt sich jetzt die am A/D-Wandler anliegende Messspannung ganz einfach durch Multiplikation des Quotienten mit der tatsächlich am Spannungsteiler anliegenden Spannung U_ges berechnen: U_A/D-Wandler = 0,29412 * U_ges

Demzufolge beträgt die am A/D-Wandler anliegende Eingangsspannung nur noch:

U_A/D-Wandler = 0,29412 * U_ges = 0,29412 * 9,41 V = 2,7677 V = 2767,7 mV

Jetzt fehlt zum Schluss nur noch die Auflösung des A/D-Wandlers. Je mehr Bits nämlich pro Volt zur Verfügung stehen, um den Messwert abzutasten, umso besser die Auflösung, d.h. Genauigkeit bei der A/D-Wandlung. Selbstverständlich spielt bei der Abtastrate auch noch die Abtastfrequenz eine maßgebliche Rolle. Denn je mehr Werte in umso kürzerer Zeit erfasst und abgefragt werden, umso genauer wird das Ergebnis der A/D-Wandlung.

Mit unserem A/D-Wandler lassen sich von 0 … 1023 = 1024 verschiedene Werte erfassen. Dazu braucht man dann 1023₁₀ Bit = 11 1111 1111₂, um den Maximalwert einer am Messeingang anliegenden, analogen Spannung erfassen zu können.

Zu der oben ermittelten Eingangsspannung von U_A/D-Wandler = 0,29412 * U_ges = 0,29412 * 9,41 V = 2,7677 V = 2767,7 mV wurde uns mit dem einfache Programm microbit_teil_03_prog_18.hex mit dem Quelltext microbit_teil_03_prog_18.js ein Binärwert von 815 in der Laufschrift des Programms angezeigt.

Demzufolge lassen sich mit 815 Bit insgesamt x Millivolt / Bit wie folgt auflösen:

2767,7 mV / 815 Bit = 3,395951 mV / Bit ≈ 3,4 mV / Bit

Mit 1024 Bit lassen sich also = 3,3959 mV / Bit * 1024 Bit = 3477,40 mV ≈ 3,48 V vom A/D-Wandler umwandeln. Da der „micro:bit“-Rechner aber intern nur über eine Betriebsspannung von V_CC = +3,3 V verfügt, folgt rückwärts gerechnet:

2767,7 mV / 815 = 3,395951 mV / Bit ≈ 3,4 mV / Bit <=>

2852,6 mV / x Bit = 3,4 mV / Bit → x Bit = 2852,6 mV / ( 3,4 mV / Bit ) = 839 Bit

Gegenüber dem vormals angezeigten Wert von 815 Bit entspricht der neue, berechnete Bitwert 839 einer Steigerung um +2,945 %. Das ist nicht viel und liegt im Rahmen akzeptierbarer Abweichungen bzw. Ungenauigkeiten.

3.8.3 Berechnung der Bereichsbreite des A/D-Wandlers

Wie bereits ausgeführt, handelt es sich bei dem integrierten A/D-Wandler des „micro:bit“-Rechners um einen 10 Bit Wandler mit dem sich Eingangsspannungen bis 3,3 V messen lassen. Dabei entsprechen 10 Bit dem Binärwert 11 1111 1111₂ = 1023₁₀ dezimal. Demzufolge verteilt sich die max. Eingangsspannung U_A/D-Wandler = 3,3 V des A/D-Wandlers auf den Bitbereich von 0 bis 1023 Bits, sodass sich 3,3 V / 1024 Bit = 0,00322265625 V/Bit = 3,223 mV auf 1 Bit wie folgt verteilen:

Bereichsbreite = 3,3 V / 1024 Bit = 3300 mV / 1024 Bit

= 3,223 mV/Bit = 0,003223 mV/Bit

Wenn sich dabei die Versorgungsspannung des „micro:bit“-Rechners, der über das Micro-USB-Kabel mit Strom versorgt wird, aber auf nur 3,24 V beläuft, dann folgt für die

Bereichsbreite = 3,24 V / 1024 Bit = 3240 mV / 1024 Bit

= 3,1640625 mV/Bit = 0,003164 V/Bit

Wie man unschwer sieht, wirkt sich die Versorgungsspannung des „micro:bit“-Rechners auch auf die Bereichsbreite des A/D-Wandlers aus, sodass diese mit in die Ergebnisse von Berechnungen einfließt und eventuell sogar verfälscht.

3.8.4 A/D-Wandler mit Spannungsteiler

Von einem Messgerät mit zwei Anschlussklemmen (= Zweipol) als Eingang zum Messen z.B. einer Gleichspannung erwartet man, dass an diesen keine Spannung anliegt, sofern man noch keine Spannungsquelle z.B. zwecks einer Widerstandsmessung angeschlossen hat.

Bei dem integrierten A/D-Wandler des „micro:bit“-Rechners würde man daher auch erwarten, dass am Messeingang ebenfalls keine Spannung anliegt! Wenn, ja wenn es die interne, elektronische Sicherung gegen Überlastung bzw. Kurzschluss an den Ports „Pin P0“ bis „Pin P2“ nicht gäbe, an denen die Sicherung wirksam ist, sofern man den „micro:bit“-Rechner mit dem Micro-USB-Kabel mit Strom versorgt!

Aber auch bei einer externen Stromversorgung mittels Batteriepack und den zwei nahezu neuen und unverbrauchten „1,5 Volt AA“-Batterien in Reihenschaltung verhält es sich so, dass am offenen, d.h. unbelasteten Eingang des A/D-Wandlers stets eine „Offset-Spannung“ von U_{A/D Offset} = 1,6 V anliegt.

Dazu muss man wissen, dass an den Eingang des A/D-Wandlers, d.h. konkret an den Port „Pin P2“ mit Pluspotential U_{A/D Offset} = 1,6 V, auch noch ein Widerstand mit R_{A/D Eingang} = 10 MΩ geschaltet ist. Aber das interne Hinzuschalten des Widerstandes allein würde nicht dazu führen, dass am Eingang des A/D-Wandlers bereits eine Spannung anliegt!

Bei der weiteren Berechnung aber darf man nun nicht den Fehler machen und annehmen, dass die bereits vorhandene Offset-Spannung von U_{A/D Offset} = 1,6 V als Spannungsabfall parallel zum Widerstand R_{A/D Eingang} = 10 MΩ anliegt, da es sich bei der Offset-Spannung nur um ein Spannungspotential gegenüber Pin „GND“ (= Masse) handelt!

Wenn aber am offenen, unbelasteten Port „Pin P2“ eine Offet-Spannung von U_{A/D Offset} = 1,6 V anliegt, dann muss es auch eine dazugehörige Spannungsquelle geben!

Diesbezüglich darf man schon jetzt richtig vermuten, dass es sich bei der Spannungsquelle um die interne Stromversorgung V_CC des „micro:bit“-Rechners handelt mit der dann auch der Widerstand R_{A/D Eingang} = 10 MΩ „am anderen Ende“ verbunden ist, sodass an diesem der Spannungsabfall wie folgt berechnet:

∆U_{A/D Eingang} = V_CC - U_A/D Offset = 3,24 V - 1,6 V = 1,64 V

∆U_{A/D Eingang} = ∆I_{A/D Offset} * R_{A/D Offset} →

∆I_{A/D Offset} = ∆U_{A/D Eingang} / R_{A/D Offset} = 1,64 V / 10 MΩ = 1,64 V / ( 10 * 10⁶ Ω )

= 1,64 V * 10^-6 / 10 Ω = 0,164 * 10^-6 V = 0,164 µA

Jetzt wissen wir zwar, welcher winzig kleiner Strom durch den Widerstand R_{A/D Eingang} fließt, aber das war’s dann auch schon.

Aber wir haben ja zum Glück noch unseren Spannungsteiler mit den Widerständen R₁ und R₂ (siehe Bild 29).

Wenn wir die Anschlussklemme des Widerstandes R₁ auf das Pluspotential der internen Versorgungsspannung am Port „Pin P2“ des „micro:bit“-Rechners mit U_3V = 3,24 V legen, dann lässt sich die Eingangsspannung U_{A/D Eingang} des A/D-Wandlers wie folgt berechnen:

U_{A/D Eingang} = U₂ = U_ges - U₁ = U_3V - U₁ = U_3V - I_ges * R₁

mit I_ges = U_ges / R_ges = U_3V / ( R₁ + R₂ ) folgt …

= U_3V - I_ges * R₁ = U_3V - U_3V / ( R₁ + R₂ ) * R₁

= U_3V * ( 1 - 1 / ( ( R₁ + R₂ ) ) * R₁

= 3,24 V * ( 1 - 240 KΩ / (240 KΩ + 100 KΩ ) )

= 3,24 V * ( 1 - 240 KΩ / 340 KΩ ) = 3,24 V * ( 1 - 0,705882353 )

= 3,24 V * ( 0,294117647 ) = 0,953 V

So weit die Theorie, d.h. die Berechnung der Eingangsspannung am A/D-Wandler.

Bei der Messung der Eingangsspannung mit dem integrierten Millivoltmeter in Form des A/D-Wandlers muss der im „5 x 5 LED-Matrix“-Display angezeigte Bitwert mittels der sogenannten Bereichsbreite wie folgt umgerechnet werden:

Bereichsbreite = Referenzspannung / ( Maximalwert + 1 )

= 3,24 V / (1023 Bit + 1) = 0,0031640625 V/Bit

= 0,003164 V/Bit = 3,164 mV/Bit

U_Mess U_{A/D Eingang} = U₂

= A/D-Messwert * Bereichsbreite

= 331 Bit * 0,003164 V/Bit = 1,047 V ( = +9,86 % gegenüber 0,953 V)

Als Nächstes messen wir mit dem Millivoltmeter des „micro:bit“-Rechners die Eingangsspanung am A/D-Wandler, indem wir den Pluspol (+) an den Widerstand R₁ des Spannungsteilers und den Minuspol (-) an den Pin „GND“ (= Masse) anschließen:

U_{A/D Eingang} = Referenzspannung * Spannungsteilerquotient ( siehe oben!)

= 9,41 V * 0,294117647 = 2,76764705827 V = 2,768 V

= A/D-Messwert * Bereichsbreite

= 932 Bit * 0,003164 V/Bit = 2,949 V ( = +6,54 % gegenüber Spannungsteiler )

3.8.5 Berechnung der A/D-Wandler-Bereichsgröße

Wird der A/D-Wandler mit 10 Bit an 3,24 V betrieben, so folgt für die Umrechnungen:

Bereichsbreite = Referenzspannung / ( Maximalwert + 1 )

= 3,24 V / ( 1023 + 1 ) Bit = 3,24 V / 1024 Bit = 0,003164 V/Bit

Umrechnung des A/D-Messwerts in eine Spannung

Spannung = A/D-Messwert * Referenzspannung / Maximalwert

= 932 Bit * 3,24 V / 1023 Bit

= 932 Bit * 0,0031671554 V/Bit

= 2,9517888328 V/Bit ≈ 2,952 V/Bit

3.8.6 Berechnung der Eingangsspannung am Spannungsteiler

Bisher wurde der Spannungsteiler mit den in Reihe geschalteten Widerständen R₁ und R₂ dazu benutzt, um die am Widerstand R₁ anliegende Spannung zu messen und auf einen Wert der Eingangsspannung ( < 3,3 V) des A/D-Wandlers zu reduzieren, sodass diese den A/D-Wandler nicht beschädigt: U_A/D-Mess = Bereichsbreite * max. A/D-Wert = 3,24 V / 1024 Bit * 1023 Bit = 3,29677734375 V ≈ 3,297 V.

Da aber der Spannungsteiler keine Einbahnstraße ist, lassen sich die bisherigen Berechnungen auch in umgekehrter Richtung anwenden (siehe Bild 29). Und zwar von dem angezeigten Bitwert des A/D-Wandlers (= analog-digital umgewandelter Bitwert der Eingangsspannung am Widerstand R₂) hin zur angelegten Spannung am Widerstand R₁ des Spannungsteilers:

U_R1 / U_ges = R₁ / R_ges = R₁ / ( R₁ + R₂ ) = 1 / ( 1 + R₁ / R₂ ) → Kehrwert →

U_ges / U_R1 = ( 1 + R₁ / R₂ ) →

U_ges = ( 1 + R₁ / R₂ ) * U_R1 = ( 1 + R₁ / R₂ ) * U_A/D-Eingang

= ( 1 + 240 KΩ / 100 KΩ ) * U_A/D-Eingang

= Teilspannungskoeffizient * U_A/D-Eingang

= Teilspannungskoeffiz. * A/D-Messw. * Ref. spannung / Maximalwert

= 3,4 * 932 Bit * 3,42 V / 1024 Bit = 3,4 * 932 * 0,00333984375

= 3,4 * 2,952 = 10,0368 V ≈ 10,0 V

= 3,4 * 839 Bit * 3,42 V / 1024 Bit = 3,4 * 839 * 0,00333984375

= 3,4 * 2,802 = 9,5268 V ≈ 9,5 V (… an der Batterie gemessen: 9,41 V)

Wie man sieht, kommt es tatsächlich darauf an, dass der A/D-Wandler einen möglichst genauen Bitwert als Messwert am Eingang ermittelt. Deshalb ist es unverzichtbar, dass man bei Berechnung der Bereichsbreite des A/D-Wandlers unbedingt vor der Messung die aktuelle Versorgungsspannung ermittelt! Dazu ist es dann auch notwendig, dass man dem „micro:bit“-Rechner entsprechend Zeit gibt, da dieser nicht besonders schnell ist und nicht über so viel Rechenleistung verfügt. Deshalb sollte man nicht nur einen Messwert über die aktuelle Versorgungsspannung ermitteln, sondern ein gutes Dutzend und aus der Summe dann den Mittelwert bilden! -

4. Das smarte Millivoltmeter bis 10 Volt

Wenn man sich von Google Translate das engl. Wort „smart“ übersetzen lässt, dann bekommt man „intelligent, klug, schlau, pfiffig, clever“ usw. zurück geliefert. Wenn aber Geräte (Hardware) oder eines unserer Programme (Software) intelligent sein soll, dann müsste man es mittels künstlicher Intelligenz (KI) programmieren oder diese implementieren und mit dem Programm und/oder dem Anwender interagieren, d.h. kommunizieren lassen.

Wenn aber weder das eine noch das andere der Fall ist, d.h. keine KI verbaut ist, dann bleiben für smarte Anwendungen nur noch zwei Dinge übrig: der sogenannte DAU und der engl. „intelligent programmer“ oder „intelligent developer“.

Im Zusammenhang mit der Computertechnik und deren Sicherheit sagt man ja, dass der größte (Sicherheits-) Fehler immer vor oder an der Tastatur sitzt. Und das sei nun mal der Mensch, der in der Hektik des Alltags oder vor schier unbändiger Neugier mal eben schnell auf eine E-Mail-Dateianlage eines ihm unbekannten Absenders klickt, diese öffnet und ausführt.

Wissen Sie was ein „DAU“ ist? Falls Sie das noch nicht wissen sollten, so könnte es sein, dass Sie hier und da von einem „Nerd“ als solcher bezeichnet werden. Wobei wir schon wieder bei den Vorurteilen und den Klischees sind. „DAU“ ist die deutsche Abkürzung für „dümmster, anzunehmender User (= Anwender)“, der Supergau (= größter anzunehmender Unfall) für jeden Programmierer, Entwickler, IT-Trainer oder Software-Verkäufer.

Bei den älteren Windows-Betriebssystemen wie z.B. Windows 95 oder 98 gab es gelegentlich eine Fehlermeldung beim Einschalten und Hochfahren des Windows-Rechners, die immer dann auftrat, wenn versehentlich keine Tastatur an den PC angestöpselt war. Sie lautete sinngemäß: „Es ist keine Tastatur angeschlossen! Drücken Sie bitte (die Funktionstaste) F1.“

DAUs würden das natürlich sofort machen, auf der Tastatur die Funktionstaste F1 drücken, dann die Kundenhotline anrufen und sich beschweren, dass das Ganze nicht funktioniert.

Technik affine Computeranwender wissen natürlich, dass alle herkömmlichen PC-Tastaturen drei Kontrollleuchten in Form kleiner LEDs haben, nämlich für „Num“ (= numerische Tastatur zur Zahleneingabe), „Shift“ (= Umschalttaste für dauerhaftes Schreiben in Großbuchstaben) und „Rollen“ (= Herauf- oder Herunterscrollen, z.B. im Fenster der „Eingabeaufforderung“ im Konsolemodus). Beim Einschalten und Hochfahren des PCs leuchten diese drei LEDs kurz auf, aber eben nur dann, wenn eine entsprechende PC-Tastatur angeschlossen ist! -

Wenn wir also unser Millivoltmeter bis 10 Volt, welch ein Widerspruch im Sinne des Wortes, da ein Millivoltmeter immer nur Spannungen bis zu einem Tausendstel misst und anzeigt, nicht aber bis 10 Volt, d.h. 10.000 Millivolt, ohne KI „smart“ machen wollen, dann bleibt nur noch der „smarte“ Intelligenzquotient (IQ) des Programmierers übrig! Und der ist natürlich begrenzt. Diesbezüglich könnte man auch sagen, dass wenn jemand merkt, dass er dumm ist, er nicht wirklich dumm ist, weil er ja seine eigene Dummheit spürt und erkennt. Dumm ist halt nur, wenn man gegen seine Dummheit im Sinne von vorsätzlicher Unwissenheit nicht ankämpft und sich nicht weiterbildet. -

Unser Millivoltmeter bis 10 Volt ist z.B. dann smart, wenn es die aktuell vorherrschende Betriebsspannung U_USB-Kabel oder U_Batterie misst und auswertet, d.h. in die Berechnung des Messwertes nebst Laufschriftanzeige mit einbezieht, sodass das Messergebnis nicht wider Erwarten z.B. wegen einer altersschwachen Batterie nebst deren abgesunkener Batteriespannung klammheimlich verfälscht wird!

Wenn also die aktuelle Betriebsspannung des „micro:bit“-Rechners an dem Rundanschluss U_{Pin 3V} = 3,24 V und nicht U_{Pin 3V} = 3,3 V beträgt, - und für ein Millivoltmeter sind das genau 60 mV (≈ 1,82 %) zu wenig - dann sollten wir diese Abweichung bei der Messung nebst Berechnung berücksichtigen!

Das Problem dabei ist aber, dass man mit dem „Basic“-Befehlsvorrat in JavaScript des „micro:bit“-Rechners wider Erwarten nicht mit Fließkommazahlen der Dezimalrechnung rechnen kann. Da wir aber trotzdem mit der Spannung von 3,24 V rechnen wollen, bleibt uns deshalb nichts anderes übrig, als den Wert 3,24 mit 100 zu multiplizieren, sodass aus den 3,24 der Wert 324 wird.

Im Prinzip haben wir aber nichts anderes gemacht als den Wert 3,24 mit 100 erweitert, sodass sich als Folge dessen das Komma um zwei Stellen nach rechts verschiebt, wobei sich der Vorgang des Erweiterns eigentlich nur auf das Bruchrechnen bezieht. Damit sich später beim Ergebniswert wieder die richtige, d.h. vorherige dezimale Wertigkeit einstellt, muss man den vorläufigen Ergebniswert wieder durch 100 dividieren! Anderenfalls würde sich ein falsches Ergebnis einstellen.

Wenn aber den Wert 324 wieder durch 100 dividiert, dann landet man wieder bei einer Dezimalzahl mit zwei Nachkommastellen mit dem das „micro:bit“-Programm nichts anfangen kann, sodass die beiden Nachkommastellen einfach abgeschnitten werden: 320 / 100 = 3,24 → 3 (siehe Programm microbit_teil_03_prog_21.hex mit dem Quelltext microbit_teil_03_prog_21.js).

So wie es im Moment aussieht, lassen sich die beiden Nachkommastellen nicht wieder zurückgewinnen, oder vielleicht doch?

Wenn es darum geht, dass sich die beiden Nachkommastellen wieder zurückgewinnen lassen und wir das im Voraus wissen, dann muss man einfach mit 100 ins Quadrat, d.h. mit 100² = 100 * 100 = 10 000 multiplizieren: 3,24 * 10 000 = 32 400, um später bei der Division durch 100 wieder auf den Wert 324 (siehe Programm microbit_teil_03_prog_22.hex mit dem Quelltext microbit_teil_03_prog_22.js).

Wenn man dann im nächsten Schritt wieder auf den Wert 3,24 kommen will, müsste man ein weiteres Mal durch 100 dividieren, aber wegen der fehlenden Fließkommarechnung würde sich dann wieder der Ergebniswert 3 einstellen.

Was wir jetzt also bräuchten, wäre ein kleiner, geschickter Trick, um die Dezimalzahl 3,24 für spätere Zwecke wieder zum Leben zu erwecken bzw. die Nachkommastellen wieder restaurieren zu können. Wenn man aber später wieder Dinge restaurieren, d.h. wieder herstellen möchte, dann müsste man diese vorab konservieren. Wie aber konserviert man die Dezimalzahl 3,24?

Wie man der Dezimalzahl 3,24 ansieht, setzt sich diese aus zwei Zahlen zusammen, nämlich aus dem ganzzahligen Wert 3 und dem Dezimalwert 24 = 24/100 = 0,24. Demzufolge müssten wir die Dezimalzahl 3,24 nur in ihre beiden Bestandteile „ganzzahlig“ und „Nachkommazahl“ zerlegen, bei der späteren Berechnung getrennt behandeln und zum Ergebniswert wieder zusammensetzen: 3,24 = 3 + 0,24 = 3 + 24/100 = 3 Einer + 24 Hundertstel = 3 Einer + 240 Tausendstel

Mit dem Programm microbit_teil_03_prog_23.hex mit dem Quelltext microbit_teil_03_prog_23.js lässt sich das Ganze problemlos ausprobieren. -

Hier geht’s dann weiter zum „micro:bit“-Programmieren, Teil 4“

[Home ] [zurück ] [ Seitenanfang ] [ Teil 2 ] [ Teil 4 ]