[ Home ] [ zurück ] [ Seitenende ]

micro:bit-Programmieren, Teil 4

Antworten auf die gestellten Fragen

Bekanntlich gibt es ja keine dumme Fragen, sondern nur dumme Antworten. Denn wer fragt, macht sich ja konkret Gedanken zu und über einen bestimmten Sachverhalt, hinterfragt diesen kritisch. Wer also nicht fragt, hat schon verloren, weil er sich nicht wirklich für bestimmte Dinge des Lebens interessiert. -

Frage 1

Jetzt wissen wir, dass wir das Anschlusskabel am Port „Pin P0“ des Sensors gefahrlos mit der Spannungsversorgung am Pin „3V“ mit U_3V = 3,17 V verbinden können, ohne dass es einen Kurzschluss gibt!

Was aber passiert mit dem „Grumpy Cat“? Wechselt dieser seinen Gesichtsausdruck zum „Smiley Cat“? Probieren Sie es aus und begründen Sie das Ergebnis!

Antwort zu Frage 1

Wie wir wissen, lässt sich die Leerlaufspannung am Port „Pin P0“ des Sensors messen. Dabei beträgt diese im vorliegenden Fall: U_{Pin P0} = 1,57 V, sodass der Port „Pin P0“ des Sensors auf positivem Spannungspotential liegt!

Wenn man dann das Anschlusskabel am Port „Pin P0“ des Sensors mit der Spannungsversorgung am Pin „3V“ mit U_3V = 3,17 V verbindet, dann hebt man das bisherige positive Spannungspotential auf einen noch höheren positiven Wert an, nämlich auf den der Spannungsversorgung am Pin „3V“, sodass überhaupt kein Strom mehr aus dem Sensor heraus in Richtung der (Geräte-) Masse (= Pin „GND“) fließen kann! Demzufolge bleibt es bei der Anzeige mit dem „Grumpy Cat“. [ zurück zur Frage 1]

Frage 2

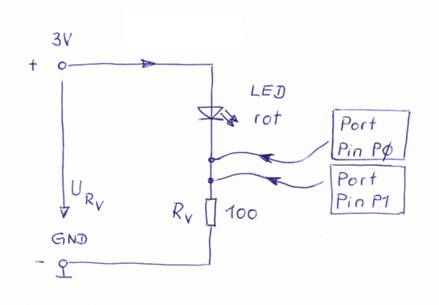
Als Nächstes verbinden wir das Anschlusskabel am Port „Pin P0“ des Sensors mit dem Spannungsteiler und zwar genau in der Mitte, d.h. am Verbindungspunkt der roten LED mit dem Vorwiderstand R_V (siehe Bild 36 – Schaltung zum „Grumpy Cat“).

Was passiert jetzt mit dem „Grumpy Cat“? Wechselt dieser jetzt endlich seinen Gesichtsausdruck zum „Smiley Cat“?

Antwort zu Frage 2

Ja, der „Grumpy Cat“ wechselt jetzt endlich seinen Gesichtsausdruck zum „Smiley Cat“, weil wir das bisher positive Spannungspotential am Port „Pin P0“ des Sensors mit der Spannungsversorgung am Pin „3V“ mit U_3V = 3,17 V maßgeblich auf den Spannungsabfall U_RV am Vorwiderstand R_V wie folgt absenken:

U = I * R →

U_RV = I * R_V = 9 mA * 100 Ω = 9 * 10^-3 A * 100 V/A = 900 * 10^-3 A = 900 mV = 0,9 V

Der Strom sucht sich ja bekanntlich immer den Weg des geringsten Widerstandes. Aber nicht nur, sondern auch das möglichst niedrigste Spannungsgefälle gegenüber Masse. Demzufolge müsste der Vorwiderstand R_V kleiner sein als der Durchflusswiderstand R_F der roten LED:

R_F = U_F / I = ( U_3V - U_RV ) / I = ( 3,17 V - 0,9 V ) / 9 mA = 2,27 V / 9 mA

= 0,252 KΩ = 252 Ω → R_V < R_F mit R_V = 100 Ω (siehe oben).

Jetzt haben wir den Beweis, dass der größere Spannungsabfall U_F an der roten LED nicht nur dafür sorgt, dass diese entsprechend hell leuchtet, sondern gleichzeitig dafür maßgeblich ist, dass der Spannungsabfall U_RV am Vorwiderstand R_V umso geringer ausfällt.

Zusammenfassend lässt sich sagen, dass der sehr kleine Strom des Sensors am Port „Pin P0“ aus diesem heraus und über den Vorwiderstand R_V gegen Masse abfließt, sodass der „Grumpy Cat“ plötzlich als „Smiley Cat“ freundlich lächelt.

Man muss also das „Grumpy Cat“ nur unter Strom setzen, damit es freundlich lächelt! Ob das bei einer Katze auch funktioniert? J [ zurück zur Frage 2]

Antwort zu Frage 3

Als Letztes verbinden wir das Anschlusskabel am Port „Pin P0“ des Sensors mit der Masse (= Pin „GND“) der „micro:bit“-Stromversorgung.

Was passiert jetzt mit dem „Grumpy Cat“? Wechselt dieser jetzt seinen Gesichtsausdruck zum „Smiley Cat“? Finden Sie es heraus, indem Sie es ausprobieren!

Ja, der „Grumpy Cat“ wechselt jetzt wieder seinen Gesichtsausdruck zum „Smiley Cat“, weil wir es dem Sensor ermöglichen, dass der winzig kleine Strom jetzt direkt ohne Umweg gegen Masse (= Pin „GND“) abfließen kann! [ zurück zur Frage 3]

Antwort zu Frage 4

Jetzt wo wir wissen, dass der Sensor am Port „Pin P0“ einen winzig kleinen Ausgangsstrom nach außen abgibt, wenn der Stromkreis gegen Masse (= Pin „GND“) der „micro:bit“-Stromversorgung geschlossen wird, stellt sich die Frage, ab welcher Ausgangsspannung der Sensor reagiert und den „Grumpy Cat“ auf „Smiley Cat“ umschaltet.

Finden Sie heraus, ab welcher Ausgangsspannung der Sensor umschaltet und begründen Sie Ihre Entscheidung bzw. Vermutung!

Wie bereits gesagt und berechnet wurde, liegt der Sensor am Port „Pin P0“ über einen quasi Offset-Widerstand von R_{Pin P0} = 10 MΩ auf dem positiven Spannungspotential von U_3V = 3,17 V, sodass sich am Sensor selbst die gemessene Leerlaufspannung von U_{Pin P0} = 1,57 V einstellt. Das wäre dann vermutlich die Spannung, wo der Sensor den „Grumpy Cat“ auf „Smiley Cat“ umschaltet. [ zurück zur Frage 4]

Frage 5

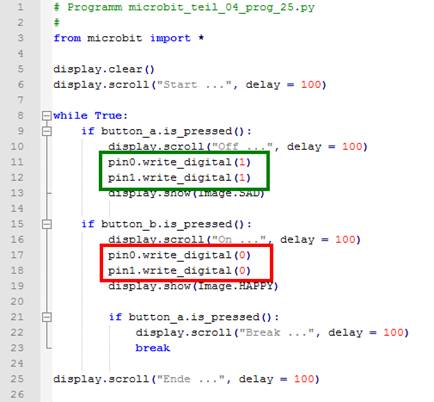
Studieren Sie das obenstehende Programm (siehe Bild 40) und probieren Sie es mehrfach aus, indem Sie die Taster A und B drücken und die rote LED mehrfach ein- und ausschalten. Schauen Sie sich außerdem die Reihenschaltung von roter LED und Vorwiderstand R_V an (siehe Bild 36).

Erklären Sie, wie man mit dem Strom vom Port „Pin P1“ des „mirco:bit“-Rechners die rote LED (fast vollständig) ausschalten kann, sodass diese nur noch glimmt.

Nach welchem Prinzip funktioniert die Reihenschaltung, sodass man mit einem Strom einen anderen Strom, nämlich den durch die rote LED, ausschalten kann?

Antwort zu Frage 5

Damit durch einen Zweipol wie z.B. durch die rote LED ein Strom fließen kann, bedarf es eines maßgeblichen Potentialunterschieds in Form eines Ladungsträgerüberschusses am Pluspol sowie eines Ladungsträgermangels am Minuspol der LED (→ techn. Stromrichtung). Dabei wird der Potentialunterschied in einem elektrischen Stromkreis mittels der elektrischen Spannung U gemessen.

Wie bereits an anderer Stelle erläutert, fängt unsere rote LED an zu leuchten, sobald die sogenannte Flussspannung U_F (= Durchlassspannung) zwischen Plus- und Minuspol der LED mehr als U_F > 1,6 V beträgt.

Bei einer sogenannten Schwellenspannung von U_Sperr < 0,7 V (… bei Siliziumdioden) sperrt die LED den Stromfluss, sodass diese nicht mehr leuchtet.

Wenn man erreichen will, dass die rote LED nicht mehr leuchtet, dann gibt es praktisch drei Methoden mit denen sich das bewerkstelligen lässt:

1. durch Abschalten der Stromzufuhr zur LED,

Diese Methode lässt sich am einfachsten durch einen Ein- und Ausschalter bewerkstelligen mit dem sich die Stromzufuhr zur LED unterbrechen lässt.

2. durch Umleiten der Stromzufuhr an der LED vorbei,

Wenn man parallel zur LED einen Ein- und Ausschalter anbringt und diesen einschaltet, dann lässt sich der Strom, der sonst die LED zum Leuchten bringen würde, parallel an dieser vorbei leiten, sodass die LED ausgeht, weil es zwischen den Anschlussklemmen der LED keinen Potentialunterschied mehr gibt.

Dabei gilt es zu beachten, dass es durch das parallele Umleiten des Stromes an der LED vorbei zu einem deutlich höheren Stromfluss kommt, da der Durchlasswiderstand der LED durch den Schalter überbrückt wird!

3. durch Herbeiführen eines höheren Spannungspotentials am Minuspol(!) der LED

Wie wir wissen, braucht die rote LED um zu leuchten eine parallel anliegende Flussspannung U_F von U_F > 1,6 V.

Im vorliegenden Fall sind das konkret U_F = 2,24 V bei einer Versorgungsspannung von U_3V = 3,16 V, sodass für den Vorwiderstand R_V nur noch ein Spannungsabfall von

U_RV = U_3V – U_F = 3,16 V – 2,24 V = 0,92 V übrig bleibt.

Wenn man nun erreichen will, dass die rote LED nicht mehr leuchtet, dann muss man dafür sorgen, dass am Minuspol(!) (= Mittelpunkt des Spannungsteilers) der LED eine Spannung von

U_off = U_RV + U_LED = 0,92 V + 2,24 V = 3,16 V

= U_3V ( → logisch!)

Für die praktische Umsetzung bräuchten wir also eine Spannungsquelle, die exakt eine Spannung von U_off = 3,16 V liefert und deren Pluspol dann an den Mittelpunkt des Spannungsteilers angeschlossen wird! Der Minuspol der Spannungsquelle muss dabei dann auf Pin „GND“ (= Masse) gelegt werden!

Wegen U_off = U_3V = 3,16 V wäre es natürlich am einfachsten, wenn wir den Mittelpunkt des Spannungsteilers mittels eines Kabels einfach auf das Pluspotential der Spannungsversorgung am großen Rundanschluss „Pin 3V“ legen würden! Aber dann ließe sich unsere rote LED quasi nur ausschalten, aber eben nicht flexibel mittels der programmierten Taster A und B ein- und ausschalten!

[ zurück zur Frage 5]

Frage 6

Wenn man die rote LED mit dem Taster A ausschaltet, dann fällt einem sofort auf, dass die LED wider Erwarten nicht ganz ausgeht, sondern immer noch etwas glimmt.

Weshalb ist das so? Versuche eine Antwort zu geben und begründe diese!

Antwort zu Frage 6

Um die rote LED mit dem Taster A ganz ausschalten zu können, müsste am Mittelpunkt des Spannungsteilers eine Spannung von U_off = U_3V = 3,16 V anliegen. Tut es aber nicht!

Da die Spannung am Mittelpunkt des Spannungsteilers nur U_off = 1,42 V beträgt, fehlen noch

∆U_off = U_3V – U_off = 3,16 V - 1,42 V = 1,74 V,

um das Spannungspotential am Mittelpunkt des Spannungsteilers noch größer werden zu lassen, sodass dann auch ein größerer Strom gegen Masse (= Pin „GND“) abfließen würde.

Der Grund dafür könnte der sein, dass die mittels Taster A und B ein- und ausschaltbare Spannungsquelle am Port „Pin P1“ entweder eine zu niedrige Spannung oder einen zu geringen Strom abgibt. Oder beides!

Wenn unsere Spannungsquelle am Port „Pin P1“ eine zu niedrige Spannung und einen zu geringen Strom abgibt, dann liegt es eindeutig daran, dass diese zu schwach ist, d.h. über zu wenig Leistung verfügt!

Damit Sie besser verstehen, was man unter Leistung versteht, nachfolgend ein Witz dazu.

Ein italienischer Bauarbeiter auf einer Baustelle in Deutschland beschwert sich bei seinem Chef und sagt: „Du Chef, ich brauche eine neue Schubkarre! Die alte quietscht andauernd! Das nervt!“

Fragt der Chef zurück: „Sag mal Adriano, wie quietscht denn die Schubkarre?“

Sagt der Adriano zum Chef: „Quietsch, … lange Pause …, quietsch, … lange Pause …, quietsch, … lange Pause …, quietsch!“

Antwortet der Chef: „Adriano, pack deine sieben Sachen ein und hau ab! Du bist mit sofortiger Wirkung fristlos entlassen!“

„Aber Chef!“ sagt Adriano „Das kannst du doch nicht machen! Ich habe doch gar nichts getan! Was ist denn der Grund für die Entlassung?“

Sagt der Chef zum Adriano: „In Deutschland macht die Schubkarre ganz schnell quietsch, quietsch, quietsch!“

So jetzt wissen Sie, wie man die Leistung verbessert! Indem man bei der Schubkarre die Drehzahl des Rades bzw. dessen Geschwindigkeit durch eine höhere Leistung vergrößert.

Und, was macht der Chef, wenn sich die Schubkarre wegen des hohen Transportgewichts und des holprigen Geländes nicht schneller bewegen lässt, sich also die Leistung einer Schubkarre nicht steigern lässt? Ganz einfach, er kauft eine zweite Schubkarre, um auf diese Weise die Transportkapazität und Transportleistung zu verdoppeln.

Mehr Leistung bedeutet nämlich nichts anderes als die gleiche Arbeit in der hälftigen Arbeitszeit zu verrichten:

Arbeit, engl. „work“, ist = mechanische Leistung x Zeit → W_mech = P_mech * t_Dauer

Ähnlich verhält es sich übrigens bei der elektrischen Leistung P_el:

W_el = P_el * t_Dauer → P_el = W_el / t_Dauer → 2 P_el = 2 W_el / t_Dauer = W_el / ( t_Dauer / 2 )

Mit P_el = U * I = I² * R = U² / R folgt für die doppelte Leistung:

2 P_el = 2 I² * R_V = 2 U² / R_V

Wenn sich also am Spannungsteiler selbst nichts ändert, weil sich an den Bauteilen nichts ändert, der Vorwiderstand R_V seinen Widerstandswert mit R_V = 100 Ω unverändert beibehält, dann lässt sich die Leistung an diesem nur verdoppeln, indem man

a) die Versorgungsspanung am oder

b) die Stromstärke

durch den Spannungsteiler verdoppelt!

Dabei lässt sich die Spannung, die wir aus der programmierten Spannungsquelle am Port „Pin P1“ beziehen nicht einfach so verdoppeln, indem man eine zweite Spannungsquelle am Port „Pin P0“ in Reihe zur ebensolchen am Port „Pin P1“ schaltet, da beide Spannungsquellen jeweils an die gemeinsame Masse (Pin „GND“) angebunden sind!

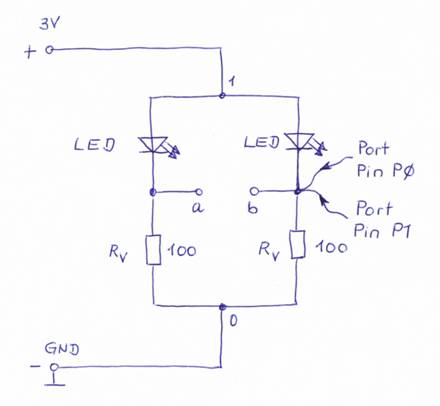
Demzufolge bleibt also nur noch die Möglichkeit übrig, dass man die Stromstärke durch den Vorwiderstand R_V verdoppelt, indem man zwei programmierbare Spannungsquellen an den Ports „Pin P0“ und „Pin P1“ parallel schaltet!

Praktisch geschieht dies, indem man den gemeinsamen Masseanschluss beider Spannungsquellen unverändert beibehält und die beiden Pluspole der einzelnen Spannungsquellen von den Ports „Pin P0“ und „Pin P1“ abgehend mit dem Mittelanschluss des Spannungsteilers, d.h. mit dem Vorwiderstand R_V wie folgt verbindet:

(Bild 41 –Stromverdoppelung durch Parallelschalten der Ports)

So, jetzt wird es vom Verständnis her schwierig. Durch das parallele Hinzuschalten der zweiten, programmierbaren Spannungsquelle haben wir den Stromfluss und die Stromstärke durch den Vorwiderstand R_V verdoppelt, von vormals I_RV = 9 mA

I_RV = U_RV / R_V = ( U_3V - U_LED ) / R_V

= ( 3,16 V - 2,26 V ) / 100 Ω = 0,9 V / 100 Ω = 0,009 A = 9 mA

auf nunmehr

I_RV = U_RV / R_V

= 2,15 V / 100 Ω = 2,15 V / 100 Ω = 0,0215 A = 21,5 mA ( … gemessen: 20,9 mA)

Leistungsaufnahme am Vorwiderstand R_V:

P_RV = U_RV * I_RV = 2,15 V * 21,5 mA = 46,225 mW ≈ 46 mW

Da der Vorwiderstand R_V bis zu 1/8 W = 0,125 W = 125 mW Wärmeverlustleistung verkraftet, liegen wir mit der Leistungsaufnahme von 46 mW absolut im grünen Bereich.

Dass jetzt der Strom durch den Vorwiderstand R_V etwas größer als 2 * 9 mA = 18 mA ausfällt, liegt daran, dass die beiden parallel geschalteten und programmierbaren Spannungsquellen an den Ports „Pin P0“ und „Pin P1“ noch nicht abgeglichen wurden, sodass diese etwas mehr Strom am Mittelanschluss des Spannungsteilers einspeisen als notwendig wäre, um die rote LED komplett dunkel werden zu lassen.

Da sich der Strom durch den Vorwiderstand R_V mit 21,5 mA / 2 = 10,75 mA für jede Spannungsquelle an den Ports „Pin P0“ und „Pin P1“ liegen wir auch hier im absolut im grünen Bereich, sodass man die Schaltung mit dem „micro:bit“-Rechner dauerhaft ohne Schaden zu nehmen eingeschaltet lassen kann!

So, nachdem nun die Hardware, d.h. der Spannungsteiler (= Reihenschaltung der roten LED mit Vorwiderstand R_V und Kabelverbindungen vom Mittelanschluss des Spannungsteilers an die Ports „Pin P0“ und „Pin P1“) entsprechend eingerichtet und hergestellt wurden, nehmen wir den „micro:bit“-Rechner mit dem neuen Programm „microbit_teil_04_prog_25.hex“ mit dem Quelltext „microbit_teil_04_prog_25.py in Betrieb:

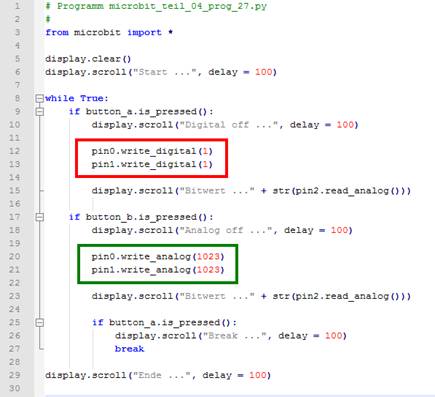
(Bild 42 – Spannungsverdoppelung am Vorwiderstand)

Wie man im obenstehenden Bild im Quellkode sieht, gibt es jetzt an den Ports „Pin P0“ und „Pin P1“ zwei digitale Spannungsquellen, die sich per Tastendruck auf die Taster A oder B ein- und ausschalten lassen (siehe grüner und roter Kasten).

Fazit

Spannungsquellen lassen sich bei gemeinsamer Masse ohne Weiteres arbeitsteilig parallel schalten, sodass dann durch den Vorwiderstand R_V nahezu ein doppelt so großer Laststrom fließt!

Aufgrund des Ohmschen Gesetzes bewirkt der doppelt so große Laststrom durch den Vorwiderstand R_V, dass an diesem auch eine nahezu doppelt so große Spannung abfällt! Dabei kann die Spannung aber nicht größer werden als die Versorgungsspannung des „micro:bit“-Rechners am großen Rundanschluss „Pin 3V“ gegen Masse mit dem Pin „GND“!

Die Spannung an einem Lastwiderstand lässt sich also nicht nur durch das in Reihe schalten zweier Spannungsquellen bei der Spannungsversorgung, sondern vielmehr auch durch das Parallelschalten zweier Spannungsquellen am Einspeisepunkt, z.B. beim Mittelanschluss eines Spannungsteilers!

Dass sich das auch mittels zweier programmierbarer Spannungsquellen des „micro:bit“-Rechners realisieren lässt, ist eine kleine Sensation, da diese Möglichkeit, eine Spannung an einem Widerstand zu verdoppeln, praktisch in keinem Lehrbuch beschrieben wird!

Das Arbeiten mit programmierbaren Spannungs- oder auch Stromquellen sollte deshalb unbedingt zum (Standard-) Repertoire bei Gerätschaften des Internets der Dinge, engl. „Internet of Things“ (IoT), gehören! -

[ zurück zur Frage 6]

Frage 7

Starte das Programm „microbit_teil_04_prog_25.hex“ mit dem Quelltext „microbit_teil_04_prog_25.py“ und betätige zuerst den Taster A, sodass die rote LED nicht mehr leuchtet und total dunkel ist.

Betätige als Nächstes den Taster B, sodass die rote LED nach 10 s ausgeschaltet wird, aber trotzdem noch still und leise vor sich hin glimmt!

Erkläre, weshalb sich die rote LED wider Erwarten nicht komplett ausschalten lässt, obwohl ja die beiden analogen Spannungsquellen an den Ports „Pin P0“ und „Pin P1“ auf ihre binären Maximalwerte von 1023₂ aufgeregelt wurden!

Antwort zur Frage 7

Kurz gesagt, darf man Äpfel nicht mit Birnen vergleichen, ist digital eben nicht analog! Demzufolge verhält sich eine analoge Spannungsquelle, auch wenn sie sich programmieren lässt, anders als eine digitale!

So lässt sich eine digitale Spannungsquelle nur ein- oder ausschalten! „Aus“ („0“) bedeutet dabei aber nicht automatisch, dass die Ausgangsspannung an der digitalen Spannungsquelle dann auch tatsächlich null Volt beträgt und der Ausgang potentialmäßig auf Masse gelegt wird!

Wenn man nämlich in der Digitaltechnik mehrere Gatter wie z.B. UND, ODER, negatives UND, negatives ODER, exklusives ODER oder NICHT, aber auch sogenannte („RS“- oder „JK“-) Flipflops zusammen schaltet, dann fällt es dem einen oder anderem Gatter schwer, einen Spannungszustand wie z.B. Masse = null Volt zu erkennen, weil z.B. die verwendeten (Silizium-) Transistoren erst ab einer Basisspannung UBE > 0,7 V elektrisch leitend werden. Wenn man einen Transistor in die sogenannte Sättigung fährt, dann beläuft sich die Kollektor-Emitter-Spannung U_CE auf den Bereich von kleiner als 0,4 < U_CE < 2 V.

>> Ist ein Transistor dagegen voll durchgesteuert (bei einem Silizium-Transistor üblicherweise bei U_BE = 0,7 V), fällt noch immer ein kleiner Teil der Betriebsspannung an der Kollektor-Emitter-Strecke ab. Im voll durchgesteuerten Zustand spricht man dann von der Sättigungsspannung eines Transistors, was auch als U_CE sat bezeichnet wird. Ein für einen Silizium-Transistor üblicher Wert ist U_{CE sat} = 0,2 V, bei Darlington-Transistoren um 0,9 bis 2,5 V. << (Quelle: Wikipedia)

>> Wird ein Flipflop zum Beispiel in Transistor-Transistor-Logik (TTL) aufgebaut, dann entspricht der Zustand „gesetzt“ einer Spannung von 2,4 bis 5 Volt am Ausgang Q. An dem negierten Ausgang Q liegen dann 0 bis 0,4 Volt an. << (Quelle: Wikipedia)

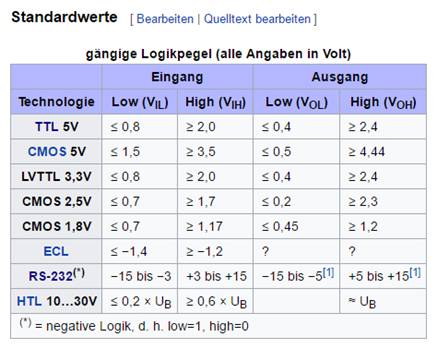
Dabei gilt es aber zu beachten, dass bei Mikroprozessoren in Mikrocontrollern aus unterschiedlichen Gründen wie z.B. Platzbedarf, Stromverbrauch, Verlustwärme usw. keine herkömmlichen Silizium-Transistoren wie in TTL-Schaltungen zum Einsatz kommen.

>> Eine hohe Spannung ist als High-Pegel (in positiver Logik eine logische 1) definiert, eine niedrige Spannung wird als Low-Pegel bezeichnet (in positiver Logik eine logische 0). Die Schaltkreise sind so dimensioniert, dass Eingangsspannungen U_E < 0,8 V als Low-Pegel, und U_E > 2,0 V als High-Pegel erkannt werden. Die Ausgangsspannung U_A beträgt typisch < 0,4 V für den Low-Pegel und > 2,4 V für den High-Pegel bei der zulässigen Last. Der statische Störabstand beträgt somit sowohl für High- als auch für Low-Pegel 0,4 V.

Logische Bausteine in TTL-Technik haben gegenüber CMOS-Bausteinen den Vorteil, dass sie unempfindlicher gegenüber elektrostatischen Entladungen sind. Der Nachteil liegt wegen der stromgesteuerten Transistoren in einer im Vergleich zu CMOS deutlich höheren Leistungsaufnahme (Stromverbrauch) bei statischem Betrieb. << (Quelle: Wikipedia)

(Bild 44 – Logikpegel in der Digitaltechnik bei Mikrocontrollern)

Was wir jetzt bräuchten, wäre eine regelbares Netzteil, um mit diesem verschiedene Logikpegel einstellen und ausprobieren zu können. Und zwar für den digitalen Eingang an einem der Ports „Pin P0“ bis „Pin P2“. Aber auch die Logikpegel am digitalen Ausgang an einem der Ports „Pin P0“ bis „Pin P2“ sollten dabei untersucht werden.

Da wir der Ursache für das schwache Glimmen der roten LED im Falle der analogen Ausgangsspannung an den beiden Ports „Pin P0“ und „Pin P1“ untersuchen und herausfinden wollen (siehe Bild 41 weiter oben), verwenden wir eine sogenannte „Wheatstone Messbrücke“ bei der zwei gegenüberliegende Spannungsteiler, ähnlich dem Großbuchstaben „H“, spannungsmäßig miteinander verglichen werden:

(Bild 45 – Wheatstone Messbrücke)

Dabei bietet die Wheatstone Messbrücke den Vorteil, dass alle beiden Spannungsteiler (links und rechts) an ein- und derselben, gemeinsamen Versorgungsspanung U_3V betrieben werden, betrieben werden müssen, damit die Brücke bestimmungsgemäß funktioniert.

Zum besseren Verständnis kann man sich die Messbrücke auch als Tafel- oder Balkenwaage vorstellen, wobei der linke Spannungsteiler der linken Waagschale und der rechte Spannungsteiler der rechten Waagschale entspricht. Dabei befinden sich die beiden Wiegezungen (=Metallfahnen) bei der Tafelwaage, mit denen sich das Gleichgewicht beider Waagschalen ablesen lässt, in der Mitte der Waage, sodass die Anzeige bei der Messbrücke der Differenzspannung U_ab entspricht (siehe oben).

Wenn man mit der Tafelwaage im Haushalt das Wägegut wie z.B. Zucker, Mehl, Milch und Zutaten für einen Kuchen messen will, dann benötigt man dazu unterschiedliche Normgewichte, die man z.B. auf die linke Waagschale legt und dann das Wägegut in der rechten Waagschale so lange nachfüllt bis das Gleichgewicht hergestellt ist. Demzufolge lässt sich mit einer Tafel- oder Balkenwaage nur das Gewicht indirekt messen. Eben genau so wie bei der Wheatstone Messbrücke.

Bei der obenstehenden Schaltung im Bild 45 wird aber die Messbrücke zweckentfremdet bzw. manipuliert, weil wir beim rechten Spannungsteiler zwei gegen Masse parallel geschaltete, programmierbare Spannungsquellen mit den Ports „Pin P0“ und „Pin P1“ zuschalten mit dem Ziel die rechte rote LED dunkel zu regeln, sodass diese entweder vollkommen erlischt oder nur noch ganz schwach glimmt.

Da die beiden gegen Masse parallel geschalteten, programmierbaren Spannungsquellen mit den Ports „Pin P0“ und „Pin P1“ am Vorwiderstand R_V einen fast doppelt so großen Strom bewirken, stellt sich an diesem gemäß dem Ohmeschen Gesetz bzw. der Spannungsteilerformel dann auch ein fast doppelt so großer Spannungsabfall U_RV ein mit der Folge, dass für die rechte rote LED nicht mehr genügend Spannung „übrig bleibt“, um noch hell leuchten zu können:

U_{LED R} = U_3V – U_RV = 3,09 V – 2,12 V = 0,97 V < U_F < 1,6 V

Zum Vergleich folgt für die linke, rote LED ohne Spannungseinspeisung:

U_{LED R} = U_3V – U_RV = 3,09 V – 1,08 V = 2,01 V > U_F > 1,6 V

Diesbezüglich muss aber noch darauf hingewiesen werden, dass bei der obenstehenden Schaltung im Bild 45 unbedingt zwei gleichartige, absolut identische rote LEDs als auch Vorwiderstände verwendet werden müssen, damit die noch folgenden Messungen und Berechnung zu richtigen Ergebnissen führen.

Erwähnt werden muss auch noch, dass der linke Spannungsteiler nicht nur als Referenz, d.h. für den Vergleich mit dem rechten Spannungsteiler dient, sondern auch dazu, die angeschlossene Spannungsversorgung mit einer „Grundlast“ zu beaufschlagen, sodass diese auch beim Zuschalten der beiden zusätzlichen Spannungsquellen am Port „Pin P0“ und „Pin P1“ stabil bleibt. Aus diesem Grund wurde dann auch die externe Stromversorgung des „micro:bit“-Rechners über das „Micro USB 2.0“-Kabel mit einer PowerBank mit Lithium-Ionen-Akku vorgenommen, da diese eine stabilere Versorgungsspannung zur Verfügung stellt als der USB-Anschluss am PC.

Zur obenstehenden Schaltung im Bild 45 mit der Wheatstone Messbrücke gehört dann natürlich auch noch das entsprechende Programm „microbit_teil_04_prog_27.hex“ mit dem Quelltext „microbit_teil_04_prog_27.py“:

(Bild 46 – Programm zur Wheatstone Messbrücke)

Bedienungsanleitung

zum Programm „microbit_teil_04_prog_27.hex“ mit dem Quelltext „microbit_teil_04_prog_27.py“

1. Starten und Ausführen des Programms

Das in den Arbeitsspeicher des „micro:bit“-Rechners geflashte Programm startet sich nach wenigen Sekunden von allein und zeigt im Display die programmierte Laufschrift „Start ...“ an.

Dabei verhält es sich, die beiden roten LEDs, die mit dem Vorwiderstand R_V in Reihe geschaltet sind, gleich hell leuchten

2. Mit Taster A die rechte LED digital ausschalten

Ein elektrischer Verbraucher wie z.B. die rechte rote LED lässt sich nicht nur durch Unterbrechen der Stromzufuhr ausschalten, sondern auch durch das Herstellen der Potentialgleichheit an den Anschlussklemmen, sodass es keinen Spannungsabfall mehr an der roten LED gibt, der diese leuchten lässt.

Durch das Betätigen des Tasters A werden die beiden digital gesteuerten und parallel geschalteten Spannungsquellen an den Ports „Pin P0“ und „Pin P1“ eingeschaltet, sodass sich die Spannung am Vorwiderstand R_V fast verdoppelt, während sie sich an der roten LED halbiert, sodass diese nicht mehr leuchtet.

Beim Betätigen des Tasters A erscheint als Erstes die Laufschrift „Digital off ...“ und anschließend nach dem Ausschalten der LED die Anzeige des Bitwertes des Spannungsabfalls U_b0 gegen Masse am Vorwiderstand R_V (siehe Bild 45).

3. Mit Taster B die rechte LED analog ausschalten

Durch das Betätigen des Tasters B werden die beiden analog gesteuerten und parallel geschalteten Spannungsquellen an den Ports „Pin P0“ und „Pin P1“ eingeschaltet, sodass sich die Spannung am Vorwiderstand R_V fast verdoppelt, während sie sich an der roten LED halbiert, sodass diese nicht mehr leuchtet, sondern nur noch ganz schwach glimmt.

Beim Betätigen des Tasters B erscheint als Erstes die Laufschrift „Analog off ...“ und anschließend nach dem Ausschalten der LED die Anzeige des Bitwertes des Spannungsabfalls U_b0 gegen Masse am Vorwiderstand R_V (siehe Bild 45).

4. Hin- und Herschalten mit den Tastern A und B

Wenn man nach dem Einschalten des Programms immer wieder mal einen der Taster A und B betätigt, um z.B. einen Messwert erneut abzulesen oder um zu testen, wie die rote LED ihre Helligkeit verändert, dann muss man jedes Mal bevor man einen anderen Taster betätigt, den „micro:bit“-Rechner mit seinem Programm resetten, d.h. neu starten, um den internen, integrierten (Kurzschlussstrom-) Schutzschalter für die Strombegrenzung wieder zu deaktiveren, damit dieser beim Betätigen des Tasters A nicht mehr aktiv ist und die Messung verfälscht!

5. Mit dem „Reset“-Taster alles wieder auf Anfang setzen

Auf der Rückseite des „micro:bit“-Rechners befindet sich ein sogenannter „Reset“-Taster mit dem sich der Rechner neu starten lässt. Dabei wird dann auch das zuvor in den Arbeitsspeicher geflashte Programm wieder neu gestartet!

Wenn man die Taster A und B abwechselnd betätigt, dann muss man jedes Mal zwischen dem Umschalten einen sogenannten „Reset“ des „micro:bit“-Rechners am rückwärtigen „Reset“-Taster durchführen, um den internen, integrierten (Kurzschlussstrom-) Schutzschalter für die Strombegrenzung wieder zu deaktiveren!

So, nun ist es an der Zeit ein paar Messungen vorzunehmen, um dem Phänomen, dass sich die rote LED wider Erwarten nicht vollständig ausschalten lässt, sodass diese stets ein wenig vor sich hin glimmt, zu ergründen.

Normalbetrieb der Messbrücke

Dazu nehmen wir die Schaltung in Betrieb ohne einen der Taster A oder B zu betätigen (siehe Bild 45) und messen als Erstes die Versorgungsspannung mit U_3V = 3,14 V Außerdem messen wir den Spannungsabfall am rechten Vorwiderstand R_V = 100 Ω mit U_RV = 1,12 V mit I_RV = U_RV / R_V = 1,12 V / 100 Ω = 0,0112 A = 11,2 mA

Die sehr geringe Differenzspannung zwischen den Anschlusspunkten „a“ und „b“ von

U_ab = -12,6 mV nach ca. 30 Sekunden ist der Bauteiletoleranz geschuldet, die bei den beiden Vorwiderständen aber nur 3 % beträgt.

Digitaler Betrieb beim Betätigen des Tasters A

Beim Betätigen des Tasters A werden die beiden parallel geschalteten, digitalen Spannungsquellen der Ports „Pin P0“ und „Pin P1“ zugeschaltet, sodass die rechte rote LED erlischt. Dabei lässt sich in der Laufschrift ein Bitwert von 706₂ in der Laufschrift ablesen:

U_{RV digital} = 707₂ Bit * 3,14 V / 1024 Bit = 2,16794922 V = 2,168 V (… gemessen: 2,14 V)

U_{LED R} = U_3V – U_{RV digital} = 3,14 V - 2,168 V = 0,972 V < U_F < 1,6 V

Dabei beträgt die Differenzspannung zwischen den Anschlusspunkten „a“ und „b“:

U_ab = -1,02 V → U_ba = 1,02 V

Vor dem Betätigen des Tasters B führen wir einen „Reset“ (= Warmstart) des „micro:bit“-Rechners durch.

Analoger Betrieb beim Betätigen des Tasters B

Beim Betätigen des Tasters B werden die beiden parallel geschalteten, analogen Spannungsquellen der Ports „Pin P0“ und „Pin P1“ zugeschaltet, sodass die rechte rote LED erlischt, aber trotzdem immer noch schwach glimmt! Dabei lässt sich in der Laufschrift ein Bitwert von 310₂ in der Laufschrift ablesen.

In der Laufschrift angezeigt wird dabei aber wider Erwarten nicht der Bitwert für den Vorwiderstand R_V, sondern für die rechte rote LED:

U_{LED R} = 310₂ Bit * 3,14 V / 1024 Bit = 0,95058594 V = 0,95 V (… gemessen: 0,99 V)

U_{RV analog} = U_3V - U_{LED R} = 3,14 V - 0,95 V = 2,19 V (… gemessen: 2,14 V)

U_{LED R} = U_3V - U_{RV analog} = 3,14 V – 2,19 V = 0,95 V < U_F < 1,6 V

Die Differenzspannung zwischen den Anschlusspunkten „a“ und „b“ beträgt unverändert:

U_ab = -1,02 V → U_ba = 1,02 V

Fazit

Zusammenfassend lässt sich feststellen, dass es problemlos möglich ist, zwei analoge oder digitale Spannungsquellen an den Ports „Pin P0“ und „Pin P1“ parallel zusammen zu schalten, um auf diese Weise einen doppelt so großen Strom aufbringen und am Mittelpunkt des rechten Spannungsteilers einleiten zu können.

Dabei dient das Ganze dazu, den Mittelpunktanschluss des rechten Spannungsteilers auf möglichst hohes positives Potential zu heben, sodass sich der Spannungsabfall an der rechten roten LED maßgeblich reduziert und die LED nicht mehr hell leuchten kann. -

Bei den anlogen oder digitalen Spannungsquellen an den Ports „Pin P0“ und „Pin P1“ scheint es ein bedeutsames Unterscheidungsmerkmal zu geben, das es stets zu beachten gilt und das man immer im Hinterkopf behalten sollte: Während sich die Ausgangsspannung der digitalen Spannungsquelle wegen der definierten und einheitlichen „On“ und „Off“-Signalpegel (siehe Bild 44) stets gegenüber dem Massepotential (= Pin „GND“) definiert, definieren muss, ist das Bezugspotential der analogen Spannungsquelle nicht zwangsläufig auf das Massepotential (= Pin „GND“) festgelegt!

Dass das Bezugspotential der analogen Spannungsquelle nicht zwangsläufig auf das Massepotential (= Pin „GND“) festgelegt ist, hängt vermutlich auch damit zusammen, dass die Rundanschlüsse der Ports „Pin P0“ bis „Pin P2“ beim Anschluss der Stromversorgung über das „Micro USB 2.0“-Kabel allesamt über eine Strombegrenzung und Stromabschaltung bei einer Überlast oder einem Kurzschluss verfügen.

Demzufolge ist jeder analoge Ein- und Ausgang über einen hochohmigen Widerstand von R_10M = 10 MΩ mit der Spannungsversorgung am Pin „3V“ verbunden, sodass im Falle eines Kurzschlusses mit U_Kurz ≈ 0 V die volle Versorgungsspannung am „10 MΩ“-Widerstand anliegt und dieser von einem Strom I_10M = U_3V / R_10M = 3,3 V / 10 MΩ = 0,33 * 10^-6 A = 0,33 µA durchflossen wird.

Ähnlich verhält es sich, wenn man z.B. den Port „Pin P2“ als analogen Messeingang mit entsprechendem A/D-Wandler für eine Spannungsmessung nutzt. Auch hier ist der Messanschluss an einem der Ports „Pin P0“ bis „Pin P2“ bei der Messung einer analogen Spannung wider Erwarten nicht auf ein negatives Bezugspotential wie der Masse (= Pin „GND“) oder ein positives wie der Spannungsversorgung (= Pin „3V“) festgelegt! Das Fatale daran ist nun, dass man bei einer Messung einer analogen Spannung nicht weiß, ob sich diese auf ein negatives oder positives Bezugspotential bezieht!

Was man jetzt also noch bräuchte, wäre ein kleines (Hilfs-) Programm mit einer grünen und roten LED mit denen sich anzeigen lässt, auf welches Bezugspotential sich die analoge Messung bezieht. Dazu müsste man aber erst mal wissen, weshalb sich bei der Messung mit dem Tasters B das Bezugspotential umkehrt!

Dabei gilt es zu beachten, dass wir bisher noch nicht wirklich mit der Wheatstone Messbrücke gearbeitet haben. Insbesondere haben wir diese zwischen den Anschlusspunkten „a“ und „b“ noch nicht abgeglichen und auch noch keine diesbezüglichen Berechnungen vorgenommen! Ob sich die Wheatstone Messbrücke letztlich eignet, um einen Potentialwechsel messtechnisch erkennen zu können, ist auch noch fraglich. Vermutlich braucht man eine Komparator, der aber nicht nur die beiden Teilspannungen am rechten Spannungsteiler (siehe Bild 45) vergleicht, sondern dabei auch noch gleichzeitig das Bezugspotential erfasst, auswertet und mittels zweier LEDs anzeigt. [ zurück zur Frage 7]

Frage 8

Demzufolge stellt sich also als Erstes die Frage, wie groß der Spannungabfall U_RV am rechten Vorwiderstand R_V = 100 Ω sein muss, damit die rechte rote LED nicht mehr leuchtet, nicht mehr leuchten kann, weil das Spannungspotential am Mittelpunkt „b“ nahezu dem der Versorgungsspannung U_3V entspricht (siehe Bild 47):

U_{LED R} = U_3V – U_RV = U_3V – I * R_V

= 3,14 V – 10 mA * 100 Ω = 3,14 V – 1000 mV = 3,14 V – 1 V = 2,14 V

Bitwert = 1024 Bit / 2,14 V = 478,5046728971963 Bit / V = 478 Bit / V

Dass wir etwas falsch gemacht haben, zeigt sich auch daran, dass in der Laufschrift der Bitwert 326 Bits / V angezeigt wird, obwohl es doch 478 Bit / V sein sollten!

Eine Spannung, einen Spannungsabfall oder einen Bitwert berechnen ist eben das eine und richtig anwenden das andere!

Was wurde also falsch gemacht? Machen Sie sich Gedanken, und finden Sie heraus, worin der Fehler besteht!

Antwort zur Frage 8

Der Spannungsumlauf

U_{LED R} = U_3V – U_RV = U_3V – I * R_V

= 3,14 V – 10 mA * 100 Ω = 3,14 V – 1000 mV = 3,14 V – 1 V = 2,14 V

Bitwert = 1024 Bit / 2,14 V = 478,5046728971963 Bit / V = 478 Bit / V

an sich ist richtig, aber falsch angewendet! Der Grund dafür ist der, dass sich mit dem analogen Eingang, mit jedem analogen oder binären Eingang an den Ports „Pin P0“ bis „Pin P2“ stets nur (Eingangs-) Spannungen gegen Masse (= Pin „GND“) messen lassen und nicht gegen das positive Potential der Spannungsversorgung U_3V am Pin „3V“!

Deshalb muss der Spannungsumlauf wie folgt lauten:

U_RV = U_3V – U_{LED R} → U_RV = U_3V wegen U_{LED R} ≈ 0 < U_F < 1,6 V

Da aber der Spannungsabfall rechnerisch U_{LED R} = 2,14 V beträgt, haben wir im Programm „microbit_teil_04_prog_33.hex“ und dem Quelltext „microbit_teil_04_prog_33.py“ den falschen Bitwert = 478 Bit / V eingesetzt (siehe oben)!

Da es sich bei Halbleitern wie der LED um nichtlineare, differentielle Widerstände handelt, lässt sich z.B. der Durchlasswiderstand für die Flussspannung U_F > 1,6 V nicht herkömmlich mittels des Ohmschen Gesetzes berechnen. Demzufolge lässt sich der Spannungsabfall U_{LED R} an der roten LED nur für den sogenannten Arbeitspunkt berechnen bei dem die LED elektrisch leitend ist.

Den Arbeitspunkt für die rote LED selbst haben wir noch nicht berechnet, da wir dazu das entsprechende Datenblatt nebst Kennlinien bräuchten!

Wir haben jetzt den gedanklichen Fehler gefunden und wissen, dass die rechte rote LED stets nur dann nicht leuchtet, wenn der Spannungsabfall an dieser null Volt beträgt: U_LED R ≈ 0 V, sodass am Vorwiderstand R_V die nahezu die gesamte Versorgungsspannung U_3V = 3,14 V abfällt: U_RV = U_3V

Demzufolge berechnet sich der Strom I_RV durch den Vorwiderstand R_V wie folgt:

I_RV = U_RV / R_V = U_3V / R_V

= 3,14 V / 100 Ω = 0,0314 A = 31,4 mA

Der Knackpunkt dabei ist nun aber der, dass die beiden parallel geschalteten analogen oder digitalen Ausgangsspannungen an den Ports „Pin P0“ und „Pin P1“ zusammen nicht ganz den Wert der Versorgungsspannung U_3V = 3,14 V erreichen, sodass an der rechten roten LED eben doch noch ein kleiner Spannungsabfall „übrig bleibt“!

Wie wir wissen, leuchtet die rechte rote LED ab einer Flussspannung U_F > 1,6 V. Ferner wissen wir, dass bei einer stromdurchlässigen, hell leuchtenden LED nicht mehr als I_F < 20 mA fließen sollen, damit diese nicht den Hitzetod stirbt.

Bei einem Strom von I_{LED max} = 20 mA durch den rechten Spannungsteiler berechnet sich der Spannungsabfall am Vorwiderstand R_V wie folgt:

U_{RV analog} = I_{LED max} * R_V = 20 mA * 100 Ω = 2000 mV = 2 V

Bitwert = 1024 Bit / 3,14 V * 2 V = 652,2292993630573 Bit / V ≈ 652 Bit / V

Für den Spannungsabfall an der rechten rote LED folgt dann:

U_{LED R} = U_3V – U_{RV analog} = 3,14 V - 2 V = 1,14 V < U_F < 1,6 V (… die LED leuchtet!)

Bei einem Strom von I_{LED max} = 10 mA durch den rechten Spannungsteiler berechnet sich der Spannungsabfall am Vorwiderstand R_V wie folgt:

U_{RV analog} = I_{LED max} * R_V = 10 mA * 100 Ω = 1000 mV = 1 V

Bitwert = 1024 Bit / 3,14 V * 1 V = 326,1146496815287 Bit / V ≈ 326 Bit / V

Für den Spannungsabfall an der rechten rote LED folgt dann:

U_{LED R} = U_3V – U_{RV analog}

= 3,14 V - 1 V = 2,14 V > U_F > 1,6 V (… LED leuchtet hell!)

Eine Siliziumdiode wird ab einer Durchbruchspannung von U_Durch > 0,7 V elektrisch leitend, d.h. stromdurchlässig. Demzufolge müsste sie bei einer Spannung von U_LED R = 0,4 V sicher sperren!

Für den Spannungsabfall am rechten Vorwiderstand R_V folgt dann:

U_{RV analog} = U_3V – U_{LED R} = 3,14 V – 0,4 V = 3,1 V

Bitwert = 1024 Bit / 3,14 V * 3,1 V

= 1010,955414012739 Bit / V ≈ 1011 Bit / V

Für den Spannungsabfall an der rechten rote LED folgt abschließend:

U_{LED R} = U_3V – U_{RV analog} = 3,14 V – 3,1 V

= 0,04 V < U_F < 1,6 V (… LED ist stockdunkel!)

Starten Sie das Programm „microbit_teil_04_prog_34.hex“ mit dem Quelltext „microbit_teil_04_prog_34.py“, und betätigen Sie den Taster B, um die rechte rote LED analog auszuschalten. Lesen Sie den in der Laufschrift angezeigten Bitwert = 705₂ ab.

Wie kommt es, dass uns jetzt in der Laufschrift ein Bitwert = 705₂ Bit/V angezeigt wird, obwohl wir doch zuvor einen Bitwert von 1011₂ Bit/V berechnet hatten?

Ganz einfach! Die Werte, die wir zuvor berechnet haben, sind zwar der Praxis entlehnt, bezogen auf den konkreten Fall, d.h. den rechten Spannungsteiler, dann aber eben doch nur teilweise relevant, weil Spannungsabfälle, Ströme, der Arbeitspunkt und die Spannungsversorgung wechselseitig voneinander abhängig sind und sich auch gegenseitig beeinflussen.

Nach dem Einschalten schwingt sich deshalb die Schaltung, quasi mit Lichtgeschwindigkeit und unter Berücksichtigung der physikalischen und ohmschen Gesetzmäßigkeit auf einen stabilen Zustand ein, sodass sich dann von außen entsprechende Spannungen, Ströme usw. messen lassen.

Diesbezügliche Messungen sind dabei aber stets nur eine Momentaufnahme, da sich diese z.B. aufgrund von Temperaturänderungen, Änderungen der Versorgungsspannung und damit auch des Arbeitspunktes geringfügig oder bei Schaltvorgängen mit elektrischer Schalthysterese auch maßgeblich ändern können. Aber nichtsdestotrotz müssen sich Schaltungen nebst Messungen praktisch jederzeit nachvollziehen und verifizieren lassen. Dabei kann aber das dynamische Verhalten von Halbleitern dem Anwender hier und da einen Strich durch die Rechnung machen.

Wenn wir also den beim Programm „microbit_teil_04_prog_34.hex“ mit dem Quelltext „microbit_teil_04_prog_34.py“ in der Laufschrift angezeigten Bitwert = 705₂ wieder ins Programm einsetzen, das Programm neu kompilieren und ein weiteres Mal starten, dann bekommen wir wieder einen anderen Bitwert angezeigt, weil es sich bei dem angezeigten Bitwert um die elektrische Reaktion der Schaltung, d.h. des rechten Spannungsteilers handelt. Dabei lässt sich dieses Spiel beliebig fortsetzen, sodass wir jedes Mal in der Laufschrift einen anderen Bitwert angezeigt bekommen! Allerdings nähern sich die in der Laufschrift angezeigten Bitwerte dem Normalzustand der Schaltung beim Einschalten an, wo noch keine Ausgangsspannungen der Ports „Pin P0“ und „Pin P1“ am Mittelpunkt „b“ des Spannungsteilers eingespeist werden!

Mathematisch handelt es sich dabei um ein iteratives Annäherungsverfahren ähnlich wie es bei der Berechnung eines Effektivzinssatzes der Fall ist.

Das Interessante dabei ist noch, dass die jeweils in der Laufschrift angezeigten Bitwerte, die später dann noch in Volt umgerechnet werden müssen, entlang der Arbeitsgeraden verlaufen, verlaufen müssen!

Der Grund für dieses anfangs ungewohnte, elektrische Verhalten ist der, dass das fast vollständige Herstellen der Potentialgleichheit zwischen den Anschlusspunkten „1“ und „b“ (= Spannungabfall an der rechten roten LED, siehe Bild 47) aus elektrotechnischer Sicht quasi einem Störfall entspricht, wobei die Schaltung mit dem Spannungsteiler stets versucht, den erzwungenen Zustand der Potentialgleichheit zu beenden, um wieder zum Normalzustand ohne Fremdeinspeisung am Mittelpunkt „b“ des Spannungsteilers zurückzukehren!

[ zurück zur Frage 8]

Frage 9

Wenn man das obenstehende Programm „microbit_teil_04_prog_38.hex“ mit dem Quelltext „microbit_teil_04_prog_38.py“ erstmals neu auf den „micro:bit“-Rechner hochgeladen und geflasht hat, dann startet sich dieses automatisch, sodass in der Laufschrift „Start …“ angezeigt und die rechte rote LED ausgeschaltet wird. Dabei befindet sich der „Up- and Down“-Zähler auf der Position „1“, die aber nach dem Programmstart nicht angezeigt wird.

a) Welcher Taster muss mehrmals nacheinander gedrückt werden, damit sich die rechte rote LED schrittweise zum immer helleren Leuchten bringen lässt?

b) Welchen Taster muss man drücken, damit sich die rechte rote LED nach dem Programmstart oder Reset schnell zum hellen Leuchten bringen lässt, ohne dass man die Helligkeit in mehren Schritten hochfahren muss?

c) Weshalb muss man den Tasters B direkt nach dem Programmstart oder Reset insgesamt zweimal drücken, damit die rechte rote LED „auf einen Schlag“ hell zu leuchten anfängt?

Antwort zur Frage 9

a) Welcher Taster muss mehrmals nacheinander gedrückt werden, damit sich die rechte rote LED schrittweise zum immer helleren Leuchten bringen lässt?

Damit sich die rechte rote LED schrittweise zum immer helleren Leuchten bringen lässt, muss man den Taster A mehrmals nacheinander drücken.

b) Welchen Taster muss man drücken, damit sich die rechte rote LED nach dem Programmstart oder Reset schnell zum hellen Leuchten bringen lässt, ohne dass man die Helligkeit in mehren Schritten hochfahren muss?

Nach dem Programmstart oder Reset lässt sich die rechte rote LED schnell zum hellen Leuchten bringen, indem man den Taster B drückt!

c) Weshalb muss man den Tasters B direkt nach dem Programmstart oder Reset insgesamt zweimal drücken, damit die rechte rote LED „auf einen Schlag“ hell zu leuchten anfängt?

Der Taster B muss direkt nach dem Programmstart oder Reset insgesamt zweimal gedrückt werden, damit die rechte rote LED „auf einen Schlag“ hell zu leuchten anfängt, weil man sich das Programm mit dem „Up- and Down“-Zähler anfangs noch nicht in der inneren „elif“-Abfrage des Tasters A befindet (siehe Bild 58).

In die innere „elif“-Abfrage des Tasters A gelangt man erst, wenn man zuvor den Taster A bereits einmal betätigt hat. Und genau dies ist direkt nach dem Programmstart oder Reset eben nicht der Fall!

[ zurück zur Frage 9]

Frage 10

Jetzt stellt sich aus der Sicht der Wheatstone Messbrücke die Frage, welcher der beiden Widerstände R₂ oder R₄ als zu messender Widerstand geeigneter wäre.

Finden Sie heraus, welcher der beiden Widerstände R₂ oder R₄ als zu messender Widerstand geeignet ist, und begründen Sie Ihre Entscheidung!

Antwort zur Frage 10

Aus der Sicht der Wheatstone Messbrücke ist der Widerstand R₂ als zu messender Widerstand am besten geeignet, weil er den bis zu neunmal höheren Querstrom aufweist. Oder anders ausgedrückt: Da der Querstrom des Widerstandes R₄ nur ein Neuntel des Querstroms vom Widerstand R₂ aufweist, belastet er das Messergebnis bzw. den Spannungsabfall U_R2,4 am wenigsten, sodass man ein besseres Messergebnis mit einer höheren Messgenauigkeit bekommt. Aber das muss erst noch ausprobiert werden!

[ zurück zur Frage 10 ]

Frage 11

Durch den neuen Abgleichwiderstand von R₄ = 991 Ω ändert sich das Verhalten des Wheatstone Messbrücke, ändern sich Spannungen und Ströme an den Widerständen R₁ = R₃ = 456 Ω, R₄ = 991 Ω und R_m = 1013 Ω, sodass diese neu abgeglichen werden muss.

Bei der abgeglichenen Messbrücke stellen sich nachfolgende Messwerte ein:

Versorgungsspannung: U_3V = 3,15 V

Abgleichspannung am Widerstand R₄: U₄ = 2,25 V

Bitwert der Abgleichspannung an R₄: 806 Bit

Brückenspannung: U_ba = 94 mV = 0,094 V

Erklären Sie wie sich der neue Abgleichwiderstand auf die Messbrücke auswirkt, wie und weshalb sich die Spannungen an den beiden Spannungsteilern rechts und links auswirken, wenn die Messbrücke abgeglichen ist.

Berechnen Sie den Querstrom im rechten Spannungsteiler R_3, R₄ und linken Spannungsteiler R₁, R_m.

Berechnen Sie die Abgleichspannung U_b am Abgleichwiderstand R₄.

Rechnen Sie den gemessenen Bitwert von 806 Bit für die Abgleichspannung am Abgleichwiderstand R₄ um in Volt, und berechnen Sie die Messgenauigkeit in % bezogen auf die gemessene Abgleichspannung U₄ = 2,25 V (siehe oben)!

Berechnen Sie die Brückenspannung U_ba an den Kontaktstellen „a“ und „b“ für die abgeglichene Messbrücke.

Antwort zur Frage 11

Durch den neuen größeren Abgleichwiderstand von R₄ = 991 Ω verringert sich der Querstrom durch den rechten Spannungsteiler R_3, R₄, sodass sich der Spannungsabfall am Abgleichwiderstand R₄ vergrößert und am Widerstand R₃ verkleinert!

Der Querstrom I_{R3, R4} im rechten Spannungsteiler R_3, R₄ berechnet sich wie folgt:

I_{R3, R4} = U_ges / R_ges = U_3V / ( R₃ + R₄ )

= 3,15 V / ( 456 Ω + 991 Ω ) = 3,15 V / 1447 Ω = 0,0021769177608846 A

= 2,1769177608846 mA = 2,177 mA

Der Querstrom I_{R1, Rm} im linken Spannungsteiler R_1, R_m berechnet sich wie folgt:

I_{R1, Rm} = U_ges / R_ges = U_3V / ( R₁ + R_m )

= 3,15 V / ( 456 Ω + 1013 Ω ) = 3,15 V / 1469 Ω = 0,00214431586113 A

= 2,14431586113 mA = 2,144 mA

Die Abgleichspannung U_b am Abgleichwiderstand R₄ berechnet sich wie folgt:

U_b = R₄ * I_{R3, R4} = 991 Ω * 2,177 mA = 2157,407 mV

= 2,157 V = 2,16 V → (… gemessen: 2,25 V siehe oben!)

Der gemessene Bitwert von 806 Bit für die Abgleichspannung am Abgleichwiderstand R₄ lässt sich wie folgt in Volt umrechnen:

U_b = U_3V / 1024 Bit * Bitwert

= 3,15 V / 1024 Bit * 806 Bit

= 2,47939453125 V = 2,48 V → (… gemessen: 2,25 V siehe oben!)

Für die Messgenauigkeit folgt:

100 % / 2,25 V * 2,48 V = 110,2222222222222 % ≈ 110 %

Die Brückenspannung U_ba an den Kontaktstellen „a“ und „b“ berechnet sich wie folgt:

U_ba = U_b - U_a = R₄ * I_{R3, R4} - R₂ * I_{R1, Rm}

= 991 Ω * 2,177 mA - 1013 * 2,144 mA = 2157,407 mV - 2171,872 mV

= 2,157407 V – 2,171,872 V = 2,16 V – 2,17 V = -0,01 V = -10 mV ≈ 0V

[ zurück zur Frage 11 ]

Frage 12

Der Messwiderstand R_m wird maßgeblich vergrößert, sodass sich vor und nach dem Brückenabgleich nachfolgende Messwerte einstellen:

Versorgungsspannung: U_3V = 3,19 V

Bitwert am Abgleichwiderstand R₄: 704 Bit vor dem Brückenabgleich!

Abgleichspannung am Widerstand R₄: U₄ = 3,05 V nach dem Brückenabgleich!

Bitwert der Abgleichspannung an R₄: 991 Bit nach dem Brückenabgleich!

Brückenspannung: U_ba = 3 mV = 0,003 V

Stellen Sie nachfolgende Berechnungen vor dem Brückenabgleich an:

1. Wandeln Sie den in der Laufschrift des „micro:bit“-Rechners angezeigten Bitwert von 704 Bit für die Abgleichspannung am Abgleichwiderstand R₄ um in Volt [V].
   
   
2. Berechnen Sie den Abgleichwiderstandes R₄ des rechten Spannungsteilers mittels der Spannungsteilerformel.

3. Berechnen Sie die Versorgungsspannung U_3V mittels der beiden Widerstände R₃ und R₄ des rechten Spannungsteilers.

Stellen Sie nachfolgende Berechnungen nach dem Brückenabgleich an:

4. Wandeln Sie den in der Laufschrift des „micro:bit“-Rechners angezeigten Bitwert von 991 Bit für die Abgleichspannung am Abgleichwiderstand R₄ um in Volt [V].

5. Berechnen Sie den Messwiderstandes R_m des linken Spannungsteilers mittels der Spannungsteilerformel.

Antwort zur Frage 12

Berechnungen diverser Spannungen vor dem Brückenabgleich:

1. Wandeln Sie den in der Laufschrift des „micro:bit“-Rechners angezeigten Bitwert von 704 Bit für die Abgleichspannung am Abgleichwiderstand R₄ um in Volt [V].

Der gemessene Bitwert von 704 Bit für die Abgleichspannung am Abgleichwiderstand R₄ vor dem Brückenabgleich lässt sich wie folgt in Volt umrechnen:

U_b = U_3V / 1024 Bit * Bitwert

= 3,19 V / 1024 Bit * 704 Bit

= 2,193125 V = 2,19 V → (… gemessen: 2,18 V siehe oben!)

2. Berechnen Sie den Abgleichwiderstandes R₄ des rechten Spannungsteilers mittels der Spannungsteilerformel.

Berechnung des Abgleichwiderstandes R₄ des rechten Spannungsteilers mittels der Spannungsteilerformel vor dem Brückenabgleich:

R₄ = R₃ / ( U_3V / U₄ - 1 )

= 456 Ω / (3,198 V / 2,19 V - 1 ) = 456 Ω / 0,4602739726027397

= 456 Ω / 0,4603 = 990,6582663480339 Ω

= 990,658 Ω = 990,7 Ω (… gemessen: 991 Ω)

3. Berechnen Sie die Versorgungsspannung U_3V mittels der beiden Widerstände R₃ und R₄ des rechten Spannungsteilers.

Berechnung der Versorgungsspannung U_3V mittels der beiden Widerstände R₃ und R₄ des rechten Spannungsteilers vor dem Brückenabgleich:

R₃ / R₄ = U₃ / U₄ = ( U_3V - U₄ ) / U₄ = ( U_3V / U₄ – 1 )

R₃ / R₄ = ( U_3V / U₄ – 1 )

U_3V = ( R₃ / R₄ + 1 ) * U₄ = ( R₃ / R₄ + 1 ) * U_b

= (456 Ω / 991 Ω + 1 ) * 2,19 V = 1,460141271442987 * 2,19 V

= 3,197709384460142 V

= 3,198 V (… gemessen: 3,19 V siehe oben!)

Berechnungen diverser Spannungen nach dem Brückenabgleich:

4. Wandeln Sie den in der Laufschrift des „micro:bit“-Rechners angezeigten Bitwert von 991 Bit für die Abgleichspannung am Abgleichwiderstand R₄ um in Volt [V].

Der gemessene Bitwert von 991 Bit für die Abgleichspannung am Abgleichwiderstand R₄ nach dem Brückenabgleich lässt sich wie folgt in Volt [V] umrechnen:

U_b = U_3V / 1024 Bit * Bitwert

= 3,19 V / 1024 Bit * 991 Bit = 3,087197265625 V

= 3,087 V → (… gemessen: 3,05 V siehe oben!)

5. Berechnen Sie den Messwiderstandes R_m des linken Spannungsteilers mittels der Spannungsteilerformel.

Berechnung des Messwiderstandes R_m des linken Spannungsteilers mittels der Spannungsteilerformel nach dem Brückenabgleich:

R_m = R₁ / ( U_3V / U₂ - 1 )

= 456 Ω / (3,19 V / 3,05 V - 1 ) = 456 Ω / 0,0459016393442623

= 456 Ω / 0,0459 = 9934,640522875817 Ω

= 9934,64 Ω = 9,935 KΩ (… gemessen: 9,95 KΩ)

[ zurück zur Frage 12 ]

Frage 13

Trotz der mit dem Digitalvoltmeter zwischen den Kontaktstellen „a“ und „b“ gemessenen Brückenspannung U_ba von null Volt und der definitiv abgeglichenen Wheatstone Messbrücke gibt es eine mit dem „micro:bit“-Rechner gemessene Potentialdifferenz von 110 Bit = 355 mV.

Geben Sie eine Erklärung wie es möglich ist, dass es bei den Messungen der Brückenspannung U_ba zwei unterschiedliche Messergebnisse hinsichtlich der Spannungsdifferenz zwischen den Kontaktstellen „a“ und „b“ gibt!

Antwort zur Frage 13

Wenn man die Brückenspannung U_ba zwischen den Kontaktstellen „a“ und „b“ der definitiv abgeglichenen Wheatstone Messbrücke mit dem Digitalvoltmeter misst, dann weiß das Voltmeter nicht, um welche Art von Schaltung sich an den Messpunkten handelt. Demzufolge stellt sich die Schaltung der Wheatstone Messbrücke aus der Sicht des Voltmeters als eine sogenannte Black Box dar, d.h. um einen Zweipol.

Wenn sich der Zweipol dabei u.a. auch aus aktiven Bauelementen wie z.B. Transistoren, Operationsverstärkern, Verstärkern, A/D-Wandlern oder wie im vorliegenden Fall um einem Pulsweitenmodulator (PWM) am Port „Pin P2“ zusammensetzt, dann spricht man auch von einem aktiven Zweipol. Dabei können aktive Zweipole auch elektrische Energie in Form einer Spannung oder eines Stromes nach außen abgeben.

Diesbezüglich ist bei dem Multimeter nebst der Spannungsmessung aber entscheidend, dass die Spannung potential- und systemunabhängig gemessen wird! Bei den Spannungsmessungen der Brückenspannung U_a und U_b mit –U_ab = U_ba = U_b – U_a mit dem „micro:bit“-Rechner ist dies nämlich genau nicht der Fall, da sich diese stets nur gegen Masse (= Pin „GND“) messen lassen. Dies ist dann auch der Grund dafür, dass wir bei den Brückenspannung U_a und U_b trotz abgeglichener Wheatstone Messbrücke mit U_a = 860 Bit und U_b = 970 Bit unterschiedlich große Spannungen messen! -

Frage 14

Berechne den Messwiderstand R_m für die abgeglichene Wheatstone Messbrücke, wenn mit dem Programm „microbit_teil_04_prog_40.hex“ und dem Quelltext „microbit_teil_04_prog_40.py nachfolgende Messwerte aufgenommen wurden:

Widerstand R₁: R₁ = 21,8 KΩ

Widerstand R₃: R₃ = 21,8 KΩ

Widerstand R₄: R₄ = 473 KΩ

Bitwert der Abgleichspannung an R₄: 671 Bit vor dem Brückenabgleich!

Bitwert am Abgleichwiderstand R₂: 65 Bit vor dem Brückenabgleich!

Bitwert der Abgleichspannung an R₄: 15 Bit nach dem Brückenabgleich!

Bitwert am Abgleichwiderstand R₂: 7 Bit nach dem Brückenabgleich!

Differenz der Bitwerte: 8 Bit nach dem Brückenabgleich!

Stromversorgungsspannung U_3V: U_3V = 3,21 V

Antwort zur Frage 14

U₄ = 3,06 V / 982 Bit * 1023 Bits = 2,164516129032258 V ≈ 2,035 V

Für den rechten Spannungsteiler mit den Widerständen R₃, R₄ folgt:

U₄ / U_3V = R₄ / R_ges = R₄ / ( R₃ + R₄ )

U_3V = U₄ / [ R₄ / ( R₃ + R₄ ) ] = U₄ * ( R₃ + R₄ ) / R₄

= U₄ * ( R₃ / R₄ +1 )

= 2,035 V * ( 21,8 KΩ / 473 KΩ + 1 ) = 2,035 V * ( 21,8 / 473 + 1 )

= 2,035 V * ( 1,046088794926004 ) = 2,035 V * ( 1,046 )

= 3,323142 V

Die Berechnung des Messwiderstandes R_m lässt sich nur durchführen, wenn mit der Versorgungsspannung U_3V gerechnet wird.

Die neue Berechnungsformel zwecks Berechnung des Messwiderstandes R_m lautet:

R_m = R₃ / ( U₃ / U₄ ) = R₃ / ( U_3V – U₄ ) / U₄

= R₃ / ( U_3V / U₄ - 1 ) → rechter Spannungsteiler!

R_m = R₁ / ( U₁ / U₂ ) = R₁ / ( U_3V – U₂ ) / U₂

= R₁ / ( U_3V / U₂ - 1 ) → linker Spannungsteiler!

= 21,8 KΩ / [ 3,21 V / ( 3,3 V / 1023 Bit * 7 Bit ) – 1 ]

= 21,8 KΩ / [ 3,21 V / (0,02258 ) – 1 ] = 21,8 KΩ / [ 3,21 V / 0,02258 - 1 ]

= 21,8 KΩ / [ 141,16 V ] = 154,4346840464721 Ω

≈ 154,4 Ω (… gemessen: 149 Ω)

U_3V = ( R₁ / R_m + 1 ) * U₂ = ( 21,8 KΩ / 154,4 Ω + 1 ) * 7 Bit

= ( 142,1917098445596 ) * 7 Bit = ( 142,192 ) * 7 Bit ≈ 995 Bit

= 3,3 V / 1023 Bit * 995 Bit = 3,21 V (… gemessen: 3,21 V)

[ zurück zur Frage 14 ]

[ Home ] [ zurück ] [ Seitenanfang ]