[ Home ] [ zurück ] [ Seitenende ] [ Teil 3 ] [ Teil 5 ]

micro:bit-Programmieren, Teil 4

1. Einleitung

Python als Programmiersprache gibt es schon seit 1991, d.h. schon zu einer Zeit, wo von „IoT“ absolut noch keine Rede war.

„IoT“ ist die englischsprachige Abkürzung für „Internet of Things“, d.h. das „Internet der Dinge (und Dienste)“. Wenn aber die Dinge „smart“, d.h. intelligent werden sollen, dann fragt man sich, wo denn die Intelligenz herkommen soll. Nämlich von den engl. „serivces“, d.h. den Dienstleistungen. Von diversen Servern einschließlich der sogenannten „Cloud“ bzw. dem „Cloud Computing“.

Wenn Sie eine sogenannte „FRITZ!Box“ mit USB-Buchse an der Rückseite als VDSL-/DSL- und WLAN-Router verwenden und dort einen USB-Speicherstick angesteckt haben, dann verfügen Sie u.a. mittels des NAS, der Benutzerschnittstelle sowie des Zugangs von außen über das Internet über Ihre eigene, engl. „private“, d.h. nicht öffentliche Cloud.

Wenn Sie an die zweite USB-Buchse der FRITZ!Box dann auch noch den „micro:bit“-Rechner anschließen, dann können Sie selbst für sich das „Internet der Dinge“ betreiben. Beispielsweise als „Smart Home“. Was dann noch fehlt, wäre eine neue Programmiersprache für das „Internet of Things“, die wiederum webbasiert, objektorientiert, ereignisgesteuert sein müsste und darüber hinaus auch noch über eine Schnittstelle für die Künstliche Intelligenz (KI) nebst Sprachein- und -ausgabe verfügt.

Google z.B. arbeitet auch am „Internet of Things“ und zwar nicht nur mit einer eigenen Entwicklungsumgebung, engl. „Software Development Kit“ (SDK), sondern auch mit einem eigenen IoT-Betriebssystem namens „Android Things“. Auf der Webseite kann man sich über die derzeit unterstützte Hardware informieren. Der „Raspberry Pi 3B“ gehört übrigens auch dazu. -

2. „Hello World!“ mit Herz

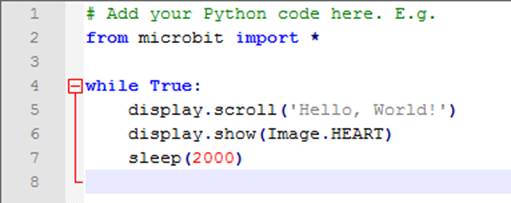
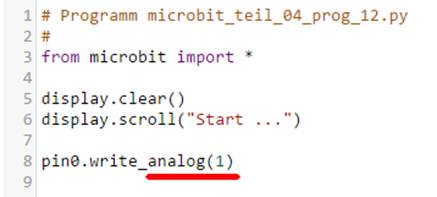
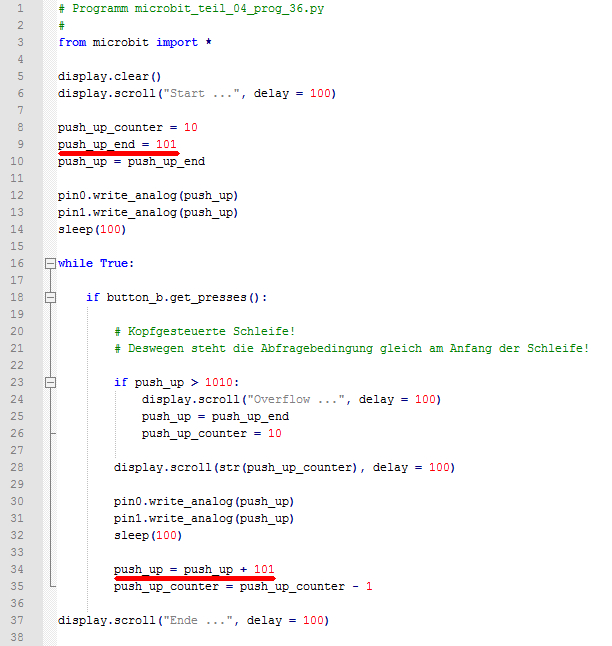
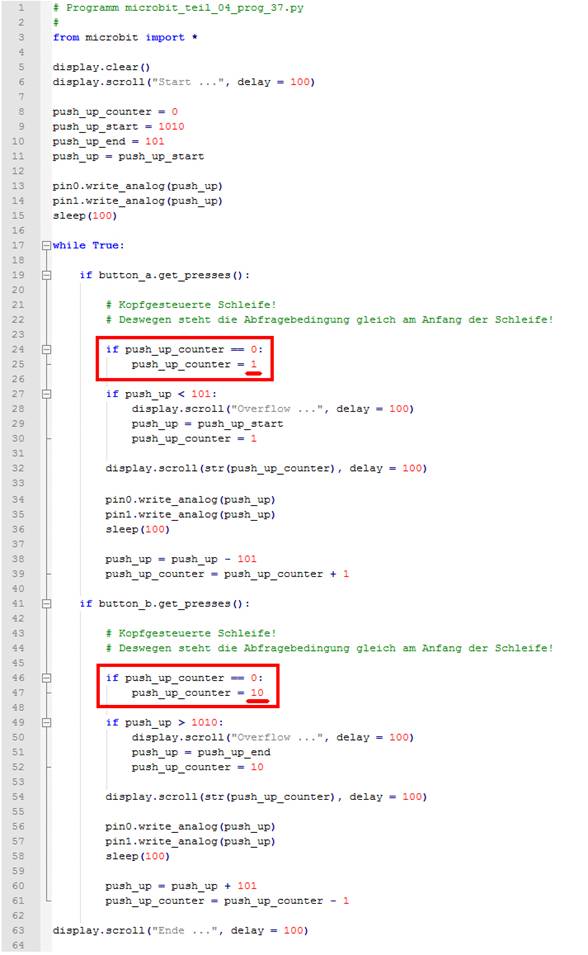
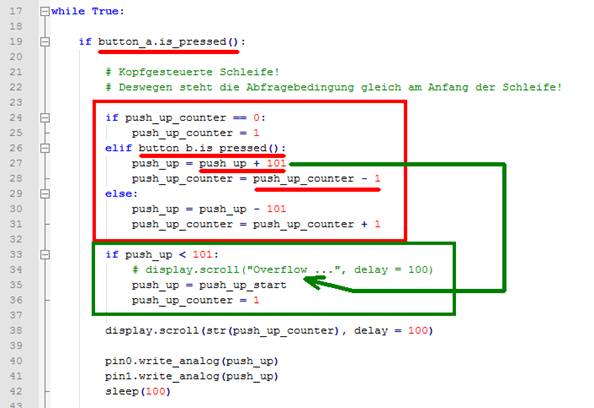
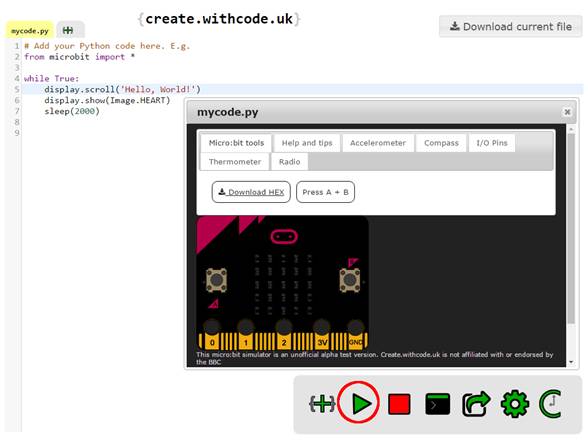
Wir legen sofort los mit der Python-Programmierung und programmieren unser erstes Programm „microbit_teil_04_prog_01.py“, das im „Notepad++“-Editor wie folgt aussieht:

(Bild 01 - Hello World! mit Herz)

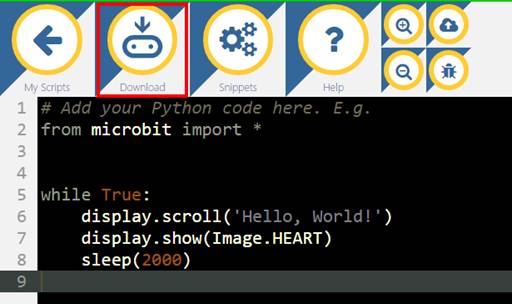
Wenn man sich das Programm, d.h. die Anzeige des Programms anschauen will, dann muss es man erst noch kompilieren/übersetzen. Dazu braucht man wiederum einen passenden Compiler, der den Sourcecode (siehe im Bild oben) in hexadezimalen Maschinenkode übersetzt. Und zwar so, dass dieser vom „micro:bit“-Rechner verstanden wird:

(Bild 02 - Python-Editor & Compiler)

Dabei geschehen das Kompilieren des Quelltextes und das Herunterladen des Kompilats, d.h. die Übersetzung in Maschinenkode, in einem Rutsch.

Die dabei herunter geladene Kompilations-Datei befindet sich auf dem Windows-PC standardmäßig im Verzeichnis \Downloads und trägt den (Datei-) Erweiterungsnamen „.hex“ (siehe Programm „microbit_teil_04_prog_01.hex“)

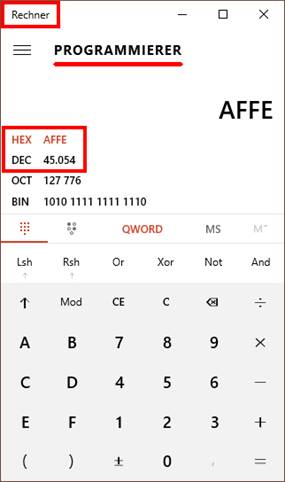
Dabei steht die Abkürzung „hex“ für hexadezimal, sodass sich der Maschinenkode aus doppelten Zahlenwerten von 0 … 9, A, B, C, D, E, F zusammensetzt. Bei den Zahlenwerten 0 … 9 handelt es sich um dezimale Zahlen und von A … F um hexwertige Zahlen von 10₁₀ bis 15₁₀.

So bedeutet die hexadezimale Zahl „AFFE₁₆“ (= 45054₁₀) keine Beleidigung, wenn man sie ausspricht oder in einer E-Mail zitiert, solange man den Index 16 für eine hexadezimale Zahl hinzufügt. Wer das nicht weiß, darf sich natürlich trotzdem beleidigt fühlen, nur strafbare wäre es im hexadezimalen Sinne nicht:

(Bild 03 – der hexadezimale AFFE)

Wie man im obenstehenden Screenshot sieht, lässt sich der integrierte Taschenrechner unter Windows in den „Programmierer“-Modus umschalten, sodass sich mit diesem ganz bequem hexadezimale Zahlen in dezimale (und umgekehrt) umrechnen lassen.

Leider gibt es auf der Homepage der „micro:bit Foundation“ für das Programmieren mit der Programmiersprache Python wider Erwarten keinen Emulator mit dem sich der Quelltext direkt im Browser ausprobieren und anzeigen lässt. Aber das ist kein Grund zu verzweifeln! Wer noch keinen „micro:bit“-Rechner (Hardware) hat, kann seinen selbst erstellten Python-Quelltext trotzdem live im Internet, d.h. im Browser ausprobieren.

Klicken Sie auf der Webseite oben in der Menüleiste auf „Create with Code“, oder starten Sie die Emulation direkt hier: https://create.withcode.uk/

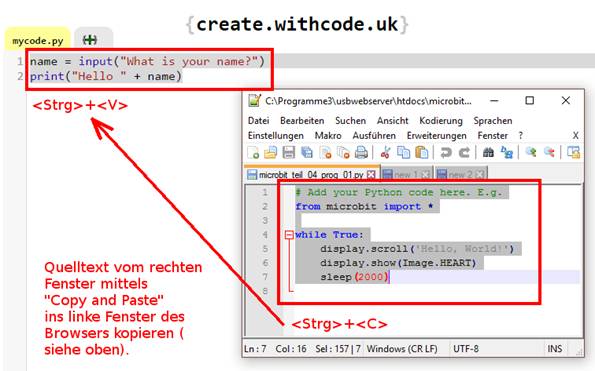
Jetzt stellt sich gleich die Frage, wie man den Quelltext (siehe Bild 01) in das Browserfenster mit der Emulation kopiert. Nämlich mittels „Copy and Paste“:

(Bild 04 – Quelltext mittels „Copy & Paste“ übertragen)

Ausgeführt wird dann das Programm „microbit_teil_04_prog_01.hex“ mit dem Quelltext „microbit_teil_04_prog_01.py“ indem man auf der Webseite mit der Entwicklungsumgebung auf das Symbol {+} klickt, sodass sich das Menüfeld öffnet. Dort lässt sich dann das Programm durch Mausklick auf das grüne Symbol ► (siehe im roten Kreis) klickt. Das Programm selbst wird dann im Fenster „mycode.py“ im siumulierten „micro:bit“-Rechner ausgeführt:

(Bild 05 – Python-Programm in der Emulation ausführen)

Wir erweitern das Programm, indem wir die Variablen „txtstr_1“ bis „txtstr_3“ deklarieren und mittels eines Textstrings, d.h. Zeichenkette initialisieren, sodass diese zu Textvariablen werden:

(Bild 06 – Menüauswahl mit Taster A und B)

Bei der „while … True“-Schleife handelt es sich um eine Endlosschleife, da die Bedingung „True“ fortwährend bis zum Stromausfall oder dem Systemabsturz erfüllt ist.

Das Problem dabei ist aber, dass sich die Endlosschleife nur mittels des Statements „break“ verlassen lässt. Und das auch nur per Knopfdruck auf den Taster B.

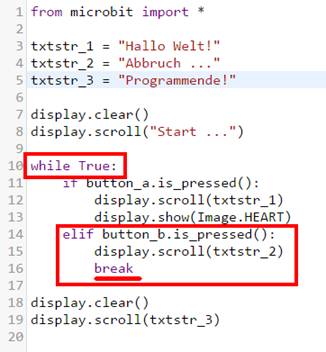
Da wir aber beim „micro:bit“-Rechner nur zwei Taster A und B haben, zahlen wir für den Programmausstieg einen hohen Preis, weil wir eben einen Taster dafür opfern müssen.

Etwas ungewöhnlich ist die „elif“-Anweisung. Dabei steht der Ausdruck „elif“ aber nur für „else if“ im Sinne von „wenn nicht, dann anderenfalls …“ (siehe Programm „microbit_teil_04_prog_02.hex“ mit dem Quelltext „microbit_teil_04_prog_02.py“).

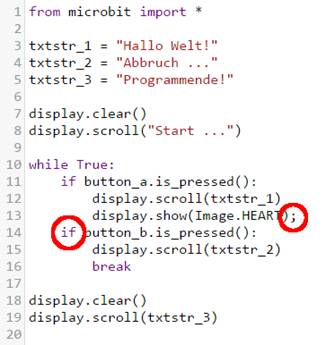
Viel gravierender ist aber der Umstand, dass der Eindruck entstehen könnte, dass eine „if …then“-Abfrage immer nur in Kombination mit der „else if“-Abfrage möglich ist. Dem ist aber genau nicht so:

(Bild 07 – Es geht auch ohne „elif“-Anweisung)

Beim Programmieren von „if“-Abfragen ist es nämlich viel besser, weil übersichtlicher und verständlicher, wenn man mehrere einzelne „if“-Abfragen programmiert als diese zu einer Kombiabfrage zu verschachteln (siehe Programm „microbit_teil_04_prog_03.hex“ mit dem Quelltext „microbit_teil_04_prog_03.py“). -

Wenn es nur darum geht, dass die Anzeige „Hallo Welt!“ der Textvariablen „txtstr_1“ nur ein einziges Mal als Laufschrift angezeigt wird und diese nicht fortwährend in einer Endlosschleife angezeigt werden soll, dann kann man das Programm bzw. die Laufschrift so programmieren, dass diese nach dem Anzeigen der Laufschrift automatisch beendet wird:

(Bild 08 – Einsparen des Tasters B)

ACHTUNG: Das was nach der Programmänderung leider nicht mehr funktioniert, ist das Statement

· display.show(Image.HEART)

Auch die beiden anderen Statements mit denen man eine Pause programmieren kann, um z.B. die Anzeige weiterhin in der „5 x 5 LED-Matrix“-Display anzuzeigen,

· sleep(1000) oder

· microbit.sleep(1000)

funktionieren wider Erwarten nicht (siehe Programm „microbit_teil_04_prog_04.hex“ mit dem Quelltext „microbit_teil_04_prog_04.py“). -

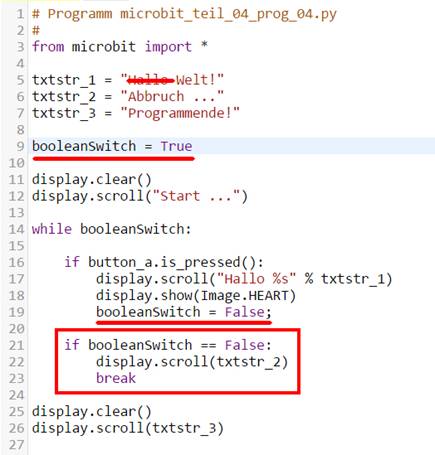
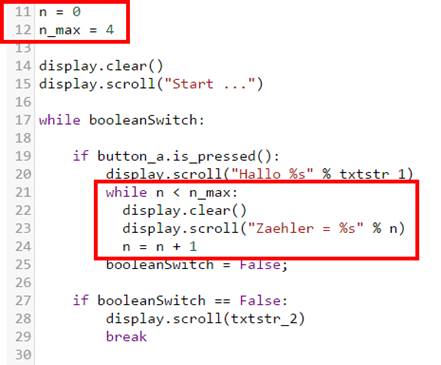
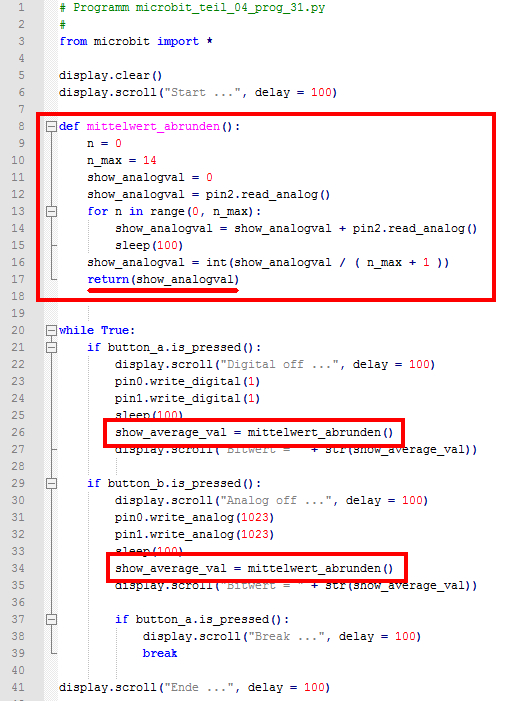
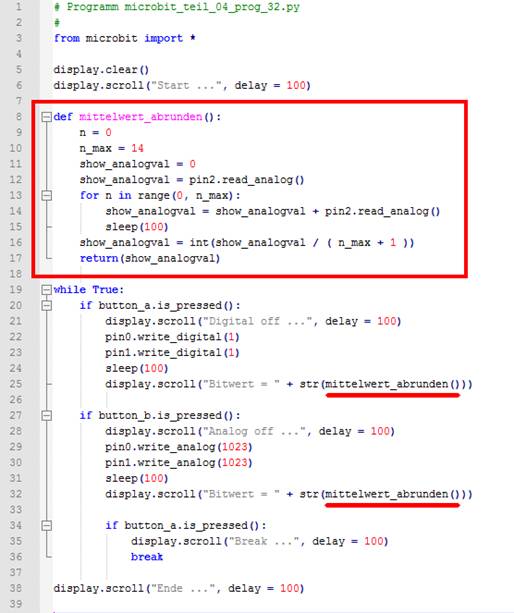
Wenn aber der „sleep“-Befehl nicht funktioniert, dann muss man sich diesen selbst programmieren. Und zwar mittels einer „while“-Schleife, wie wir sie ja bereits vom Ansatz her kennen:

n = 0

n_max = 4

while n < n_max:

display.clear()

display.scroll("Zaehler = %s" % n)

n = n + 1

Sicherlich ist Ihnen bereits die etwas eigenartige Stringausgabe beim Statement display.scroll("Zaehler = %s" % n) aufgefallen. Wenn Sie jetzt noch vermuten, dass ich mit dem „display.scroll“-Befehl nur einzelne Zeichen, engl. „characters“ oder Zeichenketten, engl. „strings“ im Sinne einer Zeichenfolge als Laufschrift wiedergeben lassen, dann liegen Sie richtig.

Wenn man dann aber eine Zahl, einen Zahlenwert in der Laufschrift wiedergeben möchte, dann muss man diesen zuvor umwandeln. Dazu muss man bereits dem String "Zaehler = %s" mitteilen, dass ein Zahlenwert im und als String angezeigt werden soll. Deshalb die Angabe „s“ für String und die Angabe „%“ für einen numerischen Wert, d.h. einen Zahlwert.

Da es sich bei der Variablen n von außen gesehen, sowohl um eine Stringvariable als auch um eine numerische Variable handeln kann und die Programmiersprache über keine hellseherische Fähigkeiten verfügt, müssen wir dem Programm, dem Statement mitteilen, dass es sich bei der Variablen n um eine numerische Variable handelt, indem man den Parameter „%“ der Variablen n voran stellt (siehe oben). -

Bei den Programmiersprachen gibt es sogenannte kopf- oder fußgesteuerte Schleifen. Dabei bedeutet „kopfgesteuert“, dass die Abfragebedingung „n < n_max“ gleich zu Beginn der Schleife, also bereits im Schleifenkopf abgefragt wird. Zu den kopfgesteuerten Schleifen zählen z.B. „for“- oder „while“-Schleifen, während die „repeat … until“-Schleifen zu den fußgesteuerten Schleifen zählen.

(Bild 09 – kopfgesteuerte „while“-Schleife)

Wenn das Programm „microbit_teil_04_prog_05.hex“ mit dem Quelltext „microbit_teil_04_prog_05.py“ ordnungsgemäß funktioniert, dann kann man die beiden Statements

display.clear()

display.scroll("Zaehler = %s" % n)

aus dem Programm entfernen und gleichzeitig den „Pausen“-Zähler z.B. auf den Wert n_max = 10000 erhöhen. Je nach dem, wie lange die Pause andauern soll. -

Werfen wir noch einen Blick auf die „for“-Schleife, die in Python etwas Besonderes ist:

(Bild 10 – kopfgesteuerte „for“-Schleife)

Was aber ist das Besondere an der „for“-Schleife? Es gibt keinen Schleifenzähler n, der am Ende der Schleife inkrementiert, d.h. um einen Schritt von n auf n + 1 erhöht wird: n = n + 1 (siehe weiter oben bei der „while“-Schleife).

Bei der „for“-Schleife mit der Angabe „range(0, n_max)“ ist nämlich der Schleifenzähler n bzw. das Inkrementieren bereits eingebaut! Was aber ist ein engl. „range“, d.h. ein Bereich, eine Reihe, eine Sammlung?

Mit der Angabe „range(0, n_max)“ wird festgelegt mit welchem Wert der Bereich beginnt (= Anfangswert, Startwert) und mit welchem dieser endet (= Endwert). Im vorliegenden Fall beginnt der „Range“ bei 0 und endet bei 3, da wir von 0 an n_max = 4 Schritte nach oben zählen, sodass der höchste von 4 Schritten bereits bei 3 erreicht ist, d.h. bei n < 4! Dabei zählt die Angabe „range(0, n_max)“ nicht nur den integrierten Schleifenzähler, sondern auch gleichzeitig dafür, dass dieser in Einerschritten, d.h. ganzzahlig hochzählt (siehe Programm „microbit_teil_04_prog_06.hex“ mit dem Quelltext „microbit_teil_04_prog_06.py“). -

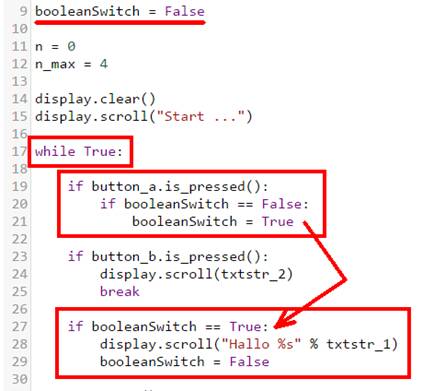
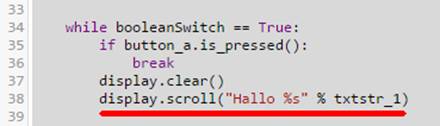
Auch wenn „while True“-Endlosschleifen sehr bequem sind, so ist der Umgang mit ihnen, d.h. das Hin- und Herschalten mit nur einem Taster trotzdem nicht so einfach und deshalb gewöhnungsbedürftig:

(Bild 11 – „while True“-Schleife mit Umschalter)

Wie man im obenstehenden Programm „microbit_teil_04_prog_07.hex“ mit dem Quelltext „microbit_teil_04_prog_07.py“ sieht, lässt sich mit dem booleschen Umschalter „booleanSwitch“ die Laufschrift display.scroll("Hallo %s" % txtstr_1) jederzeit ein- oder ausschalten.

Dabei wird aber die Laufschrift nur ein einziges Mal im „5 x 5 Matrix-LED“-Display angezeigt, da der boolesche Schalter „booleanSwitch“ anschließend sofort wieder umgeschaltet wird.

Mit dem „break“-Befehl lässt sich die „while True“-Endlosschleife wieder verlassen und das Programm beenden.

Jetzt wissen Sie, dass man mit dem logischen Schalter „booleanSwitch“ zwischen zwei Anzeigen, zwei Zuständen oder Programmen hin- und herschalten kann mit dem Vorteil, dass man dazu nur einen einzigen Taster braucht! -

In der Praxis gibt es aber auch Situationen und Erfordernisse, wo man eine Fehleranzeige, eine Meldung oder einen Infotext permanent als Laufschrift im „5 x 5 Matrix-LED“-Display anzeigen möchte und zwar so lange bis der Anwender auf die Info reagiert und diese quittiert, z.B. indem er diese per Tastendruck ausschaltet (siehe Programm „microbit_teil_04_prog_08.hex“ mit dem Quelltext „microbit_teil_04_prog_08.py“):

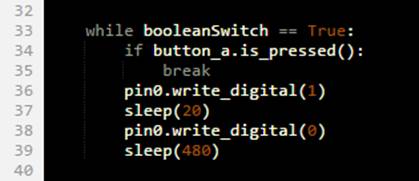
(Bild 12 – „while True“-Schleife mit Wechseltaster)

Eine Fehleranzeige, eine Meldung oder einen Infotext permanent als Laufschrift im „5 x 5 Matrix-LED“-Display anzuzeigen, ist für den „micro:bit“-Rechner im Zusammenspiel mit den beiden Tastern A und B die ultimative Kommunikationsmöglichkeit, da der Rechner selbst über keine vollwertige Tastatur oder ein mehrzeiliges LCD-Display verfügt.

Aber bei der Steuerung, Überwachung und Kontrolle von elektrischen oder elektronischen Geräten, die teilweise entfernt vom „micro:bit“-Rechner aufgestellt und betrieben werden, braucht man dann aber auch Betriebsanzeigen, das Anzeigen einer Störung oder eines Defektes usw. Beispielsweise in Form von verschieden farbigen LED-Statusanzeigen wie z.B. „grün“ für „Gerät ist eingeschaltet“, „gelb“ für „Maschine arbeitet bzw. wartet auf Bedienung“ oder „rot“ für „Störung“.

Da der „micro:bit“-Rechner u.a. auch über drei programmierbare Ports „Pin P0“ bis „Pin P2“ verfügt, lassen sich mit diesen z.B. auch LEDs ansteuern, d.h. ein- oder ausschalten. -

3. Eine LED programmiert ein- und ausschalten

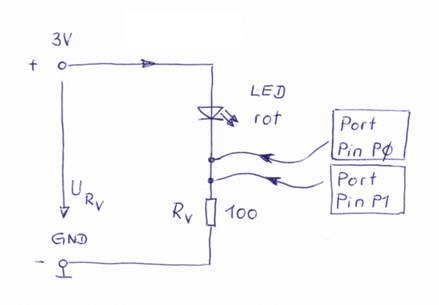
Nachfolgend geht es darum, dass wir eine rote LED zum Leuchten bringen, indem wir diese über einen entsprechenden Vorwiderstand in Reihe an den Port „Pin 0“ anschließen.

Wie man den Vorwiderstand als Funktion der roten LED sowie der entsprechenden Betriebsspannung berechnet wurde bereits im Teil 3, Kapitel „3. Es werde Licht - mit einer LED“ ausführlich behandelt.

Wie Sie sicherlich schon wissen, lassen sich die Ports „Pin 0“ bis „Pin 2“ programmieren. Und zwar als Ein- oder Ausgang. Dabei wird dann wiederum zwischen analog und digital unterschieden.

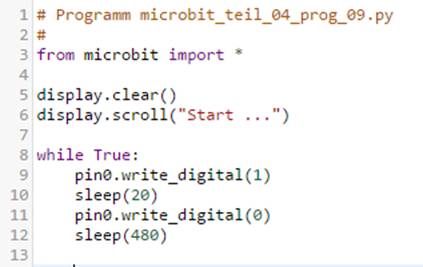
Wenn man eine LED am Port „Pin 0“ digital einschaltet, dann gibt es nur zwei Schaltzustände und zwar entweder „ein“ (= Strom ein, Stromfluss = „1“) oder „aus“ (= Strom aus, Stromfluss = „0“). Werte dazwischen gibt es nicht. Beim Einschalten liegt dann die Ausgangsspannung vom Port „Pin 0“ an. Dabei kann die Ausgangsspannung entsprechend der Stromversorgung mittels des „Micro-USB 2.0“-Kabels bis zu +3,3 V betragen.

Mit dem nachfolgenden Programm „microbit_teil_04_prog_09.hex“ mit dem Quelltext „microbit_teil_04_prog_09.py“) lässt sich die rote LED am Port „Pin P0“ zum Blinken bringen:

(Bild 13 – rote LED digital einschalten)

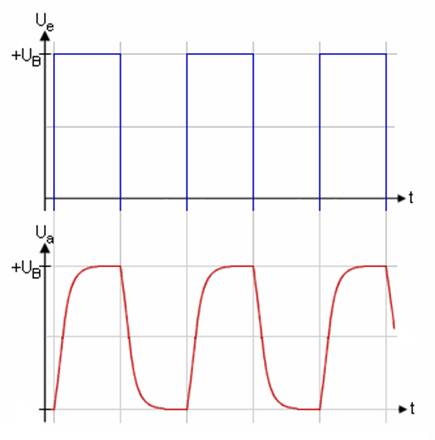
Beim Blinken der roten LED fällt auf, dass diese ziemlich hektisch blinkt, was der unterschiedlichen Ein- und Ausschaltdauer geschuldet ist. Da sich aber die rote LED nur ein- oder ausschalten lässt, lässt sich die Ein- und Ausschaltdauer nur über das Statement „sleep(20)“ und „sleep(480)“ einstellen.

Wenn man das Puls-/Pausenverhältnis (= Ein- und Ausschaltdauer) symmetrisch einstellt, sodass die beiden „sleep()“-Statements über die gleiche Zeitdauer von 250 ms verfügen, dann beträgt die Periodendauer T = 500 ms mit der Frequenz f = 1 / T = 1 / ( 500 ms ) = 1/500 Hz.

Zum Vergleich: die Frequenz des Wechselstroms in Europa beträgt f = 50 Hz = 1/T = 1 / ( 50 ms ) = 0,02 s = 20 ms. Das bedeutet nichts anderes als dass eine Glühlampe in 20 ms bis zu 50 mal an- und ausgeht. Für das menschliche Auge aber ist die Wechselfrequenz zwischen Hell und Dunkel so schnell, dass man wegen dessen Trägheit nur sieht, dass die Glühlampe einfach nur eingeschaltet ist und ununterbrochen leuchtet! Dazu muss man erwähnen, dass eine Glühlampe beide Halbwellen der sinusförmigen Wechselspannung zum Leuchten nutzt, sodass es zwischen den Wellenbergen keine größere Pause gibt, die ein Flackern des Lichts bewirken würde.

Anders verhält es sich bei einer Leuchtdiode (= LED), da diese normalerweise nur an Gleichspannung betrieben wird und deshalb nur bei richtiger Polung leuchtet. Da es sich bei einer LED im Prinzip aber um eine spezielle Siliziumdiode, die in Durchlassrichtung betrieben den größten Teil des elektrischen Stromes in sichtbares Licht umwandelt, während sie in Sperrrichtung betrieben den elektrischen Strom sperrt, handelt, ließe sich diese auch als sogenannter Einweggleichrichter verwenden und an Wechselstrom betreiben. Aber nur in Verbindung mit einem entsprechenden Vorwiderstand, der in Reihe zur LED geschaltet werden muss, damit diese im Durchlassbetrieb nicht überlastet wird und durchbrennt.

Demzufolge würde eine LED, die mit Wechselstrom betrieben wird, stets nur eine Halbwelle der Sinusschwingung durchlassen, während die andere Halbwelle wegen des Betriebs der LED in Sperrrichtung gesperrt würde. Da beim Sperren der negativen Halbwelle der Sinusschwingung der Stromfluss zum Erliegen kommt, entsteht eine entsprechende Pause bei dem die LED dunkel bleibt mit der Folge, dass die LED nur noch flackert!

Wenn also die rote LED im Zeitraum von T = 500 ms nur ein einziges Mal ein- und dann wieder ausgeschaltet wird, dann beträgt die Frequenz f = 1 / T = 1 / 500 ms = 0,002 Hz. Im Vergleich dazu würde eine Glühlampe im gleichen Zeitraum 25.000 mal an- und ausgehen. Das ist dann auch der Grund dafür, dass die „langsamere“ LED einfach nur blinkt, statt zu ununterbrochen zu leuchten.

Wenn also das Puls-/Pausenverhältnis der roten LED im Verhältnis 1:1 symmetrisch ist, dann blinkt die LED zwar immer noch ziemlich schnell, aber nicht nervös hektisch, sozusagen mehr oder weniger stressfrei. Da beim „symmetrischen Blinken“ die Lichtausbeute entsprechend größer ist, leuchtet die rote LED zudem auch noch heller (siehe Programm „microbit_teil_04_prog_10.hex“ mit dem Quelltext „microbit_teil_04_prog_10.py“). -

Wie bereits gesagt, lassen sich die Ports „Pin P0“ bis „Pin P2“ programmieren. Und zwar nicht nur als Ein- oder Ausgang, sondern auch für analoge oder digitale Anwendungen. Aber selbst wenn man eine LED digital ein- oder ausschaltet, muss man von Digitaltechnik, d.h. von Gatterschaltungen wie z.B. UND, ODER, NICHT, negatives UND (engl. „NAND“), negatives ODER (engl. „NOR“), exklusives ODER (engl. „XOR“), RS- oder JK-Flip-Flops keine Ahnung haben, sondern einfach nur wissen, dass es bei einem digitalen Schalter entweder nur den Schaltzustand „ein“ (= „1“)oder „aus“ (= „0“) gibt. Analoge Zwischenwerte wie etwas an im Sinne von halb so hell oder halb so dunkel gibt es demzufolge nicht!

Wenn man also wie im Programm oben die rote LED digital ein- und ausschaltet, sodass diese periodisch, d.h. im wiederkehrend im gleichen Rhythmus blinkt, dann benutzt man zum Ein- und Ausschalten einfach nur die beiden Statements „pin0.write_digital(1)“ oder „pin0.write_digital(0)“, sodass ich eben nicht wissen muss, dass eine LED erst bei einer Flussspannung von U_F = 1,6 V leuchtet und stets nur in Verbindung mit einem in Reihe geschalteten Vorwiderstand R_V = 100 Ω betrieben werden sollte, damit diese nicht wegen eines zu hohen Durchlassstromes I_LED < 20 mA 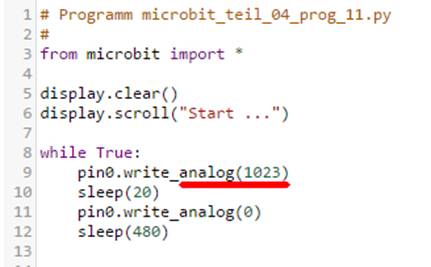durchbrennt.

Wenn man aber, wie im Programm „microbit_teil_04_prog_11.hex“ mit dem Quelltext „microbit_teil_04_prog_11.py“ zu sehen,

(Bild 14 – rote LED analog einschalten)

die rote LED analog ein- und ausschalten will, dann muss man schon wissen, dass eine LED erst bei einer Flussspannung von U_F = 1,6 V leuchtet und stets nur in Verbindung mit einem in Reihe geschalteten Vorwiderstand R_V = 100 Ω betrieben werden sollte, damit diese nicht wegen eines zu hohen Durchlassstromes I_LED < 20 mA durchbrennt. Dazu muss man dann auch wissen, welchen Wert die Betriebssspannung U_Betrieb = U_F + U_RV <= +3,3 V haben sollte, damit die rote LED beim analogen Einschalten dann auch tatsächlich leuchtet!

Wenn z.B. die zur Verfügung stehende Betriebssspannung nur U_Betrieb = 3,23 V beträgt und die rote LED zum kräftigen Leuchten eine (Durch-) Flussspannung von U_F = 1,6 V benötigt, dann bleiben für den Spannungsabfall ∆U_RV am Vorwiderstand R_V nur noch

∆U_RV = U_Betrieb - U_F = 3,23 V - 1.6 V = 1,63 V

übrig, sodass sich der Vorwiderstand R_V bei einem Strom von I_LED = 20 mA wie folgt berechnet:

R_V = U_LED / I_LED = ∆U_RV / I_F = 1,63 V / 20 mA = 0,0815 KΩ = 81,5 Ω

Wenn man aber einen Vorwiderstand mit R_V = 100 Ω verwendet, dann befindet man sich wegen des geringeren Stromes I_F mit

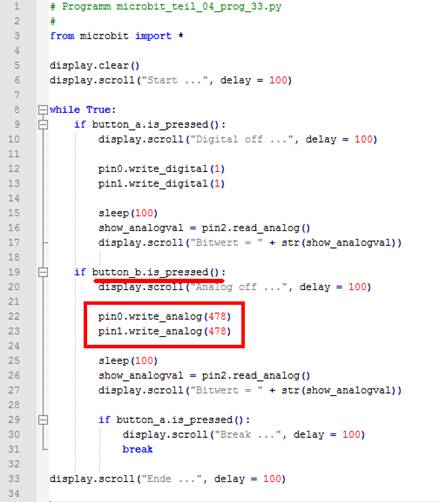
I_F = I_RV =∆U_RV / R_V = 1,63 V / 100 Ω = 0,0163 A = 16,3 mA

auf der sicheren Seite! -

Im Zusammenhang mit der Flussspannung der roten LED von U_F = 1,6 V wissen wir, dass diese ab diesem Wert zu leuchten anfängt. Bezüglich des digitalen Wertes von 1023₂ bedeutet dies, dass wir die zur Verfügung stehende Betriebssspannung von U_Betrieb = 3,23 V diesem gleichsetzen können, sodass wir gemäß Dreisatz einen analogen Wert von 1023₂ / 3,23 V * 1,6 V = 506,75₂ ≈ 507₂ einstellen müssen, damit die rote LED gerade so zu glimmen anfängt. Rechnerisch, theoretisch! In der Praxis zeigt sich nämlich, dass die rote LED selbst bei einem digitalen Wert von 1 immer noch deutlich erkennbar leuchtet:

(Bild 15 – rote LED leuchtet ganz schwach)

Da die Gesamtspannung U_{Pin P0} an der Reihenschaltung von roter LED und Vorwiderstand R_V unter Last nicht wie oben angenommen U_Betrieb = 3,23 V beträgt, sondern nur U_{Pin P0} = U_LED+RV = 2,72 V ausmacht, ergibt sich pro digitalem Wert eine Spannungsänderung am Port „Pin P0“ von 2,72 V / 1023₂ = 0,00265885 V / Bit = 2,66 mV / Bit.

Demzufolge stellt sich am Port „Pin P0“ für den digitalen Bitwert 1₂ die analoge Spannung von 2,66 mV/Bit ein, wobei die rote LED trotzdem noch ganz schwach glimmt. Besonders gut lässt sich das erkennen, wenn man direkt von oben auf die LED schaut, da diese über eine kleine eingebaute Linse verfügt, die das Licht fokussiert.

Abschließend bleibt noch zu klären, weshalb die rote LED bei einem nahezu hälftigen Bitwert von 507₂ (siehe oben) wider Erwarten nicht halb so hell leuchtet als erwartet. Der Grund dafür dürfte der sein, dass sich die Helligkeit der roten LED nicht linear, sondern eher quadratisch ändert. Das aber lässt sich wegen der fehlenden technischen Daten im Moment nicht verifizieren. -

Nachdem wir also die rote LED sowohl analog also auch digital ein- und ausschalten können, liegt es auf der Hand, dass wir diese auch programmiert, d.h. mittels des Tasters A ein- und ausschalten.

Diesbezüglich bietet es sich an, dass wir das Programm „microbit_teil_04_prog_08.hex“ mit dem Quelltext „microbit_teil_04_prog_08.py“ aufgreifen und der Einfachheit halber die Laufschrift im „5 x 5 LED-Matrix“-Display

(Bild 16 - Laufschrift gegen LED-Blinken austauschen)

gegen die Statements mit der Funktionalität des Blinkens wie folgt auswechseln:

(Bild 17 - LED-Blinken gegen Laufschrift ausgetauscht)

Wie im Screenshot von Bild 17 zu sehen ist, kommt bei den Statements mit dem Blinken u.a. auch die Statements „sleep(20)“ und „sleep(480)“ zum Einsatz. Dabei verhält es sich so, dass sich das Python-Programm mit den „sleep()“-Statements wider Erwarten nicht mit dem Emulationsprogramm auf der Homepage von „create.withcode.uk“ kompilieren lässt!

Deshalb muss man das Python-Programm mit den „sleep()“-Statements mit Compiler-Programm von MicroPython & python auf der Homepage von „https://www.microbit.co.uk/app/“ kompilieren, herunterladen und auf den „micro:bit“-Rechner flashen.

Da sich das neue Programm „microbit_teil_04_prog_13.hex“ mit dem Quelltext „microbit_teil_04_prog_13.py“ aber trotzdem an einer entscheidenden Stelle vom Ursprungsprogramm „microbit_teil_04_prog_08.hex“ mit dem Quelltext „microbit_teil_04_prog_08.py“ unterscheidet, nämlich beim booleschen Umschalter

booleanSwitch = True (… anstelle von vormals „False“ im Ursprungsprogramm),

müssen wir die Abfrageroutine

if button_a.is_pressed():

noch näher untersuchen. Beginnen wir mit dem Ursprungsprogramm:

(Bild 18 - boolesche Abfrage des Tasters A)

Im neuen Programm sieht der Quelltext praktisch genau so aus, nur halt mit negativer Logik, weil der boolesche Schalter „booleanSwitch“ anders gesetzt ist:

(Bild 19 - boolesche Abfrage des Tasters A)

Wenn also das Programm nach dem Flashen, d.h. dem Übertragen in den Arbeitsspeicher, ohne den Taster A zu drücken, startet, dann ist der boolesche Schalter „booleanSwitch“ auf „true“ gesetzt, sodass als Erstes die beiden Statements

display.clear()

display.scroll("Start ...")

ausgeführt werden und die Laufschrift „Start …“ im „5 x 5 LED-Matrix“-Display angezeigt wird. Direkt danach geht es in die äußere, große „while True:“-Endlosschleife und von dort gleich in die innere, kleine „while booleanSwitch == True“-Schleife. Wenn man dann in der inneren, kleinen Schleife den Taster A betätigt, dann verlässt man diese wieder, um gleich wieder in der inneren, kleinen Schleife zu landen, weil sich der Wahrheitswert des booleschen Schalters „booleanSwitch“ nicht geändert hat!

Erst wenn man den Taster A länger gedrückt hält, landet man nach dem Verlassen der inneren, kleinen Schleife wieder in der äußeren, großen „while True:“-Endlosschleife wo dann schließlich die Laufschrift „… on“ angezeigt wird und der boolesche Schalter „booleanSwitch“ auf den Wert „False“ gesetzt wird.

Dass der boolesche Schalter „booleanSwitch“ auf den Wert „False“ gesetzt wurde, wirkt sich aber im weiteren Programmablauf wider Erwarten nicht aus, da das Programm nach dem „break“-Befehl fortfährt und jetzt endlich die rote LED blinken lässt!

Dazu muss man wissen, dass der „break“-Befehl dazu dient, eine „while“-Schleife sofort zu verlassen, um dann irgendwann später nach dem „break“-Befehl wider mit dem normalen Programmablauf fortzufahren! Deshalb blinkt dann auch die rote LED in der inneren, kleinen „while booleanSwitch == True“-Schleife, obwohl ja die boolesche Variable „booleanSwitch“ zwischenzeitlich den Wahrheitswert „False“ angenommen hatte:

(Bild 20 - dass vollständige Programm)

Wahnsinn! Da muss man erst einmal drauf kommen bzw. auch später dran denken, dass der Programmablauf hinter dem „break“-Befehl wieder aufgenommen und fortgesetzt wird!

Apropos fortsetzen. Wenn man die innere, kleine „while booleanSwitch == True“-Schleife mittels „break“-Befehl verlässt, dann kann man jederzeit wieder in diese zurückkehren, indem man den Befehl „continue“, d.h. fortsetzen, verwendet. „break“ und „continue“ bilden also ein Geschwisterpaar und gehören deshalb zusammen.

Immer dann, wenn man eine innere Schleife mittels „break“ verlassen hat und man nicht genau weiß, was das Programm dann in der äußeren Schleife alles so macht, dann lässt sich mittels „continue“ wieder die Kontrolle zurückgewinnen, da dann das Programm wieder in die innere Schleife zurückkehrt und dort weiter macht, wo man zuvor mittels „break“ ausgestiegen war!

Mit dem Programm „microbit_teil_04_prog_14.hex“ und dem Quelltext „microbit_teil_04_prog_14.py“ lässt sich der Rücksprung in die innere, kleine „while booleanSwitch == True“-Schleife mit dem Statement „continue“ direkt ausprobieren, sodass sich das laufende Programm nicht mehr durch Tastendruck auf den Taster B beenden lässt:

(Bild 21 - die Statements „break“ und „continue“)

Wenn man auf Nummer sicher gehen und sich überzeugen will, dass man sich beim Blinken der roten LED tatsächlich in der inneren, kleinen „while booleanSwitch == True“-Schleife befindet, dann muss man nur die Kommentaranweisung „#“ entfernen, sodass man fortwährend die Laufschrift „Bin jetzt hier!“ angezeigt bekommt.

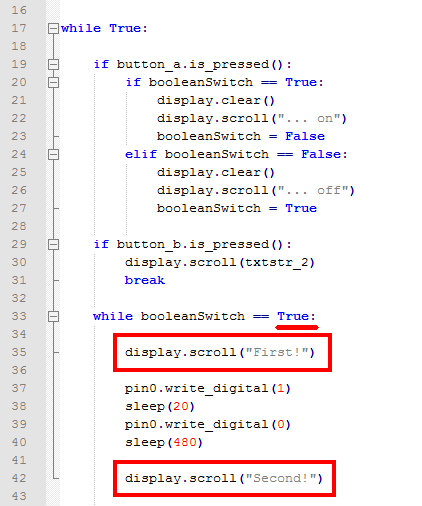
Aber das ist noch nicht alles! Schließlich hat der „break“-Befehl noch mehr zu bieten! Ein kleines Geheimnis, eine Besonderheit, die es noch zu entdecken gilt:

(Bild 22 - „break“ spaltet „while“-Schleife)

Wie man oben im Screenshot sieht, gibt es nun im Quelltext in der inneren, kleinen „while booleanSwitch == True“-Schleife zwei neue Statements und zwar

display.scroll("First!") und

display.scroll("Second!")

mit der Besonderheit, dass das erste Statement display.scroll("First!") vor dem „break“-Befehl steht und das zweite Statement display.scroll("Second!") nach dem „break“-Befehl, sodass dieser die beiden Statements nicht nur trennt, sondern auch getrennt abarbeitet (siehe Programm „microbit_teil_04_prog_15.hex“ und dem Quelltext „microbit_teil_04_prog_15.py“).

Dass man mit dem „break“-Befehl aus der inneren, kleinen „while booleanSwitch == True“-Schleife heraus verzweigt, diese also vorübergehend verlässt, wissen wir ja bereits.

Außerdem wissen wir, dass wenn der „break“-Befehl abgearbeitet wurde, die Programmausführung nach dem „break“-Befehl wieder fortgesetzt wird!

Neu und noch ungewohnt ist dabei die Erfahrung, dass sich das Ganze innerhalb der inneren, kleinen „while booleanSwitch == True“-Schleife abspielt und zwar in Abhängigkeit der booleschen Umschalt-Variablen „booleanSwitch“ mit dem Wahrheitswert „true“ (= zutreffend) oder „false“ (= unzutreffend).

Dabei wird dann je nach dem booleschen Wahrheitswert entweder die Laufschrift „First!“ oder „Second!“ im „5 x 5 LED-Matrix“-Display angezeigt! Das Besondere dabei ist also, dass sich beide Laufschriften niemals zusammen, d.h. nacheinander anzeigen lassen!

Aber ist es wirklich der „break“-Befehl, der die beiden Laufschriften voneinander trennt, sodass sich diese niemals zusammen, d.h. nacheinander anzeigen lassen?

Sie können sich die Frage selbst beantworten, indem Sie das Programm „microbit_teil_04_prog_16.hex“ mit dem Quelltext „microbit_teil_04_prog_16.py“ selbst ausprobieren:

(Bild 23 - Programmspaltung auch ohne „break“-Befehl)

Wenn Sie das obenstehende Programm starten, dann erscheint nach der Laufschrift „Start …“ die nächste Laufschriftanzeige „First!“. Dabei werden dann die nachfolgenden Programmzeilen

pin0.write_digital(1)

sleep(20)

pin0.write_digital(0)

sleep(480)

display.scroll("Second!")

wider Erwarten nicht abgearbeitet und angezeigt, blinkt keine rote LED, wird auch zum Schluss die Laufschrift „Second!“ nicht angezeigt!

Ändern Sie als Nächstes im obenstehenden Programm die Programmzeile 33

while booleanSwitch == True:

ab auf

while booleanSwitch == False:.

Kompilieren Sie den geänderten Programmkode neu, sodass eine neue, hexadezimale Programmdatei (= kompilierter Maschinenkode) entsteht, spielen Sie diese auf den „micro:bit“-Rechner, und flashen Sie den Inhalt in den Arbeitsspeicher. Nach etwa 20 Sekunden startet das geänderte und neu kompilierte Programm, sodass die Laufschriftanzeige „ Start …“ erscheint.

Nach dem Programmstart und der Laufschriftanzeige „ Start …“ blinkt die rote LED ein einziges Mal kurz auf, sodass gleich darauf die neue Laufschriftanzeige „Second!“ in der inneren, kleinen „while booleanSwitch == True“-Schleife angezeigt wird (siehe Programm „microbit_teil_04_prog_17.hex“ mit dem Quelltext „microbit_teil_04_prog_17.py“).

Jetzt steht unwiderruflich fest, dass die unterschiedliche Laufschriftanzeige sowie das einzelne Aufblitzen der roten LED nicht vom „break“-Befehl abhängt, weil es diesen in der inneren, kleinen „while booleanSwitch == True oder False“-Schleife nicht mehr gibt!

So jetzt haben wir durch Experimentieren, durch Versuch und Irrtum eine ganze Menge gelernt, ohne aber das Problem wirklich gelöst zu haben. Schließlich beschränken sich die Kommunikationsmöglichkeiten des „mini:bit“-Rechners auf das „5 x 5 LED-Matrix“-Display, die beiden Taster A und B sowie die Ports „Pin P0“ bis „Pin P2“, sofern an diese externe Gerätschaften wie z.B. die rote LED angeschlossen wurden.

Wie also soll sich der Anwender verhalten, wenn die rote LED plötzlich anfängt hektisch zu blinken, um auf diese Weise zu signalisieren, dass eine Störung vorliegt, ein Signalpegel überschritten oder ein stiller Alarm ausgelöst wurde? Da wäre es schon sehr hilfreich, wenn eine permanente Laufschrift dem Anwender mitteilen würde, um was es geht, weshalb die rote LED so heftig blinkt! Aber genau das ist uns ja bisher noch nicht gelungen, dass der Anwender parallel zur blinkenden, roten LED mittels periodisch wiederkehrender Laufschrift eingehender über ein entsprechendes Vorkommnis informiert wird. Und was ist der Grund dafür, dass uns das bisher noch nicht gelungen ist?

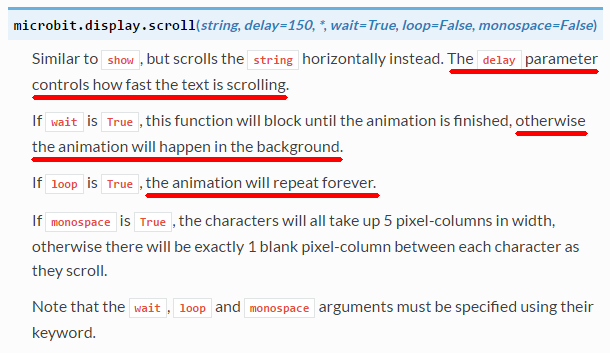
Ganz einfach, weil es sich bei dem Statement display.scroll("Text …“) in Wirklichkeit um eine „Untermenge“ eines wesentlich umfangreicheren Befehls mit insgesamt bis zu vier Parametern handelt:

display.scroll(string, delay=150, *, wait=True, loop=False, monospace=False)

(Bild 24 – „display.scroll()“ in aller Ausführlichkeit)

Nachfolgend die entsprechende Übersetzung ins Deutsche mit Google Translate:

(Bild 25 – „display.scroll()“ ins Deutsche übersetzt)

Von der „BBC micro:bit“ gibt es das obenstehende Tutorial zur Programmiersprache „MicroPython“, das ganz gut zu sein scheint. -

Was sagte der Dorfpolizist Anfang des 19. Jahrhunderts zum Bauern in dessen Haus und Hof eingebrochen wurde? „Wenn wir wüssten wie der Dieb heißt und wo er wohnt, dann hätten wir ihn schon!“. Wenn Sie kulturell gebildeter sind, dann halten Sie es mit Sokrates, der einmal sinngemäß gesagt haben soll: „Ich weiß, dass ich nichts weiß!“.

Heutzutage spricht man auch von der Halbwertszeit des Wissens, also der Zeitspanne in der Wissen veraltet, nicht mehr aktuell ist und das im Alltag und Beruf nicht mehr von Nutzen ist. Und die wird immer kürzer, sodass man einen in der frühen Jugend erlernten Beruf ohne das lebenslange Lernen ab Mitte/Ende Vierzig nicht mehr ausüben kann. Vielleicht aber auch deshalb, weil es den erlernten Beruf bis dahin nicht mehr gibt.

Wenn man also weiß, wie die Dinge funktionieren, dann verlieren sie ihren Schrecken, werden sie plötzlich ganz leicht, leicht verständlich. Im vorliegenden Fall bei der Python-Programmierung kann man als Newcomer nicht alles wissen, muss man auch nicht alles wissen! Man muss nur wissen, wo es steht! Oder man muss jemanden kennen, der sich auskennt, der weiß wie es geht (siehe Programm „microbit_teil_04_prog_18.hex“ mit dem Quelltext „microbit_teil_04_prog_18.py“):

(Bild 26 –Laufschrift und blinkende LED gleichzeitig)

Die Bedienung des obenstehenden Programms ist wegen der beiden Abfragen, ob der Taster A gedrückt wurde etwas trickreich. Demzufolge muss man beim Umschalten von „… on“ auf „… off“ den richtigen Zeitpunkt erwischen. Außerdem lässt sich das Programm durch Drücken des Tasters B nur dann abschalten und runterfahren, wenn es sich zuvor im Modus „… on“ befindet.

Damit man später noch weiß, wie das Programm bedient werden muss, nachfolgend noch die

Bedienungsanleitung

zum Programm „microbit_teil_04_prog_18.hex“ mit dem Quelltext „microbit_teil_04_prog_18.py“

1. Starten und Ausführen des Programms

Das in den Arbeitsspeicher des „micro:bit“-Rechners geflashte Programm startet sich nach etwa 20 Sekunden von allein und zeigt im Display die programmierte Laufschrift „Start ...“ an.

Nachdem die Laufschrift durchgelaufen ist, bleibt das Display zwar dunkel, aber das Programm mit den zwei Tastern A und B weiterhin aktiv.

2. Taster A zum Einschalten des Blinklichts

Nach dem selbständigen Programmstart befindet sich das Programm im Grundmodus bei dem nur der Taster A fortwährend auf einen eventuellen Tastendruck hin abgefragt wird.

Drückt man nun auf den Taster A, so kommt es auf die Länge der Zeitdauer des Drückens des Tasters an, ob die rote LED ein- oder ausgeschaltet wird. Wenn dabei die Laufschrift in den Modus, d.h. in die Anzeige „… off“ wechselt, dann muss man den Taster A ein weiteres Mal drücken, um in die Anzeige „… on“ zu wechseln.

Das Umschalten mittels des Tasters A gelingt am besten, wenn man den richtigen Zeitpunkt abpasst. Dieser ist dann gegeben, wenn die Laufschrift mit den drei Punkten „… on“ oder „… off“ exakt beim zweiten Punkt „..“ angekommen ist! Das Abpassen dieses Zeitpunkts gelingt am besten wenn man den Tasters A länger gedrückt hält und erst wieder loslässt, wenn der zweite Punkt „..“ der Laufschrift erscheint.

3. Taster A zum Ausschalten des Blinklichts

Das Blinklicht mit der roten LED wurde so programmiert, dass es sich mit nur einem Taster und zwar dem Taster A als Wechselschalter ein- und ausschalten lässt. Dabei erfolgt die Bedienung des Tasters A wie in Punkt 2.) beschrieben!

4. Taster B zum Beenden des Programms

Das Programm selbst lässt sich nur beenden, wenn es sich im Modus mit der Anzeige „…on“ befindet!

Demzufolge könnte es also sein, dass man zum Beenden des Programms erst einmal vom Modus „… off“ in „… on“ wechseln muss. Wie das geht, ist im Punkt 2.) ausführlich beschrieben.

5. Mit dem „Reset“-Taster alles wieder auf Anfang setzen

Auf der Rückseite des „micro:bit“-Rechners befindet sich ein sogenannter „Reset“-Taster mit dem sich der Rechner neu starten lässt. Dabei wird auch das zuvor in den Arbeitsspeicher geflashte Programm wieder neu gestartet, sodass sich dieses wieder im zuvor beschriebenen Grundmodus befindet! -

Wie man anhand der Bedienungsanleitung sieht, ist die Bedienung des roten LED-Blinklichts mit nur einem Taster als Umschalter leider nicht intuitiv möglich. Der Grund dafür ist der, dass sich zwei ineinander geschachtelte „while“-Schleifen nebst Tasterbedienung als logisch komplex erweist.

Deshalb werden wir solche Dinge später bei der objektorientierten Programmierung mit Python programmieren, sodass sich dann auch die Bedienung intuitiv vornehmen lässt. -

4. Dezimal Erbsen zählen

Als Erbsenzähler bezeichnet einen Menschen, der im Leben ziemlich kleinlich ist, alles überprüft, ob es ihm auch zum Vorteil gereicht und nichts ohne Gegenleistung herausrückt.

Wir wollen nachfolgend herausfinden, ob sich mit dem „micro:bit“-Rechner auch Erbsen zählen lassen. Und zwar auf’s Komma genau. Aber macht das überhaupt Sinn, Erbsen bis auf drei Nachkommastellen zu berechnen? Schließlich interessieren den Koch, wenn er eine herzhafte Erbensuppe mit Schickenspeckwürfeln kocht, nur die ganzen Erbsen und nicht die zerbröselten Erbenstückchen, die nur ein paar Milligramm wiegen.

Aber es könnte ja sein, dass die herzhafte Erbsensuppe mit Geschmacksverstärker als Tütensuppe kreiert werden soll. Mit gefriergetrockneten, zuvor zerkleinerten Erbsenstückchen, die fein dosiert der Tütensuppe beigemischt werden, wo die Zutaten dann weniger wiegen als ein Standardbrief (= 20 Gramm) der Deutschen Post AG für derzeit 70 Eurocent/Brief.

Für die herzhafte Erbsensuppe als Tütensuppe bräuchten wird dann tatsächlich eine Feinwaage nebst „micro:bit“-Rechner für das gewichtsmäßige Umrechnen der Zutaten im Gramm- und Milligrammbereich. Obwohl, wenn man zu Hause eine herzhafte Erbsensuppe kochen will, dann würde man die Erbsen nicht zählen sondern in einem Gefäß auf der Waage wiegen.

Wie man sieht, öffnet sich beim Thema „Messen, wiegen, zählen“ ein riesiges Anwendungsgebiet für Mikrocontroller und für den „micro:bit“-Rechner, da sich dieser programmieren lässt. Dazu müsste man dann aber wissen, ob sich mit dem „micro:bit“-Rechner auch tatsächlich dezimal, d.h. mit Nachkommastellen, rechnen lässt.

Eigentlich sollte das der Fall sein. Schließlich gibt es einfache Taschenrechner, die die vier Grundrechenarten und auch das Quadrieren nebst Quadratwurzelrechnen beherrschen, für um die fünf Euro. Insofern kann man eigentlich erwarten, dass der „micro:bit“-Rechner tatsächlich über einen integrierten Rechenknecht verfügt, sodass sich mit diesem auch dezimal rechnen lässt. Eigentlich! Und uneigentlich? Uneigentlich wissen wir noch nicht, ob der „micro:bit“-Rechner tatsächlich über eine arithmetische Recheneinheit, engl. ALU = „Arithmetic Logic Unit“ verfügt oder nicht.

Wenn Sie den Link anklicken und den Wikipedia-Artikel lesen, dann wissen Sie, dass jeder Prozessor über eine ALU verfügt, verfügen muss, damit er über den Adress-, Daten- und Steuerbus mit dem angeschlossenen Arbeitsspeicher (ROM = engl. „read only memory“ = Nur-Lese-Speicher, RAM = engl. „random access memory“ = frei wählbarer Schreib- und Lese-Speicher) kommunizieren, Daten austauschen und Programme ausführen kann. Aber lässt mit der ALU auch dezimal wie bei einem Taschenrechner rechnen?

>> Alle ALUs verarbeiten Festkommazahlen. Gleitkommabefehle sind in vielen aktuellen CPUs mittlerweile Standard. Ausnahmen sind kleinere Mikrocontroller, die auf geringe Stromaufnahme oder auf geringe Herstellkosten getrimmt sind. << (Quelle: Wikipedia)

Jetzt sind wir also fast genauso schlau wie vorher. Zwar wissen wir jetzt, dass Prozessoren nicht ohne die ALU auskommen, aber immer noch nicht, ob sich mit dem „micro:bit“-Rechner auch dezimal rechnen lässt.

Wenn Sie wie im Teil 3 dieses Tutorials mit JavaScript programmiert und versucht haben mit Dezimalzahlen zu rechnen, dann wissen Sie bereits, dass das wider Erwarten nicht geht. Aber das muss jetzt nicht zwangsläufig bedeuten, dass das am „micro:bit“-Rechner liegt. Schließlich sind Hardware und Software zwei verschiedene Dinge. Demzufolge könnte man auch sagen, dass die Software immer nur das kann, wozu die Hardware in der Lage ist bzw. in die Lage versetzt wurde.

Dass man beim „micro:bit“-Rechner mit JavaScript wider Erwarten nicht dezimal rechnen und programmieren kann, dürfte dann wohl daran liegen, dass das dezimale Rechnen in JavaScript des „micro:bit“-Rechners noch nicht implemeniert ist!

Wenn aber die Software bestimmte Dinge nicht oder noch nicht kann, dann bedeutet dies nicht automatisch, dass es an der Hardware liegt. Hier der Beweis:

(Bild 27 – durch Zufall entdeckt, die serielle Schnittstelle)

Wie man im obenstehenden Bild sieht, gibt es nämlich eine serielle Schnittstelle mittels der man kommunizieren und Daten austauschen kann.

>> Bei dem Programm wird der der Lichtwert von der Funktion input.lightLevel() zurückgegeben. Der Wert wird dann als Dezimalwert die über die serielle Schnittstelle mit der Funktion serial.writeNumber() ausgegeben. Danach wird noch ein Zeilenvorschub mit der Funktion serial.writeLine("") gesendet. << (Quelle: „Robotfreak Blog“ – Robotik, Elektronik, Arduino und mehr von Peter Recktenwald, Berlin)

So jetzt steht es fest, dass sich mit dem engl. „Programming Experience Toolkit“, kurz dem PXT-Entwicklungswerkzeug für Blockbefehle und dem JavaScript-Compiler von Microsoft für den „micro:bit“-Rechner im Moment noch keine Dezimalwerte berechnen, sich aber sehr wohl über die serielle Schnittstelle übertragen lassen.

Wer seinen „micro:bit“-Rechner mit dem „Micro-USB 2.0“-Kabel an eine der „USB 2.0“-Buchsen seines Windows-PCs angeschlossen hat, sodass dieser in das Windows-Dateisystem als eigenständiges USB-Laufwerk eingebunden wird, der kann sich mit dem Google Chrome-Browser oder dem kompatiblen „Vivaldi“-Browser die seriell übertragenen Daten auch in einem kleinen Fenster (siehe roter Kasten) direkt anzeigen und per Mausklick auch als sogenannte „CSV“-Textdatei in den Download-Ordner 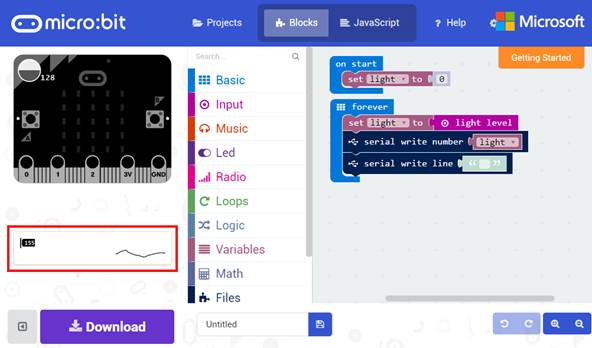des heimischen Windows-PCs herunterladen:

(Bild 28 – Daten mittels serieller Schnittstelle übertragen)

Damit sich die seriell übertragenen Daten aber im Google Chrome kompatiblen „Vivaldi“-Browser und dem von Microsoft entwickelten PXT-Entwicklungswerkzeug anzeigen und herunterladen lassen, muss man zuvor noch einen entsprechender Treiber herunterladen und installieren.

Konkret handelt es sich dabei um den „mbed Windows serial port driver“, den man sich hier von der Webseite kostenlos herunterladen kann. Unter Windows 10 ist es angeblich nicht erforderlich, den seriellen „mbed“-Treiber zu installieren. Aber es schadet nicht, wenn man es trotzdem macht.

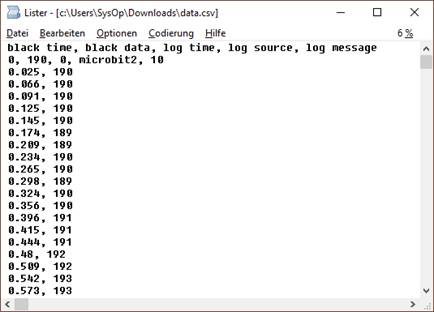
Wenn man sich die aufgezeichneten, seriellen Daten des obigen Helligkeitssensoren-Programms heruntergeladen hat, so lassen sich diese in der Textdatei „data.csv“ mit einem herkömmlichen Editor wie folgt anzeigen:

(Bild 29 – Die abgespeicherten seriellen Daten)

Wie man im obenstehenden Bild sieht, gibt es insgesamt nur zwei Spalten mit Daten. Dabei steht in der linken Spalte die während der Aufzeichnung verstrichene Zeit in Sekunden, während in der rechten Spalte die Helligkeitswerte einer der als Helligkeitssensor geschalteten LEDs des „5 x 5 Matrix LED“-Displays stehen. Dabei arbeitet die in der Mitte des Displays befindliche LED im Sperrbereich quasi als lichtempfindliche Fotodiode.

Wie man in der rechten Spalte der Helligkeitswerte sieht, handelt es sich bei aufgezeichneten Werten um ganzzahlige Werte im Messbereich von 0 bis 255, wobei eine Übersteuerung bereits bei Werten unter 255 einsetzt.

Wie man sieht, werden also nur die verstrichenen Millisekunden bei der Messwertaufnahme dezimal erfasst, während die Helligkeitswerte unterhalb von 255 liegen und mit einer Auflösung von nur 8 Bit = 1111 1111₂ erfasst werden. Das ist nicht viel, dürfte aber für das Erfassen und Reagieren auf Helligkeitsschwankungen voll und ganz ausreichen.

Jetzt bleibt noch zu klären, um welche serielle Schnittstelle es sich beim „micro:bit“-Rechner handelt. Dass es eine serielle Schnittstelle gibt, dürfte inzwischen unstrittig sein und dem Umstand geschuldet sein, dass der „micro:bit“-Rechner über das „Micro-USB 2.0“-Kabel mit Strom, Programmen und Daten versorgt wird. Dass es sich bei der seriellen Schnittstelle nicht mehr um die nur von früher bekannte „RS-232“-Schnittstelle, wie man sie von älteren PCs und Notebooks her kennt, handelt, dürft auch klar sein.

Diejenigen, die sich bereits hier und da mit neueren Peripheriegeräten oder neuerer Hardware befasst haben, wissen, dass es sich bei der seriellen Schnittstelle nur um eine „UART“-Schnittstelle, d.h. engl. „Universal Asynchronous Receiver Transmitter“ handeln kann, die auch im Datenblatt „nRF51822“ des „Nordic Semiconductor“-Herstellers genannt wird:

(Bild 30 – Die serielle UART-Schnittstelle)

>> Damit UART-Baugruppen kommunizieren können, müssen RX der einen und TX der anderen Baugruppe am Stecker gegenüberstehen. Damit sind stets zwei Steckerbelegungstypen (Master und Slave) erforderlich, auch wenn die Geräte vollkommen gleichberechtigt kommunizieren. Sollen Master mit Master oder Slave mit Slave kommunizieren können, sind Kreuzverbinder (analog dem Null-Modem-Kabel der seriellen Schnittstelle oder dem Cross-Over-Kabel des Ethernet) erforderlich.

Eine Modifikation, die Single-Wire UART (SWART) vermeidet dieses Verpolungsproblem. Werden RX und TX zusammen auf einem Pin vereint, ist zwar nur eine Simplex-Übertragung möglich, dafür aber können dann beliebige Module miteinander kommunizieren. Es können sogar mehrere UART-Module auf einem Draht kommunizieren (SWART-Bus). Die SWART ist insbesondere für kurze Entfernungen und für Datenraten bis 115.200 Baud geeignet. << (Quelle: Wikipedia)

Dabei bedeutet die im Bild stehende Bezeichnung „CTS“, engl. „clear to send“, d.h. „bereit zum senden” von Daten und „RTS“, engl. „request to send“, d.h. „bitte (Daten) senden“, „Aufforderung Daten zu senden“.

>> Die asynchrone Übertragung findet in der Datenkommunikation bei der RS-232-Schnittstelle Verwendung. Diese Schnittstelle weist eine vergleichsweise große Verbreitung auf. Ein UART erzeugt die auf der RS-232-Schnittstelle zu übertragenden Datenbits und den dazu notwendigen Datenrahmen. Die eigentliche RS-232-Schnittstelle besteht zusätzlich noch aus Pegelumsetzern und weiteren Bauelementen wie Steckern, welche nicht mehr Teil eines UART sind.

Realisiert wird ein UART meist als Kommunikationsbaustein in Mikrocontrollern oder Computern, als eigenständige integrierte Schaltung, als Teilfunktion in Chipsätzen, in Form von Hardwarebeschreibungssprachen für die Integration in Field Programmable Gate Arrays (FPGAs) oder als sogenanntes „Software-UART“, das nur durch eine Programmabfolge vorliegt und bestimmte Ein-/Ausgabepins direkt ansteuert (Bit-Banging). Die zu übertragenden bzw. die empfangenen Daten werden an das UART meist in paralleler Form, beispielsweise über einen CPU-externen Bus, geliefert.

Die Geschichte des UART ist eng verbunden mit der Standardisierung der Datenkommunikation der RS-232. Waren die ersten UARTs für Datenübertragungsraten weniger hundert Bit/s und den Anschluss an Teletypes mit Stromschnittstelle oder Modems vorgesehen, so erreichten sie in späteren Jahren als eigenständige Chips mehrere Megabit pro Sekunde. << (Quelle: Wikipedia)

Falls Sie in Ihrer PC-Bastelkiste ein überzähliges oder älteres USB-Drucker- oder USB-Modem-Kabel vom Typ „USB 2 Standard-B“ übrig haben, dann können Sie den „USB 2 Standard-B“-Stecker abschneiden, die innen liegenden Kabelenden auftrennen und abisolieren, sodass die Anschlussdrähte offen zugänglich sind.

Dabei verhält es sich bei dem von mir verwendeten Kabel so, dass am anderen Ende insgesamt vier Anschlussdrähte in den Farben rot, schwarz, weiß und grün plus Abschirmung zum Vorschein kommen. Diesbezüglich handelt es sich bei dem roten und schwarzen Kabel um die Stromversorgung, während das weiße und grüne Kabel der Datenübertragung dient. Dabei verhält es sich so, dass die beiden Datenübertragungsdrähte weiß und grün noch den schwarzen Draht als gemeinsamen Masseanschluss benötigen bzw. sich die Masse mit diesem teilen!

Weitere Infos zur UART, deren Funktionen nebst Statements finden sich auf der Homepage der BBC micro:bit MicroPython. -

So, jetzt haben wir wieder eine ganze Menge gelernt und wissen bereits jetzt, dass sich mittels der „UART“-Schnittstelle Daten seriell über das „Micro-USB 2.0“-Kabel übertragen lassen. Beispielsweise auch zwischen zwei „micro:bit“-Rechnern!

Das alles wurde aber nur möglich, weil wir bestimmte, zunächst unbekannte Dinge und Phänomene kritisch hinterfragen, recherchieren, erforschen und ausprobieren. „Dumm zu fragen“ lohnt sich also, sollte man sich nicht verbieten lassen!

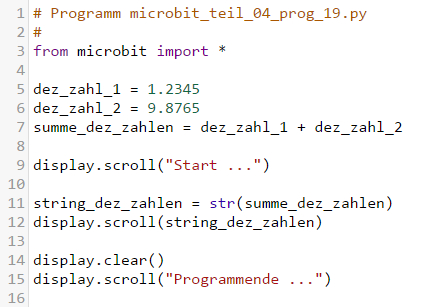
Doch nun wird es wieder Zeit, in Python zu programmieren und den Umgang mit Dezimalzahlen zu üben (siehe Programm „microbit_teil_04_prog_19.hex“ mit dem Quelltext „microbit_teil_04_prog_19.py“):

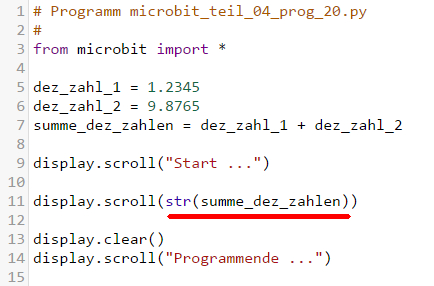
(Bild 31 – Mit dezimalen Zahlen rechnen)

Das Umwandeln der numerischen Variablen „summe_dez_zahlen“ in die String-Variable „string_dez_zahlen“ lässt sich auch wie folgt einsparen:

(Bild 32 – Noch professioneller dezimal rechnen)

4.1 Smiley oder Grumpy?

Es ist kaum zu glauben, aber amtlich! Jetzt gibt es die „Grumpy Cat“ schon in Wikipedia! Und auf dem „micro:bit“-Rechner:

(Bild 33 – Grumpy Cat)

Grumpy oder Smiley, das ist hier die Frage:

(Bild 34 – Smiley Cat)

Selbstverständlich lässt sich die „Grumpy Cat“ auch programmieren. Und auch das Umschalten auf die „Smiley Cat“. Im nachfolgenden Programm „microbit_teil_04_prog_21.hex“ mit dem Quelltext „microbit_teil_04_prog_21.py“ benutzen wir den großen Rundanschluss Port „Pin P0“ als Sensor, der auf die Berührung mit dem Finger reagiert und das „Grumpy Cat“ zum „Smiley Cat“ werden lässt. Ganz ohne Leckerlies:

(Bild 35 – Programm zum „Grumpy Cat“)

Am besten aber funktioniert der Sensor, wenn man am Port „Pin P0“ einen etwa 10 cm langen Draht anschließt, diesen am Ende ausreichend lang abisoliert und mit den Fingern der linken Hand festhält.

Ein zweiter, ebenfalls etwa 10 cm langer Draht wird am einen Ende mit dem Masseanschluss am Port „Pin GND“ des „micro:bit“-Rechners verbunden, am anderen Ende ausreichend lang abisoliert und mit den Fingern der rechten Hand festgehalten, sodass der menschliche Körper mit der rechten Hand auf Massepotential liegt und mit der linken Hand mit dem Sensor verbunden ist. Dabei wirkt dann der menschliche Körper wegen seiner großen Oberfläche als Antenne, nimmt die im Raum herrschenden elektro-magnetischen Felder nebst Strahlung (= Elektrosmog) auf und leitet diese als elektrische Körperspannung im Millivolt- und Mikroampere-Bereich (= mV = 10^-3 V, = µA = 10^-6 A) an den Sensor weiter, sodass sich das „Grumpy Cat“ zum „Smiley Cat“ verwandelt.

Wenn man sich aber mit dem „micro:bit“-Rechner in einem elektro-magnetisch abgeschirmten Raum befinden würde, im Winter auch noch eine ziemlich trockene Haut hätte und Winterstiefel mit Gummisohlen an hätte, dann würde der Sensor nicht funktionieren, weil u.a. der Körperstrom wegen des großen Hautwiderstandes zu gering wäre und der menschliche Körper wegen der fehlenden elektro-magnetischen Strahlung auch nicht als Antenne arbeiten würde.

Damit der Sensor aber trotz fehlenden Elektrosmogs zuverlässig funktioniert und man seine elektronische, Sensor unterstütze Nachttischlampe mittels leichter Berührung mit der Hand oder den Fingern ein- oder ausschalten kann, muss man etwas nachhelfen und für einen künstlichen Elektrosmog sorgen, der von der Nachttischlampe bzw. unserem Sensor am Port „Pin P0“ produziert wird, indem man den Sensor und mit ihm dann auch den Anwender im Falle der Berührung „unter Strom“ setzt.

Im vorliegenden Fall könnte dabei dann die Spannung am Sensor entsprechend der Versorgungsspannung am Rundanschluss „Pin 3V“ bis zu „gefährlichen“ 3 Volt betragen. Der Strom, der dann vom Sensor am Port „Pin P0“ vom linken Arm über den Körper zum rechten Arm gegen Masse fließt, würde dann aber nur wenige Mikroampere (= 10^-6 A) betragen und wäre damit vollkommen ungefährlich!

Wenn wir jetzt herausfinden wollen, wie der Sensor wirklich funktioniert, dann müssen wir diesen näher untersuchen und für kontrollierte, d.h. berechenbare und jederzeit nachvollziehbare, d.h. replizierbare Bedingungen sorgen.

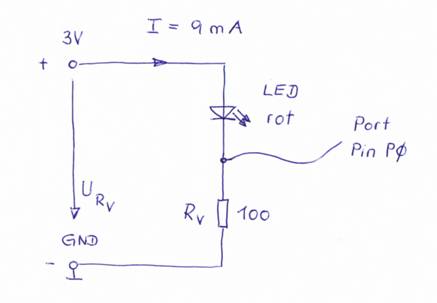
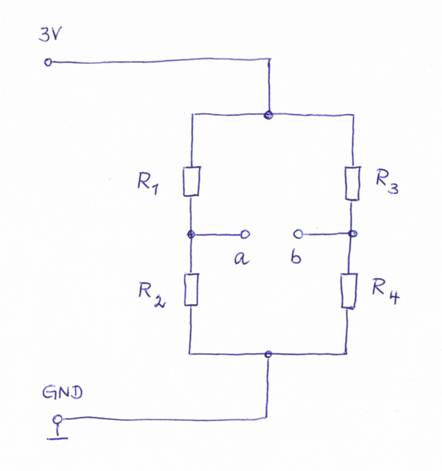
Zu diesem Zweck basteln wir uns einen sogenannten Spannungsteiler, der aus einer roten LED, einem Vorwiderstand R_V = 100 Ω, die beide in Reihe geschaltet sind, besteht und an der Spannung von U_3V = 3,17 V betrieben wird. Dabei nutzen wir die Stromversorgung am Rundanschluss „U_3V“ (= Pluspol) sowie dem Rundanschluss „GND“ (= Minuspol, Masse):

(Bild 36 – Schaltung zum „Grumpy Cat“)

Nach dem Ohmschen Gesetz berechnet sich der Spannungsabfall U_RV am Vorwiderstand R_V wie folgt:

U = I * R →

U_RV = I * R_V = 9 mA * 100 Ω = 9 * 10^-3 A * 100 V/A = 900 * 10^-3 A = 900 mV = 0,9 V

Berechnen wir nun noch den Spannungsabfall an der roten LED,

U_LED = U_3V - U_RV = 3,17 V - 0,9 V = 2,27 V

dann sieht man, dass an dieser die größere Spannung mit U_LED = 2,27 V anliegt, sodass diese ziemlich hell leuchtet und dabei über die elektrische (Licht-) Leistung P_LED wie folgt verfügt:

P_LED = U_LED * I = 3,52 V * 9 mA = 31,68 mW

Auch wenn die Kennlinie der LED im Durchlassbereich praktisch geradlinig verläuft und man die elektrische Leistung P_LED der LED herkömmlich linear berechnen kann, heißt das nicht zwangsläufig, dass sich auch die Helligkeit linear im selben Verhältnis zu Spannung oder Strom steigern lässt.

Wie Sie bereits wissen, verfügt der „micro:bit“-Rechner in der Hauptsache über drei große Rundanschlüsse Port „Pin P0“ bis „Pin P2“, die sich frei als analoge oder digitale Ein- oder Ausgänge durch Programmieren konfigurieren lassen.

Gemäß dem obenstehenden Programm „microbit_teil_04_prog_21.hex“ mit dem Quelltext „microbit_teil_04_prog_21.py“ reagiert dabei der Sensor, d.h. der Anschluss am Port „Pin P0“, auf Berührung, indem ein Stromkreis vom Sensor gegen Masse über den menschlichen Körper gebildet wird. Wie aber der Sensor tatsächlich im Detail funktioniert, wissen wir noch nicht. So wissen wir noch nicht, ob der Sensor kurzschlussfest ist, was also passiert, wenn man den Sensoranschluss auf Masse (= Pin „GND“), d.h. Minuspotential legt. Auch wissen wir nicht, ob er die Stromversorgung belastet und einen größeren Strom zieht, wenn wir den Sensor (= Port „Pin P0“) mit dem Pluspol am Rundanschluss „Pin 3V“verbinden. Geht dann die Spannungsversorgung in Knie, d.h. bricht sie zusammen, sodass die rote LED ausgeht?

Da der Sensor elektrisch recht empfindlich ist und auf kleine Körperströme reagiert, indem sich der „Grumpy Cat“ zum „Smiley Cat“ verwandelt, dürfte der Sensor nicht nur über eine hohe Verstärkung B für Gleichstrom ( oder β für Wechselstrom), sondern auch über einen hohen Eingangs- bzw. Innenwiderstand R_i verfügen, da ja bei Kontakt nur ein ganz kleiner Kontakt- bzw. Körperstrom von wenigen Mikroampere µA (= 10^-6 A) fließt.

Dabei bedeutet die Größenordnung 10^-6 A für den winzig kleinen Kontakt- bzw. Körperstrom, dass der damit verbundene Eingangs- bzw. Innenwiderstand R_i in der Größenordnung 10⁶ Ω, d.h. deutlich > 100 KΩ und < 10 MΩ sein dürfte.

Dazu muss man wissen, dass alle drei Ports „Pin P0“ bis „Pin P2“, egal wie sie beschaltet werden, praktisch kurzschlussfest sind. Aber nur, wenn der „micro:bit“-Rechner über das „Micro USB 2.0“-Kabel z.B. über den USB-Anschluss des PCs, des Notebooks oder ein USB-Steckernetzteil, mit Strom versorgt wird.

Bei der Stromversorgung über die Batterie-Anschlussbuchse durch ein extern angeschlossenes Batteriepack von zwei AA oder AAA Batterien à 1,5 Volt gibt es keine Kurzschlusssicherung!

Ferner verhält es sich so, aber das können Sie noch nicht wissen, dass alle Ports „Pin P0“ bis „Pin P2“ eingangsseitig über einen Widerstand von R_A/D = 10 MΩ auf Pluspotential von maximal U_3V = 3,3 V liegen!

Der Grund dafür dürfte der sein, dass man auf diese Weise durch den erzwungenen Spannungsabfall am hochohmigen (Offset-) Widerstadt R_A/D ( = kein Eingangswiderstand) auf diesen reagieren und die (Kurzschluss-) Strombegrenzung durch Abschalten realisieren kann!

Auf diesen Zusammenhang wurde ich auch erst durch das Kompendium „Micro:bit Praktikum“ von Burkhard Kainka, erschienen als eBook bei Amazon, aufmerksam. Dort heißt es im Kapitel 4 „Analoge Messungen“:

>> Kann es sein, dass der offene Eingang schon eine Spannung hat? Wenn ein Digital-Multimeter in Reichweite ist, kann man es ja einfach mal zwischen P0 und GND anschließen. Es zeigt dann zum Beispiel 1,7 V. Warum das so ist, muss noch untersucht werden. <<

Weitere, detaillierte Untersuchungen zu diesem Sachverhalt der quasi Offset-Spannung finden sich hier im Tutorial im Teil 3, Abschnitt „3.8.4 A/D-Wandler mit Spannungsteiler“.

Wenn man also davon ausgeht, dass die Spannung am Sensor durch die Stromversorgung am Pin „3V“ maximal bis zu 3,3 V betragen kann, dann lässt sich die Stromstärke I_Sensor, d.h. der aus dem Port „Pin P0“ heraus fließende, winzige Strom näherungsweise wie folgt berechnen:

I_Sensor = U_Sensor / R_i = U_3V / R_i

= 3,17 V / 10 MΩ = 3,17 V / ( 10 * 10⁶ Ω ) = 3, 17 V / ( 10 V/A ) * 10^-6

= 0,317 * 10^-6 A = 0,317 µA = 0,000 000 317 A ≈ 0,3 Millionstel Ampere

Mit einem Multimeter lässt sich dieser winzig kleine Strom aber schon nicht mehr messen! Stattdessen lässt sich aber die Leerlaufspannung U_{Pin P0} = 1,57 V am Port „Pin P0“ des Sensors messen, sodass für die Stromstärke des Sensors folgt:

I_{Pin P0} = U_{Pin P0} / R_{Pin P0}

= 1,57 V / 10 MΩ = 1,57 V / ( 10 * 10⁶ Ω ) = 1,57 V / ( 10 V/A ) * 10^-6

= 0,157 * 10^-6 A = 0,157 µA = 0,000 000 157 A ≈ 0,16 Millionstel Ampere

Frage 1

Jetzt wissen wir, dass wir das Anschlusskabel am Port „Pin P0“ des Sensors gefahrlos mit der Spannungsversorgung am Pin „3V“ mit U_3V = 3,17 V verbinden können, ohne dass es einen Kurzschluss gibt!

Was aber passiert mit dem „Grumpy Cat“? Wechselt dieser seinen Gesichtsausdruck zum „Smiley Cat“? Probieren Sie es aus und begründen Sie das Ergebnis!

Frage 2

Als Nächstes verbinden wir das Anschlusskabel am Port „Pin P0“ des Sensors mit dem Spannungsteiler und zwar genau in der Mitte, d.h. am Verbindungspunkt der roten LED mit dem Vorwiderstand R_V (siehe Bild 36 – Schaltung zum „Grumpy Cat“).

Was passiert jetzt mit dem „Grumpy Cat“? Wechselt dieser jetzt endlich seinen Gesichtsausdruck zum „Smiley Cat“? Finden Sie es heraus, indem Sie es ausprobieren!

Frage 3

Als Letztes verbinden wir das Anschlusskabel am Port „Pin P0“ des Sensors mit der Masse (= Pin „GND“) der „micro:bit“-Stromversorgung.

Was passiert jetzt mit dem „Grumpy Cat“? Wechselt dieser jetzt seinen Gesichtsausdruck zum „Smiley Cat“? Finden Sie es heraus, indem Sie es ausprobieren!

Frage 4

Jetzt wo wir wissen, dass der Sensor am Port „Pin P0“ einen winzig kleinen Ausgangsstrom nach außen abgibt, wenn der Stromkreis gegen Masse (= Pin „GND“) der „micro:bit“-Stromversorgung geschlossen wird, stellt sich die Frage, ab welcher Ausgangsspannung der Sensor reagiert und den „Grumpy Cat“ auf „Smiley Cat“ umschaltet.

Finden Sie heraus, ab welcher Ausgangsspannung der Sensor umschaltet und begründen Sie Ihre Entscheidung bzw. Vermutung! -

Wie wir bereits wissen, lassen sich die drei Ports „Pin P0“ bis „Pin P2“ wahlweise als analoger oder digitaler Ein- oder Ausgang programmieren. Ferner wissen wir, dass am Sensor von Port „Pin P0“ im unbelasteten Zustand eine Leerlaufspannung von U_{Pin P0} = 1,57 V anliegt, sodass man vermuten darf, dass der Sensor beim Unterschreiten dieser Spannung vom „Grumpy Cat“ auf „Smiley Cat“ umschaltet.

Um herauszufinden, dass dem wirklich so ist, programmieren als Nächstes den Port „Pin P1“ als analoge Spannungsquelle, die genau die Leerlaufspannung von U_{Pin P0} = 1,57 V abgibt. Zu diesem Zweck müssen wir aber zuvor die analoge Leerlaufspannung in einen entsprechenden binären Wert im Bereich von [ 0 … 1023₂ ] = 1024 verschiedene Spannungswerte wie folgt umrechnen:

1024₂ Bit / 3,17 V aktuelle Betriebsspannung = 323,0284 Bit / Volt ≈ 323 Bit / Volt

Gegenprobe:

323 Bit / Volt * 3,17 V = 1023,91 ≈ 1024 … was zu beweisen war!

Jetzt wo wir den Umrechnungsfaktor 323 Bit / Volt berechnet haben, lässt sich der Binärwert zum Einstellen der Leerlaufspannung von U_{Pin P0} = 1,57 V der analogen Spannungsquelle am Port „Pin P1“ ganz leicht wie folgt berechnen:

Binärwert = 323 Bit / Volt * 1,57 V = 507,11 ≈ 507 Bit

Da aber die Leerlaufspannung bei einer äußeren Beschaltung nebst geringfügiger Belastung eben nicht konstant ist, sondern in die Knie geht und sich entsprechend verringert, messen wir die Spannung am Port „Pin P0“ des Sensors noch mal nach und stellen dabei fest, dass sich diese nun auf den Wert U_{Pin P0} = 1,28 V verringert hat.

Demzufolge müssen wir den Binärwert neu berechnen:

Binärwert = 323 Bit / Volt * 1,28 V = 413,44 ≈ 413 Bit

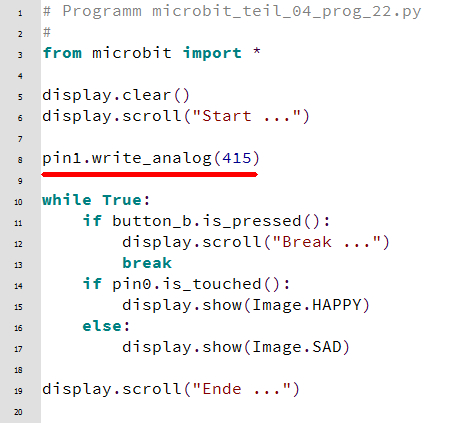
Wie man anhand des Programm „microbit_teil_04_prog_22.hex“ mit dem Quelltext „microbit_teil_04_prog_22.py“ sieht, schaltet der „Grumpy Cat“ aber erst ab einem Binärwert 415 auf den „Smiley Cat“ um:

(Bild 37 – Erweitertes Programm zum „Grumpy Cat“)

Wie man im obenstehenden Programm sieht, lässt sich der „Grumpy Cat“ durch Anlegen einer analogen Spannung mittels des Bitwertes von 415 Bit an den Sensor (= Port „Pin P0“) zum Lächeln bewegen. Wenn auch nicht ganz freiwillig. Kleine Spannungsimpulse auf den Hinterkopf erhöhen eben das Denkvermögen bzw. die gute Laune und verbessern damit das Lächeln im Gesicht.

Wenn wir wissen wollen, um welchen Spannungswert es sich dabei handelt, dann müssen wir den Bitwert 415 Bit nur mit dem Wert der aktuell anliegenden Spannungsversorgung am Pin „3V“ mit U_3V = 3,18 V wie folgt umrechnen:

U_{Pin P0} = U_3V / 1024 Bit * 415 Bit = ( 3,18 V / 1024 Bit ) * 415 Bit

= 0,00310546875 V/Bit * 415 Bit

= 3,10547 mV/Bit * 415 Bit = 3,10547 mV/Bit * 415 Bit

= 1288,77005 mV = 1,2888 V ≈ 1,29 V ( … gemessen: 1,28 V )

Für die Berechnung der A/D-Wandler-Bereichsgröße folgt:

Wird der A/D-Wandler mit 10 Bit an 3,16 V betrieben, so folgt für die Umrechnungen:

Bereichsbreite = Referenzspannung / ( Maximalwert + 1 )

= 3,18 V / ( 1023 + 1 ) Bit = 3,18 V / 1024 Bit = 0,0031055 V/Bit

Siehe auch Teil 3, Abschnitt „3.8.5 Berechnung der A/D-Wandler-Bereichsgröße“

Wir wissen jetzt, dass die Versorgungsspannung des „micro:bit“-Rechners über das „Micro USB 2.0“-Verbindungskabel im Bereich von 4,75 V - 5,50 V bei einer maximalen Stromentnahme von bis zu 500 mA teils sehr unterschiedlich ausfallen kann, was sich natürlich auch auf die interne Versorgungsspanung U_3V am Pin „3V“ und Pin „GND“ (= Masse) entsprechend auswirkt! Demzufolge gilt es, diese stets bei Berechnungen entsprechend zu berücksichtigen und mit einzubeziehen!

Jetzt wissen Sie auch, weshalb das manuelle Ermitteln des Bitwertes von 415 Bit am Sensor (= Port „Pin P0“), um den grimmigen „Grumpy Cat“ durch Anlegen einer analogen Spannung zum Lächeln zu bewegen, ziemlich aufwendig ist.

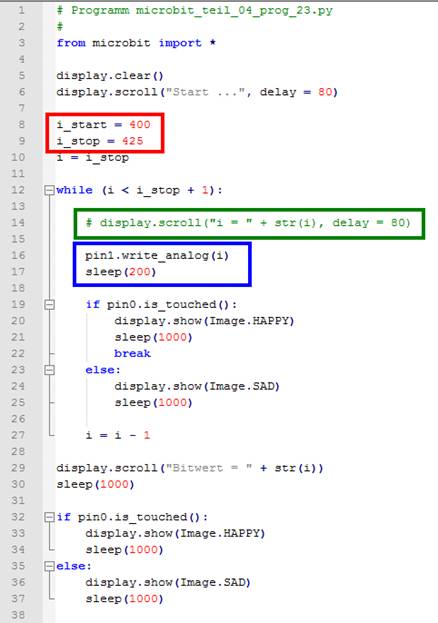
Höchste Zeit also, diesen Vorgang zu automatisieren (siehe Programm „microbit_teil_04_prog_23.hex“ mit dem Quelltext „microbit_teil_04_prog_23.py“):

(Bild 38 – Automatische Ermittlung des Bitwertes)

Kernstück des obenstehenden Programms ist die „while (i < i_stop + 1):“-Schleife, die von i_stop = 425 bis i_start = 400 rückwärts durchlaufen wird.

Dabei richtet sich der rückwärts zu durchlaufende „Stop-/Start“-Bereich mit seinen vorher festgelegten „Stop-/Start“-Werten nach dem voraussichtlich zu erwartenden Bitwert, damit sich dann später beim rückwärtigen Schleifendurchlauf auch tatsächlich ein zutreffender Bitwert ermitteln lässt mit dem sich dann der „Grumpy Cat“ auf „Smiley Cat“ umschalten lässt.

Da wir im vorliegenden Fall einen Bitwert von 715 erwarten, macht es Sinn, den Wertebereich für die Schleifendurchläufe entsprechend einzugrenzen, damit sich der zutreffende Bitwert schneller ermitteln lässt.

Sollte sich der zu erwartende Bitwert im eingegrenzten Intervall wider Erwarten nicht finden lassen, dann muss man den Schleifenbereich nach oben und/oder nach unten entsprechend vergrößern (siehe roter Kasten im obenstehenden Bild).

Wenn Sie sich die jeweiligen Bitwerte in den Schleifendurchläufen anschauen und anzeigen lassen wollen, dann müssen Sie nur im

· Statement „display.scroll("i = " + str(i), delay = 80)“

das Kommentarzeichen „#“ entfernen und das Programm neu kompilieren (siehe grüner Kasten im Bild oben).

Mit dem

· Statement „pin1.write_analog(i)“

wird die Ausgangsspannung der programmierbaren Spannungsquelle am Port „Pin P1“ als Funktion des Bitwertes des Schleifenzählers i eingestellt und mittels Verbindungskabel dem Sensor am Port „Pin P0“ zugeführt (siehe blauer Kasten).

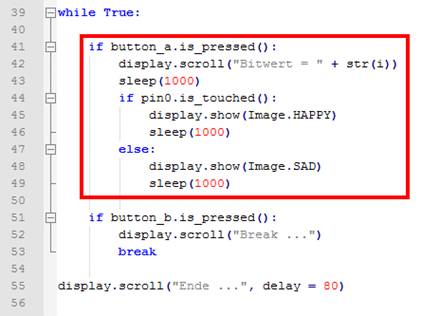
Wenn der entsprechende Bitwert, im vorliegenden Fall der Wert 417, bei den Schleifendurchläufen ermittelt wurde, wird die Schleife sofort mittels „break“ abgebrochen und verlassen. Anschließend wird dann der ermittelte Bitwert in der Laufschrift nebst Wechsel vom „Grumpy Cat“ zum „Smiley Cat“ angezeigt.

Die Anzeige des ermittelten Bitwertes lässt sich später wieder als Laufschrift nebst des „Smiley Cat“ beliebig oft anzeigen, wenn man den Taster A betätigt (siehe roter Kasten im nachfolgenden Bild):

(Bild 39 –Ermittelter Bitwert wiederholt anzeigen)

Durch Betätigen des Tasters B lässt sich die „while True:“-Endlosschleife wieder verlassen und das Programm wieder beenden.

Berechnen wir abschließend noch den zum Bitwert 417 zugehörigen Spannungswert, indem wir diesen mit der aktuell anliegenden Spannungsversorgung am Pin „3V“ mit U_3V = 3,16 V wie folgt umrechnen:

U_{Pin P0} = U_3V / 1024 Bit * 417 Bit = ( 3,16 V / 1024 Bit ) * 417 Bit

= 0,0030859375 V/Bit * 417 Bit

= 3,0859375 mV/Bit * 417 Bit = 3,08594 mV/Bit * 417 Bit

= 1286,83698 mV = 1,287 V ≈ 1,29 V ( … gemessen: 1,28 V )

Hier geht es zu Antworten der Fragen 1 bis 4. -

Bedienungsanleitung

zum Programm „microbit_teil_04_prog_23.hex“ mit dem Quelltext „microbit_teil_04_prog_23.py“

1. Starten und Ausführen des Programms

Das in den Arbeitsspeicher des „micro:bit“-Rechners geflashte Programm startet sich nach wenigen Sekunden von allein und zeigt im Display die programmierte Laufschrift „Start ...“ an.

Nach dem Programmstart zeigt sich zunächst die „Grumpy Cat“ ( L ), die dann nach etwa 10 Sekunden zum „Smiley Cat“ ( J ) wechselt. Kurz darauf wird der ermittelte Bitwert in der Laufschrift angezeigt.

Das alles erfolgt aber nur in der beschriebenen Weise, wenn sich vom Programm in der „while (i < i_stop + 1):“-Schleife tatsächlich der erwartete Bitwert ermitteln ließ!

2. Taster A zum wiederholten Anzeigen des ermittelten Bitwertes

Nach dem der erwartete Bitwert ermittelt wurde, lässt sich die Anzeige des ermittelten Bitwertes nebst des „Smiley Cat“ ( J ) durch Drücken des Tasters A beliebig oft anzeigen.

3. Taster B zum Beenden des Programms

Nachdem der ermittelte Bitwert in der Laufschrift und das „Smiley Cat“ ( J ) angezeigt wurden, lässt sich das Programm durch einmaliges Betätigen des Tasters B jederzeit wieder beenden.

4. Mit dem „Reset“-Taster alles wieder auf Anfang setzen

Auf der Rückseite des „micro:bit“-Rechners befindet sich ein sogenannter „Reset“-Taster mit dem sich der Rechner neu starten lässt. Dabei wird dann auch das zuvor in den Arbeitsspeicher geflashte Programm wieder neu gestartet! -

4.2 Strom mit Strom ausschalten

Häh? Pardon, wie bitte. Wie bitte soll das denn funktionieren? Strom mit Strom ausschalten? Das wäre ja fast so, wie wenn man Feuer mit Feuer löscht! Gibt’s das wirklich? Geht das? Ja! Feuer lässt sich beispielsweise auch mit Sprengstoff löschen. Mit viel Trinitrotoluol (= TNT) sozusagen. Und, wenn sich Feuer mit Sprengstoff löschen lässt, dann lässt es sich auch Feuer mit Feuer löschen!

Bei den Bohrfachleuten auf einer Bohrinsel, einer Erdöl- oder Erdgasförderstelle in der Wüste ist der sogenannte „Blowout“ der absolute GAU (= Größter anzunehmender Unfall). Einen „Blowout“ nennt man es, wenn sich das Erdöl oder Erdgas einer Förderstelle, d.h. eines Bohrturms entzündet und explosionsartig verbrennt. In einem Bohrturm gefördertes Erdöl oder Erdgas kann sich entzünden, wenn das Bohrgestänge aus dem Bohrloch hochgezogen werden muss, weil z.B. der Bohrkopf oder ein Teil des Bohrgestänges erneuert werden müssen. Durch den hohen Druck des Erdöls schießt dann eine bis zu fünfzig Meter hohe Fontäne in die Luft, die sich im Falle eines gefährlichen Erdöl- und Erdgasgemisches entzünden kann, Feuer fängt und den ganzen Bohrturm in die Luft sprengt oder abfackelt.

Bei einem Blowout in der Wüste ließ sich die sich bis zu fünfzig Meter hohe brennende Öl- und Gasfontäne nur durch die Druckwelle einer gewaltigen Sprengung löschen, die die brennende Feuersäule quasi wegpustete und dem Feuer den zur Verbrennung erforderlichen Sauerstoff entzog.

Ähnlich kann man kleinere oder größere Waldbrände bekämpfen und löschen. So lassen sich im Extremfall örtlich begrenzte, größere Waldbrände und deren Feuerwalze durch gezielte Gegenfeuer stoppen und bekämpfen. Einerseits in dem das Gegenfeuer der nahenden Feuersbrunst keine Nahrung, d.h. Brennstoff mehr liefert, da dieser bereits kurz zuvor absichtlich und gezielt geopfert, d.h. verbrannt wurde. Und andererseits, indem man mit dem Gegenfeuer der nahenden Feuerwalze eines Großfeuers den zur Verbrennung erforderlichen Sauerstoff entzieht, weil dieser kurz zuvor vom Gegenfeuer verbraucht wurde.

Und, was hat nun das Gegenfeuer mit dem Strom zu tun? Ganz einfach! Man kann tatsächlich mit Strom den Strom ausschalten. Präziser müsste man aber sagen, dass man mit einem Strom einen anderen ausschalten kann. Streng genommen wird aber der andere Strom nicht wirklich ausgeschaltet, sondern einfach nur durch einen „Trick“ umgeleitet! Dabei macht man sich die Eigenschaft des elektrischen Stromes zu Nutze, nämlich dass sich dieser immer den Weg des geringsten Widerstandes sucht. Und, das kann man tatsächlich wörtlich nehmen. Aber genau genommen geht es bei der Stromumleitung um das Schaffen und Ausnutzen bestimmter Spannungspotentiale. Aber im Prinzip funktioniert das Ganze dann so wie bei dem Gegenfeuer! -

Langer Rede kurzer Sinn, wenden wir uns wieder dem „micro:bit“-Rechner zu.

Nachfolgend benutzen wir weiterhin die Reihenschaltung, die aus der roten LED und dem Vorwiderstand R_V besteht (siehe Bild 36). Dabei wird der Vorwiderstand mit R_V = 100 Ω zur Strombegrenzung gebraucht, damit die rote LED im Durchlassbetrieb nicht überlastet wird und durchbrennt. Aufgrund der Reihenschaltung werden beide Verbraucher vom gemeinsamen Laststrom I_Last = 9 mA durchflossen, sodass am Vorwiderstand R_V ein Spannungsabfall von U_RV = 0,9 V abfällt und an der roten LED die Spannung U_LED = U_3V - U_RV = 3,17 V - 0,9 V = 2,27 V.

Wenn man nun erreichen will, dass die rote LED nicht mehr leuchtet, indem man mit Strom den Strom ausschaltet, dann impliziert die wörtliche Bedeutung, dass zum Ausschalten des Stromes A ein entsprechender Schalter zum Einsatz kommt, der durch den Strom B eingeschaltet wird, damit der Strom A nicht mehr fließt.

Technisch würde es sich beim Schalter in Wirklichkeit um ein Relais (bei Starkstrom um ein Schütz) handeln, dass durch einen Stromstoßschalter eingeschaltet wird, um durch dessen Relaiskontakte den Strom A zu unterbrechen. Bei dem Stromfluss durch das Relais bzw. durch die Relaisspule würde es sich dann um den Strom B handeln, der den Strom A indirekt unterbricht bzw. ausschaltet.

Da wir anstelle des mechanischen Schalters den „micro:bit“-Rechner verwenden, kann es sich bei diesem, wenn überhaupt, nur um einen elektronischen Schalter handeln. In diesem Zusammenhang stellt sich dann gleich die Frage, wie der elektronische Schalter beschaffen sein muss und er schaltungstechnisch in die Reihenschaltung eingebracht werden soll. Wenn man den „micro:bit“-Rechner als elektronischen Schalter verwendet, dann würde man z.B. mit diesem einen Strom einschalten, um einen anderen Strom auszuschalten.

Aber der „micro:bit“-Rechner ließe sich z.B. auch als elektronisch geregelte Spannungsquelle einsetzen. Dann würde man aber nicht mehr mit einem Strom einen anderen Strom ausschalten, sondern mit einer Spannung einen Strom ausschalten! Oder aber vielleicht nicht direkt ausschalten, sondern eher verhindern, vermeiden!

Die reizvollere Variante ist nun, dass man mit einer Spannung einen Strom ausschaltet, indem man diesen verhindert. Aber wie soll das funktionieren?

Um aber das Ganze besser zu verstehen, ist es didaktisch-methodisch sinnvoller, sich zuerst mit den einfachen Dingen zu befassen als mit den schweren.

4.2.1 Strom mittels Überbrückungskabel umleiten

Die sicherlich einfachste Methode, die rote LED auszuschalten, sodass diese nicht mehr leuchtet, ist die, dass man den Strom, der normalerweise die rote LED zum Leuchten bringt, einfach um diese herum leitet. Dazu muss man nur die beiden Kontakte der roten LED mittels eines Kabels überbrücken. Dabei kann man auch einen Schalter verwenden, so dass sich das einadrige Überbrückungskabel einfach parallel zur roten LED schalten lässt.

Wenn man mit dem Überbrückungskabel den Stromfluss um die rote LED herum leitet, dann entfällt nicht nur der Stromfluss durch die rote LED, sondern auch der Spannungsabfall an dieser, sodass dann am Vorwiderstand mit R_V = 100 Ω die volle Betriebsspannung mit U_RV = U_3V = 3,17 V anliegt. Demzufolge vergrößert sich dann auch die Stromstärke durch den Vorwiderstand R_V wie folgt:

I_RV = U_RV / R_V = U_3V / R_V = 3,17 V / 100 Ω = 0,0317 A = 31,7 mA

Wie man hier im Überblick zur Stromversorgung des „micro:bit“-Rechner nachlesen kann, liefert dieser bei Verwendung der Energieversorgung mittels des „Micro USB 2.0“-Kabels einen maximalen Strom von bis zu 120 mA, sodass also sichergestellt ist, dass wir den Rechner nicht überlasten.

Dies betrifft dann auch den Vorwiderstand R_V selbst. Auch für diesen müssen wir vorab die elektrische (Wärme-) Leistung wie folgt berechnen:

P_RV = U_RV * I_RV = U_3V / I_RV = 3,17 V * 31,7 mA = 100,489 mW ≈ 0,1 W

Wenn es sich bei dem Vorwiderstand um einen solchen mit 1/8 W handelt, dann sind nach Adam Riese 1/8 W = 0,125 W also 25 % mehr als in diesem an elektrischer Leistung umgesetzt wird! Demzufolge befinden wir uns auch hier auf der sicheren Seite, sodass der Vorwiderstand keine roten Bäckchen bekommt und auch nicht durchschmort.

So, jetzt können wir loslegen und das Programm „Strom mit Strom ausschalten“ programmieren:

(Bild 40 – Strom mit Strom ausschalten)

Das Programm lässt sich am besten verstehen, wenn man dieses zunächst anhand der Bedienungsanleitung ausprobiert.

Bedienungsanleitung

zum Programm „microbit_teil_04_prog_24.hex“ mit dem Quelltext „microbit_teil_04_prog_24.py“

1. Starten und Ausführen des Programms

Das in den Arbeitsspeicher des „micro:bit“-Rechners geflashte Programm startet sich nach wenigen Sekunden von allein und zeigt im Display die programmierte Laufschrift „Start ...“ an.

Dabei verhält es sich, dass die rote LED, die mit dem Vorwiderstand R_V betrieben wird, leuchtet.

2. Taster A zum Ausschalten der roten LED

Wenn die rote LED eingeschaltet ist und leuchtet, dann lässt sie sich durch Drücken des Tasters A ausschalten. Dabei erscheint die Laufschrift „Off …“, gefolgt vom Bild mit dem „Grumpy Cat“ ( L ).

Die rote LED glimmt ganz schwach als Zeichen dafür, dass sie ausgeschaltet ist!

3. Taster B zum Einschalten der roten LED

Wenn die rote LED ausgeschaltet ist und nur noch ganz schwach glimmt, dann lässt sie sich durch Drücken des Tasters B einschalten. Dabei erscheint die Laufschrift „On …“, gefolgt vom Bild mit dem „Smiley Cat“ ( J ).

Die rote LED leuchtet hell als Zeichen dafür, dass sie eingeschaltet ist!

4. Mit Tastenkombination Taster B&A das Programm beenden

Beim Beenden des Programms wird der „micro:bit“-Rechner wieder in den Ausgangszustand versetzt, sodass sich die rote LED wieder einschaltet und leuchtet.

Da sich die rote LED durch Drücken des Tasters B einschalten lässt und das Leuchten der LED dem Ausgangszustand entspricht, muss man zum Beenden des Programms zusätzlich zum Tasters B auch noch den Tasters A betätigen. Deshalb die etwas ungewöhnliche Tastenkombination B&A.

Nachdem Beenden des Programms sind die beiden Taster A und B nicht mehr in Betrieb, lässt sich die rote LED mit diesen nicht mehr ein- oder ausschalten!

5. Mit dem „Reset“-Taster alles wieder auf Anfang setzen

Auf der Rückseite des „micro:bit“-Rechners befindet sich ein sogenannter „Reset“-Taster mit dem sich der Rechner neu starten lässt. Dabei wird dann auch das zuvor in den Arbeitsspeicher geflashte Programm wieder neu gestartet! -

Frage 5

Studieren Sie das obenstehende Programm (siehe Bild 40) und probieren Sie es mehrfach aus, indem Sie die Taster A und B drücken und die rote LED mehrfach ein- und ausschalten. Schauen Sie sich außerdem die Reihenschaltung von roter LED und Vorwiderstand R_V an (siehe Bild 36).

Erklären Sie, wie man mit dem Strom vom Port „Pin P1“ des „mirco:bit“-Rechners die rote LED (fast vollständig) ausschalten kann, sodass diese nur noch glimmt.

Nach welchem Prinzip funktioniert die Reihenschaltung, sodass man mit einem Strom einen anderen Strom, nämlich den durch die rote LED, ausschalten kann?

Frage 6

Wenn man die rote LED mit dem Taster A ausschaltet, dann fällt einem sofort auf, dass die LED wider Erwarten nicht ganz ausgeht, sondern immer noch etwas glimmt.

Weshalb ist das so? Versuchen Sie eine Antwort zu geben, und begründen Sie diese! -

Es ist jetzt schon eine ganze Weile her. Ich denke so 20 bis 25 Jahre, da wurde in einer Fernsehsendung gezeigt, wie eine junge Technikerin in Japan an einem Hochspannungsmast mit einer 380 kV Höchstpannungsleitung einen meterlangen Glastellerisolator aus grünlichen Glastellern während des laufenden Betriebs(!), also unter 380 kV Höchstspannung, wechselte.

Möglich wurde das Ganze, weil man die Technikerin in einem entsprechend isolierten Transportkorb bereits auf der Erde auf eine elektrostatische Spannung von exakt 380 kV aufgeladen hatte bevor der isolierte Transportkorb vom Hubschrauber in die Höhe gehoben und zum defekten Isolator des Hochspannungsmasten transportiert wurde. Dazu muss man wissen, dass es bei einem Isolator, wie ihn der isolierte Transportkorb aus Kunststoff darstellt, keine freibewegliche Ladungsträger in Form von Elektronen wie im Kupferleiter gibt, sodass sich keine Ladungen in Form eines elektrischen Stromes transportieren lassen.

Da sich isolierte Körper je nach physikalischer Beschaffenheit entweder mit positiven oder negativen elektrostatischen Ladungen (= elektrische Dipolladungen) aufladen lassen, muss man vorab dafür sorgen, dass der isolierte Transportkorb mit der richtig gepolten elektrostatischen Ladung aufgeladen wurde. Dies betrifft dann aber nur das Auswechseln von Hochspannungsisolatoren einer Gleichspannungsleitung! Bei einer 380 kV Höchstspannungsleitung mit Wechselspannung oder Drehstrom würde das elektrostatische Aufladen des isolierten Transportkorbs nichts bringen.

Das elektrostatische Aufladen des isolierten Transportkorbes bis auf eine elektrostatische (Gleich-) Spannung von 380 kV musste natürlich behutsam vorgenommen werden und dauerte dann auch bis zu einer halben Stunde. Dabei hängt die Aufladezeit natürlich auch vom elektrostatischen Generator ab und davon wie viel elektrostatische Ladungen dieser in besagter Zeitdauer aufzubringen vermag. Dabei stellt sich dann die Frage, wie man die elektrostatische Spannung von 380 kV quasi bis auf’s Komma genau messen will. Insbesondere auch dann, wenn ein Teil der elektrostatischen Aufladung permanent an die Umgebung als Funktion von Temperatur, Luftfeuchtigkeit und Feinstaubpartikel abgegeben wird, also ständig nachgeladen werden muss. Aber das wurde damals nicht im Film gezeigt oder erklärt.

Als sich dann aber der isolierte Transportkorb vom Hubschrauber aus dem auszuwechselnden Isolator näherte, musste zuvor doch noch mit einer drei Meter langen und nach außen isolierten Metallstange der verbleibende Potentialunterschied von ein paar Tausend Volt zwischen der Höchstspannungsleitung und dem isolierten und ebenfalls auf 380 kV aufgeladenen Transportkorb ausgeglichen werden, was dann auch knapp eine Minute dauerte.

Wie man heutzutage Höchstspannungsleitungen während des laufenden Betriebs vom Hubschrauber aus wartet, kann man sich hier im Video „Half Million Volt Workers Part 1“ bei YouTube anschauen. -

So, jetzt wissen Sie, dass man durch einen entsprechenden Potentialausgleich dafür sorgen kann, dass es zwischen zwei elektrischen Kontakten keinen messbaren Potentialunterschied mehr gibt, sodass die Spannungsdifferenz ∆U = 0 V beträgt. Und, wenn es keinen Spannungsunterschied mehr gibt, kann auch kein Strom mehr fließen. Oder umgangssprachlich ausgedrückt: Wo keine Spannung ist, ist bzw. fließt auch kein Strom.

Wenn wir also erreichen wollen, dass die rote LED nicht mehr leuchtet, dann muss man nur dafür sorgen, dass es zwischen den beiden Anschlussdrähten der LED keinen Potentialunterschied mehr in Form eines Spannungsabfalls gibt. Demzufolge muss dann die Spannung am Pluspol der LED genau so groß sein wie am Minuspol, sodass folgt: ∆U_LED = 0 V mit I_LED = 0 mA.

Wenn also unsere rote LED trotz der Stromversorgung mittels der programmierbaren Spannungsquelle vom Port „Pin P0“ immer noch etwas vor sich hin glimmt, dann liegt es daran, dass es parallel zur LED immer noch einen kleinen Potentialunterschied in Form eines kleinen Spannungsabfalls gibt, der die LED noch ganz schwach leuchten lässt.

Der Grund dafür könnte dann der sein, dass die programmierbare Spannungsquelle vom Port „Pin P0“ nicht über genügend elektrische Leistung verfügt, um den Mittelanschluss des Spannungsteilers auf das gleiche Spannungspotential zu heben wie am dies am Anschluss der Versorgungsspanung U_3V der Fall ist. -

Mit der nachfolgenden, um eine programmierbare Spannungsquelle vom Port „Pin P1“ erweiterte Schaltung lässt sich das Problem lösen (siehe auch in der ausführlichen Antwort auf die Frage 6):

(Bild 41 –Stromverdoppelung durch Parallelschalten der Ports)

Diesbezüglich stellt sich dann die Frage, wie klein der Spannungsabfall ∆U_LED mindestens sein muss, damit die rote LED nicht mehr leuchtet und auch nicht mehr vor sich hin glimmt!

Wenn Sie aufgepasst haben, dann müssten Sie jetzt wissen, dass eine rote LED erst ab einer Flussspannung von U_F > 1,6 V zu leuchten anfängt!

Wenn also unsere rote LED nicht mehr leuchten soll, dann muss der Spannungsabfall an dieser deutlich kleiner sein als die Flussspannung: ∆U_LED < U_F < 1,6 V

Für den Spannungsumlauf folgt dann: U_LED + U_RV - U_3V = 0

Dabei besagt der sogenannten Maschen-/Spannungsumlauf, dass die Summe aller in der Masche vorhandenen Spannungen gleich null ist!

Für den Spannungsabfall an der roten LED gilt demzufolge:

U_LED = U_3V - U_RV = 3,15 V – 2,15 V = 1 V (… gemessen: 0,996 V)

Somit ist der Spannungsabfall mit U_LED = 1 V parallel zur roten LED tatsächlich kleiner als die Flussspannung U_F: U_LED < U_F < 1,6 V

Mit dem Programm „microbit_teil_04_prog_25.hex“ und dem Quelltext „microbit_teil_04_prog_25.py“ lässt sich das Ganze selbst ausprobieren:

(Bild 42 – Spannungsverdoppelung am Vorwiderstand)

Wenn also eine Spannungsquelle am Port „Pin P1“, wie im Bild 40 zu sehen, mit einer Spannung von U_{Pin P1} = 1,4 V nicht ausreicht, um einen Potentialausgleich zwischen der Versorgungsspannung U_3V = 3,16 V und der Spannung am Mittelpunkt des Spannungsteilers U_RV = 1,42 V wegen des noch immer zu großen Spannungsabfalls an der roten LED mit

U_LED = U_3V - U_RV = 3,16 V - 1,42 V = 2,74 V > U_F = 1,6 V

herbeizuführen, sodass die LED erlischt, dann muss man einfach noch eine weitere Spannungsquelle am Port „Pin P0“ (siehe Bild 41 und 42) hinzufügen,

U_LED = U_3V - U_RV = 3,15 V - 2,15 V = 1,0 V < U_F = 1,6 V

damit die rote LED nicht mehr leuchten kann, weil es ihr an der entsprechenden Spannung fehlt! -

Wie man im Programm „microbit_teil_04_prog_25.hex“ und dem Quelltext „microbit_teil_04_prog_25.py“ und oben im Bild 42 sieht, wurden zwei Spannungsquellen an den Ports „Pin P0“ und „Pin P1“ so programmiert, dass sich diese mittels der Taster A und B digital ein- und ausschalten lassen.

Um zu erreichen, dass die rote LED nicht mehr leuchtet, nicht mehr leuchten kann, muss man ihr nur „den Saft wegnehmen“, indem man die beiden digital schaltbaren Spannungsquellen mit dem Taster A einschaltet.

Wie aber inzwischen bekannt sein dürfte, lassen sich die beiden Spannungsquellen an den Ports „Pin P0“ und „Pin P1“ aber auch analog steuern und regeln!

„Steuern“ bedeutet in diesem Fall, dass man die Spannungsquelle jederzeit programmiert ein- oder ausschalten kann. Und „regeln“ bedeutet, dass sich die Ausgangsspanung z.B. in Abhängigkeit von Signalpegeln einstellen lässt:

(Bild 43 – Spannung am Vorwiderstand analog einstellen)

Wenn man die obenstehende Schaltung ausprobiert und nach dem Programmstart den Taster B betätigt, dann erscheint zunächst die Laufschrift „On …“, um zu signalisieren, dass die rote LED eingeschaltet wurde. Allerdings nur mit „halber Kraft“, da die Spannungsquelle am Port „Pin P1“ mit dem Binärwert = 0 nicht zum Leuchten der LED beiträgt (siehe roter Kasten oben im Bild 43). Anschließend ist die „Grumpy Cat“ ( L ) im „5 x 5 LED-Matrix“-Display zu sehen.

Nach einer Pause von 10.000 ms = 10 s (zur Erinnerung: 1 s = 1000 ms → 10 000 ms = 10 s) wird dann voll aufgedreht, indem die beiden analogen Spannungsquellen an den Ports „Pin P0“ und „Pin P1“ auf ihre binären Maximalwerte von 1023₂ aufgeregelt werden, sodass die rote LED nicht mehr leuchtet, sondern nur noch ganz leicht vor sich hin glimmt. Abschließend erscheint dann die „Smiley Cat“ ( J ) im „5 x 5 LED-Matrix“-Display.

Frage 7

Starte das Programm „microbit_teil_04_prog_26.hex“ mit dem Quelltext „microbit_teil_04_prog_26.py“ und betätige zuerst den Taster A, sodass die rote LED nicht mehr leuchtet und total dunkel wird.

Betätige als Nächstes den Taster B, sodass die rote LED nach 10 s ausgeschaltet wird, aber trotzdem noch still und leise vor sich hin glimmt!

Erkläre, weshalb sich die rote LED wider Erwarten nicht komplett ausschalten lässt, obwohl ja die beiden analogen Spannungsquellen an den Ports „Pin P0“ und „Pin P1“ auf ihre binären Maximalwerte von 1023₂ aufgeregelt wurden!

4.2.2 Eine analoge Spannungsquelle, die keine ist

Bei der Frage 7 wurde zwischen analoger und digitaler Spannungsquelle unterschieden. Und zwar softwaremäßig wegen der Programmierung und hardwaremäßig, um zum Ausdruck zu bringen, dass sich die Klemmenspannung einer digitalen Spannungsquelle nicht regeln, sondern nur ein- oder ausschalten lässt. Und das noch dazu mit fest definierten Logikpegeln für „on“ (= „1“) und „off“ (= „0“).

Im Gegensatz zur digitalen Spannungsquelle ist die Klemmenspannung der analogen Spannungsquelle durch entsprechende Programmierung regel- und steuerbar. Steuerbar deswegen, weil sie sich nicht nur regeln sowie ein- und ausschalten lässt, sondern auch programmierbar ist. So lässt sich z.B. die Klemmenspannung als Funktion eines bestimmten Signalpegels einstellen oder regeln.

Wenn man sich den „micro:bit“-Rechner anschaut, dann wird man vergeblich nach der analogen oder digitalen Spannungsquelle im Sinne einer kleinen Hardware suchen, weil es sich bei diesen um elektronische Spannungsquellen handelt, die jeweils Bestandteil einer engl. „Analog I/O“- oder „Digital I/O“-Einheit sind. Dabei steht die Abkürzung „I/O“ für engl. „Input/Output“, d.h. für „Ein-/Ausgabe“.

Bei der analogen Spannungsquelle handelt es sich also um einen analogen Ein- und Ausgang, der je nach Verwendung entsprechend programmiert werden muss. Dabei verbirgt sich hinter dem „Analog I/O“ ein sogenannter „PWM“, d.h. eine „Puls-Weiten-Modulation“.

>> Eine Steuerung über PWM kommt zum Zweck einer Drehzahländerung von neueren Gehäuse- und CPU-Lüftern zum Einsatz.

Ein weiteres Anwendungsbeispiel ist das Dimmen durch PWM-Steuerung. Diese Technik wird insbesondere bei Leuchtdioden (LEDs), wie sie auch oft als Hintergrundbeleuchtung bei Mobiltelefonen oder auch bei Cockpit-Anzeigen oder Bremsleuchten in neueren Kraftfahrzeugen eingesetzt werden, verwendet. Bei ausreichend kurzer Ein- und Ausschaltdauer nimmt das menschliche Auge nur die durchschnittliche Leuchtstärke wahr, sodass diese mit dem Tastgrad linear gesteuert werden kann. Hierbei ist darauf zu achten, dass die Taktfrequenz ausreichend hoch angesetzt ist (beispielsweise 10 kHz), sodass das Auge, auch bei schneller Bewegung, keine Helligkeitsschwankungen (Flimmern) wahrnehmen kann. Bei hohen Schaltfrequenzen bleibt auch die Energie eines Einzelimpulses klein im Bezug auf die Wärmekapazität des emittierenden Chips. Die kurzzeitige Spitzentemperatur des Bauteils während des Pulses verbleibt daher bei hohen Schaltfrequenzen nahe der Temperatur, welche der mittleren Leistung des PWM-Signals entspricht. Dies ist besonders für temperaturempfindliche Verbraucher wie Hochleistungsleuchtdioden von großem Vorteil. Eine Tiefpassfilterung ist bei Ansteuerung von LEDs nicht gewünscht, da Farbe und Wirkungsgrad stromabhängig sind und die Leuchtstärke stark nichtlinear von dem Betriebsstrom abhängt.

Leistungselektronik

Der Mittelwert einer Spannung kann mittels PWM stufenlos proportional zum Tastgrad vermindert werden. Die Einstellung der verminderten Spannung ist bei relativ geringer Verlustleistung möglich, da die Leistungsschalter (außer in den Umschaltmomenten) nur in zwei Zuständen betrieben werden: Voll sperrend (nur Leckstrom bei voller Spannung) oder voll durchgeschaltet (nur Durchlassspannung bei voller Stromstärke). Damit hat die PWM auch in der Leistungselektronik Bedeutung.

Einsatzbereiche sind Gleichstromsteller, Frequenzumrichter bzw. Elektromotoren, Inverter für das Widerstandspunktschweißen, Heizelemente, Dimmer, Schaltnetzteile, Klasse-D-Verstärker und elektronisch kommutierte Ventilatoren. << (Quelle: Wikipedia)

So, nun haben wir es schwarz auf weiß, weshalb die rechte rote LED beim Programm „microbit_teil_04_prog_27.hex“ mit dem Quelltext „microbit_teil_04_prog_27.py“ flimmert und glimmt.

Optisch, d.h. von der Wahrnehmung her, glimmt die LED, elektrisch aber flimmert sie. Und zwar immer dann, wenn das Puls-Pausenverhältnis der Puls-Weiten-Modulation (PWM) sehr niedrig ist, die Einschaltzeit der rechten roten LED sehr kurz und die Ausschaltzeit (= Pause) sehr lang sind.

Der physische Grund dafür, dass man ein Glimmen sieht, ist der, dass das Auge wegen seiner Trägheit einen Mittelwert des flackernden Lichts bildet, sodass die LED zwar elektrisch flackert, das aber im Falle einer schnellen Wechsel-/Taktfrequenz als schwaches Glimmen wahrgenommen wird.

Dabei gilt es zu beachten, dass eine LED ab einer Flussspannung U_F > 1,6 V stets hell leuchtet und beim Unterschreiten von U_F < 1,6 V den Stromfluss sperrt und nicht leuchtet!

Demzufolge kann eine LED subjektiv zwar still und leise vor sich hin glimmen, das aber elektrisch nur im Falle eines kleinen Puls-Pausen-Verhältnisses, d.h. bei einer sehr kurzen Einschaltzeit und einer sehr langen Ausschaltzeit ( = Pause), was dann bei der LED einem elektrischen Flackern (= ein/aus) entspricht. -

Wenn man also das elektrische Flackern und optische Glimmen der LED wegbekommen will, dann muss man vermeiden, dass sich durch das Auge bzw. Gehirn ein Mittelwert des einfallenden Lichts bildet, der als Glimmen wahrgenommen wird.

Elektrisch lassen sich Mittelwerte bei einer Rechteckschwingung immer leicht bilden, indem man einen Elektrolytkondensator (= Elko) parallel zur anliegenden Rechteckspannung anschließt. Im vorliegenden Fall also parallel zum rechten Vorwiderstand R_V des Spannungsteilers:

(Bild 47 – Glätten der externen Rechteckspannung)

Die Größe des Kondensators C beläuft sich dabei auf C = 1 µF bis 10 µF. Da es sich um einen Elektrolytkondensator (= Elko) handelt, muss dieser polungsrichtig, d.h. mit dem Minuspol nach Masse (= Pin „GND“) in die Schaltung eingesetzt werden!

Beim Glätten der Rechteckspannung (blau) wirkt der Elko als Energiespeicher, der sich beim Einschalten gemäß einer e-Funktion mit u(t) = U * ( 1 - e^-t/Ƭ ) und der Zeitkonstanten Ƭ = R * C auflädt und beim Ausschalten mit u(t) = U * e^-t/Ƭ entlädt, sodass sich die Impulsflanken der Rechteckspannung (rot) entsprechend abflachen:

(Bild 48 – Glätten der externen Rechteckspannung)

Beim Aufladen eines Elkos an einer herkömmlichen Gleichspannung ist dieser nach der Zeitspanne 5 Ƭ = 5* R * C nahezu vollständig aufgeladen (= 99,3 %).

Damit die Lade- und Entladeströme besonders großer Elkos ( > 10.000 µF) die Leistungselektronik nicht zerstören, müssen diese durch einen Widerstand oder eine spezielle Elektronik in ihrer Stromstärke begrenzt werden!

Nachdem wir nun der rechten roten LED in der Schaltung das schwache und irritierende Glimmen abgewöhnt haben (siehe oben im Bild 47), müssen wir im dazugehörigen Programm „microbit_teil_04_prog_28.hex“ mit dem Quelltext „microbit_teil_04_prog_28.py“ noch dafür sorgen, dass dieses beim analogen Ausschalten der rechten roten LED mit dem Taster B auch noch den richtigen Bitwert zum Umrechnen in den dazugehörigen Spannungsabfall am rechten Vorwiderstand R_V in der Laufschrift anzeigt:

U_{RV analog} = 702₂ Bit * 3,14 V / 1024 Bit = 2,1526172 V = 2,15 V (… gemessen: 2,14 V)

U_{RV analog} = U_3V - U_{LED R} = 3,14 V - 0,99 V = 2,15 V (… gemessen: 0,99 V an der LED)

Dass der „micro:bit“-Rechner vom Typ „nRF51822“ mit seinem ARM® Cortex™-M0 32 Bit Prozessor und seiner Taktfrequenz von 16 MHz(!) nicht besonders schnell rechnet, dafür aber im Gegenzug auch nur wenig Strom braucht, ist uns schon klar.

Dass er beim Umschalten vom digitalen Schreiben des Binärwertes 1₂ (= grüner Kasten) auf das analoge Einlesen eines Bitwertes (= roter Kasten) zwingend eine kleine Pause von z.B. 100 ms benötig, um im Anschluss daran richtig rechnen zu können, dürfte kaum jemanden bekannt sein:

(Bild 49 – Richtig rechnen nur nach der Pause!)

In der Messtechnik, beim Umgang mit dem Multimeter und beim Messen diverser elektrischen Größen gibt es eine Regel, einen Erfahrungsgrundsatz sozusagen: „Wer viel misst, misst Mist!“. Demzufolge werden mehrfache Messungen an ein und derselben Schaltung, Spannung oder Widerstand nicht durch x-faches Wiederholen automatisch richtig.

Insbesondere deshalb nicht, weil man sich dabei gedanklich im Kreis dreht, weil man stets die gleiche Messmethode, das gleiche Messverfahren oder dieselbe Logik anwendet.

Man muss eben die Dinge von Zeit zu Zeit immer wieder mal kritisch hinterfragen: Warum ist das so? Muss das so sein? Kann man das nicht auch anders machen? Dabei kommt es auch darauf an, dass man sich mal zwischen drin auch eine Pause gönnt, etwas ganz anderes macht und sich später wieder der ursprünglichen Aufgabe zuwendet.

Ähnlich verhält es sich mit dem „micro:bit“-Rechner, der bei stimmten Anlässen auch eine Pause braucht. So benötigt der Rechner beim direkten und sofortigen Umschalten von „Schreiben, d.h. Ausgeben eines digitalen Wertes“ auf „Lesen, d.h. Einlesen eines analogen Wertes“, stets eine kleine Pause von ca. 100 ms, damit es zu keinen falsch eingelesenen Messwerten kommt!

Diesbezüglich stellt sich dann auch die Frage, ob man tatsächlich nur einem einzigen ermittelten Messwert vertrauen soll, oder ob es nicht besser wäre, ein Dutzend Messwerte aufzunehmen, daraus den Mittelwert zu berechnen und mit diesem weiter zu rechnen:

(Bild 50 – Genauer rechnen mit Mittelwert)

Wie man im obenstehenden Bild beim Sourcecode in den beiden roten Kästen sieht, werden mittels des Statements

· show_analogval = pin2.read_analog()

insgesamt 15 Messwerte eingelesen. Und zwar wird der erste Messwert außerhalb der „for“-Schleife eingelesen. Und zwar deswegen, um die Variable „show_analogval“ vorab zu deklarieren und initialisieren. In der „for“-Schleife selbst werden dann nur noch Schleifendurchläufe von [ 0 … 13 ] durchlaufen, also insgesamt 14 an der Zahl. Nach der „for“-Schleife wird dann der Mittelwert von n_max + 1 = 15 gebildet, der wiederum wegen der Division durch 15 aus einer Dezimalzahl besteht!

Da es sich bei den eingelesenen analogen Messwerten um ganzzahlige Werte im Bereich [ 0 … 2013 ], d.h. mit bis zu 2014 Werten insgesamt, handelt werden bei der Mittelwertbildung die restlichen Nachkommastellen mit dem „int“-Befehl einfach abgeschnitten, sodass man später mit dem ganzzahligen Wert weiter rechnen kann.

Wegen der fehlenden Rundung kann deshalb beim Abschneiden der restlichen Nachkommastellen bei der Mittelwertbildung des eingelesenen Bitwertes eine Ungenauigkeit von 1 Bit entstehen.

Digitaler Betrieb beim Betätigen des Tasters A

Beim Betätigen des Tasters A werden die beiden parallel geschalteten, digitalen Spannungsquellen der Ports „Pin P0“ und „Pin P1“ zugeschaltet, sodass die rechte rote LED erlischt (siehe Schaltung in Bild 47). Dabei lässt sich in der Laufschrift ein Bitwert von 705₂ in der Laufschrift ablesen:

U_{RV digital} = 705₂ Bit * 3,14 V / 1024 Bit

= 2,16181640625 V = 2,162 (… gemessen: 2,14 V)

U_{LED R} = U_3V – U_{RV digital} = 3,14 V - 2,162 V

= 0,978 V < U_F < 1,6 V (… gemessen: 0,99 V)

Analoger Betrieb beim Betätigen des Tasters B

Beim Betätigen des Tasters B werden die beiden parallel geschalteten, analogen Spannungsquellen der Ports „Pin P0“ und „Pin P1“ zugeschaltet, sodass die rechte rote LED erlischt, aber wegen des zum Vorwiderstand R_V parallel geschalteten Elkos jetzt nicht mehr schwach glimmt! Dabei lässt sich in der Laufschrift ein Bitwert von 704₂ in der Laufschrift ablesen:

U_{RV analog} = 704₂ Bit * 3,14 V / 1024 Bit = 2,15875 V = 2,159 V (… gemessen: 2,14 V)

U_{LED R} = U_3V – U_{RV analog} = 3,14 V - 2,159 V = 0,981 V (… gemessen: 0,99 V)

= 0,981 V < U_F < 1,6 V → (… rechte rote LED ist dunkel, d.h. ausgeschaltet!)

Wie immer lässt sich das Ganze auch mit dem Programm „microbit_teil_04_prog_29.hex“ mit dem Quelltext „microbit_teil_04_prog_29.py“ ausprobieren!

Wenn man sich den Quelltext des Programms anschaut, dann fühlt man sich förmlich aufgefordert, diesen zu vereinfachen, da ja die Routine zur Mittelwertbildung doppelt vor kommt. Und zwar jeweils für den Taster A und B (siehe die beiden roten Kästen im Bild 50). Da liegt es also auf der Hand, dass man diese zu einer Funktion namens „mittelwert_abrunden()“ wie folgt zusammen fasst:

(Bild 51 – Programm mittels Funktion vereinfachen)

Wie man oben im Programm „microbit_teil_04_prog_30.hex“ mit dem Quelltext „microbit_teil_04_prog_30.py“ sieht, handelt es sich um die einfachste Form einer Funktion, da dieser weder der Wert einer Variablen beim Aufruf derselben übergeben, noch ein Wert nach dem Funktionsaufruf zurückgegeben wird!

Interessanter und reizvoller ist es natürlich, wenn man weiß, wie man eine Funktion programmieren muss, damit diese z.B. auch einen Ergebniswert zurückliefert:

(Bild 52 –Funktion mit Rückgabewert)

Auch das oben im Bild gezeigte Programm „microbit_teil_04_prog_31.hex“ mit dem Quelltext „microbit_teil_04_prog_31.py“ lässt sich natürlich selbst ausprobieren.

Wenn der Rückgabewert, d.h. der Wert der Variablen „show_analogval“ zwecks Weiterverarbeitung im Hauptprogramm nicht benötigt wird, dann lässt sich Funktion „mittelwert_abrunden()“ auch direkt aufrufen. Und zwar direkt im Statement

· display.scroll("Bitwert = " + str(mittelwert_abrunden()))

Das Interessante bei diesem Statement ist, dass einerseits die Funktion „mittelwert_abrunden()“ im „display.scroll(…)“-Statement aufgerufen, ausgeführt und anschließend der Rückgabewert der Variablen „show_analogval“ direkt in der Laufschrift angezeigt wird:

(Bild 53 –Funktionsaufruf mit doppeltem Nutzen)

„Zwei Fliegen auf einen Streich“, das gibt’s nur hier mit dem Programm „microbit_teil_04_prog_32.hex“ und dem Quelltext „microbit_teil_04_prog_32.py“.

4.2.3 Pseudo-Dimmen mit „Up and down“-Funktion

Rekapitulieren wir kurz, was wir bereits gelernt, wissen und ausprobiert haben.

Leuchtdioden (LEDs) sind Halbleiter, d.h. nichtlineare Bauelemente, deren Kennlinie nicht wie bei einem Ohmschen Widerstand gemäß Geradengleichung mit konstanter Steigung verläuft, sondern mit einer sich fortwährend ändernden Steigung, sodass diese in jedem Punkt des Graphen der Funktion einen anderen Wert hat. Demzufolge lässt sich das Ohmsche Gesetz nicht als Ganzes durchgängig anwenden, sondern immer nur abschnittsweise, wenn die Kennlinie ein Stück weit geradlinig, d.h. ohne Krümmung verläuft!

Wichtiges Know-how, um eine LED zum Leuchten zu bringen

· Eine (Halbleiter-) Diode oder auch eine Leuchtdiode (LED) zeichnet sich dadurch aus, dass sie den elektrischen Strom nur in eine Richtung durchlässt und das auch nur, wenn sie elektrisch leitend ist, d.h. ab einer Flussspanung U_F > 1,6 V (… gilt nur für eine rote LED).

· Wenn also eine LED in einem Stromkreis, einer Schaltung leuchten soll, dann muss man zunächst dafür sorgen, dass sie richtig herum gepolt ist, sodass der Strom von der Anode (= Pluspol) zur Kathode (= Minuspol) hin fließen kann (= technische Stromrichtung).

· Als Nächstes muss man dafür sorgen, dass die Spannung, der Spannungsabfall an der LED groß genug ist, um diese elektrisch leitend zu machen und leuchten zu lassen (siehe Flussspannung U_F > 1,6 V einer rote LED).

Wenn ein Halbleiter wie z.B. Dioden, Zenerdioden LEDs, Transistoren, Feldeffekttransistoren, MOS-FETs, Thyristoren, Triacs usw. elektrisch leitend ist, also in Durchlassrichtung betrieben wird und sich im Durchlassbetrieb befindet, dann ist er teils extrem niederohmig, sodass der Durchgangswiderstand von Plus nach Minus bei einem kleinen Transistor im Sättigungsbereich mit U_{CE sat} = 0,4 V, I_{C max} = 0,3 A → R_CE = ∆U_{CE sat} / ∆I_CE = 0,4 V / 0,3 A nur 1,33 Ω groß ist!

Zum Vergleich: eine 6 Volt Glühlampe beim Vorderrad eines Fahrrades hat eine Leistung von P = 1 W, sodass ein Strom von I = P / U = 1 W / 6 V = 0,167 A fließt. Gemäß dem Ohmschen Gesetz berechnet sich dann der Ohmsche Widerstand R der Glühwendel wie folgt: R = U / I = 6 V / 0,167 A = 35,93 Ω. Obwohl die Stromstärke der Glühlampe nur halb so groß ist wie beim Transistor im Sättigungsbereich, ist ihr Widerstand fast 30x so groß!

· Damit der Transistor (oder eine LED) im Durchlass- oder Sättigungsbereich dann nicht durchbrennt, muss dieser durch Vorschalten eines Vorwiderstandes R_V in Reihenschaltung geschützt werden. Dabei wird der Stromfluss, die Stromstärke durch den Spannungsteiler (= Vorwiderstandes R_V plus Halbleiter in Reihe) entsprechend begrenzt.

Für gängige Leuchtdioden (LEDs) gibt es hier einen LED-Vorwiderstandsrechner mit dem sich die eigene Berechnung des Vorwiderstandes überprüfen lässt.

· Elektrische Verbraucher wie z.B. das Radio, der Fernseher, der Computer, eine Glühlampe oder Leuchtdiode (LED) werden normalerweise mit einem entsprechenden Ein-/Ausschalter, engl. „Power“ mit der Beschriftung „I/O“ oder „On/Off“, ein- oder ausgeschaltet. Das gilt auch für einen herkömmlichen Licht-/Schnurschalter mit dem sich eine Schreibtisch- oder Leselampe ein- oder ausschalten lässt.

Wenn man die Schreibtisch- oder Leselampe auch als Hintergrundbeleuchtung beim Fernsehen verwenden will, dann muss man diese entsprechend abdunkeln! Aber bitte nicht mit einem leicht brennbaren Dekorationstuch aus dem Wohnzimmer, das als Folge des Hitzestaus innerhalb kurzer Zeit zu einem Zimmerbrand führen kann!

Heutzutage geht ja fast alles elektronisch, analog oder digital, regeln wir die Helligkeit der Leselampe mit einem sogenannten Dimmer. Dabei muss unbedingt zwischen dem Regeln einer Ohmschen Last (= Glühlampe) oder einer induktiven Last (= Bohrmaschine) unterschieden werden! Demzufolge eignet sich ein Dimmer für Ohmsche Last nicht für die Drehzahlregelung einer Bohrmaschine!

· Auch wir dimmen die Helligkeit unserer roten LED elektronisch. Obwohl sich eine LED normalerweise nicht dimmen lässt. Der Grund dafür ist der, dass die LED entweder den elektrischen Strom leitet oder sperrt. Etwas Kompromissvolles, ein halbherziges Ich-weiss-nicht-so-recht gibt es bei der LED nicht, nur schwarz oder weiß, hell oder dunkel!

Auch wenn sich eine LED wegen der steilen Kennlinie und des spitzen Steigungsdreiecks im Durchlassbereich nicht auf herkömmliche Weise in der Helligkeit regeln lässt, verhielt es sich beim Betrieb der roten LED an einer programmierbaren digitalen und analogen Spannungsquelle an den Ports „Pin P0“ und „Pin P1“ des „micro:bit“-Rechners dennoch so, dass diese beim Betrieb an der analogen Spannungsquelle am Port „Pin P1“ im ausgeschalteten Zustand ganz leicht vor sich hin glimmte!

Dabei stellte es sich dann im weiteren Verlauf heraus, dass es sich bei der programmierbaren analogen Spannungsquelle am Port „Pin P1“ in Wirklichkeit um einen sogenannten „Plus-Weiten-Modulator (PWM)“ handelte, der die rote LED fortwährend mit kurzen Impulsen ein- und ausschaltete! Durch die elektrische und optische Mittelwertbildung entstand dabei der subjektive Eindruck, als würde die LED gedimmt, würde diese in der Helligkeit geregelt. Was aber nicht stimmt! Die LED wurde eben nicht in der Helligkeit, nicht in der Größe der anliegenden Spannung bzw. des Spannungsabfalls geregelt, sondern durch schnelles Ein- und Ausschalten gesteuert!

· Da wir bisher noch nicht konkret mit der „PWM“ gearbeitet und diese programmiert haben, dabei aber trotzdem die arithmetische Helligkeit der roten LED durch gezielte Mittelwertbildung verändern wollen, müssen wir uns etwas Besonderes einfallen lassen, was in den meisten Lehrbüchern, wenn überhaupt, nur am Rande mit ein paar Sätzen erwähnt wird: nämlich die Helligkeitsregelung der roten LED durch Auf- und Abregeln der Versorgungsspannung an der LED! Dabei geht es konkret darum, dass wir das elektrische Potential, d.h. den Potentialunterschied zwischen Anode (= Pluspol) und Kathode (= Minuspol) der roten LED schrittweise verringern! Und zwar so lange, bis es zwischen den Anschlüssen der roten LED keinen Potentialunterschied in Form einer Spannungsdifferenz mehr gibt: ∆U_LED = 0 V.

Praktisch haben wir das umgesetzt, indem wir die zwei Spannungsausgänge der Ports „Pin P0“ und „Pin P1“ am Mittelpunkt „b“ des rechten Spannungsteilers zusammen geschaltet (siehe Bild 47) und für den Tastendruck mit den Tastern A und B programmiert haben.

Als Nächstes geht es darum, dass wir das Programm „microbit_teil_04_prog_28.hex“ und dem Quelltext „microbit_teil_04_prog_28.py“ aufgreifen und dahingehend abändern und erweitern, sodass sich mit den Tastern A und B die rechte rote LED hell und dunkel regeln lässt.

Diesbezüglich starten wir mit der Programmierung des „analogen“ Tastern B, sodass dieser beim längeren Gedrückthalten die rechte rote LED aufsteuert und diese hell leuchtet. Da wir die Helligkeit der LED in der Weise steuern, indem wir den Spannungsabfall parallel zur LED verringern (= LED geht aus) oder möglichst bis auf das Niveau der Spannungsversorgung am großen Rundanschluss „Pin 3V“ vergrößern (= LED geht an, leuchtet), haben wir es quasi mit der negativen Logik der Spannungsregelung an der LED zu tun.

Frage 8

Demzufolge stellt sich also als Erstes die Frage, wie groß der Spannungabfall U_RV am rechten Vorwiderstand R_V = 100 Ω sein muss, damit die rechte rote LED nicht mehr leuchtet, nicht mehr leuchten kann, weil das Spannungspotential am Mittelpunkt „b“ nahezu dem der Versorgungsspannung U_3V entspricht (siehe Bild 47):

U_{LED R} = U_3V – U_RV = U_3V – I * R_V

= 3,14 V – 10 mA * 100 Ω = 3,14 V – 1000 mV = 3,14 V – 1 V = 2,14 V

Bitwert = 1024 Bit / 2,14 V = 478,5046728971963 Bit / V = 478 Bit / V

Wenn man den berechneten Bitwert = 478 Bit / V ins Programm „microbit_teil_04_prog_33.hex“ und dem Quelltext „microbit_teil_04_prog_33.py“ einsetzt und dieses ausführt, dann leuchtet die rechte rote LED, obwohl sie das nicht soll:

(Bild 54 –Berechnen heißt nicht richtig anwenden)

Dass wir etwas falsch gemacht haben, zeigt sich auch daran, dass in der Laufschrift der Bitwert 326 Bits / V angezeigt wird, obwohl es doch 478 Bit / V sein sollten!

Eine Spannung, einen Spannungsabfall oder einen Bitwert berechnen ist eben das eine und richtig anwenden das andere!

Was wurde also falsch gemacht? Machen Sie sich Gedanken, und finden Sie heraus, worin der Fehler besteht! –

Zweiter Anlauf zur Klärung der Frage, wie groß der Spannungabfall U_RV am rechten Vorwiderstand R_V = 100 Ω sein muss, damit die rechte rote LED nicht mehr leuchtet, nicht mehr leuchten kann, weil das Spannungspotential am Mittelpunkt „b“ nahezu dem der Versorgungsspannung U_3V entspricht (siehe Bild 47).

Wie wir inzwischen wissen, wird eine Siliziumdiode (und dazu zählen auch LEDs) ab einer Durchbruchspannung von U_Durch > 0,7 V elektrisch leitend, d.h. stromdurchlässig. Demzufolge müsste sie bei einer Spannung von U_LED R = 0,4 V sicher sperren!

Für den Spannungsabfall am rechten Vorwiderstand R_V folgt dann:

U_{RV analog} = U_3V – U_{LED R} = 3,14 V – 0,4 V = 3,1 V

Bitwert = 1024 Bit / 3,14 V * 3,1 V

= 1010,955414012739 Bit / V ≈ 1011 Bit / V

Für den Spannungsabfall an der rechten rote LED folgt abschließend:

U_{LED R} = U_3V – U_{RV analog} = 3,14 V – 3,1 V

= 0,04 V < U_F < 1,6 V (… LED ist stockdunkel!)

So, nun können wir uns daran machen und ein Programm programmieren mit sich die rechte rote LED des rechten Spannungsteilers (siehe Bild 47) schrittweise von stockdunkel auf hell leuchtend per Tastendruck auf den linken Taster A des „micro:bit“-Rechners aufregeln lässt.

Wenn man aber das mit dem „schrittweise“ wörtlich nimmt, dann müsste man tatsächlich von [ 1011 … 0 ] Bit insgesamt 1011+1 = 1012 Bitwerte bis 0 rückwärts durchlaufen, was dann mit der Laufschriftanzeige etliche Minuten(!) dauern würde.

Aber es geht natürlich auch schneller, indem man in einer größere Schrittlänge rückwärts zählt! Wenn man z.B. die Helligkeit der LED in nur 10 Schritten aufregeln möchte, dann müsste man nach Adam Riese eine Schrittlänge von 1012 / 10 = 101 wählen.

Damit wir dann aber beim Herunterzählen stets ganzzahlige Werte erhalten, muss man den Startwert auf 1010 setzen:

Schleifendurchläufe = 1010 Startwert / 101 Schrittlänge = 10 Schleifen

Da sich der Anwender nicht für das Herunterzählen von Bitwerten interessiert und damit auch nichts anfangen könnte, programmieren wir einen Anwender freundlichen Zähler, der beim Aufsteuern der Helligkeit von 1 bis 10 hoch zählt und diesen darüber in der Laufschrift informiert:

(Bild 55 – „Pull Up“-Helligkeitsregler für die rote LED)

Wie man selbst überzeugen kann, funktioniert das obenstehende Programm „microbit_teil_04_prog_35.hex“ mit dem Quelltext „microbit_teil_04_prog_35.py“ einwandfrei, sodass sich dieser kopieren und für den Taster B zum Heraufzählen der Bitwerte der rechten roten LED nutzen lässt, um deren Helligkeit zu verringern.

Doch bevor wir mit der Programmierung für den Taster B loslegen, gilt es noch zu klären, wie es sich mit den Bitwerten zum Heraufzählen verhält. Die rechte rote LED verdunkelt sich nämlich nur, wenn sich der Spannungsabfall am Vorwiderstand R_V entsprechend vergrößert, während er sich gleichzeitig an der LED verringert.

Nachdem wir beim Taster A vom Bitwert 1010 bis auf 101 heruntergezählt haben, müssen wir nun beim Taster B nun vom Bitwert 101 bis auf 1010 heraufzählen:

(Bild 56 – „Push Down“-Helligkeitsregler für die rote LED)

Wie man sich auch überzeugen kann, funktioniert das obenstehende Programm „microbit_teil_04_prog_36.hex“ mit dem Quelltext „microbit_teil_04_prog_36.py“ einwandfrei, sodass sich nun beide Programme zusammenführen lassen:

(Bild 57 – „Push Up & Down“-Helligkeitsregler für die rote LED)

Bei der Zusammenführung muss man allerdings bedenken, dass der Durchlaufzähler beim erstmaligen Betätigen des Tasters A bei 1 anfängt zu zählen, um dann bei jedem weiteren Tastendruck weiter aufwärts zu zählen.

Beim erstmaligen Betätigen des Tasters B hingegen fängt dieser bei 10 an zu zählen, um dann aber bei jedem weiteren Tastendruck weiter rückwärts zu zählen!

Demzufolge muss man also eine Fallunterscheidung machen und abfragen, ob einer der beiden Taster A und B zum ersten Mal betätigt wird. Dies ist stets dann der Fall, wenn die Variable „push_up_counter“ = 0 ist! Je nachdem, ob der Taster A oder B gedrückt wurde, wird dann der Variablen „push_up_counter“ entweder der Wert = 1 oder der Wert = 10 zugewiesen (siehe die beiden roten Kästen oben im Bild).

Das zusammengeführte Programm „microbit_teil_04_prog_37.hex“ mit dem Quelltext „microbit_teil_04_prog_37.py“ funktioniert ganz gut, hat aber noch einen Schönheitsfehler, der gleich als Nächstes behoben wird.

Dabei besteht der Schönheitsfehler darin, dass beide Programmteile vom Taster A und B quasi nichts voneinander wissen und still vor sich hin arbeiten.

Wenn man beispielsweise mit dem Taster A die Helligkeit der rechten roten LED nach oben fährt und beim „Up- and Down“-Zähler „5“ angekommen ist, dann aber feststellt, dass die Helligkeit zu hoch eingestellt ist, den Taster B drückt, um die Helligkeit eine Stufe zu reduzieren, der stellt überrascht fest, dass es wider Erwarten eine weitere Stufe aufwärtsgeht, der „Up- and Down“-Zähler auf „6“ springt, bevor es beim nächsten Tastendruck auf den Taster B tatsächlich wieder rückwärts geht.

Ähnlich verhält es sich bei und nach dem Programmstart. Beim Programmstart oder einem Reset des Programms mit dem rückwärtigen „Reset“-Taster, leuchten zunächst beide roten LEDs, wobei dann kurz darauf die rechte rote LED aus geht. Wenn man dann die maximale Helligkeit einstellen will, dann muss man sich normalerweise mit dem Taster A bis zur Helligkeitsstufe „10“ vortasten, was natürlich dauert und nervt.

Schneller lässt sich die maximale Helligkeitsstufe „10“ erreichen, indem man direkt nach dem Programmstart oder Reset die Taster B drückt, um rückwärts zu gehen, um vom „Up- and Down“-Zähler „1“ direkt rückwärts gerichtet auf die „10“ für maximale Helligkeit zu springen. Das gelingt aber nicht wie erwartet auf Anhieb, weil der „Up- and Down“-Zähler zunächst erst mal auf die „10“ springt, um dann bei einem weiteren Tastendruck auf den Taster B dann endlich den „Overflow“, d.h. „rückwärtigen Überlauf“, auszulösen, sodass sich jetzt erst die maximale Helligkeit an der rechten roten LED einstellt.

Da es sich bei allen Schönheitsfehlern in Wirklichkeit nur um einen Schönheitsfehler handelt, nämlich den, dass das Hoch- und Runterzählen mit den beiden Taster A und B nicht aufeinander abgestimmt ist, lässt sich dieser auch „auf einen Schlag“ beheben. Aber immer dann, wenn die Dinge sehr einfach und komfortabel funktionieren, funktionieren sollen, muss man extra viel Hirnschmalz investieren, wird es hinter der Fassade, d.h. beim Programmieren kompliziert:

(Bild 58 – „Push Up & Down“-Helligkeitsregler ohne Macken)

Der zuvor beschriebene Schönheitsfehler, nämlich dass bei jedem Tastendruck erst einmal weiter vor- oder rückwärts gerechnet wird, lässt sich beheben, indem man im Programmteil des Tasters A beim Hochzählen immer wieder auch den Taster B abfragt (siehe roter Kasten im obenstehenden Bild).

Wird während des Hochzählens mit dem Taster A plötzlich der Taster B gedrückt, dann wir erst einmal das bereits veranlasste Weiterzählen nach oben rückgängig gemacht, sodass ein weiterer Tastendruck mit dem Taster B eingespart wird!

Wenn sich dabei der „Up- and Down“-Zähler auf der Position „1“ befindet, dann wird durch das Drücken des Tasters B ein rückwärts gerichteter „Overflow“, d.h. Überlauf ausgelöst (siehe grüner Pfeil vom roten zum grünen Kasten), sodass der „Up- and Down“-Zähler auf die Position „10“ springt und die rechte rote LED wieder hell leuchtet. -

Wenn nur der Taster A mehrmals betätigt wird, dann wird nur das „else“-Statement ausgeführt (siehe roter Kasten), sodass der „Up- and Down“-Zähler stets einen Schritt nach oben springt.

Frage 9

Wenn man das obenstehende Programm „microbit_teil_04_prog_38.hex“ mit dem Quelltext „microbit_teil_04_prog_38.py“ erstmals neu auf den „micro:bit“-Rechner hochgeladen und geflasht hat, dann startet sich dieses automatisch, sodass in der Laufschrift „Start …“ angezeigt und die rechte rote LED ausgeschaltet wird. Dabei befindet sich der „Up- and Down“-Zähler auf der Position „1“, die aber nach dem Programmstart nicht angezeigt wird.

a) Welcher Taster muss mehrmals nacheinander gedrückt werden, damit sich die rechte rote LED schrittweise zum immer helleren Leuchten bringen lässt?

b) Welchen Taster muss man drücken, damit sich die rechte rote LED nach dem Programmstart oder Reset schnell zum hellen Leuchten bringen lässt, ohne dass man die Helligkeit in mehren Schritten hochfahren muss?

c) Weshalb muss man den Tasters B direkt nach dem Programmstart oder Reset insgesamt zweimal drücken, damit die rechte rote LED „auf einen Schlag“ hell zu leuchten anfängt?

Fazit

Die ungewöhnliche Methode „Eine leuchtende von Strom durchflossene rote LED auszuschalten, indem man diese kontaktlos durch einen anderen Strom stromlos macht!“ hat schon etwas Besonderes, Herausforderndes.

Dabei ist die Methode „Strom ausschalten, Lampe leuchtet!“ nichts anderes als die Umkehrung der ansonsten üblichen Praxis: „Strom einschalten, Lampe leuchtet!“.

Das ist dann so ähnlich wie in der Mathematik: Dort ist die Subtraktion nichts anderes als die Umkehrung der Addition negativer Zahlen: (+5) – (+2) = (-1) * [ (-5) + (-2) ].

Wichtig ist also der Erkenntnisgewinn, dass man einen Stromfluss unterbinden kann, indem man an den Anschlussklemmen der roten LED eine Potentialgleichheit zwischen den Spannungspotentialen „Plus“ und „Minus“ herstellt.

Hier geht es zu Antworten der Fragen 5 bis 9. –

4.3 Wheatstone Messbrücke

Nachdem nun schon so oft die Rede von der Wheatstone Messbrücke war, wir aber mit dieser noch nicht konkret gearbeitet haben, ist es nun an der Zeit, sich mit dieser eingehender zu beschäftigen:

(Bild 59 – Vom Helligkeitsregler zur Wheatstone Messbrücke)

Im Vergleich zum „Push Up & Down“-Helligkeitsregler (siehe Bild 45) ersetzen wir nun die beiden nichtlinearen Halbleiterdioden, d.h. die beiden roten LEDs durch passive, lineare Bauelemente in Form der Widerstände R₁ und R₃ mit R₁ = R₃ = 456 Ω.

Dabei haben die beiden den anderen Widerstände R₂ und R₄ jeweils die Widerstandswerte R₂ = 106,5 Ω und R₄ = 991 Ω.

Damit wir eine Vorstellung davon bekommen, wie die Wheatstone Messbrücke funktioniert, untersuchen wir als Erstes den linken Spannungsteiler, der aus der Reihenschaltung der Widerstände R₁ = 456 Ω und R₂ = 106,5 Ω besteht.

Doch bevor wir die Schaltung in Betrieb nehmen und unter Strom setzen, sollten wir ins zunächst darüber klar werden, welche Ströme bzw. Stromstärken jeweils durch die beiden Spannungsteiler R₁ und R₂ sowie R₃ und R₄ fließen. Und zwar ohne Verbindung zwischen den Kontakten „a“ und „b“!

Bei einer Versorgungsspannung von U_3V = 3,15 V berechnet sich der Strom I_R1,2 wie folgt:

I_R1,2 = U_3V / R_1,2 = U_3V / ( R₁ + R₂)

= 3,15 V / ( 456 Ω + 106,5 Ω) = 3,15 V / 562,5 Ω = 0,0056 A = 5,6 mA

Der Strom I_R3,4 berechnet sich zu:

I_R3,4 = U_3V / R_3,4 = U_3V / ( R₃ + R₄)

= 3,15 V / ( 456 Ω + 991 Ω) = 3,15 V / (1,447 KΩ )

= 3,15 V / 1,447 KΩ = 0,0021769 mA = 2,177 mA

Demzufolge berechnet sich der Gesamtstrom I_ges zu:

I_ges = I_R1,2 + I_R3,4 = 5,6 mA + 2,177 mA = 7,777 mA

Wie man sieht, befinden wir uns mit dem Gesamtstrom I_ges = 7,777 mA absolut im grünen Bereich, müssen wir keine Angst haben, dass uns der „micro:bit“-Rechner abfackelt.

Apropos, wie war das noch mal gleich mit dem maximalen Strom, den man den drei Ports „Pin P0“ bis „Pin P2“ entnehmen darf? Hier können Sie nachschauen. Und zwar im Abschnitt „Power Supply“ (= Energieversorgung) bei „Onboard Peripherals budget“ (= Energiehaushalt der Peripheriegeräte auf der Platine).

Bei der Berechnung der Gesamtstromstärke der beiden parallel geschalteten Spannungsteiler gilt es zu beachten, dass die beiden Konstakte „a“ und „b“ nicht miteinander verbunden sein dürfen! Noch nicht!

>> Eine grafisch andere Anordnung zeigt deutlicher, dass jeweils zwei Widerstände einen Spannungsteiler bilden; zwei Spannungsteiler liegen zueinander parallel. Das Spannungsmessgerät stellt zwischen diesen eine Querbeziehung her, die der Schaltung den Namen Brückenschaltung gibt. Die unmittelbar gemessene Größe der Anordnung ist der Spannungsunterschied zwischen den Spannungsteilern, auch Diagonalspannung oder Brückenquerspannung genannt.

Die ursprüngliche Wheatstone-Brücke diente zur Messung von Widerstandswerten durch Anwendung des Abgleichverfahrens. Zunächst müssen die drei bekannten Widerstände solange variiert werden, bis die Diagonalspannung null beträgt. Anschließend lässt sich aus deren Widerstandswerten der vierte, unbekannte Wert errechnen. Durch die Verfügbarkeit günstiger Digitalmessgeräte (die mit anderen Verfahren arbeiten) wird diese Messmethode nur noch selten eingesetzt. Eine Ausnahme bilden hier Präzisionsmessungen.

Eine häufig ebenfalls als Wheatstone-Brücke (alternativ Ausschlag-Widerstandsmessbrücke) bezeichnete Methode ist die Abwandlung zum Ausschlagverfahren, bei dem nur kleine Abweichungen des Widerstands ermittelt werden können.

Erläuterndes Beispiel: Eine Brücke mit einem Temperatur-Messwiderstand in einem der Spannungsteiler befindet sich bei einer Referenztemperatur im abgeglichenen Zustand. Ändert sich die Temperatur am Messwiderstand, dann ändert sich die Diagonalspannung näherungsweise proportional zur Temperaturänderung. Das Ausschlagverfahren nimmt in der modernen Messtechnik einen festen Platz ein. << (Quelle: Wikipedia)

Jetzt wissen wir, wie die Wheatstone Messbrücke funktioniert. Nämlich indem an den Klemmen „a“ und „b“ der Potentialunterschied in Form eines mehr oder weniger großen oder kleinen Spannungsabfalls mit 0< ∆U_ab < 0 gemessen wird. Dabei kann der Spannungspfeil für die Polarität je nach Potentialgefälle von links („a“) nach rechts („b“) mit ∆U_ab > 0 oder von rechts („b“) nach links („a“) mit ∆U_ba = - ∆U_ab > 0 → ∆U_ab < 0. Mathematisch gilt dabei zu beachten, dass wenn man - ∆U_ab > 0 mit (-1) multipliziert sich das „>“-Zeichen nach „<“ umgekehrt!

Ob und wie, d.h. in welche Richtung das Potentialgefälle ausfällt, wissen wir noch nicht. Das hängt dann natürlich auch von den Widerstandswerten ab.

Wenn die Wheatstone Messbrücke halbwegs abgeglichen ist, dann fällt das Potentialgefälle recht klein aus, würde im Falle, wenn man die beiden Kontakstellen „a“ und „b“ miteinander verbindet, nur ein kleiner Ausgleichsstrom fließen.

Wenn die Wheatstone Messbrücke nicht abgeglichen ist - und das dürfte meistens der Fall sein - , dann fällt das Potentialgefälle recht groß aus, würde im Falle, wenn man die beiden Kontakstellen „a“ und „b“ miteinander verbindet, ein großer oder größerer Ausgleichsstrom fließen. Ob von rechts nach links oder umgekehrt kann man erst vorhersagen, wenn die Widerstandswerte bekannt sind.

Aber selbst dann wird die Berechnung des Ausgleichstroms nicht so einfach sein, weil es sich bei der Brückenschaltung, wenn die beiden Kontakte „a“ und „b“ z.B. mit einem Amperemeter verbunden sind, um eine kombinierte Schaltung handelt, die sich aus zwei belasteten Spannungsteilern wie folgt zusammen setzt:

(Bild 60, 61 – Wheatstone in zwei belastete Spannungsteiler unterteilt)

Jetzt müssen wir uns auch noch mit einem belasteten Spannungsteiler beschäftigen und diesen entsprechend berechnen, um dann später den Ausgleichsstrom zwischen den Kontakstellen „a“ und „b“ bestimmen zu können.

Linker Spannungsteiler (siehe Bild 60)

Der Gesamtstrom I_{ges L} durch den belasteten Spannungsteiler mit R_{ges L} = R₁ + ( R₂ // R₄) berechnet sich dann wie folgt:

R_{ges L} = R₁ + ( R₂ // R₄ ) = R₁ + ( 1 / R₂ + 1 / R₄ ) = R₁ + [ R₂ * R₄ / ( R₄ + R₂ ) ]

= 456 Ω + [ 106,5 Ω * 991 Ω / ( 991 Ω + 106,5 Ω ) ]

= 456 Ω + [ 105541,5 Ω² / 1097,5 Ω ] = 456 Ω + [ 96,16537585421412 Ω ]

= 456 Ω + [ 96,165 Ω ] = 552,165 Ω

Der Gesamtstrom I_{ges L} berechnet sich dann zu:

I_{ges L} = U_ges / R_{ges L} = 3,15 V / 552,165 Ω = 0,0057048164950694 A = 5,705 mA

Da es sich bei dem Spannungsteiler um einen belasteten handelt, interessiert noch der Teilungsverhältnis der beiden Widerstände R₂ / R₄ zueinander:

R₂ / R₄ = 106,5 Ω / 991 Ω = 0,1075 → R₂ << R₄

Oder umgekehrt:

R₄ / R₂ = 991 Ω / 106,5 Ω = 9,305164319248826 → R₄ >> R₂

Wie man unschwer sieht, ist der Widerstand R₄ = 991 Ω mehr als neunmal so groß als der Widerstand R₂ = 106,5 Ω, sodass der Querstrom I_R2 durch R₂ mehr als neunmal so groß als der Strom I_R4 durch R₄ ist!

Für einen belasteten Spannungsteiler ist das ein hervorragender Wert! Und zwar aus folgendem Grund: Damit sich bei einem belasteten Spannungsteiler am Ausgang, d.h. parallel zum Widerstand R₄ eine stabile Spannung einstellt, sollte der Querstrom durch R₂ mindestens dreimal so groß sein wie der Strom durch den Widerstand R₄.

Wenn der Trafo und der Gleichrichter in einem Netzteil das hergeben, sollte der Querstrom durch R₂ bis zu fünfmal so groß sein wie der Strom durch den Widerstand R₄, weil dann die Ausgangsspannung entsprechend stabiler ist.

Selbstverständlich gibt es elektronische (Stecker-) Netzteile für wenige Euro, die ganz ohne belasteten Spannungsteiler auskommen, die die Spannungsstabilisierung mit einem entsprechenden IC bewerkstelligen usw. Wenn man aber verstehen will, wie eine Wheatstone Messbrücke funktioniert, dann muss man sich auch mit dem belasteten Spannungsteiler auseinandersetzen. Wir werden nämlich gleich sehen, dass zur verbesserten Messgenauigkeit bei der Wheatstone Messbrücke der bis zu fünfmal so große Querstrom durch den Messwiderstand fließen sollte und gerade nicht durch den parallel geschalteten Widerstand!

Rechter Spannungsteiler (siehe Bild 61)

Eigentlich könnte man sich die nachfolgende Berechnung sparen, da sie mit der des linken Spannungsteilers identisch ist. Der Grund dafür ist der, dass die beiden Widerstände R₁ und R₃ gleich groß sind: R₁ = R₃. Ein weiterer Grund ist der, dass sich der linke und rechte Spannungsteiler den belasteten Zweig gemeinsam teilen.

Der Gesamtstrom I_{ges R} durch den belasteten Spannungsteiler mit R_{ges R} = R₃ + ( R₂ // R₄ ) berechnet sich dann wie folgt:

R_{ges R} = R₃ + ( R₂ // R₄ ) = R₃ + [ R₂ * R₄ / ( R₄ + R₂ ) ]

= 456 Ω + [ 106,5 Ω * 991 Ω / ( 991 Ω + 106,5 Ω ) ]

= 456 Ω + [ 105541,5 Ω² / ( 1097,5 Ω ) ]

= 456 Ω + [ 96,16537585421412 Ω ] = 456 Ω + [ 96,165 Ω ]

= 552,165 Ω

Der Gesamtstrom I_{ges R} berechnet sich dann zu:

I_{ges R} = U_ges / R_{ges R} = 3,15 V / 552,165 Ω = 0,0057048164950694 A = 5,705 mA

Da es sich bei dem Spannungsteiler um einen belasteten handelt, interessiert noch der Teilungsverhältnis der beiden Widerstände R₂ / R₄ zueinander:

R₂ / R₄ = 106,5 Ω / 991 Ω = 0,1075 → R₂ << R₄

Oder umgekehrt:

R₄ / R₂ = 991 Ω / 106,5 Ω = 9,305164319248826 → R₄ >> R₂

Wie man unschwer sieht, ist der Widerstand R₄ = 991 Ω mehr als neunmal so groß als der Widerstand R₂ = 106,5 Ω, sodass der Querstrom I_R2 durch R₂ mehr als neunmal so groß als der Strom I_R4 durch R₄ ist!

Frage 10

Jetzt stellt sich aus der Sicht der Wheatstone Messbrücke die Frage, welcher der beiden Widerstände R₂ oder R₄ als zu messender Widerstand geeigneter wäre.

Finden Sie heraus, welcher der beiden Widerstände R₂ oder R₄ als zu messender Widerstand geeignet ist, und begründen Sie Ihre Entscheidung! -

Das Aufspalten der Wheatstone Brückenschaltung in einen linken und rechten belasteten Spannungsteiler (siehe Bild 60, 61) geschah ursprünglich mit dem (Hinter-) Gedanken mittels einer sogenannten Superposition (= Überlagerung) später zu einer Formel zwecks Berechnung des zu erwartenden Brückenstroms I_ba (= Ausgleichstrom zwischen den beiden noch nicht abgeglichenen Spannungsteilern) zu gelangen.

Wegen der Gleichheit der beiden Widerstände R₁ und R₃ = 456 Ω und der Gleichheit der beiden belasteten Spannungsteiler ließ sich bisher noch keine Formel für das Berechnen der Brückenspannung U_ba oder des Brückenstroms I_ba herleiten. Aber das wird sich gleich ändern!

Berechnen wir als Erstes das Spannungspotential an der Kontaktstelle „a“ ohne Abgleich die Wheatstone Messbrücke, da wir ja das Potentialgefälle zwischen den Kontaktstellen „a“ und „b“ berechnen wollen!

Für den linken Spannungsteiler und den Spannungsabfällen an den beiden Widerständen R₁ und R₂ folgt:

U₂ / U_3V = R₂ / ( R₁ + R₂ ) = 1 / ( R₁ / R₂ + 1 )

Mit U₂ = U_a folgt:

U_a = 1 / ( R₁ / R₂ + 1 ) * U_3V

Berechnen wir als Nächstes das Spannungspotential an der Kontaktstelle „b“ ebenfalls ohne Abgleich die Wheatstone Messbrücke.

Für den rechten Spannungsteiler und den Spannungsabfällen an den beiden Widerständen R₃ und R₄ folgt:

U₄ / U_3V = R₄ / ( R₃ + R₄ ) = 1 / ( R₃ / R₄ + 1 )

Mit U₄ = U_b folgt:

U_b = 1 / ( R₃ / R₄ + 1 ) * U_3V

Da der Widerstand R₂ = 106,5 Ω deutlich kleiner als der Widerstand R₄ = 991 Ω ist, fließt bei der noch nicht abgeglichenen Wheatstone Messbrücke zwischen den Kontaktstellen „a“ und „b“ ein maßgeblicher Brückenstrom I_ba von rechts nach links, der von dem Potentialunterschied, d.h. der Spannungsdifferenz ∆U_ba getrieben wird:

∆U_ba = U_b - U_a = 1 / ( R₃ / R₄ + 1 ) * U_3V - 1 / ( R₁ / R₂ + 1 ) * U_3V

∆U_ba = [ 1 / ( R₃ / R₄ + 1 ) - 1 / ( R₁ / R₂ + 1 ) ] * U_3V → Formel!

= [ 1 / ( 456 Ω / 991 Ω + 1 ) - 1 / ( 456 Ω / 106,5 Ω + 1 ) ] * U_3V

= [ 1 / (1,46 ) - 1 / (5,28 ) ] * U_3V = [ 0,685 - 0,189 ] * U_3V

= [ 0,496 ] * U_3V = [ 0,496 ] * 3,14 V = 1,56 V (… gemessen: 1,6 V)

Dass der Widerstand R₂ = 106,5 Ω deutlich kleiner als der Widerstand R₄ = 991 Ω ist, wurde mit Absicht so veranlasst, um auf diese Weise das Potentialgefälle eindeutig festzulegen, nämlich von der Kontaktstelle „b“ zu „a“ mit U_ba > 0 (→ unabgeglichene Wheatstone Brückenschaltung).

Mit der Berechnung der Differenzspannung ∆U_ba = U_b - U_a haben wir jetzt indirekt eine Superposition durchgeführt ohne es zu merken, indem wir die unabgeglichene Wheatstone Brückenschaltung in eine linken und rechte Masche unterteilt und später wieder mit ∆U_ba = U_b - U_a mit U_b > U_a zusammen geführt haben.

>> Unter Superposition, auch Superpositionsprinzip (von lateinisch super = über; positio = Lage, Setzung, Stellung) versteht man in der Physik eine Überlagerung gleicher physikalischer Größen, wobei sich jene nicht gegenseitig behindern. Dieses Überlagerungsprinzip wird bei linearen Problemen in vielen Bereichen der Physik benutzt und unterscheidet sich nur in der Art der überlagerten Größen. Oft wird die Redeweise „mehrere Größen [miteinander] superponieren“ gebraucht.

Wichtige Anwendungsbereiche des Superpositionsprinzips sind elektromagnetische Wellen in der Optik und in der Funktechnik, Kräfte in der klassischen Mechanik und Zustände in der Quantenmechanik. << (Quelle: Wikipedia)

>> Als Netzwerkanalyse bezeichnet man in der Elektrotechnik die Vorgehensweise, in einem Netzwerk (siehe Bild) aus den bekannten Werten der Schaltelemente sowie den vorgegebenen Quellgrößen alle Ströme und Spannungen zu berechnen. Von Hand und mit analytischen Methoden können mit realistischem Aufwand nur lineare Systeme untersucht werden. Die rechnergestützte Schaltungssimulation dagegen beruht vorwiegend auf iterativen Näherungsverfahren, benötigt sehr viele Rechenschritte, kann aber auch mit nichtlinearen Bauelementen umgehen. (…)

In einem Netzwerk sind die Zusammenhänge zwischen allen auftretenden Strömen bzw. allen auftretenden Spannungen durch die nach dem deutschen Physiker Gustav Robert Kirchhoff benannten kirchhoffschen Regeln beschrieben. Der Zusammenhang zwischen Strom und Spannung ist durch das ohmsche Gesetz beschrieben, welches die Bauelementegleichung von Widerständen beschreibt. Voraussetzung sind reelle lineare Schaltelemente, d.h. kein kapazitiver oder induktiver Anteil und eine gerade Kennlinie im Gegensatz z.B. zur Diode.

Bei nicht reellen Widerständen wird die sogenannte komplexe Rechnung erforderlich. So lässt sich auch eine Analyse für Wechselspannung durchführen, wobei jede betrachtete Frequenz einzeln zu berechnen ist.

Damit eine Netzwerkanalyse möglich ist, werden in dem Netzwerk Knotenpunkte, Zweige und Maschen definiert. Mithilfe der kirchhoffschen Regeln und den Strom-Spannungs-Beziehungen der Zweipole können ihnen dann Gleichungen zugeordnet werden. Damit die mathematischen Gleichungssysteme zu einer eindeutigen Lösung führen, müssen die jeweiligen Gleichungen voneinander unabhängig sein. << (Quelle: Wikipedia)

So, nun wissen Sie in etwa was in der Elektrotechnik eine Superposition und die damit verbundene Netzwerkanalyse ist und, was Ihnen bisher an logischer und mathematischer Auseinandersetzung erspart geblieben ist!

Aber so ganz können wir uns wegen der Berechnung der

· Spannungsdifferenz ∆U_ba = U_b - U_a mit U_b > U_a

und des Brückenausgleichsstroms I_ba nicht vor der Superposition und dem Überlagerungsverfahren drücken.

>> Überlagerungsverfahren nach Helmholtz

Das Überlagerungsverfahren beruht auf dem Superpositionsprinzip bei linearen Systemen.

Vorgehen:

· Bis auf eine Quelle werden alle anderen entfernt. Spannungsquellen werden
durch Kurzschlüsse ersetzt bzw. Stromquellen als Unterbrechung gesehen.
Die Innenwiderstände der Quellen verbleiben jedoch in der Schaltung.

<< (Quelle: Wikipedia)

Da wir noch den Brückenausgleichsstrom I_ba der immer noch unabgeglichenen Wheatstone Messbrücke berechnen wollen, schauen wir an Kontaktstellen „a“ und „b“ in die Brückenschaltung hinein. Dabei müssen wir dann die Spannungsquelle U_3V des „micro:bit“-Rechners durch einen Kurzschluss ersetzen (siehe „Vorgehen“ oben):

(Bild 63 – Überlagerungsverfahren nach Helmholtz)

Wie man im obenstehenden Bild bei der rechten Überlagerungsschaltung unschwer sieht, sind die beiden Widerstände R₃ und R₄ wegen der gemeinsamen Masse (= Pin „GND“) parallel geschaltet. Gleiches gilt für die beiden Widerstände R₁ und R₂. Was man allerdings erst bei genauerem Hinsehen sieht, ist, dass die beiden parallel geschalteten Widerstände R₃ und R₄ mit den ebenfalls parallel geschalteten Widerstände R₁ und R₂ in Reihe geschaltet sind, sodass folgt:

R_ges = R_ba = ( R₃ // R₄ ) + ( R₁ // R₂ ) ← symbolisch!

R_ba = ( R₃ * R₄ / R₃ + R₄ ) + ( R₁ * R₂ / R₁ + R₂ ) → Formel!

= (456 Ω * 991 Ω / 456 Ω + 991 Ω ) + (456 Ω * 106,5 Ω / 456 Ω + 106,5 Ω )

= (451896 Ω² / 1447 Ω ) + (48564 Ω² / 562,5 Ω )

= (312,3 Ω ) + (86,3 Ω ) = 398,6 Ω

Mit der bereits weiter oben berechneten Differenzspannung ∆U_ba

∆U_ba = 1,56 V folgt:

I_ba = U_ba / R_ba → Formel!

I_ba = U_ba / R_ba = 1,56 V / 398,6 Ω = 3,914 mA (… gemessen: 3,9 mA)

Wie man sieht, ist die Berechnung des Brückenausgleichsstroms I_ba bei der bisher unabgeglichenen Wheatstone Messbrücke gar nicht so schwer! Man darf nur nicht den Fehler machen und die Klammerausdrücke mit den Widerständen vereinfachen, d.h. ausmultiplizieren zu wollen in der trügerischen Hoffnung, dass sich einzelne Terme gegenseitig aufheben! Tun sie nämlich nicht! -

Was jetzt noch fehlt ist die Abgleichbedingung für die Wheatstone Messbrücke.

Die Abgleichbedingung, die gleich noch hergeleitet wird, ist dann erfüllt, wenn die Messbrücke abgeglichen ist, sodass die Brückenspannung (= Differenzspannung) an den Kontaktstellen „a“ und „b“ null ist. Wo es keinen Potentialunterschied gibt (U_ba = - U_ab = 0 V), gibt es keine (Differenz-) Spannung, fließt auch kein Strom, sodass sich die Kontaktstellen „a“ und „b“ miteinander verbinden lassen:

(Bild 64 – Messanordnung Wheatstone Messbrücke)

Wenn der zu ermittelnde und zu berechnende Messwiderstand R_m kleiner als der Widerstand R₄ ist R_m < R₄ mit R₁ = R₃, die Messbrücke noch nicht abgeglichen ist und die Kontaktstellen „a“ und „b“ miteinander verbunden sind, dann fließt der Ausgleichs- und Brückenstrom I_ba > 0 von rechts nach links.

Dabei ist wichtig, dass wir es mit einer klar definierten Versuchsanordnung zu tun haben, sodass sich entsprechende Messungen sowie das spätere Einspeisen eines Abgleichsstroms an der Kontaktstelle „b“ jederzeit wieder reproduzieren und nachvollziehen lassen.

Wenn die im obenstehenden Bild zu sehende Wheatstone Messbrücke abgeglichen ist, dann wird der Potentialunterschied zwischen den Kontaktstellen „a“ und „b“ zu null, sodass folgt: U_ba = 0 V

∆U_ba = [ 1 / ( R₃ / R₄ + 1 ) - 1 / ( R₁ / R₂ + 1 ) ] * U_3V = 0 V →

Mit der mathematischen Regel „Ein Produkt wird zu null, wenn eine Faktor zu null wird!“ folgt:

1 / ( R₃ / R₄ + 1 ) - 1 / ( R₁ / R₂ + 1 ) = 0 →

1 / ( R₃ / R₄ + 1 ) = 1 / ( R₁ / R₂ + 1 )

( R₁ / R₂ + 1 ) / [ 1 / ( R₃ / R₄ + 1 ) ] = 1

( R₁ / R₂ + 1 ) = ( R₃ / R₄ + 1 )

R₁ / R₂ + 1 = R₃ / R₄ + 1 →

R₁ / R₂ = R₃ / R₄ → Abgleichformel der Wheatstone Messbrücke!

R₁ / R₂ = R₃ / R₄ →

R₁ / R_m = R₃ / R₄ →

R_m = R₁ / ( R₃ / R₄ ) → Berechnungsformel für den Messwiderstand R_m !

Um zu überprüfen, ob die Berechnungsformel für den Messwiderstand R_m funktioniert, setzen wir die Werte der entsprechenden Widerstände ein:

R₁ = 456 Ω, R_m = 106,5 Ω, R₃ = 456 Ω, R₄ = 991 Ω

R_m = R₁ / ( R₃ / R₄ )

= 456 Ω / ( 456 Ω / 991 Ω ) = 456 Ω / (0,46014 Ω )

= 991,00273829704 Ω = 991 Ω → (… nicht abgeglichene Brücke!)

Da wir den Messwiderstand R_m = 106,5 Ω kennen, haben wir es jetzt schwarz auf weiß, dass die obenstehende Wheatstone Messbrücke nicht abgeglichen ist! Aber das wussten wir ja bereits vorher. Und, wie man sieht, bestätigt es die Berechnung.

Als Nächstes stellt sich die Frage, welchen Widerstand der bisher noch immer nicht abgeglichenen Wheatstone Messbrücke man verändern muss, um diese abzugleichen.

Wegen der Symmetrie der Messbrücke mit R₁ = R₃ und R_m =? R₄ kommt eigentlich nur der Widerstand R₄ dafür in Frage:

(Bild 65 – Abgleichen der Wheatstone Messbrücke)

Wie man im obenstehenden Bild sieht, muss tatsächlich der Widerstand R₄ der Messbrücke verändert werden, um diese abzugleichen.

Wenn man in seiner Bastelkiste noch ein älteres, analoges Vielfachmessinstrument mit einem Drehspulmesswerk hat, dann lässt sich der eingangsseitige Spannungsteiler für die Wahl des Spannungsmessbereiches auch als Widerstandsdekade verwenden (siehe Bild oben).

Wem das mit dem eingangsseitigen Spannungsteiler zu kompliziert ist (siehe Bild oben), der kann sich auch die nachfolgende Widerstandsdekade zulegen:

(Bild 66 – Drehbare Widerstandsdekade)

Wenn man anstelle des statischen Widerstandes R₄ = 991 Ω die obenstehende, verstellbare Widerstandsdekade verwendet und im KΩ-Bereich startet, dann wird man schnell fündig, findet man für den Widerstand R₄ den Wert R₄ = 100 Ω, bei dem die Messbrücke abgeglichen ist, sodass die Brückenspannung U_ba zu null wird und sich der zu messende Messwiderstand R_m wie folgt berechnen lässt:

R_m = R₁ / ( R₃ / R₄ ) →

= 456 Ω / (456 Ω / 100 Ω ) = 100 Ω

Berechnen wir der Vollständigkeit halber noch die winzig kleine Brückenspannung beim abgeglichenen Zustand, so folgt:

∆U_ba = U_b - U_a

= 1 / ( R₃ / R₄ + 1 ) * U_3V - 1 / ( R₁ / R₂ + 1 ) * U_3V

= [ 1 / ( R₃ / R₄ + 1 ) - 1 / ( R₁ / R₂ + 1 ) ] * U_3V

= [ 1 / ( 456 Ω / 106,5 Ω + 1 ) - 1 / ( 456 Ω / 106,5 Ω ) ] * 3,14 V

= [ 0 ] * 3,14 V = 0 V

4.3.1 Widerstandsmessung mit Wheatstone

Nachdem nun die Funktionsweise der Wheatstone Messbrücke hinreichend bekannt und sich mit der eindeutig definierten Messanordnung die Messbrücke abgleichen lässt, stellt sich die Frage, welche Widerstandswerte sich mit der Schaltung messen lassen.

Da wir den Abgleich der Wheastone Messbrücke mit dem „micro:bit“-Rechner elektronisch vornehmen wollen, indem wir mittels der beiden parallel geschalteten analogen Ausgängen an den Rundanschlüssen Port „Pin P0“ und „Pin P1“ einen Strom am Mittelpunkt „b“ der Messbrücke einspeisen und sich die Ausgangsspannung der Rundanschlüsse stets nur auf die Masse am Pin „GND“ bezieht, muss die Bedingung U_b > U_a mit U_ba > 0 stets erfüllt sein.

In der Praxis kann es aber trotz der Bedingung U_b > U_a mit U_ba > 0 dazu kommen, dass diese nicht erfüllt wird, weil sich die Brückenspannung mit U_ab = -U_ba umkehrt! Dies ist stets dann der Fall, wenn der Messwiderstand mit R_m > 1 KΩ wird.

Immer dann, wenn R_m > R₄ wird, kehrt sich die Brückenspannung um, was ja gemäß des 2. Kirchhoffschen Gesetzes für den Maschenumlauf (= positiv im Uhrzeigersinn) unabdingbar ist:

(Bild 67 – Maschenumlauf bei der Messbrücke)

Wie man im obenstehenden Bild sieht, werden alle Spannungspfeile (= Vektoren, gerichtete Größen) der jeweiligen Teilspannungen in der unteren Masche bei der Wheatstone Messbrücke positiv im Uhrzeigersinn wie folgt aufaddiert:

U_ab + U₄ + ( -U_m ) = 0 →

U_m = U_ab + U₄

= 133 mV + 1,989 V = 0,133 V + 1,989 V

= 2,122 V (… gemessen: 2,14 V ) → U_m > U₄ → U_ab > 0

Für den Messstrom I_m durch den Messwiderstand R_m = 1 KΩ folgt:

I_m = U_m / R_m = 2,122 V / 1 KΩ = 2,122 mA

Für den Querstrom I₄ durch den Abgleichwiderstand R₄ = 106,5 Ω folgt:

I₄ = U₄ / R₄

= 1,989 V / 0,1065 KΩ = 18,67605633802817 mA

= 18,7 mA (… gemessen: 19,5 mA )

Mit dem Abgleichwiderstand R₄ = 106,5 Ω und dem zugehörigen Querstrom I₄ = 18,7 mA sind wir so ziemlich an der oberen Grenze bezüglich der Stromversorgung durch den „micro:bit“-Rechner angekommen. Schließlich brauchen wir für alle Fälle auch noch eine Reserve, um z.B. später die Schaltung erweitern zu können.

Apropos, wie war das noch mal gleich mit dem maximalen Strom, den man den drei Ports „Pin P0“ bis „Pin P2“ entnehmen darf? Hier können Sie nachschauen. Und zwar im Abschnitt „Power Supply“ (= Energieversorgung) bei „Onboard Peripherals budget“ (= Energiehaushalt der Peripheriegeräte auf der Platine). -

Nachdem nun die Wheatstone Messbrücke kein „unbekanntes Wesen“ mehr ist, wir diese gründlich erforscht und berechnet haben, ist es wieder an der Zeit, dass wir uns der Programmierung zu wenden. Ziel ist es nämlich, dass wir die Abgleich der Messbrücke per Programm automatisch vornehmen, sodass sich der Widerstandswert des Messwiderstandes R_m dann auch direkt in der Laufschrift des „5 x 5 LED-Matrix“-Display anzeigen lässt.

Zu diesem Zweck greifen wir das Programm „microbit_teil_04_prog_38.hex“ mit dem Quelltext „microbit_teil_04_prog_38.py“ auf und verbessern dieses dahingehend, dass wir das Ermitteln und Einstellen des Spannungsabfalls am Abgleichwiderstand R₄ = 106,5 Ω verfeinern, indem wir die Intervalle für das Einstellen der Abgleichspannung verkleinern, sodass wir es beim Programm „microbit_teil_04_prog_39.hex“ mit dem Quelltext „microbit_teil_04_prog_39.py“ mit 20 Stufen (vormals 10) zu tun haben, die sich jeweils um die Schrittweite von 55 Bitwerten (vormals 110) mit Taster A vergrößern und mit Taster B verkleinern lassen:

(Bild 68 – Verbesserter Abgleich der Brückenspannung bei der Messbrücke)

Wenn die Wheatstone Messbrücke mit U_ba = 54,4 mV ≈ 0 abgeglichen ist, interessiert und der Spannungsabfall am Abgleichwiderstand R₄ = 106,5 Ω, weil dieser dann dem Spannungsabfall am Messwiderstand R_m entspricht.

Aus diesem Grund wird mit dem Statement

· pin2.read_analog()

der analoge Wert des Spannungsabfalls am Abgleichwiderstand R₄ aufgenommen, mittels der Funktion

· mittelwert_abrunden()

auf den ganzzahligen Bitwert = 732 abgerundet und in der Laufschrift angezeigt, sodass sich dieser wie folgt in einen Spannungswert umrechnen lässt:

U_ab + U₄ + ( -U_m ) = 0 →

U₄ = U_m – U_ab

= U_3V / 1024 Bit * 732 Bit

= 3,13 V / 1024 Bit * 732 Bit

= 2,2374609375 V = 2,237 V (… gemessen: 2,20 V )

Da wir den Abgleichwiderstand R₄ = 106,5 Ω kennen, lässt sich mit diesem der Querstrom I₄ wie folgt berechnen:

I₄ = U₄ / R₄

= 2,237 V / 0,1065 KΩ = 21,00469483568075 mA

= 21,005 mA (… gemessen: 21,5 mA )

Da uns die anderen Widerstände R₁ = R₃ = 456 Ω, R₄ = 106,5 Ω der Wheatstone Messbrücke bekannt sind, lässt sich der Messwiderstand R_m wie folgt berechnen:

R_m = R₁ / ( R₃ / R₄ )

= 456 Ω / ( 456 Ω / 106,5 Ω ) = 106,5 Ω → (… abgeglichene Brücke!)

So, was soll man jetzt sagen? Richtig gerechnet, falsch gedacht? Dabei haben wir doch nur die (Quotienten-) Formel für die abgeglichene Brücke angewendet: R₁ / R₂ = R₃ / R₄ . Aber wegen der Symmetrie der beiden Widerstände R₁ und R₃ mit R₁ = R₃ bewegen wir uns rechnerisch stets auf der rechten Seite der Messbrücke. Was aber ist das Problem? Wie geht’s weiter?

Das Problem ist die fehlende Intelligenz der Wheatstone Messbrücke! Die merkt nämlich nicht, dass wir mittels der beiden parallel geschalteten analogen Ausgänge der Rundanschlüsse Port „Pin P0“ und „Pin P1“ einen Strom am Mittelpunkt „b“ der Messbrücke eingespeist haben, um die Messbrücke abzugleichen! Und, da es beim Ohmschen Gesetz und den Kirchhoffschen Gesetzen (= für Stromknoten und Maschenumläufe) keine virtuellen Widerstände gibt, führt die Stromeinleitung am Mittelpunkt „b“ beim Widerstand R₄ = 106,5 Ω eben nicht zu einem höheren Widerstandswert, sondern zu einem höheren Spannungsabfall mit ∆U₄ = R₄ * ∆I₄.

Weil aber der Widerstand R₄ = konstant ist, führt eine Spannungsänderung direkt proportional zu einer Stromerhöhung (und umgekehrt), sodass uns der Quotient ∆U₄ / ∆I₄ = R₄ auch nicht weiter hilft!

Aber wir sind der Lösung auf der Spur. Wenn also der Widerstand R₄ = konstant ist und die Stromeinleitung am Mittelpunkt „b“ der Messbrücke zu einem höheren Spannungsabfall ∆U₄ führt, dann lässt sich der Messwiderstand R_m im Falle des Brückenabgleichs als Funktion der beiden Teilspannungen U₃ und U₄ wie folgt berechnen:

R₁ / R₂ = R₃ / R₄ ↔ U₁ / U₂ = U₃ / U₄ → Abgleichformel Wheatstone Messbrücke!

R₁ / R_m = U₁ / U₂ = U₃ / U₄ mit R₁ = R₃ und R₂ = R_m → abgeglichene Messbrücke!

R_m = R₃ / ( U₃ / U₄ ) = R₃ / ( U_3V – U₄ ) / U₄

= R₃ / ( U_3V / U₄ - 1 ) → Neue Berechn.formel für den Messwiderstand R_m!

R_m = R₃ / ( U_3V / U₄ - 1 )

= 456 Ω / (3,12 V / 2,19 V -1 ) = 456 Ω / 0,4247 = 1073,7 Ω (…gemessen: 1,013 KΩ)

Für die Messgenauigkeit folgt:

100 % / 1013 Ω * 1073,7 Ω = 105,9921026653504 % ≈ 106 %

Wie man unschwer sieht, werden 6 % zuviel angezeigt!

U₄ = U_3V / 1024 Bit * Bitwert

= 3,12 V / 1024 Bit * 733 Bit

= 2,233359375 V = 2,23 V (… gemessen: 2,19 V )

Als Nächstes wechseln wir den Abgleichwiderstand R₄ von vormals R₄ = 106,5 Ω auf nun R₄ = 991 Ω, um auf diese Weise den Querstrom durch rechten Spannungsteiler R₃, R₄ zu reduzieren, und um höhere Widerstandswerte beim Messwiderstand R_m messen zu können. Außerdem bringen wir eine rote LED nebst Vorwiderstand als Betriebsanzeige in die Schaltung ein, um die Versorgungsspannung etwas zu belasten, sodass sich die Spannungsschwankungen beim Brückenabgleich der Wheatstone Messbrücke entsprechend verringern.

Frage 11

Durch den neuen Abgleichwiderstand von R₄ = 991 Ω ändert sich das Verhalten des Wheatstone Messbrücke, ändern sich Spannungen und Ströme an den Widerständen R₁ = R₃ = 456 Ω, R₄ = 991 Ω und R_m = 1013 Ω, sodass diese neu abgeglichen werden muss.

Bei der abgeglichenen Messbrücke stellen sich nachfolgende Messwerte ein:

Versorgungsspannung: U_3V = 3,15 V

Abgleichspannung am Widerstand R₄: U₄ = 2,25 V

Bitwert der Abgleichspannung an R₄: 806 Bit

Brückenspannung: U_ba = 94 mV = 0,094 V

Erklären Sie wie sich der neue Abgleichwiderstand auf die Messbrücke auswirkt, wie und weshalb sich die Spannungen an den beiden Spannungsteilern rechts und links auswirken, wenn die Messbrücke abgeglichen ist.

Berechnen Sie den Querstrom im rechten Spannungsteiler R_3, R₄ und linken Spannungsteiler R₁, R_m.

Berechnen Sie die Abgleichspannung U_b am Abgleichwiderstand R₄.

Rechnen Sie den gemessenen Bitwert von 806 Bit für die Abgleichspannung am Abgleichwiderstand R₄ um in Volt, und berechnen Sie die Messgenauigkeit in % bezogen auf die gemessene Abgleichspannung U₄ = 2,25 V (siehe oben)!

Berechnen Sie die Brückenspannung U_ba an den Kontaktstellen „a“ und „b“ für die abgeglichene Messbrücke. –

4.3.2 Wheatstone mit Widerstandsanzeige

Bisher verhielt es sich bei dem Programm „microbit_teil_04_prog_39.hex“ mit dem Quelltext „microbit_teil_04_prog_39.py“ so, dass wir den Brückenabgleich der Wheatstone Messbrücke manuell vornehmen mussten. Und zwar mit den Tastern A und B. Dabei stellte es sich heraus, dass man bei der Verwendung des größeren Abgleichwiderstandes R₄ = 991 Ω den höheren Bitwert = 806 Bit (siehe Frage 11 oben) einstellen musste, um die Messbrücke abzugleichen. Diesbezüglich stellt sich die

Frage 12

Der Messwiderstand R_m wird maßgeblich vergrößert, sodass sich vor und nach dem Brückenabgleich nachfolgende Messwerte einstellen:

Versorgungsspannung: U_3V = 3,19 V

Bitwert am Abgleichwiderstand R₄: 704 Bit vor dem Brückenabgleich!

Abgleichspannung am Widerstand R₄: U₄ = 3,05 V nach dem Brückenabgleich!

Bitwert der Abgleichspannung an R₄: 991 Bit nach dem Brückenabgleich!

Brückenspannung: U_ba = 3 mV = 0,003 V

Stellen Sie nachfolgende Berechnungen vor dem Brückenabgleich an:

1. Wandeln Sie den in der Laufschrift des „micro:bit“-Rechners angezeigten Bitwert von 704 Bit für die Abgleichspannung am Abgleichwiderstand R₄ um in Volt [V].
   
   
2. Berechnen Sie den Abgleichwiderstandes R₄ des rechten Spannungsteilers mittels der Spannungsteilerformel.

3. Berechnen Sie die Versorgungsspannung U_3V mittels der beiden Widerstände R₃ und R₄ des rechten Spannungsteilers.

Stellen Sie nachfolgende Berechnungen nach dem Brückenabgleich an:

4. Wandeln Sie den in der Laufschrift des „micro:bit“-Rechners angezeigten Bitwert von 991 Bit für die Abgleichspannung am Abgleichwiderstand R₄ um in Volt [V].

5. Berechnen Sie den Messwiderstandes R_m des linken Spannungsteilers mittels der Spannungsteilerformel.

Wie wir bezüglich der Wheatstone Messbrücke gelernt haben, sind die Teilspannungen am linken und rechten Spannungsteiler im Falle der abgeglichenen Messbrücke mit U_ba = 0 V von der Versorgungsspannung U_3V = 3,19 V unabhängig, sodass sich etwaige Spannungsschwankungen nicht auf das Messergebnis auswirken! Der Grund dafür ist der, dass es bei der abgeglichenen Messbrücke stets nur auf das konstante Teilungsverhältnis ankommt. Etwaige Spannungsänderungen der Versorgungsspannung U_3V wirken sich deshalb bei der abgeglichenen Messbrücke stets auf beide Spannungsteiler gleichermaßen aus! Da sich aber etwaige Spannungsänderungen der Versorgungsspannung U_3V bei der abgeglichenen Messbrücke stets auf beide Spannungsteiler gleichermaßen auswirken, kommt es zu keinem Messfehler, lässt sich der Messwiderstand R_m trotzdem berechnen.

Trotzdem gibt es aber das Problem, dass sich Spannungsschwankungen der Versorgungsspannung U_3V stets auf den „micro:bit“-Rechner auswirken, da dieser Spannungsschwankungen mit U_3V+/- = U_3V +/- ∆U_3V nicht ausgleicht, sondern vielmehr an die äußere Beschaltung wie z.B. die der drei Rundanschlüsse der Ports „Pin P0“ bis „Pin P2“ weiter reicht, sodass die am Mittelpunkt „b“ des rechten Spannungsteilers eingespeisten Ströme der analogen Spannungsquellen am Port „Pin P0“ und „Pin P1“ ebenfalls schwanken und einen neuen Brückenabgleich erforderlich machen!

Demzufolge muss die Messbrücke praktisch bei jeder Spannungsschwankung der Versorgungsspannung U_3V neu abgeglichen werden! Wahnsinn!

Höchste Zeit also, dass wir das bisherige Programm erweitern und den Brückenabgleich automatisch vornehmen! Und zwar auch und gerade bei jeder Spannungsänderung! -

Doch bevor wir uns an Programmieren machen, müssen wir noch die äußere Beschaltung der Wheatstone Messbrücke ändern.

Wie Sie ja wissen, kommt es beim Brückenabgleich darauf an, dass sich die beiden Spannungspotentiale an den Kontaktstellen „a“ und „b“ so lange einander angleichen, bis sie sich nicht mehr unterscheiden und die Potentialdifferenz zu null wird, sodass gilt: ‑ ∆U_ab = ∆U_ba = U_b – U_a = 0 mit U_b = U_a.

Da wir bei der Brückenschaltung den Widerstand R₂ des linken Spannungsteilers als Messwiderstand R_m verwenden, muss der Widerstand R₄ des rechten Spannungsteilers dementsprechend als veränderlicher Abgleichwiderstand eingesetzt werden, damit sich die Brücke abgleichen lässt (siehe Bild 65).

Wenn man allerdings den Widerstand R₄ des rechten Spannungsteilers als unveränderlichen, d.h. konstanten Festwiderstand einsetzt, dann muss man den Potentialunterschied zwischen den Kontaktstellen „a“ und „b“ auf andere Weise zu null machen, z.B. indem man am Mittelpunkt (= Stromknoten) des rechten Spannungsteilers entweder einen kräftigen Strom einleitet oder eine maßgebliche Spannung anlegt. Gemäß dem Ohmschen Gesetz führt dabei dann der eingeleitete Strom am Widerstand R₄ zu einem größeren Spannungsabfall mit U₄’ = U₄ + ∆U = U₄ + R₄ * ∆I.

Da wir aber beim „micro:bit“-Rechner noch über keine programmierbare Konstantstromquelle verfügen, wurden von uns die beiden programmierbaren Spannungsausgänge an den großen Rundanschlüssen Port „Pin P0“ und „Pin P1“ verwendet:

(Bild 69 – Bisherige Beschaltung der Wheatstone Messbrücke)

Dabei mussten wir die schmerzliche Erfahrung machen, dass es sich bei den beiden einstellbaren Spannungsausgängen wider Erwarten nicht um herkömmliche, regelbare Spannungsquellen handelte, sondern um mittels „PWM“ nebst Mittelwertbildung einstellbare Ausgangsspannungen. Deshalb wurde es zur korrekten Mittelwertbildung auch notwendig, einen entsprechenden Glättungskodensator in die Schaltung einzubringen (siehe weiter oben).

Damit sich ein automatischer Brückenabgleich programmieren lässt, müssen wir die bisherige Schaltung entsprechend abändern und dabei die beiden Spannungspotentiale U_a und U_b fortwährend mittels der A/D-Wandler an den Ports „Pin P0“ und „Pin P1“ abfragen und miteinander vergleichen:

(Bild 70 – Neue Beschaltung der Wheatstone Messbrücke)

Wie man im obenstehenden Bild sieht, bleiben von den drei Rundanschlüssen Port „Pin P0“ bis „Pin P2“ jetzt nur noch der Port „Pin P2“ für die Spannungsversorgung beim Brückenabgleich an der Kontaktstelle „b“ des rechten Spannungsteilers übrig.

Da es sich beim Port „Pin P2“ für die Spannungsversorgung um keine Spannungsquelle im herkömmlichen Sinne handelt, sondern vielmehr um einen programmierbaren Rechteckgenerator mit Pulsweitenmodulation (PWM), dessen Ausgangsspannung sich im Bereich von 0 … 1023 Bit programmieren lässt, empfiehlt es sich, diese mittels eines sogenannten Siebkondensators (Elko) zu glätten, damit sich später bei entsprechenden Spannungsmessungen mittels des A/D-Wandlers auch korrekte Mittelwerte messen lassen. Schließlich geht es ja darum, dass wir den Ohmschen Widerstandswert des Messwiderstandes R_m indirekt messen, indem wir diesen berechnen. Dazu muss aber die Wheatstone Messbrücke zuvor abgeglichen worden sein, sodass die Differenzspannung zu null wird: - ∆U_ab = ∆U_ba = U_b – U_a = 0 mit U_b = U_a.

Dabei lässt sich der Messwiderstand R_m mit der neuen Berechnungsformel wie folgt berechnen:

R₁ / R₂ = R₃ / R₄ → R₃ / R_m = U₃ / U₄ mit R₁ = R₃

R_m = R₃ / ( U₃ / U₄ ) = R₃ / ( U_3V – U₄ ) / U₄

= R₃ / ( U_3V / U₄ - 1 )

Während sich also die Brückenspannung U_ab mittels der am Kontaktstelle „b“ des rechten Spannungsteilers mit der eingespeisten Abgleichspannung U₄ vom Port „Pin P2“ einstellen lässt, wissen wir von der Versorgungsspannung U_3V nicht, wie groß diese ist.

Wenn man aber die neue Berechnungsformel nach U_3V umstellt, dann lässt sie sich berechnen! Allerdings muss man dazu wissen, wie groß der Messwiderstand R_m ist:

R_m / R₃ = 1 / ( U_3V / U₄ - 1 ) → R₃ / R_m = ( U_3V / U₄ - 1 ) → R₃ / R_m + 1 = ( U_3V / U₄ )

U_3V = ( R₃ / R_m + 1 ) * U₄ = ( 21,8 KΩ / 149 KΩ + 1 ) * 970 Bit ≈ 1112 Bit

Wenn man jetzt noch wüsste, welche Spannung U₄ dem Bitwert von 970 Bit entspräche, dann ließe sich die Versorgungsspannung U_3V sofort in die Maßeinheit [V] wie folgt umrechnen:

= 2,78 V / 970 Bit * 1112 Bit = 3,186969072164948 V

≈ 3,187 V (… gemessen: 3,195 V → - 0,25 %)

Bisher haben wir nur mit der gemessenen Abgleichspannung U₄ = 970 Bit des rechten Spannungsteilers gerechnet. Diesbezüglich gibt es aber auch noch die Spannungsmessung U₂ = 860 Bit am Messwiderstand R_m des linken Spannungsteilers. Dabei stellt sich die Frage welcher Spannungswert sich dem Bitwert 860 Bit zuordnen lässt.

Wie wir aus der Hardware-Beschreibung des „micro:bit“-Rechners wissen, beträgt die Auflösung des A/D-Wandlers 10 Bit [siehe „ADC resolution 10 bit (0..1023)]“, wobei der Wertebereich von 0 bis 1023 Bit reicht, sodass es insgesamt bis zu 1024 verschiedene Messwerte gibt. Dabei wird der Maximalwert von 1023 Bit der Spannung von 3,3 V zugeordnet (siehe „When powered from USB, the KL26 interface chip’s on-board regulator is used to provide 3.3V to the rest of the board.” im Abschnitt „Practicalities, USB Powering“).

Jetzt haben wir es erneut schwarz auf weiß, dass die Spannungsversorgung U_3V am Rundanschluss „Pin 3V“ max. 3,3 V beträgt und diese dem maximalen Bitwert 1023 entspricht!

Demzufolge kann die eingespeiste Abgleichspannung U₄ vom Port „Pin P2“ also nur einen Bitwert von bis max. 1023 annehmen, sodass theoretisch folgt:

U_{3V max} = ( R₃ / R_m + 1 ) * U₄ = ( 21,8 KΩ / 149 KΩ + 1 ) * 1023 Bit ≈ 1173 Bit

= 1173 Bit / 1023 Bit * 3,3 V ≈ 3,784 V rein rechnerisch!

Selbstverständlich kann die max. Versorgungsspannung U_{3V max} physikalisch und elektrotechnisch nicht größer werden als U_{3V max} = 3,3 V, da die interne Spannungsversorgung und –stabilisierung nebst Kurzschlußstromabschaltung keine größere Spannung zulässt!

Was läuft also schief, dass wir für U_3V ≈ 1112 Bit und U_{3V max} ≈ 1173 Bit so hohe Bitwerte bekommen, die es so eigentlich gar nicht geben dürfte? Nichts!

Wie bereits erläutert wurde, führt jede von außen zugeführte Spannung an der Kontaktstelle „b“ des rechten Spannungsteilers am Abgleichwiderstand R₄ gemäß dem Ohmschen Gesetz zu einem höheren Spannungsabfall nebst Querstrom. Das gilt auch für einen von außen zugeführten Strom z.B. von einer Konstantstromquelle. Auch dieser führt zu einem höheren Spannungsabfall am Abgleichwiderstand R₄, der dann wiederum in Form des höheren Bitwertes von U₄ = 970 Bit gemessen wird (siehe oben). Dabei gilt es zu beachten, dass sich mit dem A/D-Wandler stets nur Bitwerte von bis 1023 messen lassen, wobei eine Überschreitung wider Erwarten nicht angezeigt wird!

Jetzt steht also fest, dass sich der rechte Spannungsteiler mit dem Abgleichwiderstand R₄ sowie der vom Port „Pin P2“ eingespeisten Spannung U_{Pin P2} im Moment hauptsächlich nur zum Brückenabgleich eignet, da wir noch die weiteren Umgang mit den höheren Bitwerten untersuchen müssen.

Wenn die Wheatstone Messbrücke abgeglichen ist, und das ist im Moment der Fall, dann lässt sich die neue Berechnungsformel auch auf den linken Spannungsteiler mit dem Messwiderstand R_m wie folgt anwenden:

R_m = R₁ / ( U₁ / U₂ ) = R₁ / ( U_3V – U₂ ) / U₂

= R₁ / ( U_3V / U₂ - 1 )

Wenn, wie gehabt, der Messwiderstand R_m = 149 KΩ bekannt ist und R₁ = R₃ = 21,8 KΩ groß sind, dann lässt sich die neue Berechnungsformel II nach U_3V wie folgt umstellen und berechnen:

R_m / R₁ = 1 / ( U_3V / U₂ - 1 ) → R₁ / R_m = ( U_3V / U₂ - 1 ) → R₁ / R_m + 1 = ( U_3V / U₂ )

U_3V = ( R₁ / R_m + 1 ) * U₂ = ( 21,8 KΩ / 149 KΩ + 1 ) * 860 Bit

= 1,146308724832215 * 860 Bit = 985,8255033557047 Bit

= 985,8 Bit ≈ 986 Bit = 3,3 V / 1023 Bit * 986 Bit

= 3,180645161290323 V ≈ 3,18 V (… gemessen: 3,195 V → + 0,47 %)

Für die Berechnung des Spannungsabfalls U₂ am linken Spannungsteilers mit dem Messwiderstand R_m folgt entsprechend:

U₂ = 3,3 V / 1023 * 860 Bit = 2,774193548387097 V = 2,77 V

Wie wir bis jetzt gesehen haben und auch wissen, lässt sich die Versorgungsspannung U_3V sowohl mit dem rechten als auch linken Spannungsteiler berechnen. Allerdings mit dem Unterschied, dass man wegen des Einspeisens der Spannung U_{Pin P2} an der Kontaktstelle „b“ beim rechten Spannungsteiler einen höheren Bitwert (= 970 Bit) und demzufolge auch einen größeren Spannungsabfall U₄ = U_b bekommt, bekommen muss!

Wenn wir jetzt den linken Spannungsteiler mit dem Bitwert (= 860 Bit) und dem Spannungsabfall U₂ = U_a hinzuziehen und die Potentialdifferenz –U_ab = U_ba = U_b – U_a mit U_b > U_a bilden, so folgt:

U_b – U_a = 970 Bit – 860 Bit = 110 Bit = 3,3 V / 1023 Bit * 110 Bit

U_ba = 0,3548387096774194 V ≈ 0,355 V = 355 mV (… gemessen: 3 mV ≈ 0 V)

Das Interessante und Erstaunliche ist nun, dass sich gemäß der gemessenen Bitwerte eine Potentialdifferenz von 110 Bit = 355 mV ergibt, während die Messung mit dem Digitalvoltmeter eine Spannungsdifferenz von praktisch null Volt ergibt!

Frage 13

Trotz der mit dem Digitalvoltmeter zwischen den Kontaktstellen „a“ und „b“ gemessenen Brückenspannung U_ba von null Volt und der definitiv abgeglichenen Wheatstone Messbrücke gibt es eine mit dem „micro:bit“-Rechner gemessene Potentialdifferenz von 110 Bit = 355 mV.

Geben Sie eine Erklärung wie es möglich ist, dass es bei den Messungen der Brückenspannung U_ba zwei unterschiedliche Messergebnisse hinsichtlich der Spannungsdifferenz zwischen den Kontaktstellen „a“ und „b“ gibt! -

Frage 14

Berechne den Messwiderstand R_m für die abgeglichene Wheatstone Messbrücke, wenn mit dem Programm „microbit_teil_04_prog_40.hex“ und dem Quelltext „microbit_teil_04_prog_40.py nachfolgende Messwerte aufgenommen wurden:

Widerstand R₁: R₁ = 21,8 KΩ

Widerstand R₃: R₃ = 21,8 KΩ

Widerstand R₄: R₄ = 473 KΩ

Stromversorgungsspannung U_3V: U_3V = 3,21 V

Bitwert der Abgleichspannung an R₄: 15 Bit nach dem Brückenabgleich!

Bitwert am Abgleichwiderstand R₂: 7 Bit nach dem Brückenabgleich!

Differenz der Bitwerte: 8 Bit nach dem Brückenabgleich!

Bedienungsanleitung

zum Programm „microbit_teil_04_prog_40.hex“ mit dem Quelltext „microbit_teil_04_prog_40.py“

1. Starten und Ausführen des Programms

Das in den Arbeitsspeicher des „micro:bit“-Rechners geflashte Programm startet sich nach wenigen Sekunden von allein und zeigt im Display die programmierte Laufschrift „Start ...“ an.

2. Einstellen der Brückenabgleichspannung

Die Wheatstone Messbrücke lässt sich mittels der Taster A und B an den Kontaktstellen „a“ und „b“ des linken und rechten Spannungsteilers mittels der Brückenabgleichspannung –U_ab = U_ba mit U_b > U_a > 0 elektrisch/elektronisch abgleichen.

Zu diesem Zweck wird an der Kontaktstellen „b“ eine mittels der Taster A und B einstellbare Spannung des Pulsweitenmodulators (PWM) am Port „Pin P2“ eingespeist, die zu einer Spannungserhöhung am Abgleichwiderstand R₄ des rechten Spannungsteilers führt.

Beim Starten des Programms wird der Bitwert 512 mittels der Variablen „counter_start“ = 512 als Brückenabgleichspannung U_ba eingestellt. Dies entspricht in etwa der mittleren Spannung U_ba = 3,3 V / 1023 Bit * 512 Bit ≈ 1,652 V. Dabei handelt es sich um einen ungefähren Wert, weil die Versorgungsspannung U_3V entsprechend der Stromversorgung mittels des „Micro-USB 2.0“-Kabels bis zu +3,3 V betragen kann, meistens aber etwas kleiner ausfällt. Außerdem reagiert der rechte Spannungsteiler auf die eingespeiste Brückenabgleichspannung U_ba.

3. Taster A zum Verringern der Brückenabgleichspannung

Mit dem Taster A lässt sich die Brückenabgleichspannung U_ba bitweise verringern. Je länger der Taster A gedrückt wird, umso mehr verringert sich der Bitwert der Brückenabgleichspannung U_ba.

Da das Herunterzählen des Bitwertes etliche Sekunden dauern kann, lässt sich der aktuelle Bitwert durch gleichzeitiges, d.h. paralleles Drücken des Tasters B in der Laufschrift anzeigen.

Sobald man den Taster B wieder loslässt, der Taster A aber weiterhin gedrückt bleibt, wird weiter nach unten gezählt, bis man auch den Taster A loslässt!

Sobald man den Taster A losgelassen hat, werden die aktuell eingestellten Bitwerte für die Spannungen U_R4, U_R2, U_BA sowie für den Bitzähler der Variablen „counter“ in der Laufschrift angezeigt. Und zwar insgesamt zweimal hintereinander, damit man sich die angezeigten Bitwerte in Ruhe notieren kann!

4. Taster B zum Vergrößern der Brückenabgleichspannung

Mit dem Taster B lässt sich die Brückenabgleichspannung U_ba bitweise vergrößern. Je länger der Taster B gedrückt wird, umso mehr vergrößert sich der Bitwert der Brückenabgleichspannung U_ba.

Da das Heraufzählen des Bitwertes etliche Sekunden dauern kann, lässt sich der aktuelle Bitwert durch gleichzeitiges, d.h. paralleles Drücken des Tasters A in der Laufschrift anzeigen.

Sobald man den Taster A wieder loslässt, der Taster B aber weiterhin gedrückt bleibt, wird weiter nach unten gezählt, bis man auch den Taster B loslässt!

Sobald man den Taster A losgelassen hat, werden die aktuell eingestellten Bitwerte für die Spannungen U_R4, U_R2, U_BA sowie für den Bitzähler der Variablen „counter“ in der Laufschrift angezeigt. Und zwar insgesamt zweimal hintereinander, damit man sich die angezeigten Bitwerte in Ruhe notieren kann!

5. Mit dem „Reset“-Taster alles wieder auf Anfang setzen

Auf der Rückseite des „micro:bit“-Rechners befindet sich ein sogenannter „Reset“-Taster mit dem sich der Rechner neu starten lässt. Dabei wird dann auch das zuvor in den Arbeitsspeicher geflashte Programm wieder neu gestartet! -

Wie man weiter oben bei der Frage 14 sieht, lässt sich der Messwiderstand R_m mit der abgeglichenen Wheatstone Messbrücke nur messen, wenn die Versorgungsspannung U_3V = 3,21 V bekannt ist bzw. zuvor gemessen wurde. Der Grund dafür ist der, dass die Versorungsspannung U_3V des „micro:bit“-Rechners mittels des „Micro USB 2.0“-Kabels alles andere als stabil ist, demzufolge schwankt und das Messergebnis verfälscht! Zumindest dann, wenn man den max. Bitwert 1023 des A/D-Wandlers einfach so der max. Spannung U_3V = 3,3 V zuordnet! Auch und gerade dann, wenn diese eben niedriger ausfällt!

Wenn man also den Messwiderstand R_m mit der abgeglichenen Wheatstone Messbrücke messen und richtig umrechnen will, dann kommt man nicht umhin die Versorgungsspannung U_3V messen zu müssen. Wenn diese aber mit dem A/D-Wandler des „micro:bit“-Rechners messen will, dann braucht man dazu eine externe Referenz-Spannungsquelle wie z.B. eine 1,5 V „Mignon“-Rundzelle vom Typ „AA“.

Dabei kann dann die Nennspannung einer nagelneuen, unverbrauchten Batterie etwas mehr als 1,5 V betragen, während diese bei einer bereits „angebrochenen“ Batterie dann weniger als 1,5 V betragen dürfte.

Im vorliegenden Fall beträgt die Leerlaufspannung U_Leerlauf = 1,478 V, die sich einem vom A/D-Wandler des „micro:bit“-Rechners gemessenen Bitwert von 478 Bits zuordnen lässt. Demzufolge würde sich dann die Versorgungsspannung U_3V auf einen Wert von 1,478 V / 478 Bit * 1023 Bit = 3,163167364016736 V ≈ 3,163 V belaufen (gemessen: 3,21 V → --1,46 % Abweichung). Wenn man die Abweichung von -1,46 % mit in die Umrechnung mit einbeziehen will, dann müsste man der Batteriespannung U_Leerlauf = 1,478 V den Bitwert = 1023 Bit / 3,21 V * 1,478 V = 471 Bit zuweisen und vom gemessenen Bitwert = 478 Bit – 471 Bit = 7 Bit als Korrekturfaktor subtrahieren:

U_3V = 1,478 V / ( 478 Bit – 7 Bit ) * 1023 Bit = 1,478 V / 471 Bit * 1023 Bit

= 3,210178343949045 V ≈ 3,21 V

Hier geht es zu Antworten der Fragen 10 bis 14. –

Hier geht’s dann weiter zum „micro:bit“-Programmieren, Teil 5“

[ Home ] [ zurück ] [ Seitenanfang ] [ Teil 3 ] [ Teil 5 ]