[ easy electronik 200 ] [ Seitenende ] [ Versuch 72 ] [ Versuch 95 ]

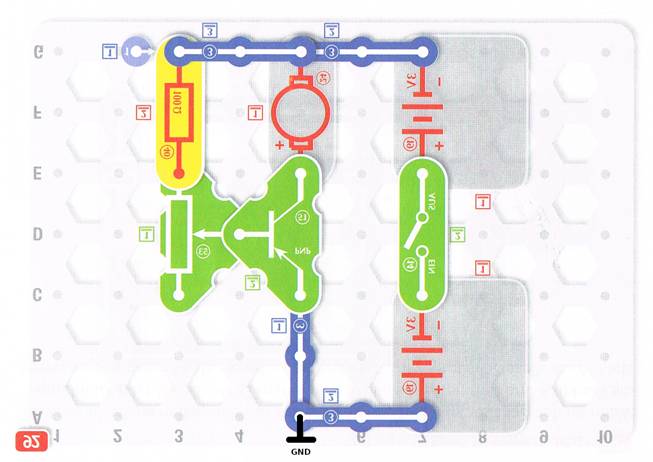
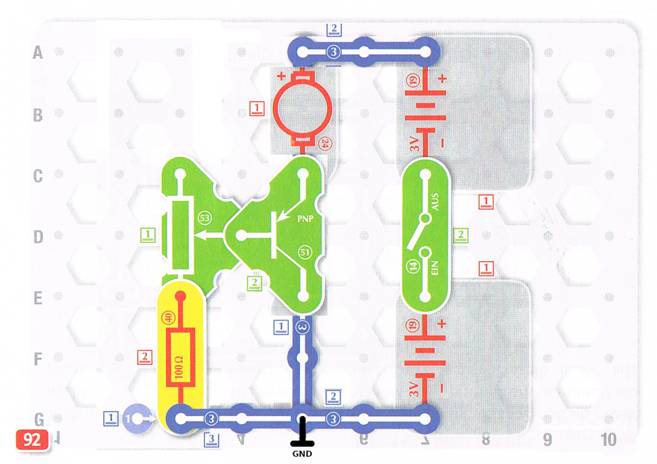
easy electronic 200 - Versuch 92

Steuerung des Motors mit einem Transistor (4)

>> Die Elektronik ist ein Hauptgebiet der Elektrotechnik. Sie ist die Wissenschaft von der Steuerung des elektrischen Stromes durch elektronische Schaltungen, das heißt Schaltungen, in denen mindestens ein Bauelement aufgrund von Vakuum- oder Halbleiter-Leitung funktioniert. Elektronische Elemente verhalten sich nichtlinear, während das Verhalten anderer elektrischer (nicht-elektronischer) Elemente als linear bezeichnet wird. Elektronik befasst sich außerdem mit der Funktion elektronischer Bauelemente selbst. Elektronikbauteile und Schaltungen in kleineren Maßstäben wird entsprechend den Strukturgrößen mit SI-Dezimalpräfixe benannt, z. B. Mikroelektronik (typisch <100 Mikrometer) oder Nanoelektronik (typisch <100 Nanometer), welche in der Regel mit dem integrierten Schaltkreis, z. B. Silizium-Chip, realisiert wird.

Elektronik verarbeitet elektrische Signale informationsmäßig oder erzeugt sie, oder verwandelt elektrische Energie hinsichtlich ihres Spannungs-Strom-Verhältnisses unter Zuhilfenahme von Verstärkern oder Gleichrichtern.

Elektronische Schaltungen werden Mithilfe der Leiterplattenbestückung zumeist auf Platinen aufgebaut und als Modul entweder zu elektronischen Geräten zusammengebaut, oder sie werden Teil elektrotechnischer Apparate. << (Quelle: Wikipedia)

Bauteileliste

Die Schaltung zum Versuch 92 setzt sich aus nachfolgenden Bauteilen zusammen (im Uhrzeigersinn von links nach rechts und von außen nach innen):

Außenschaltkreis

1. Leitleiste [2] mit 2 Steckkontakten,

2. Leitleiste [6] mit 6 Steckkontakten,

3. (Schiebe-) Schalter [14],

4. Batteriefach [19] mit 2 x 1,5 V Batterien vom Typ „Mignon AA“,

5. Leitleiste [3] mit 3 Steckkontakten,

6. Batteriefach [19] mit 2 x 1,5 V Batterien vom Typ „Mignon AA“,

7. Leitleiste [3] mit 3 Steckkontakten,

8. Leitleiste [7] mit 7 Steckkontakten,

9. Leitleiste [3] mit 3 Steckkontakten,

10. Potentiometer [53], 50 kΩ, auch als verstellbarer Widerstand „Trimmpoti“ einsetzbar,

11. Widerstand [40] mit 100 Ω,

Innenschaltkreis 1

12. Leitleiste [2] mit 2 Steckkontakten,

13. Leitleiste [2] mit 2 Steckkontakten,

14. Leitleiste [2] mit 2 Steckkontakten,

15. Glühlämpchen [18] mit 2,5 V, 0,3 A,

16. Leitleiste [2] mit 2 Steckkontakten,

17. Magnetschalter [12] mit (Rund-) Magnet,

18. Glühlämpchen [27] mit 6 V, 0,5 A,

Innenschaltkreis 2

19. Leitleiste [2] mit 2 Steckkontakten,

20. NPN-Transistor [52], rot,

21. Leitleiste [2] mit 2 Steckkontakten,

22. PNP-Transistor [51], grün,

23. Leuchtdiode rot [17]

24. Leitleiste [2] mit 2 Steckkontakten,

25. Leitleiste [2] mit 2 Steckkontakten,

Innenschaltkreis 3

26. Leitleiste [3] mit 3 Steckkontakten.

Bauteileliste nach Anzahl der Bauelemente

· 9 Stück Leitleiste [2] mit 2 Steckkontakten,

· 4 Stück Leitleiste [3] mit 3 Steckkontakten,

· 1 Stück Leitleiste [6] mit 6 Steckkontakten,

· 1 Stück Leitleiste [7] mit 6 Steckkontakten,

· 1 Stück (Schiebe-) Schalter [14],

· 2 Stück Batteriefach [19] mit 2 x 1,5 V Batterien vom Typ „Mignon AA“,

· 1 Stück Potentiometer [53], 50 kΩ, auch als verstellbarer Widerstand „Trimmpoti“ einsetzbar,

· 1 Stück Widerstand [40] mit 100 Ω,

· 1 Stück Glühlämpchen [18] mit 2,5 V, 0,3 A,

· 1 Stück Magnetschalter [12] mit (Rund-) Magnet,

· 1 Stück Glühlämpchen [27] mit 6 V, 0,5 A,

· 1 Stück NPN-Transistor [52], rot,

· 1 Stück PNP-Transistor [51], grün,

· 1 Stück Leuchtdiode rot [17].

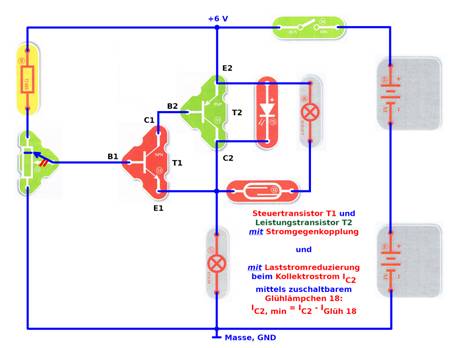
Wir haben jetzt schon eine ganze Menge über Elektronik gelernt, kennen das Wechselspiel und die Zusammenarbeit von Steuertransistor T1 und Leistungstransistor T2, wissen wie die Stromgegenkopplung funktioniert, wissen, dass man mit dem Potentiometer 53 als Basis-Spannungsteiler den Arbeitspunkt (AP) einstellt, und dass man durch paralleles Zuschalten des Strom-Entlastungszweiges mit dem Glühlämpchen 18 den Leistungstransistor T2 entlasten kann, sodass dieser keine roten Bäckchen mehr bekommt und überhitzt:

(… mit Stromentlastung! | Zum Vergrößern bitte auf das Bild klicken! | … mit Stromentlastung!)

Wenn wir als nächstes das Glühlämpchen 27 mit den Nennbetriebsdaten U_{Glüh 27} = 6,0 V, I_{Glüh 27} = 0,5 A und der Leistung P_{Glüh 27} = U_{Glüh 27} * I_{Glüh 27} = 6,0 V * 0,5 A = 3 W als Lastwiderstand R_Last gegen den Elektromotor 24 austauschen wollen, dann stellt sich sofort die Frage nach den Nennbetriebsdaten. Schließlich könnte es ja sein, dass der Elektromotor 24 einen höheren Energieverbrauch als das Glühlämpchen 27 hat und demzufolge den Leistungstransistor T2 wegen zu großer Stromstärke überhitzen und dann zerstören würde.

Schließlich heißt es in der Versuchsbeschreibung „Stelle den Schalter auf „Ein" und du kannst mit dem Potentiometer die Geschwindigkeit des Elektromotors verändern. Lass aber den Motor nicht zu lange laufen, da der Transistor durch den hohen Strombedarf des Motors heiß wird und kaputt gehen kann. (…) Aber der Motor benötigt im Vergleich zu dem Glühlämpchen einen viel stärkeren Strom. Dieser hohe Strom fließt durch den Transistor und erwärmt ihn dabei stark.“ (Quelle: Anleitung zum Experimentierkasten „KOSMOS easy electronic 200“, Seite 37)

Es geht also um Energie, d.h. konkret um Wärmeenergie die als Verlustwärme bzw. Verlustleitung den Leistungstransistor T2 mit der Zeit stark erwärmt. Energie bezeichnet man auch als Arbeit, engl. „work“. Deshalb heißt der Formelbuchstabe für Arbeit bzw. Energie „W“. Je länger also eine Maschine, ein Elektromotor läuft, umso mehr Energie „verbraucht“ er. Dabei wird aber nicht wirklich Energie verbraucht, sondern stets in eine andere Energieform umgewandelt!

Weil eben Arbeit bzw. Energie „W“ u.a. auch von der Zeit t abhängt, ist die Energie W eine Funktion der Zeit t: W = f (t).

Neben der Arbeit bzw. Energie „W“ spielt aber auch die Leistung, engl. „power“, eine Rolle, sodass folgt: W = f (P, t). Früher wurde die Leistung in Pferdestärken gemessen. Mit der Maßeinheit [ PS ], eben für Pferdestärken. So leisten 2 PS (= zwei Pferde mit 2 PS) mehr als ein Pferd mit nur 1 PS. Demzufolge lässt sich die zu vollbringende Arbeit in der Hälfte der Zeit erbringen, wenn man 2 PS statt 1 PS zur Verfügung hat.

Und, wie ist das mit den Frühstückseiern am Sonntagmorgen? Brauchen da zwei Eier doppelt so viel Wärmeenergie zum Kochen und weich werden? Ja! Und zwar beim elektrischen Eierkocher doppelt so viel elektrische Energie W_el, die dann von der Heizschlange in Wärmeenergie W_Wärme umgewandelt wird!

Aber, wenn ein Frühstücksei etwa sieben Minuten Zeit zum gar werden braucht, brauchen dann zwei Frühstückseier doppelt so lange? NEIN! Sie brauchen auch nur sieben Minuten Zeit für das Garen (= Umwandlung vom flüssigen in den gekochten Zustand), weil der elektrische Eierkocher automatisch mehr elektrische Energie W_elek über das Anschlusskabel zur Verfügung gestellt bekommt und mit der Heizschlange in Wärmeenergie W_Wärme umwandelt!

Elektrische Energie W_el ist also eine Funktion der elektrischen Leistung P_el und der Zeit t: W = f (P, t). Und die elektrische Leistung P_el ist eine Funktion der elektrischen Spannung U und des elektrischen Stroms I bzw. der elektrischen Stromstärke I: P = f ( U, I ), sodass insgesamt folgt: W = f (P, t) = f (U, I, t).

Aber es geht noch weiter! Schließlich gilt es im Anschlusskabel vom elektrischen Eierkocher noch den elektrischen (Leitungs-) Widerstand R zu überwinden, der bei einem elektrisch ungeeignetem Anschlusskabel nicht die zu kochenden Eier erhitzt, sondern das Anschlusskabel selbst, sodass sich dieses wegen der Wärmeverlustleistung P_Wärme stark erwärmt, anfängt zu schmoren, Feuer fängt und einen Zimmerbrand auslöst!

Mathematisch sieht der Zimmerbrand dann so aus: W = f (P, t) = f (U, I, t) und mit R = f(U, I) = U / I für den elektrischen Widerstand R folgt dann: W = f (P, t) = f (U, I, t) = f (U², R, t) = (I², R, t)

P = U * I = U * U / R = U² / R → P = f(U, I) = f(U², R) → sieht etwas kompliziert aus, ist es aber nicht, nur ungewohnt!

P = U * I = I * R * I = I² * R → P = f(U, I) = f(I², R) → sieht etwas kompliziert aus, ist es aber nicht, nur ungewohnt!

P = f(U, I)

→ ausgesprochen: „P ist eine Funktion von U und I“

→ bedeutet nichts anderes, als dass die Leistung P_el von der Spannung U und dem Strom I abhängt!

→ formelmäßig: P_el = U * I = U² / R = I² * R

Und für die elektrische Energie W_el mit der Maßeinheit [ Ws ], d.h. Wattsekunde, folgt dann:

W_el = P_el * t

= U * I * t

= U² / R * t = I² * R * t

Und für den elektrischen Widerstand R mit der Maßeinheit [ V/A ] = [ Ω ], d.h. Ohm, folgt dann

mit dem Ohmschen Gesetz:

R = U / I

r = ( U₂ – U₁ ) / ( I₂ – I₁ ) = ∆U / ∆I → Spannungsänderung geteilt durch Stromänderung

U = R * I → ∆U = r * ∆I

…. wie man sieht, bleibt der Widerstand r stets unverändert, d.h. konstant!

I = U / R → ∆I = ∆U / r

Wegen der Differenz (= Unterschied) von U₂ – U₁ = ∆U mit U₂ > U₁ und I₂ – I₁ = ∆I mit I₂ > I₁ nennt man den Widerstand r sozusagen unterschiedlicher Widerstand r oder auch dynamischer Widerstand r und mathematisch heißt der Widerstand r dann differentieller Widerstand r. Und weil es sich beim differentiellen Widerstand bereits Höhere Mathematik handelt, wollen wir es dabei bewenden lassen.

Aber weshalb befassen wir uns jetzt mit dem speziellen, unterschiedlichen, d.h. differentiellen Widerstand r? Weil wir die Nenn-Betriebsdaten des kleinen Elektromotor 24 nicht kennen und weil wir noch nicht wissen, ob die Motorstromstärke I_{Motor, max} unter Belastung nicht doch bis zu I_{Motor, max} < 1 A groß werden und dabei unseren Leistungstransistor T2 zerstören kann (siehe obenstehendes Bild)!

Doch zunächst müssen wir herausfinden, ob sich die Methode mit der Differenzbildung von Spannung ∆U = U₂ – U₁ und/oder Strom ∆I = I₂ – I₁ überhaupt eignet.

Zu diesem Zweck nehmen wir das Glühlämpchen 27. Und zwar deshalb, weil wir die Nennbetriebsdaten U_{Glüh 27} = 6,0 V mit I_{Glüh 27} = 0,5 A und der Leistung P_{Glüh 27} = U_{Glüh 27} * I_{Glüh 27} = 6,0 V * 0,5 A = 3 W bereits kennen! Und weil das Glühlämpchen 27 auch noch bei einer Spannung von U_{Glüh 27} < 3 V leuchtet.

Des Weiteren, weil wir uns durch das helle Leuchten des Glühlämpchen 18 eine Spannung von U_{Glüh 18} = 2,5 V bequem anzeigen lassen können und weil wir mit den beiden Batteriefächern 19 sowohl Betriebsspannungen von ca. 2,2 V bis 3,0 V mit nur einem Batteriefach 19 als auch Betriebsspannungen von ca. 4,4 V bis 6,0 V mit zwei Batteriefächern 19, je nachdem wie voll die Batterien noch sind, anwenden können. Bei den Betriebsspannungen ist nämlich nicht so sehr die Spannung an sich maßgeblich, sondern das Verhältnis in dem diese zueinander stehen:

U_{Batt 2} =5,14 V → 2 Batteriefächer 19

U_{Batt 1} =2,65 V → 1 Batteriefach 19

U_{Batt 2} / U_{Batt 1} = 5,14 V / 2,65 V = 1,9396 ≈ 1,94fache ≈ 2fache, d.h. das Doppelte!

Das Verhältnis der beiden Spannungen zueinander nennt man übrigens Quotient (= Teilungsverhältnis).

Mit U_{Batt 2} > U_{Batt 1} interessiert uns auch die Differenz (= Unterschied):

∆U = U₂ – U₁ = U_{Batt 2} - U_{Batt 1} = 5,14 V – 2,65 V = 2,49 V

P = U * I = U * U / R →

∆P = ∆U * ∆U / R

= ∆U² / R_{Glüh 27}

= ( 2,49 V )² / 12 Ω = 6,2001 V² / 12 V/A = 0,5167 VA = 0,5167 W = 516,7 mW

∆P = ∆U * ∆I →

∆I = ∆P / ∆U = 0,5167 W / 2,49 V = 0,5167 V/A / 2,49 V = 0,2075 A = 207,5 mA

Wenn man also das Glühlämpchen 27 mit nur einem Batteriefach 19, d.h. ungefähr der hälftigen Batteriespannung betreibt, dann führt die Spannungsdifferenz von ∆U = 2,49 V dazu, dass sich auch die Stromstärke entsprechend um ∆I = 207,5 mA verringert! Vorausgesetzt natürlich, dass sich der Widerstand R_{Glüh 27} des Glühlämpchens 27 nicht ändert, also konstant bleibt!

Wenn wir jetzt zweckoptimistisch annehmen, dass der Elektromotor 24 quasi über die doppelte Leistung verfügt, dann ergibt sich bei der Verwendung nur eines Batteriefaches 19 gegenüber der Verwendung von zwei Batteriefächern 19 auch die doppelt so große Leistungsänderung ∆P_neu = 2 * ∆P = 2 * 516,7 mW = 1 033,4 mW = 1,033 W

∆P_neu = ∆U² / R_{Motor 24} →

R_{Motor 24} = ∆U² / ∆P_neu

= ( 2,49 V )² / 1 033,4 mW = 6,2001 V² / 1 033,4 mVA = 6,2001 / 1 033,4 kΩ = 0,0059997 kΩ = 5,9997 Ω ≈ 6,0 Ω

∆I_neu = ∆P_neu / ∆U = 1,033 W / 2,49 V = 1,033 V/A / 2,49 V ≈ 0,4149 A = 414,9 mA

I_neu = U_{Batt 1} / R_{Motor 24}

= 2,49 V / 6,0 Ω = 0,415 A = 415 mA

I_{neu, ges} = I_neu + ∆I_neu

= 0,415 A + 0,4149 A = 0,83 A = 830 mA → bezogen auf U_{Batt 1} = 5,14 V

Unter Verwendung von zwei Batteriefächern 19 folgt gemäß dem Ohmschen Gesetz:

I_neu = U_{Batt 2} / R_{Motor 24}

= 5,14 V / 6,0 Ω = 0,8567 A = 856.7 mA

Wie man der nachfolgenden Beschreibung des kleinen Elektromotors 24 entnehmen kann, verfügt dieser in seinem Inneren über eine (oder mehrere) Magnetspulen sowie einen (oder mehrere) Magnete:

(Vergrößern: auf Bild klicken! | KOSMOS easy electronic, Seite 9)

Dass der kleine Elektromotor 24 in seinem Inneren außerdem noch über ein integriertes Getriebe verfügt, merkt man im Leerlauf des Motors, wenn dieser ohne mechanische Last, d.h. ohne Luftschraube läuft. Wegen des internen Getriebes läuft der Motor nämlich rauer und geräuschvoller (siehe nachfolgende Beschreibung).

Setzt man hingegen die Luftschraube auf die Motorachse, dann läuft der Motor unter der mechanische Last der Luftschraube wesentlich ruhiger und geräuschärmer!

(Zum Vergrößern bitte auf das Bild klicken!)

Den kleinen Elektromotor 24 kann man sich übrigens bei Amazon kaufen. Leider gibt es zu dem Motor kein Datenblatt aus dem sich die Motorleistung oder der Nennstrom I_{Motor, Nenn} bei einer Nennspannung von U_{Motor, Nenn} = 6,0 V entnehmen ließe.

Stattdessen lässt sich aber der elektrische Widerstand R_{Motor 24} der im Motor verbaute/n Spule/n mittels eines sogenannten Ohmmeters, das z.B. in einem Multimeter verbaut ist, mit R_{Motor 24} = 6,6 Ω messen!

Jetzt bestätigt sich die vorherige Annahme, dass der Motor über einen (Innen-) Widerstand von geschätzt R_{Motor 24} = 6 Ω verfügt und nehmen dies zum Anlass, die vorherige Berechnung wie folgt zu korrigieren:

Unter Verwendung von zwei Batteriefächern 19 folgt gemäß dem Ohmschen Gesetz:

I_neu = U_{Batt 2} / R_{Motor 24}

= 5,14 V / 6,6 Ω = 0,77878 A ≈ 0,779 A = 779 mA

In der Praxis ließ sich der zuletzt berechnete Motorstrom von I_neu = 779 mA nicht bestätigen.

Wenn man den Elektromotor 24 direkt an einer leistungsfähigen Powerbank anschließt und die Stromaufnahme misst, wenn man den Motor von Hand bis fast auf den Stillstand herunterbremst, dann stellt sich wegen der starken Belastung ein Laststrom von I_Last ≈ 0,5 A und einer Spannung von U_Last ≈ 4 V ein, sodass sich der Innenwiderstand des Motors wie folgt berechnet:

R_Last = U_Last / I_Last

= 4 V / 0,5 A = 8 Ω

Bezogen auf die Batteriespannung von U_{Batt 2} = 5,14 V und dem neuerlich berechneten (Innen-) Widerstand von R_{Motor 24} = R_Last = 8 Ω folgt dann für den maximalen Laststrom des Motors:

I_{Last, max} = U_{Batt 2} / R_{Motor 24}

= 5,14 V / 8 Ω = 0,6425 A = 642,5 mA

Für die Antriebsleistung P_{Last, max} des Elektromotors 24 unter maximaler Last folgt dann:

P_{Last, max} = U_{Batt 2} * I_{Last, max}

= 5,14 V * 642,5 mA = 3 302,45 mW ≈ 3,30 W → zum Vergleich mit dem Glühlämpchen 27: P_{Glüh 27} = 3,0 W

Fazit

Da es von dem Elektromotor 24 kein Datenblatt mit den Leistungsdaten gibt, wussten wir anfangs nicht welche Leistung der Motor bei welcher Drehzahl oder Spannung hat. Auch wussten wir anfangs nicht wie groß die Stromstärke des Motors bei welcher Spannung ist: I_Motor = f (U_Motor).

Mittels der Schätzung der Motorleistung P_{Motor 24} im Vergleich zum Glühlämpchen 27 war es dann möglich, den (Innen-) Widerstand R_{Motor 24} = 8 Ω des Elektromotors 24 mittels der Formel

P_{M 24} = ( U_{M 24} )² / R_{M 24} bzw. P_{M 24} = ( U_{M 24 min} + ∆U_{M 24} )² / R_{M 24}

zu berechnen!

Jetzt dürfte also endgültig klar sein, dass man in der obenstehenden Schaltung (siehe Bild) sehr wohl das Glüh-lämpchen 27 gegen den Elektromotors 24 austauschen darf:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden Bild sieht, lässt sich parallel zum Elektromotors 24 auch noch das Glühlämpchen 27 mittels Magnetschalter 12 hinzuschalten! Und da das Glühlämpchen 27 hell leuchtet, scheinen beide Verbraucher vom Leistungstransistor T2 ausreichend mit elektrischer Energie (= Spannung und Strom) versorgt zu werden. Möglich wird das aber nur deshalb, weil sich der Leistungstransistor T2 in der Sättigung mit U_{EC sat} < 1 V befindet und in diesem Modus nicht so viel Wärmeverlustleistung entsteht!

Damit der Leistungstransistor T2 nicht überhitzt und durchbrennt, sollte sich der Schieberegler des Potentiometers 53 entweder ganz oben am oberen Ende (= Elektromotor 24 läuft) oder ganz unten am unteren Ende (= Elektromotor 24 steht still) befinden!

Wenn man den Schieberegler in den mittleren Bereich des Potentiometers 53 bewegt, dann befindet sich der Leistungstransistor T2 nicht mehr gesättigten Bereich, sodass eine wesentlich größere Wärmeverlustleistung entsteht und sich der Leistungstransistor T2 stark erhitzt! Deshalb sollte der Elektromotor 24 in dieser Situation nur max. 20 Sekunden lang betrieben werden, damit der Leistungstransistor T2 nicht überhitzt und durchbrennt!

Da wir sowohl vom Glühlämpchen 27 als auch vom Elektromotor 24 die Widerstände R_{Glüh 27} = 12 Ω und R_{M 24} = 8 Ω kennen und wissen, dass beide Verbraucher parallel geschaltet sind, lässt sich die Stromteilerformel wie folgt anwenden:

I_{M 24, Nenn} / I_{Glüh 27} = R_{Glüh 27} / R_{M 24} →

I_{M 24, Nenn} = ( R_{Glüh 27} / R_{M 24} ) * I_{Glüh 27, Nenn}

= ( 12 Ω / 8 Ω ) * 0,5 A = 1,5 * 0,5 A = 0,75 A = 750 mA → Nennbetriebsstrom wegen I_{Glüh 27, Nenn} = 0,5 A

Für den Gesamtwiderstand der beiden parallel geschalteten (Last-) Widerstände folgt dann:

R_{Last, ges} = ( R_{Glüh 27} * R_{M 24} ) / ( R_{Glüh 27} + R_{M 24} )

= ( 12 Ω * 8 Ω ) / ( 12 Ω + 8 Ω ) = ( 96 Ω² ) / ( 20 Ω ) = 4,8 Ω

Demzufolge berechnet sich die Gesamtstromstärke I_ges bei einer Spannung U_{Last, ges} = 5,14 V (siehe oben) wie folgt:

I_{Last, ges} = U_Last / R_{Last, ges}

= 5,14 V / 4,8 Ω = 5,14 V / 4,8 V/A = 1,07 A → FALSCH, …

… weil u.a. der Spannungsabfall U_EC des Leistungstransistors T2 zwischen der Emitter-Kollektor-Strecke bisher unberücksichtig blieb!

Aber das lässt sich ja nachholen:

U_Last = U_{Batt, ges} – U_EC

= 4,54 V - 0,84 V = 3,7 V → mit einem Multimeter gemessene Werte!

Anhand der gemessenen Werte erkennt man, dass

· die Versorgungsspannung

mit nur noch U_{Batt, ges} = 4,54 V - gegenüber vormals 5,14 V - deutlich niedriger ausfällt (= - 11,67 %).

Dies deutet darauf hin, dass die Versorgungsspannung wegen einer sehr hohen Entnahmestromstärke
„in die Knie geht!“, da die Innenwiderstände der Batterien der beiden in Reihe geschalteten Batteriefächer 19 mit zunehmender Entladung größer werden und demzufolge die verbleibende Klemmenspannung entsprechend abnimmt.

· der Leistungstransistor T2

nicht mehr in der absoluten Sättigung, d.h. im Bereich [ 0,2 V, …, 0,4 V ], befindet. Wie bereits in früheren Versuchen erörtert wurde, erfordert eine sehr hohe Entnahmestromstärke auch eine entsprechend höhere Spannung, sozusagen als Voraussetzung einer „treibenden Kraft“.

Lässt sich die entsprechend höhere treibende Spannung wider Erwarten nicht bereitstellen, dann gibt es auch keine wesentlich höhere Entnahmestromstärke!

Da aber der Leistungstransistor T2 und die Gesamtlast, bestehend aus der Parallelschaltung von Elektromotor 24 und Glühlämpchen 27, einen Spannungsteiler bilden, gilt auch die Spannungsteilerformel, die es im vorliegenden Fall anzuwenden gilt.

Wegen der Parallelschaltung von Elektromotor 24 und Glühlämpchen 27 und dem Spannungsteiler mit dem Leistungstransistor T2 gibt es ab sofort nur noch einen belasteten Spannungsteiler, den es zu berechnen gilt.

U_EC / U_Last = r_EC / R_{Last, ges} →

r_EC = ( U_EC / U_Last ) * R_{Last, ges}

= ( 0,84 V / 3,7 V ) * 4,8 Ω = ( 0,22703 ) * 4,8 Ω = 1,089744 Ω ≈ 1,1 Ω

R_total = r_EC + R_{Last, ges} = 1,1 Ω + 4,8 Ω = 5,9 Ω

I_total = I_EC = I_{Last, ges}

= U_{Batt, ges} / R_total

= 4,54 V / 5,9 Ω = 4,54 V / 5,9 V/A = 0,76949 A ≈ 769,5 mA → FALSCH, …

… weil es sich bei dem (Innen-) Widerstand R_{Motor 24} des Elektromotors 24 um einen dynamischen Widerstand handelt, der sich eben nicht gleichförmig, d.h. linear, verhält und sich demzufolge nicht durchgängig mit dem Ohmschen Gesetz berechnen lässt. Dazu muss man wissen, dass das Ohmsche Gesetz nur für lineare, d.h. konstante Widerstände gilt!

Wenn wir die Motorkennlinie I_M24 = f(U_M24) hätten, dann könnte man sich den einen oder anderen Messwert aus der Motorkennlinie herauspicken und darauf das Ohmsche Gesetz nebst der weiteren Gesetzmäßigkeiten punktuell anwenden. Aber sobald sich irgendein Parameter ändert, z.B. weil die Klemmenspannung der ziemlich entladenen Batterie mit dem größer werdenden Innenwiderstand zunehmend verringert, stimmt die ganze Berechnung nicht mehr!

Erschwerend kommt noch hinzu, dass es sich bei der obenstehenden Schaltung mit den beiden Transistoren um eine Darlingtonschaltung, d.h. Emitterschaltung mit Stromgegenkopplung handelt, die wir bisher in Verbindung mit der nachgeschalteten Last (= Reihenschaltung von Leistungstransistor T2 und Lastwiderstand in Form der Parallelschaltung von Elektromotor 24 und Glühlämpchen 27 ) noch nicht als Ganzes berechnet haben, was auch nicht so einfach sein dürfte!

Weiterhin kommt hinzu, dass sich der Motorwiderstand R_{M 24} im Leerlaufbetrieb (= ohne Last) des Elektromotors 24 nicht allgemeingültig bestimmen und berechnen lässt, da es sich bei diesem um einen nichtlinearen Widerstand handelt und uns die Nennbetriebsdaten inkl. Motorkennlinie I_M24 = f(U_M24) nicht bekannt sind.

Wenn man aber trotzdem den Motorwiderstand R_{M 24} des Elektromotors 24 berechnen will, dann nur punktuell und unter Last! Zu diesem Zweck muss dann die rote Luftschraube (= Kreispropeller) auf die Motorachse gesetzt werden, sodass der Motor bei entsprechender „+“-Polung einen deutlich wahrnehmbaren Luftstrom nach unten (nicht nach oben) produziert!

Der von der roten Luftschraube (= Kreispropeller) produzierte Luftstrom stellt dann für den Motor eine mechanische Antriebslast dar, die wiederum in Form der zugeführten elektrischen Energie aufgebracht werden muss, sodass der Motorstrom I_{M 24} entsprechend ansteigt!

Mit dem Multimeter aufgenommene Messwerte der Versuchsschaltung unter Last, d.h. mit der aufgesetzten roten Luftschraube (= Kreispropeller):

U_{Batt, ges} = 4,32 V

U_Last = 3,41 V

I_{Last, ges} = 410 mA

R_{Last, ges} = U_Last / I_{Last, ges}

= 3,41 V / 410 mA = 0,00832 kΩ = 8,32 Ω

= 1 / ( 1 / R_{M 24} + 1 / R_{Glüh 27} )

1 / R_{Last, ges} = 1 / R_{M 24} + 1 / R_{Glüh 27} → Formel zu Berechnung parallel geschalteter Widerstände!

1 / R_{M 24} = 1 / R_{Last, ges} - 1 / R_{Glüh 27}

R_{M 24} = 1 / ( 1 / R_{Last, ges} - 1 / R_{Glüh 27} )

= 1 / ( 1 / 8,32 Ω - 1 / 12 Ω ) = 1 / ( 0,1202 - 0,0833 ) Ω = 1 / ( 0,0369 ) Ω

= 27,10 Ω → Dieser Motorwiderstand R_{M 24} des Elektromotors 24 dürfte realistisch sein!

I_{M 24} = U_Last / R_{M 24}

= 3,41 V / 27,10 Ω = 3,41 V / 27,10 V/A = 0,12583 A ≈ 125,8 mA

P_{M 24} = U_Last * I_{M 24}

= 3,41 V * 125,8 mA ≈ 430 mW

I_{Glüh 27} = U_Last / R_{Glüh 27}

= 3,41 V / 12 Ω = 3,41 V / 12 V/A = 0,284167 A ≈ 284,2 mA

P_{Glüh 27} = U_Last * I_{Glüh 27}

= 3,41 V * 284,2 mA ≈ 970 mW

Nennbetriebswerte des Glühlämpchens 27 zum Vergleich: U_{Glüh 27} = 6,0 V, I_{Glüh 27} = 500 mA → R_{Glüh 27} = 12 Ω

Berechung des Spannungsabfalls an der EC-Strecke des Leistungstransistor T2 unter Last:

U_{EC, Last} = U_{Batt, ges} - U_Last

= 4,32 V – 3,41 V = 0,91 V < 1 V → Übersteuerung, noch keine Sättigung → Wärmeverlustleistung!

P_{EC, Last} = U_{EC, Last} * I_{Last, ges}

= 0,91 V * 410 mA = 373,1 mW

Wir wenden die Stromteilerformel ein weiteres Mal an, diesmal aber mit den neuen Werten, um zu überprüfen, ob sich das Verfahren bzw. die Vorgehensweise tatsächlich eignet, um den Motorstrom I_{M 24, neu} zu berechnen.

Da wir sowohl vom Glühlämpchen 27 als auch vom Elektromotor 24 die Widerstände R_{Glüh 27} = 12 Ω und R_{M 24} = 27,10 Ω kennen und wissen, dass beide Verbraucher parallel geschaltet sind, lässt sich die Stromteilerformel wie folgt anwenden:

I_{M 24, neu} / I_{Glüh 27} = R_{Glüh 27} / R_{M 24} →

I_{M 24, neu} = ( R_{Glüh 27} / R_{M 24} ) * I_{Glüh 27}

= ( 12 Ω / 27,1 Ω ) * 0,2842 A = 0,4428 * 0,2842 A = 0,1258 A = 125,8 mA → ist richtig! Siehe weiter oben!

Wie man anhand der Stromteilerformel sieht, benötigt man den Motorwiderstand R_{M 24}, um den Motorstrom I_{M 24, neu} berechnen zu können und umgekehrt benötigt man den Motorstrom I_{M 24, neu}, um den Motorwiderstand R_{M 24} berechnen zu können! Dabei gilt es zu beachten, dass sich der Motorwiderstand R_{M 24} auf einen einzelnen, konkreten Motorstrom I_{M 24, neu} bezieht!

Konkret bedeutet dies, dass man die Motorkennlinie I_{M 24} = f( U_{M 24} ) aufnehmen muss, da man nur so für jedes einzelne Wertepaar der Wertetabelle den Motorwiderstand R_{M 24} berechnen kann!

Dabei muss die Motorkennlinie I_{M 24} = f( U_{M 24} ) des Motors direkt in der Schaltung aufgenommen werden, da die Schaltung u.a. mit der Stromgegenkopplung ständig das elektrische Verhalten beeinflusst! -

Für den Gesamtwiderstand der beiden parallel geschalteten (Last-) Widerstände folgt dann:

R_{Last, ges} = ( R_{Glüh 27} * R_{M 24} ) / ( R_{Glüh 27} + R_{M 24} ) → Spezialformel für nur zwei parallel geschaltete Widerst.

= ( 12 Ω * 27,1 Ω ) / ( 12 Ω + 27,1 Ω ) = ( 325,2 Ω² ) / ( 39,1 Ω ) = 8,32 Ω → ist richtig! Siehe weiter oben!

Zur Erinnerung: Bei der Parallelschaltung ist der Gesamtwiderstand stets kleiner als der kleinste Einzelwiderstand!

Demzufolge berechnet sich die Gesamtstromstärke I_{Last, ges} bei einer Spannung U_Last = 3,41 V wie folgt:

I_{Last, ges} = U_Last / R_{Last, ges}

= 3,41 V / 8,32 Ω = 3,41 V / 8,32 V/A = 0,4099 A ≈ 410 mA → ist richtig! Siehe weiter oben!

Vom einfachen zum stabilisierten Basis-Spannungsteiler

Dass Transistoren, wie z.B. der Leistungstransistor „PNP-Transistor 51“ (T2) zwischen Emitter und Kollektor nur dann elektrisch leitend wird (linkes Bild unten),

(Leistungstransistor T2 sperrt | Zum Vergrößern bitte auf das Bild klicken! | Leistungstransistor T2 leitet)

wenn man die Basis aufsteuert, indem man die Emitter-Basis-Diode elektrisch leitend macht, dürfte inzwischen hinlänglich bekannt sein (rechtes Bild oben).

Wie man in den beiden obenstehenden Bildern der ein und derselben Schaltung sieht, gibt es zur Stromversorgung insgesamt zwei Batteriefächer 19 mit je einer Batteriespannung von U_Batt = 3,0 V.

Dabei gilt es zu beachten, dass die beiden Batteriefächer 19 links vor dem (Schiebe-) Schalter 14 mit gleicher Polung „+“ miteinander verbunden sind, schaltungstechnisch nichts miteinander zu tun haben, da die linke Masche (= Stromkreis 1) den Emitter-Basis-Kreis und dessen Stromversorgung 1 betrifft und die rechte Masche (= Stromkreis 2) den Emitter-Kollektor-Kreis und dessen Stromversorgung 2.

Demzufolge dient die linke Masche (= Stromkreis 1) mit der Emitter-Basis-Diode als Steuerkreis und die rechte Masche (= Stromkreis 2) mit der Emitter-Kollektor-Strecke und dem Glühlämpchen 18 als Leistungskreis.

Obwohl die beiden Batteriefächer 19 links vor dem (Schiebe-) Schalter 14 mit gleicher Polung „+“ miteinander verbunden sind, schaltungstechnisch nichts miteinander zu tun haben, sind sie trotzdem elektrisch miteinander verbunden! Und zwar als Parallelschaltung zweier Spannungsquellen ( = Batteriefächer 19)!

Das ist wichtig zu wissen und zu beachten, da beide parallel geschalteten Spannungsquellen im Kurzschlussfall zwangsläufig den doppelten Kurzschlussstrom liefern!

Während also die rote Leuchtdiode 17 im linken Bild oben durch ihr Leuchten signalisiert, dass sich der Leistungstransistor „PNP-Transistor 51“ (T2) im gesperrten Zustand befindet, signalisiert das hell leuchtende Glühlämpchen 18 im linken Bild oben, dass der Leistungstransistor „PNP-Transistor 51“ (T2) jetzt voll durchgesteuert und elektrisch leitend ist!

Gemäß der Nenn-Betriebsdaten des Glühlämpchens 18 (U_{Glüh 18} = 2,5 V, I_{Glüh 18} = 0,3 A, P_{Glüh 18} = 750 mW) fließt dabei durch die elektrisch leitende Emitter-Kollektor-Strecke eine Stromstärke von bis zu I_{Glüh 18} = 300 mA, was schon ganz ordentlich ist. Dabei gilt: I_{Glüh 18} = I_E mit dem Leistungstransistor T2 als Stromknoten mit I_E = I_B + I_C und B = I_C / I_B für die Stromverstärkung des Transistors.

Mit der Stromverstärkung B des Leistungstransistors T2 stellt sich natürlich gleich die Frage, wie groß diese ist. Bezüglich des Kollektorstroms I_C kann man sich an der Nennstromstärke des Glühlämpchens 18 mit I_{Glüh 18} = 300 mA orientieren. Sofern der Leistungstransistors T2 nicht in der absoluten Sättigung, d.h. im Bereich [ 0,2 V, …, 0,4 V ] betrieben wird, sondern mit U_EC = 0,84 V, dann verbleiben für das Glühlämpchens 18 noch

U_EC + U_{Glüh 18} + ( - U_{Batt 2} ) = 0 → Spannungsumflauf im rechten Stromkreis mit dem Glühlämpchens 18

U_EC + U_{Glüh 18} - U_{Batt 2} = 0 →

U_{Glüh 18} = U_{Batt 2} – U_EC

= 2,54 V – 0,84 V = 1,7 V

Wenn man davon ausgeht, dass sich der Widerstand R_{Glüh 18} der Glühwendel des Glühlämpchens 18 auch bei der verbleibenden Spannung von U_{Glüh 18} = 1,7 V noch halbwegs linear, d.h. mit konstanter Steigung, verhält, dann lässt sich der Widerstand R_{Glüh 18} mittels Dreisatz wie folgt berechnen:

2,5 V → 8,33 Ω

1,7 V → x Ω

x = 8,33 Ω / 2,5 V * 1,7 V = 5,66 Ω

I_{Glüh 18} = I_EC = U_{Glüh 18} / R_{Glüh 18} = 1,7 V / 5,66 Ω = 1,7 V / 5,66 V/A = 0,30035 A = 300,35 mA

Bezüglich der Stromstärke des Glühlämpchens 18 mit I_{Glüh 18} = 300,35 mA gilt es zu beachten, dass sich zwar der Glühlampenwiderstand mit R_{Glüh 18} = 5,66 Ω linear verhält, nicht jedoch der Halbleiterwiderstand der Emitter-Kollektor-Strecke des Leistungstransistors T2.

Um den Basisstrom I_B des Leistungstransistors T2 berechnen zu können, müssten wir jetzt im Datenblatt nachschauen, welche Verstärkung B sich bei einem Kollektorstrom I_C = 300 mA einstellt. Zwar gibt es zum Leistungstransistors T2 ein entsprechendes Datenblatt, leider aber ohne die Kennlinie zur Verstärkung B für einen Kollektorstrom I_C = 300 mA. Erfahrungsgemäß dürfte sich die Verstärkung B bei einem Kollektorstrom I_C = 300 mA deutlich B < 100 bewegen.

Wenn man von einer Stromverstärkung B = 65 ausgeht, dann folgt für den Basisstrom I_B:

B = I_C / I_B →

I_B = I_C / B = 300 mA / 65 ≈ 4,6 mA → Der Basisstrom zum Aufsteuern des Leistungstransistors T2 ist realistisch!

Jetzt stellt sich die nächste Frage, wie sich der entsprechende Basiswiderstand R_B im linken Stromkreis mit dem Widerstand 40 und dem Potentiometer 53 berechnen lässt.

Um den Leistungstransistor T2 über die Basis voll aufsteuern zu können, muss der Schieberegler (= Poti 53), d.h. der Mittelabgriff bis auf Minimum nach oben geschoben werden, sodass der Teilwiderstand des Schiebereglers 53 zu null Ohm wird und demzufolge vernachlässigt werden darf (siehe obenstehendes Bild links).

Für den Spannungsumlauf im linken Stromkreis der Basis vom Leistungstransistor T2 mit U_{Batt 1} = 2,37 V folgt dann:

U_{R 40} + U_EB + ( - U_{Batt 1} ) = 0 →

U_{R 40} = U_{Batt 1} - U_EB → Die Durchlassspannung der EB-Diode dürfte sich auf ca. U_EB = 0,8 V belaufen, sodass folgt:

= 2,37 V – 0,8 V = 1,57 V

R₄₀ = U_{R 40} / I_{R 40}

= U_{R 40} / I_B = 1,57 V / 4,6 mA = 0,3413 kΩ = 341,3 Ω

Da wir im Experimentierkasten nur über den Widerstand 40 mit R₄₀ = 100 Ω verfügen, stellt sich die Frage, welcher Basisstrom I_B sich bei Verwendung desselben einstellt:

I_B = U_{R 40} / R₄₀

= 1,57 V / 100 Ω = 0,0157 A = 15,7 mA → Dieser Basisstrom ist definitiv zu groß!

Auch dieser Wert für den Basisstrom ist durchaus realistisch, sollte aber in der Praxis vermieden werden! Allerdings wäre der Transistor damit total übersteuert und würde sich demzufolge in der Sättigung mit 0,2 V < U_{EC sat} < 0,4 V befinden!

I_B = U_{R 40} / R₄₀

= 1,57 V / 1 kΩ = 1,57 mA → Dieser Basisstrom ist in Ordnung!

Dieser Wert für den Basisstrom ist besser geeignet, da sich mit diesem eine größere Verstärkung B einstellt und sich der Transistor im normalen Arbeitsbereich (= Arbeitsgerade) mit U_EC > U_{EC sat} befindet!

Merke:

3 Volt Stromversorgung mit einem Batteriefach 19

Emitter-Basis-Kreis:

I_B = 5 mA mit U_EB = 0,85 V →

U_RB = U_{Batt 1} – U_EB = 3,0 V – 0,85 V = 2,15 V →

R_B = U_RB / I_B = 2,15 V / 5 mA = 0,43 kΩ = 430 Ω → 100 Ω < R_B < 1 kΩ

Emitter-Kollektor-Kreis:

U_{Batt 2} = 3,0 V mit U_{Glüh 18} = 2,5 V und I_{Glüh 18} = I_EC = 0,3 A → I_C = I_EC – I_B = 300 mA – 5 mA = 295 mA

U_EC = U_{Batt 2} - U_{Glüh 18} = 3,0 V – 2,5 V = 0,5 V → keine Sättigung!

B = I_C / I_B = 295 mA / 5 mA ≈ 60fach

Da der Mensch keine hellseherische Fähigkeiten besitzt, keine infrarote Strahlung ( = TV-Fernbedienung) und auch keine elektrische Spannungen und Ströme sehen kann, sieht man es dem Transistor nicht an, in welchem elektrischen Zustand (gesperrt oder leitend) er sich befindet.

Wenn man also wissen will, in welchem elektrischen Zustand (gesperrt oder leitend) sich der Transistor befindet, dann muss man das Multimeter zu Hilfe nehmen und Spannungen und/oder Ströme an der Emitter-Basis-Diode und/oder der Emitter-Kollektor-Strecke messen! Im einen oder anderen Fall wird man dann auch Berechnungen anstellen müssen.

Wenn man aber noch kein Multimeter sein eigen nennt, dann wäre es jetzt vielleicht an der Zeit, sich mal schlau zu machen und sich zu informieren. Bei Amazon gibt es z.B. das preiswerte „CSL“-Digital-Multimeter, sozusagen für Einsteiger zum Preis von nur 11,85 €. Bei eBay findet man das gleiche Gerät für knapp die Hälfte. Allerdings dauert dort der Sparversand bis zu drei Wochen.

In der Zwischenzeit, d.h. bis zur Anschaffung eines Multimeters, behelfen wir uns, indem wir einen weiteren Indikator (= Anzeiger) in die bisherige Schaltung einbringen. Den ersten Indikator gibt es ja bereits. Und zwar in Form der roten Leuchtdiode 17, die parallel zur EC-Strecke des Leistungstransistors T2 geschaltet wurde.

Wie man im nachfolgenden Bild links unten sieht, leuchtet die rote Leuchtdiode 17 immer dann, wenn sich der Leistungstransistor T2 im gesperrten Zustand befindet. Und dies ist immer dann der Fall, wenn der Leistungstransistor T2 keinen Basisstrom I_B an seiner Basis B bezieht.

Oder anders ausgedrückt: immer wenn die EB-Spannung U_EB < 0,7 V ist, liegt der Mittelabgriff des Potentiometers 53 (= „Schieberegler“) auf dem „+“-Potential der Batterien im Batteriefach 19 (links), sodass die EB-Diode des Leistungstransistors T2 sperrt. Und wenn sich die EB-Diode im gesperrten Zustand befindet, fließt kein Strom durch sie hindurch, sodass der Bahnwiderstand R_EB > 1 MΩ (= größer als eine Million Ohm) ist und als Folge dessen die grüne Leuchtdiode 26 leuchtet (siehe nachfolgendes Bild links):

(Leistungstransistor T2 sperrt | Zum Vergrößern bitte auf das Bild klicken! | Leistungstransistor T2 leitet)

Wenn sich der Mittelabgriff des Potentiometers 53 (= „Schieberegler“) auf dem „-“-Potential der Batterien im Batteriefach 19 (links) befindet, sodass die EB-Diode und die EC-Strecke des Leistungstransistors T2 elektrisch leitend werden, dann wird der Leistungstransistors T2 aufgesteuert, sodass das Glühlämpchen 18 leuchtet (siehe obenstehendes Bild rechts).

In dem Moment, wo die EB-Diode, die EC-Strecke und der Leistungstransistor T2 selbst elektrisch leitend werden, verringert sich der Spannungsabfall an diesen auf ein Minimum, sodass für die parallel geschalteten Leuchtdioden nicht mehr genügend Spannung übrig bleibt und diese ausgehen.

Auf diese Weise lassen sich die Leuchtdioden als Indikator dafür einsetzen, um zu signalisieren, dass die EB-Diode, die EC-Strecke und der Leistungstransistor T2 elektrisch leitend sind, sobald die Leuchtdioden ausgehen. -

Frage:

Wie groß ist der Spannungsabfall U_{LED 26} an der grünen Leuchtdiode 26, wenn diese von einem Durchlassstrom I_{LED 26} = 10 mA durchflossen wird?

U_{LED 26} = U_{Batt 1} – U_R40

= U_{Batt 1} – I_R40 * R₄₀

= 3,0 V – 10 mA * 100 Ω = 3,0 V – 1000 mV = 3,0 V – 1 V = 2,0 V

Frage:

Wie groß ist der Spannungsabfall U_{LED 26} an der grünen Leuchtdiode 26, wenn diese von einem Durchlassstrom I_{LED 26} = 20 mA durchflossen wird und die Batteriespannung jetzt U_{Batt ges} = 6,0 V beträgt?

U_{LED 26} = U_{Batt ges} – U_R40

= U_{Batt ges} – I_R40 * R₄₀

= 6,0 V – 20 mA * 100 Ω = 6,0 V – 2000 mV = 6,0 V – 2 V = 4,0 V → FALSCH!

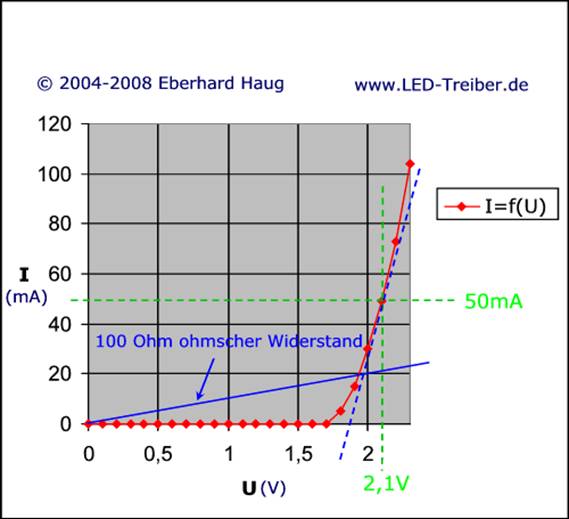
Wenn die grüne Leuchtdiode 26 hell leuchtet, dann beträgt ihre „Vorwärts“-Spannung, engl. „forward“, d.h. nach vorne, vorwärts, U_{LED 26} = U_F = 2,1 V. Dabei gilt es zu beachten, dass die Durchflussspannung U_F = 2,1 V nicht viel größer werden kann, weil es sich bei der Leuchtdiode um einen Halbleiter mit entsprechender Kennlinie handelt:

(Leuchtdiode 26 leitet | Vergrößern: auf Bild klicken! | Quelle: LED-Treiber)

U_R40 = U_{Batt ges} – U_{LED 25}

= 6,0 V – 2,1 V = 3,9 V →

I_R40 = U_{R 40} / R₄₀

= 3,9 V / 100 Ω = 0,039 A = 39 mA →

Die rote Leuchtdiode 26 brennt durch, weil der Durchflussstrom I_F nicht größter werden darf als 8 mA < I_F < 12 mA!

Damit die rote Leuchtdiode 26 eben nicht durchschmort, muss man die Batteriespannung U_Batt ges entsprechend reduzieren:

U_{Batt ges} = U_{LED 25} + U_R40

= U_{LED 25} + I_R40 * R₄₀ → I_R40 = I_F = 12 mA

= 2,1 V + 12 mA * 100 Ω = 2,1 V * 1200 mV = 2,1 V + 1,2 V = 3,3 V

Frage:

Was muss man ändern, wenn man die rote Leuchtdiode 26 trotzdem mit einer Batteriespannung von U_Batt ges = 6,0 V und einem zulässigen Durchflussstrom von I_F = 10 mA betreiben will?

U_R40 = U_{Batt ges} – U_{LED 25}

= 6,0 V – 2,1 V = 3,9 V →

R₄₀ = U_{R 40} / I_R40

= 3,9 V / 10 mA = 0,39 kΩ = 390 Ω

Wenn man die rote Leuchtdiode 26 trotzdem mit einer Batteriespannung von U_Batt ges = 6,0 V und einem zulässigen Durchflussstrom von I_F = 10 mA betreiben will, dann muss man den Vorwiderstand auf R₄₀ = 390 Ω entsprechend vergrößern, damit der Durchflussstrom von I_F = 10 mA nicht überschritten wird! -

Die bisherige Schaltung mit der separaten Ansteuerung des Leistungstransistor T2 anhand des Basis-Spannungsteilers und der Stromversorgung durch das Batteriefach 19 (links) mit U_{Batt 1} = 3,0 V hat den Vorteil, dass diese elektrisch unabhängig vom Leistungsteil der EC-Strecke des Leistungstransistor T2 mit dem Batteriefach 19 (rechts) mit U_{Batt 2} = 3,0 V funktioniert.

Demzufolge verhält es sich am Emitter E des Leistungstransistor T2 so, dass dieser einen Stromknoten darstellt, in den der Ansteuerstrom I_E1 = -I_B = I_R40, aus dem Batteriefach 19 (links) kommend, zusammen mit dem Laststrom I_E2 = - ( I_C + I_B ) = - I_C = I_Last, aus dem Batteriefach 19 (rechts) kommend, in den Emitter E hinein fließt:

I_E1 + I_E2 + ( - I_E ) = 0 → I_E = I_E1 + I_E2

Dabei gilt es zu beachten, dass alle in den Stromknoten E hinein fließenden Ströme positiv gezählt werden, während alle aus dem Stromknoten E heraus fließenden Ströme negativ gezählt werden.

Die gilt übrigens auch für den Leistungstransistor T2, der mit seinen drei Anschlüssen Emitter E, Basis B und Kollektor C ebenfalls einen Stromknoten darstellt!

Im Leistungstransistor T2 selbst teilt sich der Emitterstrom I_E = I_E1 + I_E2 wieder in seine Bestandteile - I_B und - I_C auf:

I_E = I_E1 + I_E2 = - I_B - I_C = I_R40 + I_{Glüh 18}

Der Vorteil der getrennten Stromversorgung mit dem Batteriefach 19 (links) für den Basisstrom - I_B und dem Batteriefach 19 (rechts) für den Kollektor-/Laststrom – I_C = I_Last = I_{Glüh 18} ist der, dass beide voneinander unabhängig sind!

Wenn es also im Lastkreis (rechts) zu Spannungs- oder Stromschwankungen kommt, z.B. weil sich der Lastwiderstand R_Last = R_{Glüh 18} aufgrund von Temperaturschwankungen der Außentemperatur fortwährend ändert, so bleibt die Steuerkreis (links) an der Basis B des Leistungstransistors T2 wegen seiner eigenen Stromversorgung mit dem Batteriefach 19 (links) gänzlich unbeeinflusst!

In der Praxis kommt es gelegentlich vor, dass man für die Stromversorgung der Basis B des Leistungstransistors T2 einen vom Laststrom – I_C absolut unabhängigen und stabilen Basisstrom – I_B = konstant benötigt, der sich wiederum nur mittels der Schaltung (links) realisieren lässt (siehe nachfolgendes Bild unten links):

(Energieversorgung: 2 Batteriefächer | Zum Vergrößern bitte auf das Bild klicken! | Energieversorgung: 1 Batteriefach)

Wenn man in der Praxis kein zweites Batteriefach 19 (links) mit U_{Batt 1} = 3,0 V zur Verfügung hat, es nicht zwingend erforderlich ist, dass der Basisstrom – I_B absolut unabhängig von der Stromversorgung des Lastkreises des Leistungstransistors T2 sein muss oder der Basisstrom – I_B nicht absolut stabil sein muss, dann kann man aus Gründen der Ressourcenersparnis auf das zweite Batteriefach 19 (links) mit U_Batt 1 = 3,0 V verzichten und den Basisspannungsteiler aus dem Batteriefach 19 (rechts) mit U_{Batt 2} = 3,0 V mit Strom versorgen (siehe obenstehendes Bild rechts)! –

Wenn es darum geht, den Basisstrom – I_B unabhängig von der Stromversorgung des Lastkreises des Leistungstransistors T2 stabil zu halten, dann gibt es neben der Stromgegenkopplung auch noch die Möglichkeit, den Basis-Spannungsteiler mittels eines sogenannten eingeprägten Stromes zu ertüchtigen. Dabei bezeichnet man den eingeprägten Strom im Falles des belasteten Spannungsteilers auch als Querstrom durch den Spannungsteiler.

Doch zunächst gilt es noch festzustellen, dass der Basisstrom durch den Steuertransistor „NPN-Transistor 52“ (T1) und wegen der sehr großen Verstärkung der Komplementär-Darlington-Schaltung extrem klein ist (siehe Versuch 72).

Sehr kleine Basisströme von um die 50 µA (= 50 Millionstel Ampere = 50 * 1 / 1 000 000 = 0,000 050 A) aber lassen sich nicht nur schwer messen, sondern auch nur schwierig in den Griff bekommen, d.h. steuern und regeln, eben weil sie so winzig sind.

Den nachfolgenden Berechnungen liegen folgende Messwerte zugrunde:

U_{Batt, ges} = 4,32 V

U_Last = 3,41 V

I_{Last, ges} = 410 mA

Berechnung des Lastwiderstandes:

Und wegen der Stromgegenkopplung vom Kollektor des Leistungstransistors T2 zurück zum Emitter des Steuertransistors T1 muss beim belasteten Spannungsteiler auch noch eine deutlich größere Teilspannung von

U_BE1 + U_Last = U_{LED 26} + U_{LED 17} → I_{LED, ges} = 10 mA

= 2,1 V + 1,6 V = 3,7 V

berücksichtigt werden:

U_R40 = U_{Batt, ges} – ( U_{LED 26} + U_{LED 17} )

= 4,32 V – 3,7 V = 0,62 V

R_ges = R₄₀ + r_LEDs

= R₄₀ + u_LEDs / I_{LED, ges}

= 100 Ω + 3,7 V / 10 mA = 100 Ω + 0,37 kΩ = 100 Ω + 370 Ω = 470 Ω

Berechnung mit der Spannungsteilerformel:

R₄₀ / R_ges = U_R40 / U_ges →

U_R40 = R₄₀ / R_ges * U_ges

= 100 Ω / 470 Ω * 4,32 V = 0,919 V ≈ 0,92 V

Den Teil mit der parallel geschalteten Last (Glühlämpchen + Motor) des belasteten Spannungsteilers kann man wegen des sehr kleinen Basisstroms vernachlässigen!

Frage:

Weshalb ergibt sich bei der obenstehenden Berechnung des Spannungsabfalls U_R40 am (Vor-) Widerstand 40 eine so große Abweichung: U_R40 = 0,62 V ↔ U_R40 = 0,92 V (= + 48,4 %)?

Für die große Abweichung bei der Berechnung des Spannungsabfalls U_R40 kann es verschiedene Ursachen geben.

Wenn beispielsweise ein Teil der Messungen zu einem früheren Zeitpunkt vorgenommen, während die restlichen zu einem späteren Zeitpunkt vorgenommen wurden, dann kann es vorkommen, dass die Batterien bei anderen Versuchen während dessen stärker entladen wurden, sodass die Batteriespannung zwischenzeitlich weniger geworden ist.

Es kann auch sein, dass ein Teil der Messungen mit dem Versuch A ermittelt wurden, während der andere Teil der Messungen mit einem ähnlichen Versuch B gemacht wurden.

Es kann auch sein, dass ein Teil der Messungen mit dem Glühlämpchen 18 (2,5 V, 0,3 A) gemacht wurden, während der andere Teil der Messungen mit dem anderen Glühlämpchen 27 (6,0 V, 0,5 A) durchgeführt wurden.

Was auch sein kann, ist, dass ein Teil der Messungen mit der Spannungsversorgung von 3,0 V (= 1 x Batteriefach 19) vorgenommen wurde, während der andere Teil mit der Spannungsversorgung von 6,0 V (= 2 x Batteriefächer 19) durchgeführt wurde.

Im vorliegenden Fall kommt aber die große Abweichung von + 48,4 % durch den als zu groß eingeschätzten Querstrom der beiden in Reihe geschalteten Leuchtdioden 26 und 17 von I_{LED, ges} = 10 mA zustande!

Zwar verhält es sich so, dass eine Leuchtdiode im Allgemeinen einen Durchflussstrom I_F von 8 mA < I_F < 12 mA hat.

Wenn man aber wie im vorliegenden Fall zwei wenn auch unterschiedliche Leuchtdioden hintereinander, d.h. in Reihe schaltet, dann teilt sich die von außen zugeführte Spannung auf beide Leuchtdioden auf, sodass jede Leuchtdioden annähernd nur noch mit der hälftigen Spannung versorgt wird, weil sich die beiden Widerstände wegen der Reihenschaltung addieren, also fast verdoppeln, wobei sich auch noch die Stromstärke durch die beiden Leuchtdioden auf rund die Hälfte verringert: I_{LED, ges} = ½ * 10 mA = 5 mA!

Mit den nachfolgend aktualisierten Messwerte klärt sich das Ganze sehr schnell auf:

U_{Batt, ges} = 4,45 V

U_Last = 3,31 V

I_{Last, ges} = 400 mA

I_B = 0,101 mA = 101 µA

Berechnung des Lastwiderstandes:

Und wegen der Stromgegenkopplung vom Kollektor des Leistungstransistors T2 zurück zum Emitter des Steuertransistors T1 muss beim belasteten Spannungsteiler auch noch eine deutlich größere Teilspannung von

U_BE1 + U_Last = U_{LED 26} + U_{LED 17} → I_{LED, ges} = 4,8 mA (!!!)

= 2,17 V + 1,84 V = 4,01 V

berücksichtigt werden:

U_R40 = U_{Batt, ges} – ( U_{LED 26} + U_{LED 17} )

= 4,45 V – 4,01 V = 0,44 V

R_ges = R₄₀ + r_LEDs

= R₄₀ + u_LEDs / I_{LED, ges}

= 100 Ω + 4,01 V / 4,8 mA = 100 Ω + 0,8354 kΩ = 100 Ω + 835,4 Ω = 935,4 Ω

Berechnung mit der Spannungsteilerformel:

R₄₀ / R_ges = U_R40 / U_ges →

U_R40 = R₄₀ / R_ges * U_ges

= 100 Ω / 935,4 Ω * 4,45 V = 0,4757 V ≈ 0,47 V (= + 6,82 %) 

Berechnung der Stromverstärkung B:

Wie wir bereits wissen, lässt sich die Stromverstärkung B mittels der Formel B = I_C / I_B berechnen. Ferner wissen wir bereits, dass sich die Stromverstärkung B bei zwei Transistoren, die gemäß der Darlington- oder Komplementär-Darlington-Schaltung miteinander verschaltet sind, multipliziert: B = B₁ * B₂ (siehe Versuch 72).

Bei Darlington-Transistoren, die es quasi auch im Doppelpack gibt, d.h. die zusammen in einem Gehäuse untergebracht sind, lässt sich die Stromverstärkung B logischerweise nicht mehr mit der Formel B = B₁ * B₂ berechnen, sondern nur noch direkt von außen mittels der Formel B = I_C / I_B.

Im vorliegenden Fall lässt sich die Stromverstärkung B auch direkt mittels der Formel B = I_C / I_B berechnen. Allerdings gilt es dabei zu beachten, dass sich der gesamte Kollektorstrom I_{C ges} wie folgt zusammensetzt:

I_{C ges} = I_E1 + I_C2 → I_E1 ist der Emitterstrom des NPN-Transistors 52 und

I_C2 der Kollektorstrom des PNP-Transistors 51.

Ferner gilt es zu beachten, dass sich der gesamte Laststrom I_{Last ges} aus den beiden Teilströmen I_{Motor 24} und I_{Glüh 27} wie folgt zusammensetzt:

I_{C ges} = I_{Last ges} = I_{Motor 24} + I_Glüh27 = 400 mA → der Laststrom wurde mit dem Multimeter gemessen, da man bei einer Versorgungsspannung U_{Batt, ges} < 6,0 V nicht davon ausgehen kann, dass sich bei dieser auch die Nennströme der Verbraucher wie z.B.

I_{Glüh 27, Nenn} = 0,5 A = 500 mA einstellen!

Die Nennströme der Verbraucher können sich auch deswegen nicht einstellen, weil sich diese in Reihe mit dem Leistungstransistor T2 befinden, sodass es auch den Spannungsabfall u_E2C2 an der E2C2-Strecke zu berücksichtigen gilt!

Zu guter Letzt kennen wir die Nennbetriebsdaten des Elektromotors 24 nicht. Leider!

Bevor wir den Basisstrom I_{B ges} messen, berechnen wir diesen anhand der mittleren Erfahrungswerte (s. Versuch 72):

B₂ = 25 für den Leistungstransistor T2 (in der Schaltung rechts!)

B₁ = 250 für den Steuertransistor T1 (in der Schaltung links!)

B = B₁ * B₂ = 250 * 25 = 6 250

Mit dem gemessenen Basisstrom des Steuertransistors T1 mit I_B1 = 0,10 mA folgt für die Stromverstärkung B:

B = I_{C ges} / I_B1

= I_{Last ges} / I_B1

= 400 mA / 0,1 mA = 400 * 1/10 = 4 000

Interessant dürfte in diesem Zusammenhang auch noch sein, wie groß der Bahnwiderstand r_BE1 des Steuertransistors T1 ist:

r_BE1 = u_BE1 / i_B1

= ( U_{Batt, ges} – U_R40 – U_Last ) / I_B1 →

= ( 4,45 V – 0,44 V – 3,31 V ) / 0,1 mA = ( 0,7 V ) / 0,1 mA = 0,7 V / 1/10 mA = 7 kΩ

Wie man sieht, befindet sich der Steuertransistor T1 im stromdurchlässigen, verlustbehafteten Bereich der Kennlinie. Und zwar als Regeltransistor.

Was aber ist der Unterschied zwischen einer Steuerung und einer Regelung?

Bei einer Regelung gibt es immer einen Regelkreis nebst Rückführung des Ausgangssignals auf den Eingang. Außerdem wird der IST-Wert ständig mit dem eingestellten, vorgegebenen SOLL-Wert verglichen und auf entsprechende +/- Abweichungen entsprechend reagiert. Bei der bereits behandelten Stromgegenkopplung vom Kollektor Leistungstransistor T2 auf den Emitter des Steuertransistor T1 handelt es sich um eine (analoge) Regelung.

Weil der Steuertransistor T1 den Leistungstransistor T2 über den Basisstrom ansteuert, haben wir diesen Steuertransistor genannt.

Achtung:

Stabile, d.h. nicht schwankende Messwerte stellen sich nur ein, wenn der Elektromotor 24 nicht im Leerlauf, sondern unter Last läuft! Zu diesem Zweck muss man die rote Luftschraube (= Propeller) auf die Motorachse setzen!

Um Ströme messen zu können, muss man stets die Schaltung an der entsprechenden Stelle auftrennen und zwischen die Trennstelle das Amperemeter (= Stromstärke-Meßgerät) schalten!

Zwecks Messung des Basisstromes i_B1 des Steuertransistors T1 muss dazu die blaue Leitleiste 2 zwischen dem Widerstand R₄₀, der grünen Leuchtdiode 26 und dem Potentiometers 53 entfernt werden!

Zur Messung des sehr kleinen Basisstromes i_B1 muss der Schieberegler des Potentiometers 53 ganz nach oben bzw. ganz nach rechts geschoben werden, sodass der verstellbare Teilwiderstand R_{53, 1} = 0 Ω beträgt.

Die Schaltung mit dem Stromkreis darf wegen des großen Laststromes I_Last = 400 mA und der starken Erwärmung des Leistungstransistors T2 nicht länger als 20 Sekunden in Betrieb genommen, d.h. eingeschaltet sein! -

Wie bereits erwähnt wurde, handelt es sich bei Basis-Spannungsteiler des Steuertransistors T1 um einen belasteten Spannungsteiler (SPT), der sich aus den Bauelementen Vorwiderstand R₄₀ + [ ( r_{LED 26} + r_{LED 17} ) // R₅₃ ] zusammensetzt, sodass sich dessen Gesamtwiderstand R_SPT wie folgt berechnet:

R_SPT = R₄₀ + [ ( r_{LED 26} + r_{LED 17} ) // R₅₃ ]

= 100 Ω + [ 835,4 Ω // 50 kΩ ]

= 100 Ω + [ ( 0,8354 kΩ * 50 kΩ ) / ( 0,8354 kΩ + 50 kΩ ) ]

= 100 Ω + [ ( 41,77 kΩ² ) / ( 50,8354 kΩ ) ]

= 0,1 kΩ + [ 0,82167 kΩ ] = 0,92167 kΩ ≈ 922 Ω 

Jetzt bestätigt sich, dass man den Belastungszweig des belasteten Spannungsteilers (SPT), bestehend aus dem Potentiometerwiderstand R₅₃ = 50 kΩ in der Parallelschaltung wegen seines großen Widerstandswertes gegenüber den anderen Widerständen durch Weglassen vernachlässigen kann, sodass aus dem belasteten Spannungsteiler (SPT) ein unbelasteter Spannungsteilers (SPT) wird.

Die Stromstärke durch den unbelasteter Spannungsteilers (SPT) berechnet sich nun wie folgt:

I_SPT = U_SPT / R_SPT

= U_{Batt, ges} / R_SPT

= 4,45 V / 922 Ω = 0,004826 A = 4,826 A ≈ 4,8 mA 

Vergleicht man den Querstrom I_SPT = 4,8 mA durch den Basis-Spannungsteiler mit dem Basisstrom i_B1 = 0,1 mA, so fällt auf, dass dieser insgesamt 4,8 mA / 0,1 mA = 48-mal so groß ist, sodass sich etwaige Schwankungen der Spannungsversorgung U_{Batt, ges} des belasteten Spannungsteilers so gut wie nicht auf den abgezweigten Basisstrom i_B1 auswirken:

(Zum Vergrößern bitte auf das Bild klicken!)

Den Strom durch den unbelasteten Spannungsteiler nennt man übrigens Querstrom, weil dieser quer zum Widerstand R₅₃ des Potentiometers 53 als belasteter Spannungsteiler fließt.

In der Praxis verhält es sich so, dass der Querstrom, der auch als eingeprägter Strom bezeichnet wird, in etwa viermal bis zehnmal so groß sein soll wie der Entnahmestrom im Lastzweig des belasteten Spannungsteilers.

In diesem Zusammenhang gilt es zu beachten, dass der vier- bis zehnmal so große Querstrom auch verlustleistungsbehaftet ist. Und zwar in Form von Wärmeverlustleistung.

Deshalb wird der belastete Spannungsteiler überwiegend nur zu Zwecken der Arbeitspunkteinstellung von Transistoren, deren Beschaltung gegebenenfalls temperatur- oder spannungsabhängig ist, eingesetzt.

Die obenstehende Schaltung mit den beiden Darlington-Transistoren hat den Vorteil, dass sie wegen der Darlington-Schaltung über eine sehr hohe Stromverstärkung von B = B₁ * B₂ = 4 000 verfügt, sodass sich der Leistungstransistor T2 (rechts) mit einem sehr kleinen Basisstrom I_B1 = 0,1 mA ansteuern lässt. Demzufolge ließe sich der regelbare Widerstand des Potentiometers 53 z.B. durch den Lichtsensor 16 in Form eines Fototransistors (ohne Basisanschluss) oder einer Fotodiode ersetzen. -

Teamarbeit zwischen Transistoren

Da der Leistungstransistor T2 (siehe obenstehende Schaltung) bei größeren Kollektorströmen schnell an seine Grenzen in Form der Wärmeverlustleistung gerät und demzufolge nur im Kurzzeitbetrieb (KB) von max. 20 Sekunden gefahren werden darf, bietet es sich an, größere Lastströme von Elektromotor 24 plus Glühlämpchen 27 auf zwei komplementäre Transistoren zu verteilen. Dabei bedeutet „komplementär“ so viel wie „den andern, das andere ergänzend“. Im vorliegenden Fall sind das der NPN-Transistor 52 und der PNP-Transistor 51, die entgegengesetzt zueinander verschaltet werden:

(Zum Vergrößern bitte auf das Bild klicken!)

Das besonders Interessante an der Parallelschaltung der beiden Komplementär-Transistoren gleichen Typs ist die Ansteuerung der Basisanschlüsse mit der Stromversorgung und den Basisströmen.

Da beide Transistoren vom gleichen Typ sind, wenn auch in unterschiedlicher Reihenfolge der NPN- und PNP-Halbleiterschichten, verfügen beide über gleich große Stromverstärkungsfaktoren B₁ = B₂, sodass sich bei gleich großen Lastwiderständen auch betragsmäßig (= das Vorzeichen | +/- | bleibt unberücksichtigt!) gleich große Basisströme | I_B1 | = | - I_B2 | einstellen.

Dabei gilt es zu beachten, dass der Transistor T1 (links) seinen Basisstrom I_B1 als Basisstrom - I_B2 vom Transistor T2 (rechts) bezieht. Während also der Basisstrom I_B1 an der Basis B1 in den Transistor T1 (links) hinein fließt, fließt er aus der Basis B2 vom Transistor T2 (rechts) heraus, sodass gilt: I_B1 = - I_B2.

Da der Transistor T2 (rechts) am Emitter E2 als Stromteiler arbeitet, fließt der Basisstrom I_B2 aus dem Emitter E2 heraus, wobei dieser wiederum aus dem „+“-Pol der Batterie 2 (rechts) heraus fließt.

Demzufolge stammt der Basisstrom I_B1 des Transistors T1 aus der Batterie 2 (rechts), die den Transistor T2 mit Energie versorgt! Das ist wichtig zu wissen, da elektrische Ströme immer wieder dorthin zurückfließen, von wo sie ursprünglich herkommen! Diesbezüglich wird also der Basisanschluss B1 potentialmäßig auf das Spannungsniveau des „+“-Pols der Batterie 2 (rechts) angehoben. Aber nicht nur das, wie wir gleich sehen werden!

Der Basisstrom I_B1 des Transistors T1 (links) addiert sich zum Kollektorstrom I_C1 und wird zum Emitterstrom I_E1, der aus dem Transistors T1 (links) heraus und in die Batterie 1 (links) hineinfließt. Was aber an der einen Seite in die Batterie 1 hineinfließt, muss an der anderen Seite, nämlich dem „+“-Pol der Batterie 1, wieder heraus fließen! Schließlich handelt es sich um einen oder mehrere geschlossene Stromkreise bei denen keine Ladungsträger verlorengehen oder hinzugefügt werden dürfen!

Wenn also der Emitterstrom I_E1 aus dem Transistors T1 heraus und in die Batterie 1 (links) hineinfließt, dann muss dieser auch wieder auf der anderen Seite am „+“-Pol wieder heraus fließen. Der Emitterstrom I_E1 wiederum fließt über den (Schiebe-) Schalter 14 zum Stromknoten C, um sich dort wieder in den Basisstrom I_B1 plus dem Kollektorstrom I_C1 aufzuteilen!

Während der Kollektorstrom I_C1 das Glühlämpchen 18 mit Strom versorgt, fließt der Basisstrom I_B1 weiter aus dem Stromknoten C heraus und wieder in die Batterie 2 (rechts) zurück!

Im Stromknoten D addiert sich der Basisstrom I_B1 = - I_B2 zum Kollektorstrom I_C2 und fließt als Emitterstrom I_E2 wieder in die Batterie 2 (rechts) zurück (siehe obenstehende Schaltung)!

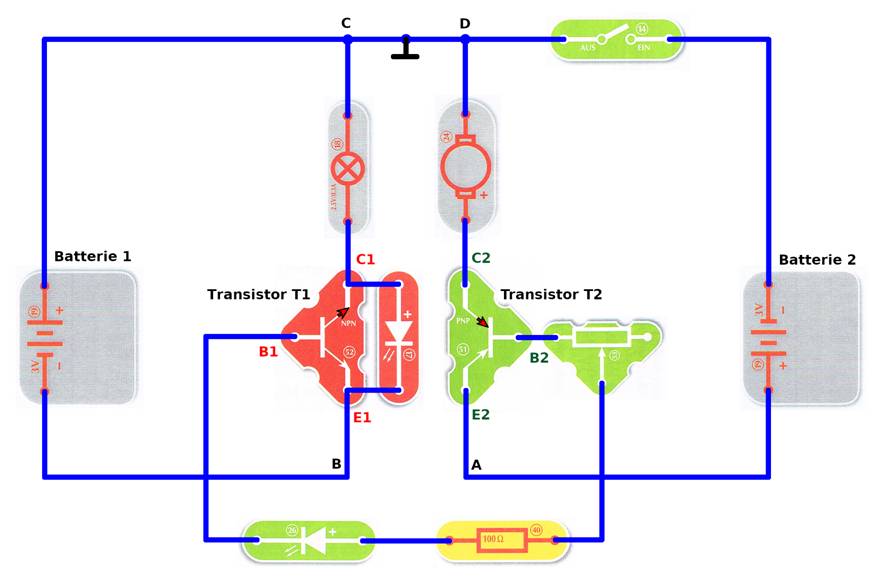
Insgesamt gibt es in der obenstehenden Schaltung und dem nachfolgenden Versuchsaufbau drei Stromkreise und zwar

· den linken Stromkreis

mit der Batterie 1 (links im Bild) als Energielieferant für das Glühlämpchen 18 und den NPN-Transistor 52,

· den rechten Stromkreis

mit der Batterie 2 (rechts im Bild) als Energielieferant für den Elektromotor 24 und den PNP-Transistor 51 und

· den Basis-Stromkreis

mit dem (Basis-) Widerstand 40 zwecks Stromzufuhr von der Basis 2 des PNP-Transistors 51 hin zur Basis 1 des NPN-Transistor 52.

Da der „+“-Pol der Batterie 1 des linken Stromkreises im oberen Teil der Schaltung direkt mit dem „-“-Pol der Batterie 2 des rechten Stromkreises verbunden ist, liegt im unteren Teil der Schaltung zwischen dem Emitter E1 des NPN-Transistors 52 (links) und dem Emitter E2 des PNP-Transistors 51 (rechts) die Gesamtspannung U_AB = U_{Batt 1} + U_Batt 2 an, sodass das Verbinden der Kontakte A und B unweigerlich zu einem Kurzschluss führt!

Der äußere Stromkreis (=Basis-Stromkreis ) mit den beiden in Reihe geschalteten Batterien 1 und 2 schließt sich über den Basis-Stromkreis, d.h. vom Emitter E2 des PNP-Transistors 51 (rechts) zum Emitter E1 des NPN-Transistors 52 (links). Dabei geht die Stromflussrichtung vom Kontakt A zum B, d.h. von der linken zur rechten Seite der Schaltung:

(Zum Vergrößern bitte auf das Bild klicken!)

Wir wissen jetzt, dass die beiden Batterien 1 und 2 im äußeren, d.h. dem Basis-Stromkreis, in Serie geschaltet sind. Dabei schließt sich der äußere Stromkreis zwischen den Kontakten A und B in Form der Beschaltung Magnet-schalter 12, Potentiometer 53 und Widerstand 40, die allesamt in Reihe geschaltet sind.

Die Reihenschaltung der beiden Batterien 1 und 2 ist es schließlich, die die Bedingung U_AB = U_{Batt 1} + U_{Batt 2} schafft, damit überhaupt eine treibende Spannung U_AB > U_{Batt 1} bzw. U_{Batt 2} zwischen den Kontakten A und B entstehen kann. Denn, obwohl im unteren Schaltungsbereich mit dem Basis-Stromkreis von Basis B2 zur Basis B1 keine Spannungsquelle vorhanden ist, fließen ja trotzdem kleine Basisströme. Aber wir wissen ja jetzt, wie diese zustande kommen!

Und, obwohl wir es ja mit den beiden Batterien 1 und 2 und den zwei getrennten Stromkreisen zu tun haben, gibt es eben doch eine elektrische Verbindung zwischen diesen, nämlich den Basis-Stromkreis zwischen den Kontakten A und B!

Aber es gibt natürlich noch etwas zu entdecken. Wenn man nämlich den (Schiebe-) Schalter 14 ausschaltet, dann wird wider Erwarten nur der rechte Schaltkreis mit dem PNP-Transistor 51 und der Batterie 2 ausgeschaltet, nicht aber der linke Schaltkreis mit dem NPN-Transistor 52 und der Batterie 1, der weiterhin „unter Strom steht“. Wer das nicht glaubt, kann gerne eine der beiden Leuchtdioden 17 oder 26 auf den NPN-Transistor 52 (links) stecken und sich selbst überzeugen:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden Bild und der Schaltung sieht, ist der (Schiebe-) Schalter 14 ausgeschaltet, so dass der rechte Schaltkreis mit dem PNP-Transistor 51 und der Batterie 2 definitiv ausgeschaltet ist, aber eben nicht der linke Schaltkreis mit dem NPN-Transistor 52 und der Batterie 1, der weiterhin „unter Strom steht“!

In diesem Zusammenhang sei daran erinnert, dass wenn der NPN-Transistor 52 (links) nicht über die Basis B1 angesteuert wird, die C1E1-Strecke sperrt, hochohmig wird mit der Folge, dass an der gesperrten C1E1-Strecke ein entsprechend großer Spannungsabfall entsteht, der die rote Leuchtdiode 17 zum Leuchten bringt!

Fazit

Jetzt steht definitiv fest, dass der rechte Schaltkreis mit dem PNP-Transistor 51 und der Batterie 2 den linken, ansonsten autonomen Schaltkreis mit dem NPN-Transistor 52 und der Batterie 1 steuert. Aber nur, wenn man die Schaltung mit dem (Schiebe-) Schalter 14 und den Basis-Stromkreis mit dem Magnetschalter 12 einschaltet.

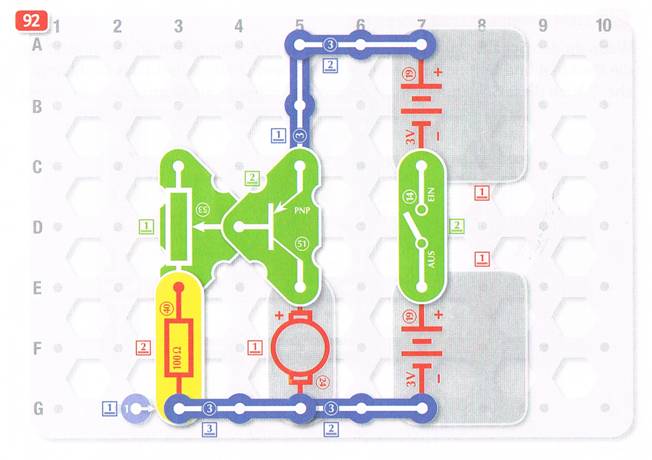
Diesbezüglich kann man sagen, dass sich mit einem Strom ein anderer Strom, nämlich der durch das Glühlämpchen 18, ein- und ausschalten lässt. Und zwar mit dem Vorteil, dass ein kleiner Basisstrom im äußeren Basis-Stromkreis einen wesentlich größeren Kollektorstrom des NPN-Transistors 52 im linken Schaltkreis mit eigener Spannungsquelle (= Batterie 1) steuert. -

Drehzahlregelung beim Elektromotor

Wenn man die Schaltung des Versuchs 92 verstehen will, dann muss man sich als Erstes nur die

verwendeten Bauteile wie z.B. Batterien, Schalter, Widerstände, Poti oder den Motor anschauen:

1. Es werden zwei Batteriefächer 19 verwendet, was bedeutet, dass die Schaltung mit einer max. Betriebsspannung von zusammen 6 Volt betrieben wird.

Demzufolge müsste man sich im Falle des Betriebs mit einem Glühlämpchen für das Glühlämpchen 27 (U_Nenn = 6,0 V, I_Nenn = 0,5 A) entscheiden, da das Glühlämpchen 18 (U_Nenn = 2,5 V, I_Nenn = 0,3 A) wegen der niedrigeren Nennspannung von U_Nenn = 2,5 V ansonsten durchbrennen würde!

2. Es wird der Elektromotor 24 verwendet, von dem wir leider nicht die Nenn-Betriebsdaten kennen und von dem es heißt: „Aber der Motor benötigt im Vergleich zu dem Glühlämpchen einen viel stärkeren Strom. Dieser hohe Strom fließt durch den Transistor und erwärmt ihn dabei stark.“

Dabei verhält es sich so, dass der Elektromotor 24 „nur“ einen Strom von I_{M 24} = 270 mA bei einer Spannung von U_{M 24} = 4,35 V verbraucht. Selbst bei der Verwendung frischer, fabrikneuer Batterien und einer Spannung von U_{M 24} = 6,0 V wären das immer noch „nur“ I_{M 24} = 372,4 mA anstatt I_{Glüh 27} = 500 mA wie beim Glühlämpchen 27.

Aber obwohl die Motorstromstärke mit 372,4 mA < I_{M 24} < 500 mA kleiner ausfällt als beim Glühlämpchen 27, erwärmt sich der Transistor 51 dabei trotzdem stark! Wie geht das zusammen? Wie kann das sein?

Wenn man den Spannungsabfall U_EC an der Emitter-Kollektor-Strecke des Transistors 51 mit U_EC = 0,31 V misst, dann stellt man fest, dass sich der Transistor 51 bereits in der sogenannten Sättigung befindet bei der die Wärmeverlustleistung am geringsten ist im Vergleich zum Normalbetrieb mit U_{EC, AP} = ½ * U_Batt ≈ 2,5 V (= mittlerer Arbeitspunkt AP_M auf der Arbeitsgeraden), wo die Wärmeverlustleistung mit am größten ist.

3. Beim Schaltungsaufbau werden auch die Widerstände 40 und 53 verwendet. Dabei wird der Widerstand 40 als Basis-Widerstand verwendet, um den Arbeitspunkt AP_M einzustellen und um den Basisstrom I_B zu begrenzen, wenn der verstellbare Widerstand (= Potentiometer 53) den Wert R_{Poti 53} ≈ 0 Ω (= Linksanschlag) annimmt:

Stromverstärkung B

B = I_C / I_B → B = 50 → Siehe auch Versuch 72 „Verstärkung B“!

I_B = I_C / B

= 500 mA / 50 = 10 mA → Erfahrungswert für I_C = 500 mA

r_EB = u_EB / I_B

= 0,8 V / 10 mA = 0,08 kΩ = 80 Ω

Zwecks Bestätigung der bisher berechneten Werte lassen sich diese auch „rückwärts“ berechnen:

I_B = u_EB / R₄₀

= 0,8 V / 100 Ω = 0,008 A = 8 mA

Wenn man sich die nachfolgende Schaltung des PNP-Transistors 51 zum Versuch 92 anschaut, dann könnte man meinen, dass es sich bei dieser um eine Kollektorschaltung handelt:

(Zum Vergrößern bitte auf das Bild klicken!)

Wenn man aber die obenstehende Schaltung vertikal spiegelt bzw. nach unten umklappt, dann sieht diese schon ganz anders aus! Dann handelt es sich plötzlich um eine Emitterschaltung:

(Zum Vergrößern bitte auf das Bild klicken!)

Was aber ist das Charakteristische an einer Emitterschaltung?

Bei einer Emitterschaltung liegt der Emitter E direkt auf Masse („┴“), engl. „ground“, abgekürzt „GND“, während der Kollektor C über den Arbeits- bzw. Lastwiderstand an die Stromversorgung der beiden Batterfächer 19 angeschlossen ist.

Bei einer Kollektorschaltung liegt der Kollektor C direkt auf Masse („┴“), engl. „ground“, abgekürzt „GND“, während der Emitter E über den Arbeits- bzw. Lastwiderstand an die Stromversorgung der beiden Batteriefächer 19 angeschlossen ist:

(Zum Vergrößern bitte auf das Bild klicken!)

Bleibt abschließend noch die Frage zu klären, weshalb der Autor der Experimentalanleitung die obenstehende Schaltung der drehzahlabhängigen Motorsteuerung so missverständlich dargestellt hat, sodass man diese mit einer Kollektorschaltung verwechseln kann, obwohl es sich ja bei dieser um eine Emitterschaltung handelt! Der Grund dafür aber ist so einfach wie verblüffend: die beiden Batteriefächer 19 lassen sich in der von mir korrigierten Darstellung so nicht auf der Aufbauplatte aufstecken! –

Weiter geht’s mit [Versuch 95 ]

[easy electronik 200 ] [ Seitenanfang ] [Versuch 72 ] [Versuch 95 ]