[ easy electronic 200 ] [ Seitenende ] [ Versuch 92 ] [ Versuch 102 ]

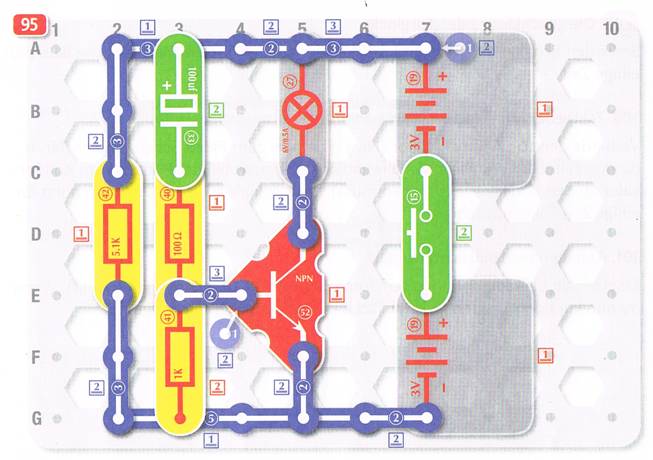
easy electronic 200 - Versuch 95

Zeit spielt eine Rolle

Der Versuch 95 ist mit „Laserstrahlen“ betitelt, die mit dem Glühlämpchen 27 erzeugt werden. Das aber ist ein Widerspruch!

Während eine Glühlampe stets diffuses, d.h. gestreutes Licht produziert, bei dem die Lichtstrahlen rund um den Glaskörper in alle Himmelsrichtungen ausgestrahlt werden, verlaufen die Lichtstrahlen beim Laser stets parallel, wobei diese gezielt in nur eine bestimmte Richtung verlaufen.

Weil aber Laserstrahlen parallel verlaufen und eben nicht diffus wie bei der Glühlampe, lässt sich beispielsweise mit einem Laserpointer kein Raum erhellen und bis in alle Ecken ausleuchten!

Würde man den Laserpointer auf eine kleine, ganz leichte und dünne in x- und y-Richtung auslenkbare Platte montieren, dann ließe sich mit dieser auch der Laserpointer horizontal in x-Richtung und vertikal in y-Richtung auslenken und bei entsprechend schneller Ablenkung eine quadratische oder rechteckige Fläche ausleuchten!

Damit die vom Laserpointer bestrahlte Rechteckfläche nicht flackert, müsste der auf der auslenkbaren Platte montierte Laserpointer sehr schnell, d.h. mit einer vertikalen Ablenkfrequenz von f_vertikal > 50 Hz, d.h. mehr als 50 Schwingungen/Sekunde, abgelenkt werden. Dazu muss man wissen, dass sich durch die Trägheit des menschlichen Auges ein flackerndes Fernsehbild ab einer Vertikalablenkfrequenz f_vertikal > 50 Hz flimmerfrei, engl. „flicker free“, wahrnehmen lässt.

Damit sich das nicht mehr flackernde Fernsehbild - und das gilt auch für das Laserpointer-Bild - über die gesamte Rechteckfläche im Format 16:9, d.h. fast doppelt so breit als hoch, gleichmäßig ausleuchten lässt, muss dieses in zwei sogenannte Halbbilder mit jeweils gerader und ungerader Zeilenzahl, engl. „frames“, aufgeteilt werden.

Bei heutigen LED-Farbfernsehern beträgt die Vertikalablenkfrequenz f_vertikal = 100 Hz und mehr, damit sich das Fernsehbild flimmerfrei darstellen lässt. Darüber hinaus müsste sich der Laserpointer durch schnelles Ein- und Ausschalten auch noch hell-dunkel tasten lassen, um ein grobes Schwarz-Weiß-Bild darstellen zu können. Für ein akzeptables Schwarz-Weiß-Bild bräuchte es aber auch noch entsprechend viele Graustufen. Demzufolge müsste sich beim Laserpointer auch noch die Helligkeit (= Intensität) für jeden einzelnen Bildpunkt individuell einstellen lassen.

Laserpointer gibt es hauptsächlich mit rotem Laserlicht, das wiederum mit nur einer roten Laser-LED erzeugt wird. Um weißes Licht für den „Laserpointer-Farbfernseher“ erzeugen zu können, bräuchte man drei unterschiedlich farbige Laser-LEDs und zwar in den Farben Rot, Grün, Blau. Deswegen nennt man Farbfernseher auch RGB-Fernseher.

Moderne LED-Fernseher verfügen zwecks Verbesserung des Kontrastes, insbesondere für Nachtaufnahmen oder Aufnahmen bei Dunkelheit, noch zusätzlich über eine LED-Matrix mit weißen LEDs, die sich bei Dunkelszenen einzeln ausschalten lassen. Demzufolge gibt es für jeden einzelnen(!) Bildpunkt - bei „High Quality (HQ) LED-Farbfernsehern“ – jeweils eine ein- und ausschaltbare LED nur für weißes Licht und tief schwarze Dunkelszenen. Wahnsinn!

Wenn also der Versuch 95 mit „Laserstrahlen“ betitelt ist, dann soll damit ausgedrückt werden, dass das Licht des Glühlämpchen 27 beim Drücken des Tasters 15 kurz aufblitzt, so als würde man im Dunkeln von einem Laserschwert getroffen.

Jetzt stellt sich gleich die Frage, ob beim Betätigen des Tasters 15, d.h. beim Einschalten und kurzen Inbetriebnehmen der Schaltung das Glühlämpchen 27 kurz aufblitzt oder nicht. Diesbezüglich stellt sich vorab auch die Frage, ob eine Glühlampe generell aufblitzen, d.h. kurz aufleuchten kann oder nicht.

Schließlich kommt bei einer Glühlampe nicht ein x-beliebiger Heizdraht zum Einsatz, sondern ein ganz spezieller Heizdraht, der sich u.a. aus Wolfram zusammensetzt. Und wegen des schlechten Wirkungsgrades hinsichtlich der Lichtausbeute handelt es sich ja bei der Glühlampe eher um ein kleines Heizöfchen als um ein Lichtenergie effizientes Leuchtmittel. Schließlich muss das elektrische Heizöfchen auch noch vorab vorgewärmt werden, bevor die Glühlampe leuchtet. Demzufolge muss die Wolfram-Glühwendel mittels elektrischen Stroms erst auf eine bestimmte Temperatur gebracht werden, bevor das Edelmetall zu glühen anfängt. Und das braucht etwas Zeit und ausreichend Energie. Und elektrische Energie W_el setzt sich aus dem Produkt von elektrischer Leistung P_el und der Zeit t wie folgt zusammen:

W_el = P_el * t

= U_{Glüh 27} * I_{Glüh 27} * t_Dauer

= 6 V * 0,5 A * 20 ms = 60 VA ms = 60 * 10^-3 VA s = 60 * 0,001 VA s = 60 mWs

Wie man anhand der Berechnung sieht, beträgt die Blitzdauer gerade mal t_Dauer = 20 ms, was natürlich sehr kurz ist.

Und, da die Trägheit des menschlichen Auges bei etwa einer (Bildwechsel-) Frequenz von f_Auge = 50 Hz liegt (siehe Fernseher) würde man den kurzen Lichtblitz auch gar nicht erst sehen:

f_Auge = 1 / T_Auge →

T_Auge = 1 / f_Auge

= 1 / ( 50 Hz ) = 1 / ( 50 Schwingungen / Sekunde ) = 1 / ( 50 * 1 Schwingung / Sekunde )

= 0,02 s = 20 ms

Damit man den „Lichtblitz“ des Glühlämpchen 27 auch wirklich sehen kann, müssen wir die Blitzdauer auf z.B. t_Dauer = 1 s vergrößern, sodass sich die im „verlängerten“ Blitz gespeicherte Energie W_el nun wie folgt berechnet:

W_el = P_el * t

= U_{Glüh 27} * I_{Glüh 27} * t_Dauer

= 6 V * 0,5 A * 1 s = 3 VAs = 3 Ws → Nennbetriebsdaten des Glühlämpchen 27: U_Nenn = 6 V, I_Nenn = 0,5 A

Ob sich die soeben berechnete elektrische Blitzlicht-Energie W_el = 3 Ws auch wirklich einstellt, muss sich aber noch herausstellen. Diese fällt nämlich geringer aus, wenn sich die vom Hersteller des Glühlämpchen 27 angegebenen Nennbetriebsdaten wider Erwarten in der nachfolgenden Schaltung nicht erreichen lassen:

(Vergrößern: auf Bild klicken! | KOSMOS easy electronic, Seite 39)

Die zuvor berechnete elektrische Blitzlicht-Energie W_el = 3 Ws lässt sich nämlich u.a. nur dann erreichen, wenn die in den beiden Batteriefächern 19 eingesetzten 1,5 V Batterien vom Typ „AA Mignon“ fabrikneu sind und ihrerseits über die maximal speicherbare Energiemenge verfügen!

Dabei kommt es dann hauptsächlich auch darauf an, dass sich die Nennbetriebsspannung von U_Nenn = 6 V des Glühlämpchen 27 bei der Blitzentladung über die Kollektor-Emitterstrecke des NPN-Transistors 52 nahezu vollständig aufbringen lässt:

U_{Glüh 27, Blitz} + u_{CE, satt} + ( - U_{Batt, ges} ) = 0 →

U_{Glüh 27, Blitz} = U_{Batt, ges} - u_{CE, satt}

= 6,0 V – 0,2 V = 5,8 V

Damit das Glühlämpchen 27 richtig hell aufblitzen kann, muss der NPN-Transistors 52 als Schalter betrieben und mit u_{CE, satt} = 0,2 V vollständig in die Sättigung gefahren werden (siehe Arbeitspunkt AP4):

(Vergrößern: auf Bild klicken! | Quelle: Elektronik-Kompendium)

Neben der treibenden Spannung von U_{Glüh 27, Blitz} = 5,8 V bedarf es aber auch eines entsprechendes Stromes von I_Nenn = 0,5 A damit das Glühlämpchen 27 richtig hell aufblitzen kann.

Wenn man dabei den NPN-Transistors 52 als Schalter in die Sättigung fährt, geht die Stromverstärkung B auf den Wert B = 25 zurück, sodass sich der dazu erforderliche Basisstrom I_B wie folgt berechnet (siehe auch Versuch 72):

B = I_C / I_B →

I_B = I_{C satt} / B =

= 0,5 A / 25 = 0,02 A = 20 mA

Berechnung der Kapazität des Kondensators

Wenn man sich die obenstehende Schaltung anschaut, dann stellt man fest, dass sich der Basis-Spannungsteiler des NPN-Transistors 52 aus den Bauelementen Kondensator 33, Widerstand 40 und Widerstand 41 in Reihenschaltung zusammensetzt.

Was aber ist ein Kondensator? Etwa ein Bauteil bei dem etwas kondensiert, bei dem sich Wassertröpfchen niederschlagen? Weit gefehlt! Im Kondensator werden logischerweise keine Wasserteilchen kondensiert, d.h. verdichtet, sondern elektrische Ladungsträger in Form von Elektronen.

Bei einem Kondensator handelt es sich also um ein elektrisches Bauteil mit dem sich elektrische Energie W_el in Form von positiv und negativ geladenen Ladungsträgern (= Elektronen) speichern lässt.

>> Ein Kondensator (von lateinisch condensare ‚verdichten‘) ist ein passives elektrisches Bauelement mit der Fähigkeit, in einem Gleichstromkreis elektrische Ladung und die damit zusammenhängende Energie statisch in einem elektrischen Feld zu speichern. Die gespeicherte Ladung pro Spannung wird als elektrische Kapazität bezeichnet und in der Einheit Farad gemessen. In einem Wechselstromkreis wirkt ein Kondensator als Wechselstromwiderstand mit einem frequenzabhängigen Impedanzwert.

Kondensatoren bestehen im Prinzip aus zwei elektrisch leitfähigen Flächen, den Elektroden, die von einem isolierenden Material, dem Dielektrikum, voneinander getrennt sind. Die Größe der Kapazität wird durch die Fläche der Elektroden, das Material des Dielektrikums und den Abstand der Elektroden zueinander bestimmt. Die Elektroden und das Dielektrikum können aufgerollt oder parallel geschaltet als Stapel angeordnet sein. Industriell hergestellte Kondensatoren werden mit Kapazitätswerten von etwa 1 Pikofarad (10⁻¹² F) bis zu etwa 1 Farad, bei Superkondensatoren bis zu 10.000 Farad geliefert.

Die mit großem Abstand am meisten produzierten Kondensatoren sind integrierte Speicherkondensatoren in digitalen Speicherschaltungen. Die wichtigsten Kondensatorarten sind Keramikkondensatoren, Kunststoff-Folienkondensatoren, Aluminium- und Tantal-Elektrolytkondensatoren und, obwohl sie auf völlig anderen Speicherprinzipien beruhen, die Superkondensatoren. Neben diesen Kondensatoren mit festen Kapazitätswerten gibt es Bauelemente mit einstellbaren Kapazitätswerten, die variablen Kondensatoren.

Kondensatoren werden in vielen elektrischen Anlagen und in nahezu allen elektrischen und elektronischen Geräten eingesetzt. Sie realisieren beispielsweise elektrische Energiespeicher als Zwischenkreiskondensatoren in Frequenzumrichtern, als Speicherkondensator in Sample-and-Hold-Schaltungen oder als Photo-Flash-Kondensatoren in Blitzlichtgeräten. Sie koppeln Signale in Frequenzweichen von Audiogeräten und bilden als hochstabile Klasse-1-Kondensatoren zusammen mit Spulen Filter und Schwingkreise. Als Glättungskondensatoren in Netzteilen und Stützkondensatoren in Digitalschaltungen sind sie im Bereich der Stromversorgung zu finden. Sie unterdrücken als Entstörkondensatoren elektromagnetische Störsignale und bewirken als Leistungskondensatoren eine erwünschte Phasenkompensation. Spezielle Bauformen von Kondensatoren werden als Sensor verwendet.

Unerwünschte kapazitive Störeinkopplungen aus elektrischen Feldern benachbarter Bauteile in Schaltungen und parasitäre Kapazitäten, sogenannte Streukapazitäten, gehören nicht zu den Kondensatoren. Ebenfalls nicht zu den Kondensatoren gehören eine Reihe von Aktoren wie piezoelektrische Wandler, elektrostatische Lautsprecher, Ablenkplatten und Bauelemente der Elektrooptik. << (Quelle: Wikipedia)

Jetzt wissen wir, dass sich die Speicherkapazität C eines Kondensators in der Maßeinheit „Farad“ [ F ] gemessen wird. Selbstverständlich lässt sich die Maßeinheit [ F ] auch wie folgt umrechnen:

[ F ] = [ As / V ] → Kapazität C [ F ] = Ladungsmenge Q [ As ] / Spannung U [ V ] →

Formel zur Berechnung der Kapazität C = Q / U mit der Ladungsmenge Q = I * t

Der in der Schaltung verwendete Kondensator 33 verfügt über eine Kapazität C von

C = 100 µF = 100 * 10^{-6 F} = 100 * 1 / 10⁶ F = 100 * 1 / 1 000 000 F = 100 * 0,000 001 F = 0,0001 F

= 0,0001 As/V = 0,1 mA s / V →

C = Q / U = I * t / U →

t = C * U / I

= 100 µF * 6,0 V / 0,5 A = 0,1 mA s / V * 6,0 V / 0,5 A = 0,1 mA s / V * 6,0 V / 500 mA

= 0,1 * 6,0 / 500 s = 0,6 / 500 s = 0,0012 s = 1,2 ms → Millisekunden!

Jetzt wissen wir, dass sich der Kondensator 33 tatsächlich blitzschnell in nur 1,2 Millisekunden aufladen lässt!

Probe:

C = Q / U = I * t / U

= 0,5 A * 1,2 ms / 6,0 V = 500 mA * 1,2 ms / 6,0 V = 500 * 1/1000 A * 1,2 * 1/1000 s / 6,0 V

= 500 A * 1,2 s / 6,0 V * 1/1 000 000 = 500 * 1,2 / 6,0 * 10^-6 As/V = 500 * 1,2 / 6,0 µF = 100 µF 

Das blitzschnelle Aufladen des Kondensator 33 in nur t_Aufladen = 1,2 ms, d.h. 1,2 Millisekunden(!) setzt voraus, dass sich beim Aufladen im Stromkreis des Kondensators kein Vorwiderstand R_Vor befindet, der den Aufladevorgang ausbremsen könnte! Auch kein noch so kleiner, winziger Leitungswiderstand in den Anschlussleitungen bei der Stromzuführung zum Kondensator.

Demzufolge findet das Berechnen der Auf- und Entladung des Kondensators unter idealisierten Bedingungen statt!

Berechnung des Basis-Spannungsteilers

Wenn man sich die obenstehende Schaltung, d.h. den Basis-Spannungsteiler, genauer anschaut, dann stellt man fest, dass es sehr wohl mehrere Widerstände in der Stromleitung vom Kondensator 33 weg gegen Masse („┴“) hin zum Minuspol der 6 Volt Batterie gibt als da sind: Widerstand 40, Widerstand 41 und der parallel geschaltete Bahnwiderstand r_BE der Basis-Emitter-Diode des NPN-Transistors 52:

r_BE = u_BE / I_B → Die Basis-Emitter-Diode wird ab einer Durchlassspannung von u_BE = 0,7 V elektrisch leitend!

= 0,7 V / 20 mA = 0,7 / 20 kΩ = 0,035 kΩ = 35 Ω

Weil der Bahnwiderstand r_BE der BE-Diode gegenüber dem (Parallel-) Widerstand 41 mit R₄₁ = 1 kΩ sehr klein ist, darf man den (Parallel-) Widerstand 41 bei der Berechnung des Basis-Spannungsteilers weglassen:

U_C33 + U_R40 + u_BE + ( - U_Batt,ges ) = 0 →

U_C33 = U_Batt,ges - U_R40 - u_BE

= U_Batt,ges - I_B * ( R₄₀ + r_BE )

= 6,0 V – 20 mA * ( 100 Ω + 35 Ω ) = 6,0 V – 20 mA * 135 Ω = 6,0 V – 20 * 135 mV

= 6,0 V – 2 700 mV = 6,0 V – 2,7 V = 3,3 V → max. Ladespannung U_C33 am C₃₃, wenn T52 elektrisch leitend ist!

Berechnung der Entladezeit des Kondensators

Nachdem der Kondensator 33 beim Betätigen des Tasters 15 aufgeladen wurde und das Glühlämpchen 27 kurz aufblitzte, kehrt der NPN-Transistors 52 wieder in den gesperrten Zustand zurück, so als ob die Stromversorgung durch die 6 Volt Batterien der Schaltung abgeschaltet wurde.

In dem Moment, wo der NPN-Transistors 52 wieder in den gesperrten Zustand zurückkehrt, kann sich der aufgeladene Kondensator 33 sofort wieder entladen. Und zwar über die in Reihe geschalteten Widerstände Widerstand 40, Widerstand 41 und Widerstand 42:

R_Ent = R₄₀ + R₄₁ + R₄₂

= 100 Ω + 1 kΩ + 5,1 kΩ = 6,2 kΩ

So wie der Kondensator nach der Zeitspanne von t = 5 τ nahezu vollständig aufgeladen ist, ist er auch nach der gleichen Zeitspanne vollständig entladen. Allerdings mit dem Entladewiderstand R_Ent = 6,2 kΩ:

t_Ent = 5 τ

= 5 * R_Ent * C₃₃ =

= 5 * 6,2 kΩ * 100 µF = 5 * 6,2 * 10³ V/A * 100 * 10^{-6 3} As/V = 3 100 * 10^-3 s = 3 100 ms = 3,1 s

Selbstverständlich lässt sich die Entladezeit t_Ent auch über die im Kondensator 33 gespeicherte Energie W_el wie folgt berechnen:

W_el = P_el * t_Ent →

t_Ent = W_el / P_el

= W_el / ( U_C33 * I_C33 ) = W_el / ( U_C33 ² / R_Ent )

= 17,8 mWs / [ ( 6 V )² / 6,2 kΩ ) ]

= 17,8 * 10^-3 V/A s / [ ( 36 V² / 6,2 * 10³ V/A ) ] = 17,8 s / [ ( 5,81 ) ] = 3,06368 s ≈ 3,1 s

Jetzt wissen wir, dass sich ein Kondensator über verschiedene elektrische „Wege“ unterschiedlich schnell auf- oder entladen kann!

Im vorliegenden Versuch braucht der Kondensator 33 rund 3,1 Sekunden, um sich vollständig zu entladen, während er für das Aufladen, erkennbar an dem kurzen Aufblitzen des Glühlämpchens 27, nur t_Aufladen = 510 ms = 0,5 s braucht (siehe Berechnung weiter unten).

Das mit der längeren Entladedauer von t_Entlade = 3,1 s lässt sich auch praktisch überprüfen, indem man das Glühlämpchens 27 durch mehrmaliges, kurzes und schnelles Drücken des Tasters 15 über den NPN-Transistors 52 einschaltet, sodass das Glühlämpchen nur noch schwach glimmt, aber eben nicht mehr hell aufblitzt!

Das, was das helle und kurze Aufblitzen des Glühlämpchens 27 nämlich signalisiert, ist der kurze Aufladeprozess des Kondensators 33, während das noch schwache Glimmen des Glühlämpchens 27 - durch mehrmaliges, kurzes und schnelles Drücken des Tasters 15 - signalisiert, dass der Entladeprozess über die Entladewiderstände R₄₀, R₄₁ und R₄₂ des vormals aufgeladenen Kondensators 33 noch nicht abgeschlossen ist.

Demzufolge erfolgt das Aufladen in nur 0,5 s und das Entladen „in ewig langen“ 3,1 s. -

Um die Funktionsweise der Schaltung zum Versuch 95 besser verstehen zu können, empfiehlt es sich, nicht nur den Auflade- und Entladevorgang des Kondensators 33 voneinander getrennt zu betrachten, sondern diesen auch schaltungstechnisch, wie nachfolgend dargestellt, umzusetzen. Zu diesem Zweck eignen sich die beiden Leuchtdioden 17 und 26 in besonderer Weise, weil sie den Stromfluss in nur eine Richtung von Plus („+“) nach Minus („-“) erlauben und dies auch noch durch entsprechendes Aufleuchten signalisieren!

Im nachfolgenden Bild links verhält es sich so, dass die Schaltung durch kurzes Drücken des Tasters 15 „unter Strom“ gesetzt wird, sodass sich der vormals entladene Kondensators 33 über den Widerstand 41 und parallel auch über die BE-Diode des NPN-Transistors 52 auflädt.

Den zur BE-Strecke und zum Bahnwiderstand r_BE = 35 Ω parallel geschalteten Widerstand 41 mit R₄₁ = 1 kΩ kann man dabei wegen r_BE << R₄₁ problemlos vernachlässigen.

Wie man an dem kurzen Aufblitzen der grünen Leuchtdiode 26 (links im Bild) erkennen kann, lädt sich der Kondensator 33 in nur t_Aufladen = 0,5 s auf, sodass dieser hochohmig wird und keinen (Basis-) Strom I_B < 20 mA mehr fließen lässt. Dabei stellt sich dann am Kondensator 33 selbst die (Leerlauf-) Spannung U_C33 = 3,3 V ein. Gäbe es dabei nicht den in Reihe geschalteten Widerstand 41, so würde sich die (Leerlauf-) Spannung U_C33 des Kondensators 33 sogar bis auf die Batteriespannung U_{Batt, ges} = 6,0 V erhöhen!

Übrigens: Wegen der sogenannten Flussspannung von U_{LED 26} = 2,1 V der grünen Leuchtdiode 26 (links im Bild), kann sich der in Reihe geschaltete Kondensator 33 nicht vollständig aufladen, sodass demzufolge das Glühlämpchens 27 wider Erwarten nicht aufblitzt (siehe nachfolgendes Bild links):

(Zum Vergrößern bitte auf das jeweilige Bild klicken!)

Im obenstehenden Bild rechts verhält es sich so, dass sich der bereits aufgeladene Kondensator 33 über den zu schließenden (Magnet-) Schalter 12 und den zum Kondensator parallel geschalteten (Entlade-) Widerstand 40 mit R₄₀ = 100 Ω entladen kann, sodass die rote Leuchtdiode 17 kurz aufblitzt.

Auch hier gilt, dass sich der aufgeladene Kondensator 33 wegen der Flussspannung von U_{LED 17} = 1,6 V der roten Leuchtdiode 17 (rechts im Bild) nicht vollständig entladen kann, sodass demzufolge das Glühlämpchens 27 wider Erwarten nicht aufblitzt (siehe obenstehendes Bild rechts). -

Wie man in den beiden obenstehenden Bildern sieht, macht es im Zweifelsfall Sinn, die Stromzweige für das Auf- und Entladen des Kondensator 33 getrennt aufzubauen und zu analysieren, um auf diese Weise das Funktionieren und Zusammenwirken der einzelnen Bauteile der Schaltung besser zu verstehen! -

Wenden wir uns nachfolgend wieder der ursprünglichen Schaltung zum Versuch 95 zu:

(Zum Vergrößern bitte auf das Bild klicken!)

Berechnung der maximalen Aufladespannung am Kondensator

Wenn sich anfangs der NPN-Transistors 52 im gesperrten Zustand befindet, dann ist der Kondensator 33 über die in Reihe geschalteten Widerstände Widerstand 40 und Widerstand 41 an die Masse („┴“) bzw. den Minuspol der 6 Volt Batterie angebunden, wobei der Bahnwiderstand r_BE der BE-Diode praktisch unendlich groß ist und gegenüber dem parallel geschalteten Widerstand 41 vernachlässigt, d.h. als nicht vorhanden angenommen werden darf.

Schaltet man dann die obenstehende Schaltung durch den Drücken des Tasters 15 einige Sekunden lang ein, dann lädt sich der Kondensator 33 sozusagen von Null an auf, stellt er im ersten Moment des Aufladens einen elektrischen Kurzschluss dar, sodass der Spannungsabfall am Kondensator mit U_C33 = 60 mV sehr klein ist (siehe weiter unten):

U_C33 = U_Batt,ges - U_R40 - U_R41

= U_Batt,ges – I_C33 * ( R₄₀ + R₄₁ // r_BE ) →

Da der NPN-Transistors 52 durch den Kurzschlussstrom des Kondensators 33 bereits voll aufgesteuert wird, ist der Bahnwiderstand r_BE der BE-Diode mit r_Be = 35 Ω sehr klein, sodass der parallel geschaltete Widerstand 41 mit R₄₁ = 1 kΩ vernachlässigt werden darf:

U_C33 ≈ U_Batt,ges – I_C33 * ( R₄₀ + r_BE ) →

= 6,0 V – 44 mA * ( 100 Ω + 35 Ω )

= 6,0 V – 44 mA * 135 Ω = 6,0 V – 5 940 mV = 6,0 V – 5,94 V = 0,06 V = 60 mV → kurz nach dem Einschalten!

Dabei wird der anfänglich große Ladestrom wegen des Kurzschlusses des Kondensators 33 durch die in Reihe geschalteten Widerstände R₄₀ und r_BE wie folgt begrenzt:

I_C33 = U_Batt,ges / ( R₄₀ + r_Be )

= 6,0 V / ( 100 Ω + 35 Ω ) = 6,0 V / 135 Ω = 0,0444 A ≈ 44 mA → max. Aufladestrom des Kondensators 33

Nach der Zeitspanne von t = 5 τ (sprich: „fünf Tau“) mit τ = R * C ist jeder Kondensator zu 99,99 % vollständig aufgeladen:

t_Auf = 5 τ = 5 * R * C

= 5 * 135 Ω * 100 µF = 5 * 135 Ω * 100 * 10^-6 As/V = 675 V/A * 100 * 10^-6 As/V

= 67 500 * 10^-6 s = 67,5 * 10^-3 s = 67,5 ms

Die nach dem Aufladen des Kondensators 33 im Kondensator gespeicherte elektrischen Energie W_el berechnet sich wie folgt:

W_el = P_el * t

= U_{C33, max} * I_C33 * t_Dauer = U_C33 * Q_C33 * t_Dauer

= 6 V * 44 mA * 67,5 ms = 264 mW * 67,5 ms = 17 820 * 10^-6 Ws = 17,8 * 10^-3 Ws

= 17,8 mWs

Weiter geht’s mit [ Versuch 102 ].

[ easy electronic 200 ] [ Seitenanfang ] [ Versuch 92 ] [ Versuch 102 ]