Künstliche Intelligenz (KI) – Grundlagen Python

[ Home ] [ Seitenende ] [ Start ] [ Teil 1 ] [ Teil 2 ] [ Teil 3 ]

Künstliche Intelligenz (KI) – Grundlagen Python

3 Python-Pakete für Datenanalysten

3.1 NumPy

NumPy dient dazu, mathematische Operationen im n-dimensionalen Raum (zum Beispiel Matrix-Vektor-Multiplikation) durchführen zu können. Die wichtigste Grundstrukur ist das Array - es entspricht einem Vektor, einer Matrix oder einem Tensor.

Ein ausführliches Tutorial findest du hier, an dieser Stelle werden wir nur die Grundlagen besprechen. -

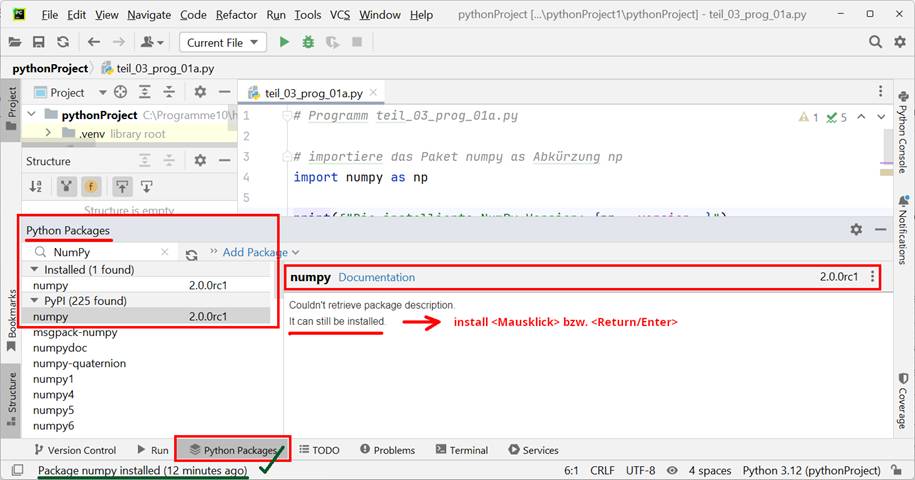
Installation des „NumPy“-Pakets unter der Entwicklungsumgebung „PyCharm“

Die Installation des engl. „Python Packages“, d.h. des Python Pakets namens „numpy 2.0.0 rc1“ (= engl. „release candidate“, d.h. Freigabe-Kandidat, Freigabeversion) in der integrierten „PyCharm“-Entwicklungsumgebung (IDE), d.h. engl. „Integrated Development Environment“, ist einfacher als man denkt:

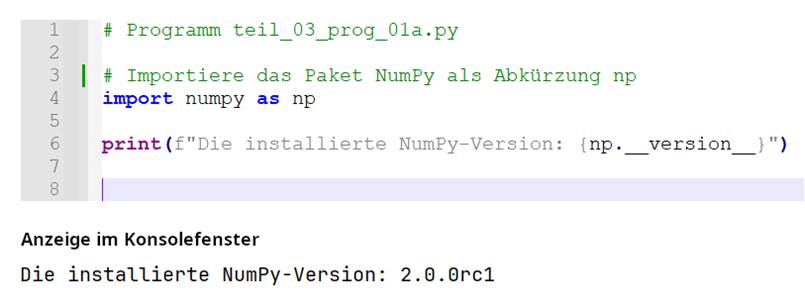
(Vergrößern: auf das Bild klicken! | Bild teil_03_prog_01a.jpg)

Mit dem nachfolgenden Programm teil_03_prog_01a.py lässt sich überprüfen, ob das „NumPy“-Paket ordnungsgemäß installiert wurde und ob es sich dabei auch um die ausgewählte „NumPy“-Version handelt:

(Vergrößern: auf das Bild klicken! | Programm teil_03_prog_01a.py)

Im Gegensatz zu anderen, höheren Programmiersprachen gibt es in Python wider Erwarten standardmäßig kein engl. „array“ im Sinne von Areal, Bereich, Anordnung, Aufstellung:

· Statement <pseudoArray : array = [ 'a', 2, 'c', 4 ]> " Fehlermeldung!

Aber wo ein Wille ist, ist auch ein Weg, könnte man meinen. Demzufolge gab es in älteren Python-Versionen sehr wohl eine <array>-Funktion, die aber ab der Python-Version 3.x aus der engl. „library“, d.h. Programmbefehls- und Funktions-Bibliothek entfernt wurde.

Hinweis:

Die Bibliothek ‚array’ ist in Python 3 veraltet und sollte nicht mehr verwendet werden! Stattdessen sollten Sie die ‚NumPy’-Bibliothek oder die integrierten Listen von Python verwenden!

Das nachfolgende Programm teil_03_prog_01b.py dient dazu, einen sogenannten Vektor namens

· Statement <my_vec = np.array([1, 2, 3, 4])>

zu programmieren, der aus vier Elementen besteht.

Der Vektor <my_vec> wiederum lässt sich nur programmieren, wenn man zuvor die Bibliothek, engl. „library“ namens ‚numpy’ wie folgt importiert:

· Statement <import numpy as np>

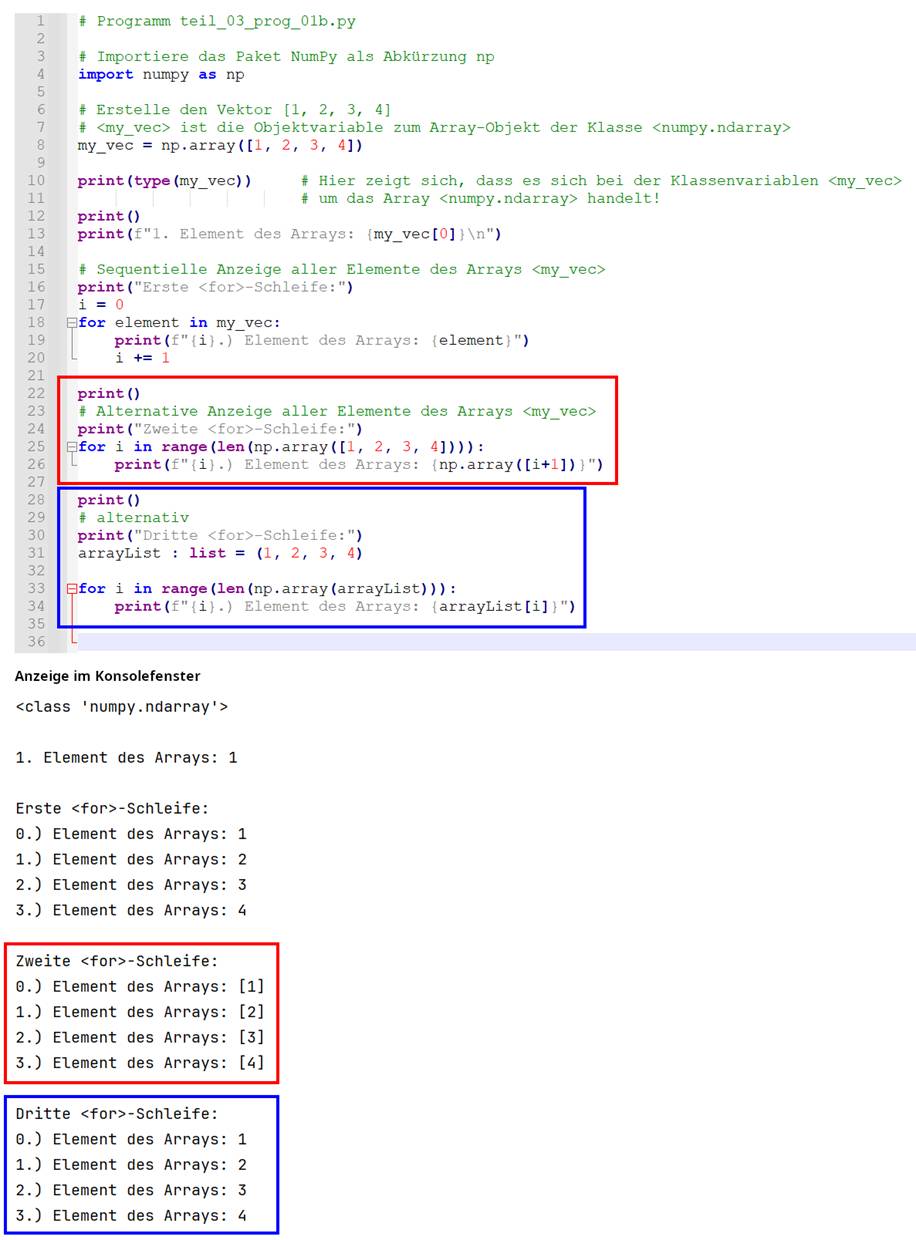
Dabei wird die Library ‚numpy’ durch den (Klassen-) Namen ‚np’ abgekürzt.

In dem Programm werden insgesamt drei verschiedene <for>-Schleifen programmiert, um den Vektor <my_vec> und dessen vier Elemente im Konsolefenster anzuzeigen. Dabei fällt auf, dass sich die vier Elemente des Vektors <my_vec> in die Liste <arrayList> auslagern lassen, sodass sich diese korrekt anzeigen lassen (siehe blauer Kasten). Ganz im Gegensatz zur zweiten <for>-Schleife, wo eben nicht die vier Elemente des Vektors <my_vec> korrekt angezeigt werden (siehe roter Kasten):

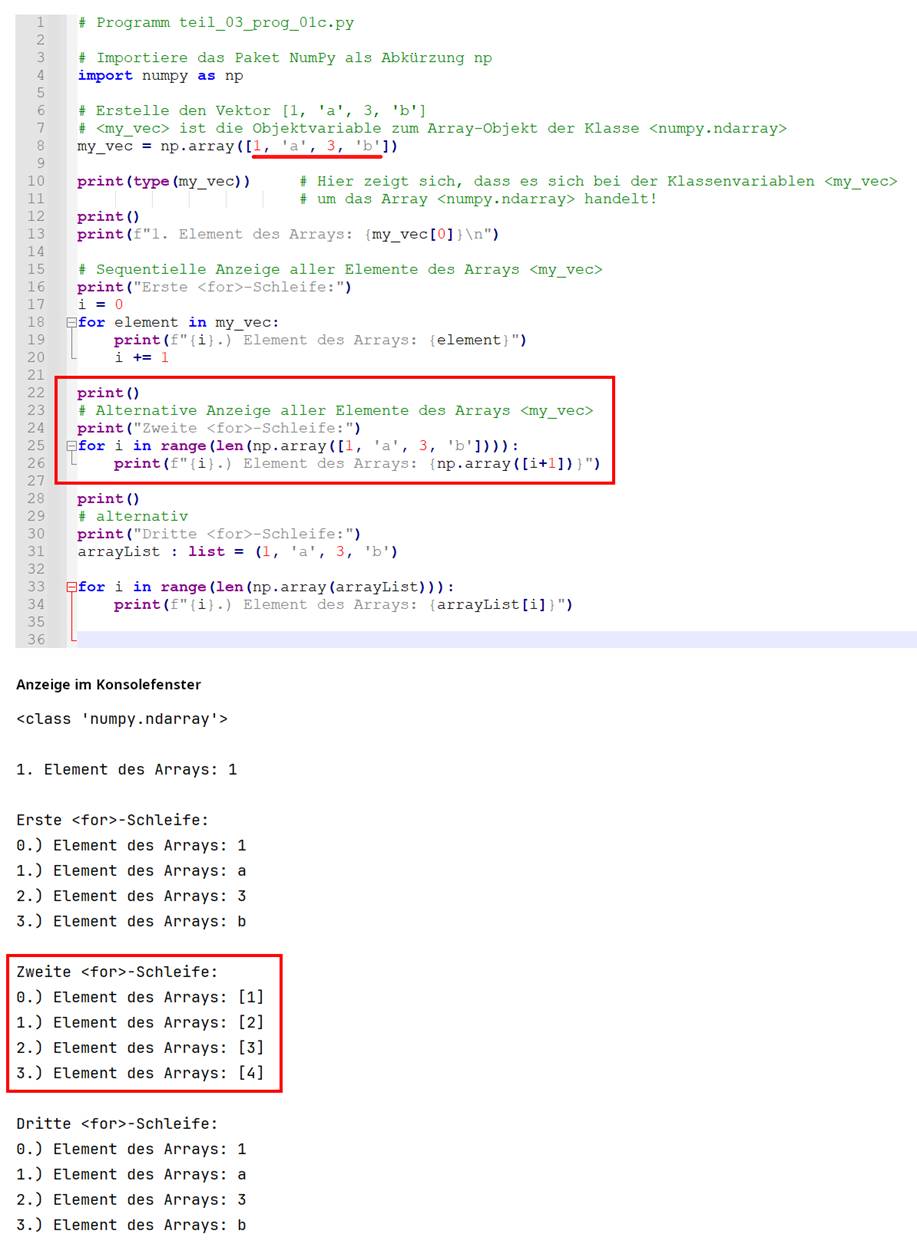
(Vergrößern: auf das Bild klicken! | Programm teil_03_prog_01b.py)

Das Problem mit der zweiten <for>-Schleife, nämlich dass die vier Elemente des Vektors <my_vec> eben nicht angezeigt werden, lässt sich mit dem nachfolgenden Programm teil_03_prog_01c.py wie folgt veranschaulichen:

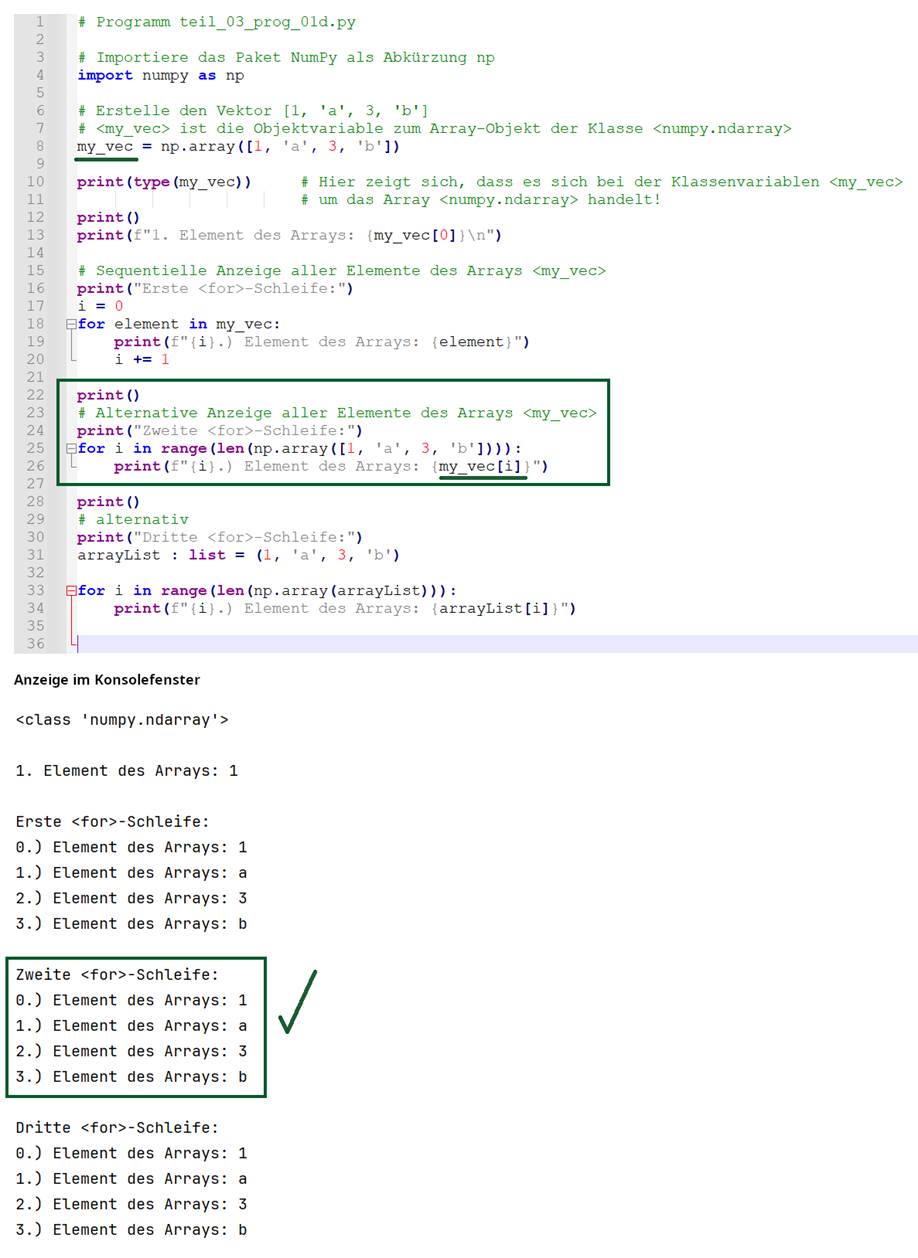
(Vergrößern: auf das Bild klicken! | Programm teil_03_prog_01c.py)

Das nachfolgende Programm teil_03_prog_01d.py bringt die Lösung, sodass nun erstmalig die vier Elemente des Vektors <my_vec> bzw. des Arrays <np.array([1, 'a', 3, 'b'])> korrekt angezeigt werden:

(Vergrößern: auf das Bild klicken! | Programm teil_03_prog_01d.py)

Um herauszufinden, weshalb das Programm teil_03_prog_01c.py mit dem

· Statement <print(f"{i}.) Element des Arrays: {np.array([i+1])}")> (siehe roter Kasten unten)

wider Erwarten nicht wie gewünscht die Inhalte [1, 'a', 3, 'b'] des

· Arrays <np.array([i+1])> im Bereich [ 1, …, 4 ] oder alternativ des

· Arrays <np.array([i])> im Bereich [ 0, …, 4 ]

anzeigt, muss man sich nur die Mühe machen und den Quellkode der beiden Programme teil_03_prog_01c.py und teil_03_prog_01d.py miteinander vergleichen:

(Vergrößern: auf das Bild klicken! | Bild teil_03_prog_01f.jpg)

Wie man im obenstehenden Screenshot sieht, werden im Programm teil_03_prog_01c.py anstatt der Inhalte(!) des

· Arrays <np.array([i+1])> im Bereich [ 1, …, 4 ]

nur die jeweiligen Indexwerte [1], [2], …, [4] angezeigt, während im Programm teil_03_prog_01d.py tatsächlich die Inhalte(!) [1], [a], [3], [b] korrekt angezeigt werden!

Diesbezüglich stellt sich die Frage, warum bzw. weshalb dem so ist. So wie es im Moment den Anschein hat, scheint es sich bei diesem Sachverhalt um eine Besonderheit der „NumPy“-Bibliothek zu handeln!

>> NumPy

NumPy ist eine Programmbibliothek für die Programmiersprache Python, die eine einfache Handhabung von Vektoren, Matrizen oder generell großen mehrdimensionalen Arrays ermöglicht. Neben den Datenstrukturen bietet NumPy auch effizient implementierte Funktionen für numerische Berechnungen an.^[4]

Der Vorgänger von NumPy, Numeric, wurde unter Leitung von Jim Hugunin entwickelt. Travis Oliphant gliederte modifizierte Funktionalitäten des Konkurrenten Numarray in Numeric ein und veröffentlichte dies 2005 als NumPy. Die Bibliothek ist quelloffen und wird von vielen Mitwirkenden weiterentwickelt.

Merkmale

Der für Python standardmäßig installierte Interpreter CPython führt Kommandos als unoptimierten Bytecode aus. Mathematische Algorithmen sind in dieser Python-Variante oft langsamer als eine äquivalente kompilierte Umsetzung. NumPy stellt hier eine performante Alternative dar. Bestehende iterative Algorithmen müssen dazu gegebenenfalls für mehrdimensionale Array-Operationen umgeschrieben werden. NumPys Operatoren und Funktionen sind optimiert für derartige Arrays und ermöglichen so eine besonders effiziente Evaluation.

Die Handhabung von NumPy-Arrays in Python ist damit vergleichbar zu MATLAB; beide ermöglichen eine schnelle Ausführung von Algorithmen, solange diese für ganze Arrays oder Matrizen statt einzelne Skalare konzipiert sind. Die Integration von NumPy in Python ermöglicht die Verwendung und Kombination mit vielen weiteren Paketen aus dem umfangreichen Python-Umfeld. Weitere MATLAB-ähnliche Funktionen bietet die Python-Bibliothek SciPy. Auch der Funktionsumfang der Matplotlib-Bibliothek zur einfachen Erstellung von Plots in Python ist den Möglichkeiten von MATLAB sehr ähnlich. Intern verwenden sowohl MATLAB als auch NumPy die beiden Programmbibliotheken BLAS und LAPACK für eine effiziente Berechnung linearer Algebra.

Die Python-Schnittstelle des weit verbreiteten Computer-Vision-Pakets OpenCV verwendet intern NumPy-Arrays zur Verarbeitung von Daten. Bilder mit mehreren Farbkanälen werden beispielsweise mit dreidimensionalen Arrays dargestellt. Indexierung, Slicing oder Maskierung mit anderen Arrays sind daher sehr effiziente Methoden um gezielt auf bestimmte Pixel zugreifen zu können. NumPy-Arrays als universelle Datenstruktur für Bilder, extrahierte Feature-Punkte, Faltungsmatrizen und vieles mehr erleichtern die Entwicklung und das Debugging von Algorithmen zur Bildverarbeitung.

Die ndarray-Datenstruktur

Die Kernfunktionalität von NumPy basiert auf der Datenstruktur „ndarray“ (n-dimensionales Array), die auch als „NumPy Array“ bezeichnet wird. Dessen wesentliche Bestandteile sind ein Zeiger auf einen zusammenhängenden Speicherbereich zusammen mit Metadaten, welche die darin gespeicherten Daten beschreiben:^[5][4]

Datentyp

Anders als in Pythons eigener List-Datenstruktur sind NumPy-Arrays homogen typisiert: Alle Elemente eines Arrays müssen vom selben Datentyp sein.

Form (engl. shape)

Definiert die Dimensionen in jeder Indexausprägung („Achse“) des Arrays und die Anzahl der Achsen (bzw. Indizes).

Schrittlängen (engl. strides)

Die Schrittlängen beschreiben für jede Achse, wie viele Bytes man im linearen Speicher springen muss, wenn ein zu dieser Achse gehöriger Index um 1 erhöht wird, zum Beispiel um zwischen zwei Zeilen oder zwei Spalten zu springen.

Einschränkungen

Tatsächliches Einfügen oder Anhängen von Array-Einträgen wie bei Pythons Listen ist nicht möglich. Die Funktion np.pad(), mit der Arrays erweitert werden können, legt neue Arrays gewünschter Größe an, kopiert bestehende hinein und liefert dies zurück. Auch bei der Aneinanderreihung zweier Arrays mit np.concatenate([a1,a2]) werden die Arrays nicht wirklich verkettet, sondern ein neues zusammenhängendes Array zurückgegeben. Bei NumPys Funktion np.reshape() ist eine Umformung auch nur möglich, wenn sich die Anzahl der Array-Einträge nicht ändert. Diese Einschränkungen sind darauf zurückzuführen, dass NumPy-Arrays im Speicher als zusammenhängender Bereich angelegt werden müssen. Das Blaze-Framework bietet hier eine Alternative, welches diese Einschränkung beheben soll.[6]

Die Verwendung von NumPy-Arrays allein gegenüber Python-Listen bringt noch keinen Geschwindigkeitsvorteil mit sich. Entsprechende Algorithmen müssen zunächst in eine vektortaugliche Form umgeschrieben werden. Dies kann von Nachteil sein, da eventuell temporäre Arrays in Größe der Eingabe angelegt werden müssen und sich damit die Speicherkomplexität von konstant zu linear vergrößert. Eine Laufzeitkompilation wurde schon in einigen Paketen implementiert, um diese Probleme zu vermeiden. Open-Source-Lösungen, die mit NumPy interagieren können, sind unter anderem numexpr[7] und Numba.[8] Außerdem gibt es mit Cython noch eine statisch kompilierbare Alternative.

NumPy Arrays werden den Anforderungen bei der Verarbeitung großer Datenmengen und denen des Deep Learnings oftmals nicht gerecht. Zum Beispiel lädt NumPy die in den Arrays enthaltenen Daten komplett in den Arbeitsspeicher eines Computers, dessen Kapazität von wissenschaftlichen Datensätzen aber oft überschritten wird. Viele Deep Learning-Anwendungen wurden erst dadurch ermöglicht, dass die dafür notwendigen Operationen der linearen Algebra auf Rechnerverbünden mit spezieller, hochparalleler Hardware wie Grafikkarten und Tensor-Prozessoren verlagert wurden, NumPy aber für die Berechnung auf dem Prozessor und auf einzelnen Computer konzipiert wurde.

Um diese Herausforderungen zu meistern, sind viele alternative Array-Implementierungen für Python erschienen, wie zum Beispiel Dask[9] zum parallelen Rechnen auf Rechnerverbünden und TensorFlow und JAX[10] für Berechnungen auf Grafikkarten. Der Einfluss NumPys wird daran deutlich, dass diese Bibliotheken meistens eine NumPy-ähnliche Programmierschnittstelle oder eine Untermenge davon zur Verfügung stellen, um Anfängern den Umstieg zu erleichtern und eine Änderung der Array-Implementierung mit nur minimalen Änderungen am Programmquelltext zu ermöglichen.[4] << Quelle: Wikipedia

Das nachfolgende Programm teil_03_prog_01b.py dient dazu, einen sogenannten Vektor namens

· Statement <my_vec = np.array([1, 2, 3, 4])>

zu programmieren, der aus vier Elementen besteht. Dabei ist „my_vec“ ein eindimensionaler Vektor, der genau eine Dimension hat. Im vorliegenden Fall repräsentiert er eine Reihe von Zahlen (1, 2, 3, 4). Im Vergleich dazu bietet ein 3D-Koordinatensystem drei Dimensionen x, y und z.

Die Interpretation eines eindimensionalen Vektors in einem 3D-System hängt vom Kontext ab:

1. Vektor als Richtung: Der Vektor kann als Richtung im Raum interpretiert werden. In diesem Fall zeigt er die Richtung und die relative Größe der Bewegung in einer der drei Dimensionen an. Beispielsweise könnte er die Bewegung eines Objekts entlang der x-Achse mit den angegebenen Größenverhältnissen (1, 2, 3, 4) beschreiben.

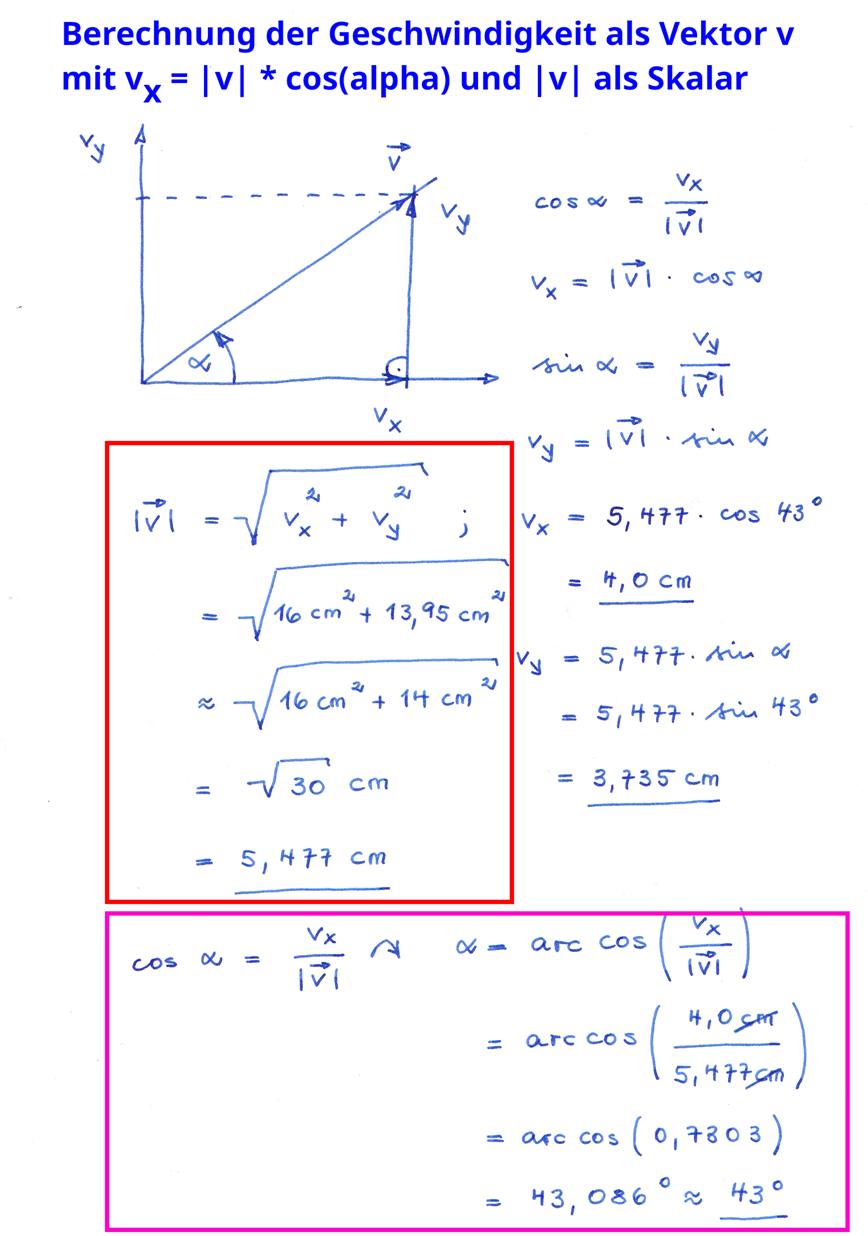
Im Mathematik- und Physikunterricht haben wir gelernt, dass ein Vektor eine bestimmte Größe hat (= Skalar = Betrag des Vektors) und in eine bestimmte Richtung (= Winkel a) zeigt. Dabei ist ein Skalar ein einzelner numerischer Wert, während ein Vektor eine Sammlung von numerischen Werten ist, die als gerichtete Größe (mit z.B. dem Winkel a) in einem mehrdimensionalen Raum interpretiert werden kann.

Ein Geschwindigkeitsvektor v beispielsweise hat eine bestimmte Länge l für das Maß der Geschwindigkeit (= Skalar, d.h. Betrag von | v | ) und den Winkel a in Bezug auf die x-Achse:

(Vergrößern: auf das Bild klicken! | Bild teil_03_prog_01g.jpg)

2. Vektor als Projektion: Der Vektor kann als Projektion eines mehrdimensionalen Vektors auf eine der drei Achsen des 3D-Systems betrachtet werden. In diesem Fall repräsentieren die Werte die Komponenten des ursprünglichen Vektors in der jeweiligen Dimension.

Jetzt wissen wir u.a. auch anhand des

· Statements <my_vec = np.array([1, 2, 3, 4])> im Programm teil_03_prog_01b.py,

dass es sich bei dem Vektor <my_vec> und dem NumPy-Array <np.array([1, 2, 3, 4])> um einen eindimensionalen Vektor handelt:

Ein eindimensionaler Vektor hat genau eine Dimension. Im vorliegenden Fall repräsentiert er eine Reihe von Zahlen (1, 2, 3, 4).
Ein 3D-Koordinatensystem hingegen bietet drei Dimensionen: x, y und z.
Die Interpretation eines eindimensionalen Vektors in einem 3D-System hängt vom Kontext ab:

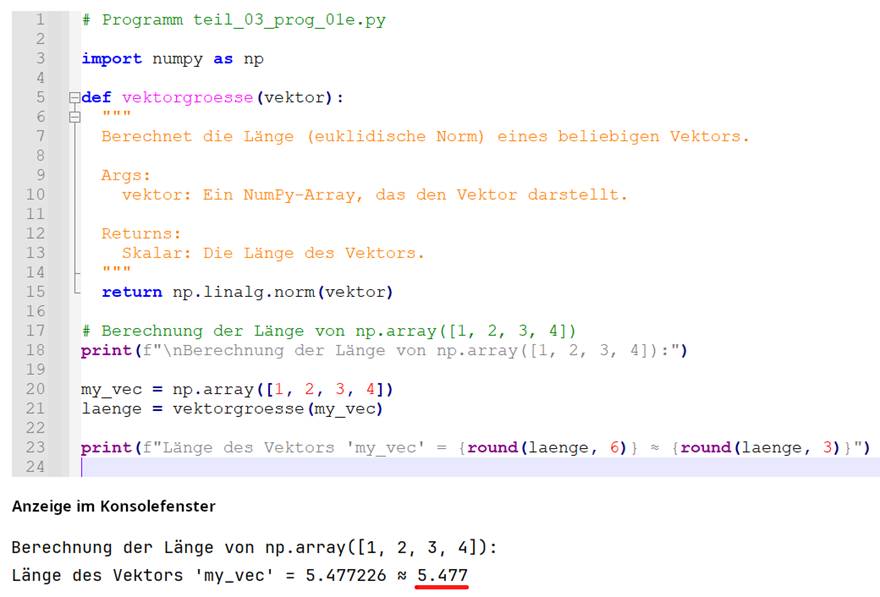
Die Bewegung eines eindimensionalen Vektors in einem 3D-System ist also nicht auf eine Achse beschränkt, sondern hängt von der Interpretation und dem Kontext ab. Er kann eine Richtung, eine Projektion oder eine andere abstrakte Größe darstellen.

2. Berechnung der Länge des Vektors:

Die Länge eines Vektors lässt sich als Skalar des NumPy-Arrays <np.array([1, 2, 3, 4])> unabhängig von seiner Dimensionalität mit der euklidischen Norm wie folgt berechnen:

(Vergrößern: auf das Bild klicken! | Programm teil_03_prog_01e.py)

So, jetzt wissen wir, dass sich die Länge eines eindimensionalen Vektors nicht nur gemäß Pythagoras (siehe handschriftliches Skript), sondern auch mittels der euklidischen Norm (siehe auch euklidischer Raum) berechnen lässt, wobei die KI letzteres Verfahren bevorzug, u.a. deswegen, weil in dieser keine Quadratwurzel berechnet werden muss.

Außerdem lässt sich die Länge eines eindimensionalen Vektors, der sich wiederum aus z.B. vier Einzelvektoren unterschiedlicher Länge gemäß dem NumPy-Array <np.array([1, 2, 3, 4])> zusammensetzt, mit dem euklidischen Verfahren aus der Sicht der KI besser berechnen, was aber nicht heißt, dass sich dieses auch einfacher verstehen oder programmieren lässt!

Wie wir nämlich gleich sehen werden, hat das euklidischen Verfahren nämlich auch -, wenn auch eher indirekt, - mit dem Pythagoras bzw. den Quadraten der vier Einzelvektoren unterschiedlicher Länge gemäß dem NumPy-Array <np.array([1, 2, 3, 4])> zu tun:

Berechnen der quadratischen Summe der vier Einzelvektoren:

Summe S² = 1² + 2² + 3²+ 4² = 1 + 4 + 9 + 16 = 30 "

Länge des Vektors <my_vec> = Ö S² = Ö 30 = 5,47722557505 ≈ 5,477 (siehe oben!)

Wie wir jetzt wissen, setzt sich die Länge des eindimensionalen Vektors <my_vec> aus vier Einzelvektoren unterschiedlicher Länge gemäß dem NumPy-Array <np.array([1, 2, 3, 4])> zusammen.

Dabei verhält es sich so, dass die vier Einzelvektoren unterschiedlicher Länge ebenfalls eindimensional sind und in die gleiche Richtung verlaufen wie der eindimensionale Vektor <my_vec>. Das ist dann auch der Grund und zugleich die Bedingung dafür, dass sich die vier Einzelvektoren unterschiedlicher Länge geometrisch (= quadratisch) addieren lassen!

Diesbezüglich bedeutet „eindimensional“ nicht, dass sich die betreffenden Vektoren ausschließlich auf der x- oder y-Achse befinden oder parallel zu den x- oder y-Achsen verlaufen! Vielmehr verhält es sich so, dass sich die Vektoren beliebig räumlich im zwei-, drei- oder multi-dimensionalen Raum angeordnet befinden!

Dabei gilt es zu beachten, dass sich die vier Einzelvektoren unterschiedlicher Länge, wenn sie in die gleiche Richtung wie der eindimensionale Vektor <my_vec> verlaufen, programmiertechnisch mittels des

· Statements <my_vec = np.array([1, 2, 3, 4])>

geometrisch addieren lassen (siehe oben)! –

Die Länge des Vektors <np.array([1, 2, 3, 4])> kann mit der euklidischen Norm berechnet werden. Diese Norm ist eine Verallgemeinerung des absoluten Betrags für mehrdimensionale Vektoren und misst die Entfernung eines Punktes vom Ursprung im Koordinatensystem.

Mathematische Formel:

Die euklidische Norm eines Vektors x mit n Einträgen (in diesem Fall n=4) berechnet sich wie folgt:

||x|| = √( Σ x_i² ) im Bereich von i = 1 bis n

Dabei sind:

· ||x|| die Länge (Norm) des Vektors x

· Σ Summensymbol

· i Laufindex über die Dimensionen des Vektors (1 bis n)

· x_i die i-te Komponente des Vektors x

Berechnung am Beispiel:

Gegeben sei der Vektor x = np.array([ 1, 2, 3, 4 ]).

1. Quadrieren jeder Komponente: x₁² = 1², x₂² = 2², x₃² = 3², x₄² = 4² => [ 1, 4, 9, 16 ]

2. Summierung der quadrierten Komponenten: Σ(x_i²) = 1 + 4 + 9 + 16 = 30

3. Quadratwurzel ziehen aus der Summe: √30 ≈ 5.477

Ergebnis:

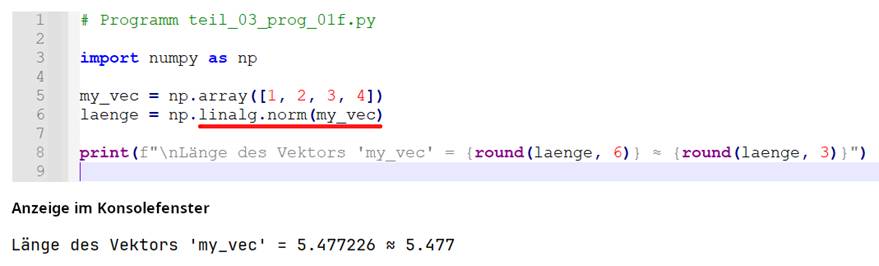
Die Länge des Vektors np.array([1, 2, 3, 4]) beträgt ca. 5,48 (siehe auch weiter oben!)

Alternative Berechnung mit NumPy:

NumPy bietet die Funktion np.linalg.norm(), die direkt die euklidische Norm eines Vektors berechnet:

(Vergrößern: auf das Bild klicken! | Programm teil_03_prog_01f.py)

Python: Arbeiten mit Datenstrukturen - Listen und NumPy-Arrays

Keine eingebaute "array"-Bibliothek:

Leider verfügt Python 3 nicht über eine eingebaute Bibliothek namens "array". Das array-Modul wurde in Python 2.x eingeführt und gilt seit Python 3 als veraltet. Stattdessen bietet Python zwei wichtige Alternativen für die Arbeit mit Datenstrukturen:

NumPy-Arrays: NumPy (Numerical Python) ist eine beliebte Erweiterungsbibliothek für Python, die effiziente und leistungsstarke Werkzeuge für die Arbeit mit mehrdimensionalen Arrays (Datenfeldern) bereitstellt. Sie bietet umfangreiche Funktionen zum Erstellen, Bearbeiten, Durchführen mathematischer Operationen und Analysieren von Daten in Arrays.
Eingebaute Listen: Pythons eingebaute Listen sind vielseitige Datenstrukturen, die zum Speichern und Verwalten von Sammlungen von Elementen verwendet werden können. Listen sind zwar nicht so gut für numerische Berechnungen optimiert wie NumPy-Arrays, aber sie sind einfacher zu verwenden und bieten mehr Flexibilität für die dynamische Datenhandhabung.

Funktionen für NumPy-Arrays:

NumPy bietet eine Vielzahl von Funktionen für die Arbeit mit Arrays. Einige häufig verwendete Funktionen sind:

array(): Erstellt ein Array aus einer Liste oder einem anderen iterierbaren Objekt.
arange(): Erzeugt einen Bereich von gleichmäßig verteilten Werten.
reshape(): Verändert die Form eines Arrays.
dtype: Ruft den Datentyp eines Arrays ab oder setzt ihn.
copy(): Erstellt eine Kopie eines Arrays.
zeros(): Erstellt ein Array, das mit Nullen gefüllt ist.
ones(): Erstellt ein Array, das mit Einsen gefüllt ist.
empty(): Erstellt ein leeres Array (keine Initialwerte).
nditer(): Iteriert über die Elemente eines Arrays.
where(): Wählt Elemente basierend auf einer Bedingung aus.
sort(): Sortiert ein Array.
mean(): Berechnet den Mittelwert eines Arrays.
std(): Berechnet die Standardabweichung eines Arrays.
sum(): Berechnet die Summe eines Arrays.
dot(): Berechnet das Skalarprodukt zweier Arrays.
linalg.solve(): Löst ein System linearer Gleichungen.
fft.fft(): Berechnet die Fast Fourier Transformation (FFT).

Funktionen für Python-Listen:

Auch die eingebauten Listen von Python bieten verschiedene Funktionen zum Bearbeiten von Listen:

· append(): Fügt ein Element am Ende einer Liste hinzu.

· insert(): Fügt ein Element an einer bestimmten Position in eine Liste ein.

· remove(): Entfernt das erste Vorkommen eines Elements aus einer Liste.

· pop(): Entfernt und gibt das letzte Element aus einer Liste zurück.

· index(): Findet den Index eines Elements in einer Liste.

· count(): Zählt die Vorkommen eines Elements in einer Liste.

· sort(): Sortiert die Elemente einer Liste.

· reverse(): Kehrt die Reihenfolge der Elemente in einer Liste um.

· clear(): Entfernt alle Elemente aus einer Liste.

· copy(): Erstellt eine Kopie einer Liste.

Dies sind nur einige wenige Beispiele der vielen Funktionen, die in Python für die Arbeit mit Arrays und Listen zur Verfügung stehen. Die spezifischen Funktionen, die Sie verwenden werden, hängen von Ihren konkreten Aufgaben der Datenanalyse und -bearbeitung ab.

In Kürze geht es hier weiter u.a. mit „Was bedeutet 'koinzidieren'?“

[ Home ] [ Seitenanfang ] [ Start ] [ Teil 1 ] [ Teil 2 ] [ Teil 3 ]