|
|
[ NodeESP ] [ Seitenende ] |
|
|||||||||
|
|
NodeESP – Programmieren 5 Digitale Spannungsmessung mit dem A/D-Wandler bis 3,3 Volt Der Mikrocontroller
„NodeESP“ lässt sich von Haus
aus in der Programmiersprache „Sketch“, bei der es sich um eine für Mikrocontroller
abgespeckte Variante der „C++“-Programmierung handelt,
programmieren. Dabei kommt die engl. „Integrated Development Environment“ (IDE),
d.h. die Integrierte
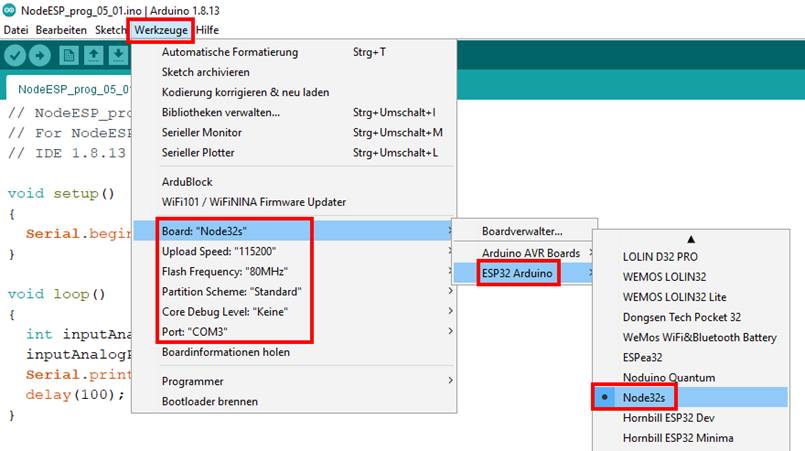
Entwicklungsumgebung der „Arduino“ zum Einsatz. Damit sich das „Sketch“-Programm „NodeESP_prog_05_01.ino“ gleich auf dem Mikrocontroller „NodeESP“ hochladen,
kompilieren und ausführen lässt, müssen in der Entwicklungsumgebung (IDE) des „Arduino IDE“ nachfolgende Einstellungen
vorgenommen werden: (Zum Vergrößern bitte
auf das Bild klicken!) „Sketch“-Programme setzen sich insgesamt
aus vier Programmblöcken
zusammen: 1.
Titel des Programms Was wird programmiert? Worum geht es? Die entsprechenden Angaben zum Programm werden
ganz am Anfang des Programms als /* Kommentarzeilen */ eingetragen. 2.
Variablen Im Programmblock
„Variablen“ werden Konstanten,
Variablen und die PINs von Bauelementen festgelegt.
3.
setup() Im Programmblock
„setup()“ erfolgt die Initialisierung bei dem entsprechende
Grundeinstellungen festgelegt werden. Dabei wird die Funktion „setup()“ gleich zu Beginn beim Starten des Programms
ausgeführt. Und zwar nur ein einziges Mal! 4.
loop() Bei dem Programmblock
„loop()“ handelt es sich um eine
Endlosschleife, die direkt nach dem Ausführen des Programmblocks „setup()“ fortwährend ausgeführt wird! Die beiden Programmblöcke „setup()“ und „loop()“ werden als sogenannte
Funktion vom Typ „void“ deklariert. Dabei bedeutet engl. „void“
so viel wie leer im Sinne von Nichts. Damit ist gemeint, dass eine leere Funktion vom Typ „void“ nichts macht. Demzufolge hat die leere Funktion vom Typ „void“ keine Attribute im Sinne von Eigenschaften oder
Fähigkeiten, sodass sich mit dieser auch keine Objekte definieren oder
deklarieren lassen (siehe „OOP“ = „Objekt
orientierte Programmierung“): (Bild vergrößern: auf
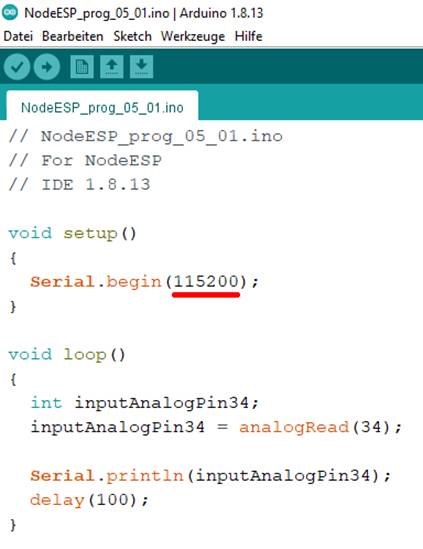
Bild klicken! Webverzeichnis | NodeESP_prog_05_01.ino) Was
aber macht das „Sketch“-Programm „NodeESP_prog_05_01.ino“ im Einzelnen? Im Programmblock
„setup()“ gibt es nur das ·
Statement < Serial.begin(115200) > mit dem die sogenannte
Baudrate festgelegt wird.
Dabei handelt es sich bei der Baudrate
um die Übertragungsgeschwindigkeit von Symbolen
aus der Nachrichtentechnik und Fernmeldetechnik. Wenn ein Symbol
datenmäßig sehr klein ist, dann entspricht 1 Baud = 1 Bit. Ist ein zu
übertragendes Symbol größer, dann
werden mehrere Bits für die Übertragung
benötigt: wie z.B. 1 Baud = 4 Bit. Bei der Baudrate von 115200 Baud werden 115200
Bits/Sekunde = 14 400 Bytes/Sekunde = 14 Kilobytes/Sekunde übertragen. Immer vorausgesetzt, dass nur einfache
Symbole der Größe 1 Bit übertragen werden! Dabei entsprechen 8 Bit = 1 Byte und 1024
Bytes = 1 Kilobyte! Dabei gilt es zu beachten, dass 1 Kilobyte = 1024 Bytes entspricht, da wir nicht
im Dezimalzahlensystem, sondern im binären Zahlensystem des Computers
rechnen! In
der Endlosschleife, d.h. dem Programmblock „loop()“, wird mit dem ·
Statement < int inputAnalogPin34 > die Variable „inputAnalogPin34“ zunächst nur deklariert. Und zwar als Typ „integer“, sodass die Variable mit positiven oder negativen
ganzzahligen Werten rechnen und diese speichern kann. Dabei verhält es sich
so, dass sich mit 1 Byte = 8
Bit
insgesamt 28 = 256
ganzzahlige positive oder negative Werte darstellen lassen, die sich
im Bereich von [ 0, …, 28 - 1 ] = [ 0, …, 255 ] bewegen! Wenn man bei dem 8-Bit-Wert von 255 Bit + 1 Bit
addiert, dann erfolgt ein sogenannter dekadischer Überlauf, sodass alles wieder bei null anfängt: 25510 Bit + 110 Bit =
1111 11112 + 0000 00012 = 1 0000 00002 = 256
Bit10 → Überlauf! Wenn sich mit dem 8-Bit-Wert auch ganzzahlige negative Werte darstellen
lassen sollen, dann halbiert sich der 8-Bit-Wert auf 2 x 4 Bit wie folgt: 12710 Bit + 110 Bit =
11112 + 00012 = 1 00002 = 128 Bit10 → Überlauf! 4-Bit-Zahlenbereich für positive Werte = [ 0, …, 127 ] und für negative Werte = [ -127, …, 0 ]. Wenn man auch mit negativen
Zahlen im Bereich [ -127, …, 0 ]
rechnen will, dann muss man sich bei der Programmierung
selbst um diese kümmern, da es per se keine negativen Bits gibt. Es sei denn, man rechnet binär,
dann lassen sich mit einem entsprechenden Logikgatter
vom Typ engl. „NOT“, d.h. „NICHT“ (= -1 ) positive Werte in ihr negatives Pendant umwandeln, indem sich das digitale
Ausgangssignal (= Reckeckimpuls!)
von z.B. vormals +3,3 V auf
nunmehr -3,3 V oder
von +5 V auf
nunmehr -5 V invertiert!
·
Statement < inputAnalogPin34 = analogRead(34) > die zunächst nur deklarierte
Variable inputAnalogPin34 nun initialisiert,
sodass dieser ein konkreter Wert zugewiesen wird!
Und zwar mit dem „integer“-Wert, der
am Port „Pin 34“ mit dem A/D-Wandler eingelesen wird. Wegen
der hohen Auflösung des A/D-Wandler
lassen sich mit diesem dezimale Werte
im Bereich [ 0, …, 4095 ] =
4096 verschiedene Dezimalwerte
inkl. der Null berechnen!
·
Statement
< Serial.println(inputAnalogPin34) > die
am Port „Pin 34“ mit dem A/D-Wandler eingelesene Eingangsspannung UPin
34 wird mittels der Klasse
„Serial“ und
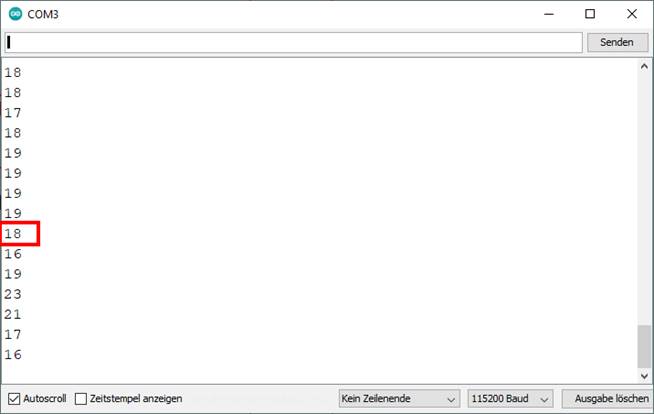
dem „println()“-Befehl fortlaufend im Konsolefenster,
d.h. im seriellen Monitor
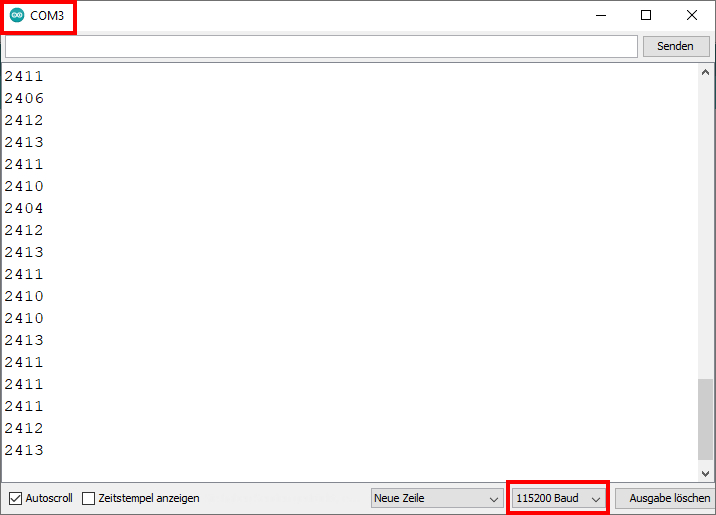
untereinander angezeigt: (Zum
Vergrößern bitte auf das Bild klicken!) Bei den angezeigten,
ganzzahligen Messwerten handelt es sich um Bitwerte im Bereich
[ 0, …, 4095 ]. Dabei ist der angezeigte Bitwert eine direkte Funktion der am Port „Pin 34“ anliegenden Spannung UPin
34.
Wenn man konkret
wissen will, um welche Spannung UPin 34 es sich dabei aktuell
handelt, so muss man den angezeigten Bitwert
= 2413 wie folgt umrechnen: 4095
Bit → 3,3 V 2413
Bit → x V x
= 3,3 V / 4095 Bit * 2413 Bit = 1,94454 V
≈ 1,95 V Probe: 4095 Bit / 3,3 V * 1,94454 V
≈ 2.413 Bit
·
Statement < delay(100)“ eine Verzögerung von 100 ms ausgeführt, sodass sich die fortlaufende Anzeige der Bitwerte entsprechend verlangsamt und
der Anwender diese besser, d.h. stressfrei ablesen kann. Wem die Anzeige der Bitwerte im seriellen Monitor (siehe
oben) noch immer zu schnell und hektisch durchläuft, der kann den Verzögerungswert jederzeit von 100 ms
auf z.B. 1000 ms abändern! Wir erweitern und verbessern noch das „Sketch“-Programm „NodeESP_prog_05_01.ino“, indem wir die beiden
Statements ·
Statement < int inputAnalogPin34 > # → Deklaration der Variablen
inputAnalogPin34 ·
Statement < inputAnalogPin34 = analogRead(34) > # → Initialisierung der Variablen
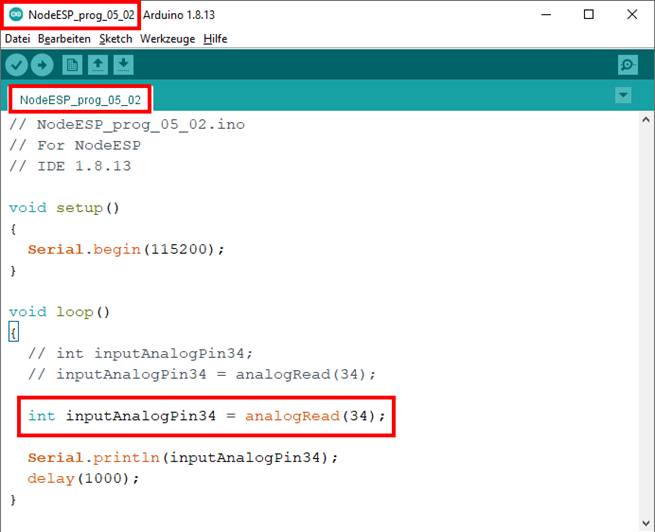
inputAnalogPin34 zu nur noch einem wie folgt zusammenfassen: ·
Statement < int inputAnalogPin34 = analogRead(34) > # → Deklaration und Initialisierung
(Bild vergrößern: auf
Bild klicken! Webverzeichnis | NodeESP_prog_05_02.ino) So, jetzt sind wir schon mittendrin in der „Sketch“-Programmierung und dem abgespeckten C++, obwohl wir noch gar nicht
wissen, wie die am Port „Pin 34“ des A/D-Wandlers
anliegenden Spannung UPin 34 zustande kommt.
Höchste Zeit also, einen Blick auf die Schaltung
mit dem Breadboard
(= Experimentier- und Montagebrett) zu werfen: (Zum Vergrößern bitte
auf das Bild klicken!) Da es sich bei dem oben im Bild zu sehenden Breadboard um
ein Longboard
(= Langbrett) handelt, setzt sich dieses aus zwei einzelnen, kurzen Breadboards
zusammen. Demzufolge müssen beide Breadboards bezüglich der Stromversorgung von 3,3 V
und 5,0 V über die doppelten
Verbindungsbügel oben und unten
miteinander verbunden werden (siehe obenstehendes Bild)! Wer noch nie mit einem Breadboard experimentiert und
gearbeitet hat, kann mit der oben im Bild gezeigten Verdrahtung
wahrscheinlich auf Anhieb nicht so viel anfangen, diese nicht verstehen. Dazu
muss man nämlich wissen, dass das schmale Longboard um je eine weitere
schmale zweireihige Kontaktleiste
oben und unten erweitert wurde. Dabei dienen die beiden zweireihigen Kontaktleisten ausschließlich der Stromversorgung, d.h. der Stromzufuhr (= obere Kontaktleiste) und der
Stromrückführung auf Massepotential (= untere Kontaktleiste). Breadboards sind auf der Plattenunterseite sowohl horizontal (siehe obere und
untere zweireihige Kontaktleiste
für die Stromversorgung) und auf der
Rückseite des mittleren Longboards vertikal verdrahtet, wobei beide Hälften
des mittleren Longboards
in der Mitte durch eine Rinne
voneinander elektrisch getrennt sind, sodass man gelegentlich beide
Teile des Longboards
durch eine Brücke in vertikaler
Richtung miteinander verbinden
muss (siehe rote
Kabelbrücke
rechts vom 10 kΩ Potentiometer): (Zum Vergrößern bitte
auf das Bild klicken!) Wie man im obenstehenden Bild sieht, wird der
analoge Eingang des A/D-Wandlers
am Port „Pin 34“ vom Potentiometer über
den Mittelabgriff mit „Strom“ versorgt, obwohl der A/D-Wandler selbst gar keinen Strom
„verbraucht“, d.h. benötigt, sondern für die A/D-Wandlung nur das Spannungspotential in Form des Spannungsabfalls ∆UPin 34 auswertet und in
einen entsprechenden Bitwert
umwandelt.
Aus diesem Grund macht es Sinn, dass man
zunächst die minimale Leistung PPoti, max
des Potentiometers anhand des Potentiometerwiderstandes RPoti = 10 kΩ sowie der anliegenden
Versorgungsspannung von UPin 3V3 = 3,3 V wie folgt berechnet: PPoti = UPin 3V3 * IPoti →
IPoti
= UPin 3V3 / RPoti
= UPin 3V3
* UPin 3V3 / RPoti
= ( 1 / RPoti ) * ( UPin 3V3 )2
PPoti = 1 / RPoti * UPin 3V32 = 1 /
10 kΩ
* ( 3,3 V )2 = 1 / ( 10 * 103 Ω ) * 10,89 V2 = 1 / ( 10 * 103 V/A ) * 10,89 V2 = 1 / 10 * 10-3 V/A
* 10,89 V2 = 1,089 V IPoti = UPin 3V3 / RPoti
= 3,3 V / 10 kΩ = 3,3 V / ( 10 * 103 Ω
) = 0,33 * 10-3 A = 0,33 mA = 330 µA
Wenn man davon ausgeht, dass das Potentiometer mit einer maximal
zulässigen (Gesamt-) Leistung von PPoti, max = 250 mW betrieben werden darf, dann berechnet sich
die maximal zulässige Stromstärke IPoti, max wie folgt: IPoti, max = PPoti,
max
/ UPin 3V3 = 250 mW / 3,3 V =
0,250 W / 3,3 V = 0,07576 A ≈ 75,8 mA Diesbezüglich stellt sich dann gleich die
Frage, wie klein der Potentiometerwiderstand
RPoti, min bei der maximal
zulässigen Stromstärke IPoti, max ist: PPoti = UPin 3V3 * IPoti →
UPin 3V3 = IPoti
* RPoti
=
IPoti
* RPoti
* IPoti
PPoti = RPoti * IPoti2 → RPoti,
min =
PPoti / IPoti, max2 =
250 mW /
( 75,8 mA
)2 = 250 * 10-3
VA / ( 75,8 * 10-3 A )2 = 250 V =
250 V / ( 5745,64 * 10-3 A ) = 250 V / 5,7456 A = 43,512 Ω ≈ 43,5 Ω
Alternative Berechnung: RPoti,
min =
UPoti / IPoti, max
= UPin 3V3 / IPoti, max
= 3,3 V / 75,8 mA = 0,0435356 kΩ ≈ 43,5 Ω Wer
unsicher ist, ob bisher alles richtig überlegt und berechnet wurde, kann auf
einfache Weise wie folgt die Probe auf’s Exempel (=
Beispiel, Musterbeispiel, Musterfall) machen: Ua = UPin 34 = IPoti, max * RPoti, min = 75,76 mA * 43,5 Ω = 3 295,56 mV
= 3,29556 V ≈ 3,3 V → Wir haben bisher
alles richtig berechnet! Wenn also der Potentiometerwiderstand insgesamt RPoti = 10 kΩ groß ist und der
kleine, verstellbare Potentiometer-widerstand
wegen der zulässigen (Wärme-)
Verlustleistung nicht kleiner als RPoti, min = 43,5 Ω werden darf, wo
befindet sich dieser dann? Da wir die Spannung stets gegen Masse
(„┴“) bzw. Port „Pin GND“ messen, befindet sich der kleine, verstellbare Potentiometerwiderstand RPoti,
min = R2 = 43,5 Ω zwischen dem Mittelpunkanschluss (= Anschlusspunkt R3 bzw. Ua)
des Potentiometers und der Masse („┴“) bzw. dem Port „Pin GND“ (siehe Bild im Bild): (Bild
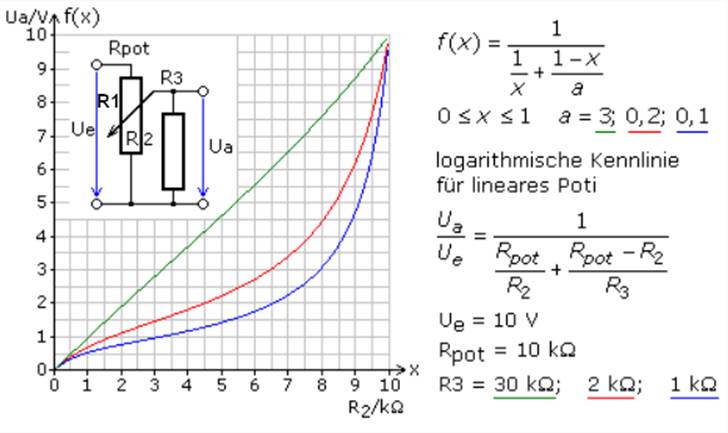
vergrößern: auf Bild klicken! Belasteter Spannungsteiler: Elektroniktutor) Achtung: Die im obenstehenden Bild stehenden
Widerstandswerte für R3 und Ue = 10 V stehen nicht
im Zusammenhang mit unser bisherigen und weiteren Berechnung! Wenn man die Ausgangsspannung Ua = UEingang, Pin 34 des belasteten
Spannungsteilers (= Potentiometer) am A/D-Wandler
des „NodeESP“ berechnen will, dann
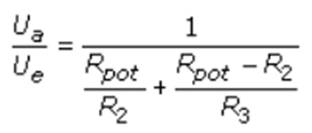
muss man die entsprechende Formel verwenden: Ue / Ua = RParallel / Rges → RParallel = R2 // RLast = R2 // R3 und Rges = R1 + ( R2 // R3 ) = ( R2 // R3 ) / ( R1 + ( R2 // R3 ) ) Ue =
[ ( R2 // R3 ) / ( R1 + ( R2 // R3 ) ) ] * Ua Leider hat die Berechnungsformel zur Berechnung des belasteten Spannungsteilers (= Potentiometer) einen entscheidenden Schönheitsfehler! Und zwar den des (Potentiometer-) Widerstandes R1 als großen Unbekannten, der sich leider nicht
auf herkömmliche Weise berechnen lässt, da es mit diesem mehr als eine
Unbekannte gibt!
So lange es nur darum geht, eine der Spannungen Ue oder
Ua zu berechnen, ist
dies problemlos möglich. Wenn es aber darum geht, eine der Widerstandswerte Rpot,
R2 oder R3 als Unbekannte zu berechnen, wird es kompliziert, ist dies auf
herkömmliche Weise z.B. durch Umstellen, Erweitern, Kürzen, Ausklammern oder
nach einer der Unbekannten
Rpot, R2 oder
R3 auflösen, leider nicht
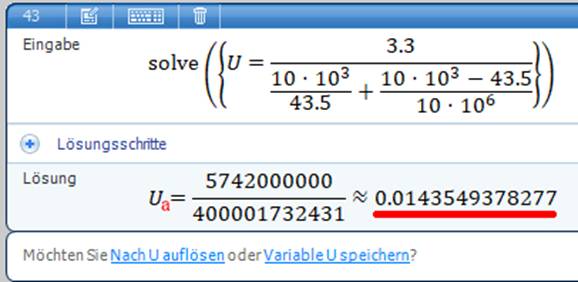
mehr möglich! Aber zum Glück gibt es ja das Rechenprogramm „Microsoft
Mathematics“ mit dem sich die im weißen Kasten stehende Formel mühelos
berechnen lässt: (Zum Vergrößern bitte
auf das Bild klicken!) Wegen der hohen Bitauflösung von 4095 Bits und der hohen Eingangsempfindlichkeit des A/D-Wandlers von 0,80586 mV/Bit dürfte der Eingangswiderstand R3 des A/D-Wandlers größer als R3 = REingang,
Pin 34 = 10 MΩ sein, sodass der Spannungsteiler praktisch nicht belastet wird bzw. die
Belastung vernachlässigbar klein ist, sodass sich die Ausgangsspannung Ua am Spannungsteiler ( = Eingangsspannung UEingang,
Pin 34
am A/D-Wandler) wie folgt
berechnet: Ue / Ua = RParallel / ( R1 + ( R1 + ( R2 // R3 ) ) ) Mit R3 = REingang,
Pin 34 = 10 MΩ >
R2 = RPoti, min = 43,5 Ω folgt, dass man den Eingangswiderstand R3 = REingang, Pin 34 des A/D-Wandlers am Port „Pin 34“ vernachlässigen und
deshalb weglassen darf: Ue / Ua = RParallel / ( R1 + ( R2 // R3 ) ) = R2 ≈ R2 / ( R1 + R2 ) = R2 / RPoti = R2 / RPoti * Ua = 43,5 = 14,355 mV = 0,014355 V (siehe oben im weißen Kasten!)
Abschließend stellt sich noch die Frage, wie
viele Bits man am Potentiometer beim „Sketch“-Programm „NodeESP_prog_05_02.ino“ einstellen muss,
damit sich am Eingang des Ports „Pin 34“ die analoge Eingangsspannung Ua =
14,355 mV
einstellt: 3,3 V → 4095 Bit 1
V → x Bit x = 4095 Bit / 3,3 Anzahl Bits =
Skalierungsfaktor Bit/V * Ua =
1 241 Bit/V * 14,355 mV
= 1 241 Bit/ = 17,814555 Bit ≈ 18
Bit
Wenn man mit dem „Sketch“-Programm „NodeESP_prog_05_02.ino“ und durch Drehen des Rändelrades am Potentiometer RPoti
= 10 kΩ nach links bis kurz vor dem
Anschlag versucht, den Bitwert
= 18
einzustellen, dann wird man
(Zum Vergrößern bitte
auf das Bild klicken!) erstaunt feststellen, dass das gar nicht so
einfach ist. Einerseits weil man sich mit der Einstellung fast schon am linken
Anschlag des Potentiometers befindet und zum
anderen, weil die Winkeleinstellung
von 1,2 Grad auf 18 Bit doch sehr
klein ist: 4095 Bit
→ 270 Grad 1
Bit → x Grad X
= 270 Grad / 4095 Einstellwinkel in Grad = Skalierungsfaktor
0,066 Grad/ (Zum Vergrößern bitte
auf das Bild klicken!) Bei dem obenstehenden Potentiometer lässt sich noch ein
entsprechendes Rändelrad aufstecken, sodass
sich dieses ohne Kreuzschlitz-Schraubendreher von Hand einstellen
lässt. Wir
behalten die Winkeleinstellung von
1,2 Grad am Potentiometer mit 18 Bit unverändert bei und starten
das „Sketch“-Programm „NodeESP_prog_05_03.ino“:
(Bild vergrößern: auf Bild
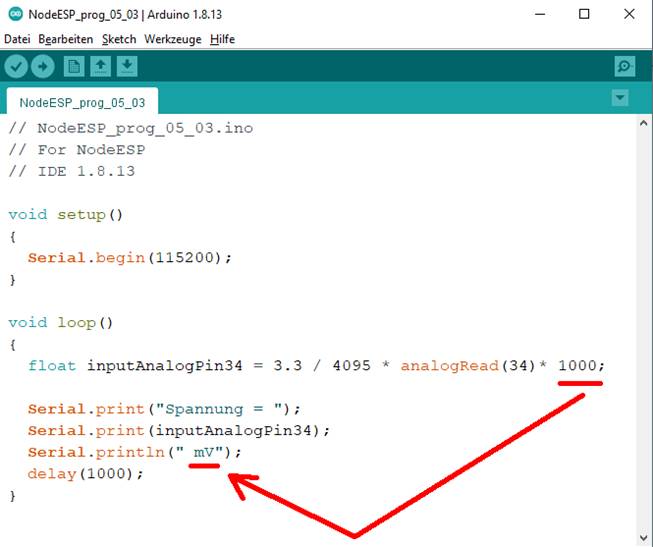
klicken! Webverzeichnis | NodeESP_prog_05_03.ino) Wenn man das „Sketch“-Programm „NodeESP_prog_05_03.ino“ startet, dann wird
als erstes die Baud-Übertragungsrate von 115 200 Baud und als Nächstes die Funktion loop()
vom Typ „void“ ausgeführt. Innerhalb der Funktion loop() wird dann als erstes
das ·
Statement < inputAnalogPin34 = 3.3 / 4095 * analogRead(34) * 1000“ > ausgeführt. Dabei wird über mit dem Statement < analogRead(34) > der Port „Pin 34“ analog ausgelesen und der vom A/D-Wandler umgewandelte Bitwert mit den Skalierungsfaktor 3.3 / 4095 = 0,806 [ mV/Bit ]
multipliziert. Das Zwischenergebnis wiederum wird mit dem Faktor 1000 multipliziert, damit sich
der Ergebniswert in Millivolt [ mV ]
ausgeben und anzeigen lässt: 4095 Bit
→ 3,3 V 1
Bit → x
V x = 3,3 V / 4095 Probe: 4095
Bit / 3,3 Der endgültige Ergebniswert von 0,806
mV/ (Bild vergrößern: auf
Bild klicken! Webverzeichnis | NodeESP_prog_05_04.ino) Gemäß dem „EVA-Prinzip“,
d.h. „Eingabe, Verarbeitung, Ausgabe“, werden zuerst Daten eingegeben/eingelesen, dann verarbeitet/berechnet und als
Letztes auf den Bildschirm, den Drucker oder über Lautsprecher/Kopfhörer in
gesprochener Form, d.h. engl. „Text-to-Speech“
( = Sprache zu Text), ausgegeben. Dazu dienen die drei
nachfolgenden Statements: ·
Statement
< Serial.print("Spannung = ") > Die Ausgabeanweisung < Serial.print() >
setzt sich aus der (Befehls-) Klasse „Serial“ und
der Anweisung < print("Spannung
= ") > zusammen, sodass
folgende Anzeige erscheint: →Spannung_=_← mit „_“ als engl. „space“,
d.h. Leerzeichen. Dabei
verhält es sich so, dass mit der Anweisung
< print() > kein engl. „Line feed“ (LF), d.h. keine Zeilenschaltung
veranlasst wird, sodass sich die nächste folgende „print()“-Anweisung und dessen anzuzeigende Zeichenkette, engl.
„string“, direkt ohne Leerzeichen, engl. „space“, angefügt angezeigt wird. ·
Statement
< Serial.print(inputAnalogPin34) > Der
gespeicherte Inhalt der Variablen „inputAnalogPin34“ vom Typ „float“, d.h. Fließkommarechnung mit
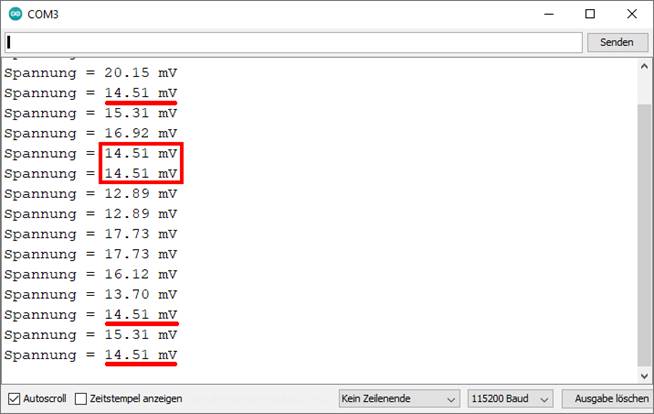
zwei Nachkommastellen, wird wie folgt angezeigt: →14,51← ohne voran- oder
nachgestellte engl. „spaces“, d.h. Leerzei-chen. ·
Die beiden Statements zusammen führen zur Anzeige: →Spannung_=_14,51← mit „_“ als engl. „space“, d.h. Leer-zeichen. ·
Statement
< Serial.println("
mV") > Die Ausgabeanweisung < Serial.print() >
setzt sich aus der (Befehls-) Klasse „Serial“ und
der Anweisung < print("
mV") > zusammen, sodass
nachfolgende Anzeige erscheint: →_mV← mit „_“ als engl. „space“,
d.h. Leerzeichen. Das
Besondere an dem Statement mit der
Anweisung println("
mV") ist,
dass jetzt wegen der Angabe „ln“,
d.h. engl. „Line feed“, eine Zeilenschaltung
(„◄┘“) am Ende
des anzuzeigenden Strings veranlasst
wird. Dabei
werden aber Sonderzeichen bzw.
Kodierungen wie
die der Zeilenschaltung („◄┘“) am
Ende des anzuzeigenden Strings nicht
angezeigt: →_mV← ·
Die drei Statements zusammen führen zur Anzeige: →Spannung_=_14,51_mV←
ohne dass
die Kodierung Zeilenschaltung
(„◄┘“) am
Ende des anzuzeigenden Textes angezeigt wird! ·
Statement
< delay(1000) > Das
letzte Statement sorgt dafür, dass
das „Sketch“-Programm für
die Zeit von 1000 Millisekunden [ms]
angehalten wird, sodass der Anwender die Displayanzeige
im Konsolefenster stressfrei
lesen kann (siehe oben): →Spannung_=_14,51_mV←
Jetzt
wissen wir, dass sich mittels der drei Statements Serial.print("Spannung =
"); Serial.print(inputAnalogPin34); Serial.println(" mV"); quasi ein durchgängiger Zeichen- bzw. Textstring der Form „Spannung = 14,51 mV“ im Konsolefenster
angezeigen lässt. Dabei stellt sich natürlich die Frage, ob es
nicht auch ohne diese „Trickserei“ mit den drei
Statements schneller und kürzer
geht, sodass sich der Textstring
auch mit nur einem „Serial.println“-Statement darstellen lässt: ·
Statement < Serial.println("Spannung =
" + inputAnalogPin34 + " mV"); > In der Tat lassen sich statische Textstrings wie "Spannung = " und
" mV" zu "Spannung = " + " mV" miteinander
„addieren“ bzw. mittels „+“ miteinander verbinden.
Um aber die Variable „inputAnalogPin34“ ebenfalls mittels „+“ mit einem statischen Textstring verbinden zu können, müsste diese vom Typ „String“
(→ „C++“) sein oder vom Typ „char“ (→ „C“) nebst Umwandlung mittels ·
Statement < inputAnalogPin34_String = inputAnalogPin34_Array > Demzufolge ist
das ·
Statement < inputAnalogPin34_String = inputAnalogPin34_Array > die Transformation von der „C”-Programmierung zur „C++“-Programmierwelt. >>
C ist eine imperative
und prozedurale
Programmiersprache, die der Informatiker Dennis Ritchie in
den frühen 1970er Jahren an den Bell Laboratories entwickelte. Seitdem ist
sie eine der am weitesten verbreiteten Programmiersprachen. Die Anwendungsbereiche von C
sind sehr verschieden. Sie wird zur System- und Anwendungsprogrammierung eingesetzt. Die
grundlegenden Programme aller Unix-Systeme und die Systemkernel
vieler Betriebssysteme sind in C programmiert.
Zahlreiche Sprachen, wie C++, Objective-C, C#,
D, Java, JavaScript,
LSL, PHP, Vala oder Perl, orientieren sich an der Syntax
und anderen Eigenschaften von C. (…) C wurde
1969–1973 von Dennis Ritchie[2] in den Bell Laboratories für die Programmierung des damals neuen Unix-Betriebssystems entwickelt. Er stützte sich dabei auf die
Programmiersprache B, die Ken Thompson und Dennis Ritchie in den Jahren
1969/70 geschrieben hatten – der Name C entstand als Weiterentwicklung von B.
B wiederum geht auf die von Martin Richards Mitte der 1960er-Jahre
entwickelte Programmiersprache BCPL zurück.[3] Ursprünglich war der Name NB ("New B")
vorgesehen, daraus wurde schließlich C.[4] Ritchie schrieb auch den ersten Compiler für C. 1973 war die Sprache so weit ausgereift, dass man
nun den Unix-Kernel für die PDP-11 neu in C schreiben konnte. << (Quelle: Wikipedia) >>
C++ ist eine von der ISO genormte Programmiersprache. Sie wurde ab
1979 von Bjarne Stroustrup bei AT&T als
Erweiterung der Programmiersprache C entwickelt. C++ ermöglicht sowohl die effiziente und maschinennahe
Programmierung als auch eine Programmierung auf hohem Abstraktionsniveau.
Der Standard definiert auch eine Standardbibliothek, zu der verschiedene
Implementierungen existieren. << (Quelle: Wikipedia) Was jetzt noch fehlt, ist die Verbindung bzw.
Transformation vom Maschinenkode (→ Hardware, → Mikrocontroller),
engl. „Assembler“
zur höheren Programmiersprache „C“ mit dem ·
Statement „dtostrf()“ = d(ouble) to str(ing) f(loat), Sodas sich die eingelesene, analoge Spannung des A/D-Wandlers
am Port „Pin 34“ in einen entsprechenden digitalen Bitwert im Bereich [0, …, 4095] umwandeln und der Variablen „inputAnalogPin34“ vom Typ „float“
oder „double“ zuweisen lässt (siehe
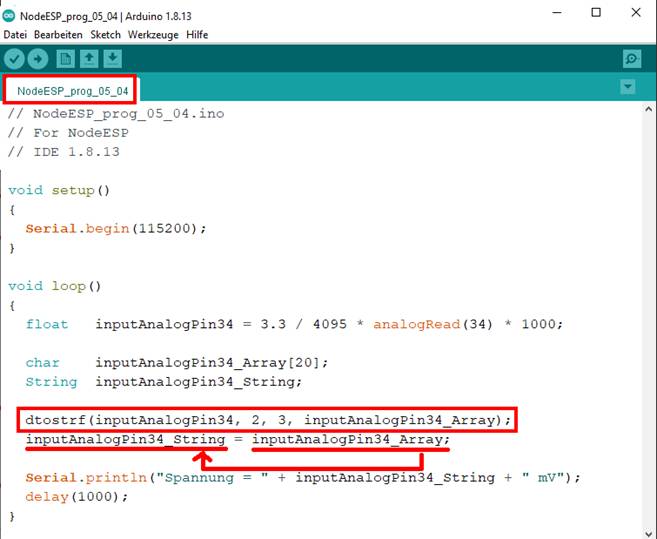
„Sketch“-Programm „NodeESP_prog_05_04.ino“): (Bild vergrößern: auf
Bild klicken! Webverzeichnis | NodeESP_prog_05_04.ino) Dazu muss man wissen, dass es nicht nur „C“ und „C++“ als Programmiersprache
gibt, sondern auch, dass sich die für Mikrocontroller
entwickelte „Sketch“-Programmiersprache bei beiden Programmiersprachen bedient.
Demzufolge gibt es in „C“ als die ältere
Programmiersprache standardmäßig keine Stringverarbeitung bzw. keine
Variablen vom Typ „String“, sondern nur vom Typ „char“, d.h. vom Typ „einzelner Buchstaben,
Ziffern, Zeichen und kodierten Symbolen“, die als quasi „Zeichenfolge“ einzelner
Zeichen in einem Array
gespeichert werden. Bei „C++“
als die neuere Programmiersprache gibt es zwar die Stringverarbeitung mit Variablen vom Typ „String“, dafür aber keine
Variablen vom Typ „char“, sodass man
demzufolge beide Typen mittels entsprechender Zuweisung konvertieren
muss: ·
Statement < inputAnalogPin34_String = inputAnalogPin34_Array; > Demzufolge umfasst das Array der Variablen „inputAnalogPin34_Array“ in der „C“-Programmierung
insgesamt [20] Felder, die im Bereich
von [0, …, 19] durchnumeriert sind: ·
Statement < char
inputAnalogPin34_Array[20]; > Mit dem Statement
„dtostrf“ = d(ouble) to str(ing)
f(loat) lässt sich die
eingelesene, analoge Spannung des A/D-Wandlers am Port „Pin 34“ in einen
entsprechenden digitalen Bitwert im Bereich [0, …, 4095] umwandeln und der Variablen „inputAnalogPin34“ vom Typ
„float“ oder „double“ zuweisen, in das „char(acter)“-Array mit der Variablen „inputAnalogPin34_Array“ vom Typ
„char“ konvertieren
und der Variablen „inputAnalogPin34_Array“ wie folgt zuweisen: ·
Statement < dtostrf(inputAnalogPin34, 2, 3, inputAnalogPin34_Array); > Dabei legt der Parameter „2“ fest, wie viele Zeichen, engl. „character“,
der Fließkommazahl vor dem Dezimalkomma zugewiesen werden
dürfen, nämlich zwei Zeichen. Der Parameter
„3“ legt fest, wie viele Zeichen, engl. „character“,
der Fließkommazahl nach dem
Dezimalkomma als Dezimalstellen zugewiesen werden
dürfen, nämlich drei Zeichen: (Bild vergrößern: auf
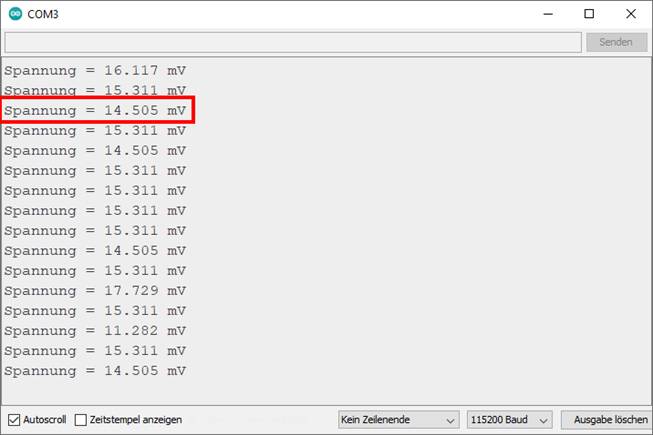
Bild klicken! Webverzeichnis | NodeESP_prog_05_04.ino) Im obenstehenden Bild (siehe roter Kasten) sieht man jetzt auch sehr deutlich, dass die
drei Nachkommastellen
tatsächlich kaufmännisch gerundet werden, sodass der Wert 14,505 mV auf 14,51 mV mit zwei Nachkommastellen kaufmännisch aufgerundet
wird: (Zum
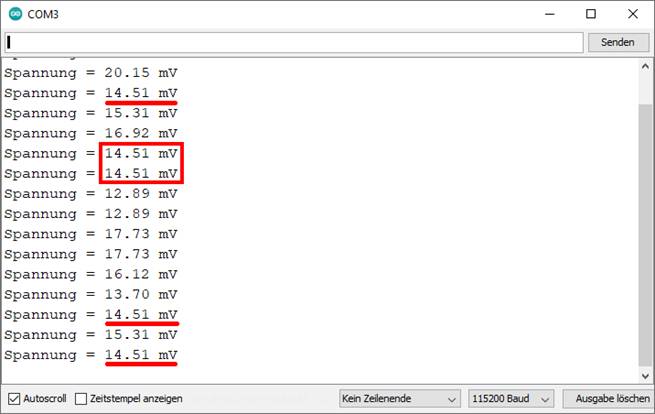
Vergrößern bitte auf das Bild klicken!) Wenn man sich die im
obenstehenden Bild angezeigten Messwerte anschaut, dann fällt sofort auf,
dass diese teils doch erheblich voneinander abweichen. Demzufolge hat die kleinste
angezeigte Spannung den Wert UPin 34, min = 12,89 mV
und die größte den Wert UPin 34, max = 20,15 mV, sodass sich die Abweichung vom Mittelwert UPin 34, mittel = 16,52 mV
wie folgt berechnet: ∆UPin 34, min = ( UPin 34, max + UPin 34, min ) / 2 = ( 20,15 mV + 12,89 mV ) / 2 = 16,52 mV →
+/- 3,63
mV →
+/- 21,97 % Abweichung vom Mittelwert. Die absolute Abweichung aber beträgt: ∆UPin
34, abs = UPin 34, max - UPin 34, min = 20,15 mV - 12,89 mV = 7,26 mV → 36,03 % absolute Abweichung.
Aber bevor wir eine weiteres Verfahren zur genaueren Messwerterfassung
kennenlernen und ausprobieren, müssen wir uns noch weitere
Programmierkenntnisse aneignen. Bisher haben wir nur zwei Funktionen kennengelernt und zwar die beiden ·
Statements < void setup() und void loop()
> Nun erzeugen wir eine weitere, sozusagen eigene Funktionen namens ·
Statement
< void inputAnalogPin34_String() > Dabei soll die Funktion „inputAnalogPin34_String()“
wie der Name schon sagt, später den analogen Port „Pin 34“ des A/D-Wandlers
einlesen, dessen Dezimalwert im Bereich [ 0, …, 4095 ] in einen Millivolt-Wert [ mV ]
umrechnen und in eine Zeichenkette,
engl. „string“, umwandeln. Doch zunächst ist die Funktion „inputAnalogPin34_String()“
vom Typ „void“,
d.h. so viel wie leer und zwar in dem Sinne, dass diese nichts
Verwertbares wie z.B. ein Ergebnis
oder ähnliches ans Hauptprogramm
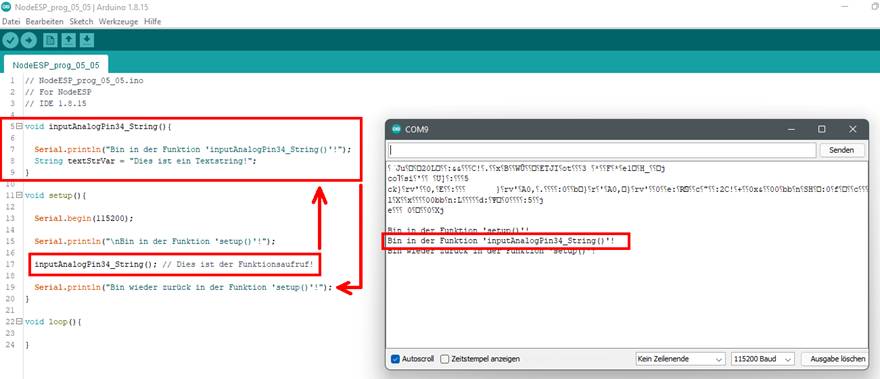
zurückliefert: (Bild vergrößern: auf
Bild klicken! Webverzeichnis | NodeESP_prog_05_05.ino) Wenn man nun erreichen
will, dass die Funktion „inputAnalogPin34_String()“
den Variableninhalt
der Stringvariablen „textStrVar“ nach
dem Funktionsaufruf mit dem ·
Statement
< Serial.println("Textausgabe
= " + inputAnalogPin34_String() ); > an das Hauptprogramm
bzw. die Funktion „void
setup()“ zurück liefert, dann muss
man das ·
Statement
< return(textStrVar);
> ans Ende der Funktion
„inputAnalogPin34_String()“
setzen! Da die Funktion „inputAnalogPin34_String()“ den Variableninhalt
der Stringvariablen „textStrVar“ an
das Hauptprogramm bzw. die Funktion „void setup()“ zurück liefert, ist sie nicht
mehr leer, d.h. nicht mehr vom Typ
„void“, sondern vom Typ „String“, weil der zurück zu liefernde Inhalt der Variablen „textStrVar“
vom Typ „String“
ist!
Da das zurück gelieferte
Ergebnis, nämlich der Variableninhalt der Stringvariablen „textStrVar“,
vom Typ „String“
ist, lässt sich dieser bei der Textanzeige
zum vorangestellten Text „Textausgabe = “
mittels „+“ quasi
addieren, d.h. wie folgt hinzufügen: ·
Statement
< Serial.println("Textausgabe
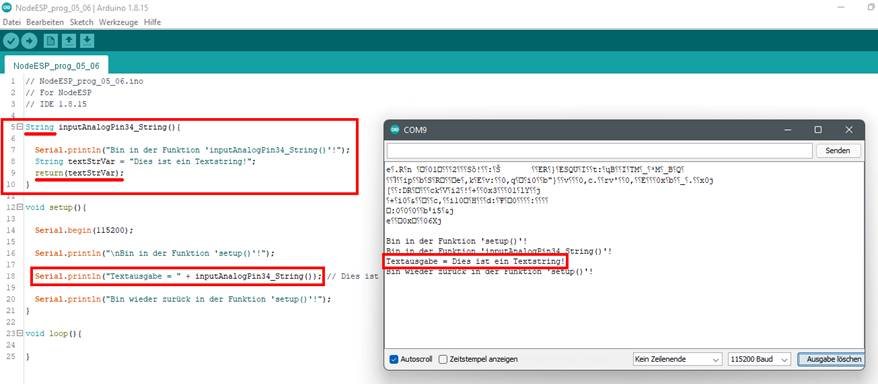
= " + inputAnalogPin34_String() ); > (Bild vergrößern: auf
Bild klicken! Webverzeichnis | NodeESP_prog_05_06.ino) Kennen Sie das „EVA“-Prinzip?
„EVA“ ist die Abkürzung für „Eingabe, Verarbeitung, Ausgabe“. Um Daten mittels Computer be- und verarbeiten zu können, muss man diese
zunächst in den Computer eingeben, d.h. in den Arbeitsspeicher
bringen. Beispielsweise durch (Tastatur-) Eingaben oder durch Einlesen einer Datei. Und um mit den Daten rechnen zu können, benötigt man
ein entsprechendes Computerprogramm.
Nachdem die Daten entsprechend den Anweisungen
des Computerprogramms berechnet
und verarbeitet
wurden, lassen sie sich wieder ausgeben, d.h. auf dem Display
anzeigen, auf dem Drucker
ausdrucken oder wieder in eine Datei
abspeichern. Gemäß dem „EVA“-Prinzip
wurden in der Funktion „inputAnalogPin34_String()“
bis jetzt Daten, und zwar der Variableninhalt
der Stringvariablen „textStrVar“, verarbeitet
und mittels des ·
Statements
< return(textStrVar);
> wieder an das Hauptprogramm
„setup()“ ausgegeben und in
der „Arduino“-Konsole
angezeigt. Doch wenn Daten in der Funktion „inputAnalogPin34_String()“ verarbeitet
werden sollen, dann müssen sie zuvor, d.h. vor der Verarbeitung,
„irgendwie“ in die Funktion
gebracht, d.h. eingelesen werden: ·
Statement < String inputAnalogPin34_String(String getInputString)
> Besonders interessant und wichtig ist tatsächlich, dass man
innerhalb des ·
Statements
< Serial.println("Textausgabe
= " + inputAnalogPin34_String("Dies ist ein Textstring!") ); > nicht nur die Funktion „inputAnalogPin34_String()“
selbst aufrufen kann, sondern dieser auch noch beim Funktionsaufruf
den Textstring "Dies ist ein
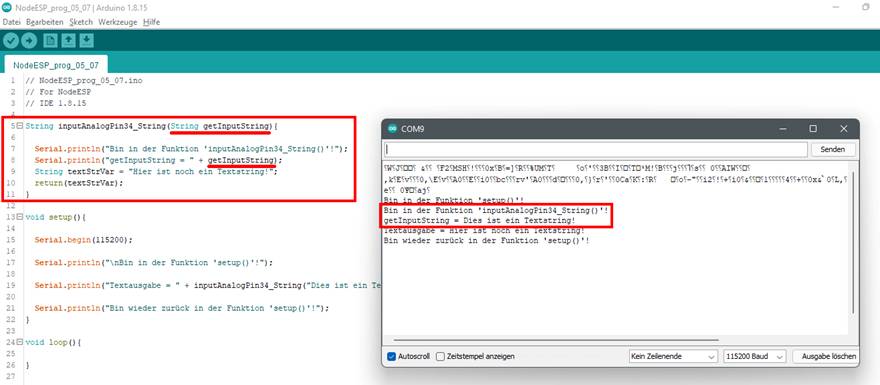
Textstring!" mit auf den Weg geben, d.h. einlesen kann: (Bild vergrößern: auf
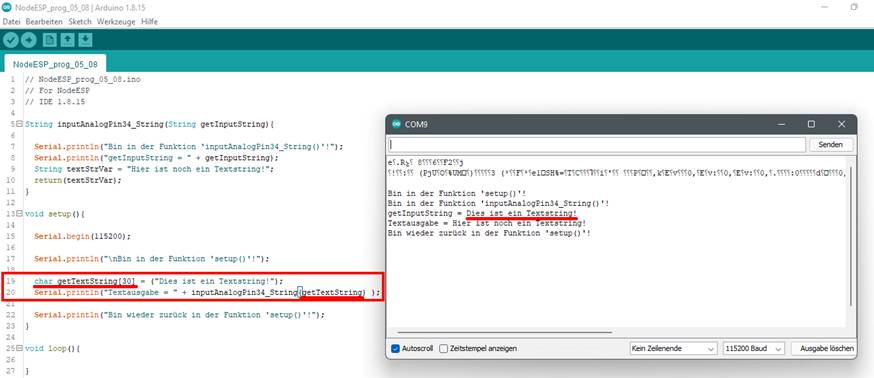
Bild klicken! Webverzeichnis | NodeESP_prog_05_07.ino) Selbstverständlich lässt sich nicht nur konstanter
Text in Form des Textstrings „Dies ist ein Textstring!“
oder z.B. mittels der Textvariablen
„getTextString“ vom Typ „String“ übergeben, ·
Statement
< String getTextString = "Dies ist ein
Textstring!";
> sondern auch Text in Form eines Zeichen-Arrays
vom Typ „char“,
engl. „character“, d.h. Buchstaben, Ziffern und Zeichen:
·
Statement
< char getTextString[30]
= ("Dies
ist ein Textstring!");
> ·
Statements
< Serial.println("Textausgabe
= " + inputAnalogPin34_String(getTextString) ); > (Bild vergrößern: auf Bild
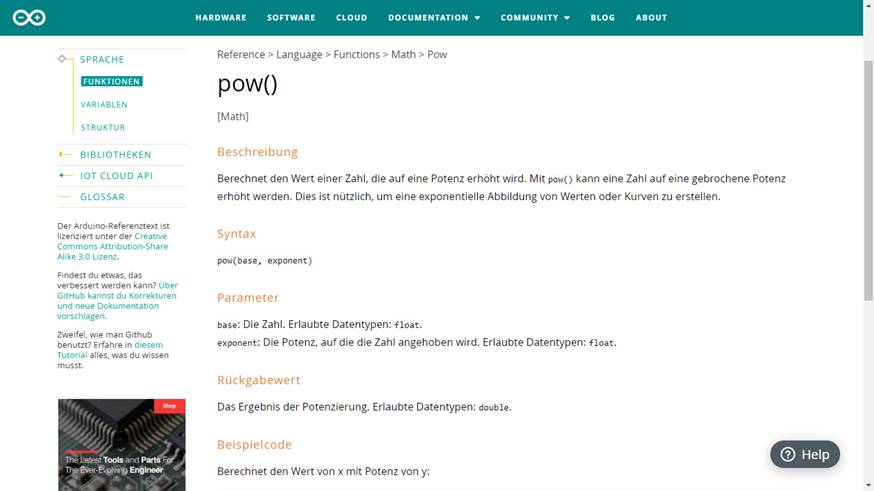
klicken! Webverzeichnis | NodeESP_prog_05_08.ino) Als nächstes lernen wir
einen neuen Befehl kennen. Und zwar den „Sketch“-Befehl „pow()“ mittels dem sich eine
beliebige Zahl ins Quadrat erheben, d.h. quadrieren lässt: (Bild vergrößern: auf
Bild klicken! Quelle: Arduino) Wie kann man sich den Befehl „pow()“ am
besten merken? Im Englischen steht der Ausdruck „power“ für Macht, Leistung,
Kraft, Strom, Energie, Stärke, Potenz. Im
weitesten Sinne spielt engl. „Power“,
d.h. auf Deutsch „Potenz“ auch
beim Potenzieren
eine Rolle. Übersetzt man „Potenzieren“ ins Englische, so heißt es übersetzt,
engl. „raise to the power of“,
d.h. „erhebe in
die Potenz von x2“. Dabei steht engl. „raise“
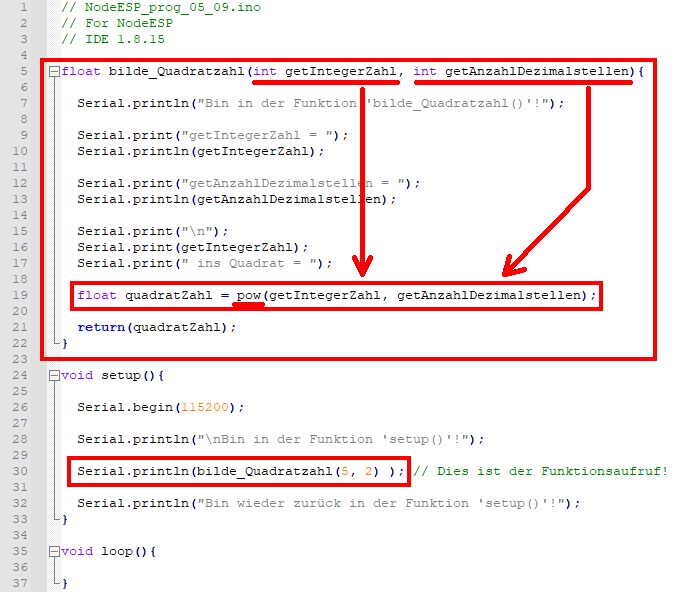
für „sich erheben“, „sich erhöhen“, womit im vorliegenden Fall der Exponent ^2 (= hoch 2) gemeint ist. Dabei gibt der zweite
Parameter „getAnzahlDezimalstellen“ im
·
Statement
< float quadratZahl = pow(getIntegerZahl, getAnzahlDezimalstellen); > an, wie viele Dezimalstellen
(= 2) im
Ergebnis ausgegeben werden sollen: (Bild vergrößern: auf
Bild klicken! Webverzeichnis | NodeESP_prog_05_09.ino) Das Besondere
an dem „pow()“-Befehl
und dem ·
Statement
< float quadratZahl = pow(getIntegerZahl, getAnzahlDezimalstellen); > aber ist, dass sich nicht
nur ganzzahlige Werte wie
z.B. die Zahl „5“ ins Quadrat
erheben lässt = 25,
sondern auch rationale Zahlen
wie z.B. die Zahl „5,5“. Was aber sind rationale
Zahlen? Der Begriff „Vernunft“ kommt aus dem Lateinischen
und nennt sich „ratio“ (siehe Google
Translate). „Rationale Zahlen“
sind also vernünftige Zahlen.
Die Zahl „5,5“ z.B ist vernünftig, d.h. rational und die Kreiszahl Pi (= „π“)
mit π = 3,1415926535897932384626433832795… ≈ 3,14159… ist unvernünftig, d.h. irrational, weil
die Kreiszahl π
praktisch unendlich viele Nachkommastellen
hat, sodass sich die Dezimalstellen
nach dem Komma nicht als rationaler, d.h. vernünftiger
Bruch
darstellen lassen: 3,14159… = 3 + 0,14159… = 3 + ( 14159…
/ 100 000… ) = 3 + 0,141592…
= 3 + ( 141592… / 1 000 000… ) = 3 + 0,1415926… = 3 + ( 1415926… / 10 000 000… ) = 3 + 0,14159265… = 3 + ( 14159265… / 100 000 000… ) = … Die Zahl „5,5“ ist also deshalb vernünftig, d.h. rational,
weil sie eine endliche Zahl
von Nachkommastellen
hat, nämlich gerade mal eine und weil sich die Zahl „5,5“ als vernünftiger Bruch wie folgt darstellen
lässt: 5,5 = 5 + 0,5 = 5 + 5 / 10 = 5 + ½ = 11 / 2 Und, wenn die Zahl
„5,5“
als vernünftiger Bruch darstellen lässt, dann gilt das auch für das Quadrat
der Zahl „5,5“: 5,5
^2 = ( 11 / 2 )^2 = ( 11 / 2 ) * ( 11 / 2 )
= ( 11 * 11 ) / ( 2 * 2 ) = 121 / 4
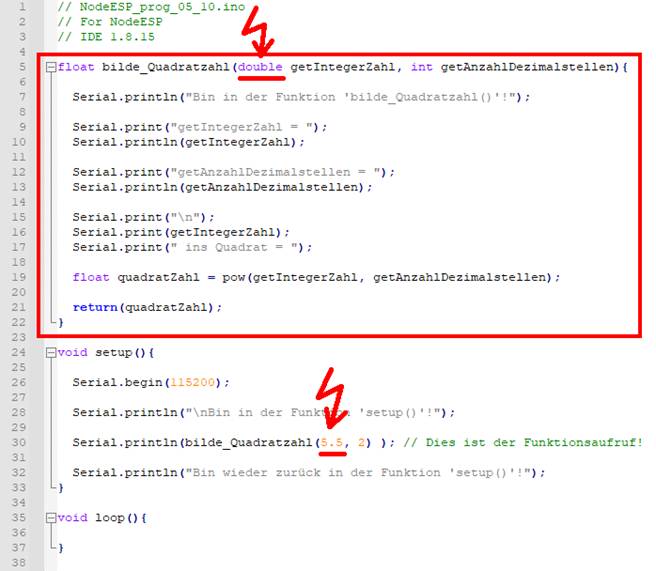
= 30,25 (Bild vergrößern: auf
Bild klicken! Webverzeichnis | NodeESP_prog_05_10.ino) Wenn man, wie im
obenstehenden Programmkode zu sehen ist, die rationale Zahl „5,5“ quadrieren will, dann muss
die Variable „getIntegerZahl“
von nun an immer vom Typ „double“
sein, damit es beim Kompilieren keine Fehlermeldung gibt! Außerdem sollten wir im nächsten
Programm die Variable „getIntegerZahl“ in
Variable „getRationaleZahl“ umbenennen:
(Bild vergrößern: auf
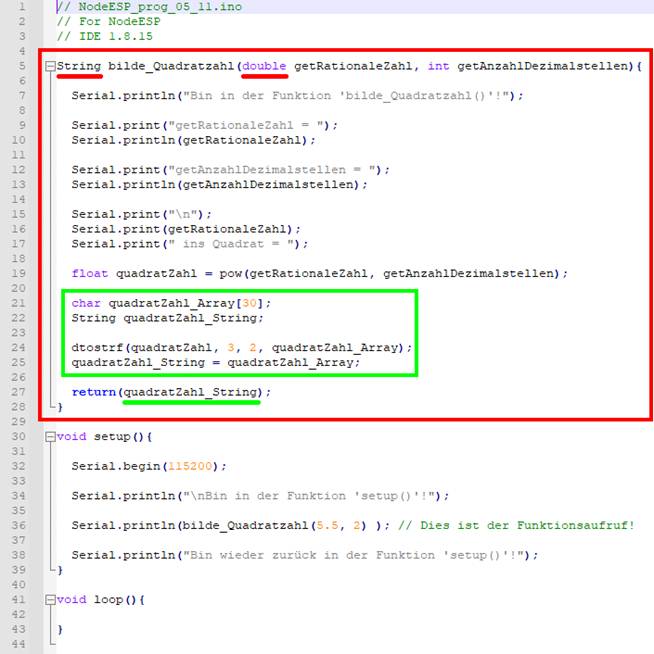
Bild klicken! Webverzeichnis | NodeESP_prog_05_11.ino) Wie man im Programmkode im grünen Kasten sieht, wird im ·
Statement „dtostrf()“ = d(ouble) to str(ing) f(loat), konkret im ·
Statement
< dtostrf(quadratZahl,
3, 2, quadratZahl_Array); > das Ergebnis der Quadratur 5,5^2 = 30,25,
d.h. der Inhalt der Variablen „quadratZahl“ zunächst
in die Variable „quadratZahl_Array“ vom Typ „char“,
d.h. engl. „character“,
im Sinne eines Zeichen-Arrays,
das sich aus einzelnen Buchstaben, Ziffern oder Zeichen zusammensetzt,
umgewandelt! Diesbezüglich sei daran erinnert, dass der Befehl „dtostrf()“der
Programmiersprache „C“
entstammt. Da aber das Ergebnis
als Textstring
vom Typ „String“
angezeigt werden soll, muss der Inhalt der Variablen „quadratZahl_Array“
noch in den der „String“-Variablen „quadratZahl_String“
wie folgt umgewandelt werden: ·
Statement
< quadratZahl_String = quadratZahl_Array; > Auch hier sei daran
erinnert, dass der Typ „String“
der Variablen „quadratZahl_String“
der Programmiersprache „C++“
entstammt. Deshalb auch die entsprechende Umwandlung. Sozusagen von „C“
nach „C++“
(siehe im grünen Kasten
oben). Wenn also der Variableninhalt
der Variablen „quadratZahl_String“
vom Typ „String“
ist, dann muss die Funktion „bilde_Quadratzahl()“
mit dem ·
Statement
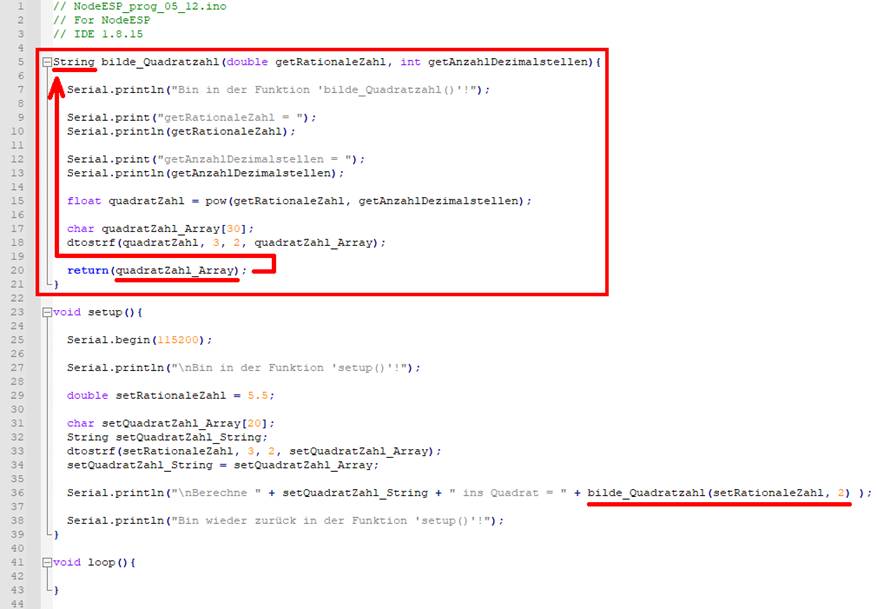
< return(quadratZahl_String); > ebenfalls vom Typ „String“ sein: (Bild vergrößern: auf
Bild klicken! Webverzeichnis | NodeESP_prog_05_12.ino) Wir optimieren weiterhin das
Programm, indem wir eine Funktion „doubleToString()“
programmieren mit der sich eine Fließkommazahl
vom Typ „float“
oder „double“
wie z.B. die rationale Zahl „5,5“ in
einen Textstring
umwandeln lässt, damit sich dieser bei der Anzeige mittels String.println() zu
anderen Textstrings hinzufügen lässt: ·
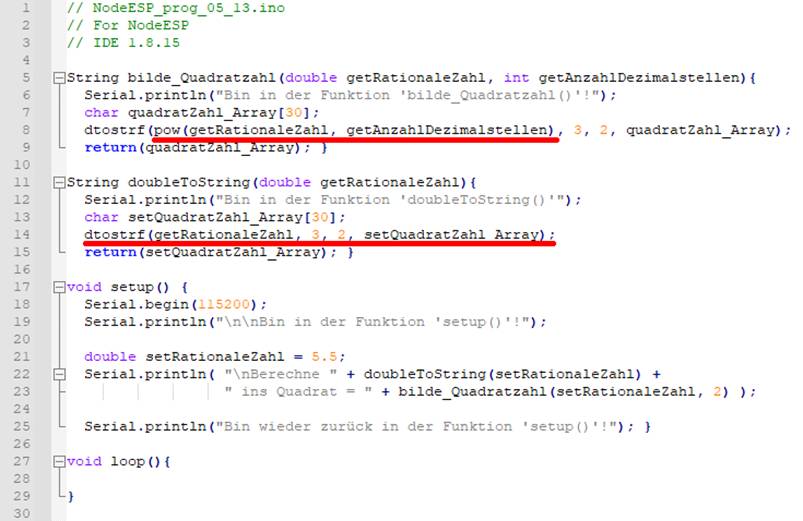
Statement (Bild vergrößern: auf
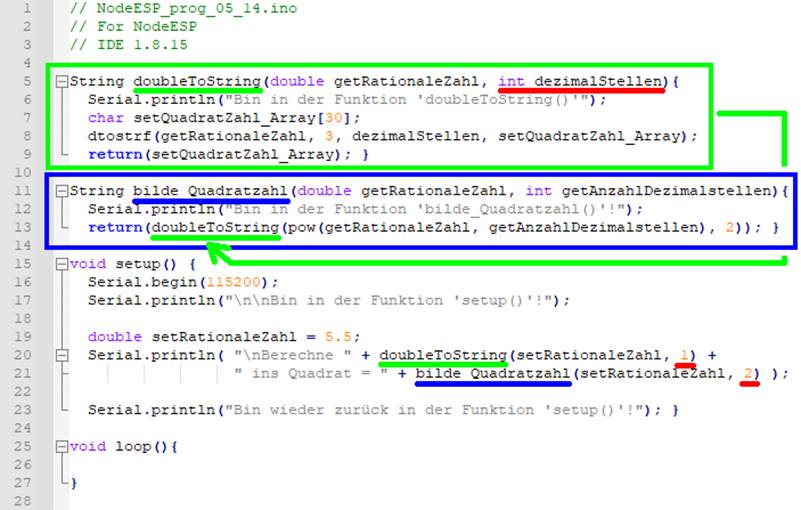
Bild klicken! Webverzeichnis | NodeESP_prog_05_13.ino) Wir optimieren das Programm
ein weiteres Mal, indem wir die Funktion
„doubleToString()“ innerhalb des Quellkodes vor die Funktion „bilde_Quadratzahl()“ positionieren,
damit diese bereits dem Compiler bekannt ist, bevor
diese in der Funktion „bilde_Quadratzahl()“
aufgerufen und ausgeführt wird. Außerdem führen wir in der Funktion „doubleToString()“
eingangsseitig im Kopf der Funktion
einen weiteren Parameter ein. Und
zwar die Variable „getAnzahlDezimalstellen“
vom Typ „int“,
d.h. engl. „integer“, ganzzahlig, sodass sich die Anzeige der darzustellenden
Nachkommastellen vorab festlegen
und mit auf den Weg geben lässt (siehe rote Unterstreichung): (Bild vergrößern: auf Bild
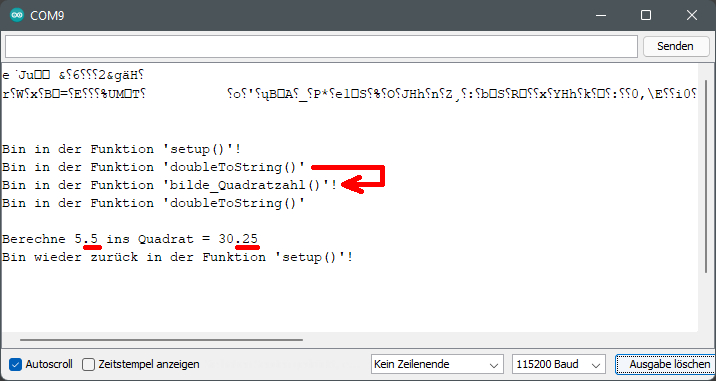
klicken! Webverzeichnis | NodeESP_prog_05_14.ino) Werfen wir in diesem
Zusammenhang noch einen Blick auf die Bildschirmanzeige: (Bild vergrößern: auf
Bild klicken! Webverzeichnis | NodeESP_prog_05_14.ino) Wie man im obenstehenden
Screenshot des Konsolefensters
sieht, wird bei der Programmausführung
des „Sketch“-Programms „NodeESP_prog_05_14.ino“
durch den „NodeESP“-Mikrocontroller standardmäßig
als erstes die Funktion „setup()“
aufgerufen und ausgeführt. Innerhalb dieser wird dann
als nächstes die Funktion „doubleToString()“ aufgerufen
und ausgeführt, um den Dezimalwert „5.5“
mit nur einer Nachkommastelle
des ·
Statements
< double setRationaleZahl = 5.5; > in einen Textstring umzuwandeln, damit sich dieser in der „Serial.println()“-Textanzeige
mit dem ·
Statement
< Serial.println(
"\nBerechne " + doubleToString(setRationaleZahl, 1 ) + … );
> anzeigen lässt. Anschließend wird die Funktion „bilde_Quadratzahl()“
aufgerufen und ausgeführt, um den Dezimalwert
„5.5“
wie folgt zu quadrieren: 5.52 = 5.5^2 = 30.25. Zwecks Textanzeige
muss der Ergebniswert = 30.25
ebenfalls mit der Funktion „doubleToString()“ in einen Textstring umgewandelt werden, sodass sich dieser
dann abschließend mit dem ·
Statement
< Serial.println( … +
" ins Quadrat = " + bilde_Quadratzahl(setRationaleZahl, 2) ); >; im oben gezeigten Konsolefenster
anzeigen lässt. Auch wenn sich das Ganze
etwas kompliziert anhört bzw. liest, so geht es doch nur um eines, nämlich,
ob und wie man z.B. die Funktion „doubleToString()“
aufruft, wie eine Funktion eine andere
Funktion aufruft und vor allem, wie Funktionen im Programmkode eines „Sketch“-Programms angeordnet sein müssen! Und
zwar in welcher Reihenfolge! Dabei geht es um
gegenseitige und wechselseitige, logische Abhängigkeiten von Funktionen,
wenn z.B. eine Funktion von einer
anderen abhängig ist, diese also voraussetzt, bevor sie sich
aufrufen und starten lässt. Dann muss nämlich die eine Funktion von der anderen
wissen und wissen, dass es diese überhaupt gibt! Wie aber machen das die Funktionen? Schließlich sind Funktionen
nicht per se intelligent oder hellseherisch! Ganz einfach! Die
„künstliche“ Intelligenz spielt sich im Kopf des engl. „developer“,
d.h. des Entwicklers, des Programmierers ab, der im Programm festlegen muss, an welcher Position die eine oder andere
Funktion positioniert werden muss.
Bei älteren, höheren
Programmiersprachen müssen Funktionen, Methoden (Funktion eines Objektes)
oder Objekte im Quellkode vor
dem des Hauptprogramms stehen. Bei
anderen können diese entweder vor oder hinter dem Quellkode des Hauptprogramms stehen. Falls eine (Sub-) Funktion (eine Methode oder
ein Objekt) eine andere voraussetzt, also auf diese aufbaut, dann
muss diese innerhalb des Quellkodes
vor der aufrufenden (Main-)
Funktion stehen! Dann weiß der Compiler nämlich, dass
er zuerst die (Sub-) Funktion
kompilieren muss und anschließend erst die (Main-) Funktion. Im vorliegenden Fall der
modernen „Sketch“-Programmierung
für Mikrocontroller mit dem „NodeESP“
spielt es keine Rolle, ob Funktionen
innerhalb des Programmkodes vor
dem Hauptprogramm „setup()“
platziert werden oder nicht, da der Compiler
bereits vor dem eigentlichen Kompilieren
untersucht und prüft, welche Programmteile
ob und wie von anderen abhängen, diese also voraussetzen!
[ Zurück
] zum NodeESP –
Versuch 5 |
|
|||||||||
|
|
[
NodeESP
] [ Seitenanfang ] |
|