[ NodeESP ] [ Seitenende ]

NodeESP – Versuch 5

Vom analogen zum digitalen Spannungsmessgerät

Rufen wir uns kurz mittels Wikipedia in Erinnerung, was ein Spannungsmessgerät ist:

>> Ein Spannungsmessgerät (auch als Spannungsmesser oder umgangssprachlich als Voltmeter^[1] bezeichnet) dient zur Messung elektrischer Spannungen.

Bei der Messung wird die Messgröße in eine Anzeige ihres Vielfachen der Einheit Volt umgeformt. Das Spannungsmessgerät besteht aus dem eigentlichen Messwerk bzw. der Messelektronik, einer Anzeige und gegebenenfalls einem Vorwiderstand oder Spannungsteiler zur Anpassung des Messbereiches. Für Laboranwendungen gibt es umschaltbare Vielfachmessgeräte mit mehreren Messbereichen und für weitere Messgrößen, die als Multimeter bezeichnet werden. << (Quelle: Wikipedia)

Früher, d.h. vor der Erfindung von Halbleitern, d.h. von Dioden, Zenerdioden, Transistoren, Feldeffekttransistoren (MOS-) FETs), Thyristoren und Triacs, gab es nur analoge Voltmeter bzw. analoge Multimeter (= Zeigermessgeräte):

>> Bei Analogmultimetern wird der Messwert auf einem Zeigermessgerät mit mehreren Skalen für unterschiedliche Messbereiche angezeigt. Die Ablesewerte sind durch diskrete Teilstriche dargestellt, Zwischenwerte können interpoliert werden. Die Fehlergrenzen von analogen Messgeräten können bei hochwertigen Geräten durchaus weniger als ein Prozent des Messbereichsendwertes betragen. Als entscheidendes Bauteil, das die Anzeige liefert, kommt in der Regel ein Drehspulmesswerk zum Einsatz.

Die Messbereiche von Drehspulgeräten erstrecken sich so etwa bei Gleichspannungen von 100 mV bis 1000 V, für Gleichströme von 100 µA bis 10 A, hochwertige Geräte weisen teilweise noch kleinere Bereiche auf. Analoge Multimeter haben bei Spannungsmessung im Regelfall einen wesentlich geringeren Innenwiderstand als Digitalmultimeter, was bei hochohmigen Spannungsquellen zu Messabweichungen (Schaltungseinfluss) führen kann. Der Einfluss des Innenwiderstands bei Strom- und Spannungsmessung kann durch eingebaute Verstärker verringert werden, wodurch solche Analogmultimeter bei Spannungsmessung einen hohen Innenwiderstand erreichen, der dem von Digitalmultimetern entsprechen kann.

Zur Widerstandsmessung wird der Strom gemessen, den eine eingebaute Batterie durch den Widerstand fließen lässt. Der Zusammenhang ist stark nichtlinear; die Messung eignet sich nur für grobe Aussagen. Auch bei Widerstandsmessung kann bei sehr hochwertigen Geräten eine Verstärkerelektronik zur Skalenlinearisierung eingesetzt werden. << (Quelle: Wikipedia)

Mit der Entwicklung der Digitaltechnik und der logischen Gatterschaltungen, der Verdichtung, d.h. der Unterbringung von abertausenden Transistoren auf einem kleinen, quadratmillimeter großen Silizium-Chip in Form eines „Integrierten Schaltkreises“, engl. „Integrated Circuit“ (IC) sowie der Entwicklung der „Operationsverstärker“ (OPs) ab Anfang der 1960er Jahre gab es dann auch digitale Voltmeter bzw. digitale Multimeter (= Messgeräte mit digitaler Anzeige in Form mehrstelliger 7-Segment-Anzeigen auf Basis von LEDs oder eines mehrzeiligen LCD-Displays):

>> Bei Digitalmultimetern wird das Signal elektronisch mit einem Analog-Digital-Umsetzer aufgenommen und der gemessene Wert als numerischer Wert angezeigt. Die Messbereiche erstrecken sich in der Regel von 200 mV bis 1000 V und von 20 µA bis 20 A. Digitale Multimeter weisen bei der Spannungsmessung meist einen hohen Innenwiderstand von 1 bis 20 MΩ auf, Standard ist 10 MΩ. Die relative Fehlergrenze ist je nach Messbereich meist kleiner als 1 %, in den Gleichspannungsbereichen liegt sie bei hochwertigeren Geräten in der Regel unter 0,2 %.

Die Messung von Strom wird durch Messung der Spannung an umschaltbaren Shuntwiderständen durchgeführt. Die Messung von Widerständen wird auf die Messung von Spannung aufgrund einer umschaltbaren Konstantstromquelle zurückgeführt.

Vorteile von Digitalmultimetern sind der relativ einfache mechanische Aufbau und in Massenfertigung produzierbare elektronische Bauteile, wodurch sie schon relativ preiswert erhältlich sind, meist billiger als ein gutes Analoggerät. Die Bedienung ist durch die Einblendung der Maßeinheiten im Display sowie durch die Vermeidung mehrerer Skalen sehr einfach. Ferner besitzen manche Digitalgeräte Schutzschaltungen gegen Überlast und Verpolung. Komfortable Geräte können den Spannungsmessbereich automatisch wählen (Auto-Range-Funktion). Gegen Stöße und Stürze sind sie relativ unempfindlich, da keine empfindliche Mechanik beschädigt werden kann.

Bedingt durch die interne Elektronik zur Signalverarbeitung und Anzeige auf dem Display sind Digitalmultimeter immer auf eine Versorgung aus einer Batterie, Netzgerät oder Solarzelle angewiesen.

Einige Geräte weisen auch Messmöglichkeiten für Frequenzen, Kapazitäten, Induktivitäten sowie Transistor- und Diodeneigenschaften auf. Mittels eingebauter oder externer Sensoren sind mit manchen Geräten auch Luftfeuchtigkeits-, Schall- oder Temperaturmessungen möglich. Auch ein akustischer Durchgangsprüfer ist bei fast allen Digitalgeräten eingebaut. << (Quelle: Wikipedia)

Jetzt wissen wir, dass die analoge (Gleich-) Spannung beim digitalen Spannungsmessgerät (= Voltmeter) zwecks Umwandlung in einen digitalen Messwert dem sogenannten Analog-/Digital-Wandler (= A/D-Wandler), engl. „analog-to-digital converter)“ (= ADC) zugeführt wird.

Da sich das analoge Eingangssignal des A/D-Wandlers nicht nur wertmäßig in Form kleiner Spannungsänderungen ∆U fortwährend ändern, d.h. schwanken kann, sondern auch zeitmäßig während des Messintervalls mit ∆t ändern, d.h. dehnen, strecken und stauchen kann, muss das analoge Eingangssignal des A/D-Wandlers sowohl zeitlich also auch wertmäßig, d.h. amplitudenmäßig, erfasst und ausgewertet werden, sodass der analoge Messwert sowohl eine Funktion der Spannung U als auch der Zeit t ist bzw. diese bei der Umrechnung berücksichtigen muss! 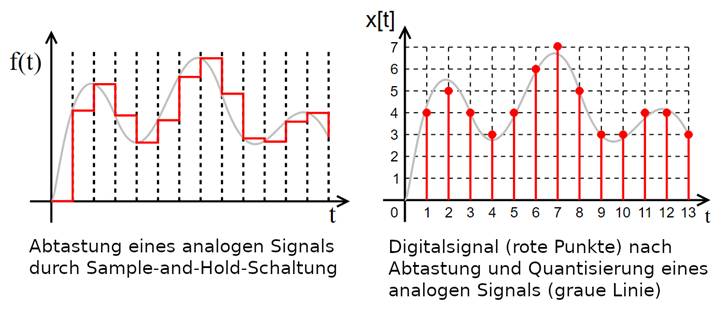Demzufolge ergibt sich ein zeitlicher (links) und Bitwerte mäßiger (rechts) Verlauf (siehe Wikipedia):

(Zum Vergrößern bitte auf das Bild klicken!)

Im linken Bild oben wird also das analoge Signal mittels Rechteckimpulse stufenweise abgetastet. Dabei moduliert der sinusförmige Signalverlauf hinsichtlich seiner Amplitude die einzelnen Rechteckimpulse ebenfalls in der Amplitude. Das Abtasten des sinusförmigen Signalverlaufs durch Rechteckimpulse nennt man übrigens engl. „samplen“, d.h. abtasten.

Je größer die Samplingrate, d.h. je größer die Abtastfrequenz ist, umso genauer wird das Ergebnis!

Die A/D-Wandler (= ADCs) des ESP32 im „NodeESP“ arbeiten mit T = 200 000 Messungen/Sekunde, d.h. mit einer Samplingfrequenz von

f_Sample = 200 000 / s = 200 000 s^-1 = 200 000 Hz = 200 kHz mit f = 1 / T oder

T = 1 / f = T_Sample = 0,000005 s = 0,005 ms = 5 * 10^-6 s = 5 µs

Das klingt nicht nur sehr vielversprechend, sondern ist es auch!

Im rechten Bild oben sieht man das aus dem analogen Signal umgewandelte Digitalsignal (= rote Punkte), dessen Bitwerte aber nach der Umwandlung nicht exakt auf dem Kurvenverlauf des analogen Ursprungssignals liegen. Dabei verhält es sich so, dass die Ungenauigkeiten umso kleiner sind, je kleiner, d.h. schmäler und umso zahlreicher die einzelnen, roten Abtastbalken (siehe Bild links oben) sind. Demzufolge verringern sich die Ungenauigkeiten umso mehr, je größer die Samplingfrequenz ist.

Zum Erzeugen der Samplingfrequenz braucht man einen Sinusgenerator, der wie im vorliegenden Fall mit einer (Resonanz-) Frequenz von f_Sample = 200 kHz schwingt. Dem Sinusgenerator nachgeschaltet wird dann ein sogenannter Komparator, d.h. Signalvergleicher im Sinne eines Spannungsvergleichers, der das Eingangssignal mit einer fest vorgegebenen, Vergleichs- bzw. Konstantspannung vergleicht. Demzufolge verfügt ein Komparator über zwei Eingänge, aber nur einen Ausgang an dem die umgewandelten Sinusschwingungen (= hochfrequente Wechselspannung) in Form von Rechteckimpulsen anliegen.

Sobald eine Sinusschwingung der Samplingfrequenz den Nulldurchgang auf der Zeitachse (vormals x-Achse im Koordinatensystem) durchläuft, sodass die sinusförmige Wechselspannung u_Sinus(t) > 0 V_~ mit t > t₀ größer null Volt wird und dabei die vorgegebene Vergleichsspannung am zweiten Eingang mit u_Sinus(t) > U_Referenz übersteigt, schaltet der Ausgang des Komparators sprunghaft auf den ungefähren Maximalwert der anliegenden Versorgungsspannung von z.B. U_Rechteck < 3,3 V oder U_Rechteck < -3,3 V je nach Polariät der eingangsseitigen Halbwelle der Sinusschwingung. Wenn man die beiden Eingänge gegen Masse („┴“) miteinander vertauscht, dann wird die Ausgangsspannung (= Reckeckspannung) des Komparators invertiert!

>> Ein Komparator ist typischerweise eine Schaltung mit Operationsverstärker. Ein Operationsverstärker eignet sich als Komparator im Bereich niedriger Frequenzen und hat die Eigenschaft von Kippschaltungen, die beim Über- oder Unterschreiten der Referenzspannung Uref definierte Spannungswerte am Ausgang annehmen. Diese Spannungswerte sind durch die Betriebsspannung +UB und -UB vorgegeben. Wird die Referenzspannung Uref an den positiven Eingang gelegt, so wird die Ausgangsspannung invertiert.

Für höhere Frequenzen kommen echte Komparatoren zum Einsatz, welche aus denselben Grundfunktionen bestehen, jedoch nur als Komparatoren und nicht auch noch als Verstärker arbeiten können. Wegen der hohen Verstärkung reagiert diese Schaltung schon bei kleinen Spannungsunterschieden am invertierenden und nichtinvertierenden Eingang. Bei normalen Operationsverstärkern springt die Ausgangsspannung nicht sofort von Ua max zu Ua min bzw. umgekehrt. Es tritt eine Verzögerung durch die Slew Rate und Erholzeit des Operationsverstärkers auf.

Für kürzere Verzögerungszeiten gibt es spezielle Komparatoren. Bei ihnen (sind) ist die Verstärkung und die Genauigkeit der Umschaltschwelle etwas geringer. Dafür eignen sie sich in der Regel zur Ansteuerung von Digitalschaltungen. << (Quelle: Elektronik-Kompendium)

Neben der Abtastfrequenz (= Samplingrate) spielt für die Genauigkeit auch die sogenannte Auflösung des A/D-Wandlers bei der Umwandlung des analogen Eingangssignals ins digitale Ausgangssignal in Form von Bitwerten eine entscheidende Rolle.

So verfügt z.B. der „Arduino UNO“ mit seinem A/D-Wandler über eine Auflösung von nur 1024 Bit bezogen

auf 3,3 V Gleichspannung des digitalen Ausgangssignals:

3,3 V → 1023 Bit

1,0 V → x Bit

x = 1023 Bit / 3,3 V * 1,0 V = 310 Bit → 310 Bit/V

Probe:

310 Bit/V * 3,3 V = 1023 Bit

Wie man unschwer sieht, geht dabei der Bitwertebereich von [ 0, , 1023 ], sodass sich insgesamt 1024 verschiede Bitwerte ergeben! Der Bitwert 1024₁₀ selbst aber schon zur nächsten Bitdekade 0100 0000 0000₂ gehört, während der vorherige Bitwert 1023₁₀ dem Bitwert = 1024₁₀ - 1₁₀ = 0100 0000 0000₂ - 0000 0000 0001₂ = 0011 1111 1111₂ entspricht.

Im Gegensatz zum „Arduino UNO“ verfügt der „NodeESP“ mit einem seiner A/D-Wandler über eine Auflösung von 4096 Bit bezogen auf 3,3 V Gleichspannung des digitalen Ausgangssignals:

3,3 V → 4095 Bit

1,0 V → x Bit

x = 4095 Bit / 3,3 V * 1,0 V = 1 241 Bit → 1 241 Bit/V

Probe:

1 241 Bit/V * 3,3 V = 4095 Bit

Wie man unschwer sieht, ist die Bitauflösung des A/D-Wandlers vom „NodeESP“ insgesamt viermal so groß als die des „Arduino UNO“.

Beispiel

Welcher Bitwert stellt sich am Ausgang des A/D-Wandlers ein, wenn am analogen Eingang desselben eine Gleichspan-nung von U_Eingang = 1,25 V anliegt?

3,3 V → 4095 Bit

1,25 V → x Bit

x = 4095 Bit / 3,3 V * 1,25 V = 1 551 Bit → 1 551 Bit / 1,25 V = 1 241 Bit/V

Probe:

1 241 Bit/V * 1,25 V = 1 551 Bit

So, nun haben wir noch ganz nebenbei herausgefunden, dass nicht nur die Bitauflösung von 4095 Bit des A/D-Wandlers vom „NodeESP“ von Bedeutung ist, sondern auch die Bitzahl pro einem Volt = 1 241 Bit/V.

Demzufolge ist die Bitauflösung immer dann am größten und damit am genauesten, wenn sich möglichst viele Bitwerte einem Volt zuordnen lassen: 1 241 Bit/V.

Der Vorteil der Bitzahl pro Volt = 1 241 Bit/V ist nämlich der, dass man diesen Quotienten nur mit dem eingangsseitigen Analogwert der Spannung von z.B. U_Eingang = 1,25 V multiplizieren muss, um rechnerisch auf den ausgangsseitigen, digitalen Bitwert von 1 551 Bit zu kommen: 1 241 Bit/V * 1,25 V = 1.551 Bit.

Dabei lässt sich der Quotient als Bitzahl pro Volt auch als Skalierungsfaktor = 1 241 Bit/V bezeichnen, der die Umrechnung von analogen Volt in digitale Bitwerte erleichtert, sodass man nicht jedes Mal die Dreisatzrechnung bemühen muss! -

Umgekehrt, d.h. rückwärts von digital zu analog geht die Umrechnung natürlich auch:

4095 Bit → 3,3 V

1 Bit → x V

x = 3,3 V / 4095 Bit * 1 Bit = 8,06 * 10^-4 V = 0,806 mV → 0,806 mV/Bit

Probe:

0,806 mV/Bit * 4095 Bit = 3,3 V

Wenn wir z.B. am Ausgang des A/D-Wandlers einen digitalen Bitwert von 1 551 Bit messen bzw. angezeigt bekommen, dann entspricht dieser der analogen Eingangsspannung von U_Eingang = 0,806 mV/Bit * 1 551 Bit = 1 250,106 mV = 1,25 V.

Demzufolge macht es also auch Sinn, einen ausgangsseitigen Bitwert mittels des ausgangsseitigen Quotienten bzw. Skalierungsfaktors = 0,806 mV/Bit in einen zugehörigen, eingangsseitigen Spannungswert U_Eingang = 0,806 mV/Bit * 1 551 Bit = 1 250,106 mV = 1,25 V umzurechnen!

Mit dem ausgangsseitigen Quotienten bzw. Skalierungsfaktors = 0,806 mV/Bit wird sofort deutlich, dass der A/D-Wandler des „NodeESP“ über einen sehr empfindlichen, analogen Spannungseingang U_Eingang verfügt!

Ganz im Gegensatz zum sehr unempfindlichen, analogen Spannungseingang U_Eingang des „Arduino UNO“ mit

1023 Bit → 3,3 V

1 Bit → x V

x = 3,3 V / 1023 Bit * 1 Bit = 0,0032258 V = 3,226 mV → 3,226 mV/Bit

Probe:

3,226 mV/Bit * 1023 Bit = 3 300,198 mV = 3,3 V

Auch beim direkten Vergleich der eingangsseitigen, analogen Spannungsempfindlichkeit = 3,226 mV/Bit des „Arduino UNO“ mit der eingangsseitigen, analogen Spannungsempfindlichkeit = 0,806 mV/Bit des „NodeESP“ zeigt sich sofort, dass die Spannungsempfindlichkeit des „NodeESP“ viermal so empflindlich ist als die des „Arduino UNO“!

Wenn es also darum geht, eine sehr kleine, analoge Eingangsspannung von U_Eingang < 1 mV zu messen und in einen entsprechenden ausgangsseitigen digitalen Bitwert umzurechnen, dann es ist man gut beraten, einen sehr empfindlichen A/D-Wandler mit einem sehr großen ausgangsseitig maximalen Bitwert von z.B. 4095 Bit/3,3 V wie beim „NodeESP“ zu verwenden!

So, nun wird es langsam Zeit, dass wir uns der Praxis zuwenden und das erste Messprogramm zur Messung einer analogen Gleichspannung von bis zu 3,3 V programmieren.

[ Weiter ] zur Programmierung des „Sketch“-Programms „sketch_prog_05_01.ino“

Spannungsmessung mit höherer Genauigkeit

Obwohl der A/D-Wandler des „NodeESP“ über eine sehr hohe Bitauflösung von 4096 verschiedenen Messwerten im Bereich [ 0, …, 4095 ] Bits verfügt - bezogen auf eine analoge Eingangsspannung von max. U_{e, max} = 3,3 V - , verhält es sich dennoch so, dass die Messwerte selbst, wenn auch in einem kleinen Korridor, ziemlich stark schwanken (siehe Bild oben).

Einer der Gründe dafür dürfte der sein, dass der A/D-Wandler kein Hellseher ist und demzufolge bei der Messung des ersten Messwertes nicht weiß, nicht wissen kann, wie groß der Spitzenwert (= max. Ausschlag) der Amplitude ist, sodass dieser geschätzt werden muss. Wie aber soll man etwas schätzen von dem man keine Ahnung hat bzw. das man noch nicht kennt?

„Vorsicht heißt die Mutter der Porzellankiste“ könnte man sagen. Mein Bruder musste als Jugendlicher in der Jugendherberge Teller abtrocknen. Dabei blieb es nicht aus, dass ihm ein großer Teller aus den Händen glitt und zerbrach und er diesen bezahlen musste. Von diesem Tag an zog er es vor, nur noch kleine Teller abzutrocknen, weil diese nicht so viel gekostet hätten, falls doch noch mal einer zu Bruch gegangen wäre. Man muss sich eben nur zu helfen wissen.

So ähnlich macht es auch der A/D-Wandler. Er fängt ganz bescheiden mit 1 Bit als Messvergleichsspannung an

4095 Bit → 3,3 V

1 Bit → x V

x = 3,3 V / 4095 Bit * 1 Bit = 8,0586 * 10^-4 V = 0,806 mV → Skalierungsfaktor 0,806 mV/Bit

Probe:

0,806 mV/Bit * 4095 Bit = 3.300,57 V ≈ 3,3 V þ

und fährt diese dann sukzessive hoch. Demzufolge verfügt der A/D-Wandler in seinem Inneren z.B. über einen sogenannten Sägezahn-Generator mit dem sich eine langsam oder auch schnell ansteigende Spannung in Form eines Sägezahns innerhalb eines definierten Zeitfensters erzeugen lässt. Dabei vergleicht dann ein sogenannter Komparator (= Signalpegel-Vergleicher) das analoge Eingangssignal (= Messsignal) mit der ansteigenden, analogen Sägezahnspannung, um beim Überschreiten derselben einen zeitabhängigen Triggerimpuls auszulösen, der wiederum dafür sorgt, dass das analoge Eingangssignal vom A/D-Wandler in ein binäres Ausgangssignal, d.h. in einen entsprechenden Bitwert umgewandelt und z.B. im Konsolefenster des „NodeESP“ angezeigt wird.

Wegen des Skalierungsfaktors von 0,806 mV/Bit ≈ 1 mV/Bit werden also die berechneten und angezeigten Spannungswerte immer um rund +/- 1 mV zu groß oder zu klein sein. Mindestens! Wobei sich trotz des 32-Bit-Prozessors stets auch maßgebliche Rundungsfehler einstellen dürften.

(Bild vergrößern: auf Bild klicken! Quelle: PDF-Datei des Physikers Dr. rer. nat. Andreas M. Seifert)

>> Die Regressionsanalyse ist ein Instrumentarium statistischer Analyseverfahren, die zum Ziel haben, Beziehungen zwischen einer abhängigen (oft auch erklärte Variable, oder Regressand genannt) und einer oder mehreren unabhängigen Variablen (oft auch erklärende Variablen, oder Regressoren genannt) zu modellieren. 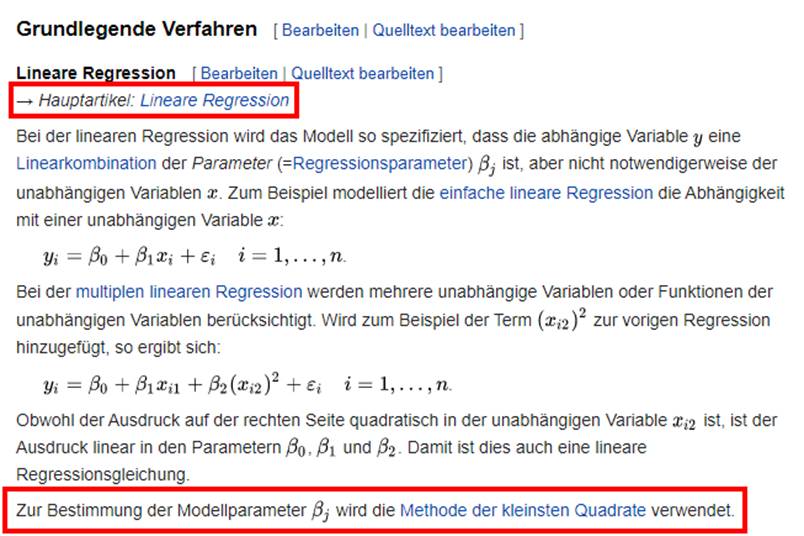Die Durchführung einer Regression wird verwendet, um Zusammenhänge quantitativ zu beschreiben oder Werte der abhängigen Variablen zu prognostizieren.^[1] Die häufigste Form der Regressionsanalyse ist die lineare Regression, bei der der Anwender eine Gerade (oder eine komplexere lineare Funktion) findet, die den Daten nach einem bestimmten mathematischen Kriterium am besten entspricht. 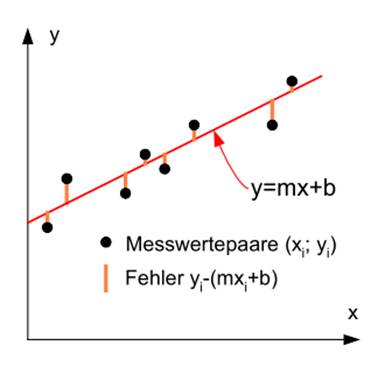Beispielsweise berechnet die gewöhnliche Methode der kleinsten Quadrate eine eindeutige Gerade (oder Hyperebene), die die Summe der Abweichungsquadrate zwischen den wahren Daten und dieser Linie (oder Hyperebene), d. h. die Residuenquadratsumme minimiert. Aus bestimmten mathematischen Gründen kann der Anwender den bedingten Erwartungswert der abhängigen Variablen schätzen, wenn die unabhängigen Variablen eine bestimmte Menge von Werten annehmen. Weniger gebräuchliche Formen der Regression verwenden geringfügig unterschiedliche Verfahren zum Schätzen alternativer Lageparameter (z. B. die Quantilsregression) oder zum Schätzen des bedingten Erwartungswertes für eine breitere Klasse nichtlinearer Modelle (z. B. nichtparametrische Regression).

Die Regressionsanalyse wird hauptsächlich zu zwei konzeptionell unterschiedlichen Zwecken verwendet. Erstens wird die Regressionsanalyse häufig für Schätzungen und Vorhersagen verwendet, bei denen sich ihre Verwendung erheblich mit dem Bereich des maschinellen Lernens überschneidet, siehe auch symbolische Regression. Zweitens kann in einigen Situationen eine Regressionsanalyse verwendet werden, um auf kausale Beziehungen zwischen den unabhängigen und abhängigen Variablen zu schließen. Wichtig ist, dass Regressionen für sich genommen nur Beziehungen zwischen einer abhängigen Variablen und einer oder mehrerer unabhängiger Variablen in einem gegebenen Datensatz aufzeigen. Um Regressionen für Vorhersagen zu verwenden oder Kausalzusammenhänge herzuleiten, muss der Anwender sorgfältig begründen, warum bestehende Beziehungen Vorhersagekraft für einen neuen Kontext haben oder warum eine Beziehung zwischen zwei Variablen eine Kausalzusammenhangsinterpretation hat (Korrelation und Kausalzusammenhang). Letzteres ist besonders wichtig, wenn Anwender mithilfe von Beobachtungsdaten kausale Zusammenhänge abschätzen möchten. (…)

<<

(Bild vergrößern: auf Bild klicken! Quelle: Wikipedia)

(Zum Vergrößern bitte auf das Bild klicken!)

(Bild vergrößern: auf Bild klicken! Quelle: PDF-Datei des Physikers Dr. rer. nat. Andreas M. Seifert)

[ NodeESP ] [ Seitenanfang ]