[ Proxi-Roboter ] [ Seitenende ] [ Montage 1 ] [ Coding 2 ]

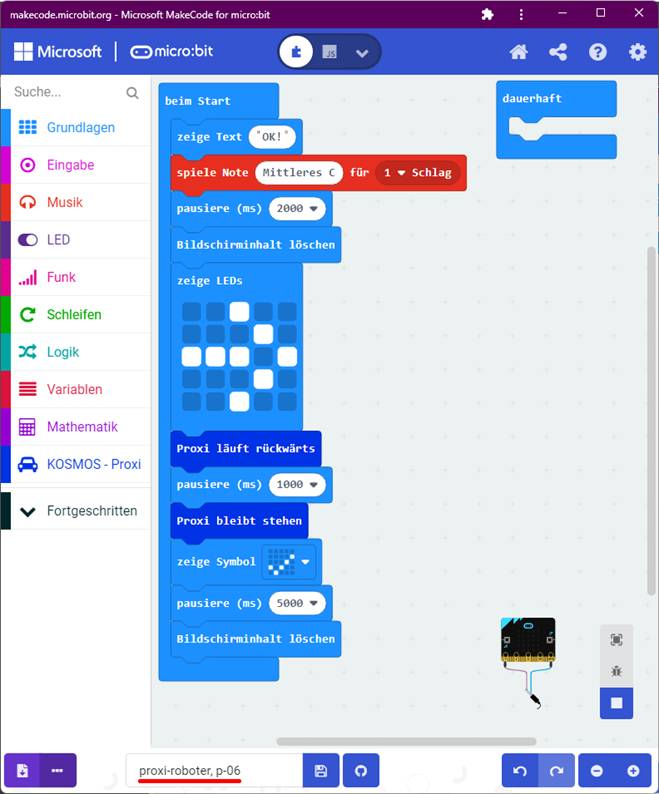
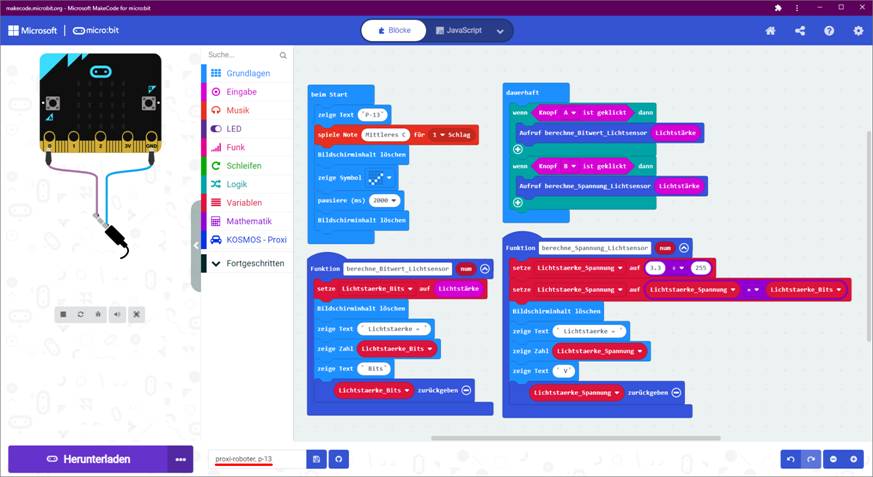
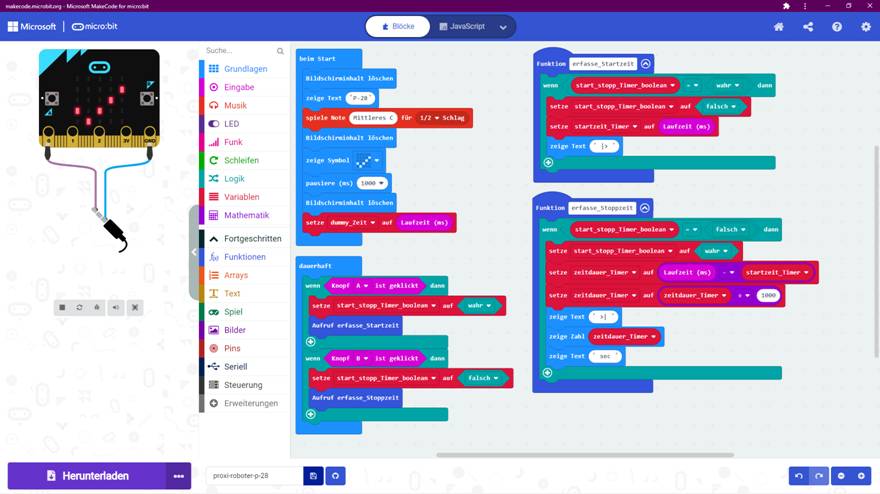
KOSMOS – der programmierbare Proxi-Roboter

Rechts- und Linksdrehung beim Proxi-Roboter

Wir befinden uns auf dem Windows-PC, starten den Microsoft „MakeCode“-Editor als „Google Chrome“-App(!) durch Mausklick auf das Icon , importieren das „Proxi-Roboter“-Programm „proxi-roboter, p-02“ in den „MakeCode“-Editor und speichern das ursprüngliche Programm als neues Projekt mit dem Dateinamen „proxi-roboter, p-03“ ab:

(Zum Vergrößern bitte auf das Bild klicken!)

Dann erweitern wir das Projekt „proxi-roboter, p-03“ wie folgt

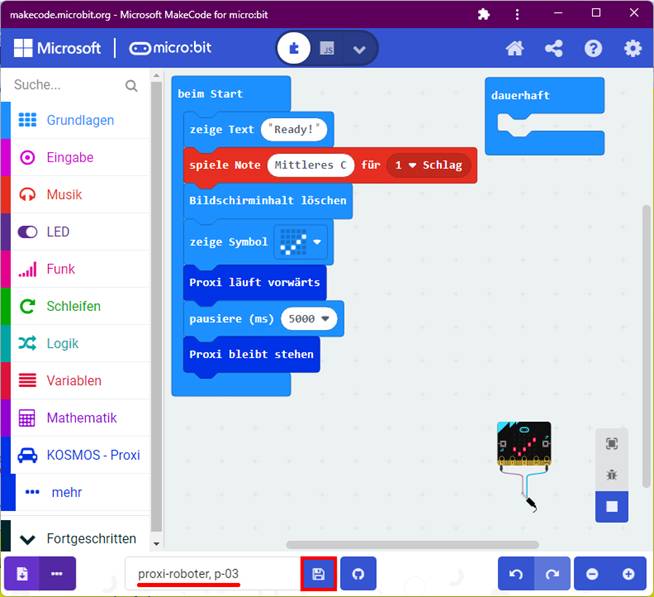
(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden Screenshot sieht, meldet sich der Proxi-Roboter nach dem Programmstart mit der Laufschriftanzeige „Ready!“, d.h. „Fertig!“ im Sinne von „Alles okay!“. Nachdem die Laufschrift durchgelaufen ist, wird das Tonsignal „Mittleres C“ zu Gehör gebracht, der Bildschirm (= 5 x 5 Matrix LED-Display) gelöscht und das Symbol „Häkchen P“ angezeigt. Damit soll ebenfalls signalisiert werden, dass alles in Ordnung ist. Dabei wird das „Häkchen P“ zunächst dauerhaft im Display angezeigt. 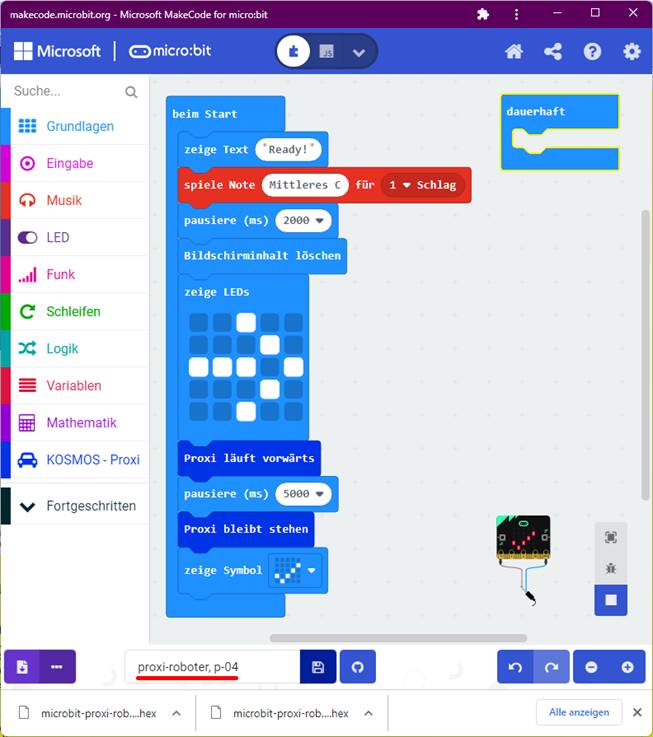Man kann aber das „Häkchen P“ auch erst später, nachdem das Programm vollständig abgearbeitet wurde, anzeigen lassen:

(Zum Vergrößern bitte auf das Bild klicken!)

Über die Art und Weise, ob und wie der Proxi-Roboter mit dem Anwender kommuniziert, kann man natürlich streiten. Dabei könnte man die optische und akustische Signalisierung, darüber was der Roboter gerade macht bzw. gemacht hat, auch als überflüssig abtun.

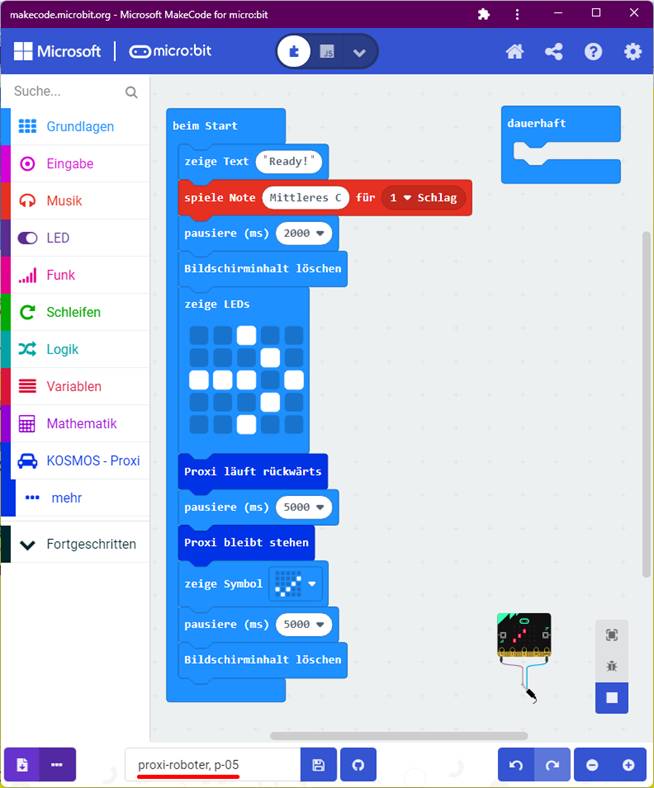
Trotzdem bin ich der Meinung, dass die optische und akustische Kommunikation mit dem Anwender Sinn macht, da man anhand der Signalisierung genau verfolgen kann, ob der Roboter auch das macht, was er machen soll bzw. was programmiert wurde! Schließlich findet man sich anhand der Signalisierung auch schneller und besser im Programm zurecht:

(Zum Vergrößern bitte auf das Bild klicken!)

Bezüglich der Programmierung des Antriebsmotors P13 für die Vorwärtsbewegung geht es darum herauszufinden, wie lange ein kompletter Umlauf des Motors nebst Untersetzung des Getriebes andauert, um die Umlaufzeit für einen Umlauf des Motors später einem Vollkreis von 360 Grad zuordnen zu können. Deshalb nähern wir uns schrittweise der Umlaufzeit für einen Vollkreis der beiden schwarzen Zahnräder B9 (links) und A6 (rechts) an:

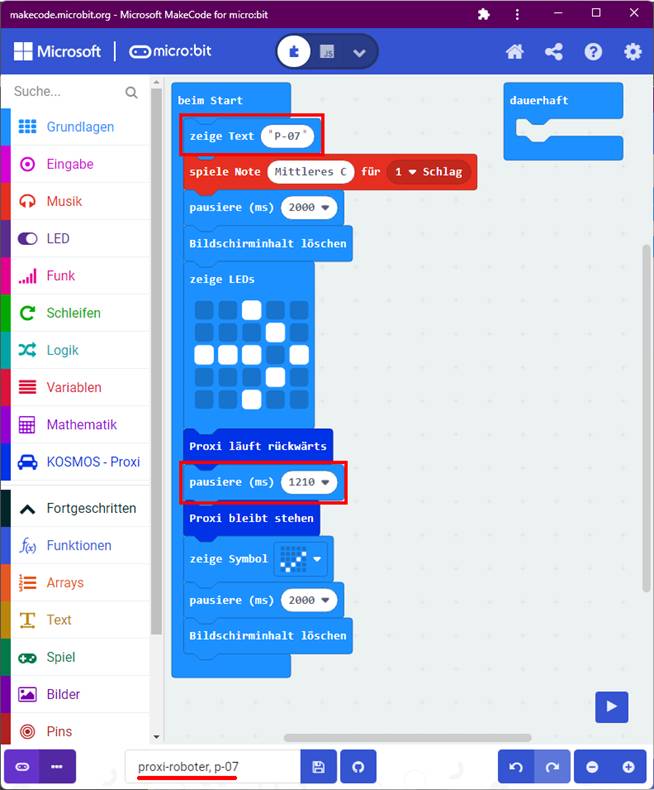
(Zum Vergrößern bitte auf das Bild klicken!)

Mit dem Statement <pausiere (ms) 1210> lässt sich ziemlich genau ein Vollkreis umrunden:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden Screenshot sieht, dauert ein vollständiger Umlauf für der beiden schwarzen Zahnräder B9 (links) und A6 (rechts) t_Umlauf = 1210 ms = 1,21 s:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man ferner im obenstehenden Bild im rot umrandeten Oval sieht, stehen sich die beiden Markierungspfeile "! der beiden schwarzen Zahnräder B9 (links) und A6 (rechts) nach einem Umlauf, d.h. nach t_Umlauf = 1210 ms = 1,21 s nicht mehr exakt gegenüber. Demzufolge muss man im laufenden Betrieb mit n Umläufen stets damit rechnen, dass es z.B. aufgrund von, wenn auch geringen, Spannungsschwankungen bei der 5 V USB-Stromversorgung über das „Micro USB 2.0“-Kabel oder durch die Erwärmung des Antriebsmotors P13 zu mehr oder weniger großen oder kleinen Abweichungen bei der Drehzahl des Motors und damit auch bei der zugrunde gelegten Umlaufzeit kommt.

Wenn aber Versorgungsspannung und Betriebstemperatur des Proxi-Roboters die Motordrehzahl n und damit die Umlaufzeit t_Umlauf beeinflussen, dann müssen wir diese im Auge behalten, d.h. beobachten und diese der jeweils zugrunde gelegten Umlaufzeit zuordnen.

Mathematisch sagt man dazu, dass die Motordrehzahl n eine Funktion f der Spannung U_Motor des Motors ist:

n = f( U_Motor ).

Praktisch bedeut dies, dass die Motordrehzahl n von der am Motor anliegenden Spannung U_Motor abhängt bzw. abhängig ist.

Wenn wir den Proxi-Roboter mit den 4 Mignon-Batterien vom Typ „AA“ im Batteriefach P15 betreiben,

(Zum Vergrößern bitte auf das Bild klicken!)

dann ließe sich der Motor ohne Spannungsstabilisierung und ohne Regelung mit einer Versorgungsspannung von max. U_Batt = 4 * 1,5 V = 6,0 V betreiben. Da der Motor aber an der Zusatzplatine P16 mit den vier Infrarot-LEDs angeschlossen ist und sich u.a. zeitabhängig steuern lässt, kann man davon ausgehen, dass die tatsächliche Betriebsspannung des Motors wegen der vorgeschalteten Elektronik nebst des „micro:bit“-Rechners entsprechend niedriger ausfällt.

Wenn man aber den Proxi-Roboter u.a. beim Programmieren mit dem „Micro USB 2.0“-Verbindungskabel und der USB-Stromversorgung vom Windows-PC aus betreibt, dann beträgt die „USB 2.0“-Spannung für die Stromversorgung ohnehin nur noch 4,75 V - 5,25 V.

Spannungsmessungen direkt am Motor haben ergeben, dass die

· Spannung bei Batteriebetrieb U_{M, Batt} = 5,74 V beträgt, und dass die

· Spannung bei „USB 2.0“-Betrieb U_{M, USB} = 2,38 V beträgt.

In der Praxis hat sich dies auch auf die Weise bestätigt, dass der Motor bei Batteriebetrieb mit U_{M, Batt} = 5,74 V praktisch doppelt so schnell lief als bei dem „USB 2.0“-Betrieb mit U_{M, USB} = 2,38 V. Demzufolge müsste man dies bei der Programmierung des Proxi-Roboters entsprechend berücksichtigen und auch dem Anwender über das LED-Display mitteilen für welchen Betriebsmodus (Batterie oder USB 2.0) das entsprechende Programm programmiert wurde!

Im Umkehrschluss bedeutet dies, dass man anhand der jeweiligen Drehzahl n mit n = Anzahl Umdrehungen / Minute herausfinden und berechnen kann, ob der Proxi-Roboter mit Batterien oder mittels „USB 2.0“-Spannungsversorgung betrieben wird. Wenn man dabei auch noch über einen Referenzspannungswert U_Ref als Bezugsspannung (= Soll-Wert) verfügt, dann ließe aus der Änderung der Umdrehungszahl n direkt die zum Betrieb des Motors erforderliche Spannung U_{M, Batt} oder U_{M, USB} berechnen! -

Bezüglich des Proxi-Roboters verhält es sich derzeit so, dass wir die am Antriebsmotors P13 anliegende Spannung von U_{M, Batt} = 5,74 V bzw. U_{M, USB} = 2,38 V nicht mit dem „micro:bit“-Rechner anhand eines analogen Spannungseingangs nebst Analog-/Digitalwandlung (A/D-Wandler) erfassen und auswerten können. Deshalb kommen wir an dieser Stelle nicht weiter.

Was sich an dieser aber noch zeigen lässt, ist, wie man eine analoge Spannung am Eingang eines analogen Ports einliest, in einen digitalen Bitwert mittels des integrierten A/D-Wandlers des „micro:bit“-Rechners umwandelt und diesen in die analoge Spannung einer „USB 2.0“-Spannungsversorgung umrechnet.

Bei dem „micro:bit“-Rechner gibt es am unteren Rand eine Leiste mit 5 großen Rundlöchern , engl. „Edge Connector“, in die sich sogenannte Bananenstecker mit Verbindungskabeln einstecken lassen.

Bei der großen Rundbuchse „3V“ handelt es sich um einen besonderen Anschluss, engl. „port“ genannt. Demzufolge handelt es sich bei dem Port mit dem Pin „3V“ um eine interne, stabilisierte Spannungsquelle mit U_{Pin 3V} = 3,3 V, deren stabilisierte Spannung sich sehr gut als Referenzspannung nutzen lässt.

(Vergrößern: auf das Bild klicken! | Quelle: BBC micro:bit Hardware)

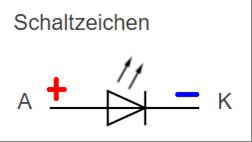
Bei dem Projekt „proxi-roboter, p-08“ erfassen wir erstmalig die Umgebungshelligkeit des „micro:bit“-Rechners, die als dezimaler Binärwert in der Systemvariablen <Lichtstärke> gespeichert wird.

Leuchtdioden (LEDs), engl. „Light Emitting Diodes“, d.h. Licht emittierende Halbleiterdioden bestehen aus einer p- und n-leitenden Halbleiterschicht, die an der Sperrschicht einen PN-Übergang ausbilden. Dabei werden Leuchtdioden (LEDs) stets in Durchlassrichtung

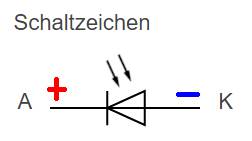
betrieben, sodass sich die Sperrschicht am PN-Übergang räumlich verkleinert und der Durchlassstrom I_F mittels eines entsprechenden Vorwiderstandes R_Vor = 100 … 240 Ω entsprechend begrenzt werden muss, damit die LED keinen Schaden nimmt und durchschmort!

Betreibt man eine LED hingegen in Sperrrichtung,

dann vergrößert sich am PN-Übergang die Sperrschicht und mit ihr auch der Sperrschichtwiderstand R_Sperr.

Durch die Beleuchtung der Sperrschicht am PN-Übergang sorgen die eintreffenden, elektrisch geladenen Photonen dafür, dass die Ladungsmenge Q und mit ihr auch die Sperrspannung U_Sperr und elektrische Feldstärke E in der Sperrschicht ansteigen, sodass sich auch die in der Sperrschicht gespeicherte elektrische Energie W_el im Mittel vermeintlich vergrößert:

W_el = ½ U_Sperr * Q = ½ U_Sperr * I_Sperr * t "

Für die Sperrschichtkapazität folgt mit C_Sperr = Q / U_Sperr = 2 Q / 2 U_Sperr = … = n Q / n U_Sperr = konstant!

Das bedeutet, dass die Sperrschichtkapazität C_Sperr trotz Zunahme der Ladungsmenge Q an Photonen wegen der ebenfalls zunehmenden Sperrspannung U_Sperr konstant bleibt!

E = U_Sperr / d_Sperr " Sperrschichtlänge d_Sperr = U_Sperr / E = 2 * U_Sperr / 2 * E = … = n * U_Sperr / n * E = konstant!

Jetzt wissen wir wegen d_Sperr = konstant, dass der eintreffende Photonenstrom wegen der konstanten Ausdehnung der Sperrschicht zwangsweise zu einer Zunahme der elektrischen Feldstärke E an der Sperrschicht führt, sodass als Folge dessen größere elektrische Kräfte auf die Ladungsträger wirken, die früher oder später zu einem Spannungsüberschlag im Sinne einer zwangsweisen Entladung und Zerstörung der Sperrschicht beim PN-Übergang führt!

Das Besondere ist aber, dass es zu keinem Spannungsüberschlag kommt, kommen kann, weil der äußere Druck der elektrischen Feldstärke E auf die Ladungsträger in der Sperrschicht dazu führt, dass sich der Sperrstrom I_Sperr in der Sperrschicht maßgeblich vergrößert und zu einem Ladungsträgerabfluss im PN-Übergang führt. Dabei entspricht der Ladungsträgerabfluss in Form des vergrößerten Sperrstroms I_Sperr direkt dem Photonenstrom bzw. der Umgebungshelligkeit, die sich ja rechnerisch mittels des Statements

auswerten, d.h. in einen dezimalen Bitwert und in einem weiteren Programmierschritt in eine adäquate Spannung umrechnen lässt!

Übrigens: Die Sperrschicht des PN-Übergangs selbst ist halbleiterphysikalisch elektrisch neutral, weil sich in dieser p- und n-leitende Ladungsträger in Form von freibeweglichen Elektronen und Defektelektronen (= Elektronenlöcher) gegenseitig kompensieren, d.h. ladungsmäßig ausgleichen!

Demzufolge lassen sich in der Sperrschicht selbst auch keine Ladungsträger jedweder Art speichern! Deshalb wirkt dann auch die elektrische Feldstärke E über die elektrisch neutrale Sperrschicht hinweg! -

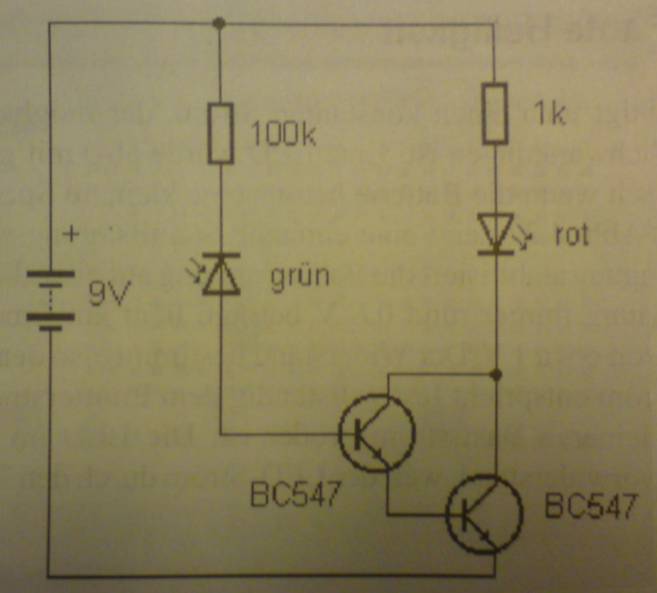
Die nachfolgende Abbildung zeigt eine elektronische Schaltung mit zwei NPN-Transistoren, die als Darlington zusammengeschaltet sind und somit über eine Stromverstärkung B = B1 * B2 im Bereich von B = [ 20 000 bis 50 000 ] verfügen, so dass sich der sehr kleine Sperrstrom I_{B Sperr, grün} ≈ 1 µA (= 1 Millionstel Ampere) auf bis zu I_{C, Mittel} = 35 000 µA = 35 * 10³ µA = 35 * 10³ * 10^-6 A = 35 * 10^-3 A = 35 mA (= Mittelwert) verstärken lässt.

In der Schaltung selbst berechnet sich aber der Kollektorstrom I_{C T1,T2} durch den Vorwiderstand R_Vor = 1 kΩ zum Schutz der roten LED wie folgt:

I_{C T1,T2} = ( U_Batt – U_LED – U_{CE, satt} ) / R_Vor " Sättigungsspannung U_{CE, satt} = 0,4 V

= ( 9 V – 1,6 V – 0,4 V ) / 1 kΩ = 7 V / 1 kΩ = 7 mA " Stromstärke durch die rote LED

>> Standard-Leuchtdioden haben einen Durchmesser von 5 mm. Sie sind die häufigsten verwendeten Leuchtdioden in elektronischen Schaltungen. Sie beginnen bei 8 bis 12 mA zu leuchten. Erhöht man den Strom leuchten Sie heller. Bei 20 mA ist die maximale Leuchtkraft erreicht. Der Unterschied zu 15 mA ist aber nur minimal. Meist ist ein Strom von 10 mA schon ausreichend, um sie ausreichend zum Leuchten zu bringen. < (Quelle: Elektronik-Kompendium)

Wenn man möchte, dass die rote LED mit I_F = 15 mA richtig hell leuchtet, dann müsste man den Vorwiderstand von derzeit R_Vor = 1 kΩ entsprechend der nachfolgenden Berechnung auf R_Vor = 470 Ω verkleinern:

R_Vor = ( U_Batt – U_LED – U_{CE, satt} ) / I_{C T1,T2} " I_{C T1,T2} = I_F

= ( U_Batt – U_LED – U_{CE, satt} ) / I_F

= ( 9 V - 1,6 V – 0,4 V ) / 15 mA = 7 V / 15 mA = 0,467 kΩ ≈ 470 Ω

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man in der obenstehenden Schaltung sieht, wird die grüne LED in Sperrrichtung betrieben, sodass diese als lichtempfindliche Leuchtdiode arbeitet. Dabei entspricht der Sperrstrom durch die grüne LED gleich dem Basisstrom I_B T1 durch die beiden Basis-Emitter-Dioden in Reihe von zusammen U_BE = 2 * 0,7 V = 1,4 V:

U_{LED, Sperr} = U_Batt - U_{R 100k} - U_BE

= U_Batt – ( I_{R 100k} * R_100k ) - U_BE " I_{R 100k} = I_{Sperr, LED} = 1 µA (entsprechend der bisherigen Annahme!)

= 9 V - ( 1 µA * 100 kΩ ) - 1,4 V

= 9 V - ( 100 mV ) - 1,4 V = 9 V - 0,1 V - 1,4 V = 7,5 V

R_{Sperr, LED} = U_{LED, Sperr} / I_{Sperr, LED}

= 7,5 V / 1 µA = 7,5 MΩ " Widerstand R_{Sperr, LED} der grünen LED in Sperrrichtungg!

Berechnung der Stromverstärkung B der Darlington-Schaltung:

B = I_C / I_B = I_{C T1,T2} / I_{Sperr, LED}

= 15 mA / 1 µA = 15 * 10^-3 A / 1 * 10^-6 A = 15 * 10^-3 * 10⁶ = 15 * 10³ = 15 000 fach!

Jetzt wo wir wissen, dass sich eine herkömmliche Leuchtdiode (LED) auch als Fotodiode verwenden lässt, sofern sie in Sperrrichtung betrieben wird, kann man sich jetzt auch vorstellen, dass sich die 5 x 5 Matrix des LED-Displays des „micro:bit“-Rechners zusammen mit 5 x 5 = 25 Einzeldioden quasi als einzelne Fotodiode betreiben lässt.

Dabei lässt sich die Umgebungshelligkeit mittels der 5 x 5 Matrix des LED-Displays als Fotodiode erfassen und der Variablen <Lichtstärke> wie folgt zuweisen:

Dabei gilt es unbedingt zu beachten, dass die maximale Lichtstärke den dezimalen Bitwert = 255 annehmen kann, sodass sich der Bereich von dunkel bis hell über die Bitwerte [ 0, … 255 ] = 256 Werte erstreckt!

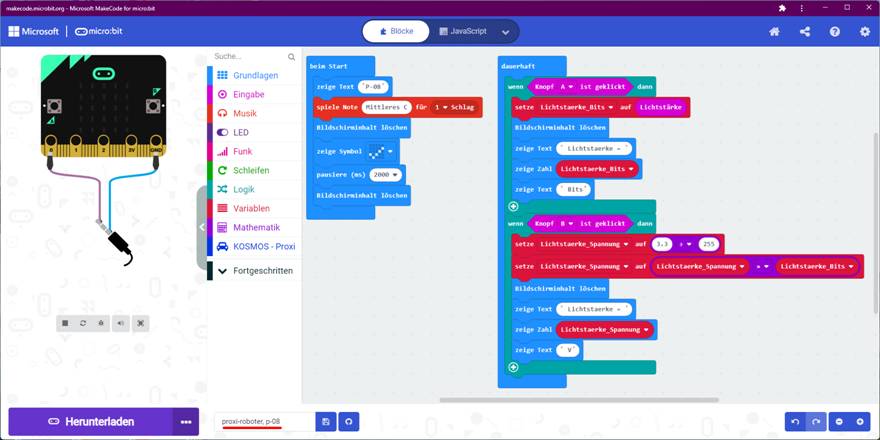
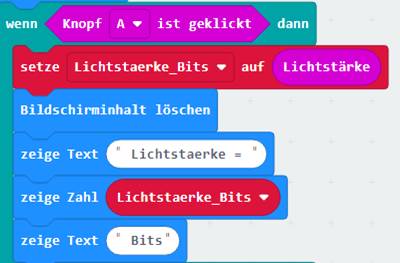
Wenn man bei dem nachfolgenden Projekt „proxi-roboter, p-08“ nach dem Programmstart den <Knopf A> drückt, dann wird mittels des 5 x 5 Matrix des LED-Displays als Fotodiode die Umgebungshelligkeit erfasst, als dezimaler Bitwert der Variablen <Lichtstärke> zugewiesen und der entsprechende Bitwert als Laufschrift auf dem LED-Display angezeigt:

(Zum Vergrößern bitte auf das Bild klicken!)

Wenn man dann bei dem obenstehenden Projekt „proxi-roboter, p-08“ als Nächstes den <Knopf B> drückt, dann wird der Bitwert der Variablen <Lichtstärke> in eine analoge Spannung umgerechnet, die wiederum der Variablen <Lichtstaerke> zugewiesen wird, sodass der vormals gespeicherte Bitwert überschrieben wird! Der Wert der umgerechneten analogen Spannung wird dann als Laufschrift auf dem LED-Display angezeigt.

Demzufolge wird beispielsweise der Bitwert = 200 Bit in die analoge Spannung

1023 Bit " 3,3 V

200 Bit " x V

_______________

x = 3,3 V / 1023 Bit * 200 Bit = 0,6451612903225806 V = 0,64516129 V ≈ 0,65 V þ

umgerechnet!

Bezogen auf die maximale Spannung von 3,3 V erscheinen die 0,65 V aber recht wenig. Der Grund dafür ist der, dass wir die Skala der zur Verfügung stehenden Bitwerte [ 0, …, 1023 ] nicht ausnutzen, weil der Wert der Variablen <Lichtstärke> selbst nur Bitwerte bis 255 annehmen kann!

Wenn wir also tatsächlich den Bereich der maximal möglichen Spannung von 3,3 V ausnutzen wollen, dann müssen wir den maximal möglichen Bitwert 255 der Lichtstärke auf bis zu 1023 skalieren, d.h. hochrechnen:

1023 Bit " 3,3 V

255 Bit " x V

_______________

x = 3,3 V / 1023 Bit * 255 Bit = 0,8225806451612903 V = 0,82258 V ≈ 0,823 V þ

255 Bit " 0,823 V

1023 Bit " x V

_________________

x = 0,823 V / 255 Bit * 1023 Bit = 3,301682352941176 V = 3,30168 V ≈ 3,3 V þ " Logisch!

Demzufolge beträgt der Skalierungsfaktor

3,3 V / 0,823 V = 4 fach analog!

Wenn man die Spannung von 0,65 V der gemessenen Lichtstärke mit dem Skalierungsfaktor 4 wie folgt hochrechnet,

U_Licht = 0,65 V * 4 = 2,6 V

dann folgt für die skalierten Bitwerte:

3,3 V " 1023 Bit

2,6 V " x Bit

_______________

x = 1023 Bit / 3,3 V * 2,6 V = 806 Bit skaliert auf die Basis von 1023 Bit

Der Knackpunkt dabei ist nämlich der, dass sich die Lichtstärke mit dem maximalen Bitwert 255 - Hardware bedingt und aus Sichtweise des Fotodioden LED-Displays - nicht auf maximal 1023 Bit hoch skalieren lässt!

Deshalb dürfen wir genau diesen Denkfehler nicht machen, obwohl man es ja theoretisch machen kann, aber es wegen der Hardware des Lichtsensors(!) praktisch nicht funktioniert, nicht funktionieren kann!

Deshalb müssen wir zwecks Berechnung der analogen Spannung von bis zu 3,3 V und wegen der Hardware des A/D-Wandlers(!) immer von diesen 3,3 V ausgehen und eben diese dem maximalen Bitwert 255 des Lichtsensors wie folgt zuordnen:

255 Bit " 3,3 V

200 Bit " x V

______________

x = 3,3 V / 255 Bit * 200 Bit = 2,588235294117647 V = 2,588 V ≈ 2,59 V

Probe:

3,3 V " 255 Bit

2,59 V " x Bit

_______________

x = 255 Bit / 3,3 V * 2,59 V = 200,1363636363636 Bit = 200,136 Bit ≈ 200 Bit skaliert auf die Basis von 255 Bit þ

Tja, das Leben kann so einfach sein, wenn man weiß wie es geht! Aber hinterher ist man ja immer schlauer!

Ausschlaggebend beim „micro:bit“-Rechner ist nämlich, dass sich alle analogen und digitalen Ports wie z.B. die großen Rundbuchsen „0“, „1“ und „2“, aber auch die stabilisierte Spannungsversorgung „3V“ mit den A/D-Wandlern auf eine analoge Ausgangsspannung von U_Port = 3,3 V beziehen!

Das aber kann der Lichtstärkensensor in Form des Fotodioden LED-Displays nicht „wissen“ und liefert demzufolge nur Bitwerte bis 255 Bit anstelle von bis zu 1023 Bit.

Wenn man z.B. aber später einen analogen Port wie z.B. den Port „Pin 0“ benutzt und diesem den Bitwert = 200 zuweist, dann liefert dieser Hardware bedingt eine maximale analoge Ausgangsspannung von bis zu 3,3 V.

Wenn sich aber die maximale Lichtstärke technisch bedingt nur auf den Bereich [ 0, …, 255 ] Bit bezieht, dann muss man eben diesen vorhandenen Bit-Bereich der maximalen analogen Ausgangsspannung von 3,3 V zuordnen! -

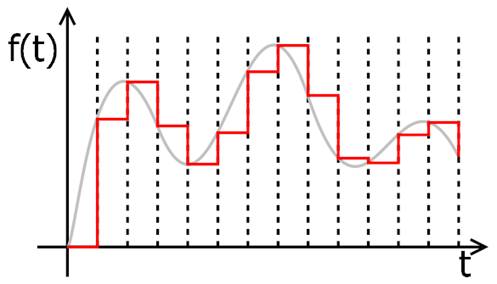
Werfen wir bei dieser Gelegenheit noch kurz einen Blick auf den zeitabhängigen Prozess der Analog-zu-Digital-Wandlung beim A/D-Wandler.

Dazu muss man wissen, dass der A/D-Wandler über einen Abtastbereich der analogen Spannung (= grauer Kurvenverlauf) im Bereich von [ 0, …, 1023 ] mit 1024 verschiedenen Abstufungen verfügt:

(Vergrößern: auf das Bild klicken! | Quelle: Wikipedia)

Ferner sollte man wissen, dass es auch höher auflösende A/D-Wandler mit z.B. einem Abtastbereich der analogen Spannung (= grauer Kurvenverlauf) im Bereich von [ 0, …, 4095 ] mit 4096 verschiedenen Abstufungen gibt, die z.B. bei Multimetern oder Oszilloskopen eingesetzt werden und dementsprechend auch mehr kosten!

Abschließend sei noch kurz die Funktionsweise des Projekts „proxi-roboter, p-08“ erläutert. Wenn man nach dem Programmstart, d.h. nach dem Hochfahren des „micro:bit“-Rechners und der Anzeige des Häkchens „P“ in der Laufschrift auf den <Knopf A> drückt, dann wird mittels des 5 x 5 Matrix des LED-Displays, das kurz als Fotodiode arbeitet, die Umgebungshelligkeit erfasst, als dezimaler Bitwert der Variablen <Lichtstärke> zugewiesen und der entsprechende Bitwert als Laufschrift auf dem LED-Display angezeigt.

Wenn sich also im Laufe des Tages fortwährend die Umgebungshelligkeit verändert und man auf diese Änderungen laufend reagieren möchte, dann muss man dementsprechend oft auf den <Knopf A> drücken, da nur dieser Programmblock den Bitwert der Variablen <Lichtstärke> abruft:

Wenn man sich darüber hinaus den zuvor mittels <Knopf A> eingelesenen Bitwert der Variablen <Lichtstärke> auch als elektrische Spannung mittels der Variablen <Lichtstaerke_Spannung> anzeigen lassen möchte, weil diese für den ambitionierten Anwender und angehenden Elektrotechniker wesentlich aussagekräftiger ist, dann muss man den <Knopf B> je nach Erfordernis entsprechend oft drücken, weil nur dessen Programmblock den Bitwert der Variablen <Lichtstärke> in die analoge Spannung der Variablen <Lichtstaerke_Spannung> umrechnet:

Das Arbeiten mit Funktionen

Wenn es in der Physik, der Elektrizitätslehre als Teilgebiet der Physik oder in der Elektrotechnik in einem Stromkreis einen rechnerischen bzw. mathematischen Zusammenhang zwischen Spannung U und Strom I gibt, nämlich den, dass der Strom I umso größer wird, je größer die Spannung U ist, dann spricht man von der Proportionalität zweier Größen.

Wenn sich also der Strom I proportional (~) zur Spannung U verhält, dann gilt: I ~ U.

Wenn darüber hinaus die doppelt so große Spannung 2 * U = 2 U auch einen doppelt so großen Strom 2 * I = 2 I zur Folge hat, dann folgt: 2 * I ~ 2 * U " I ~ U

Die Proportionalität 2 * I ~ 2 * U verfügt also auf beiden Seiten des Proportionalitätszeichens ~ über ein- und denselben (Multiplikations-) Faktor = 2, sodass sich mit diesem aus der Proportionalität immer

· die Proportionalität Faktor n * I = Faktor n * U ableiten lässt.

Wenn darüber hinaus der Quotient n * I / n * U = I / U mit I / U = k und k als Konstante stets konstant ist, dann handelt es sich bei der Konstanten k gemäß dem Ohmsches Gesetz um den sogenannten

· elektrischen Leitwert G mit k = I / U bzw. G = I / U

Mit dem Kehrwert von k ergibt sich dann wiederum der

· elektrische Widerstand R mit 1 / k = 1 / G und R = U / I

Den Quotienten 1 / k bezeichnet man als elektrischen Widerstand R und die dazugehörige Gleichung bzw. Formel nennt man

Ohmsches Gesetz mit

R = U / I

= ∆U / ∆I

= ( U₂ – U₁ ) / ( I₂ – I₁ ) mit U₂ > U₁ und I₂ > I₁

Dabei lässt sich das Ohmsche Gesetz wie folgt in eine Gleichung umwandeln:

R = U / I "

I = U / R "

I = 1 / R * U " Gerade, die durch den Ursprung im Koordinatensystem verläuft.

Wenn die sogenannte Widerstandsgerade bzw. die Funktion I = f(U) = 1 / R * U nicht durch den Ursprung im Koordinatensystem verläuft, dann gilt für die Geradengleichung:

I = 1 / R * U + I₀ mit I₀ > 0 " Konstantstrom einer (Konstant-) Stromquelle

Dabei gilt es zu beachten, dass der Konstantstrom I₀ sowohl positive als auch negative Stromstärkewerte wie z.B. I₀ = 10 mA oder I₀ = -10 mA annehmen kann!

So, nun wissen wir nicht nur was eine mathematische Funktion ist, sondern haben ganz nebenbei auch noch das Ohmsche Gesetz kennengelernt!

Bei der Programmierung von höheren Programmiersprachen wie z.B. JavaScript, PHP, C, C# von Microsoft, Java von Sun Microsystems jetzt Oracle oder Python gibt es auch Funktionen, die aber keine mathematischen Funktionen sind, aber trotzdem mathematische Funktionen im Sinne von Gleichungen in der Programmierung enthalten können.

Was also sind programmiertechnisch Funktionen?

Umgangssprachlich könnte man sagen, dass alles was funktioniert, eine oder mehrere Funktionen enthält. Dabei bezieht sich das Funktionieren von Geräten und Maschinen hauptsächlich auf die dazu verwendete Technik. Eine Kaffeemaschine funktioniert, wenn sie nicht nur heißes Wasser produziert, sondern damit auch zur richtigen Zeit, nämlich nach dem Einschalten, das Kaffeepulver aufbrüht. Wenn eine Kaffeemaschine nach geraumer Zeit stark verkalkt ist, funktioniert sie nicht mehr oder nur noch eingeschränkt, sodass das Kaffeeaufbrühen immer länger dauert, weil der Boiler wegen der Verkalkung nicht mehr genügend heißes Wasser liefert und stattdessen mehr Wasserdampf als Heißwasser produziert.

Lässt sich eine Kaffeemaschine programmieren? Ja! So gibt es z.B. Kaffeemaschinen mit einer eingebauten Zeitschaltuhr, sodass man sich Sonntagmorgen um 10 Uhr vom Kaffeeduft wecken lassen kann. Auch ließen sich die Stromaufnahme und die Brühzeit mittels Sensoren erfassen und mittels Mikroprozessorprogramm auswerten. Wenn dann z.B. die Zeitdauer der Stromaufnahme und Brühzeit im Laufe der Zeit immer länger wird, dann kann man davon ausgehen, dass die Kaffeemaschine wegen zunehmender Verkalkung immer weniger wie erwartet funktioniert.

Das Auswerten der Brühzeit wiederum würde aber nur dann richtig funktionieren, wenn man dabei auch die eingefüllte Wassermenge für z.B. vier Tassen Kaffee mittels einer Füllstandsanzeige erfassen würde und der Anwender nach dem Einschalten der Kaffeemaschine dieser mitteilt, wie viele Tassen Kaffee aufgebrüht werden sollen. Nur dann ließe sich nämlich eine Kennlinie erstellen, hinsichtlich der Brühzeit auswerten und ein entsprechender Alarm zum Entkalken der Maschine auslösen.

Eine Funktion leistet also etwas, indem sie z.B. über Sensoren Soll- und Ist-Werte miteinander vergleicht, auswertet und etwas veranlasst, etwas tut.

Demzufolge verfügt eine Funktion über einen oder mehrere Eingangskanäle für Signale, Messwerte und Parameter, liest diese ein, berechnet und verarbeitet diese, um schließlich das Ergebnis über den Ausgangskanal wieder an das Hauptprogramm zurückzugeben. Deshalb heißt das Prinzip auch EVA-Prinzip: Daten eingeben, verarbeiten und wieder als Ergebnis ausgeben.

Dabei haben Funktionen den Vorteil, dass sie sich jederzeit und beliebig oft anwenden und wiederholen lassen!

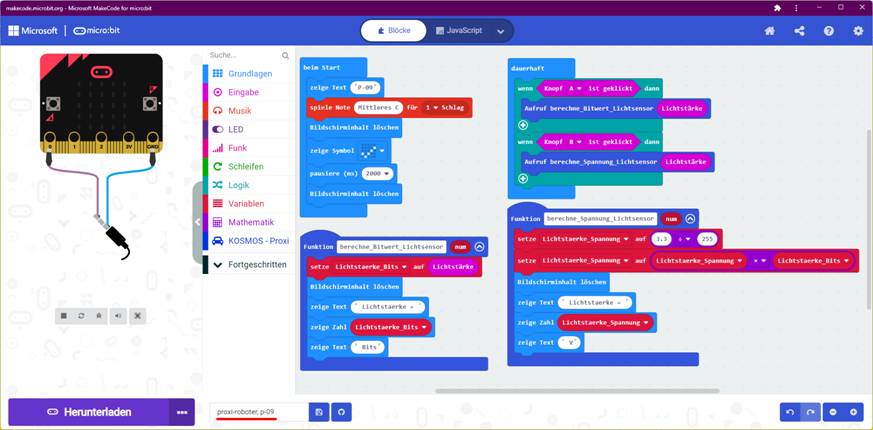
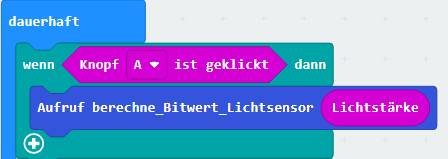
Bei den beiden Projekten „proxi-roboter, p-08“ und „proxi-roboter, p-09“ gibt es noch einen „Schönheitsfehler“ im Programmkode, den es zu beheben gilt. Und zwar benutzen wir im

· Programmblock <dauerhaft>

sowie in den

· Funktionen <berechne_Bitwert_Lichtsensor> und <berechne_Spannung_Lichtsensor>

die Variable <Lichtstärke> ohne diese zuvor deklariert und initialisiert zu haben.

Als Variable bezeichnet man in der Mathematik einen rechnerisch oder zeitlich jederzeit veränderlichen Wert. Dabei dient die Variable als Platzhalter, bildlich gesprochen als Schublade, in die man aus verschiedenen Anlässen und zu unterschiedlichen Zeiten z.B. mal mehr, mal weniger Schokolade aufbewahrt. Dabei ist dann die Schokolade der Inhalt, der mathematische Wert und die Schublade die dazugehörige Variable.

Wenn die Schublade aus Holz ist, dann sieht man ihr nicht an, was sich in ihr befindet, ob sich wirklich Schokolade in der Schublade befindet oder nicht, weil sie zwischenzeitlich heimlich aufgegessen wurde.

Wäre die Schublade aus Glas oder durchsichtigem Kunststoff, dann könnte man schon von außen sehen, ob sich wirklich Schokolade in der Schublade befindet oder nicht.

Eine Kommode hat oftmals drei oder vier Schubladen, die von außen alle gleich aussehen, wenn sie einheitlich weiß lackiert sind, sodass man diese ohne abzuzählen nicht auseinanderhalten könnte, weil sie eben alle gleich aussehen.

Würden wir die Schubladen mit n = 0, n = 1, n = 2 numerieren, d.h. indexieren, dann könnte man die gleich aussehenden Schubladen ganz einfach anhand des jeweiligen Index problemlos auseinanderhalten. Dabei beginnt die Indexierung bei n = 0, weil der Computer nur zwei Finger zum Zählen hat, nämlich „0“ = „Strom aus“ (= logisch „false“) und „1“ = „Strom ein“ (= logisch „true“).

Was aber passiert bzw. was macht man, wenn die Schublade n = 2 - also die dritte Schublade - voll ist und fast schon überquillt? Ganz einfach! Man sucht sich eine leere Schublade n = 0 und tut dort die neuen Schokoladentafeln hinein:

1. Schublade(0) = neue_Schokoladen " Die Schublade(0) wird ausschließlich mit neuer Schokoladen gefüllt!

2. Schublade(0) = Schublade(0) + neue_Schokoladen " Die Schublade(0) wird mit weiterer Schokolade aufgefüllt!

Oder, wenn in der neuen Schublade(0) mehr Platz für Schokolade ist als in der alten Schublade(2), dann folgt:

3. Schublade(0) = Schublade(2) + neue_Schokoladen "

Jetzt wissen wir, dass sich einer Variablen jederzeit neue Inhalte, neue Werte zuweisen lassen (siehe 1.)! Außerdem wissen wir, dass sich einer Variablen, die bereits Inhalte, Werte enthält, weitere neue Inhalte, neue Werte hinzufügen lassen (siehe 2.). Ferner wissen wir, dass sich einer Variablen Variableninhalte, Variablenwerte einer anderen Variablen zuweisen und zusätzlich auch noch weitere neue Inhalte, Werte hinzufügen lassen (siehe 3.).

Dabei gilt es zu beachten, dass die Zuweisungen 1.), 2.) und 3.) von Inhalten oder Werten zu einer Variablen immer von links nach rechts „gelesen“ werden!

Aber auch wenn eine Schublade (= Variable) noch keine Schokolade im Sinne von Inhalten oder Werten enthält, kann man die Schublade zuvor darauf festlegen, dafür bestimmen, dass sie nur Schokolade aufnehmen darf und nichts anderes!

In der Programmierung nennt man das Festlegen einer Variablen auf einen bestimmten Typus (numerisch, alphanumerisch oder boolesch) kurz „deklarieren“ oder „Deklaration!“

Und das Zuweisen von Inhalten oder Werten an eine Variable bestimmten Typs nennt man „initialisieren“ oder „Initialisierung“.

Wenn man eine Variable initialisiert, dieser also Inhalte oder Werte zuweist, dann wird sie zuvor automatisch auch deklariert!

Bei den beiden Projekten „proxi-roboter, p-08“ und „proxi-roboter, p-09“ besteht der „Schönheitsfehler“ im Programmkode darin, dass zwar die Variable <Lichtstärke> in beiden Programmen angesprochen und

benutzt wird, ohne diese zuvor im Hauptprogramm initialisiert zu haben!

Wenn man demzufolge die Variable <Lichtstärke> in der Funktion <berechne_Bitwert_Lichtsensor> des Projekts „proxi-roboter, p-09“ das erste Mal benutzt,

um dieser den dezimalen Bitwert zuzuweisen, dann gelingt das nur deswegen, weil die Variable <Lichtstärke> bereits zuvor beim Kompilieren mit Lichtstärke = 0 als dezimalem Bitwert initialisiert wurde!

Bevor also der Compiler den Quellkode, engl. „source code“, des Projekts „proxi-roboter, p-09“ in Maschinenkode des „ARM Cortex M0“-Prozessors des „micro:bit“-Rechners übersetzt, schaut dieser u.a. zuvor nach, ob und welche Variablen es im Programm gibt und initialisiert diese vorsorglich. Dabei werden automatisch Rechen-Variablen mit dem Wert = 0 und Text-Variablen mit dem leeren Textstring „“, d.h. mit null Zeichen bzw. mit der Textstringlänge = 0 initialisiert, damit es später beim Programmstart und der Programmausführung wider Erwarten keine Probleme im Sinne eines sogenannten „Laufzeitfehlers“ gibt!

Dass dem wirklich so ist, lässt sich auch beweisen! Nämlich indem man sich in einem der beiden Projekte

„proxi-roboter, p-08“ oder „proxi-roboter, p-09“ direkt nach dem Programmstart den umgerechneten Wert der Variablen <Lichtstaerke_Spannung> durch Drücken von <Knopf B> im LED-Display anzeigen lässt:

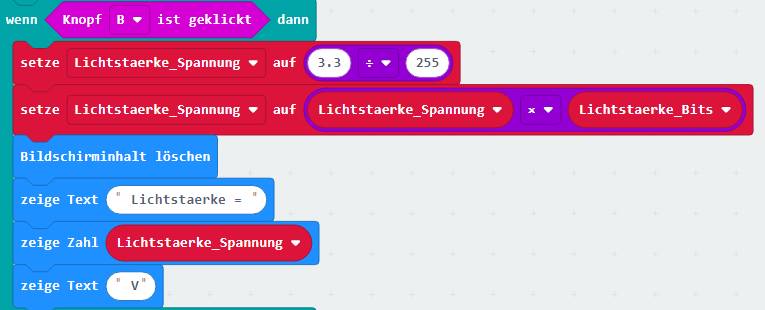
Wie man im obenstehenden Programmblock [ wenn < Knopf B ist geklickt >, dann ] sieht, lässt sich das Statement

mit der Division 3,3 / 255 problemlos berechnen und das Ergebnis der Variablen <Lichtstaerke_Spannung> zuweisen.

Bei dem nachfolgenden Statement

sieht es wegen der Multiplikation schon etwas anders aus, weil die Variable <Lichtstaerke_Bits> den Bitwert = 0 hat und das Rechenwerk des „micro:bit“-Rechners die mathematische Regel „Eine Zahl mit Null multipliziert ergibt Null!“ beherrschen muss:

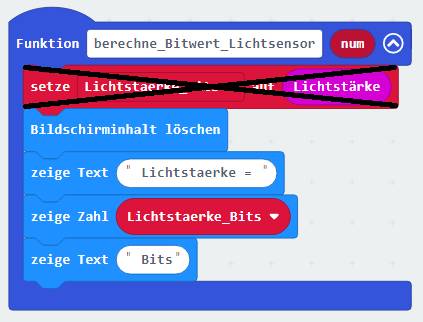
(Zum Vergrößern bitte auf das Bild klicken!)

Wir verändern den Quellkode im obenstehenden Projekt, indem wir in der Funktion <berechne_Bitwert_Lichtsensor> das Statement

einfach entfernen,

sodass die Variable <Lichtstaerke_Bits> nicht mehr mit dem Wert der Variablen <Lichtstärke> initialisiert wird!

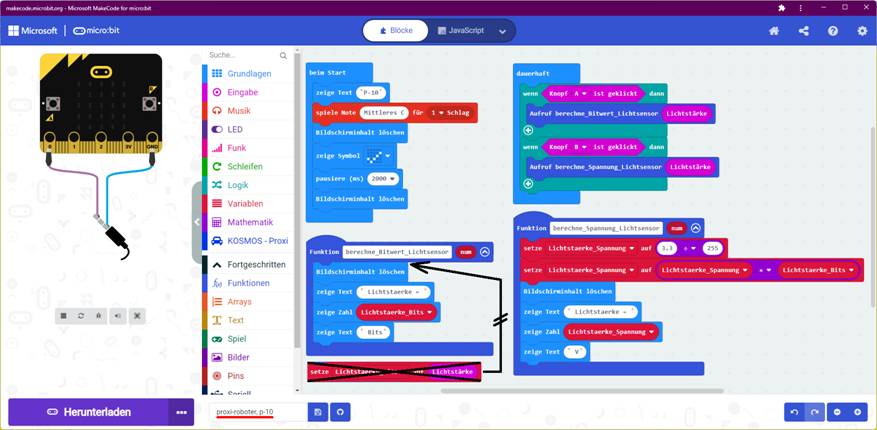
Wir speichern die Änderung des Quellkodes im neuen Projekt „proxi-roboter, p-10“ ab,

(Zum Vergrößern bitte auf das Bild klicken!)

starten das Programm und betätigen nach dem Programmstart den <Knopf A>, um zu sehen, welcher Bitwert in der Laufschrift „Lichtstaerke = ? Bits“ angezeigt wird.

Obwohl beim Funktionsaufruf der Funktion <berechne_Bitwert_Lichtsensor> der Bitwert der Variablen <Lichtstärke> für die Umgebungshelligkeit „mit auf den Weg gegeben“, d.h. eingelesen wird, sodass dieser innerhalb der Funktion zur Verfügung steht,

wird mit dem Bitwert der Variablen <Lichtstärke> nicht gearbeitet, d.h. nicht der Variablen <Lichtstaerke_Bits> zugewiesen, da wir das Statement

aus dem Programmkode entfernt haben! Deshalb lässt sich in der Funktion <berechne_Bitwert_Lichtsensor> mittels der Variablen <Lichtstaerke_Bits> nur der Bitwert = 0 in der Laufschrift anzeigen! -

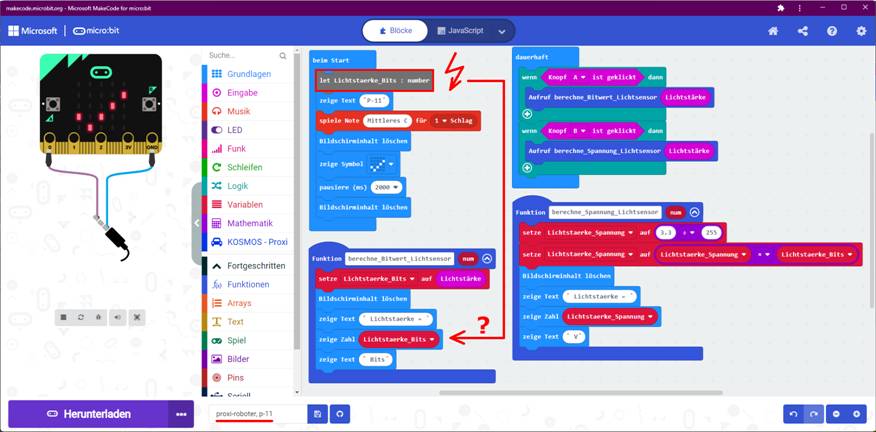
Werfen wir einen Blick auf das nächste Projekt „proxi-roboter, p-11“ mit dem interessanten Statement

,

das es zu klären und erklären gilt:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man sieht, ist das neue Statement

nicht nur farblich grau hinterlegt, sondern auch auf englisch, also nicht ins Deutsche übersetzt, was darauf hin deutet, dass sich dieses Statement nicht in der eingedeutschten Befehlsbibliothek befindet, sich demzufolge dort auch nicht anklicken und in das Programm übernehmen lässt!

So wie es aussieht, geht es bei dem Statement um die Variable <Lichtstaerke_Bits>, die vom Typ engl. „number“, d.h. numerisch ist. Dabei bedeutet „number“ übersetzt „Anzahl, Nummer, Zahl, Ziffer“.

Mathematisch gehören zu „number“ natürliche (positive) Zahlen, ganze (positive und negative) Zahlen, aber auch (positive oder negative) Dezimalzahlen, umgangssprachlich Kommazahlen genannt.

Interessant ist außerdem, dass der Variablen <Lichtstaerke_Bits> kein konkreter Wert wie z.B. Null zugewiesen wird!

Demzufolge handelt sich bei dem Statement

um das Deklarieren der Variable <Lichtstaerke_Bits>, d.h. das Festlegen, dass die Variable vom Typ „number“, d.h. numerisch sein soll.

Wenn aber eine Variable wie z.B. die Variable <Lichtstaerke_Bits> bereits deklariert wurde, dann lässt sich diese auch jederzeit initialisieren, lässt sich dieser jederzeit ein Zahl wie z.B. der Bitwert der Systemvariablen <Lichtstärke> zuweisen:

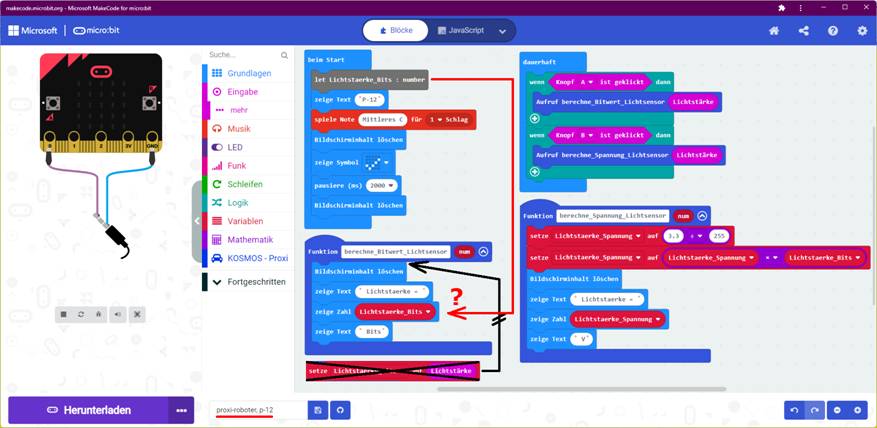
Jetzt bleibt nur noch zu klären, welcher Bitwert der Variablen <Lichtstaerke_Bits> beim Bestätigen von <Knopf A> in der Laufschrift auf dem LED-Display angezeigt wird. Und zwar im unbeleuchteten Zustand des 5 x 5 Matrix großen LED-Diesplays. Ich weiß es zwar, aber ich verrate es nicht. Mein Tipp: das Projekt „proxi-roboter, p-11“ starten und dann <Knopf A> drücken! -

Weiter geht’s mit dem Projekt „proxi-roboter, p-12“ bei dem zwar die Variablen <Lichtstaerke_Bits>

deklariert, aber eben nicht deklariert wird, weil das Statement

weggelassen wurde:

(Zum Vergrößern bitte auf das Bild klicken!)

Was bedeutet die Anzeige „NaN“ in der LED-Laufschrift, wenn man das Projekt „proxi-roboter, p-12“ startet und nach dem Hochfahren des „micro:bit“-Rechners den <Knopf A> drückt?

Hier noch ein Tipp dazu: Positioniere den Mauszeiger im „MakeCode“-Programm von Microsoft (= „Blöcke“) auf das Statement

Bewege den Mauszeiger auf dem Statement langsam hin und her bis dieser zu einer kleinen, weißen Hand verändert und warte einen kleinen Moment, bis die kleine Kontext-Anzeige

erscheint!

Jetzt wissen wir endlich, was es mit dem Statement auf sich hat und weshalb es dunkelgrau hinterlegt ist! Nämlich deshalb, weil es sich bei dem Statement in Wirklichkeit um einen „JavaSricpt“-Befehl handelt, der sich logischerweise nicht in ein „Block“-Statement der „MakeCode“-Entwicklungsumgebung von Microsoft umwandeln lässt!

Und das „JavaScript“-Statement

zum Deklarieren der Variable <Lichtstaerke_Bits> ist es dann auch, was später den Fehler „NaN“, engl. „Not a Number“, d.h. keine Anzahl, Nummer, Zahl, Ziffer bedeutet. Dabei gilt es anzumerken, dass sich mit einer Ziffer nicht rechnen lässt, es sei denn, dass diese zuvor in eine Zahl umgewandelt wird! -

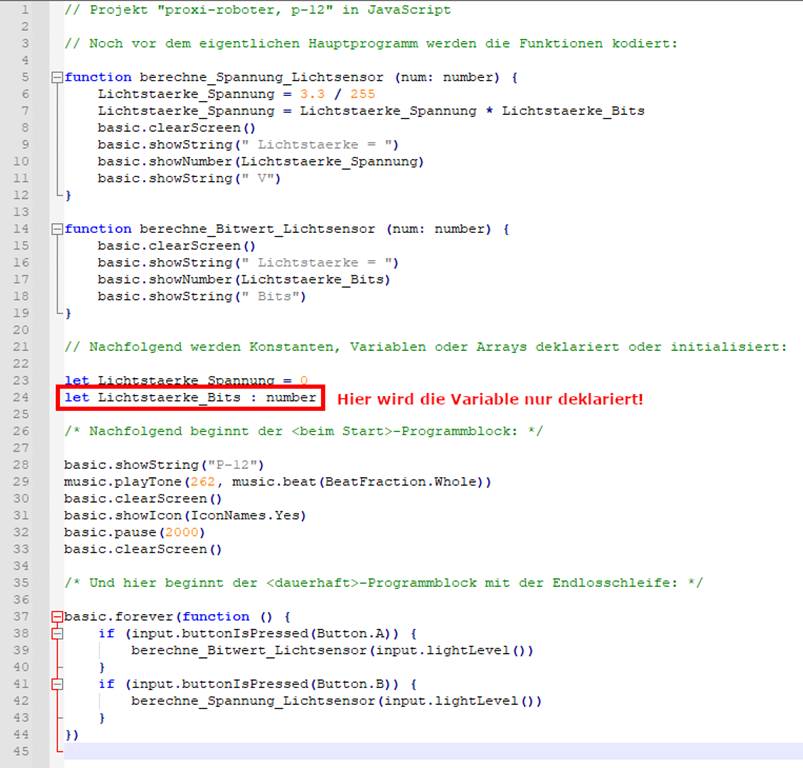
Werfen wir bei dieser Gelegenheit einen Blick auf den „JavaScript“-Quellkode:

(Zum Vergrößern bitte auf das Bild klicken!)

So, jetzt ist es raus! Ich habe bei der Programmierung geschummelt und dem „MakeCode“-Programm, d.h. dem Programmieren in Blöcken heimlich das „JavaScript“-Statement

untergeschoben, um den Unterschied zwischen dem Deklarieren und Initialisierung besser verdeutlichen zu können. Diesbezüglich könnte man auch sagen, dass das Initialisieren einer Variablen das Deklarieren einschließt bzw. vorwegnimmt.

Wie wir jetzt ferner wissen, lässt sich die „micro:bit“-Programmieroberfläche, die übrigens auch von Microsoft mitentwickelt wurde, jederzeit vom „Block“-Programmieren mit „MakeCode“ von Microsoft auf das „JavaScript“-Programmieren umschalten!

In diesem Zusammenhang dürfen wir schon jetzt gespannt sein, ob und wie die Roboter-Befehle vom KOSMOS „Proxi“-Roboter in JavaScript übersetzt werden!

Funktionen mit Eingang und Ausgang

Bisher benutzen wir Funktionen hauptsächlich dazu, bestimmte, sich teils wiederholende Dinge, insbesondere Programmkode in diese auszulagern, um dementsprechend die Lesbarkeit und Übersichtlichkeit des Programms zu verbessern.

Funktionen bewerkstelligen und leisten nicht nur etwas, sondern verhalten sich auch programmiertechnisch teils unterschiedlich!

So kann eine Funktion z.B. das Ergebnis einer Berechnung als zutreffend, d.h. richtig, engl. „true“ (= „1“) oder als unzutreffend, d.h. falsch, engl. „false“ (= „0“) charakterisieren und bewerten.

Wenn eine Funktion eine Berechnung durchführt, die entweder richtig oder falsch sein kann, dann hätte sie den Charakter „1“ für richtig oder „0“ für falsch.

Programmiertechnisch nennt man „0“ = „false“ oder „1“ = „true“ auch vom Typ her, engl. „boolean“, deutsch „boolesch“, d.h. wahrheitsgemäß.

Bisher verhielten sich die beiden Funktionen „numerisch“, d.h. rechnerisch!

Funktionen dienen aber nicht nur dazu, funktionelle Programmteile zusammenzufassen und in eine Funktion auszulagern, sondern können auch die in der Funktion berechneten Ergebniswerte wieder an das Hauptprogramm <beim Start> oder an die nächste Funktion zurückgeben:

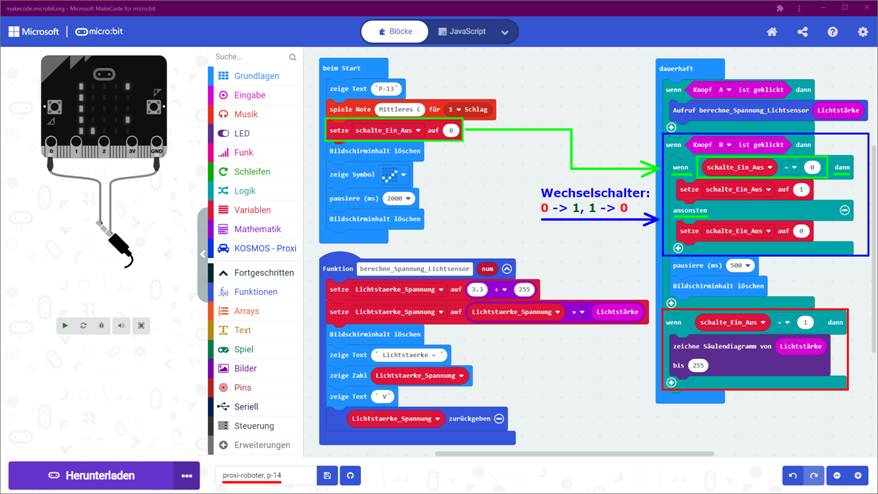
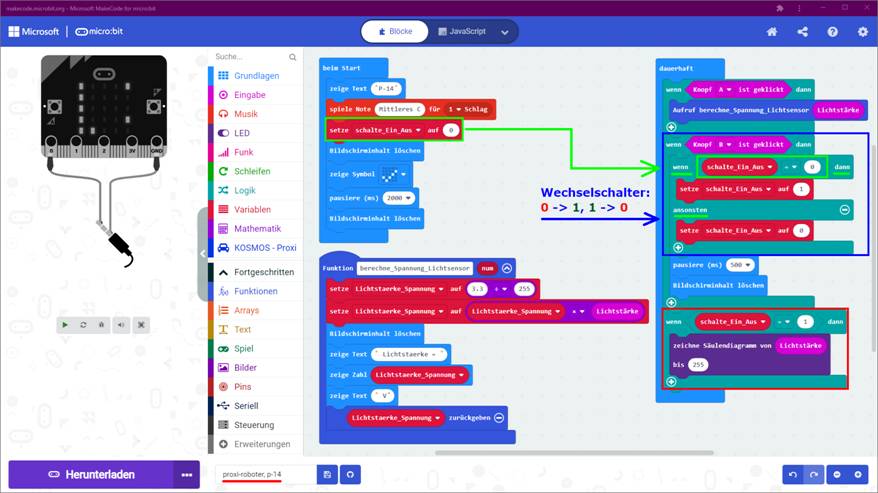
(Zum Vergrößern bitte auf das Bild klicken!)

Beim nächsten Projekt „proxi-roboter, p-14“ wird mit dem Statement

die Variable <schalte_Ein_Aus> auf den logischen Wert = 0 gesetzt (siehe im Hauptprogramm <beim Start>), um auf diese Weise den booleschen, d.h. logischen „Ein-/Aus-“-Schalter auf den Anfangswert „Aus“ (= 0) zu setzen.

Dabei ist es wichtig, den booleschen, d.h. logischen „Ein-/Aus-“-Schalter von Anfang an auf einen definierten Zustand (= „Aus“) zu setzen, damit es später beim Umschalten (siehe blauer Kasten) zu keinen Missverständnissen kommt, weil man nicht weiß, ob der boolesche „Ein-/Aus-“-Schalter aktuell ein- oder ausgeschaltet ist!

Die Umgangssprache verfügt im Gegensatz zur Hochsprache nur über einen begrenzten Wortschatz, was aber nicht zwangsweise ein Nachteil sein muss. Schließlich hilft uns die Umgangssprache dabei, Dinge schneller zu verstehen und zu begreifen. Wenn also die Umgangssprache von einem Schalter spricht, dann denkt der Technik affine Mensch sofort an einen Lichtschalter in der Wohnung, im Wohnungsflur, im Hausflur oder Treppenhaus.

Doch seit der Erfindung des Transistors Anfang der 50er Jahre müsste die Umgangssprache auch von einem Taster bzw. Tastschalter sprechen.

Bei einem längeren Hausflur liegen die Lichtschalter logischerweise ziemlich weit auseinander. Mit dem Vorteil, dass ich das Flurlicht mit dem Lichtschalter A einschalten und am anderen Ende des Flures mit dem Lichtschalter B wieder ausschalten kann.

Der Strippenzieher, d.h. der Elektroinstallateur, nennt eine solche Schaltung, die aus zwei Schaltern A und B besteht, Wechselschaltung. Dabei schaltet der Lichtschalter A die Stromzufuhr „auf dem Hinweg“ vom Außenleiter bzw. Stromleiter L (= Phase) über die Glühlampe hin zum Neutralleiter N (= geeignet niederohmig geerdet) ein und der Lichtschalter B „auf dem Rückweg“ zum Stromleiter L (= Phase) wieder aus.

Wenn aber die Glühlampe „auf dem Rückweg“ ausgeschaltet wird, dann kann es sein, dass sie, obwohl ausgeschaltet, auf der spannungsführenden Seite, d.h. dem Stromleiter L (= Phase) liegt! Achtung: Gefahr eines Stromschlags!

Deshalb müssen Wechselschaltungen bei Wartungs- oder Reparaturarbeiten stets am Sicherungskasten durch Ausschalten der Sicherung stromlos gemacht werden!

Wenn in einem längeren Wohnungs- oder Hausflur mehr als zwei Lichtschalter verbaut sind, dann handelt es sich bei diesen in Wirklichkeit um Taster zum Ein- oder Ausschalten der Beleuchtung.

Was aber ist der Unterschied zwischen einem Lichtschalter und einem Lichttaster?

Während ein Lichtschalter tatsächlich die Stromzufuhr zur Glühlampe ein- oder ausschaltet, gibt man über den Lichttaster nur den Befehl dazu, die Stromzufuhr zur Glühlampe ein- oder auszuschalten! Ob der Befehl zum Ein- oder Ausschalten dann tatsächlich ausgeführt, d.h. umgesetzt wird, erkennt man dann nur an der Glühlampe selbst, wenn diese an- oder ausgeht! Demzufolge erfolgt das Ein- und Ausschalten über ein entsprechendes Relais im Sicherungskasten!

Der „micro:bit“-Rechner verfügt übrigens über drei Taster und zwar auf der Vorderseite die beiden Taster A und B und an der Rückseite den „Reset“-Taster, der sich neben der „Micro USB 2.0“-Anschlussbuchse befindet. Dabei dient der „Reset“-Taster dazu, den „micro:bit“-Rechner neu zu starten, wobei dann auch das im Arbeitsspeicher nichtflüchtig gespeicherte Programm automatisch gestartet und ausgeführt wird.

Die beiden Taster A und B auf der Vorderseite des „micro:bit“-Rechners lassen sich programmieren. Beim Programmieren mit „MakeCode“ (= Blöcke) heißen die beiden Taster „Knopf A“ und „Knopf B“, so die Übersetzung.

Beim nachfolgenden Projekt „proxi-roboter, p-14“ kann man im Programmblock „dauerhaft“ im blauen Kasten sehr gut sehen, dass man mit dem <Knopf B> lediglich den logischen Schalter, d.h. die Variable <schalte_Ein_Aus> von logisch „0“ (= engl. „false“, unwahr, unzutreffend, aus) auf logisch „1“ (= engl. „true“, wahr, zutreffend, ein) und umgekehrt umschaltet!

Dabei verhält es sich so, dass der Umschaltvorgang mittels Drücken des Tasters „Knopf B“ zunächst ohne Folgen, ohne Reaktion bleibt, da das eigentliche Umschalten separat veranlasst und demzufolge mittels Statement im roten Kasten programmiert werden muss:

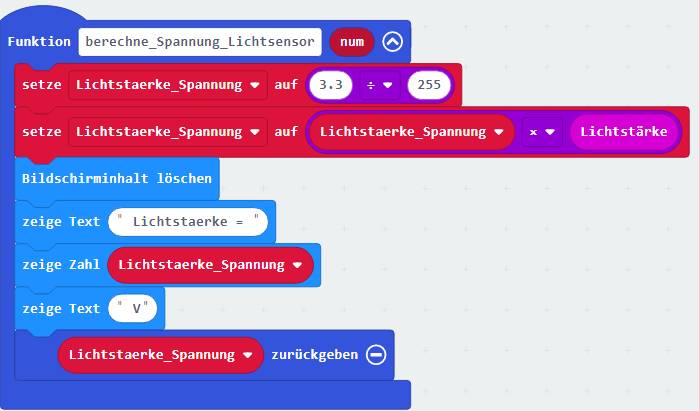
(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden Bild des Projektes „proxi-roboter, p-14“ sieht, gibt die Funktion <berechne_Spannung_Lichtsensor> zwar die berechnete Spannung in Form der Variablen <Lichtstaerke_Spannung> wieder an das Hauptprogramm <beim Start> sowie an das Programm <dauerhaft> zurück,

ohne aber später beim Programmblock <zeichne Säulendiagramm> wieder auf diese zurückzugreifen:

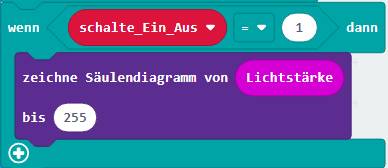
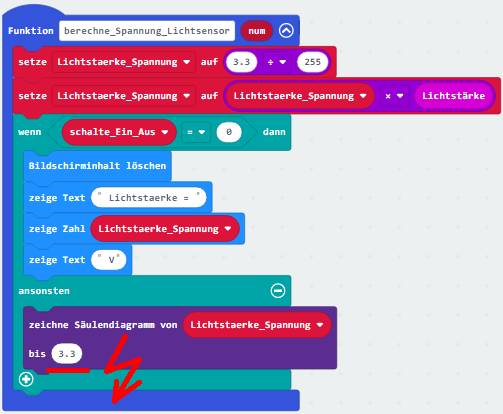
(Zum Vergrößern bitte auf das Bild klicken!)

Wir nehmen den zuvor beschriebenen „Schönheitsfehler“ zum Anlass, um diesen zu beheben und verlagern dabei gleichzeitig den Programmblock <zeichne Säulendiagramm> in die Funktion <berechne_Spannung_Lichtsensor>

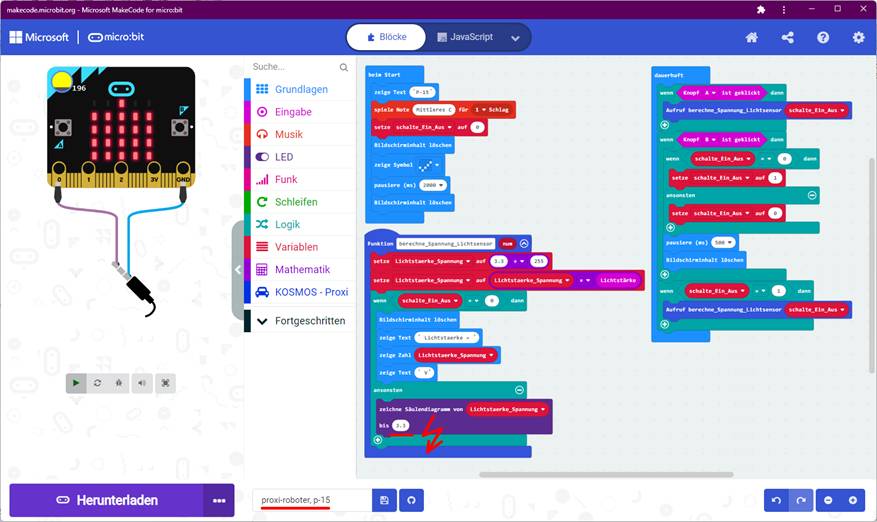
und passen bei dieser Gelegenheit das Säulendiagramm an die umgerechnete Spannung als Funktion der Lichtstärke an, indem wir den vormaligen Bitwert 255 auf nunmehr 3,3 V abändern, sodass sich jetzt das Säulendiagramm auf die maximale Spannung U_Säule = 3,3 V bezieht! Dabei ändert sich aber nichts an der grafischen Darstellung (siehe Projekt „proxi-roboter, p-15“

(Zum Vergrößern bitte auf das Bild klicken!)

Vom Klickzähler zum Rundenzähler

Mit dem Projekt „proxi-roboter, p-07“ (siehe weiter oben) brachten wir den Proxi-Roboter dazu, dass er mit dem Motor P13, dem Untersetzungsgetriebe und der Hub- und Schubstange B2 genau einen Zahnradumlauf (= 360 Grad) in der Zeit von t_Einzel = 1210 ms (= Millisekunden) = 1,210 s ( = Sekunden) durchführte.

Da sich die tatsächliche Umlaufzeit u.a. wegen der Reaktionszeit der Zeitnehmerperson nicht absolut exakt stoppen lässt, greifen wir zu einem Trick und lassen den Motor P13 mit den beiden gleichlaufenden Zahnrädern und der Hub- und Schubstange B2 insgesamt eine Minute lang laufen und zählen dabei die Drehzahl, d.h. Anzahl der Umläufe wie folgt:

Zeitdauer T = 1 min = 60 s insgesamt

t_Einzel = 1,210 s

Drehzahl n = Umdrehungen " dimensionslos, d.h. ohne Maßeinheit!

Berechnung der Drehzahl n pro Minute:

n = T / t_Einzel

= 1 min / 1,210 s = 60 s / 1,210 s = 49,58677685950413 ≈ 49,587 ≈ 49,6 Umdrehungen

Da es bei der Drehzahl n um ganzzahlige Umdrehungen geht, also um n = 50 Umdrehungen, rechnen wir wie folgt „rückwärts“, um die Rundenzeit t_Einzel einer einzelnen Umdrehung wie folgt zu berechnen:

t_Einzel = T / n

= 1 min / 50 = 60 s / 50 = 1,20 s = 1200 ms

Jetzt wo wir die Rundenzeit t_Einzel kennen, lässt sich diese entsprechend dem Vollkreis = 360⁰ wie folgt aufteilen:

t_Einzel / 360⁰ = 1200 ms / 360⁰ = 3,333 ms/1⁰ = 19,998 ms/6⁰ ≈ 20 ms/6⁰

Wie man sieht, lässt sich der Vollkreis von 360⁰ in insgesamt 60 schmale „Tortenstücke“ à 6⁰ Winkel pro „Tortenstück“ unterteilen. Das ist wichtig, wenn es später darum geht, dass sich der Proxi-Roboter schrittweise vor- oder zurückbewegt.

Damit man später weiß, wie viele Schritte sich der Proxi-Roboter vor- oder zurückbewegt hat, muss man später auch noch einen Schrittzähler in das Programm einbauen.

Das nachfolgende Projekt „proxi-roboter, p-16“ dient dazu, die Drehung der schwarzen Zahnräder B9 (links) und A6 (rechts) nebst der Auf- und Abbewegung der senkrechten Zug- und Druckstange bezüglich der Rotation der beiden Zähnräder zu erfassen

(Zum Vergrößern bitte auf das Bild klicken!)

mit dem Ziel, den Bewegungsapparat und dessen Drehung nach links und rechts zu steuern, um diesen beim späteren Zusammenbau in eine vorteilhafte Montageposition zu bringen, sodass sich später der Dreh- und Bewegungsmechanismus der 2 x 3 Krabbenbeine leichter montieren lässt.

Das Projekt „proxi-roboter, p-16“ bzw. das dazugehörige, kompilierte und ausführbare Programm „microbit-proxi-roboter-p-16.hex“ besteht dabei aus drei Programmblöcken:

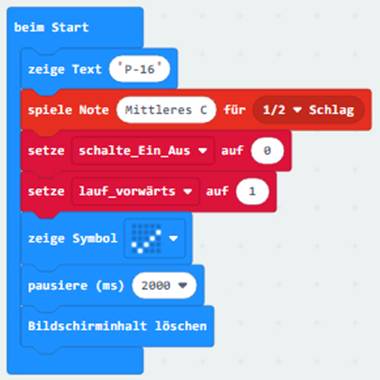
1. dem Programmblock <beim Start>,

bei dem die beiden Variablen <schalte_Ein_Aus> = 0 und <lauf_vorwärts> = 1 initialisiert werden. Demzufolge ist der Antriebsmotor P13 beim Einschalten und Hochfahren des Proxi-Roboters ausgeschaltet, wohingegen die Bewegungsrichtung mit der Variablen <lauf_vorwärts> = 1 mit logisch „zutreffend“ (= 1) bereits vorgegeben ist, sodass sich der Motor P13 beim Einschalten mittels Druck auf den Taster „Knopf A“ in kleinen 6⁰ Schritten im Uhrzeigersinn nach rechts bewegt (siehe orangefarbenes Zahnrad, d.h. Ritzel P8, auf der Motorachse des Motors P13 mit den blau und schwarzen Stromversorgungskabeln).

Dabei lässt sich der Antriebsmotor P13 jederzeit durch erneutes Betätigen des Tasters „Knopf A“ wieder anhalten bzw. ausschalten (siehe Punkt 2.).

(Zum Vergrößern bitte auf das Bild klicken!)

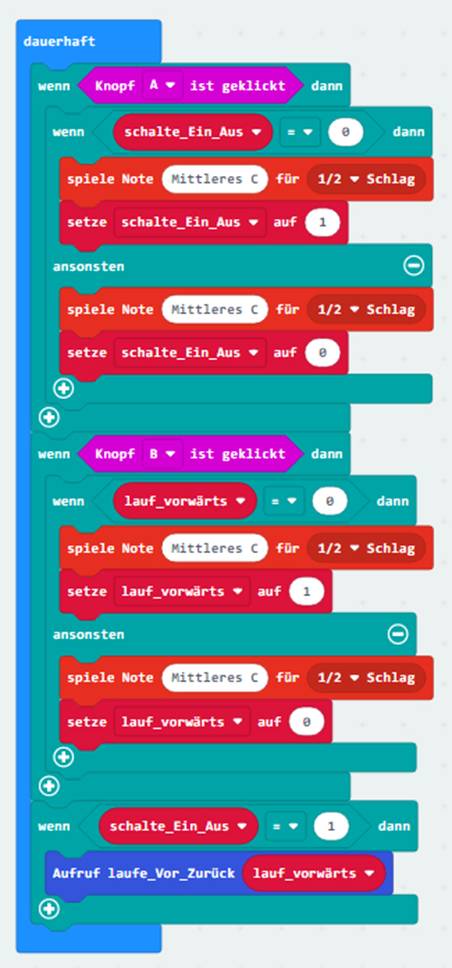
2. dem Programmblock <dauerhaft>,

das aus insgesamt drei weiteren Teilblöcken <wenn Knopf A ist geklickt, dann>, <wenn Knopf B ist geklickt, dann> und <wenn schalte_Ein_Aus = 1, dann> besteht.

Dabei dient der Teilblock <wenn Knopf A ist geklickt, dann> dazu, den Antriebsmotor P13 umzuschalten. Ist der Motor ausgeschaltet, dann lässt er sich durch einfachen Tastendruck auf den Taster <Knopf A> einschalten und umgekehrt, indem die Variable <schalte_Ein_Aus> entweder auf logisch „1“ (= ein, zutreffend) oder „0“ (= aus, unzutreffend) gesetzt wird.

Der Teilblock <wenn Knopf B ist geklickt, dann> dient dazu, den Antriebsmotor P13 in seiner Drehrichtung umzuschalten. Ist die Variable <lauf_vorwärts> auf logisch „1“ (= ein, zutreffend) gesetzt, dann dreht sich die Motorachse mit dem orangefarbenen Ritzel P8 im Uhrzeigersinn rechts herum. Bei logisch „0“ (= aus, unzutreffend) dreht sie sich gegen den Uhrzeigersinn links herum. Dabei verhält es sich so, dass sich der Antriebsmotor P13 jederzeit während seiner Bewegung in seiner Drehrichtung umschalten lässt, sodass er beim Richtungswechsel nicht extra angehalten werden muss! Der Richtungswechsel lässt sich auch im Stillstand vornehmen, wenn der Antriebsmotor P13 steht!

Achtung: Die beiden Teilblöcke <wenn Knopf A ist geklickt, dann> und <wenn Knopf B ist geklickt, dann> dienen nur dazu, die eine oder andere Aktion zu veranlassen, d.h. anzustoßen, selbst aber nicht auszuführen!

Demzufolge dient der letzte Teilblock <wenn schalte_Ein_Aus = 1, dann> ausschließlich dazu, nur die Funktion <laufe_Vor_Zurück> aufzurufen! Aber eben nur dann, wenn die Variable <schalte_Ein_Aus> = 1 ist, d.h. nur wenn der Antriebsmotor P13 eingeschaltet ist und sich entweder rechtsherum oder linksherum dreht!

Wenn aber die Variable <schalte_Ein_Aus> = 1 ist und der Antriebsmotor P13 eingeschaltet ist, dann wird die Funktion <laufe_Vor_Zurück> dauerhaft aufgerufen und ausgeführt!

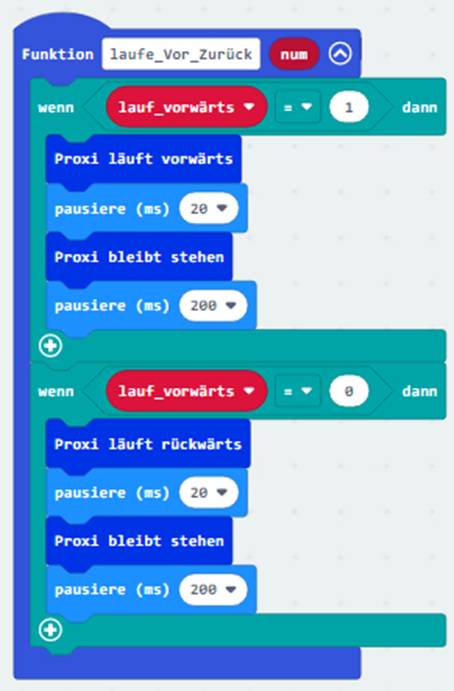
(Zum Vergrößern bitte auf das Bild klicken!)

und

3. dem Programmblock <Funktion <laufe_Vor_Zurück>,

der sozusagen das ausführende Organ, bei der staatlichen Gewaltenteilung in Deutschland auch Exekutive genannt, ist und dafür sorgt, dass die zuvor mittels Taster „Knopf A“ oder „Knopf B“ veranlassten Aktionen umgehend ausgeführt und in die Tat umsetzt werden.

Besonders interessant dabei ist, wie sich der Proxi-Roboter bewegt, wie erläuft! Einmal losgefahren, läuft er wie der VW Käfer: „… und läuft und läuft und läuft!“ Bis der Tank leer ist oder beim Proxi-Roboter die Batterien leer sind.

Demzufolge besitzt das Statement <Proxi läuft vorwärts> oder <Proxi läuft rückwärts> wider Erwarten keine zeitliche Befristung, kein zeitliches Limit, sodass sich der Programmierer selbst darum kümmern muss und ein Stoppsignal setzen muss, wenn der Proxi-Roboter zum Stillstand kommen soll.

Und da der Proxi-Roboter im vorliegenden Fall immer nur kleine Vor- oder Rückwärtsbewegungen machen soll, folgt auf jeden Laufbefehl, der Befehl zum Stehenbleiben. Und zwar alle 20 Millisekunden! Und bei 60 kleinen Trippelschritten dauert die vollständige Umlaufzeit für nur einen Vollkreis der beiden schwarzen Zahnräder B9 (links) und A6 (rechts) trotzdem nur 1200 Millisekunden = 1,2 Sekunden!

Damit aber der Benutzer des Proxi-Roboters später die kleinen Vor- oder Rückwärtsbewegungen koordinieren und jederzeit anhalten kann, gibt es zwischen jeder Bewegung eine zehnmal längere Kunstpause von 200 Millisekunden.

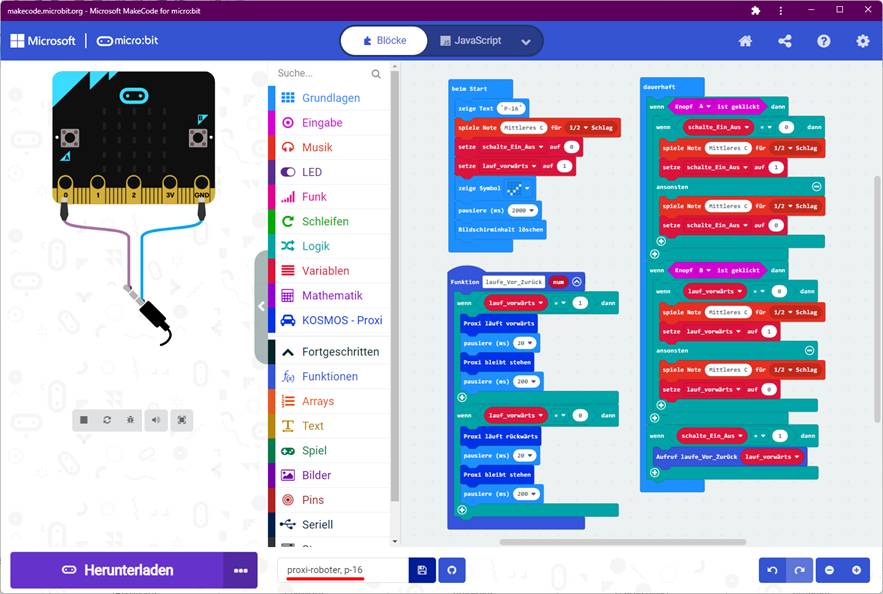
(Zum Vergrößern bitte auf das Bild klicken!)

Nachfolgend das Projekt „proxi-roboter, p-16“ mit dem vollständigen „MakeCode“-Programmkode:

(Zum Vergrößern auf das Bild klicken!)

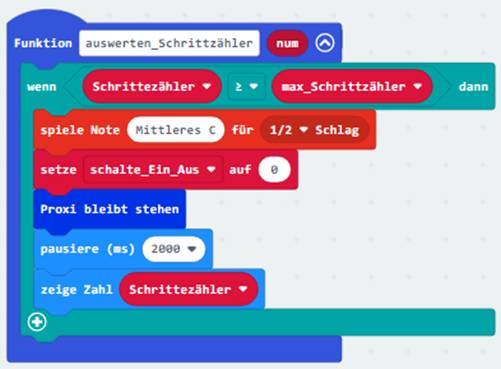
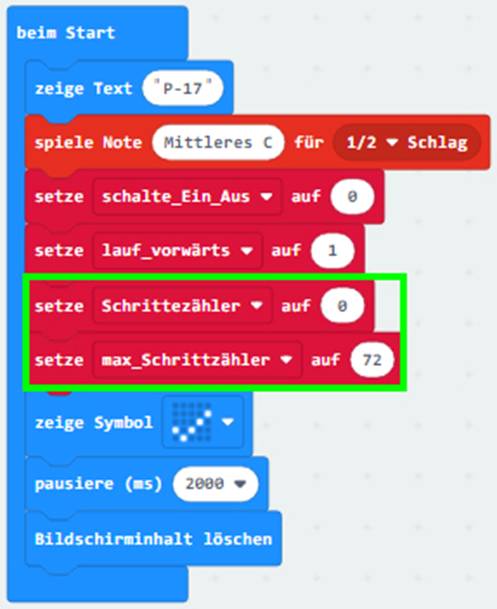
Wir erweitern das obenstehende Programm um die <Funktion auswerten_Schrittzähler>.

Dabei fällt sofort auf, dass es zwei neue Variablen gibt. Und zwar die Variable <Schrittzähler> und <max_Schrittzähler>.

Während die Variable <Schrittzähler> bei jedem Durchlaufen der < Funktion laufe_Vor_Zurück> um einen Schritt erhöht wird (siehe hellgrüner Kasten), wird diese fortwährend mit der Variablen <max_Schrittzähler> und dem Maximalwert = 72 Schritte verglichen:

(Zum Vergrößern bitte auf das Bild klicken!)

Beim Überschreiten des Maximalwertes ≥ 72 Schritte wird der Antriebsmotor P13 ausgeschaltet und der aktuelle Wert des Schrittzählers in der Laufschrift des LED-Displays angezeigt (siehe oben).

Damit sich die beiden Variablen <Schrittzähler> und <max_Schrittzähler> auch tatsächlich problemlos, d.h. ohne eine Fehlermeldung zu bewirken, nutzen lassen, sollten diese zuvor im Hauptprogramm <beim Start> wie folgt initialisiert werden (siehe hellgrüner Kasten):

(Zum Vergrößern bitte auf das Bild klicken!)

Wie bereits an anderer Stelle besprochen, verfügt der Proxi-Roboter leider über keine präzisen Schrittmotoren, sondern aus Kostengründen nur über herkömmliche, sehr preiswerte Gleichstrommotoren, deren Antrieb demzufolge Bauart bedingt über keine Nullstellung (= 0⁰ Winkel der Motorachse) verfügt. Demzufolge dauert der 360⁰ Durchlauf eines Vollkreises je nach teils unterschiedlicher Versorgungsspannung über das „Micro USB 2.0“-Kabel mal 70, 71 oder 72 Schritte der festen Schrittlänge von derzeit 20 Millisekunden.

Und da die Netzspannung tagsüber eher etwas niedriger und abends eher etwas höher ausfällt, kommt man nicht umhin, den Maximalwert = 72 des Schrittzählers öfters mal korrigieren zu müssen!

Da trifft es sich gut, dass die Variablen <max_Schrittzähler> bereits im Hauptprogramm <beim Start> initialisiert wird, sodass man nicht überall in allen Programmteilen nach dieser suchen muss, um den Maximalwert = 72 des Schrittzählers jeweils einzeln abändern zu müssen (siehe Projekt „proxi-roboter, p-16“):

(Zum Vergrößern bitte auf das Bild klicken!)

Jetzt steht eindeutig fest, dass eine teils zu niedrige Versorgungsspannung über das angeschlossene „Micro USB 2.0“-Kabel des Windows-PCs unmittelbar dazu führt, dass der Antriebsmotors P13 langsamer läuft und wegen der geringeren Drehzahl dabei weniger Schritte (= 70) pro 360⁰ Durchlauf eines Vollkreises ausführt.

Umgekehrt würde der Antriebsmotors P13 bei einer teils höheren Versorgungsspannung etwas schneller laufen und wegen der höheren Drehzahl dabei mehr Schritte (= 72) pro 360⁰ Durchlauf eines Vollkreises ausführen.

Demzufolge gibt es also einen Zusammenhang zwischen der Änderung der Versorgungsspannung ∆U und der sich ändernden Drehzahl ∆n:

∆U ~ ∆n " ∆n ~ 1 / ∆t " ∆n = 1 / ∆t * Konstante c " ∆n = Konstante c / ∆t " ∆n = 2 π / ∆T

∆n = 2 π / ∆T " n = 2 π / T "

ω = 2 π / T = 2 π f " Winkelgeschwindigkeit " T = Umlaufzeit für einen 360⁰ Vollkreis!

Mit der Winkelgeschwindigkeit ω = 2 π f bestätigt sich, dass es sich bei der Konstante c tatsächlich um die Konstante 2π handelt (siehe auch weiter unten).

Da es sich bei der Vor- und Rückwärtsbewegung des Proxi-Roboters mittels Antrieb durch den Antriebsmotor P13 und den beiden schwarzen Zahnrädern B9 (links) und A6 (rechts) um Kreisbewegungen handelt, haben wir es mit der Kreiszahl Pi „π“ mit π = 3,14159 ≈ 3,14 zu tun. Und wenn sich dabei auch noch die Zahnräder mit einer bestimmten Geschwindigkeit drehen, dann kommt noch die sogenannte Winkelgeschwindigkeit Omega „ω“ ins Spiel.

So sind z.B. die Holzräder einer Kutsche mit einem rundum laufenden, flachen Stahlband der Länge bzw. des Umfangs U = 2 π r versehen. Und wenn sich die Holzräder während der Fahrt drehen, dann geht es bei diesen auch um die Umlaufgeschwindigkeit v_Umlauf = s / t mit s = zurückgelegte Wegstrecke und t = verstrichene Zeit während eines Umlaufs:

v_Umlauf = s / t " s = Umfang U = 2 π r

= 2 π r / t " Mit dem Radius r als sogenannter Einheitsvektor gilt: r = 1 und für einen Umlauf folgt: t = T

= 2 π 1 / T "

= 2 π / T " v_Umlauf entspricht wegen der Kreisbewegung der Winkelgeschwindigkeit ω

ω = 2 π / T " mit f = 1 / T

ω = 2 π f " f = Kreisfrequenz, gemessen in Hertz [Hz]; Kreisfrequenz wegen der sich drehenden Zahnräder

= 2 π * 1 / T = 2 π / T = n " Drehzahl n, gemessen in Umdrehungen n / Sekunde = [ 1 / s ] = [ s^-1 ]

Dazu muss man wissen, dass man bei der Winkelgeschwindigkeit ω und den 2 π sowohl dezimal mit 6,28 rechnen kann als auch mit 360⁰ Winkelgraden für einen Vollkreis:

1. Fortbewegung des Proxi-Roboters anhand von selbst definierten Schritten

Mit n = 72 Schritte für einen 360⁰ Vollkreis folgt:

72 Schritte " 360⁰

5 Schritte " n ⁰

n = 360⁰ / 72 Schritte * 5 Schritte = 25⁰ Winkeländerung bei 5 Schritten oder 5⁰ Winkeländerung / 1 Schritt!

Dabei geht es nur um die zurückgelegten Schritte und zwar unabhängig von der dazu benötigten Zeit!

Wenn später der Proxi-Roboter wegen der leicht angestiegenen 5 V USB-Stromversorgung über das „Micro USB 2.0“-Kabel etwas schneller läuft als bisher, dann ändert sich an den 72 Schritten für den Umlauf eines 360⁰ Vollkreises nichts! Auch und obwohl der 360⁰ Vollkreis schneller durchlaufen wird!

Der Knackpunkt dabei ist aber, dass dem so sein sollte, aber wider Erwarten dem nicht so ist. Zwar bewegt sich der Proxi-Roboter schrittweise, weil wir das so gewollt und auch entsprechend programmiert haben, indem dieser nach jedem Einzelschritt eine Pause von 20 ms + 200 ms = 220 ms einlegt (siehe Bild 26). Davon aber, dass sich der Antriebsmotor P13 des Proxi-Roboters bei einer etwas höheren Versorgungsspannung schneller dreht, ändert nichts daran, dass der Schrittzähler weiterhin mit n = 72 Schritte rechnet!

Wenn wir aber die bei den 72 Schritten zurückgelegte Wegstrecke s eines der beiden schwarzen Zahnräder B9 (links) oder A6 (rechts) mit dem Radius r = 10 mm wie folgt berechnen (siehe Bild 7),

U = 2 π * r = 6,28318 * 10 mm ≈ 6,283 * 10 mm = 62,83 mm ≈ 6,28 cm

wird der Zusammenhang gleich deutlicher, wenn man die Umlaufgeschwindigkeit v für einen Umlauf mit einbezieht:

v₁ = s₁ / t₁ = 6,28 cm / 18,81 s = 0,33386496 cm/s ≈ 0,334 cm/s

v₂ = s₂ / t₂ = 6,28 cm / 18,08 s = 0,347345 cm/s ≈ 0,347 cm/s " Motor läuft schneller!

s₃ = v₂ * t₁ = 0,347 cm/s * 18,81 s = 6,52707 cm ≈ 6,53 cm "

Wie man sieht, legt der Motor in der gleichen Zeit t = 18,81 s eine deutlich größere Wegstrecke s₃ = 6,53 cm zurück! Wenn aber der Motor in der gleichen Zeit eine deutlich größere Wegstrecke zurücklegt, dann macht der auch deutlich mehr Schritte:

6,28 cm " 72 Schritte

6,53 cm " x Schritte

x = 72 / 6,28 cm * 6,53 cm = 74,86624 Schritte ≈ 74,9 Schritte ≈ 75 Schritte

Umgekehrt verhält es sich so, dass der schneller laufende Motor die gleiche Strecke s₂ = 6,28 cm in kürzerer Zeit t₂ = 18,08 s zurücklegt:

s₄ = v₂ * t₂ = 0,347345 cm/s * 18,08 s = 6,2799976 cm ≈ 6,28 cm

18,81 s " 72 Schritte

18,08 s " x Schritte

x = 72 / 18,81 s * 18,08 s = 69,2057 Schritte ≈ 69,21 Schritte ≈ 69 Schritte

Wie man im Vergleich sieht, führt der Motor in der bisherigen Zeit t₁ = 18,81 s mit der zurückgelegten, größeren Strecke s₃ = 6,53 cm und mit 75 Schritten auch mehr Schritte aus. Eben, weil der Motor schneller läuft!

Umgekehrt bedeutet dies, dass der schneller laufende Motor in der kürzeren Zeit t₂ = 18,08 s trotzdem weniger Schritte ausführt: nämlich nur 69 Schritte gegenüber bisher 72 Schritte!

Spätestens jetzt bestätigt sich, dass es bezüglich eines Umlaufs zwischen der dazu benötigten Zeit t, der Anzahl der zurückgelegten Schritte und der Änderung der Motorgeschwindigkeit ∆v einen unmittelbaren, proportionalen Zusammenhang gibt:

" Legt der Motor in der bisher gleichen Zeit t₁ = 18,81 s mehr als 72 Schritte zurück und in der kürzeren Zeit t₂ = 18,08 s weniger als 72 Schritte zurück, dann muss der Motor schneller laufen!

Dabei muss die Differenz zwischen dem Maximalwert und dem Basiswert = (75 – 72) Schritte = 3 Schritte und zwischen dem Minimalwert und dem Basiswert = (72 – 69) Schritte = 3 Schritte gleich groß sein!

" Legt der Motor in der bisher gleichen Zeit t₁ = 18,81 s weniger als 72 Schritte zurück und in der kürzeren Zeit t₂ = 18,08 s noch weniger Schritte, dann muss der Motor langsamer laufen!

Demzufolge kommen wir nicht umhin, bei der Programmierung von Vor- oder Rückwärtsbewegungen mittels Antriebsmotor P13 neben der Anzahl der zurückgelegten Schritteanzahl auch die dazu benötigte Zeit zu erfassen und auszuwerten, um definitiv zu wissen, ob sich der Motor schneller oder langsamer dreht und dabei eine längere oder kürzere Strecke zurücklegt.

Dafür, dass sich der Antriebsmotor P13 langsamer oder schneller dreht, gibt es im Wesentlichen folgende Gründe:

1. Der Motor läuft wegen der niedrigeren oder höheren 5 V USB-Stromversorgung über das „Micro USB 2.0“-Kabel deutlich wahrnehmbar langsamer oder schneller.

2. Der Motor läuft wegen der niedrigeren oder höheren Stromversorgung mittels Batteriebetrieb im Laufe der Zeit deutlich wahrnehmbar langsamer, weil sich die Batterien nach und nach entladen.

3. Der Motor läuft deutlich wahrnehmbar langsamer, weil es eine Rampe nebst Steigung hinauf geht, der Motor bei gleicher Geschwindigkeit bzw. Drehzahl entsprechend mehr leisten müsste, weil er einen Teil der Antriebskraft in die Überwindung der Steigung investieren muss, dies aber nicht zu leisten vermag, weil die Motorleistung begrenzt ist!

Demzufolge muss der Motor beim Hinauffahren auf einen Hügel wegen der begrenzten Leistung langsamer werden und dabei gleichzeitig mehr Zeit aufwenden!

4. Der Motor läuft deutlich wahrnehmbar schneller, weil es eine Rampe nebst Gefälle hinab geht und sich die Antriebskraft aufgrund der Hangabtriebskraft deutlich verringert!

Wenn man also zukünftig wissen will, ob der Proxi-Roboter eine Steigung hinauf klettert oder herunter läuft, dann muss man u.a. nachfolgende Dinge berechnen:

1. die potentielle Energie W_pot des Hügels mit W_pot = F_G * h " F_G = Gewichtskraft, h = Höhe des Hügels

F_G = m * g " m = Masse des Proxi-Roboters in Kg (Kilogramm), g = 9,81 m/s² für die Erdbeschleunigung

W_pot = F_G * h = m * g * h mit der Maßeinheit [ kg * m/s² * m ] = [ kg (m/s)² ] = [ 9,81 Nm ]

2. die zurückgelegte Wegstrecke s (= Länge der Steigung) mit s = ½ a t² und v = a * t

a = Beschleunigung des Fahrzeugs bzw. des Proxi-Roboters, gemessen in [ m/s² ]

v = Geschwindigkeit des Fahrzeugs bzw. des Proxi-Roboters, gemessen in [ m/s ]

3. die elektrische und mechanische Antriebsleistung des Motors:

P_elek = U_Motor * I_Motor " P_mech = F_mech " F_mech = Antriebskraft, gemessen in Newton [ N ]

4. die verrichtete elektrische Arbeit W_elek = P_elek * t_Motor = U_Motor * I_Motor * t_Motor, gemessen in [ VAs ]

5. die verrichtete mechanische Arbeit W_mech = F_mech * s, gemessen in Newtonmeter [ Nm ] = [ VAs ]

6. die kinetische Energie W_kin (= Arbeit), die im Fahrzeug bzw. Roboter auf der Höhe des Hügels gespeichert ist: W_kin = ½ m v², gemessen in [ kg (m/s)² ] bzw.

W_kin = ½ m ( a * t )², gemessen in [ kg * ( m/s² * s )² ] = [ kg (m/s)² ]

Umrechnung der Maßeinheit [ kg (m/s)² ] = [ 9,81 Nm ] (siehe oben)

Ob der Proxi-Roboter eine Steigung hinauf klettert oder herunter läuft, lässt sich zum Glück auch ganz ohne Berechnung herausfinden, nämlich indem man den im „micro:bit“-Rechner verbauten Beschleunigungssensor, engl. „accelerator“, bemüht:

(Zum Vergrößern bitte auf das Bild klicken!)

>> Beschleunigungsmesser

Was ist das? Ein Beschleunigungssensor misst die Beschleunigung des micro:bit; diese Komponente erkennt, wenn der micro:bit bewegt wird. Es kann auch andere Aktionen erkennen, wie z.B. Schütteln, Kippen und freier Fall. << (Quelle: Archive micro:bit)

Nachfolgend zwei kleine Beispielprogramme: Wasserwaage und Neigungssensor.

2. Fortbewegung des Proxi-Roboters anhand der Drehzahl

Wenn der Proxi-Roboter zum Umrunden eines 360⁰ Vollkreises insgesamt n = 72 Schritte benötigt, dann folgt daraus, dass sich der 360⁰ Vollkreis in 72 schmale und spitze Kreissegmente in Form von sehr schmalen Tortenstücken aufteilt. Dabei ist jeder Winkel des schmalen und spitzen Tortenstückes = 360⁰ / 72 Kreissegmente = 5⁰ groß.

Leider bringt uns die geometrische Aufteilung des 360⁰ Vollkreises wegen der fehlenden Zeitabhängigkeit nicht weiter. Wie wir aber wissen, dauert eine Umrundung des 360⁰ Vollkreises bis zu T = 18,81 s pro Umdrehung.

n = 1 / T " ω = 2 π / T = 2 π f " ω = 2 π * 1 / T = 2 π * n " ω = 2 π * n " n = ω / 2 π

= 1 / 18,81 s = ( 1 / 18,81 ) s^-1 = 0,0531632110579479 s^-1 ≈ 0,0532 s^-1

Für die Winkelgeschwindigkeit ω folgt dann:

ω = 2 π * n

= 6,28 * 0,0532 s^-1

= 0,334096 s^-1

≈ 0,334 s^-1 " Die Winkelgeschwindigkeit wird nur für die Umrechnung benötigt!

Für die Berechnung der Drehzahl n folgt:

n = ω / 2π = ( 2π / T ) / 2π = 1 / T

= 0,334 s^-1 / 6,28 = 0,0531847133757962 s^-1 ≈ 0,0532 s^-1 ≈ 5/100 Umdrehungen pro Sekunde!

Probe:

n * T = 0,0532 s^-1 * 18,81 s = 1,000692 ≈ 1 þ

Da die Berechnung der Drehzahl n für sich allein steht und eben nicht in Relation zu einem 5⁰ Tortenstück von 72 Teilstücken mit ein Vollkreis von 360⁰ steht, bringt uns die Drehzahl-Berechnung nicht weiter!

3. Fortbewegung des Proxi-Roboters mittels Zeitdauer pro Einzelschritt

So wie man den 360⁰ Vollkreis in 72 Tortenstücke zu je 360⁰ / 72 = 5⁰ / Tortenstück aufteilen kann, lässt sich dieser auch in 18,81 s / 72 Schritte = 0,26125 s / 1 Schritt = 0,26125 s / 5⁰ Tortenstück = 0,05225 s / 1⁰ Tortenstück * 360⁰ = 18,81 s þ aufteilen. Ähnlich verhält es sich mit dem zeitlichen Maßstab 0,26125 s / 1 Schritt * 72 Schritte = 18,81 s þ

So wie sich die 360⁰ / 72 Schritte = 5⁰ pro Schritt (= 5⁰ pro Tortenstück) als Maßstab festlegen lassen, lassen sich die 18,81 s / 72 Schritte = 0,26125 s pro Schritt (= 0,26125 s pro Tortenstück) als zeitlicher Maßstab festlegen!

Jetzt verfügen wir endlich über die Möglichkeit, die 72 Einzelschritte für die Fortbewegung zu programmieren und dabei jeden Einzelschritt der dazu benötigten Zeitdauer von 0,26125 s pro Einzelschritt als zeitlichen Maßstab zuzuweisen!

Praktisch bedeutet dies, dass wir programmiertechnisch an den 72 Einzelschritten für die Fortbewegung niemals etwas ändern, sondern im Falle von zeitlichen Abweichungen immer nur den zeitlichen Maßstab neu anpassen!

Ähnlich verhält es sich auch beim Menschen im Alltag. So ist die allgemeine, d.h. durchschnittliche Schrittlänge eines Menschen u.a. biologisch durch die Körpergröße und den Körperbau der Gliedmaßen festgelegt.

Wenn wir also auf dem Weg zur Straßenbahn oder dem Omnibus zu spät dran sind und Gefahr laufen, diese oder diesen zu verpassen, dann schalten wir einfach „einen Gang höher“ und laufen schneller, um pünktlich an der Haltestelle anzukommen! Dabei verändern wir nicht die gewohnte Schrittlänge, sondern die Taktfrequenz (= Drehzahl = Anzahl der Schritte pro Minute), indem wir bei gleicher Schrittlänge einfach schneller laufen und dabei mehr Schritte in kürzerer Zeit zurücklegen! Das Interessante und Wichtige dabei ist, dass sich an der Weglänge von und zu der Haltestelle nichts ändert, sodass nur das Ziel in kürzerer Zeit erreicht wird: v = s / t " v + ∆v = s / ( t - ∆t )!

Beispiel:

s = 1 km, v = 5 km/h, Verspätung ∆t = 2 min "

t = s / v

= 1 km / 5 km/h = 1/5 h = 0,2 h = 0,2 * 1 h = 0,2 * 60 min = 12 min

Verspätung ∆t = 2 min "

v’ = v + ∆v

= s / ( t - ∆t )

= 1 km / ( 12 min - 2 min ) = 1 km / 10 min = 1 km / ( 10 * 1 min ) = 1 km / ( 10 * 1/60 h )

= 1 km / ( 1/6 h ) = 6 km/h

Bei einer Schrittlänge sl = 50 cm berechnet sich die Anzahl ns der Schritte wie folgt:

ns = s / sl

= 1 km / 50 cm = 1 * 1 km / ( 50 * 1 cm ) = 1 * 1000 m / ( 50 * 1 * 1/100 m ) = 1 * 1000 m * 100 / ( 50 * 1 * 1/100 m )

= 1 * 1000 m * 100 / ( 50 m ) = 100 000 / 50 = 10 000 / 5 = 2 000 Schritte

Dabei berechnet sich die Drehzahl n beim Laufen wie folgt:

ω = 2π n "

n = ω / 2π = ( 2π / T ) / 2π = 1 / T

= 1 / ( 12 min ) = 1 / ( 12 * 1 min ) = 1 / ( 12 * 60 sec ) = 1 / 720 sec^-1

= 0,0013888888888889 sec^-1 ≈ 0,0014 sec^-1 " bezogen auf t = 12 min " ohne Verspätung!

= 1 / ( 10 min ) = 1 / ( 10 * 1 min ) = 1 / ( 10 * 60 sec ) = 1 / 600 sec^-1

= 0,0016666666666667 sec^-1 ≈ 0,0017 sec^-1 " bezogen auf t’ = 10 min " mit Verspätung!

Wie wir bereits weiter oben festgestellt haben, bringt uns die Drehzahl n nicht weiter.

Berechnung der Einzelschritte pro Zeitdauer:

2000 Schritte / 12 min = 2000 Schritte / 12 * 1 min = 2000 Schritte / 12 * 60 sec = 2000 Schritte / 720 sec

= 2,777777777777778 Schritte / sec ≈ 2,78 Schritte / sec "

( 2,78 Schritte * 50 cm ) / sec = ( 2,78 Schritte * 50 * 1 cm ) / sec = ( 2,78 Schritte * 50 * 0,01 m ) / sec

= ( 2,78 Schritte * 0,50 m ) / sec = 1,39 m / sec für je einen Schritt "

= Schrittgeschwindigkeit 1,39 m / sec = 1,39 * 1 m / ( 1 * 1 sec ) = 1,39 * 0,001 km / ( 1 * 1 / 3600 h )

= 0,00139 * 3600 km / h = 5,004 km/h ≈ 5,0 km/h bezüglich der Zeitdauer t = 12 min.

Formelmäßig folgt daraus:

ns = 2000 " Anzahl der Schritte

sl = 50 cm = 50 * 1 cm = 50 * 0,01 m = 0,5 m " Schrittlänge

t = 12 min = 12 * 1 min = 12 * 60 s = 720 s " Zeitdauer t in Sekunden

Berechnung der Schrittgeschwindigkeit pro Stunde:

v_Schritt = s_Entfernung / t

= ( sl * ns ) / t

= 0,5 m * 2000 / 12 min = 1000 m / ( 12 * 1 min ) = 1000 m / ( 12 * 1/60 h ) = 1 km * 60 / ( 12 h )

= 1 km * 5 / ( 1 h ) = 5 km/h " Schrittgeschwindigkeit bezüglich der Zeitdauer t = 12 min

Was bedeutet es, wenn sich wegen der Verspätung des Fahrgastes(!) die verbleibende Zeitdauer auf t = 10 min verringert, um die Straßenbahn oder den Bus zu erreichen?

Wenn sich wegen der Verspätung die verbleibende Zeitdauer auf t = 10 min verringert, dann muss man „einen Zahn zulegen“ und die Schrittgeschwindigkeit auf 6 km/h wie folgt erhöhen:

v_Schritt = s_Entfernung / t

= ( sl * ns ) / t

= 0,5 m * 2000 / 10 min = 1000 m / ( 10 * 1 min ) = 1000 m / ( 10 * 1/60 h ) = 1 km * 60 / ( 10 h )

= 1 km * 6 / ( 1 h ) = 6 km/h " Schrittgeschwindigkeit bezüglich der Zeitdauer t = 10 min

Wenn der Fahrgast seine Schrittgeschwindigkeit steigert, um die Verspätung aufzuholen, dann muss er seine Antriebsleistung steigern, sodass sich sein Puls (= Herzfrequenz, Drehzahl) und Blutdruck erhöhen. Demzufolge darf ein älterer Mensch mit Herz-Kreislauf-Problemen eben nicht schneller laufen und seine Schrittgeschwindigkeit erhöhen, weil der dann außer Atem kommt und sein Herz nicht mit spielt.

Was also muss sich ändern, wenn die Schrittgeschwindigkeit mit 5 km/h beibehalten wird und sich auch die zur Verfügung stehende Zeitdauer t = 10 min nicht ändert?

v_Schritt = s_Entfernung / t

= ( sl * ns ) / t "

v_Schritt * t = sl * ns "

sl = v_Schritt * t / ns

= 5 km/h * 10 min / 2000 = 5 * 1000 m / 3600 s * 10 * 60 s / 2000

= 50 m / 36 s * 600 s / 2000 = 0,4166666666666667 m ≈ 0,42 m " FALSCH! Worin liegt der Fehler?

Wenn die Schrittgeschwindigkeit mit 5 km/h beibehalten wird, während sich gleichzeitig die zur Verfügung stehende Zeitdauer auf nur noch t = 10 min verringert, dann verkürzt sich automatisch auch die in der kurzen Zeit zurücklegbare Strecke s_NEU wie folgt:

v_Schritt = s_NEU / t "

s_NEU = v_Schritt * t_NEU

= 5 km/h * 10 min = 5 * 1 km / h * 10 * 1 min = 5 * 1000 m / 3600 s * 10 * 60 s

= 50 m / 36 s * 600 s = 833,3333333333333 m ≈ 833 m þ

Zum Vergleich:

S_VORHER = v_Schritt * t_VORHER

= 5 km/h * 12 min = 5 * 1 km / h * 12 * 1 min = 5 * 1000 m / 3600 s * 12 * 60 s

= 50 m / 36 s * 720 s = 1000 m þ

Wenn man zum Zurücklegen der Strecke S_VORHER = 1000 m nur noch t_NEU = 10 min zur Verfügung hat, dann bleibt einem nichts anderes übrig als entweder

a) die Schrittgeschwindigkeit v_Schritt zu erhöhen oder

b) die Schrittlänge sl zu vergrößern,

wobei sich dann zwangsläufig auch die Anzahl der Schritte ns verringert (siehe oben!).

Um die geänderte, neue Schrittlänge sl_NEU berechnen zu können, muss man die alte und neue Streckenlänge ins Verhältnis setzen, den Quotienten s_VORHER / s_NEU bilden und dem Quotienten sl_NEU / sl_VORHER wie folgt gleichsetzen:

sl_NEU / sl_VORHER = s_VORHER / s_NEU "

sl_NEU = ( s_VORHER / s_NEU ) * sl_VORHER

= ( 1000 m / 833 m ) * 0,5 m = 1,20048 * 0,5 m ≈ 1,2 * 0,5 m = 0,6 m

Schrittlänge sl und Anzahl der Schritte ns bedingen einander, wobei das Produkt Schrittlänge sl * Anzahl der Schritte ns gleich der Streckenlänge s entspricht:

s_Entfernung = sl_NEU * ns_NEU "

ns_NEU = s_Entfernung / sl_NEU

= 1000 m / 0,6 m = 1666,666666666667 Schritte ≈ 1667 Schritte

Probe:

s_Entfernung = sl_NEU * ns_NEU

= 0,6 m * 1667 (Schritte, dimensionslos!) = 1000,2 m ≈ 1 km þ

Von der Streckengeschwindigkeit zur Einzelschrittgeschwindigkeit

Fassen wir kurz zusammen: Die Entfernung zur nächsten Haltestelle von Bus oder Straßenbahn beträgt Streckenlänge s = 1000 m, wozu in der zur Verfügung stehenden Zeit t_VORHER = 12 min insgesamt

ns_VORHER = s_Entfernung / sl_VORHER

= 1000 m / 0,5 m = 2000 Schritte

bei einer Streckengeschwindigkeit v_Strecke = 5 km/h zurückgelegt werden müssen.

Demzufolge berechnet sich die Zeitdauer t_Einzelchritt eines einzelnen Schrittes der Schrittlänge s_{Einzelschritt} = 0,5 m wie folgt:

t_Einzelchritt = t_VORHER / ns_VORHER

= 12 min / 2000 = 12 * 1 min / 2000 = 12 * 60 s / 2000 = 720 s / 2000 = 0,36 s

v_Einzelchritt = sl_VORHER / t_{Einzelschritt}

= 0,5 m / 0,36 s = 50 / 36 m/s = 1,388888888888889 m/s ≈ 1,4 m/s

Probe durch Umrechnen in km/h:

= 1,4 * 1 m / ( 1 s ) = 1,4 * 0,001 km / ( 1 / 3600 h )

= 1,4 * 0,001 * 3600 km/h = 1,4 * 1/1000 * 3600 km/h = 1,4 * 3,6 km/h = 5,04 km/h ≈ 5 km/h

v_Strecke = s_Entfernung / t_Strecke

= 1000 m / ( 12 min ) = 1000 * 1 m / ( 12 * 1 min ) = 1000 * 0,001 km / ( 12 * 1/60 h )

= 1 * 60 / 12 km/h = 5 km/h þ

Demzufolge berechnet sich die Zeitdauer t_Einzelchritt eines einzelnen Schrittes der Schrittlänge sl_NEU = 0,6 m wie folgt:

t_Einzelchritt = t_NEU / ns_NEU

= 10 min / 1667 = 10 * 1 min / 1667 = 10 * 60 s / 1667 = 600 s / 1667

= 0,3599280143971206 s ≈ 0,359928 s ≈ 0,36 s

v_Einzelchritt = sl_NEU / t_NEU

= 0,6 m / 0,36 s = 60 / 36 m/s = 1,666666666666667 m/s ≈ 1,7 m/s

Probe durch Umrechnen in km/h:

= 1,7 * 1 m / ( 1 s ) = 1,7 * 0,001 km / ( 1 / 3600 h )

= 1,7 * 0,001 * 3600 km/h = 1,7 * 1/1000 * 3600 km/h = 1,7 * 3,6 km/h = 6,12 km/h ≈ 6 km/h

v_Strecke = s_Entfernung / t_Strecke

= 1000 m / ( 10 min ) = 1000 * 1 m / ( 10 * 1 min ) = 1000 * 0,001 km / ( 10 * 1/60 h )

= 1 * 60 / 10 km/h = 6 km/h þ

Es ist natürlich trivial, d.h. naheliegend, für jedermann leicht ersichtlich oder erfassbar, dass die höhere Geschwindigkeit von v_Strecke = 6 km/h zur Bewältigung der Strecke s_Entfernung = 1000 m in der kürzeren Zeit t_Strecke = 10 min identisch ist mit der Einzelschritt-Geschwindigkeit v_Einzelchritt = 1, 7 m/s, da der Benutzer des ÖPNVs während des Hinlaufens zur Haltestelle der Straßenbahn oder des Omnibusses weder seine Schrittlänge von 0,6 m noch seine Schrittgeschwindigkeit von 6 km/h ändert! Wäre dem wider Erwarten nicht so, käme der Benutzer des ÖPNVs entweder zu früh oder zu spät an der Haltestelle an!

Übrigens:

Der Umrechnungsfaktor von [ km/h ] " [ m/s ] beträgt allgemein:

[ km/h ] = 1 / 3,6 * [ m/s ]

und von [ m/s ] " [ km/h ]:

[ m/s ] = 3,6 * [ km/h ]

So, nun haben wir eine ganze Menge zur Kinematik, d.h. der Bewegungslehre aus dem Bereich der Mechanik gelernt, sodass wir uns wieder dem Proxi-Roboter und dem Projekt „proxi-roboter, p-17“ zuwenden können. Dabei geht es nachfolgend darum, dass wir die Zeit t bei der schrittweisen Vor- oder Rückwärtsbewegung des Roboters mit erfassen und auswerten, um die Schrittweite und Schrittanzahl pro Umdrehung überwachen und einhalten zu können.

Doch zunächst müssen wir herausfinden, ob und wie sich Zeit überhaupt messen lässt. In der Schule haben wir gelernt, dass das Jahr 365 Tage hat, ein Tag 24 Stunden lang ist und sich eine Stunde aus 60 Minuten zusammensetzt. Aus dem Sportunterricht bzw. der Leichtathletik wissen wir, dass ein 100 m Lauf durchschnittlich in 12 bis 14 Sekunden, vielleicht auch 17 Sekunden absolviert werden kann, je nach Kondition, Körpergröße und Körpergewicht. Dabei werden mit herkömmlichen Stoppuhren nicht nur Minuten gemessen, sondern auch 1/10 Sekunden. Aber es gibt natürlich auch noch kleinere Maßeinheiten wie z.B. eine hundertstel (= 1/100) oder eine tausendstel (= 1/1000) Sekunde mit 1/1000 s = 0,001 s = 1 ms („Millisekunde“):

Beispiel einer Umrechnung:

t = 5000 ms = 5000 * 1 ms = 5000 * 1 ( „Milli“ * s) = 5000 * 1 ( 1/1000 * 1 s)

= ( 5000 * 1 * 1 / 1000 ) * 1 s = 5000 / 1000 s = 5 s

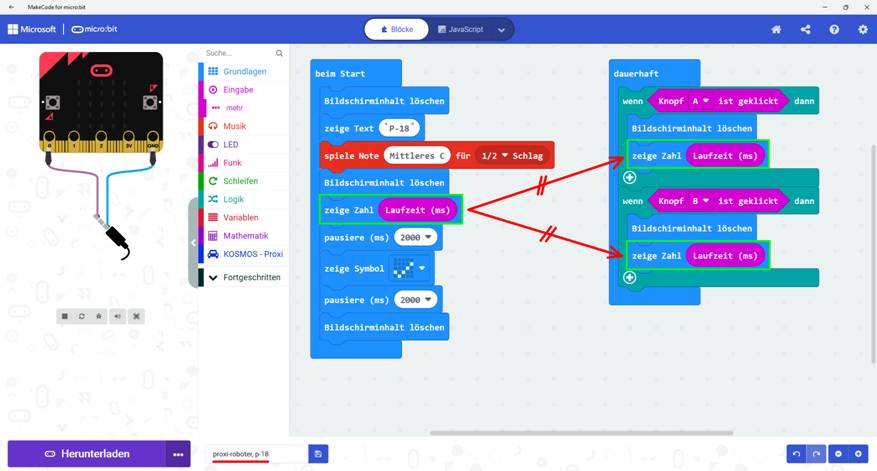
Mit dem Parameter <Laufzeit (ms)> lässt sich also die Laufzeit des „micro:bit“-Rechners auslesen!

Dabei könnte man meinen, dass es sich dabei um die Laufzeit seit dem Einschalten des Rechners handelt. Dem ist aber nicht so, weil es sich bei dem „micro:bit“-Rechner und dem Parameter <Laufzeit (ms)> eben nicht um einen Betriebsstundenzähler, eine Uhr oder eine Stoppuhr handelt (siehe Projekt „proxi-roboter, p-18“):

(Zum Vergrößern bitte auf das Bild klicken!)

Wenn man das obenstehende Projekt „proxi-roboter, p-18“ startet, dann bekommt man direkt nach dem Programmstart den Zeitstempel = 4962 ms angezeigt. Und zwar beim Betrieb mit der 5 V USB-Stromversorgung über das „Micro USB 2.0“-Kabel vom Windows-PCs.

Wenn man das „Micro USB 2.0“-Kabel vom Windows-PC abzieht und die Stromversorgung über das 6 Volt Batteriepack des Proxi-Roboters vornimmt, dann bekommt man direkt nach dem Programmstart den Zeitstempel = 5917 ms angezeigt.

Wenn man den rückwärtigen „Reset“-Taster drückt, um einen sogenannten Warmstart des Programms auszulösen, dann bekommt man nach dem Programmstart von 20 Sekunden beim Betätigen eines der Taster „Knopf A“ oder „Knopf B“ den Zeitstempel = 20174 ms angezeigt, was der seit dem Programmstart verstrichenen Zeit von 20,174 s = 20 Sekunden und 174 Tausendstel = 20 Sekunden und 174 Millisekunden entsprechen dürfte.

Wir ändern das obenstehende Programm dahingehend ab, indem wir uns die nach zwei Minuten verstrichene Zeit mit der Umrechnung = 2 min = 2 * 1 min = 2 * 60 s = 2 * 60 * 1 s = 120 * 1000 ms = 120 000 ms anzeigen lassen (siehe Projekt „proxi-roboter, p-19“):

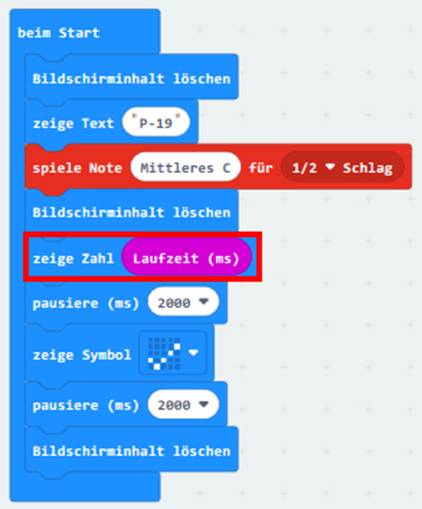
(Zum Vergrößern bitte auf das Bild klicken!)

Schauen wir uns das obenstehende Projekt „proxi-roboter, p-19“ näher an und beginnen wir beim Programmblock „beim Start“:

(Zum Vergrößern bitte auf das Bild klicken!)

Wie wir wissen, wird der obenstehende Programmblock „beim Start“ nach dem Herunterladen und Starten des Programms auf dem „micro:bit“-Rechner als Erstes ausgeführt.

Dabei dient das Statement <zeige_Zahl [ Laufzeit (ms) ]> dazu, die aktuelle Laufzeit mit der Maßeinheit [ ms ] auszulesen und als Laufschrift im LED-Display anzuzeigen. Wie bereits weiter oben erwähnt, wird dabei der Zeitstempel = 4962 ms angezeigt.

Lässt man das Programm in der „MakeCode“-Entwicklungsumgebung von Microsoft laufen, dann bekommt man die Zeitstempel 4601, 4605 oder 4622 angezeigt, was darauf hindeutet, dass es sich beim Parameter [Laufzeit (ms)] zunächst um Zufallswerte handelt. Insbesondere deshalb, weil es sich bei dem Parameter um eine interne Variable des „micro:bit“-Rechners handeln dürfte, die bisher noch nicht initialisiert wurde.

Praktisch bedeutet dies, dass die interne Variable < Laufzeit (ms)> beim ersten Aufruf mit einem Zufallswert initialisiert wird, den man wegwerfen sollte, weil erst der zweite Aufruf zu einem richtigen, tatsächlich verwertbaren Ergebnis führt!

Demzufolge ist man gut beraten, den ersten Aufruf der internen Variablen < Laufzeit (ms)> ins Hauptprogramm <beim Start> aufzunehmen, ohne diesen jedoch auszuwerten oder zu berücksichtigen!

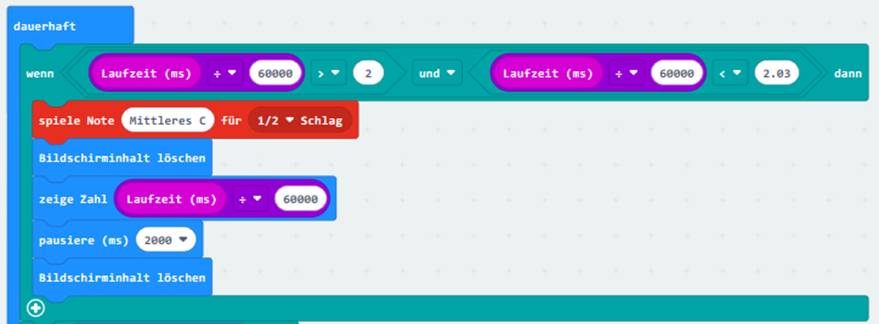
Dies ist dann auch der Grund dafür, dass es im gesamten Projekt „proxi-roboter, p-19“ zunächst keine einzige frei definierte Variable gibt, die gegebenenfalls initialisiert werden müsste.

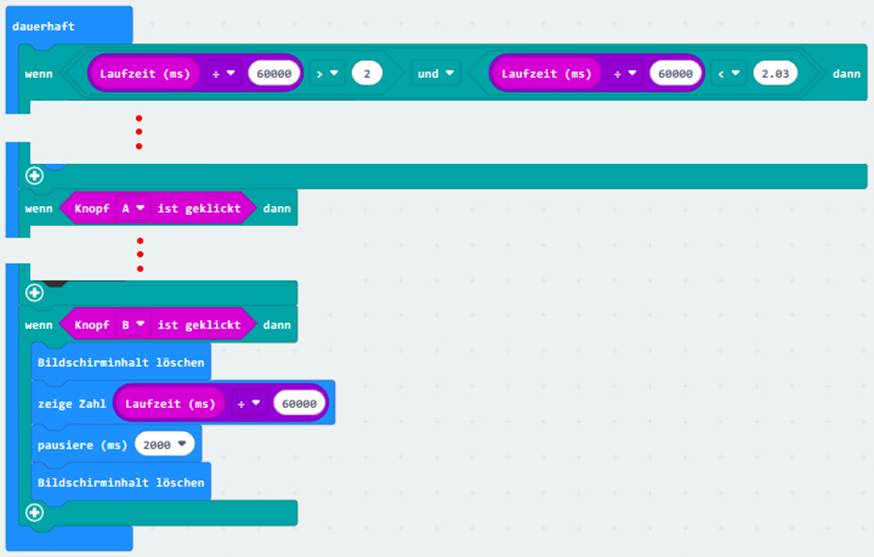
Im Programmblock <dauerhaft> wird als Erstes zwei Minuten lang gewartet bis die Laufzeit > 2 Minuten und < 2,03 Minuten erreicht ist:

2 min = 2 * 1 min = 2 * 60 sec = 2 * 60 * 1 sec = 2 * 60 * 1 000 ms (" Millisekunden) = 120 * 1 000 ms = 120 000 ms

120 000 ms / 60 000 ms = 2 Minuten

2,03 min = 2,03 * 1 min = 2,03 * 60 sec = 2,03 * 60 * 1 sec = 2,03 * 60 * 1 000 ms = 121,8 * 1 000 ms = 121 800 ms

121 800 ms / 60 000 ms = 2,03 Minuten

Die Zeitspanne von 2 Minuten wurde extra so gewählt, weil man auf diese Weise mit der Stoppuhr auf dem Smartphone sehr gut und einfach überprüfen kann, ob die Zeitfunktion auch zuverlässig funktioniert. Und in der Tat verhält es sich so, dass die Timerfunktion < Laufzeit (ms)> erstaunlich präzise funktioniert!

Dazu muss man wissen, dass jede CPU, engl. „Central Processing Unit“, d.h. Zentraleinheit, über einen internen quarzstabilisierten Taktgenerator verfügt, der den Mikroprozessor, auch den des „micro:bit“-Rechners, mittels des sogenannten Prozessortaktes präzise steuert.

Dabei gilt es zu beachten, dass dem Mikroprozessor mit jedem Programmbefehl, jedem Statement eine bestimmte Taktzahl und Taktfolge zugewiesen wird, innerhalb denen ein Befehl schritt- und taktweise abgearbeitet wird. Schließlich geht es beim Mikroprozessor auch darum, dass z.B. der Datenaustausch zwischen dem Prozessor, der ALU, engl. „arithmetic logic unit“, d.h. Rechenwerk, dem Arbeitsspeicher und der Peripherie wie z.B. Festplatte, USB-Speicherstick usw. synchronisiert wird, damit keine Daten verlorengehen. Demzufolge läuft der Prozessortakt, währenddessen der Prozessor mehrere Befehle abarbeitet, ununterbrochen und hochpräzise weiter! Das gilt auch für den Mikroprozessor „ARM Cortex M0“ des „micro:bit“-Rechners.

(Zum Vergrößern bitte auf das Bild klicken!)

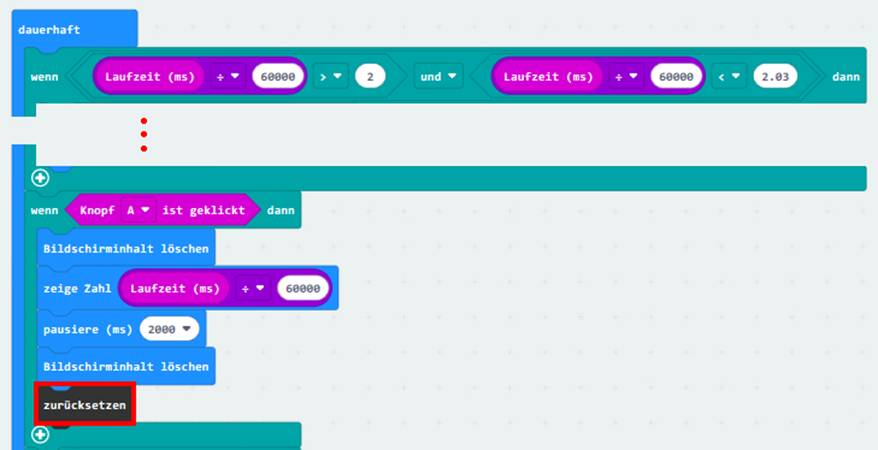
Mit dem Programmblock <wenn Knopf A ist geklickt dann> lässt sich jederzeit der aktuelle Status des Hochzählens auf Knopfdruck „A“ abrufen und dezimal mit zwei Nachkommastellen in der Maßeinheit [ min ] (" Minuten) anzeigen:

1 min = 1 * 1 min = 1 * 60 s = 60 * 1 s = 60 * 1/1 000 ms = 60 000 ms

Am Ende des Programmblocks wird dann der „micro:bit“-Rechner auf Neudeutsch „resettet“, d.h. zurückgesetzt, sodass der Rechner einen sogenannten Warmstart (= Neustart im eingeschalteten Zustand) durchführt und das Projekt

„proxi-roboter, p-19“ neu startet:

(Zum Vergrößern bitte auf das Bild klicken!)

Mit dem Programmblock <wenn Knopf B ist geklickt dann> lässt sich zwar die zweiminütige Laufzeit mit den 120 000 ms nicht verkürzen, aber der aktuelle Status des Hochzählens auf Knopfdruck „B“ abrufen und dezimal mit zwei Nachkommastellen in der Maßeinheit [ min ] (" Minuten) anzeigen:

(Zum Vergrößern bitte auf das Bild klicken!)

Mit dem nachfolgenden Projekt „proxi-roboter-p-20“ entwickeln wir das bisherige Programm weiter, indem wir nun Variablen verwenden.

Dabei wird die Variable <dummy_Zeit> mit dem Statement <setze [dummy_Zeit] auf Laufzeit (ms)> dazu verwendet, um den ersten Wert des Zeitstempels <Laufzeit (ms)>, der ja wegen der erstmaligen und einmaligen Initialisierung in Wirklichkeit ein Zufallswert ist, einzulesen und zu verwerfen, indem wir diesen nicht weiter benutzen!

>> Technik:

· einen Platzhalter oder eine vorerst nicht benötigte Variable beim Programmieren

· in der Computertechnik eine Datei, die angelegt wird,

um die Funktionsweise eines Programms oder Versuchsaufbaus zu testen

· in der Regression (Statistik) eine Dummy-Variable

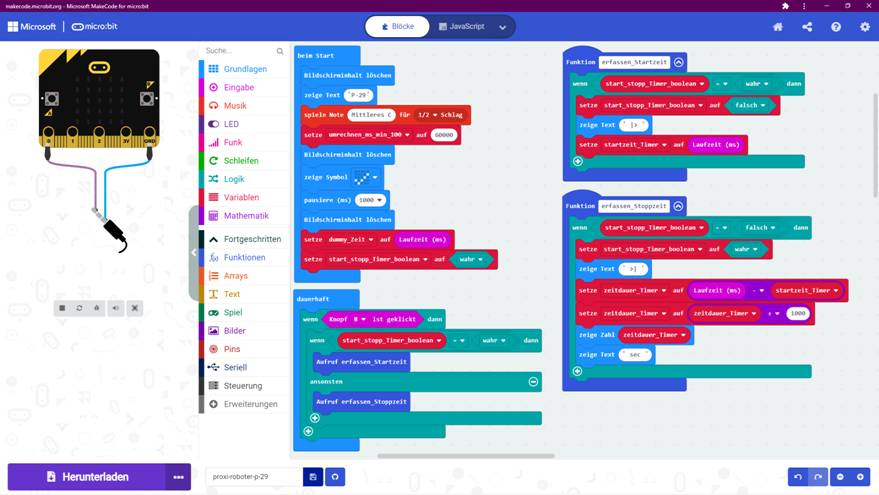
· eine unter Elektrotechnikern verbreitete engl. Bezeichnung für Ersatzlast << (Quelle: Wikipedia)

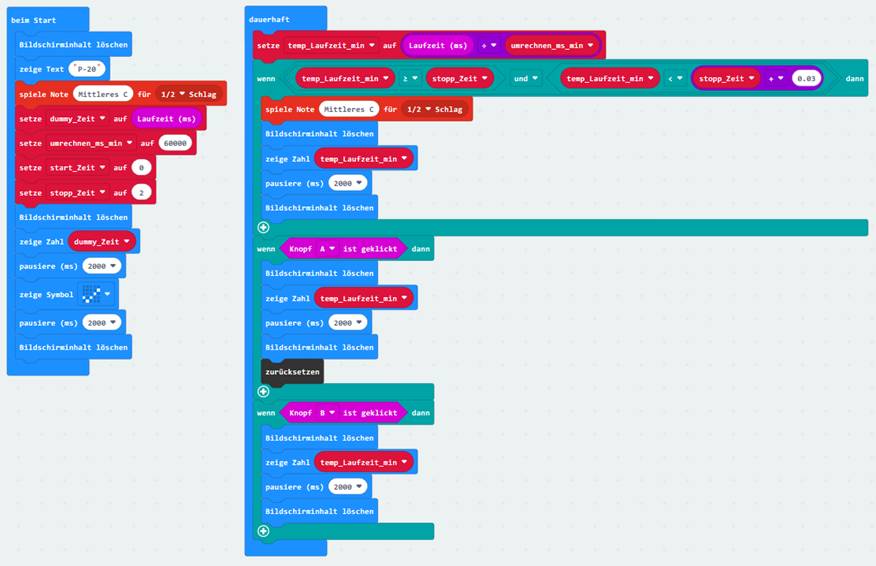
Zwecks besserer Lesbarkeit des Programms und zu Zwecken des besseren Verständnisses rechnen wir ab sofort nur noch in Minuten [ min ] = [ ’ ] und nicht mehr in Millisekunden [ ms ] = [ 0,001 s ] = [ 1/1000 s ] = [ 1/1000 ’’ ] (= tausendstel Sekunden).

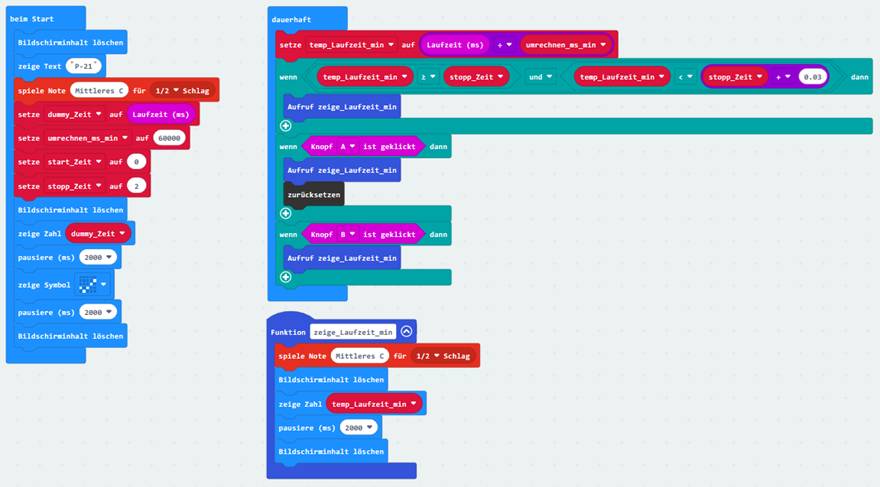
Demzufolge wird der Zeitstempel <Laufzeit (ms)> gleich zu Beginn des Programmblocks <dauerhaft> eingelesen und mittels der mit dem Wert 60 000 initialisierten Variablen <umrechnen_ms_min> in Minuten umgerechnet und in der Variablen <temp_Laufzeit_min> zur weiteren Verwendung gespeichert:

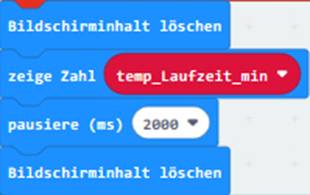
(Zum Vergrößern bitte auf das Bild klicken!)

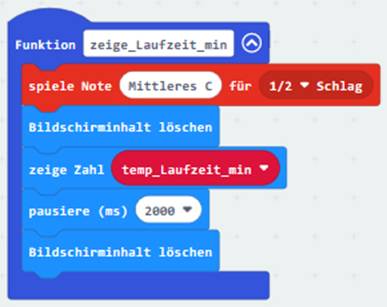
Selbstverständlich lässt sich auch das obenstehende Programm weiter verbessern, indem wiederkehrende und sich wiederholende Programmteile

(Zum Vergrößern bitte auf das Bild klicken!)

in die Funktion <zeige_Laufzeit_min> wie folgt auslagern:

(Zum Vergrößern bitte auf das Bild klicken!)

Schauen wir uns noch den vollständigen Microsoft „MakeCode“ des Projektes „proxi-roboter-p-21“ an:

(Zum Vergrößern bitte auf das Bild klicken!)

Vom guten alten VW Käfer der Volkswagen AG wurden in 65 Jahren von 1938 bis 2003 insgesamt 21,5 Millionen Fahrzeuge gebaut. Dabei lautete einer der bekanntesten Werbesprüche „Und läuft und läuft und läuft …“. Obwohl doch ein Auto fährt und nicht läuft.

Wenn also das Auto fährt und nicht läuft, weil es keine Beine und Füße hat, weshalb sagt dann der Werbespruch, dass der VW Käfer läuft und läuft und läuft? Wahrscheinlich deswegen, weil die Automobilverkäufer und Marketing-Fuzzis (= engl. „Fuzzy“, umgangssprachlich „beliebige männliche Person, die nicht ernst genommen wird“) keine Physiker oder Techniker sind, sondern Kaufleute. Denn wenn etwas gut läuft, dann sprechen die Kaufleute von einem „Selbstläufer“. Damit ist gemeint, dass sich eine Sache wie der VW Käfer wie von allein verkauft, sich der Verkäufer beim Verkaufsgespräch nicht anstrengen muss, keine Überzeugungsarbeit leisten oder den Kunden überreden muss.

Aber obwohl der VW Käfer fährt und nicht läuft, läuft trotzdem etwas! Und zwar im Hintergrund! Ab Anfang 1970 gab es nämlich ein neues Modell, den VW Käfer 1302 mit stärkerem Motor und höherem Gewicht. Und seitdem läuft er, der Sprit, d.h. der Kraftstoff im Tank und der Mehrverbrauch, der sich bei der Tankuhr direkt an der Bewegung des Füllstandsanzeigers ablesen lies. Dabei belief sich der Spritverbrauch bei sportlicher Fahrweise auf teilweise bis zu 14 Litern pro 100 km! Dabei bewegte sich der Füllstandsanzeiger so flott in Richtung der 5 Liter Reserveanzeige, dass man gar nicht auf die Uhr schauen musste, um zu wissen was die Stunde geschlagen hat.

Wobei wir beim Stichwort „Zeit“ angelangt sind. Die läuft und läuft und läuft nämlich auch beim Proxi-Roboter. Aber eben still und leise, sodass man sie nicht ticken hört.

Wie bereits erwähnt, hängt das mit der Taktfrequenz des „ARM Cortex M4 32 Bit“-Prozessors des „micro:bit“-Rechners der Version 2.x zusammen. In dem Moment, wo man den Proxi-Roboter durch Einschalten der Stromzufuhr in Betrieb nimmt, läuft die Zeit mit der Taktfrequenz von f = 64 MHz (= „Megahertz“ = 10⁶ Hz = 1 000 000 Hz = 1 Million Schwingungen pro Sekunde).

T = 1 / f

= 1 / 64 MHz = 1 / ( 64 * 1 MHz ) = 1 / ( 64 * 1 * 10⁶ Hz ) = 1 / ( 64 * 1 * 10⁶ s^-1 ) = ( 10^-6 / 64 ) s

= ( 10^-6 / 64 ) s = ( 1 / 64 ) µs = 0,015625 µs ≈ 0,016 µs

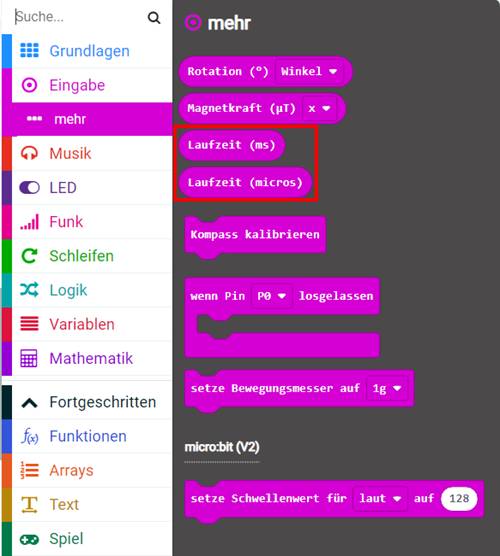
Und siehe da, gibt es bei der „MakeCode“-Programmierung tatsächlich auch eine Systemvariable <Laufzeit (micros)> mit der sich die Laufzeit in „Mikrosekunden“ [µs] abfragen lässt:

(Zum Vergrößern bitte auf das Bild klicken!)

Ob wir früher oder später auch mit den „Mikrosekunden“ [µs] und der Systemvariable <Laufzeit (micros)> arbeiten werden, wird sich aber noch zeigen.

Wie aber soll man mit der Laufzeit umgehen, wie lässt sich diese am besten handhaben? Dabei ist das mit der Laufzeit so ähnlich wie mit dem Geist, den man aus der Flasche gelassen hat und der sich nicht wieder einfangen lassen will (siehe Grimms Märchen). Wenn die Zeit erst einmal läuft, dann läuft sie und läuft und läuft.

Wie aber wird die Zeit gestartet und wie kann man sie sich jederzeit wieder anzeigen lassen?

Wie wir ja bereits wissen, leitet sich die Zeit aus dem Prozessortakt ab, sodass man diese nicht extra starten muss. In dem Moment, wo man den „micro:bit“-Rechner „unter Strom setzt“, d.h. einschaltet, startet sich mit dem Prozessortakt auch die Zeit, die wiederum im Hintergrund im Stillen vor sich hin werkelt.

Wenn man dann aber nach dem Programmstart <beim Start> oder im Programmblock <dauerhaft> mit der Zeit arbeiten will, dann geht das nur in Verbindung mit der Systemvariablen <Laufzeit (micros)>, die wiederum beim Erstgebrauch zuvor noch initialisiert werden muss:

(Zum Vergrößern bitte auf das Bild klicken!)

Dabei gilt es, wie bereits erwähnt, zu beachten, dass der erste Wert der Laufzeit weggeworfen werden muss und nicht verwendet werden darf! Ferner stellt sich die Frage, wie sich alle anderen, nachfolgenden Werte der Systemvariablen <Laufzeit (micros)> speichern lassen, da mit jedem Knopfdruck auf den Taster < Knopf A> ein neuer Laufzeitwert generiert wird, den es abzuspeichern gilt.

Die Möglichkeit, dass man für jeden neuen Laufzeitwert auch eine neue

· Variable <Laufzeit_1>, <Laufzeit_2>, …, <Laufzeit_n> oder

· Variable <Laufzeit₁>, <Laufzeit₂>, …, <Laufzeit_n> generiert, scheidet aus,

da sich diese programmiertechnisch nicht indexieren lassen!

Programmiertechnisch indexieren lässt sich hingegen die nachfolgende Syntax

· Variable <Laufzeit[0]>, Variable <Laufzeit[1]>, <Laufzeit[2]>, …, <Laufzeit[n]>

Dabei steht der Index [n] für eine beliebige Anzahl von n Einzelelementen, die sich in einem engl. „Array“, d.h. einer Liste oder Tabelle zusammenfassen lassen.

Mit dem nachfolgenden Statement wird das leere Array namens „list“ deklariert:

(Zum Vergrößern bitte auf das Bild klicken!)

Dabei verhält es sich so, dass man bei der Deklaration des Arrays <list> nicht angeben muss, aus wie vielen Elementen n das Array bestehen soll bzw. mit wie vielen Elementen n das Array später datenmäßig gefüllt werden soll!

Demzufolge ist die Größe des Arrays nicht statisch festgelegt, sodass dieses später dynamisch wachsen und nahezu beliebig groß werden kann!

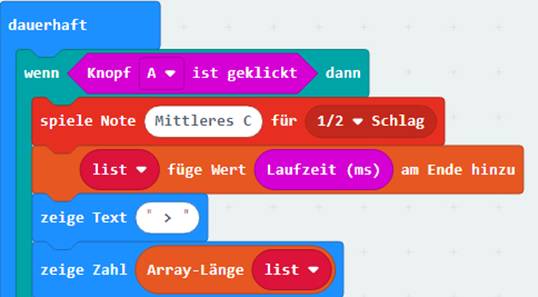
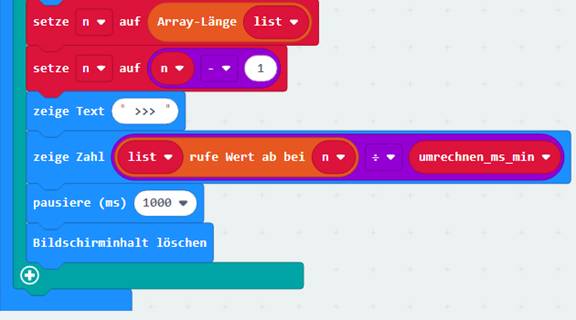
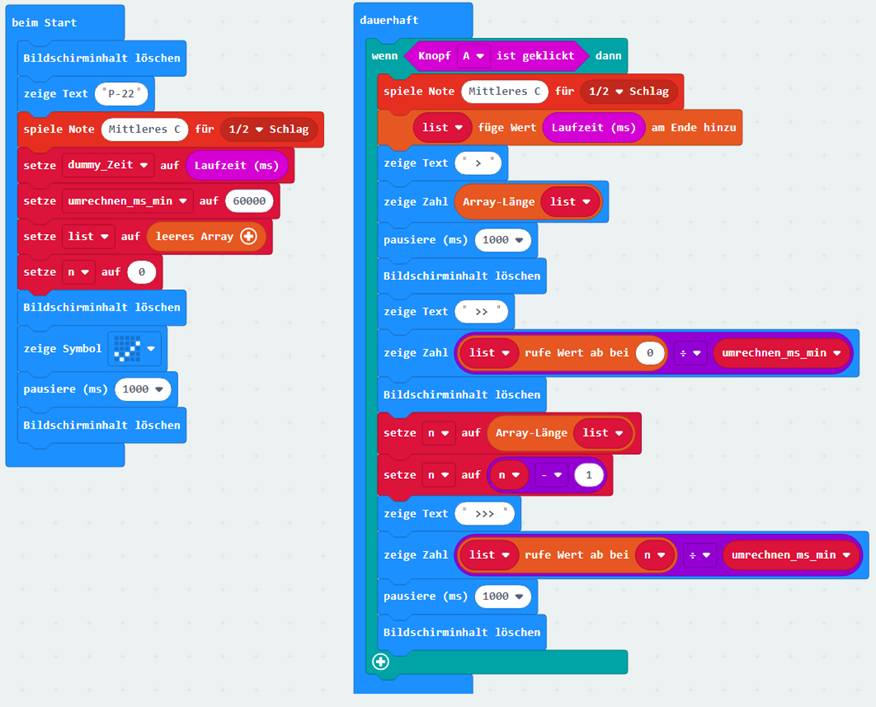
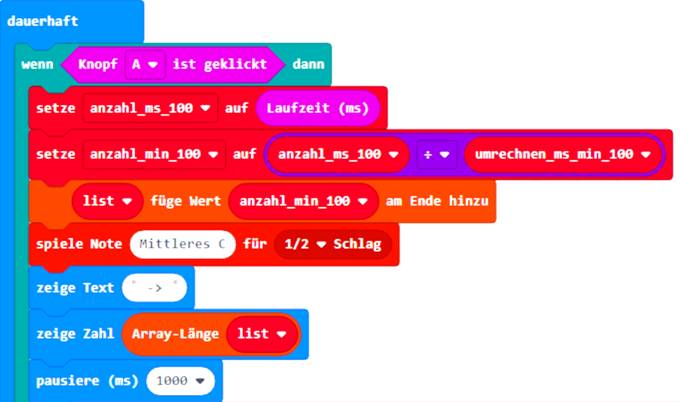
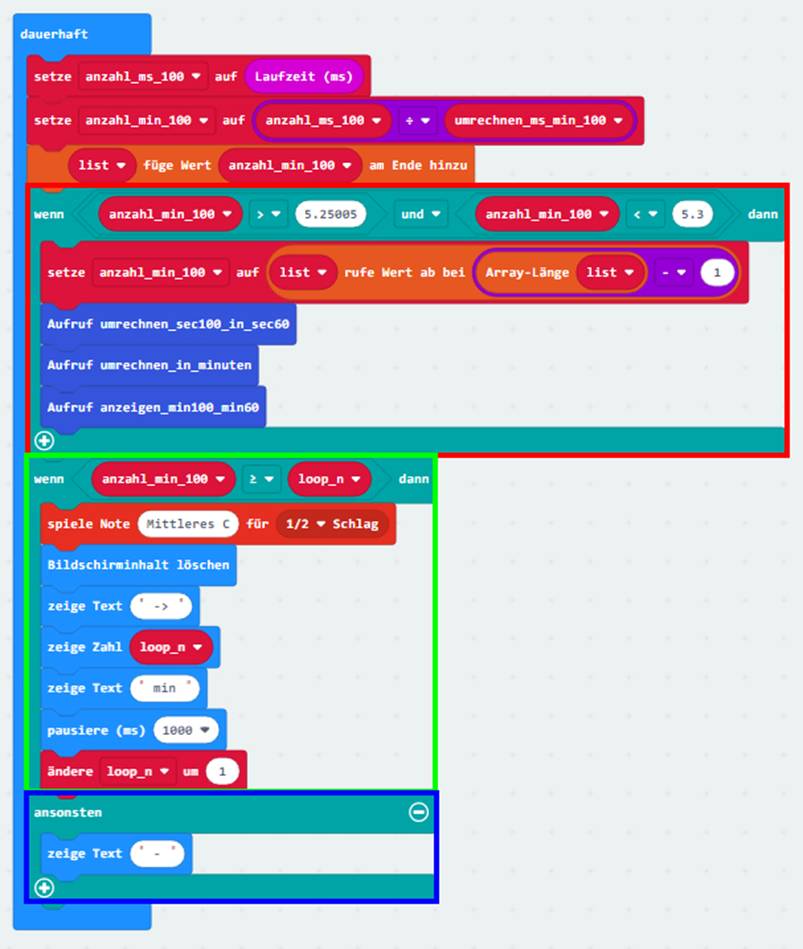
Wenn man nachfolgend zum ersten Mal den Taster <Knopf A> drückt, dann wird dem Array <list> nach dem Signalton <Mittleres C> der aktuelle Wert der Systemvariablen <Laufzeit (micros)> am Ende des Arrays hinzugefügt:

(Zum Vergrößern bitte auf das Bild klicken!)

Nach der Laufschriftanzeige „ > “ wird dann noch die Länge „1“ des Arrays <list> angezeigt. Damit ist die Anzahl n = 1 der im Arrays <list> gespeicherten Elemente gemeint!

Im vorliegenden Fall gibt es also zum jetzigen Zeitpunkt nur ein einziges Element des Arrays <list> mit der Array-Variablen list[0] = 0,35 min (als Beispielwert). Wichtig dabei ist, dass das erste Element den Index [0] trägt!

Der Grund dafür ist der, dass sowohl in der Mathematik als auch in der Informatik die Zahl 0 (nicht Ziffer „0“) eine vollwertige, quasi emanzipierte Zahl ist, mit der sich auch rechnen lässt und mit der auch gerechnet wird!

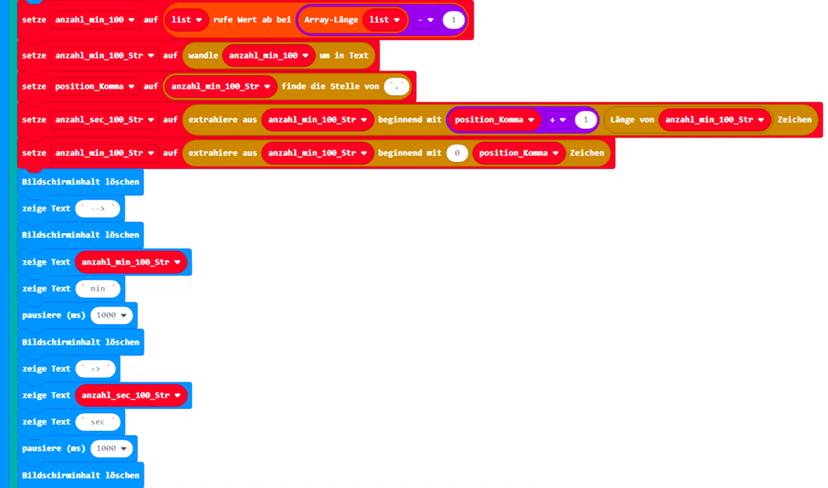
Mittels des nachfolgenden Programmblocks wird nach der Laufschriftanzeige „ >> “ der Inhalt des ersten Array-Elments list[0] = 0,35 min angezeigt und dabei sofort in Minuten [min] umgerechnet:

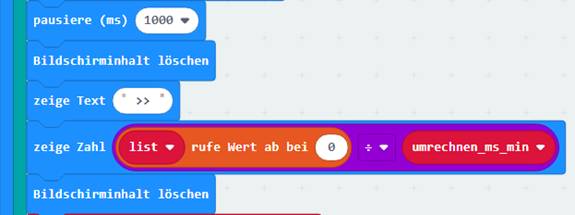
(Zum Vergrößern bitte auf das Bild klicken!)

Beim letzten Programmblock wird nach der Laufschriftanzeige „ >>> “ der Inhalt des letzten Array-Elments list[0] = 0,35 min angezeigt und dabei sofort in Minuten [min] umgerechnet:

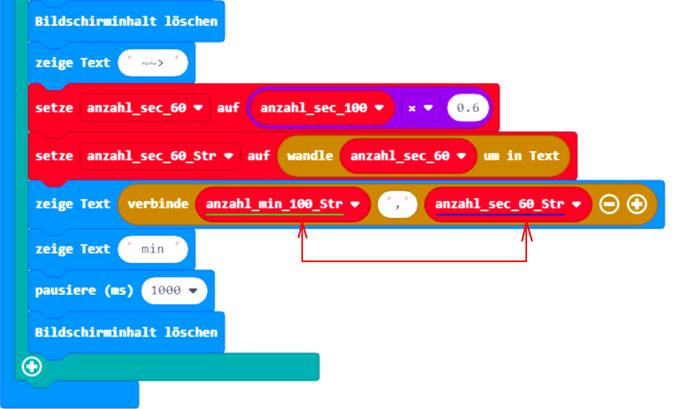
(Zum Vergrößern bitte auf das Bild klicken!)

Interessant und beachtenswert ist dabei, dass mit dem Statement

(Zum Vergrößern bitte auf das Bild klicken!)

zunächst die Array-Größe des Arrays <list> mit der Array-Länge auf die Zählvariable n gesetzt wird. Dabei ist n = 1, weil das Arrays <list> zum derzeitigen Zeitpunkt nur ein einziges Array-Element enthält: list[0] = 0,35 min.

Und da das erste Array-Element list[0] = 0,35 min mit dem Index n = 0 beginnt, muss man von der ermittelten Array-Länge n = 1 noch den Wert = 1 subtrahieren,

sodass der erste Wert list[0] = 0,35 min des Arrays <list> gleich dem letzten Wert list[0] = 0,35 min des Arrays ist!

Demzufolge muss man immer daran denken, dass der erste Wert eines Arrays stets beim Index = 0 beginnt (siehe Projekt „proxi-roboter-p-22“):

(Zum Vergrößern bitte auf das Bild klicken!)

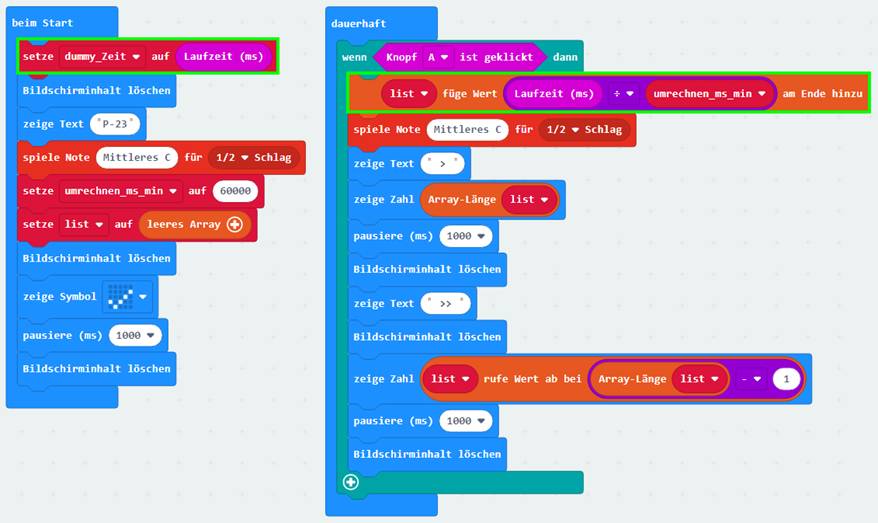
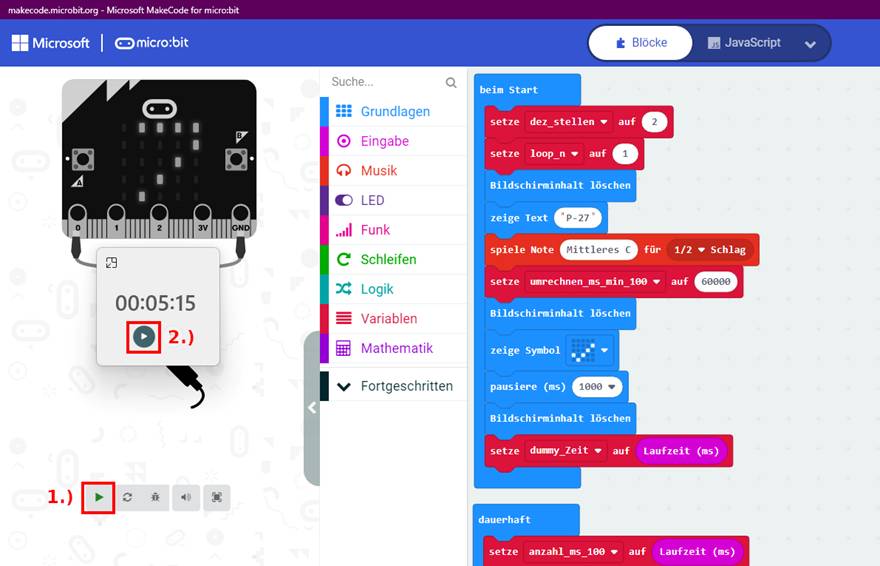
Im Zusammenhang mit dem obenstehenden Projekt „proxi-roboter-p-22“ stellt sich noch die Frage, ab wann die „Laufzeit (ms)“-Millisekunden-Uhr zu laufen beginnt, d.h. gestartet wird:

1. sofort beim Starten des Programms mit dem Programmblock ,

2. beim Ausführen des Statements ,

3. beim erstmaligen Drücken des Tasters oder

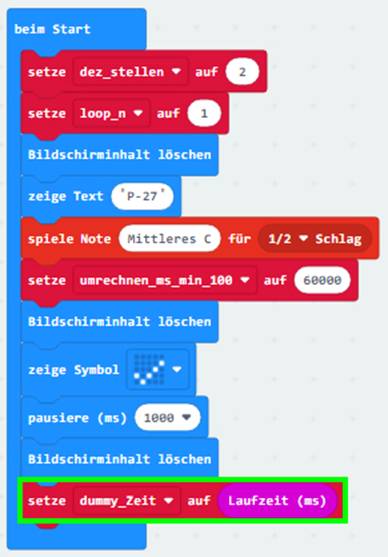
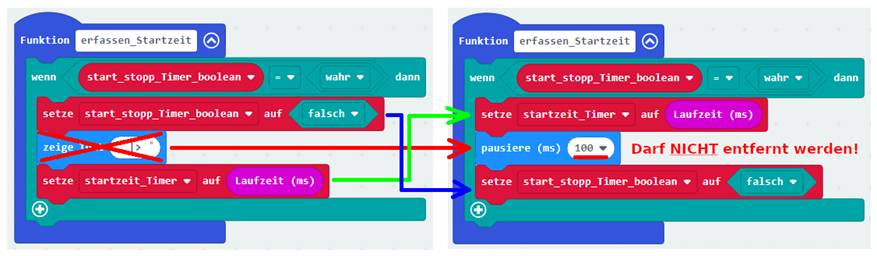
4. beim Ausführen des Statements ?

Antwort: >> Beim Ausführen des Statements <setze dummy_Zeit auf [ Laufzeit (ms) ]>

Begründung: Wie bereits weiter oben erklärt, wird die „Laufzeit (ms)“-Millisekunden-Uhr in dem Moment gestartet, wo man sich die interne Systemvariable <Laufzeit (ms)> in der Laufschrift des LED-Displays anzeigen lässt oder, wie im vorliegenden Fall, diese der Variablen <dummy_Zeit> mittels Deklaration zuweist. Dabei spielt es keine Rolle, ob der erste Zeitwert einen gültigen, d.h. zutreffenden Zeitstempel enthält oder nicht. <<

Wenn du die Antwort nebst Begründung sehen willst, dann musst du nur im Browser die linke Maustaste gedrückt halten und mit dem Mauszeiger über die Kennzeichnung im Bereich >> ___ << fahren und diesen entsprechend markieren!

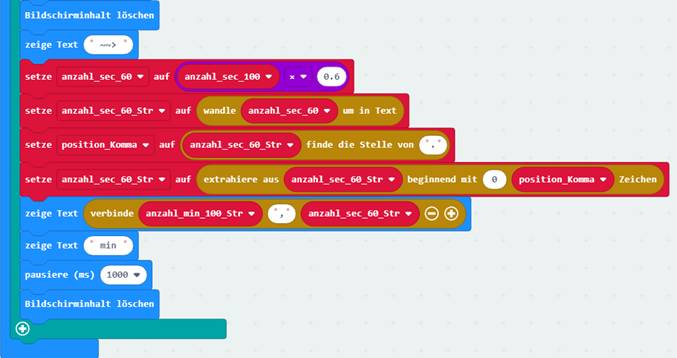
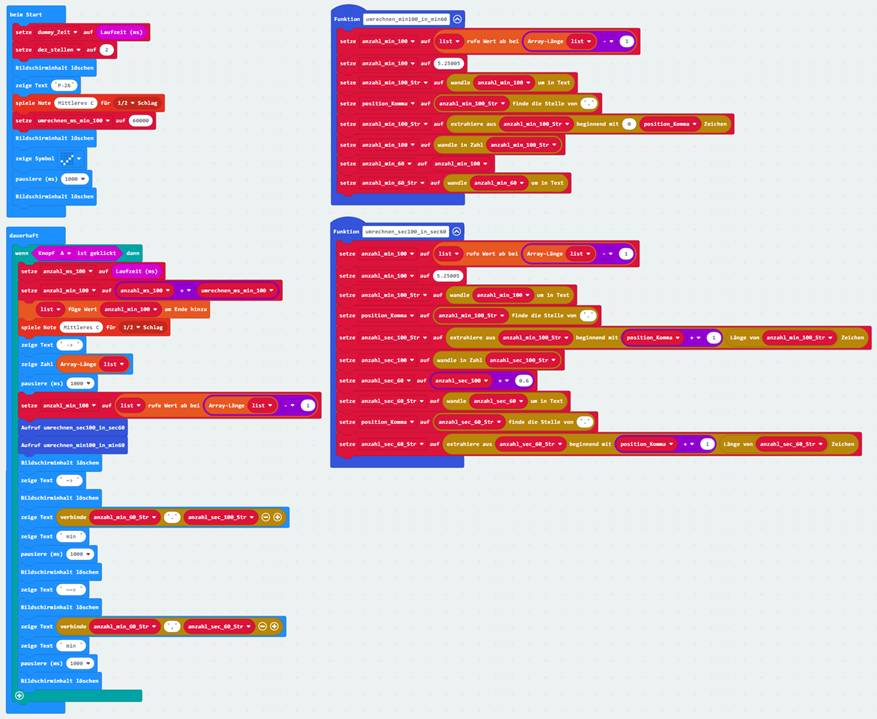
Der Trick dabei ist nämlich der, dass die gelbe Textfarbe die gleiche ist wie für die Hintergrundfarbe der Schrift!

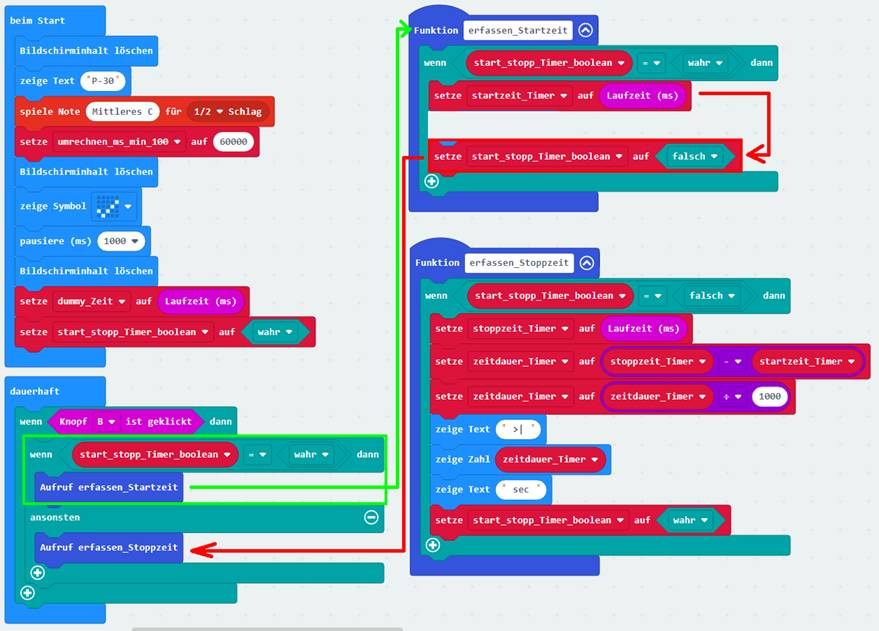
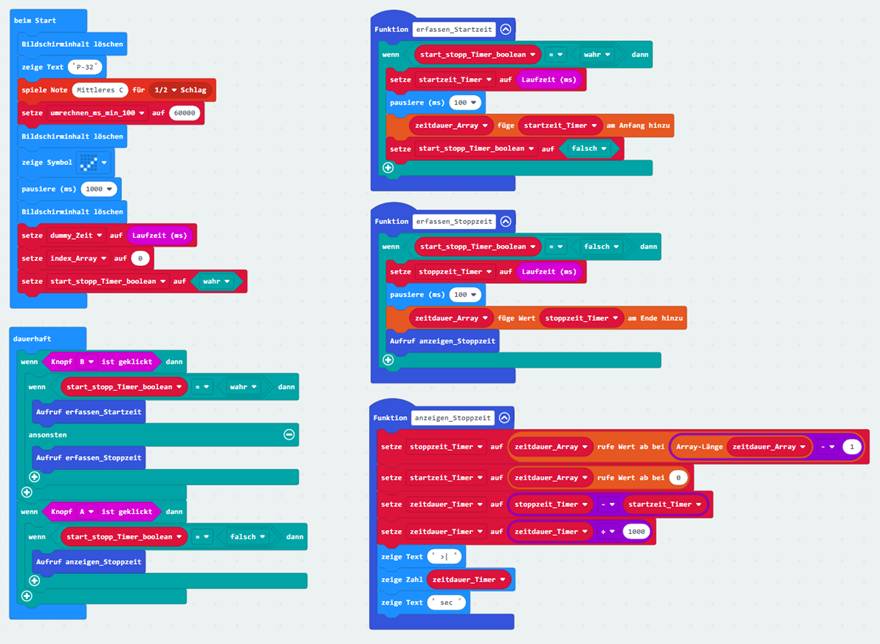
Wir entwickeln das Programm weiter, sodass es sich als Stoppuhr verwenden lässt. Dabei achten wir darauf, dass die zeitkritischen Statements (siehe grüne Kästen) gleich zu Beginn des Quellkodes im Projekt „proxi-roboter-p-23“ stehen:

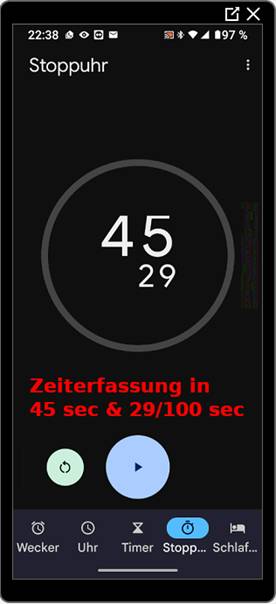
(Zum Vergrößern bitte auf das Bild klicken!)

Wenn man mit der Stoppuhr auf dem Smartphone die gemessene bzw. gestoppte Zeit mit der des obenstehenden Programms vergleichen will, dann muss man die Stoppuhr des Smartphones zeitgleich mit dem Programmstart des obenstehenden Programms starten!

Beim Vergleich der auf dem Smartphone angezeigten Stoppzeit fällt auf, dass diese

· erst in 1/100 Sekunden,

· dann in Sekunden und 1/100 Sekunden,

(Zum Vergrößern bitte auf das Bild klicken!)

· anschließend in Minuten:Sekunden und 1/100 Sekunden und

· später auch in Stunden:Minuten:Sekunden angezeigt wird.

Im Programm des Projekts „proxi-roboter-p-23“ wird aber die Stoppzeit wegen des Umrechnungsfaktors von Millisekunden auf Minuten = 1000 ms * 60 s = 60 000 min

nur in Minuten gefolgt von einem Dezimalpunkt plus zwei Dezimalstellen wie z.B. 2.25 min angezeigt! Dabei stehen die zwei Dezimalstellen „.25“, aber eben nicht für 25/100 Sekunden, sondern für 25/100 Minuten(!), da wir ja die gemessenen Millisekunden [ms] im obenstehenden Programm in Minuten [min] nebst zweier Dezimalstellen wie folgt umgerechnet haben:

2,25 min = 2,25 * 1 min = 2,25 * 60 sec = 135 sec = 135 * 1 sec = 135 * 1000 ms = 135 000 ms

135 000 ms = 135 000 * 1 ms = 135 000 * 1/1000 s = 135 000 * 0,001 s = 135 s = 135 * 1 s = 135 * 1/60 min = 2,25 min

Demzufolge muss man den im Programm angezeigten Wert von 2,25 min noch wie folgt in „echte“ Sekunden umrechnen:

2 Min. + 25/100 Minuten. = 2,25 Min. = 2,25 * 1 Min. = 2,25 * 60 Sek. = 2 Min. + 15/60 Minuten = 2 Min. + 15 Sekunden

0,25 Minuten = 25/100 Minuten(!) = 1/4 Min. = 1/4 * 1 Min. = 1/4 * 60 Sek. = 15 Sekunden(!) = 15/60 Minuten(!)

" 2,25 = 2 * 60 sec + 0,25/100 * 60 sec = 120 sec + 0,25/100 * 60 sec = 120 sec * 15 sec = 2 min + 15 sec

Aus der Umrechnung

0,25 Minuten = 25/100 Minuten(!) = 1/4 Min. = 1/4 * 1 Min. = 1/4 * 60 Sek. = 15 Sekunden(!) = 15/60 Minuten(!)

lässt sich der Umrechnungsfaktor k (= „k“ wie Koeffizient) wie folgt berechnen:

0,25 min₁₀₀ * k = 0,15 min₆₀ " mit k = 0,6

k = 0,15 min / ( 0,25 min ) = 15 / 25 = 3 / 5 = 3 * 10 / ( 5 / 10 ) = 30 / 5 / 10 = 6 / 10 = 0,6

Mit dem Statement

lassen sich z.B. die 0,25 min₁₀₀ * k = 0,25 min₁₀₀ * 0,6 = 0,15 min₆₀ problemlos umrechnen. Dabei gilt es zu beachten, dass wir wegen des Koeffizienten k = 0,6 dezimal mit zwei Nachkommastellen rechnen. Und zwar inklusive der internen, kaufmännischen Rundung! Durch den Koeffizienten k = 0,6 erzwingt man sozusagen das dezimale Rechnen mit zwei Nachkommastellen!

Da bei der Umrechnung mittels des Koeffizienten k = 0,6 sozusagen die einhundertstel Minuten in sechzigstel Minuten umgerechnet werden, könnte man auch auf die Idee kommen und nachfolgendes Statement

mit der Kettenrechnung <anzahl_sec_100 / 100 * 60> programmieren, weil dieses den Zusammenhang zwischen Hundertstel und Sechzigstel besser veranschaulicht als die nackte Dezimalzahl 0,6. Leider funktioniert das Statement aber wider Erwarten nicht, weil der „MakeCode“-Interpreter und Kompiler offensichtlich aufgrund eines Programmierfehlers die Kettenrechnung nicht beherrscht!

Das Projekt „proxi-roboter-p-24“ basiert auf dem Vorgänger-Projekt „proxi-roboter-p-23“, sodass der Programmblock <beim Start> beider Programme identisch ist.

Der Programmblock <dauerhaft> hingegen wurde erweitert und zwar dahingehend, dass sich mit diesem jetzt zwei verschiedene Arten von Stoppzeiten anzeigen lassen:

1. Anzeige der gestoppten Zeit in Minuten und hundertstel Minuten,

wie z.B. 2,25 min₁₀₀ = 2 Minuten und 25/100 Minuten = 2 Minuten und 25 Sekunden₁₀₀

2. Anzeige der gestoppten Zeit in Minuten und sechzigstel Minuten,

wie z.B. 2,15 min₆₀ = 2 Minuten und 15/60 Minuten = 2 Minuten und 15 Sekunden₆₀

Dabei entspricht die Anzeige der gestoppten Zeit in Minuten und sechzigstel Minuten der unseres Alltags, d.h. unserer Armbanduhr, Stoppuhr oder Stoppuhr auf dem Smartphone usw.

Dementsprechend muss man bei der Addition („+“) oder Subtraktion („-“) zweier Minutenanzeigen diese wie folgt be- und umrechnen:

2,15 min₁₀₀ + 2,55 min₁₀₀ = 2 min₆₀ + 15/100 * 60 sec₆₀ + 2 min₆₀ + 55/100 * 60 sec₆₀

= 2 min₆₀ + 15 * 0,6 sec₆₀ + 2 min₆₀ + 55 * 0,6 sec₆₀

= 2 min₆₀ + 9 sec₆₀ + 2 min₆₀ + 33 sec₆₀ = 4 min₆₀ + 42 sec₆₀

= 4 min₆₀ + 42 * 1 sec₆₀ = 4 min₆₀ + 42 * 1/60 * 100 sec₁₀₀ ≈ 4 min₆₀ + 42 * 1,667 sec₁₀₀

= 4 min₆₀ + 70 sec₁₀₀ = 4 min₆₀ + 70 * 1 sec₁₀₀ = 4 min₆₀ + 70 * 1/100 min₁₀₀

= 4 min₆₀ + 0,7 min₁₀₀ = 4,7 min₁₀₀

Spätestens jetzt sieht man sehr deutlich, dass die in der Schule gelernte Zeitrechnung von 1 Tag = 24 Std. sowie 1 Std. = 60 Min. und 1 Min. = 60 Sekunden mit 1 std = 60 min = 60 * 1 min = 60 * 60 sec = 3600 sec zwar inzwischen „in Fleisch und Blut“ übergegangen ist, aber trotzdem rechnerisch sehr unpraktisch ist, weswegen Mikrocontroller wie der „micro:bit“-Rechner mit der „MakeCode“-Block-Programmierung ausschließlich dezimal rechnen:

2,25 min₁₀₀ + 2,917 min₁₀₀ = 5,167 min₁₀₀ = 5 min₆₀ + 0,167 min₁₀₀ = 5 min₆₀ + 167/1000 min₁₀₀

= 5 min₆₀ + 167/1000 * 1 min₁₀₀ = 5 min₆₀ + 167/1000 * 1/100 * 60 min₆₀

= 5 min₆₀ + 167/1000 * 0,6 min₆₀ = 5 min₆₀ + 0,1002 min₆₀ ≈ 5,1 min₆₀

= 5 min₆₀ + 1/10 * 1 min₆₀ = 5 min₆₀ + 1/10 * 60 sec₆₀ = 5 min₆₀ + 6 sec₆₀

= 5 min₆₀ + 6 * 1 sec₆₀ = 5 min₆₀ + 6 * 1/60 min₆₀ = 5 min₆₀ + 0,1 min₆₀

= 5 min₆₀ + 0,1 * 1 min₆₀ = 5 min₆₀ + 0,1 * 1/60*100 min₁₀₀

= 5 min₆₀ + 0,1 * 1,667 min₁₀₀ = 5 min₆₀ + 0,1667 min₁₀₀ ≈ 5,167 min₁₀₀

In diesem Zusammenhang sei nochmals darauf hingewiesen, dass man bei der dezimalen Minutenangabe stets mit angeben muss, ob sich diese auf 100 Sekunden pro 1 Min₁₀₀ wie z.B. 5,167 min₁₀₀ oder aber auf 60 Sekunden pro Min₆₀ wie z.B. 5,1 min₆₀ = 5 min₆₀ + 0,1 min₆₀ = 5 min₆₀ + 1/10 * 60 sec₆₀ = 5 min₆₀ + 6 sec₆₀ bezieht!

Dabei gilt es ferner zu beachten, dass der Minutenwert vor dem Dezimalkomma niemals in hundert Minuten [min₁₀₀] im Sinne von 1 std₁₀₀ = 100 min₁₀₀ umgerechnet wird!

Es gilt immer 1 std₆₀ = 60 min₆₀ und z.B.

0,1 min₆₀ = 1/10 * 60 sec₆₀ = 6 sec₆₀ oder 0,1 min₁₀₀ = 1/10 * 100 sec₁₀₀ = 10 sec₁₀₀

Siehe auch:

„Wie es zur 12-Stunden-Anzeige für die Uhr kam“

„Dezimalzeit“

Gemäß dem sogenannten „EVA“-Prinzip besteht der Programmblock <beim Start> aus zwei Teilen und zwar

1. dem Einlesen des aktuellen Zeitstempels <Laufzeit (ms)>

beim Drücken des Tasters „Knopf A“, dem anschließenden Umrechnen des Zeitstempels von Millisekunden in Minuten₁₀₀ mit zwei Nachkommastellen für die hundertstel Minuten₁₀₀ (= Sekunden₁₀₀) und der Wertezuweisung an das numerische Array <list>.

Dabei gilt es zu beachten, dass mit jedem Drücken des Tasters „Knopf A“ ein neuer und aktueller Zeitstempel dem numerischen Array <list> automatisch am Ende hinzugefügt wird:

(Zum Vergrößern bitte auf das Bild klicken!)

2. dem Auslesen des gespeicherten Zeitstempels <Laufzeit (ms)> aus dem numerische Array <list>. Dabei gilt es zu beachten, dass immer der letzte, aktuelle Wert am Ende des numerischen Arrays <list> ausgelesen wird.

Zu diesem Zweck muss man natürlich zuvor noch die Länge des numerischen Arrays <list> bestimmen.

Von der Länge des numerischen Arrays <list> muss man dann noch -1 subtrahieren, um auf die tatsächliche Länge zu kommen, weil das erste Element des Arrays <list> immer beim Index = 0 beginnt:

(Zum Vergrößern bitte auf das Bild klicken!)

Als nächstes wird der letzte Wert mit Index = n-1 des numerischen Arrays <list> eingelesen und der Variablen <anzahl_min_100> zugewiesen, im nächsten Statement in eine Zeichenkette, engl. „string“, umgewandelt und der alphanumerischen Variablen <anzahl_min_100_Str> zugewiesen.

Dabei wird der bisher numerische Wert wie z.B. der Zeitstempel 5,167 [min₁₀₀] in den String „5.167“ in Form von alphanumerischen Zeichen (= Buchstaben, Ziffern(!), Leer- oder Sonderzeichen) umgewandelt.

Während man mit Zahlen rechnen kann, handelt es sich bei den Ziffern quasi um entsprechende Symbole mit denen sich nicht mehr rechnen lässt; ähnlich wie bei den römischen Ziffern auf dem Ziffernblatt (nicht Zahlenblatt!) einer analogen Wanduhr.

Übrigens: Das römische Zahlensystem konnte sich weltweit nicht dauerhaft durchsetzen, weil sich mit den römischen Zahlen nicht rechnen lässt: MMXXII = M + M + X + X + II = 1000 + 1000 + 10 + 10 + 2 = 2000 + 20 + 2 = 2022 .

Der Grund dafür ist der, dass es bei den „römischen Zahlen“ keine Wertigkeit (= Stufigkeit im Sinne eines 10er Multiplikators) wie z.B. Einer (= E, 1 = 10⁰ ), Zehner(= Z, 10 = 10¹ ), Hunderter (= H, 100 = 10² ), Tausender (= T, 1000 = 10³ ) usw. gibt:

2022 = 2 * 10³ + 0 * 10² + 2 * 10¹ + 2 * 10⁰ = 2 * 1000 + 0 * 100 + 2 * 10 + 2 * 1 = 2000 + 0 + 20 + 2

Zurück zum String „5.167“, der mittels des Statements

auf den Dezimalpunkt „ . “ hin durchsucht wird. Demzufolge befindet sich dieser beim String „5.167“ an der Position = 1, weil die erste Stelle „5“ des Strings der Position = 0 entspricht!

Mit der bekannten Position des Dezimalpunktes „ . “ lässt sich nun der String „5.167“ in den linken Teil mit den ganzzahligen Werten inkl. der Null (" Variable <anzahl_min_100_Str>) und in den rechten Teil mit den Dezimalstellen (" Variable <anzahl_sec_100_Str>) aufteilen.

Dabei handelt es sich bei beiden Variablen <anzahl_min_100_Str> und anzahl_sec_100_Str um Variablen vom Typ „string“ (= alphanumerische Zeichenkette), sodass sich mit diesen nicht rechnen lässt!

Da das Statement mit der Variablen <anzahl_min_100_Str>

(Zum Vergrößern bitte auf das Bild klicken!)

den ursprünglichen Variableninhalt (= String „5.167“) mit dem Ergebniswert (= String „5“) überschreibt, der Originalwert also verlorengeht, müssen wir als Erstes das Statement mit der Variablen <anzahl_sec_100_Str> und den Nachkommastellen (= String „167“) programmieren:

(Zum Vergrößern bitte auf das Bild klicken!)

Nach der „string“-mäßigen Aufspaltung des ursprünglichen Variableninhalts (= String „5.167“) in Vor- und Nachkommastellen möchte man natürlich auf Nummer sicher gehen und wissen, ob die Aufspaltung erwartungsgemäß funktioniert und das richtige Ergebnis liefert:

(Zum Vergrößern bitte auf das Bild klicken!)

Selbstverständlich lässt sich der aufgespaltete String (= String „5.167“ = String „5“ + String „167“ ) auch als Ganzes darstellen:

(Zum Vergrößern bitte auf das Bild klicken!)

Ähnlich verhält es sich bei der zusammengesetzten Darstellung mit der Anzeige der 60er Sekunden. Dabei lässt sich die Umrechnung von 100er Sekunden in 60er Sekunden wie folgt vornehmen:

0.167 s₁₀₀ ≈ 0.17 * 1 s₁₀₀ = 0.17 * 1/100 * 60 s₆₀ = 0.17 * 0,6 s₆₀ = 0,102 s₆₀ ≈ 0,10 s₆₀

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden Screenshot des Quellkodes vom Projekt „proxi-roboter-p-24“ sieht, werden nur die Nachkommastellen von 100er Sekunden in 60er Sekunden umgerechnet!

Außerdem gibt es noch einen Programmierfehler, den es noch zu beheben gilt. Und zwar den, dass die Nachkommastellen der Variablen <anzahl_sec_60> vor der Umwandlung in die Variable <anzahl_sec_60_Str> wider Erwarten nicht abgeschnitten werden.

Zwar werden bei der Stoppzeit von 5.167 min₁₀₀ nur zwei Nachkommastellen = 16 sec₁₀₀ von vormals 167 sec₁₀₀ berücksichtigt

16 sec₁₀₀ = 16 * 1 sec₁₀₀ = 16 * 0,6 * 1 sec₆₀ = 9,6 sec₆₀ ,

trotzdem aber beim Ergebniswert = 9,6 sec₆₀ nicht auf die ganzzahlige Nachkommastelle = 9 sec₆₀ abgeschnitten, sodass man mit dem Statement

die Laufschriftanzeige „3,9,6 min“ und eben nicht „3,9 min“ angezeigt bekommt.

Mit dem Projekt „proxi-roboter-p-25“ und dem erweiterten Programmkode

(Zum Vergrößern bitte auf das Bild klicken!)

wird das Problem behoben.

Wenn man das Projekt „proxi-roboter-p-25“ testen will, dann muss man die Stoppuhr auf dem Smartphone zeitgleich zusammen mit dem Programm starten und bei diesem exakt beim Zeitstempel 3 Min. 10 Sek. auf den Taster „Knopf A“ des „micro:bit“-Rechners drücken. In der Laufschrift bekommt man dann sowohl die Anzeige „~> 3.16 min“ (= min₁₀₀) als auch „~~> 3,9 min“ (= min₆₀) angezeigt.

Dabei sei nochmals daran erinnert, dass nur die Nachkommastellen von 100er Sekunden in 60er Sekunden umgerechnet und angezeigt werden!

Wir erweitern den Programmkode des Projektes „proxi-roboter-p-25“ dahingehend, dass wir die Umrechnung der 100er Minuten in 60er Minuten und der 100er Sekunden in 60er Sekunden in die beiden Funktionen

1.

2.

auslagern, sodass sich der Programmkode im Projekt „proxi-roboter-p-26“ entsprechend übersichtlicher gestaltet. Dabei gilt es zu beachten, dass die vorgenannte Reihenfolge der Funktionen 1.) und 2.) bei der Umrechnung zwingend einhalten werden muss, weil Ergebniswerte verschiedener Variablen im Laufe der Umrechnung überschrieben werden:

(Zum Vergrößern bitte auf das Bild klicken!)

Wenn man sich bei der Umrechnung von 100er Minuten in 60er Minuten mangels Übung wieder unsicher ist, wie man den Umrechnungsfaktor k ermittelt, dann hilft einem nachfolgende Vorgehensweise wieder auf die Sprünge:

1 min₁₀₀ " 1 min₆₀ "

1 min₁₀₀ = k * 1 min₆₀ " mit 1 min₁₀₀ = 1/100 std₁₀₀

1/100 std₁₀₀ = k * 1/60 std₆₀ "

k = 1/100 std₁₀₀ / ( 1/60 std₆₀ )

= 1/100 std₁₀₀ / ( 1/60 std₆₀ )

= 1/100 * 60

= 60 / 100 = 0,6

1 min₁₀₀ = k * 1 min₆₀

k * 1 min₆₀ = 1 min₁₀₀

1 min₆₀ = 1 min₁₀₀ / k

= 1 min₁₀₀ / 0,6 = 1 min₁₀₀ / ( 6/10 ) = 10/6 * 1 min₁₀₀

≈ 1,67 * 1 min₁₀₀

oder

1 min₁₀₀ ≈ 1 min₆₀ / 1,67 = 0,6 * 1 min₆₀

Beispiel (siehe oben)

5.167 min₁₀₀ = 5,167 * 0,6 * min₆₀

= 3,1002 min₆₀ ≈ 3,10 min₆₀ " 3 min₆₀ und 10 sec₆₀

Ansonsten lässt sich die Umrechnung auch mittels Dreisatz wie folgt lösen:

100 min₁₀₀ " 1 Std₁₀₀

60 min₆₀ " x Std₆₀

___________________

x = 1 Std₁₀₀ / 100 min₁₀₀ * 60 min₆₀ = 60/100 Std₆₀ = 0,6 Std₆₀

Auch obwohl es zwei verschiedene Zeitmessverfahren gibt, nämlich

1. die Zeitmessung in 60 Minuten [ ’ ] [ min ], 100 Sekunden [ “ ] [ s ]

und Millisekunden [ ms ] (=1/1000 Sekunden) beim „micro:bit“-Rechner und

2. die Zeitmessung in 60 Minuten [ ’ ] [ min ], 60 Sekunden [ “ ] [ s ]

bei Armband-, Wand- und Küchenuhren und Kurzzeitmessern für das hart gekochte 7-Minuten-

oder weiche 4-Minuten-Frühstücksei und mit 1/10 Sekunden [ s ] und 1/100 [ s ] bei der Stoppuhr

für den 100 m Lauf im Alltag gibt,

so bewegen sich trotzdem beide im Dezimalsystem, sodass sich mit diesen rechnen lässt.

Wenn man aber beim Taschenrechner z.B. die Zeit von 4 Minuten und 45 Sekunden in der Form 4,45 min₆₀ eintastet und den Wert 30 Sekunden addiert, dann bekommt man als Ergebnis = 4,45 + 30 = 34,45 ý angezeigt, weil der Taschenrechner von sich aus nicht weiß, nicht wissen kann, dass es sich bei dem Wert 30 um Sekunden und nicht um Minuten handelt. Der Taschenrechner rechnet nämlich dimensionslos, d.h. ohne irgendwelche Maßeinheiten!

Bei dem Wert 30 kann man nämlich sehr wohl zum Ausdruck bringen, dass es sich bei diesem um Sekunden handelt, nämlich mit 30 s = 30/60 min = 1/2 min = 0,5 min

Wer darüber hinaus meint, dass es sich bei 4,45 min um 4 Minuten und 45 Sekunden (= 4’ 45“ = 4:45) handelt, liegt wegen der Zehntel und Hundertstel der Dezimalstellen falsch!

Trotzdem kann man natürlich zum Ausdruck bringen, dass es sich bei der Angabe 4,45 um 4 Minuten und 45 Sekunden handeln soll, d.h. mit sechzigstel Minuten gerechnet werden soll. Nur muss man das entsprechend zum Ausdruck bringen bzw. kenntlich machen! Mit der Angabe 4 Minuten + 45/60 Minuten = 4 Minuten + 3/4 Minuten = 4 Minuten und 45 Sekunden gibt es aber keine Missverständnisse:

4,45 min₆₀ = 4 min₆₀ + 45/100 min₆₀ = 4 min₆₀ + 45/100 * 1 min₆₀ = 4 min₆₀ + 0,45 * 1 min₆₀

= 4 min₁₀₀ + 0,45 * 1,667 min₁₀₀ = 4 min₁₀₀ + 0,75 min₁₀₀ = 4 min₁₀₀ : 75 sec₁₀₀ = 4,75 min₁₀₀

4,45 min₆₀ = 4 min₆₀ + 45/60 min₆₀ = 4 min₆₀ + 3/4 min₆₀ " gesprochen: „vier Dreiviertel Minuten“ " 1 min = 60 sec

Durch die Erweiterung von 25 in Zähler und Nenner wird sozusagen klammheimlich die Umwandlung von 60 Sekunden auf 100 Sekunden pro Minute vorgenommen:

= 4 min₁₀₀ + ( 3 * 25 ) / ( 4 * 25 ) min₁₀₀

= 4 min₁₀₀ + 0,75 min₁₀₀ = 4,75 min₁₀₀ " gesprochen: „vier Dreiviertel Minuten“ " 1 min = 100 sec

4,75 min₁₀₀ = 4 min₁₀₀ + 75/100 min₁₀₀ = 4 min₁₀₀ + 75/100 * 1 min₁₀₀ = 4 min₁₀₀ + 0,75 * 1 min₁₀₀

= 4 min₆₀ + 0,75 * 0,6 min₆₀ = 4 min₆₀ + 0,45 min₆₀ = 4 min₆₀ : 45 sec₆₀ = 4,45 min₆₀

Die Unterteilung eines Vollkreises mit 360⁰ in sechzigstel oder hundertstel Teilsegmente, ähnlich eines Tortenstückes, kann man sich auch bildlich vorstellen. Demzufolge ist ein Vollkreis mit 1 min₁₀₀ und hundertstel Sekunden Unterteilung deutlich größer, d.h. auch zahlenmäßig(!), als ein Vollkreis mit min₆₀ und sechzigstel Sekunden Unterteilung.

Wenn man also sechzigstel Minuten in hundertstel Minuten umrechnen will, dann muss man wegen des größeren Vollkreises bei den hundertstel Minuten den größeren Umrechnungsfaktor 1 min₆₀ = 1,667 * 1 min₁₀₀ wählen.

Wenn man hingegen hundertstel Minuten in sechzigstel Minuten umrechnen will, dann muss man wegen des kleineren Vollkreises bei den sechzigstel Minuten den kleineren Umrechnungsfaktor 1 min₁₀₀ = 0,6 * 1 min₆₀ wählen.

Wenn man die nackten Zahlenwerte 4,45 Minuten und 4,75 Minuten miteinander vergleicht, dann kann es sich bei dem Wert 4,75 nicht um einen Wert mit sechzigstel Minuten Unterteilung handeln, da der Dezimalwert 75 bereits einen Überlauf bei den sechzigstel Minuten zur Folge hätte: 4,75 min₆₀ = 5,15 min₆₀.

Demzufolge kann der Wert 4,75 durchaus als Unterteilung mit hundertstel Minuten verstanden werden: 4,75 = 4,75 min₁₀₀ = 4 min₁₀₀ + 75/100 min₁₀₀. Und umgekehrt kann der kleinere Wert 4,45 als Unterteilung mit sechzigstel Minuten aufgefasst werden: 4,45 = 4,45 min₆₀ = 4 min₆₀ + 45/60 min₆₀ = 4 min₆₀ + 3/4 min₆₀.

Wenn also zu der Zeit von 4 Minuten und 45 Sekunden (= 4,45 min₆₀) insgesamt 30 Sekunden addiert werden sollen, dann folgt entsprechend der Unterteilung mit sechzigstel Minuten:

4,45 min₆₀ + 30 sec = 4,45 min₆₀ + 30 * 1 sec₆₀ = 4,45 min₆₀ + 30 * 1/60 min₆₀ = 4,45 min₆₀ + 30/60 min₆₀

Die nachfolgende Umrechnung ist mathematisch korrekt, aber zeitmäßig falsch:

= 4,45 min₆₀ + 1/2 min₆₀ ¹ 4,45 min₆₀ + 0,5 min₁₀₀ = 4,95 min₆₀ ý = 5,35 min₆₀ ý " FALSCH!

Die nachfolgende Umrechnung ist mathematisch und zeitmäßig richtig:

= 4,45 min₆₀ + 1/2 min₆₀ = 4,45 min₆₀ + 30 sec₆₀ = 5,15 min₆₀ þ " RICHTIG!

30 sec₆₀ = 0,5 * min₁₀₀ " 30 sec₆₀ = 50 sec₁₀₀ = 50 / 100 * 60 sec₆₀ = 30 sec₆₀

5,15 min₆₀ = 5 min₆₀+ 0,15 * 1 min₆₀ = 5 min₆₀+ 0,15 * 1,667 min₁₀₀ = 5 min₆₀+ 0,25005 min₁₀₀ ≈ 5,25 min₁₀₀

4,45 min₆₀ + 30 sec = 4 min₆₀ + 45/60 * 100 min₁₀₀ + 30/60 * 100 sec₁₀₀

= 4 min₆₀ + 75 min₁₀₀ + 50 sec₁₀₀ = 4,75 min₁₀₀ + 0,50 min₁₀₀ = 5,25 min₁₀₀

Interessant, aber auch gleichzeitig trivial (= alltäglich, gewöhnlich) ist, dass sich beide Ergebniswerte 4,75 min₆₀ = 5,15 min₆₀ jeweils in hundertstel Minuten wie folgt umrechnen lassen:

5,15 min₆₀ = 5 min₆₀ + 0,15 * 1 min₆₀ = 5 min₆₀ + 0,15 * 1,667 min₁₀₀ ≈ 5,25 min₁₀₀

4,75 min₆₀ = 4 min₆₀ + 0,75 * 1 min₆₀ = 4 min₆₀ + 0,75 * 1,667 min₁₀₀ ≈ 5,25 min₁₀₀

Was aber bedeutet es praktisch, wenn beide Umrechnungen

= 5,15 * 1 min₆₀ = 5 min₆₀ + 0,15 * 1,667 min₁₀₀ = 5,25005 min₁₀₀ ≈ 5,25 min₁₀₀

= 4,75 * 1 min₆₀ = 4 min₆₀ + 0,75 * 1,667 min₁₀₀ = 5,25025 min₁₀₀ ≈ 5,25 min₁₀₀

zum selben Ergebnis führen?

>> Wenn beide Umrechnungen zum selben Ergebnis führen, dann muss es sich bei beiden um ein und dieselbe Umrechnungsverfahren handeln! <<

Was bedeutet es ferner, wenn alle drei Ergebniswerte 4,75 * 1 min₆₀ = 5,15 * 1 min₆₀ = 5,25 min₁₀₀ gleichbedeutend und gleichwertig sind?

>> Wenn alle drei Ergebniswerte 4,75 * 1 min₆₀ = 5,15 * 1 min₆₀ = 5,25 min₁₀₀ gleichbedeutend und gleichwertig sind, d.h. zum selben Ergebnis führen, dann haben wir es mit zwei verschiedenen Messverfahren(!) (= sechzigstel und hundertstel Minuten) zu tun! Demzufolge wurden beide Messverfahren in ein und demselben Inertialsystem (= Bezugssystem) durchgeführt, sodass es sich deshalb bei allen drei Ergebniswerten um ein und dieselbe Zeitspanne bzw. ein und dasselbe Zeitfenster handelt! <<

Wenn du die Antwort nebst Begründung sehen willst, dann musst du nur im Browser die linke Maustaste gedrückt halten und mit dem Mauszeiger über die Kennzeichnung im Bereich >> ___ << fahren und diesen entsprechend markieren!

Praktisch ließe sich das damit vergleichen, dass wir bei der Messung zwei verschiedene Stoppuhren verwenden, die beide zum selben Zeitpunkt t = 0 gestartet wurden. Während also eine Stoppuhr mit sechzigstel Minuten rechnet, rechnet die andere mit hundertstel Minuten.

Beide Stoppuhren messen aber dieselbe Zeitspanne, sodass diese unabhängig voneinander zum selben Zeitpunkt t = 5,15 min₆₀ = 5,25 min₁₀₀ die Messung beenden, eben weil die unterschiedlichen Stoppuhren nur die Zeit unterschiedlich berechnen, d.h. unterschiedlich maßstäblich anzeigen! -

Siehe auch:

„Minute im Arbeitsstudium“ …mit REFA-Stoppuhr in hunderter Minuteneinteilung 15 sec₁₀₀ = 15/100 min₁₀₀

„Industrieminute“

„Excel: Rechnen mit 100 Industrieminuten pro Stunde“

Mit dem Programm des Projektes „proxi-roboter-p-26“ lässt sich der vorgegebene Zeitstempel = 5,25005 min₁₀₀ problemlos in

5,25005 min₁₀₀ = 5 min₁₀₀ + 0,25005 * 1 min₁₀₀ = 5 min₁₀₀ + 0,25005 * 0,6 min₆₀ = 5 min₁₀₀ + 0,15003 min₆₀

= 5,15003 min₆₀

umrechnen.

Damit man nicht warten muss bis die Zeit des Zeitstempel = 5,25005 min₁₀₀ erreicht ist, wurde diese bereits mit dem Statement

ins Programm und zwar in die beiden Funktionen

aufgenommen. Um den vorgegebenen Zeitstempel = 5,25005 min₁₀₀ von hundertstel in sechzigstel Minuten (= 5,15003 min₆₀) umrechnen zu lassen, muss man nach dem Programmstart nur den Taster „Knopf A“ drücken.

Obwohl mit dem Programmstart auch die Zeiterfassung der Systemvariablen <Laufzeit (ms)> fortwährend mit läuft, dient das Programm nur dazu den vorgegebenen Zeitstempel umzurechnen!

Dabei lässt sich die Umrechnung von hundertstel in sechzigstel Minuten durch Drücken des Tasters „Knopf A“ beliebig oft wiederholen!

Mit dem Programm des Projektes „proxi-roboter-p-27“ lässt sich die Zeitdauer des vorgegebenen Zeitstempels = 5,25005 min₁₀₀ nicht nur von hundertstel in sechzigstel Minuten = 5,15003 min₆₀ umrechnen, sondern auch wie bei einer Stoppuhr messen!

Dabei beginnt die Zeitmessung automatisch in dem Moment wo das Statement <setze dummy_Zeit auf Laufzeit (ms)> (siehe grüner Kasten) ausgeführt wird:

(Zum Vergrößern bitte auf das Bild klicken!)

Diesbezüglich sei wieder daran erinnert, dass der erste Messwert der Systemvariablen <Laufzeit (ms)> fehlerhaft ist, da diese erst beim Aufruf derselben initialisiert wird. Trotzdem verhält es sich so, dass die Zeitmessung sofort mit dem ersten Aufruf der Systemvariablen <Laufzeit (ms)> automatisch startet (siehe Statement im grünen Kasten)!

Wenn man also die Zeitmessung mittels einer separaten Stoppuhr oder wie im vorliegenden Fall mittels eines Zeitgebers überprüfen will, dann muss man diesen genau in dem Moment starten, wenn das Symbol des Häkchens „P“ nach der Pause von einer Sekunde in der LED-Anzeige des „micro:bit“-Rechners gelöscht wird!

Wie allgemein bekannt sein dürfte, liefert Windows standardmäßig von Haus aus eine multifunktionale Uhr mit, die sich als Zeitgeber, Alarm, Stoppuhr und Weltuhr direkt am Windows-PC bzw. auf dem Desktop nutzen lässt.

Um die (Windows-) Uhr zu starten, muss man nur mittels der Maus in der sogenannten System Tray auf das Symbol „Windows-Fenster“ klicken, dann im nächsten Fenster auf <Alle Apps> klicken, sodass alle unter Windows installierten Programme und Apps in alphabetischer Reihenfolge aufgelistet werden. Nun muss man nur noch bis zum Buchstaben „U“ nach unten scrollen und das „Uhr“-Programm starten.

In der linken oberen Fensterecke des „Uhr“-Programms klickt man dann auf das „Menü“-Symbol „“, um die Funktion „Zeitgeber“ auszuwählen.

Mittels Mausklick auf den kleinen Stift „“ unten rechts im Fenster lässt sich dann die Zeitdauer (= 5’ 15“ = 5:15 = 5 min₆₀ : 15 sec₆₀) für den Countdown, d.h. das Rückwärtszählen einstellen!

Abschließend klickt man oben rechts im Fenster auf das Verkleinerungs-Symbol „“, sodass sich der Zeitgeber in etwa auf Briefmarkengröße verkleinert und sich als permanente Anzeige beliebig auf dem Desktop positionieren lässt:

(Zum Vergrößern bitte auf das Bild klicken!)

Zusammen mit dem Programm des Projektes „proxi-roboter-p-27“ und dem Zeitgeber sieht das Ganze dann so aus:

(Zum Vergrößern bitte auf das Bild klicken!)

Vorgehensweise beim Überprüfen der zu messenden Zeitdauer:

1. Wie bereits erwähnt wurde, muss zwecks Überprüfens der zu messenden Zeitdauer von 5 min₆₀ 15 sec₆₀ als Erstes das Projektprogramm „proxi-roboter-p-27“ auf dem „micro:bit“-Rechners gestartet werden!

2. Nach dem Programmstart muss dann als Zweites der Countdown des Windows-Zeitgebers genau in dem Moment gestartet werden, wenn das Symbol des Häkchens „P“ in der LED-Anzeige des „micro:bit“-Rechners verschwindet!

Da es im Programm des Projektes „proxi-roboter-p-27“ jetzt keinen Taster „Knopf A“ mehr gibt, mit dem sich die zu messende Zeitdauer von 5 min₆₀ 15 sec₆₀ stoppen ließe, gibt es stattdessen die <Wenn … dann>-Abfrage mit dem Statement

,

(Zum Vergrößern bitte auf das Bild klicken!)

bei der der aktuelle Zeitwert der Variablen <anzahl_min_100> mit der festgelegten Stoppzeit von 5.25005 min₁₀₀ = 5,15003 min₆₀ verglichen wird. Sobald die festgelegte Stoppzeit von 5.25005 min₁₀₀ überschritten wurde, erfolgt die Auswertung und Anzeige der gemessenen Stoppzeit mittels der drei Funktionen (siehe weiter unten im roten Kasten):

(Zum Vergrößern bitte auf das Bild klicken!)

Damit dem Anwender bei der fünfminütigen Messung nicht langweilig wird, wird zu jeder ganzzahligen, d.h. vollen Minute, die bereits verstrichene Zeit in der LED-Laufschrift des „micro:bit“-Rechners angezeigt. Dabei werden aber die bereits verstrichenen, vollen Minuten nicht extra berechnet, sondern einfach nur mittels der Variablen <loop_n> (= Schleifenzähler n) durchgezählt und ganzzahlig angezeigt (siehe weiter unten im grünen Kasten):

(Zum Vergrößern bitte auf das Bild klicken!)

Zu guter Letzt wird im blauen Kasten mit dem Statement

fortwährend ein sich wegen der Laufschriftanzeige von rechts nach links bewegender „Fortschrittsbalken“ angezeigt, um dem Anwender zu signalisieren, dass das Programm des Projektes „proxi-roboter-p-27“ still im Hintergrund vor sich hin werkelt und der kleine „micro:bit“-Rechner nicht zwischenzeitlich abgestürzt ist.

Dabei ist der Programmkode im blauen Kasten Bestandteil der <wenn … dann>- oder <ansonsten>-Abfrage:

…

(Zum Vergrößern bitte auf die Einzelbilder klicken!)

Immer dann, wenn es im grünen Kasten nichts zu tun gibt, d.h. wenn es keine bereits verstrichenen, vollen Minuten anzuzeigen gibt, wird im blauen Kasten der sich von rechts nach links bewegende „Fortschrittsbalken“ angezeigt (siehe oben).

Wie man anhand des nachfolgenden Quellkodes sieht, wurden die Ausgabe- und Anzeige-Statements der hundertstel und sechzigstel Minuten

(Zum Vergrößern bitte auf die einzelnen Bilder klicken!)

in die Funktion

ausgelagert, sodass sich die Lesbarkeit des Programms weiter verbessert:

(Zum Vergrößern bitte auf das Bild klicken!)

Beim bisherigen Programm des Projektes „proxi-roboter-p-27“ verhält es sich so, dass man die Zeitdauer des Zeitstempels = 5,25005 min₁₀₀ für den Countdown, d.h. das Herunterzählen, händisch in den Programmkode des Programms einpflegen musste:

(Zum Vergrößern bitte auf das Bild klicken!)

Elektronische Wecker, Alarmgeber, Stoppuhren oder Zeitschaltuhren wie z.B. beim Backofen verfügen zwecks der Einstellung der aktuellen Uhrzeit oder der Zeitdauer der Gar- bzw. Backzeit oftmals nur über zwei Tasten und zwar über eine „Minus“-Taste („-“) zum Abwärtszählen und eine „Plus“-Taste („+“) zum Heraufzählen der einzustellenden Zeitdauer:

(Zum Vergrößern bitte auf das Bild klicken!)

Bei der Bedienung der beiden „Plus“- und „Minus“-Tasten verhält es sich zweckmäßigerweise so, dass die einzustellende Zeitdauer umso schneller im Display durchläuft, je länger man eine der beiden Tasten gedrückt hält. Demzufolge wird die einzustellende Zeitdauer erst ganz langsam in einzelnen Minuten hoch gezählt und wird dann immer schneller, je länger man eine der beiden Tasten gedrückt hält, sodass die Stunden am Ende nur so durch das Display rasen. Sobald man aber eine der jeweiligen Tasten loslässt, stoppt die angezeigt Zeitdauer und fängt beim erneuten Drücken einer der Tasten wieder ganz langsam an zu zählen (siehe YouTube-Video).

Nachfolgend geht es aber erst einmal darum, die Eingabe der Zeitdauer des Zeitstempels für den Countdown mittels der beiden Tasten <Knopf A> und <Knopf B> zu programmieren, um dann zu sehen, ob und wie sich die Funktion der Zeitschaltuhr des Backofens nachprogrammieren lässt.

Beim Programm des Projektes „proxi-roboter-p-28“ handelt es sich erstmals um ein richtiges „Stoppuhr“-Programm, das sich mit den beiden Tastern <Knopf A> und <Knopf B> bedienen lässt. Dabei dient die Taste <Knopf A> dazu, die Stoppuhr zu starten („|>“) und mit der Taste <Knopf B> zu beenden („>|“):

(Zum Vergrößern bitte auf das Bild klicken!)

Das Besondere an dem Programm des Projektes „proxi-roboter-p-28“ ist, dass die beiden Taster <Knopf A> und <Knopf B> wider Erwarten nicht die „Start“- und „Stopp“-Funktion direkt veranlassen und ausführen, sondern nur einen Umschalter in Form der booleschen Variablen <start_stopp_Timer_boolean>, der von „wahr“, engl. „true“, auf „falsch“, engl. „false“ und umgekehrt hin und her geschaltet wird.

Demzufolge gibt es immer nur ein „Entweder“ oder ein „Oder“, d.h. <wenn … dann>- oder <ansonsten>-Abfrage, aber niemals ein „Und“ (siehe grüner Kasten):

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man anhand der Wahrheitstabelle im grüner Kasten sieht, muss immer einer der beiden Taster <Knopf A> oder <Knopf B> gedrückt werden, um die Stoppuhr zu starten („|>“) oder anzuhalten („>|“).

Das Interessante dabei ist noch, dass sich der eigentliche Wechselschalter aus den beiden Einzelschaltern in Form der beiden Taster <Knopf A> und <Knopf B> zusammensetzt, was sozusagen materialmäßig eine Ressourcenverschwendung ist.

Weil aber die Umschaltlogik mittels der booleschen Variablen <start_stopp_Timer_boolean> etwas komplex ist und das Umschalten der Stoppuhr von Start („|>“) zu Anhalten („>|“) indirekt erfolgt, macht es Sinn, das Umschalten der Stoppuhr mit den einzelnen Tastern <Knopf A> oder <Knopf B> vorzunehmen, weil man dann sofort sieht, ob das Ganze funktioniert oder nicht.

Wir hatten ja schon mal die Rede von der sogenannten Treppenhausbeleuchtung mittels Wechselschalter, wo man das Treppenhauslicht mit dem Schalter A einschalten und am anderen Ende mit dem Schalter B wieder ausschalten kann.

Dabei erkennt man Wechselschalter daran, dass sich der Wippschalter entweder in der einen Wipp-Position befindet oder in der anderen, sodass sich anhand der Wipp-Position von außen nicht feststellen lässt, ob sich der Wippschalter im eingeschalteten oder ausgeschalteten Zustand befindet!

Und, da die Treppenhauslampen der Treppenhausbeleuchtung immer nur einphasig geschaltet werden, kann eine ausgeschaltete Treppenhauslampe trotzdem unter „Strom“ stehen, nämlich dann, wenn zufälliger Weise die stromführende braune Phase L1 nicht ausgeschaltet/getrennt wird, sondern nur der nicht Strom führende blaue Neutralleiter N für den Stromrückfluss!

Moderne Wohnungsflur- oder Treppenhausbeleuchtungen arbeiten aber heutzutage nur noch mit einem sogenannten Stromstoßrelais bei denen auf den Wohnetagen und im Treppenhaus stets nur Niedervolt-Taster für die Steuerung, d.h. das Ein- oder Ausschalten der Beleuchtung verbaut werden.

Jetzt kennen wir auch den Unterschied zwischen einem Schalter und einem Taster!

Ein (Ein-/Aus-) Schalter schaltet bzw. unterbricht immer selbst den Stromfluss zur Glühlampe, während ein Taster den Stromfluss zur Glühlampe immer nur indirekt über das Stromstoßrelais steuert!

Wenn man also die Arbeits- und Funktionsweise nebst Algorithmus des Programms beim Projekt „proxi-roboter-p-28“ verstanden hat, dann lässt sich dieses auch so programmieren, dass man für die Stoppuhr, d.h. für das Starten und Stoppen der Stoppzeit, nur noch einen Taster benötigt (siehe Projekt „proxi-roboter-p-29“):

(Zum Vergrößern bitte auf das Bild klicken!)

Wie man im obenstehenden „MakeCode“-Programmkode sieht, arbeitet der Taster <Knopf B> sowohl zum Starten als auch zum Stoppen der Stoppuhr, eben weil sich der Taster <Knopf B> mit jedem Knopfdruck umschalten lässt!

Leider eignet sich das Programm des Projektes „proxi-roboter-p-29“ noch nicht dazu, um festzustellen zu können wie lange der Taster <Knopf B> gedrückt wurde, da sich dieser immer erst dann wieder erneut drücken lässt, wenn die Laufschriftanzeige in der LED-Laufschrift durchgelaufen ist:

1. Laufschriftanzeige „|>“ohne weitere Anzeige

zwecks Mitteilung, dass die Stoppuhr gestartet wurde.

2. Laufschriftanzeige „>|“ mit Auswertung und Anzeige der gestoppten Zeitdauer

zwecks Mitteilung, dass die Stoppuhr angehalten wurde.

Aber immerhin wissen wir jetzt, dass sich die LED-Laufschriftanzeige wider Erwarten nicht durch Tastendruck auf den Taster <Knopf B> unterbrechen lässt.

Damit durch das Drücken des Tasters <Knopf B> sofort die Startzeit zum Zeitpunkt des Tastendrucks erfasst wird, positionieren wir das Statement <setze startzeit_Timer auf Laufzeit (ms)> direkt an den Anfang der Funktion <erfassen_Startzeit>.

Um das bisherige Programm des Projektes „proxi-roboter-p-29“ schneller zu machen, entfernen wir in diesem das Statement <zeige Text „ |> “> und ersetzen dieses durch das Statement <pausiere (ms) 100“>, sodass sich jetzt mit dem Programm des Projektes „proxi-roboter-p-30“ Stoppzeiten größer 100 ms ( > 0,010 s) zwischen dem ersten und zweiten Tastendruck des Tasters <Knopf B> stoppen lassen:

(Links: Projekt „proxi-roboter-p-29“ | Rechts: Projekt „proxi-roboter-p-30“)

(Zum Vergrößern bitte auf die Bilder klicken!)

Zum Vergleich: Junge Leute, die mit 18 Jahren den PKW-Führerschein machen erreichen eine Reaktionszeit von um die 25/100 s = 0,25 s = 25 ms.

Auf das Statement <setze startzeit_Timer auf Laufzeit (ms)> muss sofort das Statement <pausiere (ms) 100“> folgen, damit das Programm des Projektes „proxi-roboter-p-30“ später auch ordnungsgemäß funktioniert!

Der Grund dafür dürfte der sein, dass mit der Systemvariablen <Laufzeit (ms)> der Prozessortakt abgefragt wird. Und zwar mittels eines sogenannten Interrupts, d.h. einer kurzzeitigen Unterbrechung des laufenden Programms.

Damit der Prozessor nach dem Interrupt wieder mit dem laufenden Programm fortfahren kann, muss intern die zuvor gesetzte Sprungmarke wieder angesprungen werden. Die Wiederaufnahme des laufenden Programms braucht aber etwas Zeit, d.h. ein paar Taktzyklen der Rechenzeit des Prozessors.

Wenn man das Statement <pausiere (ms) 100“> aus dem Programmkode entfernt, dann setzt der Prozessor nach der Abfrage der Systemvariablen <Laufzeit (ms)> wieder seine Arbeit, d.h. den Programmablauf fort und zwar wider Erwarten beim vorherigen Statement <wenn Knopf B ist geklickt dann> …<ansonsten> …, sodass ohne erneutes Drücken des Tasters <Knopf B> die bisher verstrichene Zeitdauer beim Ausführen des Interrupts mit t_Interrupt = 0,02 s = 20 ms in der Laufschrift angezeigt wird:

(Zum Vergrößern bitte auf das Bild klicken!)

Offensichtlich handelt es sich hier um einen Programmierfehler der „MakeCode“-Programmiersprache von Microsoft oder um einen Fehler im Betriebssystem des „micro:bit“-Rechners. Um das herauszufinden, müsste man das obenstehende „MakeCode“-Programm in einer anderen Programmiersprache wie z.B. Python nachprogrammieren. Wenn sich in Python der gleiche Fehler zeigt, dann dürfte es sich tatsächlich um einen Fehler im Betriebssystem des „micro:bit“-Rechners handeln!

Bei dem Programm des Projektes „proxi-roboter-p-31“ wurde die Anzeige der gestoppten Zeitdauer in die Funktion <anzeigen_Stoppzeit> ausgelagert. Außerdem werden die gestoppte Start- und Stoppzeit im Array <zeitdauer_Array> gespeichert:

(Zum Vergrößern bitte auf das Bild klicken!)

Das obenstehende Programm des Projektes „proxi-roboter-p-31“ hat noch den Nachteil, dass sich mit diesem immer nur jeweils eine Start-Stopp-Messung durchführen lässt, weil am Ende des Programmkodes der Funktion <erfassen_Stoppzeit> und der Funktion <anzeigen Stoppzeit> wiederholt das Statement <setze start_stopp-Timer_boolean auf wahr> gesetzt wird, sodass wieder alles „auf Anfang“ gesetzt wird und die Zeitmessung beim Drücken des Tasters <Knopf B> von vorne beginnt.

In der Praxis hat es sich aber herausgestellt, dass es oftmals vorteilhaft ist, wenn man die laufende Start-Stopp-Messung durch erneutes Drücken des Tasters <Knopf B> fortsetzen kann! Deshalb wurde im nachfolgenden Programm des Projektes „proxi-roboter-p-32“ das Statement <setze start_stopp-Timer_boolean auf wahr> in den Funktionen <erfassen_Stoppzeit> und <anzeigen Stoppzeit> weggelassen:

(Zum Vergrößern bitte auf das Bild klicken!)

Mit zurzeit 143 DinA4-Seiten im Querformat und 99 Bildern ist es an der Zeit, das Tutorial über das Kodieren von „MakeCode“-Programmen in einer neuen Webseite fortzusetzen. [ Hier geht’s dann weiter! ]

[ Proxi-Roboter ] [ Seitenanfang ] [ Montage 1 ] [ Coding 2 ]