[ easy electronik 200 ] [ Seitenende ] [ Versuch 8 ] [ Versuch 10 ] [ Versuch 17 ]

easy electronic 200 – Lösung zur Aufgabe 10-1

Einfache Schaltung mit einem ohmschen Widerstand

Eine elektrische Schaltung besteht u.a. aus einem ohmschen Widerstand R, dessen Widerstandswert nicht explizit bekannt ist.

Zu dem ohmschen Widerstand R gibt es aber eine Wertetabelle mit I = f(U), sprich „I ist eine Funktion von U“ als sogenannte Widerstandsgerade im Sinne einer Kennlinie:

U[V]	-3	-2	-1	0	1	2	3
I[mA]	L	-5	L	L	10	L	L

Leider ist das Aufgabenblatt mit der obenstehenden Wertetabelle durch versehentliches Verschütten von etwas Wasser aus der Trinkflasche teilweise unleserlich geworden, sodass sich nur noch zwei Stromstärkewerte I_R erkennen und ablesen lassen.

Aufgabe

a) Berechne den ohmschen Widerstand R mittels der zwei Messwerte aus der gegebenen Wertetabelle!

b) Berechne den Konstantstrom I₀ an der Stelle I₀ = f(U₀) mit U₀ = 0 V (siehe Wertetabelle).

c) Wird bei der elektrischen Schaltung die Stromstärke I_R durch den Widerstand R mittels einer Spannungs-, Strom- oder Spannungs- und Stromquelle aufgebracht?

d) Wie groß muss die Spannung U der Spannungsquelle sein, damit durch den Widerstand R exklusiv ein Strom I_R der Stromstärke I_R = 20 mA fließt? Der zuvor berechnete und zugrunde gelegte Konstantstrom I₀ sowie der Widerstand R sollen dabei unverändert bleiben!

e) Zeichne den Graphen der Funktion I_R = f(U_R) zur obenstehenden Wertetabelle mit dem Maßstab 1 V " 2 cm
und 5 mA " 2 cm.

f) Welche Stromstärke I₀ lässt sich am Schnittpunkt der Widerstandsgeraden mit der Stromachse (= Senkrechte) ablesen?

g) Interpretiere den Wert der Stromstärke I₀ > 0 am Schnittpunkt mit der Spannung U₀ = 0.

h) Wende die (mathematische) Geradengleichung auf die (elektrotechnische) Widerstandsgerade an!

Bemerkung:

Die Begriffe „Widerstandsgerade“, „Widerstandsgleichung“ und „Widerstandskennlinie“ sind heutzutage nicht mehr so geläufig und finden sich demzufolge wider Erwarten auch nicht in Wikipedia. Den älteren Semestern unter den Ingenieuren dürften aber die Begriffe noch geläufig sein.

So lautete beispielsweise eine Prüfungsfrage in Messtechnik im 4. Semester, Mitte der 1975er Jahre an der damaligen Technischen Hochschule Darmstadt (heute: Technische Universität Darmstadt): „Erklären Sie, was das Charakteristische einer Widerstandsgeraden ist.“ Dabei hätte man natürlich auch direkt nach der Kennlinie eines linearen, konstanten Widerstandes fragen können, was viel einfacher und weniger trickreich gewesen wäre.

Der Ausdruck/Begriff „Widerstandsgleichung“ hingegen ist in der Tat missverständlich. Schließlich beschreibt das Ohmsche Gesetz R = U / I = einen konstanten(!) Quotienten und nicht eine lineare Gleichung vom mathematischen Typ y = f(x) = ax + b bzw. im elektrotechnischen Sinn I = f(U) = 1 / R * U + I₀.

Lösung zur Aufgabe a)

a) Berechne den ohmschen Widerstand R mittels der zwei Messwerte aus der gegebenen Wertetabelle!

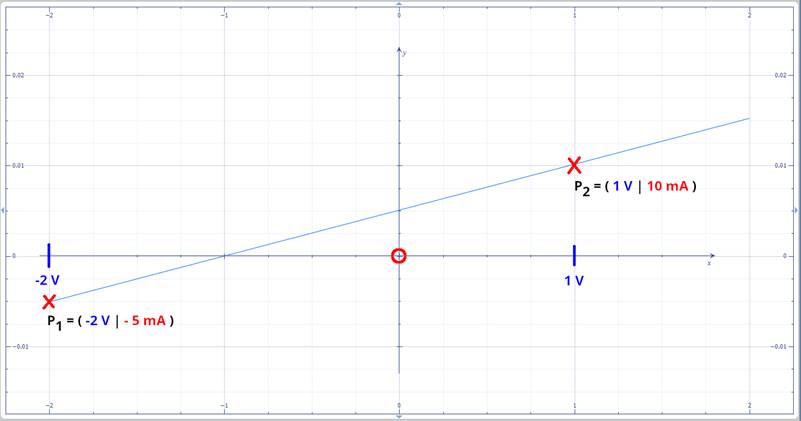
Der Umstand, dass der Widerstandswert vom ohmschen Widerstand R nicht explizit bekannt ist, lenkt den Blick automatisch auf die Wertetabelle, von der wiederum nur zwei Messpunkte P₂ = ( 1 V | 10 mA ) und P₁ = ( -2 V | - 5 mA ) mit P₂ > P₁ vorhanden sind. Diesbezüglich handelt es sich bei P₂ > P₁ um eine wichtige Bedingung, die im vorliegenden Fall aber erfüllt ist.

Wie man anhand der Maßeinheiten der zwei Messpunkte P₂ und P₁ unschwer sieht, lassen sich diese problemlos in die Maßeinheit Ohm [ V / A ] = [ W ] bzw. Kiloohm [ V / mA ] = [ kW ] umformen!

Die Maßeinheit Ohm [ W ] bzw. Kiloohm [ kW ] führt den angehenden Wissenschaftler in die Elektrizitätslehre der Physik oder den angehenden Ingenieur der Elektrotechnik/Elektronik in die Honig süße Versuchung, sofort das Ohmsche Gesetz mit der Formel für den Widerstand R = U / I kritiklos, unkritisch und blauäugig anzuwenden!

Als angehender Wissenschaftler oder Ingenieur sollte man aber beizeiten lernen, sich zukünftig nicht mehr automatisch und spontan auf das Bauchgefühl allein zu verlassen, sondern bereits vorhandenes Wissen analytisch und kritisch zu hinterfragen und zu überprüfen!

Selbstverständlich hindert einen niemand daran, das Ohmsche Gesetz der Form R = U / I ad hoc wie folgt anzuwenden:

R = U / I

= 1 V / 10 mA = 1 V / ( 10 * 10^-3 A ) = 1 V * 10³ / ( 10 A ) = 0,1 * 10³ V/A = 0,1 kW = 100 W " FALSCH!

„Gut gemeint und richtig gerechnet, aber trotzdem falsch gedacht!“ könnte man meinen.

Wenn man sich nämlich die beiden Messpunkte P₂ = ( 1 V | 10 mA ) und P₁ = ( -2 V | - 5 mA ) in ein entsprechendes Koordinatensystem einzeichnet, dann erkennt man sofort, dass die Verbindungsgerade der beiden Messpunkte P₂ und P₁ eben nicht durch den Koordinatenursprung verläuft,

(Zum Vergrößern bitte auf das Bild klicken!)

sodass das Ohmsche Gesetz der Form R = U / I wider Erwarten nicht angewendet werden darf!

Das Ohmsche Gesetz in der Form R = U / I darf nämlich nur dann angewendet und berechnet werden,

· wenn die sogenannte Widerstandsgerade (= Kennlinie) exakt durch den Ursprung des Koordinatensystems verläuft!

Vom Quotienten zum Differenzenquotient

Doch bevor wir die Begriffe „Quotient“ und „Differenzenquotient“ klären, gilt es noch einen weiteren Begriff, der mit dem Begriff „Quotient“ im Zusammenhang steht, zu klären. Und zwar den Begriff „Quote“, den die meisten vom Glückspiel, dem Gewinnspiel oder den Sportwetten her kennen.

In Deutschland ist die Gewinnausschüttung bei Glückspielautomaten in der Spielverordnung geregelt. Die Verordnung schreibt vor, dass die Gewinnausschüttung bei Spielautomaten in Gaststätten, Spielotheken und Bars mindestens 70 % betragen muss. Bei Spielautomaten in Spielhallen und Spielbanken muss die Gewinnausschüttung mindestens 80 % betragen.

Die Gewinnausschüttung wird in Prozent angegeben und bezeichnet den Anteil des eingesetzten Geldes, der an die Spieler ausgeschüttet wird. Eine Gewinnausschüttung von 70 % bedeutet also, dass von 100 Euro Einsatz 70 Euro an die Spieler ausgeschüttet werden und 30 Euro vom Betreiber behalten werden.

Die Gewinnausschüttung ist ein wichtiger Faktor für die Attraktivität von Glückspielautomaten. Spieler möchten natürlich möglichst hohe Gewinne erzielen. Eine hohe Gewinnausschüttung kann dazu beitragen, dass Spieler häufiger spielen und mehr Geld einsetzen.

Demgemäß beträgt die Gewinnquote q der Gewinnausschüttung bei Spielautomaten mindestens q = 80 % = 80 pro ein Hundertstel = 80/100 = 8/10 " 1 : 8/10 = 1 : 0,8.

Vereinfacht ausgedrückt ist eine Quote mathematisch nichts anderes als die Angabe eines Verhältnisses wie z.B. bei einem Bruch, der aus einem ganzzahligen(!) Zähler und Nenner besteht: 8/10. Dabei zählt der Zähler wie oft das Teilungsverhältnis, d.h. der Nenner, angewendet werden soll! Hier also 8 mal so oft: 8/10 = 8 * 1/10 = 8 * 0,1 = 0,8 dezimal = 8/10 = 80/100 = 80 % prozentual.

Im Gegensatz zum Ausdruck „Quote“ bezieht sich der Begriff „Quotient“ rein auf das Mathematische, aber auch auf das Formelmäßige nebst der zugehörigen Maßeinheiten, wie z.B. R = U / I = 25 / 100 V/A = 1 / 4 W = 0,25 W = 250 mW " Maßeinheiten: [ V ] / [ A ] = [ V/A ] = [ W ].

Beim Ohmschen Gesetz R = U / I " konstant(!) " besteht der Widerstand R aus dem Quotienten = U / I.

Wie man unschwer sieht, setzt sich der Begriff „Differenzenquotient“ aus den beiden Begriffen „Differenz“ und „Quotient“ zusammen.

Mathematisch und elektrotechnisch stellt man den Begriff „Differenz“ auch durch den großen, griechischen Buchstaben „∆“ - sprich „Delta“ - dar!

Dabei setzt sich eine Differenz ∆ stets aus einem größeren Zahlenwert abzüglich einem kleineren Zahlenwert zusammen:

∆ = großer Wert W₂ – kleiner Wert W₁

= W₂ – W₁ " W₂ = 10; W₁ = 6 mit W₂ > W₁

= 10 – 6 = 4

Vom Ohmschen Gesetz I über den Differenzenquotienten hin zum Ohmschen Gesetz II

Während

· das Ohmsche Gesetz I in der Form R = U / I

nur dann angewendet und berechnet werden darf, wenn die sogenannte Widerstandsgerade (= Kennlinie) exakt durch den Ursprung des Koordinatensystems verläuft,

muss(!)

· das Ohmsche Gesetz II in der Form R = ∆U / ∆I

stets dann angewendet werden, wenn die Widerstandsgerade (= Kennlinie) nicht durch den Ursprung des Koordinatensystems verläuft, sondern aus dem Ursprung des Koordinatensystems heraus parallel verschoben ist!

Was aber steckt hinter dem Differenzquotienten ∆U / ∆I ?

Das Ohmsche Gesetz II

In der Mathematik beschreibt der Graph der Funktion y = f(x) = 2x + 1 eine Gleichung ersten Grades, d.h. eine linear ansteigende Gerade mit konstanter Steigung m = 2, die aber nicht direkt durch den Ursprung des Koordinatensystems verläuft, sondern aus dem Ursprung heraus um den Wert b = 1 nach oben in Richtung der y-Achse parallel verschoben ist:

(Zum Vergrößern bitte auf das Bild klicken!)

Dabei lässt sich die Steigung m = 2 der Geradengleichung y = 2x + 1 auch mittels des Quotienten ∆y / ∆x wie folgt berechnen:

m = ∆y / ∆x

= 3 / 1,5 = 2 þ

Dabei lässt sich die Steigung m auch mittels des Tangens, abgekürzt „tan“ und des Winkels a wie folgt berechnen:

tan a = Gegenkathete ∆y / Ankathede ∆x

= 3 / 1,5 = 2

Mittels des „Arcus Tangens“, abgekürzt „arctan“, lässt sich schließlich auch noch der Winkel a des Steigungsdreiecks berechnen:

a = arctan(2) = 63,43^o

Wegen des unterschiedlichen Maßstabes bei der Bemaßung des Koordinatensystems lässt sich der Winkel a des Steigungsdreiecks nicht maßstabsgerecht bzw. im 1:1 Seitenverhältnis darstellen. -

In der Physik, der Elektrizitätslehre, dem Ohmschen Gesetz und der Elektrotechnik lässt sich die mathematische Geradengleichung auf die elektrotechnische Widerstandsgerade (= Widerstandskennlinie) wie folgt übertragen:

y = 2x + 1 "

I = 1 / R * U + I₀

= 2 A/V * U + 1 A " 1 / R = 2 A/V " R = ½ V/A = 0,5 W " … und dem Konstantstrom I₀ = 1 A

Für U = 1 V folgt gemäß der Gleichung für die Widerstandsgerade:

I = 1 / R * U + I₀

= 1 / ( 0,5 W ) * 1 V + 1 A

= 1 / ( 1/2 V/A ) * 1 V + 1 A = 2 A + 1 A = 3 A þ (Siehe oben im Kennliniendiagramm!)

U = R * ( I - I₀ )

= 0,5 W * ( 3 A – 1 A ) = 0,5 V/A * 2 A = 1 V þ (Siehe oben im Kennliniendiagramm!)

Jetzt wissen wir, dass die mathematische Steigung m der elektrischen Steigung 1 / R entspricht! Dabei bezeichnet man die elektrische Steigung 1 / R auch als Leitwert G mit der Maßeinheit „Siemens“ = [ S ]

G = 1 / R

= I / U

= ∆I / ∆U " Steigung der Widerstandsgeraden!

= 3 A / 1,5 V = 2 A/V = 2 S = 2 W^-1

= 1 / ( 0,5 W ) = ( 1/2 W )^-1 = 2 W^-1

Winkel a im Steigungsdreieck berechnen

tan a = Länge der Gegenkathete ∆y / Länge der Ankathete ∆x

= Länge der Gegenkathete ∆I / Länge der Ankathete ∆U

= ∆I / ∆U

= 3 A / 1,5 V = 2 A/V = 2 S = 2 W^-1

a = arctan ( 2 ) = 63,4349^o ≈ 63,4^o

Der Winkel a = 63,4^o ist schon ziemlich groß, sodass dementsprechend auch die Steigung der Widerstandsgeraden ziemlich groß ist und die Widerstandskennlinie von links unten vom Ursprung aus steil nach rechts oben verläuft (siehe Diagramm oben). -

Bildet man vom bisherigen Differenzquotienten ∆U / ∆I den reziproken, d.h. umgekehrten Differenzquotienten mit ∆I / ∆U so entspricht dieser der Steigung m = 1 / R = ∆I / ∆U der Widerstandsgeraden (= Kennlinie) auf die sich u.a. mathematisch die Punkt-Steigungs-Form anwenden lässt:

m = 1 / R = ∆I / ∆U "

1 / R = ∆I / ∆U

= ( I₂ – I₁ ) / ( U₂ – U₁ ) mit I₂ > I₁ und U₂ > U₁ oder

= ( I – I₁ ) / ( U – U₁ ) mit I > I₁ und U > U₁ oder

= ( I – I₀ ) / ( U – U₀ ) mit I > I₀ und U > U₀

" Quellenspannung U₀ einer idealen Spannungsquelle

" Konstantstrom I₀ einer idealen Stromquelle

I = 1 / R * ( U – U₀ ) + I₀ " Schaltung mit einer idealen Spannungs- und Stromquelle I₀

oder

R = ∆U / ∆I

= ( U – U₀ ) / ( I – I₀ ) mit U > U₀ und I > I₀

U = R * ( I – I₀ ) + U₀ " Schaltung mit einer idealen Strom- und Spannungsquelle U₀

Für den Fall, dass es keine Spannungsquelle U₀ gibt, folgt: U₀ = 0 "

1 / R = ( I – I₀ ) / ( U – U₀ ) mit I > I₀ und U > U₀ = 0

1 / R * ( U – U₀ ) = ( I – I₀ ) "

1 / R * U = I – I₀ "

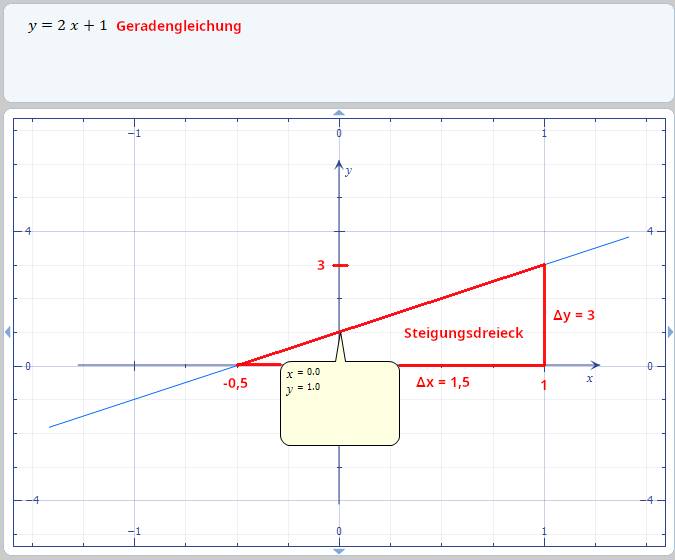
I = 1 / R * U + I₀ mit I₀ ¹ 0 " Gleichung zur Widerstandsgeraden, die sich aus dem Ohmsches Gesetz II ableitet.

Ruft man sich an dieser Stelle die mathematische Geradengleichung in Erinnerung,

y = f(x) = a x + b " a = Steigung, b = Parallelverschiebung aus dem Koordinatenursprung!

so fällt sofort die äquivalente Übereinstimmung zur Gleichung mit der Widerstandsgeraden (= Kennlinie, Geradengleichung) auf!

Für den Fall, dass es keine Stromquelle I₀ gibt, folgt: I₀ = 0 "

1 / R = ( I – I₀ ) / ( U – U₀ ) mit I > I₀ = 0 und U > U₀

1 / R * ( U – U₀ ) = ( I – I₀ ) "

1 / R * ( U – U₀ ) = I "

I = 1 / R * ( U – U₀ ) mit U > U₀ " Gleichung zur Widerstandsgeraden, abgeleitet aus dem Ohmsches Gesetz II.

Da man den beiden Messwerten aus der Wertetabelle mit den Messpunkten P₂ = ( 1 V | 10 mA ) und P₁ = ( -2 V | - 5 mA ) nicht auf Anhieb ansieht, ob die Widerstandsgerade (= Kennlinie) des Widerstandes R eventuell aus dem Koordinatenursprung heraus parallel verschoben ist, gehen wir auf Nummer sicher und berechnen den Widerstand R mittels des zu vor erläuterten Differenzquotienten ∆U / ∆I:

R = ∆U / ∆I

= ( U₂ – U₁ ) / ( I₂ – I₁ )

= [ 1 V – ( -2 V ) ] / [ 10 mA – ( -5mA ) ]

= ( 1 V + 2 V ) / ( 10 mA + 5mA )

= 3 V / 15 mA = 0,2 kW = 200 W þ

Lösung zur Aufgabe b)

b) Berechne den Konstantstrom I₀ an der Stelle I₀ = f(U₀) mit U₀ = 0 V (siehe Wertetabelle).

Mit der erweiterten Widerstandsgeraden (= Kennlinie) gemäß dem Ohmschen Gesetz II

I = 1 / R * ( U – U₀ ) + I₀ " Schaltung mit einer idealen Spannungsquelle U₀ und einer idealen Stromquelle I₀

I = 1 / R * U + I₀ " Schaltung nur mit einer idealen Stromquelle I₀

I₀ = I – ( 1 / R * U )

Für den Messpunkt P₂ = ( 1 V | 10 mA ) folgt dann

I₀ = I₂ – ( 1 / R * U₂ )

= 10 mA – ( 1 / 200 W * 1 V )

= 10 mA – ( 0,005 W^-1 * 1 V )

= 10 mA – ( 0,005 A/V * 1 V ) = 10 mA – 5 mA = 5 mA þ

und für den Messpunkt P₁ = ( -2 V | -5 mA )

I₀ = I₁ – ( 1 / R * U₁ )

= -5 mA – ( 1 / 200 W * -2 V )

= -5 mA – ( 0,005 W^-1 * -2 V )

= -5 mA – ( 0,005 A/V * -2 V ) = -5 mA + 10 mA = 5 mA þ

Logisch, dass sich für die beiden Messpunkte P₂ und P₁ derselbe Konstantstrom I₀ = 5 mA einstellt, da sich ja beide Messpunkte auf der gleichen Widerstandsgeraden (= Kennlinie) befinden!

Demzufolge ergibt sich auch für den Messpunkt P_0V = ( 0 V | ? mA ) an der Stelle I₀ = f(U₀) mit U₀ = 0 V derselbe Konstantstrom I₀ = 5 mA:

I = 1 / R * ( U – U₀ ) + I₀ " Schaltung mit einer idealen Spannungsquelle U₀ und einer idealen Stromquelle I₀

I = 1 / R * U + I₀ " Schaltung nur mit einer idealen Stromquelle I₀

I_0V = 1 / R * U_0V + I₀

= 1 / 200 W * 0 V + 5 mA = 5 mA

oder

U = R * ( I – I₀ )

U_0V = R * ( I_0V – I₀ ) = 0 V " Ein Produkt wird zu Null, wenn ein Term zu Null wird! "

I_0V = I₀ = 5mA

Achtung! Streng genommen wissen wir mathematisch nicht wirklich, ob der Messpunkt P_0V = ( 0 V | 5 mA ) tatsächlich auf der Widerstandsgeraden liegt oder eben nicht! Wenn man aber den Graph der Funktion I = f(U) = 1 / R * U + I₀ zeichnet, dann sieht man sehr wohl, dass der Messpunkt P_0V = ( 0 V | 5 mA ) auf der Widerstandsgeraden liegt!

Umgekehrt wird aber ein Schuh aus dem Ganzen. Nämlich dann, wenn die Werte des Messpunktes P_0V = ( 0 V | 5 mA ) die Geradengleichung der Widerstandsgeraden (= Kennlinie) erfüllen, sodass sich als Ergebnis der Konstantstrom I₀ wie folgt bestätigt:

I = 1 / R * U + I₀ "

I₀ = I_0V – ( 1 / R * U_0V )

= 5 mA – ( 1 / 200 W * 0 V ) = 5 mA þ " siehe Kennlinie weiter oben!

Lösung zur Aufgabe c)

c) Wird bei der elektrischen Schaltung die Stromstärke I_R durch den Widerstand R mittels einer Spannungs-, Strom- oder Spannungs- und Stromquelle aufgebracht?

Gemäß dem Ohmschen Gesetz II (siehe oben) stehen uns im Wesentlichen zwei Berechnungsformeln bzw. Geradengleichungen zur Verfügung, als da sind:

I = 1 / R * ( U – U₀ ) + I₀ " Schaltung mit einer idealen Spannungs- und Stromquelle I₀

U = R * ( I – I₀ ) + U₀ " Schaltung mit einer idealen Strom- und Spannungsquelle U₀

Wie man unschwer sieht, kommen sowohl die ideale Spannungsquelle U₀ als auch die idealen Stromquelle I₀ in beiden Geradengleichungen vor.

Dies ist weiter nicht verwunderlich, da sich beide Geradengleichungen aus dem Differenzenquotienten

R = ( U – U₀ ) / ( I – I₀ ) = ∆U / ∆I = 1 / m mit der Steigung m

zusammensetzen!

Setzt man nämlich die Geradengleichung U = f(I) in die Geradengleichung I = f(U) ein, so folgt:

I = 1 / R * ( U – U₀ ) + I₀

= 1 / R * ( R * ( I – I₀ ) + U₀ – U₀ ) + I₀

= ( I – I₀ ) + I₀ = I þ

Demzufolge bleibt es also uns überlassen, ob wir mit

I = 1 / R * U + I₀ " Schaltung mit einer idealen Stromquelle I₀

oder

U = R * ( I – I₀ )

rechnen:

(Vergrößern: auf Bild klicken! | Circuit JS1, aufgabe_c1.js1)

Messpunkt P₂:

I = 1 / R * U + I₀

I₂ = 1 / R * U₂ + I₀ " Messpunkt P₂ = ( U₂ / I₂ ) = ( 1 V / 10 mA )

= 1 / ( 200 W ) * 1 V + 5 mA = 0,005 A/V * 1 V + 5 mA

= 0,005 A + 5 mA = 5 mA + 5 mA = 10 mA þ

U = R * ( I – I₀ )

U₂ = R * ( I₂ – I₀ )

= 200 W * ( 10 mA - 5 mA )

= 200 V/A * 5 mA = 1000 mV = 1 V þ

Messpunkt P₁:

I = 1 / R * U + I₀

I₁ = 1 / R * U₁ + I₀ " Messpunkt P₁ = ( U₁ / I₁ ) = ( -2 V / -5 mA )

= 1 / ( 200 W ) * ( -2 V ) + 5 mA = 0,005 A/V * ( -2 V ) + 5 mA

= 0,005 A * ( -2 ) + 5 mA = -10 mA + 5 mA = -5 mA þ

U = R * ( I – I₀ )

U₁ = R * ( I₁ – I₀ )

= 200 W * ( -5 mA - 5 mA )

= 200 V/A * -10 mA = -2000 mV = -2 V þ

Messpunkt P_0V:

I = 1 / R * U + I₀

I_0V = 1 / R * U_0V + I₀ " Messpunkt M_0V = ( U_0V / I_0V ) = ( 0 V / 5 mA ) " Konstantstrom I₀ bei U₀ = 0 V

= 1 / ( 200 W ) * ( 0 V ) + 5 mA = 0,005 A/V * ( 0 V ) + 5 mA

= 0,005 A * ( -0 ) + 5 mA = 0 mA + 5 mA = 5 mA þ

U = R * ( I – I₀ )

U_0V = R * ( I_0V – I₀ )

= 200 W * ( 5 mA - 5 mA )

= 200 V/A * 0 mA = 0 V þ

Um die obenstehende Frage, ob es sich bei der Stromversorgung der einfachen Widerstandsschaltung um eine Spannungs- oder Stromquelle handelt, beantworten zu können, muss man wissen, dass es sich beim Strom I₀ um den Konstantstrom einer Konstantstromquelle I₀ handelt, die die Schaltung mit dem ohmschen Widerstand R = 200 W mit Strom versorgt.

Der Unterschied zwischen einer idealen und realen Spannungs- oder Stromquelle

Eine ideale Spannungs- oder Stromquelle, wie hier in der Aufgabe(!), verfügt über keinen Innenwiderstand R_i, sodass sich diese in Verbindung mit dem Ohmsches Gesetz I und/oder II, der Widerstandsgeraden (= Kennlinie) als Funktion I = f(U) mit I = 1 / R * U + I₀ leichter berechnen lässt!

Eine reale Spannungs- oder Stromquelle, wie nachfolgend dargestellt, verfügt sehr wohl über einen Innenwiderstand R_i, sodass sich diese in Verbindung mit dem Ohmsches Gesetz I und/oder II, der Widerstandsgeraden (= Kennlinie) als Funktion I = f(U) mit I = 1 / R * U + I₀ schwerer berechnen lassen!

Dementsprechend braucht es bei der Berechnung der realen Spannungs- oder Stromquelle entsprechende Kenntnisse bezüglich der sogenannten Maschenumläufe (= für Spannungen) und Stromknoten sowie der Superposition (= Überlagerung).

Wegen des Innenwiderstandes R_i von realen Spannungs- oder Stromquellen verfügen diese auch über sogenannte Leerlaufspannungen oder Kurzschlussströme, sodass z.B. die Leerlaufspannung U_leer gleich der Ursprungsspannung U₀ entspricht: U_leer = U₀.

Beim Betrieb einer realen Spannungsquelle sind Ursprungsspannung U₀ und Klemmenspannung U_kl wegen des Innenwiderstandes R_i unterschiedlich groß.

Dabei verhält es sich so, dass sich eine reale, lineare Spannungsquelle U₀ jederzeit in eine reale, lineare Stromquelle I₀ umrechnen lässt (und umgekehrt). Und zwar ganz einfach durch Umplatzieren des Innenwiderstandes R_i:

(Wikipedia: Von Saure, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=12632634 )

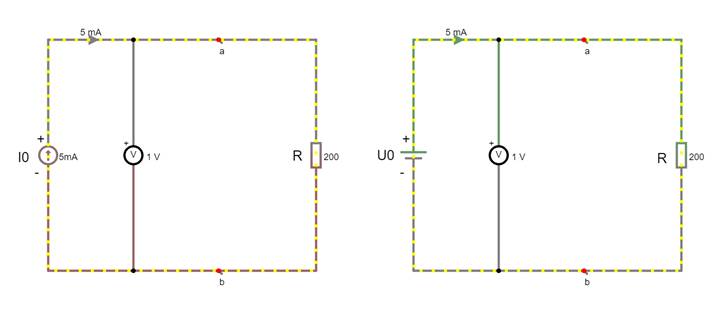
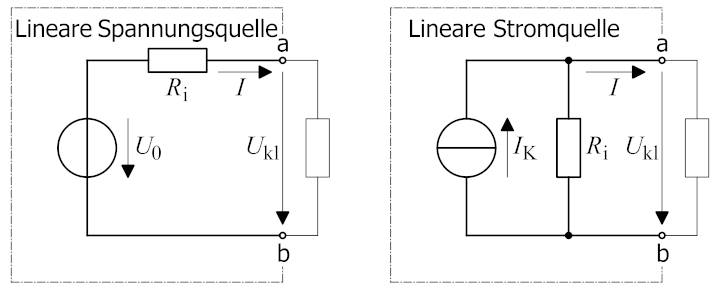
Da sich beide Schaltungen elektrisch äquivalent zueinander verhalten, lässt sich der Kurzschlussstrom I_Kurz am besten links bei der linearen Spannungsquelle U₀ mittels Maschenumlauf wie folgt berechnen:

U_Ri + U_kl – U₀ = 0 " U_kl = U₀ - U_Ri = 0 (!) " Im Kurzschlussfall ist die Klemmenspannung U_kl = 0 V

U₀ = U_Ri

= I₀ * R_i

= 5 mA * 200 W = 1000 mV = 1 V

Zusammen mit der Klemmenspannung U_kl = 0 V folgt für den Kurzschlussstrom I_Kurz:

I_Kurz = I₀ " I_Kurz darf nicht mit dem Konstantstrom I_K der linearen Stromquelle I₀ verwechselt werden!

I₀ = U₀ / R_i

= 1 V / 200 W = 1 V / ( 200 V/A ) = 1 / 200 A = 0,005 A = 5 mA

Während die lineare Spannungsquelle U₀ kurzzeitig durchaus kurzgeschlossen werden darf ( " Kurzschlussspannung U_kl = 0 ), ohne dass die treibende Spannungsquelle U₀ Schaden nimmt und durchbrennt, weil der maximale Kurzschlussstrom I_Kurz durch den in Reihe geschalteten Innenwiderstand R_i begrenzt wird, verhält es sich bei der linearen Stromquelle anders.

Bei der linearen Stromquelle gibt es nämlich keinen in Reihe geschalteten Widerstand, der den maximalen Kurzschlussstrom I_Kurz begrenzen würde!

Was aber ist das Charakteristische einer linearen Stromquelle?

Das Charakteristische einer linearen Stromquelle ist, dass sich die Größe der Klemmenspannung U_kl stets nach dem angeschlossenen Lastwiderstand R_ab an den Anschlussklemmen a und b richtet!

Ist beispielsweise der Lastwiderstand R_ab unendlich groß (R_ab " ¥), dann ist auch die Klemmenspannung U_kl unendlich groß (U_ab " ¥), sodass die lineare Stromquelle wegen der unendlich großen, parallel anliegenden Klemmenspannung U_kl und eines eventuellen Spannungsüberschlages in Form eines Lichtbogens durchschmort!

Des Weiteren würde die unendlich große, parallel anliegende Klemmenspannung U_kl einen unendlich großen Strom I_Ri (I_Ri " ¥) durch den Innenwiderstand R_i der linearen Stromquelle jagen, sodass diese unverzüglich den Hitzetod stirbt!

Jetzt wo wir wissen, worin der Unterschied zwischen einer Strom- und Spannungsquelle besteht, wenden wir uns wieder der Frage c) zu:

c) Wird bei der elektrischen Schaltung die Stromstärke I_R durch den Widerstand R mittels einer Spannungs-, Strom- oder Spannungs- und Stromquelle aufgebracht?

Damit sich die Dinge besser verstehen und leichter berechnen lassen, geht es in der Aufgabe nur um ideale Spannungs- und Stromquellen ohne Innenwiderstand R_i.

Diesbezüglich betrachten wir als Erstes die ideale Spannungsquelle mit der veränderlichen Spannung U₀ und dem (Last-) Widerstand R an den Anschlussklemmen a, b und dem Maschenumlauf im Uhrzeigersinn:

U_ab + ( -U₀ ) = 0 " U_ab = U₀

Da bei der Schaltung mit der idealen Spannungsquelle keine (Konstant-) Stromquelle I₀ vorhanden ist, lässt sich das Ohmsche Gesetz I wie folgt anwenden:

R = U / I " U = R * I "

I = f(U)

= 1 / R * U₀

= 1 / ( 200 W ) * 1 V = 1 / ( 200 V/A ) * 1 V = 0,005 A/V * 1 V = 0,005 A = 5 mA

(Vergrößern: auf Bild klicken! | Circuit JS1, aufgabe_c3a.js1)

Selbstverständlich lässt sich auch das Ohmsche Gesetz II, auch obwohl noch keine (Konstant-) Stromquelle I₀ vorhanden ist, wie folgt anwenden:

R = ∆U / ∆I "

∆I = 1 / R * ∆U

I₂ – I₁ = 1 / R * ( U₂ – U₁ )

I – I₀ = 1 / R * ( U – U₀ )

I = 1 / R * ( U – U₀ ) + I₀

I = 1 / R * ( U – 0 ) + 0

= 1 / R * U " Für U = 1 V einsetzen liefert (siehe oben):

= 1 / ( 200 W ) * 1 V = 1 / ( 200 V/A ) * 1 V = 0,005 A/V * 1 V = 0,005 A = 5 mA þ

Bei der Schaltungssimulation „Circuit Simulator 2.8.1js“ lässt sich die Spannung U der spannungsgesteuerten Spannungsquelle am Schieberegler „Spannung“ im Bereich von [ -2 V, …, +2 V ] beliebig einstellen, sodass sich auf diese Weise die komplette Wertetabelle durchlaufen lässt!

Wie man anhand der letzten Berechnung sieht, stellt sich für I = f(U) = 1 / R * U an der Stelle U = U₀ = 1 V die Stromstärke I = 5 mA ein.

Gemäß der Wertetabelle und der Widerstandsgeraden (= Kennlinie) aus der Aufgabe sollten es aber I = I₂ = 10 mA sein, sodass bezüglich der bisherigen Stromstärke noch 5 mA fehlen, die noch von der Konstantstromquelle I₀ = 5 mA im zweiten, erweiterten Schaltungsteil beigesteuert werden müssen (siehe Stromknoten):

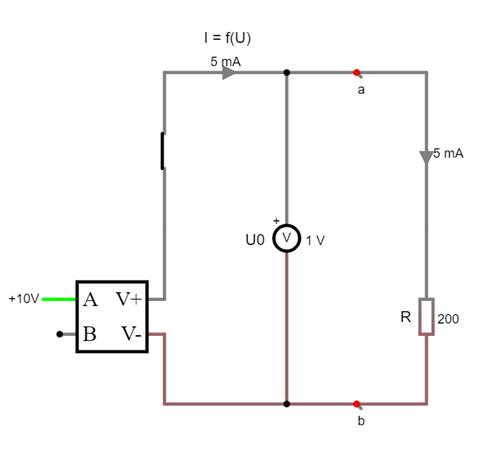
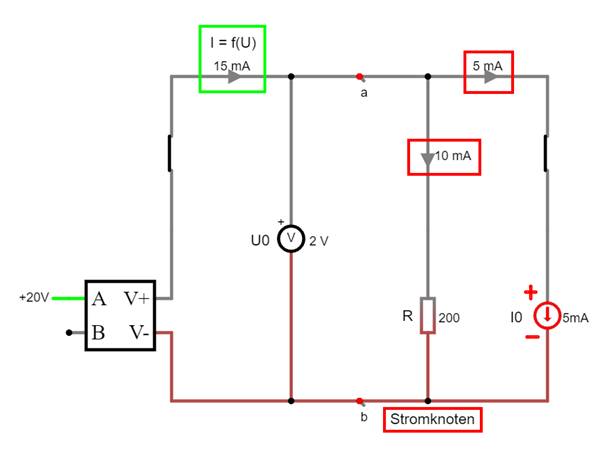
(Vergrößern: auf Bild klicken! | Circuit JS1, aufgabe_c3b.js1)

Wie man anhand der Spannungsmessung durch das Voltmeter mit U₀ = 1 V sieht, führt der Konstantstrom der Stromquelle I₀ mit I₀ = 5 mA am Widerstand R = 200 W zu dem Spannungsabfall von U = U₀ = 1 V.

Der Knackpunkt ist nun aber der, dass auch die spannungsgesteuerte Spannungsquelle links einen Spannungsabfall von U = U₀ = 1 V bewirkt, sodass zwischen beiden Spannungsabfällen wider Erwarten kein spannungsmäßiger Potentialunterschied besteht, der zu einen Gesamtstrom I = 10 mA im Messpunkt P₂ = ( 1 V | 10 mA ) führen würde :

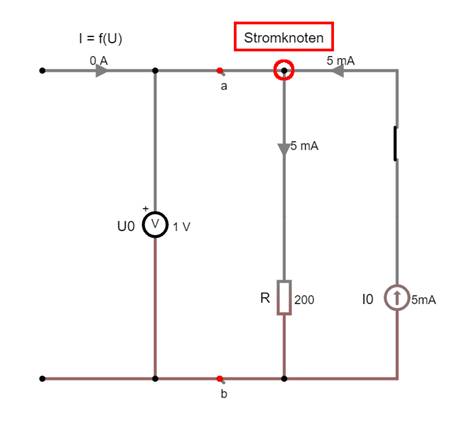
(Vergrößern: auf Bild klicken! | Circuit JS1, aufgabe_c3c.js1)

Der eben beschriebene Sachverhalt lässt sich auch anders beschreiben bzw. ausdrücken, nämlich, dass der Konstantstrom der Stromquelle I₀ mit I₀ = 5 mA den im Stromknoten entgegengesetzt fließenden Strom gleicher Stromstärke der spannungsgesteuerten Spannungsquelle kompensiert, d.h. aufhebt: I = f(U) = 0 A (siehe im Bild oben!).

Gemäß der Funktion I = f(U) = 1 / R * U + I₀ ist aber die spannungsgesteuerte Spannungsquelle V+ der „Antreiber“ der Schaltung, sodass sich gemäß der Widerstandsgeraden (= Kennlinie) für U = U₀ = 1 V eine Stromstärke von

I = f(U)

= 1 / R * U + I₀

= 1 / ( 200 W ) * 1 V + 5 mA = 1 / ( 200 V/A ) * 1 V + 5 mA

= 0,005 A/V * 1 V + 5 mA = 5 mA + 5 mA = 10 mA þ

einstellen muss!

Demzufolge müssen wir schaltungstechnisch dafür sorgen, dass der Konstantstrom der Stromquelle I₀ mit I₀ = 5 mA eben nicht die Stromstärke I = f(U) der spannungsgesteuerten Spannungsquelle V+ von vormals I = f(U) = 5 mA auf nur noch I = 0 A kompensiert!

Die naheliegende Lösung, den Abgabestrom der spannungsgesteuerten Spannungsquelle V+ mittels Verdoppeln der Abgabespannung auf U = U₀ = 2 V mit der Folge, dass sich der dann der Abgabestrom wieder auf I = f(U) = 5 mA vergrößert, ist wider Erwarten nicht zielführend, da sich mit der Spannungsverdoppelung die Wertetabelle und die Kennlinie verändern würden! Gemäß der Kennlinie muss sich aber für eine Abgabespannung von U = U₀ = 2 V eine Stromstärke von I = 15 mA einstellen (siehe orangefarbene Spalte):

I = f(U)

= 1 / R * U + I₀

= 1 / ( 200 W ) * 2 V + 5 mA = 1 / ( 200 V/A ) * 2 V + 5 mA

= 0,005 A/V * 2 V + 5 mA = 10 mA + 5 mA = 15 mA þ

U [V]	-3	-2	-1	0	1	2	3
I [mA]	L	-5	L	5	10	15	L

Wie aber lässt sich die spannungsgesteuerten Spannungsquelle V+ dazu bringen, einen größeren Abgabestrom von I = f(U) = 15 mA zu bewerkstelligen, wenn eine Spannungsverdoppelung aus den genannten Gründen nicht in Frage kommt?

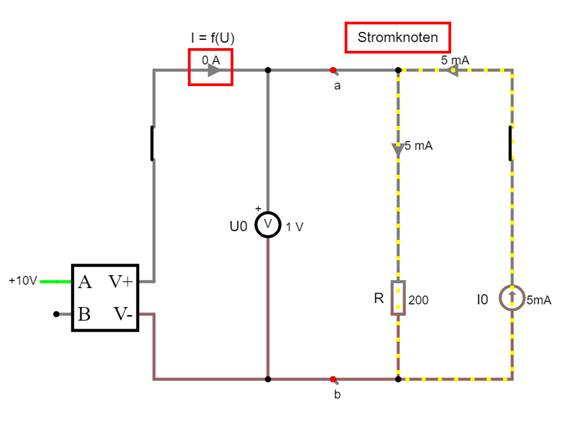
Da eine Spannungsverdoppelung aus den genannten Gründen nicht in Frage kommt, muss man die spannungsgesteuerte Spannungsquelle V+ quasi dazu „zwingen“, einen größeren Abgabestrom von I = f(U) = 15 mA bereitzustellen, indem man diese durch Umpolen der Konstantstromquelle I₀ „anzapft“:

(Vergrößern: auf Bild klicken! | Circuit JS1, aufgabe_c3d.js1)

Wenn man nun noch den Stromknoten betrachtungsmäßig nach unten legt,

(Vergrößern: auf Bild klicken! | Circuit JS1, aufgabe_c3d.js1)

dann lässt sich die Widerstandsgerade (= Kennlinie) in Form der Geradengleichung wieder aus dem rein ohmschen Stromanteil mit I_R = 1 / R * U plus dem Konstantstromanteil I₀ wie folgt zusammensetzen:

I = f(U)

I_ges = 1 / R * U + I₀

= 1 / ( 200 W ) * 2 V + 5 mA

= 10 mA + 5 mA = 15 mA þ

Lösung zur Aufgabe d)

d) Wie groß muss die Spannung U der Spannungsquelle sein, damit durch den Widerstand R exklusiv ein Strom I_R der Stromstärke I_R = 20 mA fließt? Der zuvor berechnete und zugrunde gelegte Konstantstrom I₀ sowie der Widerstand R sollen dabei unverändert bleiben!

Wegen der Reihenschaltung der Spannungsquelle mit dem Widerstandes R lässt sich die Stromstärke auf I_R = 20 mA nur vergrößern, indem man die Spannung U der Spannungsquelle entsprechend vergrößert, da ja der zugrunde gelegte Konstantstrom mit I₀ = 5 mA sowie der Widerstand mit R = 200 W unverändert bleiben sollen!

Wer jetzt meint, einfach mit dem Ohmschen Gesetz I drauflos rechnen zu können, muss aufpassen, dass er mit dem „richtigen“ Strom rechnet:

U = R * I " Ohmschen Gesetz I allgemein!

U_R = R * I_R " Ohmschen Gesetz I …" darf in der Schaltung nur auf den Widerstand R angewendet werden!

= 200 W * 20 mA = 4000 mV = 4 V "

Die Berechnung ist richtig, da ja der zugrunde gelegte Konstantstrom I₀ in der Berechnung unberücksichtigt geblieben ist!

Achtung!

Ab jetzt müssen wir höllisch aufpassen, ob wir mit I = I_ges = I_R + I₀ rechnen oder nur mit I_R = I – I₀.

Dies betrifft insbesondere auch die Wertetabelle, die sich stets auf I = I_ges = I_R + I₀ bezieht!

Schließlich geht es jetzt bei der Aufgabenstellung exklusiv darum, dass die Stromstärke durch den Widerstand R auf I_R = 20 mA angehoben wird. Aber eben nicht mittels des Konstantstroms von I₀ = 5 mA, sondern mittels der Spannungsquelle U = U₀ = 4 V.

Alternativ lässt sich das Ganze auch mit dem Ohmschen Gesetz II wie folgt berechnen:

I_ges = 1 / R * U + I₀ "

… Wegen der Parallelschaltung von Widerstand R und der Konstantstromquelle I₀ gilt: U = U_R

= 1 / R * U_R + I₀ "

U_R = R * I_R

= R * ( I_ges - I₀ )

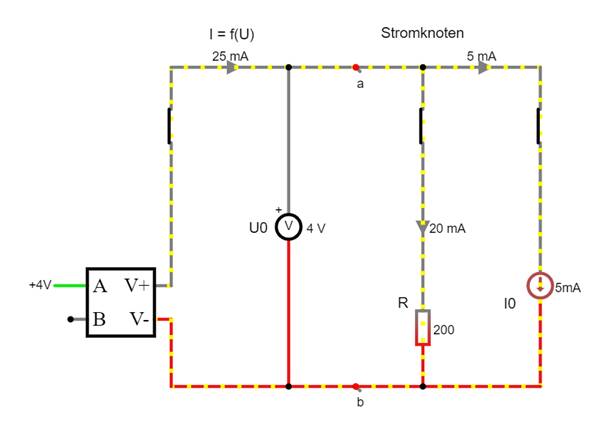
= 200 W * ( 25 mA – 5 mA )

= 200 W * 20 mA = 200 V/A * 20 mA = 4000 mV = 4 V " RICHTIG wegen I_ges = I_R + I₀

Für den oberen Stromknoten gilt nämlich:

I_ges + ( -I_R ) + ( -I₀) = 0 "

I_ges = I_R + I₀

= 20 mA + 5 mA = 25 mA þ

Dabei gilt vereinbarungsgemäß für den oberen Stromknoten:

Alle in den Stromknoten hinein fließenden Ströme werden positiv gezählt und alle aus dem Stromknoten heraus fließenden Ströme werden negativ gezählt!

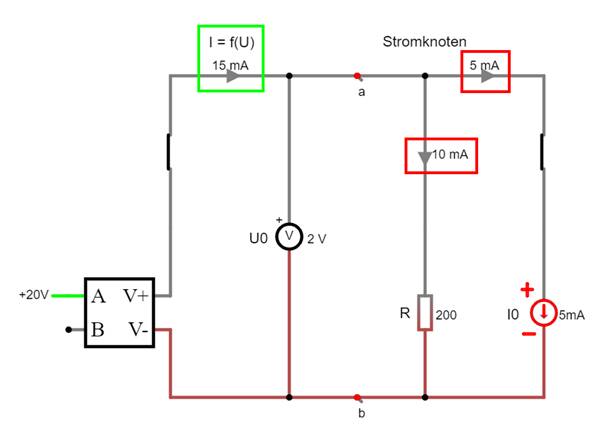
Nur wer die Schaltung richtig versteht und bei der Berechnung den Stromknoten mit einbezieht,

(Vergrößern: auf Bild klicken! | Circuit JS1, aufgabe_c3f.js1)

ist auch in der Lage richtig zu rechnen! –

Wie man sieht, lässt sich die Wertetabelle jetzt wie folgt erweitern:

U [V]	-3	-2	-1	0	1	2	3	4
I [mA]	L	-5	L	5	10	15	L	25

Allerdings mehr theoretisch, weil wir nicht wissen, welche maximale Spannung sich mittels der regelbaren Spannungsquelle einstellen bzw. realisieren lässt. -

Hinweis zum Thema „Stromquellen“:

Stromquellen gibt es z.B. im Facheinzelhandel nicht einfach so zu kaufen wie herkömmliche Batterien (= Spannungsquellen) in Form von 1,5 Volt Rundzellen vom Typ „AA“ (= „Mignon“), Typ „AAA“ (= „Micro“) oder 9 Volt Blockbatterien, da Stromquellen meistens nur in Labornetzgeräten und deren Elektronik verbaut sind!

Immer dann, wenn sich bei einem (Labor-) Netzgerät die abgegebene Stromstärke, z.B. im Bereich von [ 0, …, 2 ] A, mittels eines Reglers (= Potentiometer) einstellen lässt,

(Programmierbare Labornetzteile mit zwei Ausgängen | Quelle: Wikipedia)

hat man es im Inneren bei der Elektronik mit einer einstellbaren Konstantstromquelle zu tun:

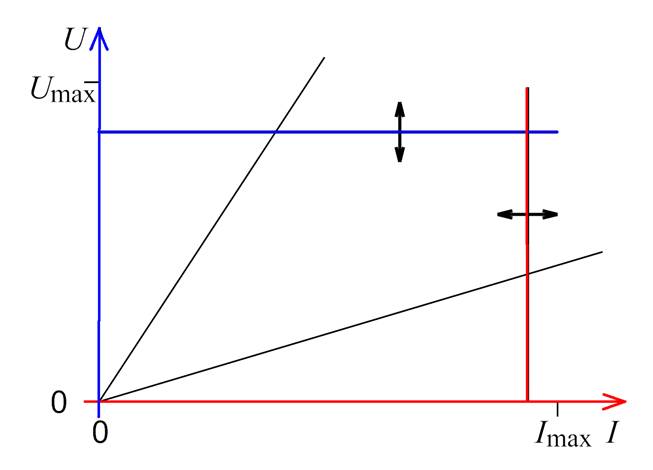
(Kennlinie eines Labornetzgerätes mit einstellbarer Spannungs- und Strombegrenzung;

ferner zwei Last-Kennlinien (dünne Linien)
Quelle: Wikipedia)

Lösung zur Aufgabe e)

e) Zeichne den Graphen der Funktion I_R = f(U_R) zur obenstehenden Wertetabelle mit dem Maßstab 1 V " 2 cm
und 5 mA " 2 cm.

In der Mathematik, aber auch in der Elektrotechnik, gibt zu jeder rechnerischen, formelmäßigen Lösung oder Lösung mittels der Geradengleichung y = m x + b bzw. der Widerstandsgeraden I = 1 / R * U * I₀ eine grafische, d.h. zeichnerische Lösung.

So auch im vorliegenden Fall, wo ausgehend von der Wertetabelle zunächst die zeichnerische, d.h. grafische Lösung in Form der Widerstandsgeraden vorgenommen werden soll, um dann später auf die mathematische bzw. elektrotechnische Lösung mittels der entsprechenden Funktionsgleichung I = f(U) = 1 / R * U * I₀ zu gehen.

Wenn man als geübter und erfahrener Elektrotechniker die bruchstückhafte Wertetabelle aus dem Schlaf heraus lesen und interpretieren kann, weil man bei den beiden Messwerten bzw. Messpunkten P₂ = ( U₂ / I₂ ) = ( U_1V / I_{10 mA} ) = ( 1V / 10 mA) und P₁ = ( U₁ / I₁ ) = ( U_-2V / I_{-5 mA} ) = ( -2 V / -5 mA ) mit P₂ > P₁ sofort

· die Zwei-Punkte-Form,

· die Geradengleichung und

· die Widerstandsgerade I = 1 / R * U * I₀ vor dem geistigen Auge sieht, wozu dann auch

· der mathematische Differenzenquotient m = ∆y / ∆x für die Steigung der Geradengleichung mit

Steigung m = tan α = Gegenkathede ∆y / Ankathede ∆x

· der elektrotechnische, rezibroke Differenzenquotient 1 / R = ∆I / ∆U und

· der differentielle Widerstand R = ∆U / ∆I " r = dU / dI gehören,

dann sei es einem vergönnt, dass man sich anstelle der händischen, zeichnerischen Lösung eines entsprechenden Werkzeuges in Form einer Software bedient.

Und zwar des Programms „Microsoft Mathematics“ von Microsoft, das es kostenlos für das Windows-Betriebssystem zum Herunterladen gibt:

(Vergrößern: auf Bild klicken! | MS Mathematics, widerstandsgerade_03.gcw)

Lösung zur Aufgabe f)

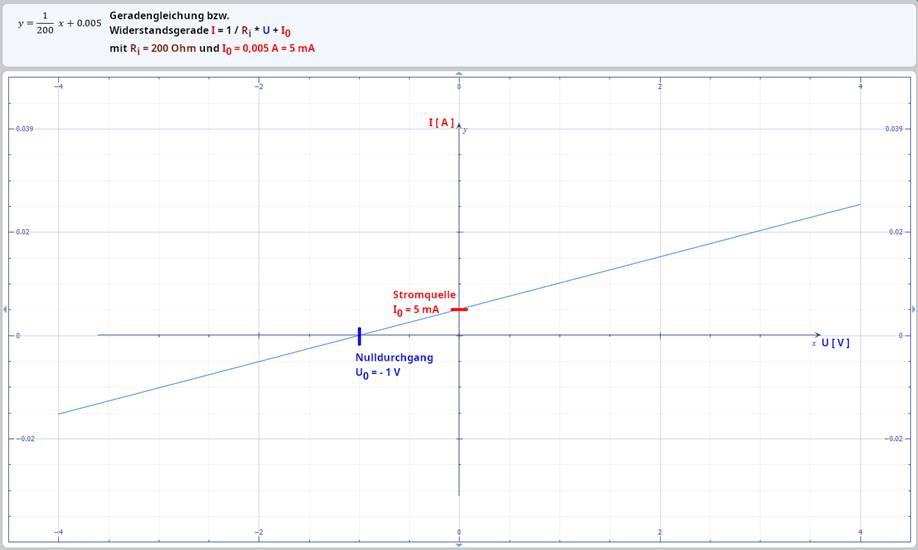
f) Welche Stromstärke I₀ lässt sich am Schnittpunkt der Widerstandsgeraden mit der Stromachse (= Senkrechte) ablesen?

Am Schnittpunkt der Widerstandsgeraden mit der Stromachse (= Senkrechte) lässt sich die Stromstärke I₀ = 5 mA ablesen! -

Lösung zur Aufgabe g)

g) Interpretiere den Wert der Stromstärke I₀ > 0 am Schnittpunkt mit der Spannung U₀ = 0.

Die Stromstärke I₀ = 5 mA > 0 am Schnittpunkt mit der Spannung U₀ = 0 V deutet darauf hin, dass die einfache Widerstandsschaltung mittels einer linearen (Konstant-) Stromquelle I₀ mit Strom versorgt wird! Deswegen auch die Parallelverschiebung der Widerstandsgeraden aus dem Koordinatenursprung heraus!

Wegen der Parallelverschiebung der Widerstandsgeraden aus dem Koordinatenursprung heraus, d.h. wegen des Vorhandenseins der linearen (Konstant-) Stromquelle I₀, muss dann auch zwingend mit der (linearen) Gleichung für die Widerstandsgeraden gerechnet werden: I = 1 / R * U + I₀.

Und zwar mit R_i = 200 W und I₀ = 5 mA (siehe Schnittpunkt bei U = 0 V ). -

Lösung zur Aufgabe h)

h) Wende die (mathematische) Geradengleichung auf die (elektrotechnische) Widerstandsgerade an!

Mathematisch lässt sich die obenstehende Widerstandsgerade für einen linearen, d.h. rein ohmschen Widerstand mittels der Geradengleichung wie folgt berechnen:

y = m x + b " mathematische Geradengleichung

m = Steigung der Geraden mit m = ∆y / ∆x

b = Parallelverschiebung der Geraden aus dem Koordinatenursprung heraus

Elektrotechnisch lässt sich die obenstehende Widerstandsgerade für einen linearen, d.h. rein ohmschen Widerstand, wie folgt berechnen:

I = 1 / R * U + I₀ " elektrotechnische Geradengleichung (= Kennlinie)

1 / R = Steigung der Widerstandsgeraden mit 1/R

= ∆I_R / ∆U_R

= ( 10 mA – (-5 mA ) ) / ( 1 V – (-2 V) )

= ( 10 mA + 5 mA ) / ( 1 V + 2 V ) = 15 mA / 3 V = 5 mA / V = 5 mW^-1

R = ∆U_R / ∆I_R

= 1 / ( 5 mW^-1 ) = 1 / ( 5 * 10^-3 W^-1 ) = 1 * 10³ W / 5 = 1000 / 5 W = 200 W

I₀ = Konstantstrom, d.h. Parallelverschiebung der Widerstandsgeraden aus dem Koordinatenursprung heraus

= Schnittpunkt der Widerstandsgeraden mit der Senkrechten, d.h. der Stromachse I = f(U)

= I_R – 1 / R * U_R

= 10 mA – 1/200 W * 1 V = 0,010 A – 1 / ( 200 V/A ) * 1 V = 0,010 A – 1 / 200 A = 0,010 A – 0,005 A

= 10 mA - 5 mA = 5 mA

[ easy electronik 200 ] [ Seitenanfang ] [ Versuch 8 ] [ Versuch 10 ] [ Versuch 17 ]