[ easy electronic 200 ] [ Seitenende ] [ Versuch 95 ]

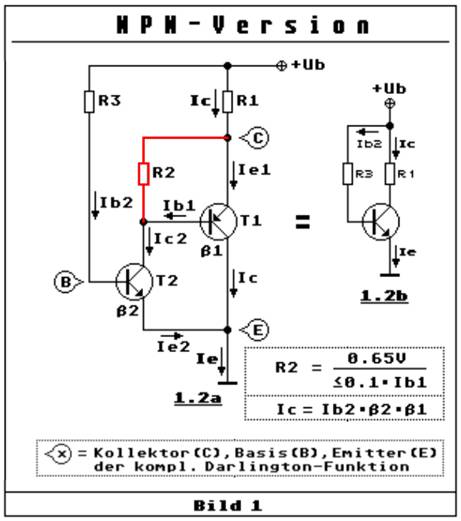
easy electronic 200 - Versuch 102

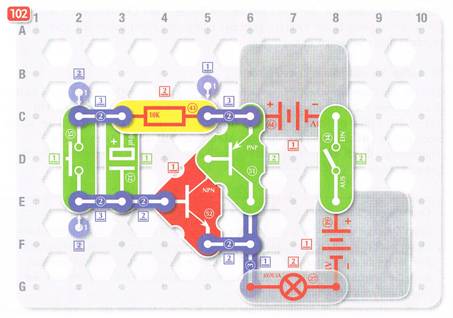
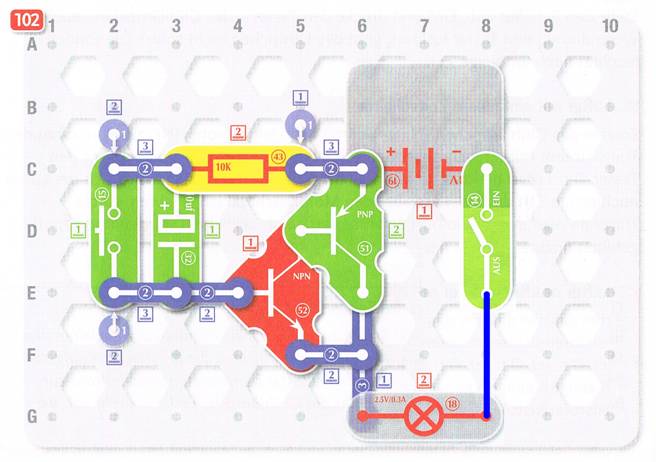
Lampe mit Zeitverzögerung (1)

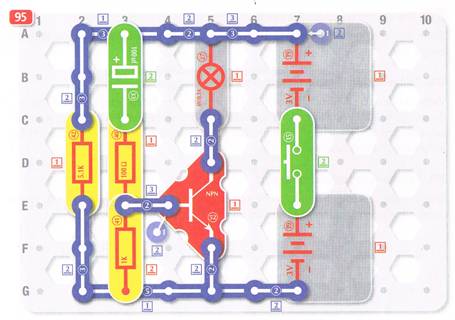
Wenn man die Schaltung vom Versuch 102 (nachfolgendes Bild links) mit der vom Versuch 95 (nachfolgendes Bild rechts) vergleicht, dann stellt man fest, dass beide mit den in Reihe geschalteten Batteriefächern 19 an einer Batteriespannung von U_{Batt, ges} = 6,0 V betrieben werden.

Ferner fällt auf, dass sich der Kondensator beider Schaltungen im Basis-Kollektor-Kreis des NPN-Transistors 52 befindet. Dabei fällt aber auch auf, dass beim Versuch 102 (links) der kleinere Kondensator 32 mit C₃₂ = 10 µF und beim Versuch 95 (rechts) der größere Kondensator 33 mit C₃₃ = 100 µF verwendet wird.

Während also der Kondensator in der linken Schaltung nur 1/10 so groß ist wie in der rechten Schaltung, verhält es sich bei den beiden Aufladewiderständen Widerstand R₄₃ = 10 kΩ (links) und Widerstand R₄₀ = 100 Ω genau umgekehrt, ist der Widerstand R₄₃ in der linken Schaltung 100x so groß als der Widerstand R₄₀ in der rechten Schaltung!

Um herauszufinden, was es mit den beiden Kondensatoren 32 und 33 sowie den Aufladewiderständen R₄₀ und R₄₃ auf sich hat, berechnen wir die jeweilige Zeitkonstante τ = R * C wie folgt:

τ_C32 = R₄₃ * C₃₂ → Aufladedauer t_{Auf, C32} = 5 * τ_C32

t_{Auf, C32} = 5 * 10 kΩ * 10 µF = 5 * 10 * 10³ V/A * 10 * 10^{-6 3} As/V

= 5 * 10 * 10 * 10^-3 s = 500 * 10^-3 s = 500 ms (Bild unten, links)

τ_C33 = R₄₀ * C₃₃

t_{Auf, C33} = 5 * 100 Ω * 100 µF = 5 * 100 V/A * 100 * 10^-6 As/V

= 50 000 * 10^{-6 3} s = 50 * 10^-3 s = 50 ms (Bild unten, rechts)

Zum Vergleich der Aufladungszeiten t_Auf: t_{Auf, C33} < t_Auf < t_{Auf, C32}

Wenn man nun die beiden Aufladungszeiten t_{Auf, C32} von der linken Schaltung (Versuch 102) mit t_{Auf, C33} von der rechten Schaltung (Versuch 95) vergleicht, dann fällt sofort auf, dass sich der große Kondensator 33 mit C₃₃ = 100 µF viel schneller auflädt als der kleinere Kondensator 32 mit C₃₂ = 10 µF: t_{Auf, C33} < t_Auf < t_{Auf, C32}.

Und das, obwohl ja gerade der große Kondensator 33 mit C₃₃ = 100 µF wegen seiner um den Faktor 10x größeren Kapazität eigentlich viel länger bräuchte, um sich vollständig aufzuladen!

Aber im Gegensatz zum größeren Kondensator 33 mit C₃₃ = 100 µF „fährt“ der kleinere Kondensator 32 mit C₃₂ = 10 µF, der sich ja eigentlich viel, viel schneller aufladen könnte, sozusagen mit „angezogener Handbremse“, weil er vom großen (Auflade-) Widerstand R₄₃ = 10 kΩ „ausgebremst“ wird (siehe nachfolgende Schaltung links):

(Zum Vergrößern bitte auf das Bild klicken!)

Wenn man die beiden obenstehenden Schaltungen weiter miteinander vergleicht, dann fällt noch auf, dass die linke Schaltung (Versuch 102) mit zwei nacheinander geschalteten Transistoren arbeitet. Und zwar mit dem roten NPN-Steuertransistor 52, gefolgt vom nachfolgenden grünen PNP-Leistungstransistor 51.

Dabei gilt es zu beachten, dass der Emitter des roten NPN-Steuertransistors 52 direkt mit dem Emitter des grünen PNP-Leistungstransistors 51 verbunden ist! Deshalb spricht man auch von einer sogenannten komplementären Darlington-Schaltung, die man auch Sziklai-Paar (-Schaltung) nennt.

Und da sich das Glühlämpchen 27 als Lastwiderstand (= Verbraucher) ausgangsseitig im Emitterkreis beider Transistoren befindet, handelt es sich bei der links obenstehenden Sziklai-Paar (-Schaltung) um eine Kollektorschaltung bei der der Emitter des grünen PNP-Leistungstransistors 51 (links) auf den „+“-Pol der 6 V Batterie als Masse („┴“) gelegt ist. Und weil das Glühlämpchen 27 als Lastwiderstand den zusammengeschalteten Emittern folgt, nennt man die Kollektorschaltung auch Emitterfolger.

Frage:

Braucht man, damit das Glühlämpchen 27 beim Einschalten als auch beim Drücken des Tasters 15 länger leuchtet unbedingt die links obenstehende Schaltung (Versuch 102) mit zwei Transistoren?

Ja, da beide Transistoren in der Sziklai-Paar-Schaltung über eine mehrfach so große Stromverstärkung B = B1 * B2 verfügen als wenn man nur einen Transistor verwenden würde:

B = B1 * B2

= B_T52 * B_T51

= 250 * 50 = 12 500-fache Stromverstärkung!

Wie man sieht, verfügt der rote NPN-Steuertransistor 52 über ein 50-fach größere Stromverstärkung als der grüne PNP-Leistungstransistor 51 (siehe auch Versuch 72).

Dabei bietet die hohe Stromverstärkung den entscheidenden Vorteil, dass sich der kleine Kondensator 32 mit C₃₂ = 10 µF mit dem sehr kleinen Basisstrom von I_B1 = 230 µA (Berechnung sie weiter unten) über einen sehr langen Zeitraum aufladen lässt, sodass das Glühlämpchen 27 entsprechend lange leuchtet!

Bevor wir nun aber fortfahren, gilt es noch sich mit der Wärmeverlustleistung des grünen PNP-Leistungstransistors 51 zu befassen. Und zwar aus folgendem Grund:

(Zum Vergrößern bitte auf das Bild klicken!)

Immer dann, wenn man mit einem Transistor die Leistung (= Spannung und Strom) eines Verbrauchers wie die des Glühlämpchens 27 bezüglich der Helligkeit regelt, entsteht im Transistor schädliche, weil Lebensdauer verkürzende Wärmeverlustleistung am Emitter-Kollektor-Bahnwiderstand r_EC mit

P_EC = u_EC * i_EC = u_EC * u_EC / r_EC = u_EC² / r_EC

= i_EC * r_EC * i_EC = i_EC² * r_EC ,

die es zu beobachten und zu reduzieren gilt!

Im vorliegenden Fall mit den zwei Batteriefächern 19 und der 6 Volt Spannungsversorgung sowie dem Glühlämpchen 27 wird nämlich der grüne PNP-Leistungstransistor 51 während des Dimmens (= Abdunkelns) mittels Verlustleistung behaftetem Längsregler sehr heiß, sodass man sich an diesem die Finger verbrennen kann!

Damit der grüne PNP-Leistungstransistor 51 nicht vorzeitig das Zeitliche segnet, entfernen wir ein Batteriefach 19, sodass die Schaltung (Versuch 102) nur noch mit U_Batt = 3,0 V Spannung versorgt wird!

Zu diesem Zweck wird dann auch das 6 Volt Glühlämpchen 27 gegen das 2,5 Volt Glühlämpchen 18 ausgewechselt:

(Zum Verbessern bitte auf das Bild klicken!)

Ausgehend von dem Glühlämpchen 18 mit den Nenn-Betriebswerten U_{Glüh 18, Nenn} = 2,5 V und I_{Glüh 18, Nenn} = 0,3 A mit R_Glüh 18 = U_{Glüh 18, Nenn} / I_{Glüh 18, Nenn} = 2,5 V / 0,3 A = 8,33 Ω folgt für den Kollektorstrom I_C2 des grünen PNP-Leistungstransistor 51 (T2):

I_C2 = ( U_{Batt, ges} – U_{CE2, satt} ) / R_{Glüh 18, Nenn}

= ( 3,0 V – 0,2 V ) / 8,33 Ω = 2,8 V / 8,33 Ω = 0,33613 A ≈ 336 mA → U_{CE2, satt} = 0,2 V → Sättigung von T2!

I_C2 = ( U_{Batt, ges} – U_CE2 ) / R_{Glüh 18, Nenn}

= ( 3,0 V – 1,2 V ) / 8,33 Ω = 1,8 V / 8,33 Ω = 0,2161 A ≈ 216 mA → U_CE2 = 1,2 V → Normalbetrieb von T2!

In diesem Zusammenhang sei nochmals daran erinnert, dass sich der Transistor nicht nur als analoger Spannungsregler (oder Stromregler) betreiben lässt mit dem sich die Spannung am Lastwiderstand einstellen oder regeln lässt, sondern auch als quasi digitaler Ein- und Ausschalter (Ein = engl. „On“ = „1“, Aus = engl. „Off“ = „0“).

Diesbezüglich gilt es zu beachten, dass sich ein Transistor, der ausschließlich als elektronischer Schalter betrieben wird, mit größeren Einschaltströmen betreiben lässt, weil die Wärmeverlustleistung der Kollektor-Emitter-Strecke im sogenannten Sättigungsbetrieb deutlich niedriger ausfällt!

>> Als Sättigung (auch Sättigungsbetrieb) wird der vollständig leitende Zustand bei Halbleiterelementen wie Bipolar-Transistoren bezeichnet. Bevor ein Halbleiter in die Sättigung kommt, geht dieser zuerst in die sogenannte Kompression. Kompression bedeutet, dass die Verstärkung (Gain) eines Verstärkers mit größer werdender Eingangsleistung abnimmt.

Eine Erhöhung der Steuerspannung oder des Steuerstromes bewirkt keine nennenswerte Änderung des Ausgangssignals.

Befindet sich der Transistor in Sättigung, ist die Kollektor-Emitter-Spannung U_CE kleiner als seine Basis-Emitter-Spannung U_BE. Die Sättigungsspannung U_CEsat ist von der Übersteuerung, der Vorwärtsverstärkung und der Inversverstärkung des BJT abhängig und kann bis auf wenige zehn mV sinken.

Ein Transistor wird bewusst in Sättigung betrieben, wenn dieser als Schalter eingesetzt wird. << (Quelle: Wikipedia)

(Vergrößern: auf das Bild klicken! | Quelle: Elektronik-Kompendium)

Mit den Stromverstärkungen B1 = 250 für den Steuertransistor T1 und B2 = 25 für den Leistungstransistor T2 folgt:

I_B1 = 1 / B * I_C2

= 1 / ( B2 * B1 ) * I_C2

= 1 / ( 25 * 250 ) * 336 mA = 1 / ( 6 250 ) * 336 mA = 0,00016 * 336 mA = 0,05376 mA ≈ 53,76 µA

R_B1 = U_{Batt, ges} + ( - U_E1B1 - U_{Glüh 18} ) / I_B1

= 3,0 V + ( - 0,7 V - 1,97 V ) / 53,76 µA

= 0,33 V / 53,76 µA = 0,006138 * 10⁶ Ω ≈ 6,14 * 10³ Ω = 6,14 kΩ

Da es im Experimentierkasten keinen Widerstand R_B1 = 6,14 kΩ gibt, nehmen wir den nächst größeren Widerstand R₄₃ = 10 kΩ als Basis- und Aufladewiderstand, insbesondere dann, wenn es darum geht, dass das Glühlämpchen 18 längere Zeit nachleuchtet!

Mit dem Widerstand R₄₃ = 10 kΩ muss man den Basisstrom I_B1 wie folgt neu berechnen:

R₄₃ = U_{Batt, ges} + ( - U_E1B1 - U_{Glüh 18} ) / I_B1

I_B1 = ( U_{Batt, ges} - U_E1B1 - U_{Glüh 18} ) / R₄₃

= ( 3,0 V - 0,7 V - 1,97 V ) / 10 kΩ = 0,33 V / 10 kΩ = 0,033 mA = 33 µA → … gemessen: 25 µA mit t_Auf ≈ 10 s

Wenn man die Nachleuchtdauer des Glühlämpchen 18 stoppt, dann stellt man erstaunt fest, dass diese bei t_{Glüh 18} ≈ 10 s liegt, obwohl sich für die Aufladezeit t_{Auf, C32} nur ein Wert von t_{Auf, C32} = 0,5 s berechnen ließ (siehe obenstehendes Bild, links).

Frage:

Wie lässt sich der große Unterschied zwischen der Aufladezeit t_{Auf, C32} und der Nachleuchtdauer t_{Glüh 18} des Glühlämpchens 18 erklären?

Um die Frage beantworten zu können, müssen wir die beiden gegensätzlichen Schaltungen analysieren:

(Zum Vergrößern bitte auf eines der Bilder klicken!)

In der links obenstehenden Schaltung (Versuch 102) handelt es sich aus der Sicht des roten NPN-Steuertransistors 52 um eine Kollektorschaltung, bei dem das Glühlämpchen 18 als Lastwiderstand R_{Glüh 18} dem Emitter gegen Masse („┴“) folgt:

(Vergrößern: auf Bild klicken! | Quelle: Wikipedia)

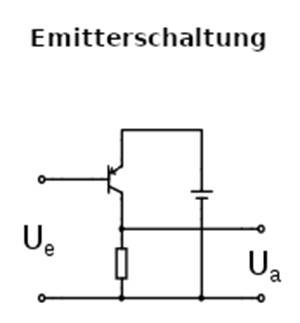
Und aus der Sicht des grünen PNP-Leistungstransistors 51 handelt es sich bei diesem um eine Emitterschaltung, bei dem das Glühlämpchen 18 als Lastwiderstand R_{Glüh 18} dem Kollektor gegen Masse („┴“) folgt (siehe rechts obenstehende Schaltung).

Da es sich beim roten NPN-Steuertransistor 52 und dem grünen PNP-Leistungstransistor 51 um komplementär zusammengeschaltete Transistoren handelt, haben wir es bei der links obenstehenden Schaltung (Versuch 102) wieder bzw. immer noch mit einer Sziklai-Paar-Schaltung zu tun:

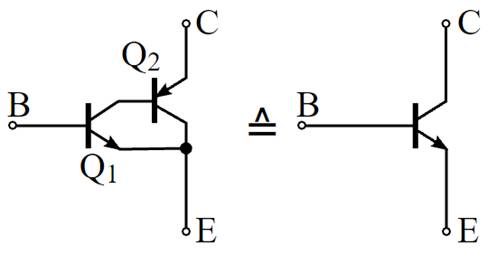
(Vergrößern: auf Bild klicken! | Quelle: Wikipedia)

Wie man anhand des obenstehenden Bildes sieht, lassen sich hier im Versuch 102 die beiden komplementär zusammengeschalteten Transistoren zu einem NPN-Transistor zusammenfassen. Im vorliegenden Fall wäre das dann der rote NPN-Steuertransistor 52 und zusammen mit dem nachgeschalteten Glühlämpchen 18 als Lastwiderstand R_Glüh 18 handelt es sich dann bei der Schaltung um einem sogenannten Emitterfolger (= Kollektorschaltung) mit Stromgegenkopplung:

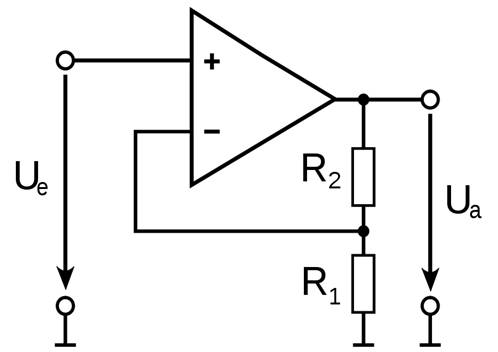
(Vergrößern: auf Bild klicken! | Quelle: Wikipedia)

Wie man anhand der obenstehenden Schaltung mit einem Operationsverstärker (OPV) sieht, gibt es im Ausgangsbereich (rechts) einen Spannungsteiler, der sich aus den beiden Widerständen R₂ und R₁ und dem Mittelabgriff zusammensetzt, sodass ein Teil der Ausgangs- bzw. Lastspannung wieder auf den invertierenden Spannungeingang („-“) des OPVs zurückgeführt wird und dabei die Verstärkung des OPVs entsprechend verringert.

Tauscht man in der obenstehenden Schaltung den OPV gegen den grünen PNP-Leistungstransistor 51 aus, dann entspricht der Widerstand R₂ dem Bahnwiderstand r_EC der Emitter-Kollektor-Strecke und der Widerstand R₁ dem Lastwiderstand R_Last = R_{Glüh 18} (= Glühlämpchen 18):

α = R₁ / ( R₁ + R₂ )

= R_{Glüh 18} / ( R_{Glüh 18} + r_EC2 ) →

Nebenrechnung:

R_{Glüh 18} = U_{Glüh 18} / I_{Glüh 18}

= ( U_Batt – u_EC2 ) / I_{Glüh 18}

= ( 3,0 V – 0,4 V ) / 336 mA = 2,6 V / 336 mA = 7,738 Ω ≈ 7,7 Ω

r_EC2 = u_EC2 / i_EC

= ( U_Batt – U_{Glüh 18} ) / i_EC ≈ ( U_Batt – U_{Glüh 18} ) / I_{Glüh 18}

= ( 3,0 V – 2,6 V ) / 336 mA = 0,4 V / 0,336 A ≈ 1,19 Ω

α = R_{Glüh 18} / ( R_{Glüh 18} + r_EC2 ) →

= 7,7 Ω / ( 7,7 Ω + 1,19 Ω ) = 7,7 Ω / 8,89 Ω ≈ 0,866

Immer dann, wenn die Verstärkung einen Wert wie z.B. α = 0,866 < 1 aufweist, handelt es sich bei dieser um eine Dämpfung bei der die Verstärkung mittels Rückkopplung verringert wird.

Berechnung der Stromgegenkopplung - zum Ersten

Der Begriff „Stromgegenkopplung“ hört sich einerseits interessant an, andererseits auch etwas mysteriös. Aber das liegt daran, weil wir uns unter dem Begriff noch nichts Praktisches vorstellen können. Wenn man den Ausdruck analysiert, dann wird ein Strom gegengekoppelt. Aber welcher? Und gegen was gegengekoppelt? An was lässt sich ein Strom koppeln?

Wenn man sich die Funktion I = f(U), sprich „Der Strom I ist eine Funktion der Spannung U“, dann bedeutet das, dass der Strom I von der Spannung U abhängt bzw. an diese gekoppelt ist. Das bedeutet elektrotechnisch, dass wenn sich die Spannung U mit +/- ∆U ändert, dann ändert sich im gleichen Maße auch der Strom I mit I +/- ∆I. Und wenn es eine Spannungsänderung ∆U gibt, dann gibt es auch eine Stromänderung ∆I, lässt sich der Quotient (= Teilungsverhältnis) R = ∆U / ∆I bilden, ändert sich mit diesem die Steigung m = ∆y / ∆x → m = ∆I / ∆U = 1 / ( ∆U / ∆I ) = 1 / R der Widerstands- bzw. Arbeitsgeraden mit I = 1 / R * U + I₀ mit I₀ = Konstantstrom; erfordert Konstantstromquelle!

Da wir es bei dem Versuch 102 mit zwei Transistoren zu tun haben, die noch dazu komplementär gemäß der Sziklai-Paar-Schaltung zusammengeschaltetet sind. Demzufolge gibt es auch zwei Arbeitsgeraden - für jeden Transistor eine - , die noch dazu funktional unterschiedlich sind, da der grüne PNP-Leistungstransistor 51 vom roten NPN-Steuertransistor 52 gesteuert wird. Erschwerend kommt aber eben noch die Stromgegenkopplung hinzu, die die arbeitsteilige Arbeitsweise der beiden Transistoren zusätzlich beeinflusst.

Da wir von der Stromgegenkopplung bisher nur eine vage Vorstellung haben und wir von den beiden Transistoren keine Datenblätter, insbesondere Kennlinienfelder, haben, in die sich die Arbeitsgeraden eintragen ließen, verzichten wir bis auf Weiteres darauf mit Arbeitsgeraden zu arbeiten und diese zu berechnen. -

Kehren wir also wieder zu den Wurzeln zurück, nämlich zu dem was uns bekannt ist und zu den beiden Hauptdarstellern, die die Leuchtdauer des Glühlämpchens 18 (wegen der 3 Volt Stromversorgung) beeinflussen: Kondensator 32 und (Auflade-) Widerstand 43 und dem Verbündeten dieser beiden, nämlich der Zeit t.

Wie wir ja inzwischen wissen, lädt sich ein Kondensator in der Zeitspanne t_Auf = 5 τ nahezu vollständig auf 99,9 % auf:

t_Auf = 5 τ = 5 * R * C mit τ = R * C →

Dabei gilt es zu beachten, dass sich ein Kondensator schneller auf- als entladen kann und umgekehrt!

Mit den Werten der Bauelemente Kondensator 32 (→ C₃₂ = 10 µF) und Widerstand 43 (→ R₄₃ = 10 kΩ) folgt für das Aufladen des Kondensators C₃₂:

t_Auf = 5 τ = 5 * R * C

= 5 * R₄₃ * C₃₂

= 5 * 10 kΩ * 10 µF = 5 * 10 * 10³ Ω * 10 * 10^{-6 F} = 500 V/A * 10^-3 As/V = 500 * 10^-3 s = 500 ms → Aufladung!

t_Auf = 5 τ = 5 * R * C = 10 s →

R_Auf = t_Auf / ( 5 C₃₂ )

= 10 s / ( 5 * 10 µF ) = 1 10 s / ( 5 * 10 * 10^-6 As/V ) = 1 / 5 * 10⁶ V/A = 0,2 * 10⁶ Ω = 200 * 10³ Ω = 200 kΩ

Damit das Glühlämpchen 18 nach dem Drücken des Tasters 15 bis zu 10 s lang leuchtet, d.h. die beiden Transistoren über die Basis mit Strom versorgt werden, muss man diese entsprechend „bremsen“ und die Aufladestromstärke durch den Widerstand R_Auf = 200 kΩ entsprechend verringern! Auf welchen Wert die Aufladestromstärke reduziert werden muss, damit das Glühlämpchen 18 tatsächlich 10 Sekunden lang leuchtet, werden wir gleich noch berechnen.

Auch wenn der Kondensator 32 eine Kapazität von C₃₂ = 10 µF hat, muss dies nicht zwangsläufig dazu führen, dass dieser beim Betrieb der Schaltung (Versuch 102) möglichst schnell oder vollständig aufgeladen wird. Gleiches gilt auch für das Entladen des Kondensators bei dem es vorkommen kann, dass dieser wider Erwarten nicht ganz schnell, sondern langsamer und noch dazu auch nicht vollständig entladen wird.

Das unterschiedlich schnelle oder langsame, auch unvollständige Aufladen eines Kondensators wird durch das Zeitfenster 0 < t < 5 τ bestimmt und durch die in diesem Zeitfenster übertragbar Ladungsmenge Q mit Q = I * t.

Neben Stromstärke I und Zeit t spielt beim Aufladen aber auch noch der sogenannte „Treiber“, d.h. eine antreibende (oder abbremsende) elektrische Kraft F eine wichtige Rolle. Und zwar die Kräfte im elektrischen Feld des Kondensators zwischen den Kondensatorplatten (Pluspol = Anode, Minuspol = Kathode) nebst Dielektrikum als Isolierschicht.

Demzufolge ist die elektrische Feldstärke E bei einem Plattenkondensator umso größer, je größer die anliegende, treibende Spannung U und umso kleiner der Plattenabstand d ist: E = U / d mit der Maßeinheit [ Volt / Meter ] = [ V / m ]. Umso mehr man den Plattenabstand d verringert, umso größer werden die elektrischen Kräfte F auf die Ladungsträger im Dielektrikum, sodass es letztlich zu einem Spannungsüberschlag kommt, die den Kondensator beschädigt (siehe auch Durchschlagsfestigkeit).

Wenn man sich die Maßeinheit [ As / V ] der Kapazität von C₃₂ = 10 µF des Kondensators 32 anschaut, dann stellt man unschwer fest, dass sich diese gemäß der Formel C = Q / U = I * t / U wie folgt berechnen lässt:

C = Q / U

= I * t / U →

U_C32 = I_C32 * t_Auf / C₃₂

= 33 µA * 500 ms / 10 µF = 33 * 10^{-6 A} * 500 * 10^-3 s / 10 * 10^{-6 F}

= 16 500 * 10^-3 As / ( 10 As/V ) = 16,5 / ( 10 V ) = 1,65 V → gemessen: 2,41 V aufgeladen nach t_Auf ≈ 21,4 s

Da der Unterschied zwischen der berechneten, maximalen Kondensatorspannung von U_C32 = 1,65 V nach erfolgter Aufladung mit t_Auf = 5 τ = 10 s und der gemessenen, maximalen Kondensatorspannung von U_{C32, Mess} = 2,41 V mit t_{Auf, Mess} = 5 τ = 21,4 s sehr groß ist, müssen wir, bevor wir mit Berechnungen usw. fortfahren, den Grund für das abweichende Rechenergebnis herausfinden!

Ein wichtiger Grund und zugleich Ursache der ungenauen Berechnung der maximalen Kondensatorspannung U_C32 = 1,65 V ist der, dass wir angenommen haben, dass die Aufladung des Kondensators 32 mit dem Erlöschen des Glühlämpchen 18 tatsächlich nach 10 Sekunden abgeschlossen ist. Dem ist aber nicht so!

Vielmehr verhält es sich so, dass der Kondensator 32 erst viel später, nämlich nach t_{Auf, Mess} = 5 τ = 21,4 s vollständig auf die maximale Kondensatorspannung von U_{C32, Mess} = 2,41 V aufgeladen ist, obwohl das Glühlämpchen 18 schon lange nicht mehr leuchtet!

Der Grund dafür ist der, dass jede Glühlampe wegen der Glühwendel aus Wolfram und deren Material- und Werkstoffeigenschaften erst ab einer Temperatur von mehr als 3 000 °C zu leuchten und bei 3 422 °C zu schmelzen anfängt. Demzufolge braucht es vorab eine gewissen Anfangsleistung, um es mittels Spannung und Strom zum Leuchten zu bringen. Eine Glühlampe „verbraucht“ also bereits Strom, obwohl sie noch gar nicht leuchtet, solange sie noch nicht auf Betriebstemperatur zum Leuchten gebracht wurde.

Den Effekt des Vorwärmens macht man sich übrigens bei blinkenden Warnleuchten an Baustellen zunutze, um auf diese Weise die Lebensdauer der Glühlampe zu verlängern! Wenn man nämlich die Glühwendel einer hell blinkenden oder blitzenden Warnleuchte mit einem kleinen Ruhestrom vorwärmt, dann wirkt sich der plötzliche und wiederkehrende Einschaltstromstoß beim Aufblitzen der Warnleuchte nicht Material verschleißend und Lebensdauer verkürzend aus, weil die Heizwendel durch das Vorglühen bereits einen entsprechenden Widerstand hat!

Wenn der Kondensator 32 nach dem Loslassen des Tasters 15 und nach der Zeitspanne 5 τ vollständig aufgeladen ist, sodass dieser keine Ladungsträger mehr in Form von Elektronenüberschuss am Minuspol und Elektronenmangel am Pluspol aufnehmen kann, dann verhält sich dieser wie ein hochohmiger Widerstand von R_Auf = 428 kΩ, der nur noch einen sehr kleinen (Rest-) Strom fließen lässt:

C = Q / U → Q = C * U

= I * t / U →

U_C32 = I_C32 * t_Auf / C₃₂ →

= 48,2 µA * 0,5 s / 10 µF = 24,1 As / 10 As/V = 2,41 V 

t_Auf = 5 τ = 5 * r * C → r = f(t) ≠ R = konstant im Sinne des Ohmschen Gesetzes!

Der Quotient Q / U beschreibt das (Teilungs-) Verhältnis zwischen der im Kondensator gespeicherten Ladungsträgermenge, wobei das Q für lateinisch „Quantum“, d.h. Menge, steht.

Wie die Formel Q = I * t besagt, ist die im Kondensator gespeicherte Ladungsträgermenge zeitabhängig mit Q = f(t). Und der zeitliche Verlauf beim Auf- und Entladen ist wider Erwarten nicht gleichförmig im Sinne von konstant, d.h. linear (siehe Kondensator-Ladekurven).

Gleichzeitig ist aber die im Kondensator gespeicherte Ladungsträgermenge Q auch eine Funktion der Spannung U mit Q = f(U). Und die Spannung U mit U = f(t) verläuft beim Auf- und Entladen ebenfalls nicht linear, sodass sich das Rechnen mit dem Ohmschen Gesetz - und der Formel R = U / I → zeitlich konstant → linear - verbietet!

Wenden wir uns also wieder dem vermeintlichen Geheimnis der Stromgegenkopplung zu.

Bei dem Glühlämpchen 18 mit den Nenn-Betriebswerten U_{Glüh 18, Nenn} = 2,5 V und I_{Glüh 18, Nenn} = 0,3 A berechnet sich der Widerstand R_Glüh 18 des Glühlämpchens wie folgt:

R_Glüh 18 = U_{Glüh 18, Nenn} / I_{Glüh 18, Nenn} = 2,5 V / 0,3 A = 8,33 Ω

I_{Glüh 18} = U_{Glüh 18} / R_Glüh 18

= 1,97 V / 8,33 Ω = 1,97 V / 8,33 V/A = 0,236497 A ≈ 236,5 mA

Dabei gehen wir der Einfachheit halber davon aus, dass der Widerstandsverlauf (= Kennlinie) des Glühlämpchens 18 über weite Teile des Spannungsbereichs von [ 1 V, …, 3,2 V ] praktisch gleichförmig, d.h. linear mit R_Glüh 18 = 8,33 Ω = konstant verläuft.

Die Stromverstärkung B1 des NPN-Steuertransistors 52 berechnet wie folgt:

I_E1 = I_Last = I_{Glüh 18}

= I_B1 + I_C1

Da der Laststrom des Glühlämpchens 18 mit I_{Glüh 18} = 236,5 mA bereits ziemlich groß ist, muss von einer eher kleinen Stromverstärkung B1 von z.B. um die 20 ausgegangen werden.

Geht man davon aus, dass sich mit einem Basisstrom von I_B1 = 10 mA der Kollektorstrom I_C1 = I_E1 – I_B1 steuern lässt, so folgt für das Berechnen der Stromverstärkung B1:

I_C1 = I_E1 – I_B1

= 236,5 mA – 10 mA = 226,5 mA

B1 = I_C1 / I_B1

= 226,5 mA / 10 mA = 22,65 →

I_E1 = I_Last = I_{Glüh 18} = 236,5 mA und I_E1 = I_C1 + I_B1 = 226,5 mA + 10 mA = 236,5 mA 

Wenn es an dem Glühlämpchen 18 als Lastwiderstand und Emitterwiderstand des NPN-Steuertransistors 52 zu einem Spannungsanstieg ∆U kommt, dann vergrößert sich der Spannungsabfall auf,

U_{Glüh 18, neu} = U_{Glüh 18} + ∆U

= 1,97 V + 0,1137 V = 2,084 V

I_{Glüh 18, neu} = ( U_{Glüh 18} + ∆U ) / R_{Glüh 18}

= I_{Glüh 18} + ( ∆U / R_{Glüh 18} )

= 236,5 mA + ( 0,1137 V / 8,33 Ω ) = 236,5 mA + ( 0,1137 V / 8,33 V/A )

= 236,5 mA + ( 0,1137 V / 8,33 A ) = 236,5 mA + 13,65 mA = 250,15 mA

sodass der Emitter E1 des roten NPN-Steuertransistors 52 auf ein höheres Spannungsniveau gehoben wird. Und mit diesem natürlich auch die Basis B1 des NPN-Steuertransistors 52, sodass dieser erst ab einer höheren Basisspannung U_{B1, neu} elektrisch leitend werden kann:

U_{B1, neu} = U_BE1 + U_{Glüh 18, neu}

= 0,7 V + 2,084 V = 2,784 V

Mit der erhöhten Stromstärke I_{Glüh 18, neu} = 250,15 mA berechnet sich die neue, verringerte Stromverstärkung B1, neu wie folgt:

B1, neu = I_{C1, neu} / I_{B1, neu}

= 236,5 mA / 13,65 mA = 17,33 →

I_{E1, neu} = I_{Last, neu} = I_{Glüh 18, neu} = 250,15 mA und I_E1 = I_C1 + I_B1 = 236,5 mA + 13,65 mA = 250,15 mA 

Jetzt wissen wir, dass der Stromanstieg des Laststromes durch den Lastwiderstand R_{Glüh 18} des Glühlämpchen 18 auch zu einem größeren Spannungsabfall am Glühlämpchen selbst führt, und dass der Stromanstieg des Laststromes über den Kollektor C1 des NPN-Steuertransistors 52 an die Basis B2 des grünen PNP-Leistungstransistors 51 weitergeben wird. Allerdings mit einer zeitlichen Verspätung sozusagen, da der rote NPN-Steuertransistor 52 erst ab der größeren Basisspannung von U_{B1, neu} = 2,784 V elektrisch leitend wird.

Dabei stellt sich dann gleich die Frage, was das mit dem Kondensator 32 als Energiespeicher macht. Schließlich ist der Kondensator vor dem Einschalten noch ungeladen, sodass er sich sofort nach dem Einschalten des Schalters 14 auflädt bzw. aufzuladen versucht. Dabei gilt es zu bedenken, dass sich der Kondensator 32 als temporärer Energiespeicher nur aufladen kann, wenn man diesem von außen über den Pluspol der 3 Volt Batterie des Batteriefachs 19 entsprechend elektrische Energie zuführt.

Weil sich aber der Kondensator 32 von außen nur über den Pluspol der 3 Volt Batterie des Batteriefachs 19 und den Stromrückfluss über den Minuspol der 3 Volt Batterie aufladen kann, muss zuvor noch der rote NPN-Steuertransistor 52 elektrisch leitend werden und die Kollektor-Emitter-Strecke C1E1 aufsteuern, sodass der Bahnwiderstand r_C1E1 niederohmig wird.

Dabei gilt es aber stets zu bedenken, dass der Kondensator 32 im ungeladenen Zustand, d.h. zum Zeitpunkt des Einschaltens, einen Kurzschluss darstellt, sodass die Basis B1 potentialmäßig über den Widerstand R₄₃ = 10 kΩ an den Pluspol der 3 Volt Batterie des Batteriefachs 19 angebunden ist. Demzufolge berechnet sich der Basisspannungsteiler des roten NPN-Steuertransistor 52 wie folgt:

U_{Glüh 18} + U_BE + U_R43 – U_Batt = 0 →

U_R43 = U_Batt - U_BE - U_{Glüh 18}

= 3,0 V – 0,7 V - 1,97 V = 0,33 V = 330 mV

I_B1 = U_R43 / R₄₃

= 330 mV / 10 kΩ = 330 * 10^-3 V / 10 * 10³ V/A = 33 * 10^{-6 A =} 33 µA

Da der rote NPN-Steuertransistor 52 mit dem grünen PNP-Leistungstransistor 51 zusammenarbeitet, diesen also ansteuert, verfügt der Leistungstransistor 51 über eine kleine Stromverstärkung von B2 = 25 und der Steuerungs-transistor 52 über eine große Stromverstärkung von B1 = 250, sodass folgt:

I_C1 = B1 * I_B1

= 250 * 33 µA = 8 250 µA = 8,25 mA

I_E1 = I_B1 + I_C1

= 33 µA + 8,25 mA = 0,033 mA + 8,25 mA = 8,283 mA ≈ 8,3 mA

Um herauszufinden, ob sich der grüne PNP-Leistungstransistor 51 tatsächlich aufsteuern lässt, berechnen wir abschließend noch den Emitterstrom I_E2 wie folgt:

I_E2 = B2 * I_C1

= 25 * 8,25 mA = 206,25 mA

I_C2 = I_E2 - I_B2

= I_E2 – I_C1

= 206,25 mA - 8,25 mA = 198 mA → Zum Vergleich: I_{Glüh 18} = 236,5 mA (siehe ziemlich weit oben!)

Jetzt haben wir den Beweis, dass der rote NPN-Steuertransistor 52 nach dem Einschalten des Schalters 14 sofort den grünen PNP-Leistungstransistor 51 aufsteuert, sodass sich anschließend der Kondensator 32 über den elektrisch leitenden Steuertransistor gegen Masse („┴“), d.h. den Minuspol der 3 Volt Batterie aufladen kann:

(Zum Vergrößern bitte auf eines der Bilder klicken!)

Spätestens jetzt gilt es einen möglichen Irrtum aufzuklären: Nämlich den, dass der Kondensator 32 die elektrische Energie liefert, um das Glühlämpchen 18 bis zu t_Auf = t_{Glüh 18} ≈ 10 s leuchten zu lassen!

Vielmehr verhält es sich einerseits so, dass der Aufladevorgang des Kondensators 32 die Basis B1 des roten NPN-Steuertransistors 52 ansteuert und beeinflusst, andererseits beeinflusst die Transistorbeschaltung mit der Stromgegenkopplung auch die Zeitdauer der Aufladung des Kondensators 32!

Demzufolge kann sich der Kondensator 32 „nicht einfach so auf die Schnelle aufladen, wie er gerne möchte“, sondern nur so wie es die weitere Beschaltung mit dem NPN-Steuertransistor 52 zu lässt!

Die im Kondensator 32 gespeicherte, elektrische Energie berechnet sich wie folgt:

W_C32 = ½ C * U² → Mittelwert! Die elektrische Energie steigt rampenförmig linear an!

= ½ * 10 µF * ( 2,41 V )² = 5 * 10^-6 As/V * 5,8081 V² = 29,0405 µVAs ≈ 29,04 µWs ≈ 29,0 µWs 7

Kurz Frage:

Wie berechnet sich die Dreiecksfläche eines rechtwinkligen Dreiecks?

Dreiecksfläche A = Rechtecksfläche / 2 = ( Grundseite g * Höhe h ) / 2 →

Die Hälfte ( = ½ ) einer Rechtecksfläche ergibt die Dreiecksfläche eines rechtwinkliges Dreiecks!

W_el = P_el * t_Auf = U_el * I_el * t_Auf

= U_Glüh * I_Glüh * t_Auf

= 1,97 V * 236,5 mA * 10 s = 4 659,05 mVAs ≈ 4,70 Ws 7

Frage:

Welche Kapazität müsste der Kondensator 32 haben, um die Energie W_el = 4,70 Ws des Glühlämpchens 18 zu speichern, damit es bei einer Spannung von U_{Glüh 18} = 1,97 V bis zu 10 Sekunden lang leuchten kann?

W_C32 = ½ C * U² →

C = 2 * W_C32 / U²

= ( 2 * 4,7 Ws ) / ( 1,97 V )² ≈ ( 9,4 VAs ) / 3,88 V² = 2,42268 As/V ≈ 2,4 F → 2,4 Millionen Mikrofarad [ µF ]

(Zum Vergrößern bitte auf das Bild klicken!)

Um die 2,4 Millionen µF aus mehreren, parallel geschalteten Elektrolytkondensatoren (Elkos) mit je einer Kapazität C von C = 10 000 µF zu erhalten, müsste man die Anzahl n Elkos zum Stückpreis von 6,43 € kaufen:

Anzahl n

= 2 400 000 µF / 10 000 µF pro Elektrolytkondensator

= 2 400 000 µF / 10 000 µF pro Elektrolytkondensator

= 240 Stück * 6,43 € pro Einzelstück ≈ 1 543,- € insgesamt!

Wie man sieht, ist das Speichern von elektrischer Energie W_el in mehreren, parallel geschalteten Elkos nicht nur ziemlich teuer, sondern auch technisch entsprechend aufwendig, weil man bis zu 240 Elkos miteinander verschalten muss.

Für das Parallelschalten von Kondensatoren gilt:

C_ges = C₁ + C₂ + …+ C_n

n = Anzahl der Kondensatoren

Wenn alle einzelnen Kondensatoren vom gleichen Typ sind und alle aus der gleichen Produktionsserie stammen (→ gleiche Toleranz bei der Kapazität C), dann lassen sich deren Einzelkapazitäten wie folgt zusammenfassen:

C_ges = C₁ + C₂ + …+ C_n

Mit C₁ = C₂ = …= C_n folgt:

= C₁ + C₁ + …+ C₁

C_ges = n * C₁

n = Anzahl der Kondensatoren

Da alle Elkos parallel geschaltet sind, werden alle an ein und derselben Spannung U betrieben!

So wie sich bei der Parallelschaltung alle Einzelkapazitäten zur Gesamtkapazität addieren, addieren sich die einzelnen Lade- oder Entladeströme auch zum Gesamtstrom:

I_{C ges} = I_C1 + I_C2 + …+ I_Cn

n = Anzahl der Kondensatoren

Wenn alle einzelnen Kondensatoren vom gleichen Typ sind:

I_{C ges} = n * I_C1

n = Anzahl der Kondensatoren

Aufgabe:

a) Berechne den Kurzschlussstrom I_Kurz der 240 parallel geschalteten Elkos, wenn sich diese mit einer Gesamtkapazität von C = 2,4 F innerhalb von t_Kurz = 10 ms bei einer Kurzschlussspannung von U_Kurz = 100 mV entladen!

b) Berechne den Kurzschlussstrom I_Kurz eines einzelnen Kondensators.

c) Berechne die Entladedauer t_Ent der in einem der 240 parallel geschalteten Elkos gespeicherten elektrischen Energie W_C32, wenn dieser mit einem Entladewiderstand von R_Ent = 1 kΩ entladen wird!

d) Berechne den Entladestrom I_Ent, wenn einer der 240 parallel geschalteten Elkos mit einem Entladewiderstand von R_Ent = 1 kΩ entladen wird!

Lösung:

a) Berechne den Kurzschlussstrom I_Kurz der 240 parallel geschalteten Elkos, wenn sich diese mit einer Gesamtkapazität von C = 2,4 F innerhalb von t_Kurz = 10 ms bei einer Kurzschlussspannung von U_Kurz = 100 mV entladen!

W_C32 = ½ C * U² → … mit C = Q / U = I * t / U folgt:

= ½ * I * t / U * U²

= ½ * I_Kurz * t_Kurz * U_Kurz

I_Kurz = W_C32 / ( ½ t_Kurz * U_Kurz )

= 4,7 Ws / ( ½ * 10 ms * 100 mV )

= 2 * 4,7 Ws / ( 1 000 µVs ) = 9,4 Ws / ( 1 mVs ) = 9,4 W / ( 1 * 10^-3 V ) = 9,4 VA * 10³ / ( 1 V ) = 9,4 kA

Im Abschnitt „Verteilereinbauten“ von Wikipedia sieht man rechts im Bild einen Straßenverteilerkasten mit insgesamt drei waagrechten und ca. 6 cm breiten Stromschienen für die Energieversorgung mit Drehstrom (= dreiphasiger Wechselstrom) von bis zu 10 kA Stromstärke je Phase.

An dieser Stelle sei aber ausdrücklich darauf hingewiesen, dass Elkos (= Elektrolytkondensatoren) stets nur mit Gleichstrom aufgeladen werden dürfen!

Bei der UKW, DAB+ und Fernsehsendestation „Hoher Meißner“ ( = 710 m hoch) in Nordhessen des Hessischen Rundfunks mussten bei Wartungsarbeiten die Gleichstromversorgung der wassergekühlten Rundfunkröhren vorübergehend abgeschaltet werden. Dazu mussten dann auch die Tonnen(!) großen Elkos, die zu Zwecken der Glättung der welligen Gleichspannung eingesetzt werden, vorschriftsgemäß mittels Entladewiderstand über mehrere Stunden(!) entladen werden.

Das aber dauerte dem Starkstromelektriker zu lange, schließlich wollte dieser keine unbezahlten Überstunden machen und demzufolge auch wieder pünktlich zu Hause ein. Kurzerhand nahm er deshalb seinen 40 cm langen Chrom-Vanadium-Schraubendreher mit der fingerdicken Klinge und überbrückte damit die beiden Kontakte eines der Tonnen(!) großen Elkos, sodass dieser kurzgeschlossen wurde! Durch den starken Kurzschlussstrom gab es einen Lichtblitz und für ein paar Sekunden einen hellen Lichtbogen, der den dummen und unvorsichtigen Starkstromelektriker so stark blendete, sodass dieser minutenlang nichts sehen konnte.

Als der Elektriker wieder sehen konnte, war von seinem 40 cm langen Schraubendreher nur noch der isolierte Griff vorhanden, war das Chrom-Vanadium der fingerdicken Klinge komplett geschmolzen und die beim Lichtbogen verflüssigten Chrom-Vanadium-Tröpfchen in die Umgebung verspritzt! Die hätten dann sprichwörtlich auch ins Auge gehen können! -

Lösung:

b) Berechne den Kurzschlussstrom I_Kurz eines einzelnen Kondensators.

Auch die Stromstärke des Kurzschlussstromes I_{Kurz, einzel} eines der 240 parallel geschalteten Elkos ist beachtlich:

I_{Kurz, einzel} = 1 / 240 * I_{Kurz, ges}

= 1 / 240 * 9,4 kA = 1 / 240 * 9 400 A = 39,167 A ≈ 39,2 A

Lösung:

c) Berechne die Entladedauer t_Ent der in einem der 240 parallel geschalteten Elkos gespeicherten elektrischen Energie W_C32, wenn dieser mit einem Entladewiderstand von R_Ent = 1 kΩ entladen wird!

τ_Ent = R_Ent * C → Entladedauer t_Ent = 5 * τ_Ent

t_Ent = 5 * 1 kΩ * 10 000 µF = 5 * 10³ V/A * 10 * 10³ * 10^-6 As/V

= 5 * 10 * s = 50 s

Wie man sieht, wird ein einzelner Kondensator der Kapazität C₃₂ = 10 000 µF trotz des Entladewiderstandes von R_Ent = 1 kΩ doch in recht kurzer Zeit entladen!

Probe:

Q = I_Ent * t_Ent

= 31 mA * 50 s = 1 550 mAs = 1,55 As

C = Q / U = I_Ent * t_Ent / U = 1 / R * t → t = 5 * τ = 5 * R * C

t_Ent = 5 * R * C

= 5 * 1 kΩ * 10 000 µF = 5 * 10³ V/A * 10 * 10³ * 10^-6 As/V

= 5 * 10 * s = 50 s 

W_C32 = ½ C * U²

= ½ C * ( I_Ent * R_Ent )²

= ½ 10 000 µF * ( 31 mA * 1 kΩ )²

= ½ 10 * 10³ * 10^-6 As/V * ( 31 mA * 1 * 10³ V/A )²

= 5 * 10^-3 As/V * ( 31 V )² = 5 * 10^-3 As/V * 961 V² = 5 * 10^-3 * 961 VAs = 4 805 * 10^-3 Ws ≈ 4,8 Ws 

Lösung:

d) Berechne den Entladestrom I_Ent, wenn einer der 240 parallel geschalteten Elkos mit einem Entladewiderstand von R_Ent = 1 kΩ entladen wird!

W_C32 = ½ C * U² = ½ C * ( I_Ent * R_Ent )² →

I_Ent = [ W_C32 / ( ½ C ) / R_Ent² ]^1/2 = [ W_C32 / ( ½ C ) ]^1/2 / R_Ent

= [ 4,7 Ws / ( ½ * 10 000 µF ) ]^1/2 / 1 kΩ = [ 4,7 VAs / ( ½ * 10 000 * 10^{-6 3} As/V ) ]^1/2 / 10³ V/A

= [ 4,7 / ( ½ * 10 * 10^-3 V² ) ]^1/2 / 10³ V/A = [ 4,7 / 5 * 10³ V² ]^1/2 / 10³ V/A

= [ 4,7 / ( 5 * 10³ V² ) ]^1/2 / 10³ V/A = 940^1/2 V / 10³ V/A ≈ 30,66 * 10^-3 A ≈ 31 mA

Wie man sieht, ist der Entladestrom mit I_Ent = 31 mA eines einzelnen Elkos nicht besonders groß, aber in der Summe, d.h. bei insgesamt 240 Elkos dann eben doch: I_{Ent. ges} = 31 mA * 240 = 7 440 mA = 7,44 A.

Deshalb macht es Sinn, jeden der 240 einzelnen Kondensatoren mit einem Entladewiderstand auszustatten, damit auf diese Weise alle Kondensatoren beim Ausschalten der Stromversorgung gleichzeitig entladen werden. Dies hat dann auch noch den Vorteil, dass sich die kleinen Entladeströme mit I_Ent = 31 mA elektrisch gut beherrschen lassen und man herkömmliche Widerstände als Entladewiderstände verwenden kann. Dabei berechnet sich die Wärmeverlustleistung P_R Wärme im Entladewiderstand wie folgt:

W_C32 = ½ C * U² →

U² = 2 * W_C32 / C →

U_C = ( 2 * W_C32 / C )^1/2

= [ 2 * 4,7 Ws / ( 10 000 µF ) ]^1/2

= [ 9,4 VAs / ( 10 * 10³ * 10^-6 As/V ) ]^1/2

= [ 9,4 / 10 * 10³ V² ]^1/2 = [ 0,94 * 10³ V² ]^1/2 = [ 940 ]^1/2 V = 30,6594 V ≈ 30,7 V

Jetzt wissen wir endlich, wie groß die maximale Betriebsspannung an einem einzelnen Elko, aber auch an den insgesamt 240 Elkos werden kann, da diese ja alle parallel zusammen geschaltet sind!

P_{R Wärme} = U_C * I_Ent

= 30,7 V * 31 mA = 951,7 mW = 0,9517 W ≈ 1 W

Jetzt bestätigt sich, dass man tatsächlich herkömmliche Widerstände mit einer zulässigen Verlustleistung von bis zu 1 Watt als Entladewiderstand verwenden kann. -

Berechnung der Stromgegenkopplung - zum Zweiten

PNP- oder NPN-Transistoren lassen sich prinzipiell als Emitter-, Kollektor- oder Basis-Schaltung betreiben.

Dabei ist die Emitterschaltung (siehe Versuch 95 „Zeit spielt eine Rolle“) gerade für Elektronik-Einsteiger am besten zu verstehen.

Immer dann wenn die Basis-Emitter-Diode des NPN-Transistors mit U_BE ≥ 0,7 V elektrisch leitend und damit stromdurchlässig wird, wird auch die Kollektor-Emitter-Strecke mit dem dynamischen Bahnwiderstand r_CE ≤ 2 Ω stromdurchlässig. Und zwar mit dem Stromverstärkungsfaktor B = I_C / I_B ≈ I_E / I_B . Dabei gilt es zu beachten, dass der kleine Basisstrom I_B den großen, dicken Kollektorstrom I_C auf und zu steuert!

Bei einem Stromverstärkungsfaktor von B = 250 lässt sich z.B. mit einem kleinen Basisstrom von I_B = 1 mA ein Kollektorstrom I_C von

I_C = B * I_B = 250 * 1 mA = 250 mA steuern.

Bei einem Stromverstärkungsfaktor von B = 250 lässt sich z.B. mit einem kleinen Basisstrom von I_B = 0,01 mA ein Kollektorstrom I_C von

I_C = B * I_B = 250 * 0,01 mA = 2,5 mA steuern.

Die Emitterschaltung mit dem grünen PNP-Leistungstransistor 51 erkennt man daran, dass der Lastwiderstand R_Last in Form eines elektrischen Verbrauchers (Glühlämpchen, Elektromotor, Leuchtdiode, Widerstand usw.) direkt am Kollektor C angeschlossen ist, während der Emitter E direkt am Pluspol („+“) der Spannungsversorgung anliegt.

Wenn man also die Schaltung zum Versuch 102 (links) ganz einfach vertikal spiegelt, dann sieht man sofort, dass sich der grüne PNP-Leistungstransistor 51 in einer Emitterschaltung und der rote NPN-Steuertransistor 52 in einer Kollektorschaltung befindet (siehe nachfolgendes Bild rechts):

(Zum Vergrößern bitte auf eines der Bilder klicken!)

Damit der grüne PNP-Leistungstransistor 51 (T2) in Emitterschaltung das Glühämpchen 18 zum Leuchten bringen kann, muss dieser an seiner Basis B2 entsprechend aufgesteuert werden. Dabei lässt sich dieser an seiner Basis B2 nur dann aufsteuern, wenn die Basis-Emitter-Spannung U_BE2 > 0,7 V wird.

Die BE-Spannung von T2 wiederum kann nur dann größer als U_BE2 > 0,7 V werden, wenn der NPN-Steuertransistor 52 (T1) an seiner Basis B1 aufgesteuert wird.

Wenn man davon ausgeht, dass die Stromverstärkung B2 des PNP-Leistungstransistors 51 (T2) wegen des deutlich größeren Laststroms von I_Last = I_{Glüh 18}

I_{Glüh 18} = U_{Glüh 18} / R_Glüh 18

= 1,97 V / 8,33 Ω = 1,97 V / 8,33 V/A = 0,236497 A ≈ 236,5 mA

mit B2 = 25 angenommen werden kann (siehe auch Versuch 72), berechnet sich der zugehörige Basisstrom I_B2 wie folgt:

B2 = I_C2 / I_B2 →

I_B2 = I_C2 / B2

= 236,5 mA / 25 = 9,46 mA

Demzufolge berechnet sich der Spannungsabfall U_EC2 am EC-Bahnwiderstand r_EC2 wie folgt (siehe Bild oben links):

U_EC2 = U_Batt - U_{Glüh 18}

= 3,0 V - 1,97 V = 1,03 V → … an der Grenze zum Sättigungsbereich!

Dabei gilt es zu beachten, dass sich ein Transistor, der im Sättigungsbereich betrieben wird, nicht regeln lässt!

Da sich aber der Kondensator C₃₂ beim Einschalten des Schalters 14 sofort auflädt, sodass anfangs kurz ein großer Ladestrom fließt, der dann allerdings gemäß der Aufladekurve schnell wieder abflacht, befindet sich der grüne PNP-Leistungstransistor 51 (T2) nur für einen kurzen Moment in der Sättigung!

Zum Vergleich (siehe Arbeitsstromverschiebung):

I_C2 = ( U_{Batt, ges} – U_{CE2, satt} ) / R_{Glüh 18, Nenn}

= ( 3,0 V – 0,2 V ) / 8,33 Ω = 2,8 V / 8,33 Ω = 0,33613 A ≈ 336 mA → U_{CE2, satt} = 0,2 V → Sättigung von T2!

I_C2 = ( U_{Batt, ges} – U_CE2 ) / R_{Glüh 18, Nenn}

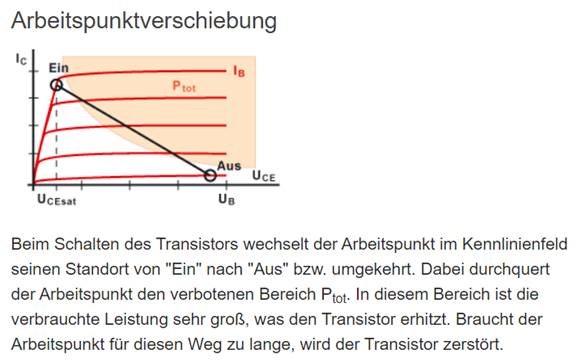
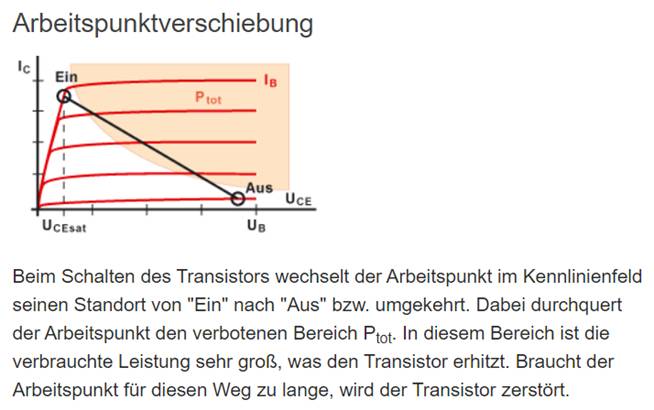
= ( 3,0 V – 1,2 V ) / 8,33 Ω = 1,8 V / 8,33 Ω = 0,2161 A ≈ 216 mA → U_CE2 = 1,2 V → Normalbetrieb von T2!

Beim Einschalten des (Ein-/Aus-) Schalters 14 wird nicht nur der Kondensator 32 aufgeladen, sondern währenddessen auch die Arbeitsgerade vom grünen PNP-Leistungstransistor 51 (T2) von oben links (= „Ein“) nach rechts unten (= „Aus“) durchlaufen:

(Vergrößern: auf Bild klicken! | Quelle: Elektronik-Kompendium)

Während des Durchlaufens der Arbeitsgeraden durch den grünen PNP-Leistungstransistor 51 (T2) von oben links (= „Ein“) nach rechts unten (= „Aus“) ändert sich fortwährend die Stromverstärkung B2 im Bereich [ 10, …, 50, … 250 ], sodass diese beim Einschalten den Wert B2_sat = 10 und beim Ausschalten bzw. Erlöschen des Glühlämpchens 18 den Wert B2_dunkel = 250 annimmt.

Während des Durchlaufens der Arbeitsgeraden von oben links (= „Ein“) nach rechts unten (= „Aus“) vergrößert sich gleichzeitig der Bahnwiderstand r_EC der Emitter-Kollektor-Strecke und die Emitter-Kollektor-Spannung U_EC, sodass sich im Gegenzug gleichzeitig der Kollektorstrom I_C2 entsprechend verringert und das Glühlämpchen 18 erlischt:

I_B2sat = I_C2sat / B2_sat = 336 mA / 10 = 33,6 mA → Sättigung (= „Ein“)!

I_{B2 hell} = I_{C2 hell} / B2_hell = 216 mA / 50 = 4,32 mA → Normalbetrieb (= Arbeitspunkt in der Mitte der Arbeitsgeraden)!

I_{B2 dunkel} = I_{C2 dunkel} / B2_dunkel = 8,25 mA / 250 = 33 µA → Sperrbetrieb (= „Aus“)!

Woran aber lässt sich erkennen, dass die Stromverstärkung B2 des grünen PNP-Leistungstransistor 51 (T2) während des Durchlaufens der Arbeitsgeraden von oben links (= „Ein“) nach rechts unten (= „Aus“) fortwährend vergrößert, während sich gleichzeitig der Basisstrom I_B2 verkleinert (siehe im obenstehenden Diagramm „Arbeitspunktverschiebung“ die verschiedenen roten Basisstrom-Kennlinien I_B = f(U_CE) )?

Die Stromverstärkung B bzw. B2 für den grünen PNP-Leistungstransistor 51 (T2) mit dem Quotienten B2 = I_C2 / I_B2 sollte ja über einen großen Bereich der Arbeitsgeraden möglichst konstant sein, damit sich beim Durchlaufen derselben möglichst keine Verzerrungen einstellen. Und solange wir auf der Arbeitsgeraden nicht in die Sättigung mit U_CEsat < 1,2 V fahren, darf man sehr wohl davon ausgehen, dass die Stromverstärkung B2 annähernd konstant, d.h. linear, verläuft.

Da aber die Stromverstärkung B2 mit dem Quotienten B2 = I_C2 / I_B2 wider Erwarten nicht die Steigung a = ∆y / ∆x mit

a = ∆I_C2 / ∆I_B2 angibt, bedarf es eines weiteren Diagramms und zwar den des Stromsteuerkennlinienfeldes:

(Vergrößern: auf Bild klicken! | Quelle: Elektronik-Kompendium)

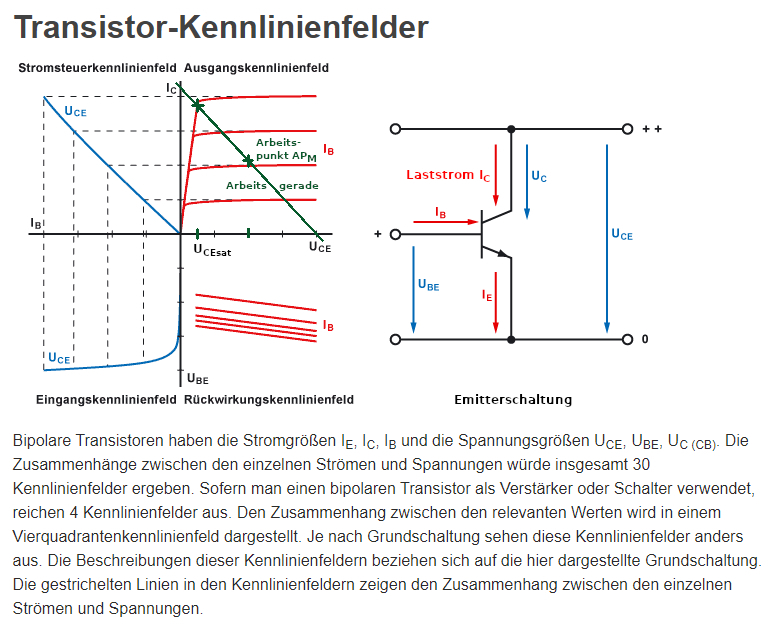
Wenn man sich die obenstehende Steuerstromkennlinie I_C = f(I_B) zum ersten Mal anschaut, ohne den nachfolgenden Text genau durchgelesen zu haben, dann könnte man meinen, dass diese für verschiedene Spannungen U_CE gilt. Dem ist aber nicht so; die Steuerstromkennlinie gilt immer nur für eine bestimmte Spannung U_CE!

Wie man im nachfolgenden Bild sieht, wurde die Steuerstromkennlinie den Transistor-Kennlinienfeldern entnommen:

(Vergrößern: auf Bild klicken! | Quelle: Elektronik-Kompendium)

Leider lässt sich mit der oben im Bild zu sehenden Stromsteuerkennlinie nicht so viel anfangen, weil das Entstehen der U_CE-Kennlinie formelmäßig nicht erklärt und hergeleitet wird. Gemäß der Kennlinie wird die Funktion I_C = f(I_B) dargestellt, die größtenteils als angenähert linear aufgefasst werden darf: B = f(I_B, I_C) = I_C / I_B = konstant. Dabei bezieht sich U_CE im Falle der Emitterschaltung (siehe Bild 15) auf den Spannungsabfall zwischen Kollektor und Emitter, der durch den Bahnwiderstand r_CE = u_CE / i_C = u_CE / ( B * I_B ) entsteht. Setzt man die Messwerte des Messpunktes P₁ ein, so folgt:

r_CE = u_CE / i_C

= u_CE / ( B * I_B )

= 835 mV / 203,93 * 0,738 mA = 835 mV / 150,5 mA = 5,548 Ω →

u_CE = r_CE * ( B * I_B ) →

Mit größer werdendem Basisstrom I_B (und Kollektorstrom I_C) werden die Stromverstärkung B sowie der Spannungsabfall u_CE immer kleiner, wenn man die Arbeitsgerade von rechts unten (= „Aus“, T2 sperrt) nach links oben (= „Ein“, T2 in Sättigung) durchläuft. Wenn sich der Transistor T2 in Sättigung befindet, ändern sich U_CEsat = 0,2 V und die Verstärkung B nicht mehr:

r_CEsat = u_CEsat / i_Csat

= 0,8 V / 152,4 mA = 800 mV / 152,4 mA ≈ 5,25 Ω → Werte vom und zum Messpunkt P₂

Um zu sehen, wie sich der grüne PNP-Leistungstransistor 51 (T2) beim Durchlaufen der Arbeitsgerade von rechts unten (= „Aus“, T2 sperrt) nach links oben (= „Ein“, T2 in Sättigung) verhält, nehmen wir alternativ zwei Messwerte für den Basis- und Kollektorstrom des grünen PNP-Leistungstransistor 51 (T2) auf:

a) Messpunkt P₂, Widerstand R₄₁ = 1 kΩ:

I_{B2 P2} = 0,967 mA, I_{C2 P2} = 152,4 mA, U_{CE2 P2} = 800 mV → Sättigung!

Berechnung der Stromverstärkung B2 des Transistors T2:

B2_P2 = I_{C2 P2} / I_{B2 P2}

= 152,4 mA / 0,967 mA = 157,601 ≈ 157,6

b) Messpunkt P₁, Widerstand R₄₃ = 10 kΩ:

I_{B2 P1} = 0,738 mA, I_{C2 P1} = 150,5 mA, U_{CE2 P1} = 835 mV → Sättigung!

Berechnung der Stromverstärkung B2 des Transistors T2:

B2_P1 = I_{C2 P1} / I_{B2 P1}

= 150,5 mA / 0,738 mA = 203,9295 ≈ 204

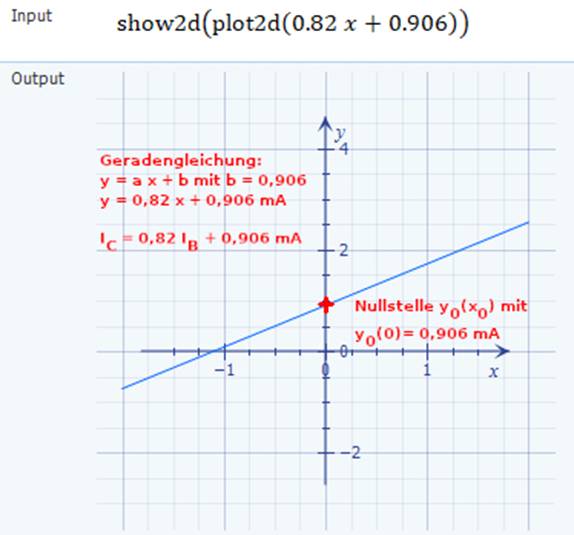
Hier bestätigt sich erneut, dass die Stromverstärkung B = I_C / I_B mit steigendem Kollektorstrom I_C abnimmt! -

Mittels der sogenannten Zwei-Punkte-Form stellen wir die zugehörige Geradengleichung wie folgt auf:

y – y₁ / x – x₁ = y₂ – y₁ / x₂ – x₁

= ∆y / ∆x

= Steigung a der Geradengleichung y = ax + b mit b = Parallelverschiebung aus dem Koord.ursprung!

I_C2 – I_{C2 P1} / I_B2 – I_{B2 P1} = I_{C2 P2} – I_{C2 P1} / I_{B2 P2} – I_{B2 P1}

= ∆I_C / ∆I_B

= Steigung a der Geradengleichung I_C = a I_B + b →

mit b = Parallelverschiebung aus dem Koordinatenursprung!

I_C2 – 150,5 mA / I_B2 – 0,738 mA = ( 152,4 mA – 150,5 mA ) / ( 0,967 mA – 0,738 mA )

= ( 1,9 mA ) / ( 0,229 mA )

= 8,2969 ≈ 8,3 → Steigung a = 8,3

I_C2 – 150,5 mA = 8,3 * ( I_B2 – 0,738 mA )

I_C2 = 8,3 I_B2 – 0,738 mA + 150,5 mA

I_C2 = 8,3 I_B2 + 144,4 mA → Geradengleichung mit a = ∆I_C2 / ∆I_B2 = 8,3 für den Basiswiderstand R₄₃ = 10 kΩ

Probe:

Für den Messpunkt P₂ folgt:

I_{C2 P2} = 8,3 I_{B2 P2} + 144,4 mA = 8,3 * 0,967 mA + 144,4 mA = 8,026 mA + 144,4 mA ≈ 152,4 mA 

Für den Messpunkt P₁ folgt:

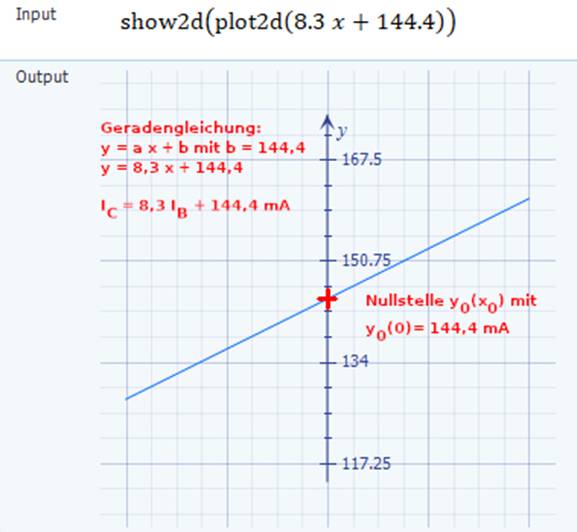
I_{C2 P1} = 8,3 I_{B2 P1} + 144,4 mA = 8,3 * 0,738 mA + 144,4 mA = 6,125 mA + 144,4 mA ≈ 150,5 mA 

Wenn man die Geradengleichung I_C2 = 8,3 I_B2 + 144,4 mA mathematisch mit der Normalform y = a x + b = a x + y₀ vergleicht, dann sieht man sofort, dass diese als Funktion I_C2 = f(I_B2) an der Stelle I_B2 = 0 um den Wert I_C2(0) = f(I_B2=0) = 144,4 mA parallel nach oben in Richtung der y-Achse (= I_C2-Achse) aus dem Koordinatenursprung heraus verschoben ist:

(Vergrößern: auf Bild klicken! | Quelle: Microsoft Mathematics)

Berechnen der Nullstelle I_C2(0) der Geradengleichung I_C2 = 8,3 * I_B2 + 144,4 mA:

I_C2(0) = I_C2(I_B2 = 0)

= 8,3 * I_B2 + 144,4 mA = 8,3 * 0 + 144,4 mA = 144,4 mA

Berechnung der Nullstelle I_C2(I_B2) = 0 (= Schnittstelle mit der x-Achse bzw. I_B2-Achse):

I_C2(0) = 8,3 * I_B2 + 144,4 mA = 0 →

8,3 * I_B2 = - 144,4 mA

I_B2(I_C2 = 0) = I_B2(0)

I_B2(0) = - 144,4 mA / 8,3

= - 17,39759 mA ≈ - 17,4 mA

(Vergrößern: auf Bild klicken! | Quelle: Microsoft Mathematics)

Jetzt wissen wir, dass wenn man zwei Messwerte für Spannung und Strom aus der Schaltung zum Versuch 102 aufnimmt und diese in die Zwei-Punkte-Form einsetzt, auf diese immer Verlass ist und sich auf diese Weise sowohl die Geradengleichung herausfinden als auch der Graph der Funktion als grafische Lösung zeichnen lässt!

Dabei ist das kostenlose Programm „Microsoft Mathematics“, das es auch als Smartphone-App gibt, ein mächtiges und hilfreiches Werkzeug.

Aufgrund der Geradengleichung und der Parallelverschiebung des Graphen aus dem Koordinatenursprung heraus, wissen wir jetzt, dass sich der grüne PNP-Leistungstransistor 51 (T2) beim Einschalten kurzzeitig in der Sättigung befindet und sich dabei als gesteuerte Stromquelle verhält, d.h. kurzzeitig einen von der Versorgungsspannung unabhängigen Strom von insgesamt I_{C2 P1} ≈ 150,5 mA zum Leuchten des Glühlämpchens 18 bereit stellt! -

Nachdem wir den grünen PNP-Leistungstransistor 51 (T2), der sich beim Einschalten kurzzeitig in der Sättigung befindet und dabei als gesteuerte Stromquelle verhält, berechnet haben, geht es nachfolgend darum, den roten NPN-Steuertransistor 52 (T1) und dessen unbelasteten Basis-Spannungsteiler, bestehend aus den beiden Widerständen R₁ = 10 kΩ und R₂ = 1 MΩ ( → ∞ ), zu berechnen:

(Quelle: electronicsplanet.ch | Vergrößern: auf Bild klicken! | Lampe mit Zeitverzögerung (1))

>> Von der Spannungsquelle zur Stromquelle...

Im Gegensatz zur Konstantspannungsquelle gibt die Konstantstromquelle immer denselben Strom ab. Und zwar unabhängig vom angeschlossenen Widerstand. Ändert sich bei einer Stromquelle der Lastwiderstand, ändert sich anstatt des Stroms die Spannung. Der einfachste Weg, eine Stromquelle mit konstantem Ausgangsstrom aufzubauen, ist die Kombination einer Spannungsquelle mit einer Stromstabilisierungsschaltung. Nach diesem Prinzip funktioniert auch die (Schaltung mit dem NPN Transistor als Stromquelle).

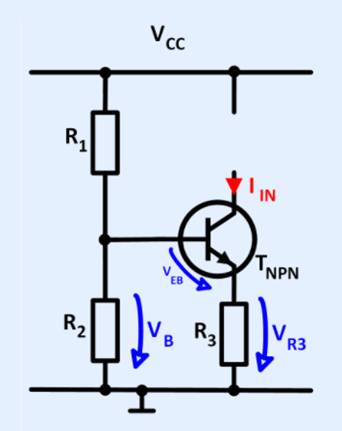
Der NPN Transistor als Stromquelle

In dieser Schaltung ist V_cc die konstante Spannung eines Netzgeräts, einer Batterie oder eines Spannungsreglers. Indem man zu V_cc einen NPN Transistor und drei Widerstände zuschaltet, entsteht eine Schaltung, die an ihrem Eingang einen geregelten Strom zieht. Solche Schaltungen, die an einem Stromeingang einen geregelten Strom ziehen, anstatt ihn zu liefern, nennt man auch Stromsenken. Die Last wird zwischen V_cc und den Stromeingang angeschlossen.

Funktionsweise der Stromquellenschaltung

An der Basis des NPN Transistors erzeugt der Spannungsteiler von R₁ und R₂ eine konstante Basisspannung V_B = V_R2. Die Emitterspannung V_R3 ist ebenfalls konstant und um V_BE kleiner als die Basisspannung V_B. Daraus folgt, dass die Spannung, die über R₃ (= R_Last = R_{Glüh 18}) abfällt ebenfalls konstant ist. Genauso wie der Strom durch R₃ (= Prinzip des belasteten Spannungsteilers).

Der Strom, der durch R₃ fließt, wird vom Transistor geliefert. Und da der Emitterstrom des Transistors hauptsächlich von seinem Kollektor kommt, fließt dort der Strom I_IN hinein, der durch R₃ fliest. Dieser Kollektrostrom wird bestimmt durch R₁, R₂, V_cc, V_BE und R₃.

Ein Lastwiderstand ( = Kollektorwiderstand R_C), der zwischen V_cc und dem Kollektor angeschlossen wird, wird vom Strom I_IN durchflossen, ohne dass er ihn beeinflusst. So wirkt diese Schaltung (für den Kollektorwiderstand R_C) als Konstantstromquelle für jedes Bauteil zwischen V_cc und dem Kollektor. << (Quelle: electronicsplanet.ch)

Der abgespeckte Basis-Spannungsteiler, der zunächst ohne den Transistor aus den beiden in Reihe geschalteten Teilwiderständen R₁ und R₂ besteht, wird um den Lastzweig des Bahnwiderstandes r_BE2 = U_BE2 / I_B2 der BE-Diode plus Lastwiderstand R₃ (= R_Last = R_{Glüh 18}) erweitert. 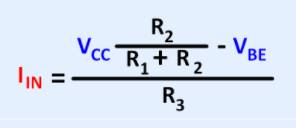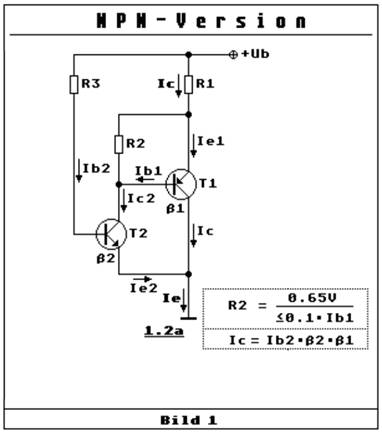Dabei entsteht aber wider Erwarten kein belasteter Spannungsteiler, da der kleine Basisstrom I_B2 des Transistors gegenüber dem großen Emitterstrom I_E2 vernachlässigt werden darf: I_E2 = I_B2 + I_C2 ≈ I_C2.

Für den durch den Transistor unbelasteten Spannungsteilers gilt die Spannungsteilerformel:

U_R2 / U_CC = R₂ / ( R₁ + R₂ )

( U_BE2 + U_R3 ) / U_CC = R₂ / ( R₁ + R₂ )

U_BE2 + U_R3 = U_CC * [ R₂ / ( R₁ + R₂ ) ]

U_R3 = U_CC * [ R₂ / ( R₁ + R₂ ) ] - U_BE2

I_E2 * R₃ = U_CC * [ R₂ / ( R₁ + R₂ ) ] - U_BE2

I_C2 * R₃ ≈ U_CC * [ R₂ / ( R₁ + R₂ ) ] - U_BE2

I_IN ≈ { U_CC * [ R₂ / ( R₁ + R₂ ) ] - U_BE2 } / R₃ → Zähler und Nenner durch R₂ dividieren!

(Quelle: electronicsplanet.ch)

I_IN ≈ { U_CC * 1 / [ ( R₁ / R₂ ) + 1 ] - U_BE2 } / R_{Glüh 18}

≈ { 2,83 V * 1 / [ ( 10 kΩ / 1 MΩ ) + 1 ] - 0,7 V } / 8,33 Ω

≈ { 2,83 V * 1 / [ ( 10 * 10³ Ω / 1 * 10⁶ Ω ) + 1 ] - 0,7 V } / 8,33 Ω

≈ { 2,83 V * 1 / [ ( 10 * 10^-3 ) + 1 ] - 0,7 V } / 8,33 Ω

≈ { 2,83 V * 1 / [ 0,010 + 1 ] - 0,7 V } / 8,33 Ω

≈ { 2,83 V / [ 1,010 ] - 0,7 V } / 8,33 Ω

= { 2,80 V - 0,7 V } / 8,33 V/A = { 2,10 V } / 8,33 V/A = 0,2521 A = 252,1 mA

Bezüglich der obenstehenden Berechnung des unbelasteten Spannungsteilers muss noch erwähnt werden, dass es den Teilwiderstand R₂ des Basis-Spannungsteilers in der Schaltung zum Versuch 102 nicht wirklich gibt.

Um aber trotzdem mit der Spannungsteilerformel für den unbelasteten Spannungsteiler rechnen bzw. herausfinden zu können, ob uns diese Berechnung weiter bringt, wurde der Teilwiderstand R₂ des Basis-Spannungsteilers mit einem sehr großen, hochohmigen Wert von R₂ = 1 MΩ hypothetisch angenommen mit dem Effekt, dass sich ein sehr kleiner Wert für den Quotienten R₁ / R₂ = 0,010 + 1 = 1,010 ≈ 1 einstellt, der das Rechenergebnis nur ganz geringfügig verfälscht.

So wie es aussieht, scheint der Ergebniswert I_IN ≈ 252,1 mA größenordnungsmäßig im Vergleich zu den Nennbetriebsdaten des Glühlämpchens 18 mit U_Nenn = 2,5 V, I_Nenn = 300 mA richtig zu sein.

Bezüglich der Schaltung zum Versuch 102 gilt es aber zu bedenken, dass der Eingangsstrom I_C1 = I_IN = I_{B2 P1} = 0,738 mA (siehe weiter oben beim Messpunkt P₁, Widerstand R₄₃ = 10 kΩ) sehr, sehr viel kleiner ist als der bisherige Eingangsstrom.

Selbstverständlich lässt sich die obenstehende Berechnung des unbelasteten Spannungsteilers auch mit dem sehr viel kleineren Eingangsstrom von I_IN = I_{B2 P1} = 0,738 mA wie folgt durchführen:

I_IN ≈ { U_CC * 1 / [ ( R₁ / R₂ ) + 1 ] - U_BE2 } / R_{Glüh 18} → Formel nach R_{Glüh 18} = R₃ umstellen!

R₃ ≈ { U_CC * 1 / [ ( R₁ / R₂ ) + 1 ] - U_BE2 } / I_IN → Der Eingangsstrom I_IN wird zu I_{B2 P2}.

R₃ ≈ { U_CC * 1 / [ ( R₁ / R₂ ) + 1 ] - U_{BE2 P2} } / I_{B2 P2}

R₃ ≈ { U_CC * 1 / [ ( R₁ / R₂ ) + 1 ] - U _{BE2 P2} } / I_{B2 P2}

≈ { 2,83 V * 1 / [ ( 10 kΩ / 1 MΩ ) + 1 ] - 0,7 V } / 0,738 mA

≈ { 2,83 V * 1 / [ ( 10 * 10³ Ω / 1 * 10⁶ Ω ) + 1 ] - 0,7 V } / 0,738 mA

≈ { 2,83 V * 1 / [ ( 10 * 10^-3 ) + 1 ] - 0,7 V } / 0,738 mA

≈ { 2,83 V * 1 / [ ( 0,01 ) + 1 ] - 0,7 V } / 0,738 mA

≈ { 2,83 V * 1 / [ 1,01 ] - 0,7 V } / 0,738 mA

≈ { 2,83 V * 0,99 - 0,7 V } / 0,738 mA

R₃ ≈ { 2,8 V - 0,7 V } / 0,738 mA = 2,1 V / 0,738 mA ≈ 2,85 kΩ

U₃ / I₃ = R₃

U₃ / R₃ = I₃ →

I₃ = U₃ / R₃

= U_{Glüh 18} / R₃ → Nennbetriebsdaten des Glühlämpchens 18: U_Nenn = 2,5 V, I_Nenn = 0,3 A

= 2,5 V / 2,85 kΩ = 0,877 mA → I₃ = I_E1 = I_B1 + I_C1 → I_E1 > I_C1 = 0,738 mA ( vormals I_{B2 P2} )

An dieser Stelle muss noch daran erinnert werden, dass sich die Berechnung des unbelasteten Spannungsteilers auf den Schaltungsteil mit dem roten NPN-Steuertransistor 52 (T1) bezieht, sodass dies auch auf den Lastwiderstand R₃ zutrifft. Demzufolge ist der Lastwiderstand R₃ = 2,85 kΩ des unbelasteten Spannungsteilers dem Lastwiderstand R_{Glüh 18} = 8,33 Ω parallel geschaltet und darf wegen R₃ >> R_{Glüh 18} bei der Parallelschaltung vernachlässigt werden!

Nachdem wir den Basis-Spannungsteiler des roten NPN-Steuertransistors 52 (T1) berechnet haben und die Berechnung stillschweigend davon ausgeht, dass mit diesem das Glühlämpchens 18 direkt, d.h. ohne den nachgeschalteten grünen PNP-Leistungstransistor 51 (T2) als Verstärker, mit Strom versorgt werden soll, sodass dieses hell leuchtet, ist es für das Verständnis über das Funktionieren der Schaltung wichtig zu wissen, wie sich der rote NPN-Steuertransistor 52 (T1) elektrisch verhält.

Um zu sehen, wie sich der rote NPN-Steuertransistor 52 (T1) beim Durchlaufen der Arbeitsgerade von rechts unten (= „Aus“, T1 sperrt) nach links oben (= „Ein“, T1 in Sättigung) verhält, nehmen wir auch bei diesem zwei Messwerte für den Basis- und Kollektorstrom des roten NPN-Steuertransistors 52 (T1) wie folgt auf:

c) Messpunkt P₂, Widerstand R₄₁ = 1 kΩ:

I_{B1 P2} = 0,132 mA, I_{C1 P2} = 1,018 mA, U_{CE P1} = 8,6 mV → Sättigung!

Berechnung der Stromverstärkung B1 des Transistors T1:

B1 = I_C1 / I_B1

= I_{C1 P2} / I_{B1 P2}

= 1,018 mA / 0,132 mA )

= 7,712 ≈ 7,7

d) Messpunkt P₁, Widerstand R₄₃ = 10 kΩ:

I_{B1 P1} = 0,021 mA, I_{C1 P1} = 0,907 mA, U_{CE1 P1} = 41,4 mV → Sättigung!

Berechnung der Stromverstärkung B1 des Transistors T1:

B1_P1 = I_{C1 P1} / I_{B1 P1}

= 0,927 mA / 0,021 mA = 44,1429 ≈ 44

Hier bestätigt sich ein weiteres Mal, dass die Stromverstärkung B = I_C / I_B mit fallendem Kollektorstrom I_C zunimmt! -

Mittels der sogenannten Zwei-Punkte-Form stellen wir die zugehörige Geradengleichung wie folgt auf:

y – y₁ / x – x₁ = y₂ – y₁ / x₂ – x₁

= ∆y / ∆x

= Steigung a der Geradengleichung y = ax + b mit b = Parallelverschiebung aus dem Koord.ursprung!

I_C1 – I_{C1 P1} / I_B1 – I_{B1 P1} = I_{C1 P2} – I_{C1 P1} / I_{B1 P2} – I_{B1 P1}

= ∆I_C / ∆I_B

= Steigung a der Geradengleichung I_C = a I_B + b →

mit b = Parallelverschiebung aus dem Koordinatenursprung!

I_C1 – 0,927 mA / I_B1 – 0,021 mA = ( 1,018 mA – 0,927 mA ) / ( 0,132 mA – 0,021 mA )

= ( 0,091 mA ) / ( 0,111 mA )

= 0,8198 ≈ 0,82 → Steigung a = 0,82

I_C1 – 0,927 mA = 0,82 * ( I_B1 – 0,021 mA )

I_C1 = 0,82 I_B1 – 0,021 mA + 0,927 mA

I_C1 = 0,82 I_B1 + 0,906 mA → Geradengleichung mit a = ∆I_C1 / ∆I_B1 = 0,82 für den Basiswiderstand R₄₃ = 10 kΩ

Probe:

Für den Messpunkt P₂ folgt:

I_{C1 P2} = 0,82 I_{B1 P2} + 0,906 mA = 0,82 * 0,132 mA + 0,906 mA = 0,108 mA + 0,906 mA ≈ 1,014 mA 

Für den Messpunkt P₁ folgt:

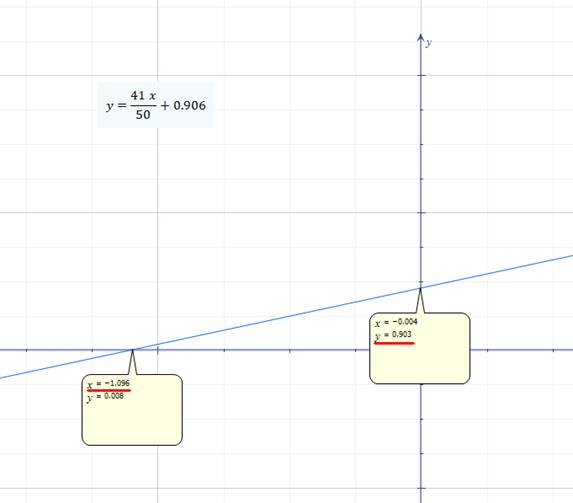
I_{C1 P1} = 0,82 I_{B1 P1} + 0,906 mA = 0,82 * 0,021 mA + 0,906 mA = 0,017 mA + 0,906 mA ≈ 0,923 mA 

Wenn man die Geradengleichung I_C1 = 0,82 I_B1 + 0,906 mA mathematisch mit der Normalform y = a x + b = a x + y₀ vergleicht, dann sieht man sofort, dass diese als Funktion I_C1 = f(I_B1) an der Stelle I_B1 = 0 um den Wert I_C1(0) = f(I_B1=0) = 0,906 mA parallel nach oben in Richtung der y-Achse (= I_C1-Achse) aus dem Koordinatenursprung heraus verschoben ist:

(Vergrößern: auf Bild klicken! | Quelle: Microsoft Mathematics)

Berechnen der Nullstelle I_C1(0) der Geradengleichung I_C1 = 0,82 * I_B1 + 0,906 mA:

I_C1(0) = I_C1(I_B1 = 0)

= 0,82 * I_B1 + 0,906 mA = 0,82 * 0 + 0,906 mA = 0,906 mA

Berechnung der Nullstelle I_C1(I_B1) = 0 (= Schnittstelle mit der x-Achse bzw. I_B1-Achse):

I_C1(0) = 0,82 * I_B1 + 0,906 mA = 0 →

0,82 * I_B1 = - 0,906 mA

I_B1(I_C1 = 0) = I_B1(0)

I_B1(0) = - 0,906 mA / 0,82

= -1,1049 mA ≈ -1,105 mA

(Vergrößern: auf Bild klicken! | Quelle: Microsoft Mathematics)

Jetzt wissen wir, dass, wenn man zwei Messwerte für Spannung und Strom aus der Schaltung zum Versuch 102 aufnimmt und diese in die Zwei-Punkte-Form einsetzt, auf diese immer Verlass ist und sich auf diese Weise sowohl die Geradengleichung herausfinden als auch der Graph der Funktion als grafische Lösung zeichnen lässt.

Transistor-Betriebsdaten im direkten Vergleich
NPN-Steuertransistor 52 (T1)				PNP-Leistungstransistor 51 (T2)
Bezeichnung	Wert	Bemerkung		Bezeichnung	Wert	Bemerkung
Basiswiderstand R43	10 kΩ
UCE1 P1	40,3 mV	Sättigung		UCE2 P1	836 mV	Sättigung
IB1 P1	0,019 mA	= 19 µA	┌	IB2 P1	0,907 mA	IB2 P1 = IC1 P1
IC1 P1	0,907 mA	IC1 P1 = IB2 P1	┘	IC2 P1	144,1 mA
B1P1	47,7	Stromverstärk.		B2P1	158,9	Stromverstärk.
rCE1 P1 = UCE1 P1 / IC1 P1	44,4 Ω	Bahnwiderst.		rCE2 P1 = UCE2 P1 / IC2 P1	5,8 Ω	Bahnwiderst.
IC1 = 0,98 IB1 + 0,888 mA		Geradengleich.		IC2 = 138,3 IB2 + 143,2 mA		Geradengleich.

Da der Basisstrom I_{B2 P1} des PNP-Leistungstransistors 51 (T2) gleich dem Kollektorstrom I_{C1 P1} des NPN-Steuertransistors 52 (T1) (siehe hellgelbe Tabellenzeile oben), mussten die Messwerte für den Messpunkt P₁ mit dem Widerstand R₄₃ = 10 kΩ neu gemessen werden, sodass ab sofort für die weitere Berechnung der beiden Geradengleichungen mit den neuen Messwerten aus der obenstehenden Tabelle gerechnet werden muss!

Zwei-Punkte-Form für den NPN-Steuertransistor 52 (T1)

I_C1 – 0,907 mA / I_B1 – 0,019 mA = ( 1,018 mA – 0,907 mA ) / ( 0,132 mA – 0,019 mA )

= ( 0,111 mA ) / ( 0,113 mA )

= 0,982301 ≈ 0,98 → Steigung a = 0,98

I_C1 – 0,907 mA = 0,98 * ( I_B1 – 0,019 mA )

I_C1 = 0,98 I_B1 – 0,019 mA + 0,907 mA

I_C1 = 0,98 I_B1 + 0,888 mA → Geradengleichung mit a = ∆I_C1 / ∆I_B1 = 0,98 für den Basiswiderstand R₄₃ = 10 kΩ

Zwei-Punkte-Form für den PNP-Leistungstransistor 51 (T2)

I_C2 – 144,1 mA / I_B2 – 0,907 mA = ( 152,4 mA – 144,1 mA ) / ( 0,967 mA – 0,907 mA )

= ( 8,3 mA ) / ( 0,06 mA )

= 138,333 ≈ 138,3 → Steigung a = 8,3

I_C2 – 144,1 mA = 138,3 * ( I_B2 – 0,907 mA )

I_C2 = 138,3 I_B2 – 0,907 mA + 144,1 mA

I_C2 = 138,3 I_B2 + 143,2 mA → Geradengleichung mit a = ∆I_C2 / ∆I_B2 = 138,3 für den Basiswiderstand R₄₃ = 10 kΩ

Da die beiden komplementär geschalteten Transistoren wie ein Sziklai-Paar geschaltet sind, ist der Basisstrom I_{B2 P1} des PNP-Leistungstransistors 51 (T2) gleich dem Kollektorstrom I_{C1 P1} des NPN-Steuertransistors 52 (T1), sodass sich beide Geradengleichungen zu einer wie folgt zusammensetzen lassen:

I_C1 = 0,98 I_B1 + 0,888 mA → Geradengleichung zum roten NPN-Steuertransistor 52 (T1)

= I_B2 → mit I_B2 = 0,98 I_B1 + 0,888 mA →

I_C2 = 138,3 I_B2 + 143,2 mA → Geradengleichung zum grünen PNP-Leistungstransistor 51 (T2)

I_C2 = 138,3 * 0,98 I_B1 + 0,888 mA + 143,2 mA

= 138,3 * 0,98 I_B1 + 0,888 mA + 143,2 mA

I_C2 = 135,5 I_B1 + 144,1 mA → neue Geradengleichung für den zusammengesetzten, fiktiven Transistor T3

Wir messen die Basisstrom I_B1 des roten NPN-Steuertransistor 52 (T1) mit I_B1 = 0,02 mA und setzen diesen Wert in die neue Geradengleichung ein, sodass folgt:

I_C2 = 135,5 I_B1 + 144,1 mA 

= 135,5 * 0,02 mA + 144,1 mA = 2,71 mA + 144,1 mA ≈ 146,8 mA → (gemessen: 142,3 mA → -3,1 % Abweichung)

Im Elektronik-Kompendium des Patrick Schnabel gibt es die Abhandlung „Die komplementäre Darlington-Schaltung“ (Sziklai-Connections) von Thomas Schaerer mit der ich mich nachfolgend befasse, in der Hoffnung, eine Antwort darauf zu bekommen, wie die sogenannte Stromgegenkopplung der Kollektorschaltung des Steuertransistors T1 mit nachgeschaltetem Lastwiderstand R_Last = Vorwiderstand R₁ + LED-Durchlasswiderstand r_LED funktioniert:

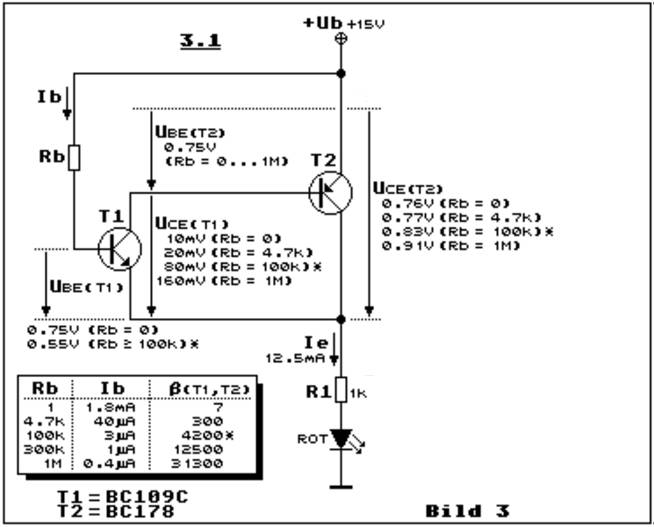
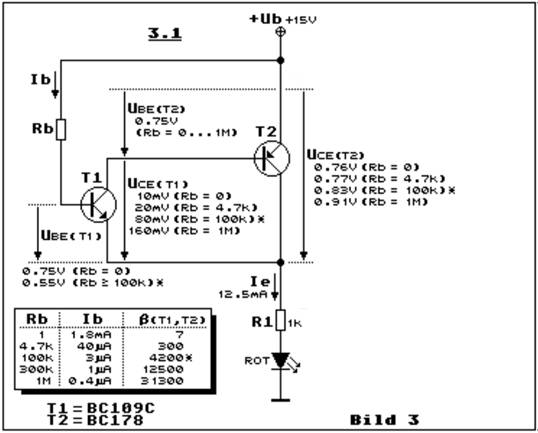
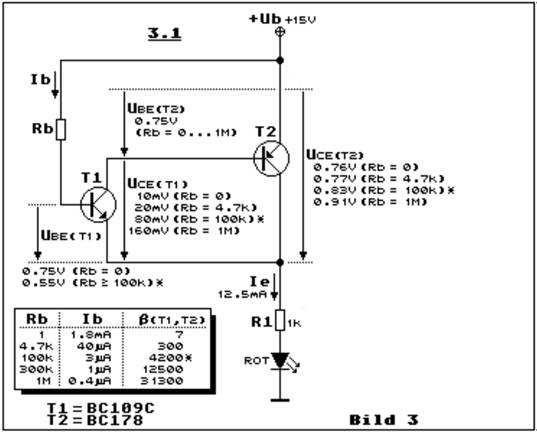
(Vergrößern: auf Bild klicken! | Quelle: Elektronik-Kompendium)

>> Teilbild 3.1 zeigt die komplementäre Darlingtonschaltung mit einem NPN- (T1) und mit einem PNP-Transistor (T2). Wie schon zu Bild 1 erwähnt, bestimmt der eingangsseitige Transistor, also T1, die Charakteristik der Darlingtonstufe. Es ist also eine komplementäre NPN-Darlingtonstufe. Wir betrachten hier vor allem die Spannungen und ich bitte beim Weiterlesen des Textes Teilbild 3.1 mit den Zahlenwerten und der Tabelle unten links genau zu beachten.

Wir beginnen mit einem Rb-Widerstandswert von 0 Ohm.

Das bedeutet, dass der Emitter von T2, der an +Ub angeschlossen ist, direkt mit der Basis von T1 verbunden ist. Was bei der "normalen" Darlingtonschaltung selbstverständlich erlaubt ist, ist hier total verboten! <<

Die Formulierung „Das bedeutet, dass der Emitter von T2, der an +Ub angeschlossen ist, direkt mit der Basis von T1 verbunden ist.“ ist zwar elektrotechnisch in Ordnung, erklärt aber nicht, weshalb man die Basis eines Transistors niemals direkt, d.h. ohne Basisvorwiderstand Rb, auf den Pluspol der Spannungsversorgung Ub = 15 V legen darf!

Wenn man nämlich den Basisvorwiderstand Rb weglässt, d.h. einfach entfernt, indem man diesen überbrückt, dann fließt der größte Teil des Laststromes Ie nicht mehr über den Leistungstransistor T2 als Längsregler (= Spannungsregler), sondern eben direkt über die BE-Diode BE(T1) vom Steuertransistor T1 und den Lastwiderstand R_Last = R1 + r_LED gegen Masse (= Minuspol der Spannungsquelle Ub) ab. Dabei kann der irregeleitete Basisstrom Ib so groß wie der Laststrom Ie selbst werden und als Folge dessen die BE-Diode BE(T1) des Steuertransistors T1 (und damit natürlich auch den Transistor selbst) zerstören:

Ub = U_BE(T1) + Ie * R1 + u_LED → u_LED = i_LED * r_LED → siehe Standard-LEDs

u_LED = Ub – ( U_BE(T1) + Ie * R1 )

= 15 V – ( 0,75 V + 12,5 mA * 1 kV/A ) = 15 V – ( 0,75 V + 12,5 V ) = 15 V – 13,25 V = 1,75 V

I_BE(T1) = U_BE(T1) / r_BE(T1) →

r_BE(T1) = U_BE(T1) / I_BE(T1)

= 0,75 V / 12,5 mA = 750 mV / 12,5 mA = 60 Ω → Annahme: Leistungstransistor T2 sperrt.

Der Bahnwiderstand r_BE(T1) (= Durchlasswiderstand) der BE-Diode BE(T1) des Steuertransistors T1 beträgt r_BE(T1) = 60 Ω unter der Annahme, dass der Leistungstransistor T2 sperrt, weil er einen zu geringen Basisstrom IB(T2) bekommt, sodass die BE-Diode BE(T1) des Steuertransistors T1 den kompletten Laststrom I_Last = Ie übernimmt.

Ob der Leistungstransistor T2 tatsächlich vollständig sperrt, wissen wir aber noch nicht! Nur, wenn er sperrt, dann vergrößert sich der Spannungsabfall U_Last am gesamten Lastwiderstand R_Last = R1 + r_LED wie folgt:

U_Last = Ub – U_BE(T1)

= 15 V – 0,75 V = 14,25 V

U_R1 = U_Last – u_LED

= 14,25 V – 1,75 V = 12,5 V

I_Last = Ie = I_BE(T1)

I_BE(T1) = U_R1 / R1

= 12,5 V / 1 kΩ = 12,5 mA 

Zum Vergleich berechnen wir noch den Bahn- bzw. Durchlasswiderstand r_LED der roten LED:

r_LED = u_LED / I_LED

= u_LED / Ie

= 1,75 V / 12,5 mA = 1,75 V / 12,5 kΩ = 0,14 kΩ = 140 Ω

Da an der roten LED ein größerer Spannungsabfall in Form der Durchlassspannung U_F = U_LED = 1,75 V im Vergleich zur BE-Diode BE(T1) des Steuertransistors T1 mit U_BE(T1) = 0,75 V entsteht, ist auch deren Durchlasswiderstand r_LED = 140 Ω entsprechend größer als der der BE-Diode BE(T1) mit r_BE(T1) = 60 Ω.

>> Wenn man im Testaufbau diese Schaltungskonfiguration ausmisst, d.h. man misst an Rb mit einem ganz niedrigen Ohmwert von nur 1 Ohm die Spannung über Rb um den Strom Ib zu errechnen, stellt man fest, dass der Stromverstärkungsfaktor B_T1 der gesamten Darlingtonschaltung nur einen Wert von B_T1 = 7 hat. <<

B_T1 = I_C(T1) / I_B(T1) ≈ I_E(T1) / I_B(T1)

= Ie / Ib →

Ib = I_C(T1) / B_T1

≈ Ie / B_T1

= 12,5 mA / 7 = 1,7857 mA ≈ 1,8 mA

U_Rb = Ib * Rb

= 1,8 mA * 1 Ω = 1,8 mV

Der Basisstrom von Ib = 1,8 mA an sich würde normalerweise schon ausreichen, den Steuertransistor T1 aufzusteuern. Und der Stromverstärkungsfaktor B_T1 = 7 wäre für einen Leistungstransistor auch noch in Ordnung. Allerdings müsste dabei der Kollektorstrom I_C(T1) mehr als 20-fach so groß sein: I_C(T1) ≥ 250 mA. Ist er aber nicht, weil die Basisspannung mit U_Rb = 1,8 mV viel zu klein ist, um den Steuertransistor T1 aufzusteuern:

U_CE(T1) + U_BE(T2) = U_Rb + U_BE(T1)

= 1,8 mV + 750 mV = 751,8 mV

U_CE(T1) = U_Rb + U_BE(T1) - U_BE(T2)

= 751,8 mV – 750 mV = 1,8 mV → U_CE(T1) = U_Rb

Weil sich aber der Steuertransistor T1 wegen der zu kleinen Basisspannung mit U_Rb = U_CE(T1) = 1,8 mV eben nicht aufsteuern lässt, fließt der Laststrom I_Last = 12,5 mA ausschließlich über die BE-Diode BE(T1), die wiederum bei einem Durchlassstrom von mehr als I_BE(T1) > 50 mA durchbrennen würde!

Demzufolge dürfen in der obenstehenden, komplementären Darlington-Schaltung (= Sziklai-Paar-Schaltung) der Vorwiderstand R1 und die rote LED z.B. nicht durch zwei 7 Volt Glühlämpchen à 2 W (= Kolbenlampen für die Skalenbeleuchtung bei alten Röhrenradios) in Reihenschaltung ersetzt werden:

P_Glüh = U_Glüh * I_Glüh →

I_Glüh = P_Glüh / U_Glüh

= 2 W / 7 V = 2 VA / 7 V = 0,2857 A ≈ 286 mA 7

R_Glüh = U_Glüh / I_Glüh

= 7 V / 286 mA = 0,0244755 kΩ ≈ 24,5 Ω

I_Reihe = 2 * U_Glüh / 2 * R_Glüh

= 7 V / 24,5 Ω = 0,2857 A ≈ 286 mA 7

Jetzt wissen wir, dass man nicht nur Leuchtdioden (= LEDs) mit einem Vorwiderstand vor dem Durchbrennen schützen muss, sondern auch BE-Dioden von Transistoren durch den Basiswiderstand (als Vorwiderstand)!

Insbesondere dann, wenn der Transistor im absoluten Sättigungsbereich mit U_CEsat < 50 mV betrieben wird!

>> Das bedeutet, T1 wäre bezüglich Kollektorstrom praktisch genau so belastet wie T2 und das ist in der Realität unzulässig, weil ein solcher Darlington ganz einfach nicht funktionieren kann. T1 würde, weil er in der Regel schwächer ist als T2, kaputt gehen. Selbst dann wenn Rb in diesem Beispiel 4,7 k-Ohm hätte, wäre die Stromverstärkung des Darlington mit etwa 300 noch immer viel zu niedrig. Dies kommt ganz einfach davon, weil T1, mit U_CE(T1) = 20 mV, noch immer viel zu stark gesättigt ist. <<

Mit dem Basiswiderstand Rb = 4,7 kΩ und B_T1 = 300 folgt:

Ib = I_C(T1) / B_T1

≈ Ie / B_T1

= 12,5 mA / 300 = 0,04167 mA ≈ 0,042 mA = 42 µA

>> Das kommt davon, weil der Basisstrom Ib in Relation zu Ie, verglichen an der möglichen Gesamtstromverstärkung noch immer viel zu hoch ist. Erst wenn Rb mindestens einen Wert von 100 k-Ohm hat und dabei Ib etwa 3 µA unterschreitet, kommt diese komplementäre Darlingtonschaltung in den Bereich einer Stromverstärkung die der Bezeichnung Darlington würdig ist. Noch besser sieht es aus, wenn Rb einen Wert von 300 k-Ohm hat und dadurch Ib bei 1 µA liegt. Dann liegt die Stromverstärkung sicher über 10'000 und bei 1 M-Ohm und 0.4 µA werden sogar mehr als 30'000 erreicht, wobei UCE(T1) nur 160 mV hat. (…)

Welchen Vorteil hat also diese komplementäre Darlingtonschaltung? Man kann ohne zusätzliche externe Spannung, den T1-Basisstrom so definieren, dass UCE(T1) etwa 150 mV beträgt und so die Stromverstärkung der gesamten Darlingtonschaltung ausreichend hoch und T1 nur schwach gesättigt ist. Eine schwache Sättigung bedeutet eine relativ rasche Reaktionsfähigkeit des Darlingtons auf schnelle Stromänderungen. (…)

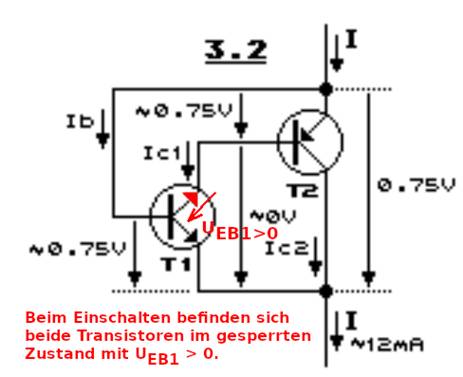
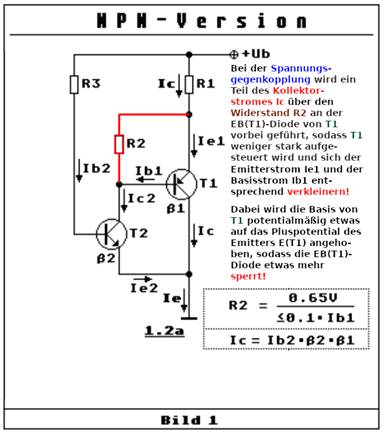
(Vergrößern: auf Bild klicken! | Quelle: Elektronik-Kompendium)

An Teilbild 3.2 wollen wir jetzt verstehen warum die Verstärkung der gesamten Darlingtonschaltung extrem niedrig werden muss, wenn Rb einen Wert von (fast) 0 Ohm hat, also der Emitter von T2 mit der Basis von T1 kurzgeschlossen (direkt verbunden) ist. <<

Wenn man dann die Darlingtonschaltung einschaltet, dann „sucht“ sich der Strom I entweder den kürzesten Weg oder den Weg mit dem geringsten Widerstand zum Potentialausgleich, d.h. zum Minuspol der Spannungsversorgung.

Dabei wäre für den Strom I der Weg über die EC(T2)-Strecke des Leistungstransistors T2 der kürzestete, vorausgesetzt, dass dieser bereits beim Einschalten über die Basis aufgesteuert, d.h. stromleitend wäre und sich im gesättigten Zustand befände.

Ist er aber eben nicht, weil sich der Leistungstransistor T2 beim Einschalten der Darlingtonschaltung noch im gesperrten Zustand befindet! Schließlich muss der Leistungstransistor T2 kurz nach dem Einschalten der Darlingtonschaltung ja erst noch mittels des Steuertransistors T1 und dessen Kollektorstroms Ic1 aufgesteuert und stromdurchlässig gemacht werden!

Demzufolge bleibt dem Strom I nichts anderes übrig, als sich den Weg des geringsten Widerstandes über die BE(T1)-Diode des Steuertransistors T1 zu suchen!

Dabei gilt es aber noch zu beachten, dass sich der Steuertransistor T1 zum Zeitpunkt des Einschaltens der Darlingtonschaltung ebenfalls im gesperrten Zustand befindet, sodass der Strom I nur über die BE(T1)-Diode von T1 fließen kann, ohne dass die CE(T1)-Strecke und der Transistor T1 selbst stromleitend wären!

Den gesperrten Zustand des Steuertransistors T1 erkennt man übrigens an dem Spannungsabfall parallel zur CB(T1)-Diode von T1 mit U_{CB (T1)} > 0.

Die BE(T1)-Diode von T1 wiederum wird aber erst in dem Moment stromleitend, wenn sich an dieser ein Spannungsabfall von U_{BE (T1)} > 0,75 V aufgebaut hat!

Wenige Millisekunden nach dem Einschalten der Darlingtonschaltung wird die BE(T1)-Diode des Steuertransistors T1 elektrisch leitend, sodass sich der Spannungsabfall parallel zur CB(T1)-Diode von T1 mit U_{CB (T1)} < 0 umkehrt und als Folge dessen der Steuertransistors T1 und mit ihm der Leistungstransistor T2 aufgesteuert werden!

Kurz nachdem der Steuertransistor T1 und mit ihm der Leistungstransistor T2 aufgesteuert wurden, teilen sich diese wie bei einem Stromknoten den Strom I untereinander auf: I = Ic1 + Ic2.

>> Nun ist es so, dass die Summe von Ic1 und Ic2 nicht größer sein kann als der Strom durch die gesamte Darlingtonschaltung. In einem inneren Regelprozess teilt sich (deshalb) der Strom I sehr schnell mit nur sehr kleinen Unterschieden in die Teilströme Ic1 und Ic2 auf.

Woher weiß man dies, ohne dass man die Ströme direkt misst? Ganz einfach deshalb, weil die Basis-Emitter-Schwellenspannungen von T1 und T2 praktisch gleich hoch sind. Dies ist so, weil die Kollektor-Emitter-Spannung von T1 im gesättigten Zustand nur gerade etwa 10 mV beträgt. Diese niedrige Spannung bildet zwischen Kollektor und Basis von T2 praktisch einen Kurzschluss, was T2 zu einer Diode macht. Deshalb ist die Kollektor-Emitter-Spannung von T2 gleich groß wie dessen Basis-Emitter-Schwellenspannung. Fragt sich jetzt noch, woher man weiß, wie hoch die Stromverstärkung in diesem Sonderfall ist.

Ganz einfach, man setzt in die T1-Basisleitung einen Widerstand Rb von 1 Ohm. Das ist fast so gut wie ein Kurzschluss, denn es fällt an Rb, wie Teilbild 3.1 zeigt, nur eine Spannung von weniger als 2 mV ab. Damit kennt man Ib und wegen I = 12,5 mA die Stromverstärkung des gesamten Schaltung. << (Quelle: Elektronik-Kompendium, Abschnitt „Kollektorschaltung mit komplementärem Darlington“.)

>> Ganz einfach, man setzt in die T1-Basisleitung einen Widerstand Rb von 1 Ohm. Das ist fast so gut wie ein Kurzschluss, denn es fällt an Rb, wie Teilbild 3.1 zeigt, nur eine Spannung von weniger als 2 mV ab. <<

U_Rb = U_EC(T2) – U_BE(T1)

= 760 mV – 750 mV = 10 mV

>> Wenn man im Testaufbau diese Schaltungskonfiguration ausmisst, d.h. man misst an Rb mit einem ganz niedrigen Ohmwert von nur 1 Ohm die Spannung über Rb um den Strom Ib zu errechnen, stellt man fest, dass der Stromverstärkungsfaktor B_T1 der gesamten Darlingtonschaltung nur einen Wert von B_T1 = 7 hat. <<

B_T1 = I_C(T1) / I_B(T1) ≈ I_E(T1) / I_B(T1)

= Ie / Ib →

Ib = I_C(T1) / B_T1

≈ Ie / B_T1

= 12,5 mA / 7 = 1,7857 mA ≈ 2 mA

U_Rb = Ib * Rb

= 2 mA * 1 Ω = 2 mV

In diesem Zusammenhang ist es falsch, wenn man den kleinen Spannungsabfall von U_Rb = 2 mV mit einem Kurzschluss vergleicht bzw. zu erklären versucht. Es ist zwar naheliegend, dies zu tun, ist aber trotzdem nicht zutreffend. Schließlich gibt es in der Elektronik (= Elektrotechnik u.a. mit aktiven Bauelementen wie z.B. Transistoren) nicht nur Spannungsquellen, sondern auch Stromquellen, wenn auch nur in elektronischer Form, die man nicht einfach so im Elektromarkt kaufen kann!

Schließlich handelt es sich bei der Transistor-Vorstufe mit dem Steuertransistor T1 um eine Stromquelle, auch wenn man es dieser nicht auf den ersten Blick ansieht (siehe hier im Abschnitt „Funktionsweise der Stromquellenschaltung“).

Demzufolge befindet sich der Leistungstransistor T2 mit seiner BE(T2)-Diode im Konstantstromzweig des Kollektors C(T1) des Steuertransistors T1!

Und bei dem Steuertransistor T1 als (Konstant-) Stromquelle richtet sich die (Klemmen-) Spannung derselben stets nach dem angeschlossenen Lastwiderstand R_Last = R1 + r_LED und im Basis-Eingangskreis von T1 nach dem Basiswiderstand Rb = 1 Ω.

Gemäß dem Ohmschen Gesetz gilt dabei für den kleinen Basiswiderstand RB = 1 Ω, dass an einem kleinen Widerstand stets ein kleiner Spannungsabfall und an einem großen Widerstand stets ein großer Spannungsabfall entsteht! -

Im Vergleich zum Standarddeutsch (= Hochdeutsch) gibt es auch noch die Umgangssprache, die u.a. über einen kleineren Wortschatz verfügt. Menschen mit einem höheren Bildungsabschluss wie z.B. Abitur (= Allgemeine Hochschulreife) verfügen oftmals über einen Wortschatz von mehr als 6 000 Worten, während Menschen ohne Bildungsabschluss oder Hauptschulabschluss über einen Wortschatz von teils weniger als 2 000 Worten verfügen. Da sich das Denken nicht nur im Kopf abspielt, sondern auch im Stillen als Zwiesprache (= gesprochenes Denken), verhält es sich so, dass die Umgangssprache in vielen Bereichen des Alltags wegen des kleineren Wortschatzes ungenauer, unpräziser und missverständlicher ist, was sich auch auf das Denken auswirkt. Aber der Mensch mit dem kleineren Wortschatz merkt es nicht direkt oder sofort, sondern z.B. erst bei der Kommunikation mit einem sprachgewandten, kulturell gebildeten Menschen.

So spricht der Volksmund umgangssprachlich z.B. von einer 12 Volt Auto- bzw. Starterbatterie, obwohl es sich bei dieser um einen Akku handelt. Bei Batterien in Haushalts- und Unterhaltungselektronikgeräten spricht der Volksmund auch von Stromquellen, obwohl es sich bei diesen um Spannungsquellen handelt! Und bei einer Stromquelle handelt es sich genau genommen um eine Konstantstromquelle, die es oftmals nur in elektronisch geregelten Netzteilen oder Labornetzgeräten gibt.

Bereits im Versuch 1 „Der Stromkreis“ wurde die Begrifflichkeit „spannungs- oder stromführend“ erläutert.

Wenn sich z.B. der Ein-/Ausschalter gleich zu Beginn der Schaltung am Plus- („+“) oder Minuspol („-“) der Spannungsquelle befindet, dann ist die Stromzuführung von der Spannungsquelle hin zur Anschlussklemme des Ein-/Ausschalters bereits spannungsführend, während die Stromrückführung nach dem Verbraucher (= Lastwiderstand) erst dann stromführend ist, wenn man den I/0-Schalter (= Ein-/Ausschalter) einschaltet.

Demzufolge macht es also einen lebensgefährlichen 7 Unterschied, ob ich versehentlich das braune Stromleitungskabel (= „Phase“, = spannungsführender Leiter L1 einer Wechselstromleitung), ohne zwischengeschalteten Lichtschalter, an der Deckenlampe berühre oder das blaue stromrückführende Kabel (= Neutralleiter, Nullleiter).

Lichtschalter sollten deshalb immer das braune Stromleitungskabel (= „Phase“, = spannungsführender Leiter L1 einer Wechselstromleitung) ein- oder ausschalten und niemals(!) das blaue Strom rückführende Kabel (= Neutralleiter, Nullleiter). Bei Arbeiten z.B. an der Deckenlampe sollte man sich aber auch Sicherheitsgründen nicht darauf verlassen und deshalb den entsprechenden Sicherungsautomaten ausschalten, d.h. vom Stromnetz trennen! -

Im weitesten Sinne könnte man also bei der „Phase“, d.h. dem spannungsführenden braunen Leiter L1 einer Wechselstromleitung von einer (Wechselspannungs-) Quelle, engl. „source“ sprechen und bei dem blauen Strom rückführenden Kabel (= Neutralleiter, Nullleiter) von der (Wechselspannungs-) Senke, engl. „drain“.

Streng genommen sind aber die Begriffe „source“ (= Quelle) und „drain“ (= Senke) der Elektronik bzw. Halbleitertechnik, speziell den sogenannten „MOS-FET-Transistoren“ vorbehalten.

Bei den „FETs“, d.h. den Feldeffekt-Transistoren, handelt es sich vereinfacht ausgedrückt um Spannung gesteuerte Transistoren, sodass an deren Gate-Anschluss keine Steuerströme fließen und die Steuerung der FETs demzufolge leistungslos erfolgt:

>> Feldeffekttransistoren (FETs) sind eine Gruppe von Transistoren, bei denen im Gegensatz zu den Bipolartransistoren nur ein Ladungstyp am elektrischen Strom beteiligt ist – abhängig von der Bauart: Elektronen oder Löcher bzw. Defektelektronen. Sie werden bei tiefen Frequenzen – im Gegensatz zu den Bipolartransistoren – weitestgehend leistungs- bzw. verlustlos geschaltet. Die am weitesten verbreitete Art des Feldeffekttransistors ist der MOSFET (Metall-Oxid-Halbleiter-Feldeffekttransistor).

Entdeckt wurde das Prinzip des Feldeffekttransistors im Jahr 1925 von Julius Lilienfeld. Damals war es aber noch nicht möglich, einen solchen FET auch tatsächlich herzustellen. Halbleitermaterial der notwendigen Reinheit als Ausgangsmaterial kommt in der Natur nicht vor und Methoden zur Erzeugung hochreinen Halbleitermaterials waren noch nicht bekannt. Insofern waren auch die speziellen Eigenschaften von Halbleitern noch nicht ausreichend erforscht. Erst mit der Herstellung hochreiner Halbleiterkristalle (Germanium) Anfang der 1950er-Jahre wurde dieses Problem gelöst.^[1] Aber erst durch die Silizium-Halbleitertechnologie (u. a. thermische Oxidation von Silizium) in den 1960er-Jahren konnten erste Labormuster des FET hergestellt werden.^[2][3] << (Quelle: Wikipedia)

Während eine

· Spannungsquelle, engl. „voltage source“,

am Pluspol ein positives Spannungspotential in Form eines Ladungsträgerüberschusses zur Verfügung stellt, sodass eine entsprechend kleine oder große, positive (Quellen-) Spannung, ohne dass ein Strom fließt, an den Anschlussklemmen anliegt,

stellt eine

· Spannungssenke, engl. „voltage drain“,

am Minuspol ein negatives Spannungspotential in Form eines Ladungsträgermangels bereit, sodass eine entsprechend kleine oder große, negative (Quellen-) Spannung, ohne dass ein Strom fließt, an den Anschlussklemmen anliegt.

Wie wir alle wissen, kann man sich im Super- oder Elektromarkt verschiedene Spannungsquellen wie z.B. 9 Volt Blockbatterien, 1,5 Volt Batterien vom Typ „AAA“ oder „AA“ usw. kaufen, Spannungssenken hingegen nicht! Und zwar aus einem einfachen Grund, nämlich den, dass die bei einer Batterie oder einem Akku unbedingt erforderliche Spannungssenke bereits in der Spannungsquelle, d.h. im gleichen Gehäuse mit enthalten ist!

In der Praxis gibt es allerdings einen speziellen Akku bei dem Spannungsquelle und Spannungssenke physisch und physikalisch voneinander getrennt sind! Und zwar bei der sogenannten „Redox-Flow-Batterie“.

Wie wir ferner wissen, kann man sich im Super- oder Elektromarkt keine verschiedenen Stromquellen kaufen, auch wenn der Volksmund umgangssprachlich bei den Batterien, Akkus, Steckernetzgeräten, Netzteilen usw. von Stromquellen spricht. Das gilt natürlich auch für die Stromsenken, die man sich ebenfalls nicht einfach so kaufen kann.

Und trotzdem gibt es sie, die Stromquellen und die Stromsenken, wenn auch in versteckter Form, sodass man schon etwas genauer hinschauen muss, um diese in den beiden nachfolgenden Schaltungen zu entdecken:

(Vergrößern: auf Bild klicken! | Quelle: Elektronik-Kompendium)

Wenn man aber bereits weiß, was eine Stromquelle und eine Stromsenke ist und worin sich beide voneinander unterscheiden, dann sieht man sofort, dass sich in der linken Schaltung eine Stromquelle und in der rechten Schaltung eine Stromsenke befindet.

Da wir es bei beiden Schaltungen mit Elektronik zu tun haben, braucht es sowohl für die Stromquelle als auch für die Stromsenke aktive Bauelemente und zwar in Form der PNP- und NPN-Transistoren.

Außerdem müssen wir schauen, wo sich der Lastwiderstand R1 befindet. Und zwar gleich als Erstes nach der Spannungsversorgung +Ub (siehe rechte Schaltung) oder als Letztes vor dem Masseanschluss („┴ “) (siehe linke Schaltung).

Als gedankliche Eselsbrücke kann man sich merken, dass die

· Stromquelle
den elektrischen Strom in die Schaltung „drückt“,

während die

· Stromsenke
den elektrischen Strom aus der Schaltung „saugt“ und in der Senke „verschwinden“ lässt.

Wie wir bereits von der komplementären Darlington-Schaltung (= Sziklai-Paar-Schaltung) anhand der Geradengleichungen bzw. Arbeitsgeraden wissen, werden sowohl der NPN-Steuertransistor T1 als auch der PNP-Leistungstransistor T2 als Stromquelle betrieben (siehe obenstehendes Bild links).

Demzufolge „drückt“ der PNP-Leistungstransistor T2 als Stromquelle seinen Emitterstrom Ie = 12,5 mA in die Schaltung bzw. den Lastwiderstand R_Last = R1 + r_LED hinein, indem er das Spannungspotential am Emitter E(T2) anhebt.

Dabei gilt es zu bedenken, dass der PNP-Leistungstransistor T2 als Stromquelle(!) das Spannungspotential am Emitter E(T2) eben nicht anheben, sondern nur den Emitterstrom Ie vergrößern kann!

Da aber das Ohmsche Gesetz gilt, wird die Änderung der Stromstärke ∆Ie durch den Lastwiderstand R_Last sofort in eine entsprechende Spannungsänderung ∆U_Last umgesetzt!

Und, da wir gerade bei der Änderung der Stromstärke ∆Ie sind, klären wir noch auf, was es mit der sogenannten Stromgegenkopplung bzw. Gleichstromgegenkopplung auf sich hat.

Wenn sich der PNP-Leistungstransistor T2 als Stromquelle im laufenden Betrieb erwärmt, z.B. weil sich der Lastwiderstand R_Last wider Erwarten verkleinert hat und einen größeren Laststrom Ie zieht oder sich die Versorgungsspannung +Ub aus irgendeinem Grund vergrößert hat, dann wird der Transistor elektrisch leitender, d.h. zwischen Emitter und Kollektor niederohmiger!

Als Folge dessen verkleinert sich der Bahnwiderstand r_EC(T2) zwischen Emitter und Kollektor, sodass ein größerer Kollektorstrom I_C(T2) ≈ Ie fließt, der wiederum einen größeren Spannungsabfall am Emitter- bzw. Lastwiderstand R_Last = R1 + r_LED zur Folge hat.

Wegen der Reihenschaltung des PNP-Leistungstransistors T2 mit dem Lastwiderstand R_Last führt der größere Spannungsabfall am Emitter- bzw. Lastwiderstand R_Last zu einer Verringerung der Betriebsspannung U_EC(T2) am Transistor, sodass auch die Emitter-Basisspannung U_EB(T2) von T2 abnimmt und der Transistor etwas mehr sperrt.

In diesem Zusammenhang gilt es zu beachten, dass die Art der Stabilisierung des Arbeitspunktes von der Transistorgrundschaltung prinzipiell unabhängig ist!

Jetzt, wo wir schon sehr viel über die komplementäre Darlington-Schaltung (= Sziklai-Paar-Schaltung) im Bild 3 gelernt haben und wissen, dass diese als Stromquelle betrieben wird, die den elektrischen Strom in die Schaltung „drückt“, lässt sich auch klären, weshalb es anfangs beim NPN-Steuertransistors T1 mit der Dimensionierung des Basiswiderstandes Rb solche Probleme gab.

Da die komplementäre Darlington-Schaltung (im obenstehenden Bild links) als Stromquelle betrieben wird und sich diese in Reihe mit dem Emitter- bzw. Lastwiderstand R_Last = R1 + r_LED = 1,14 kΩ befindet, entfällt auf den Laststromzweig die weit aus größere Teilspannung U_Last:

U_Last = R_Last * I_Last

= 1,14 kΩ * 12,5 mA = 14,25 V,

sodass für die Spannungsversorgung der komplementären Darlington-Schaltung nur die kleinere Teilspannung U_EC(T2) übrig bleibt:

U_EC(T2) = Ub - U_Last

= 15 V – 14,25 V = 0,75 V,

sodass sich der PNP-Leistungstransistors T2 wegen der kleinen Teilspannung praktisch nur im Sättigungsbereich betreiben lässt!

Der Betrieb des PNP-Leistungstransistors T2 mit der kleinen Teilspannung hat zur Folge, dass sich die Arbeitsgerade nur über einen kleinen Spannungsbereich erstreckt, also ziemlich zusammengestaucht ist, sodass sich das Einstellen des Arbeitspunktes schwierig gestaltet. Erschwerend kommt noch hinzu, dass sich die Stromverstärkung B der komplementären Darlington-Schaltung multipliziert, sodass bereits kleinste Änderungen der Basisstromstärke Ib im µA-Bereich des NPN-Steuertransistors T1 zu großen Änderungen im Regelverhalten des PNP-Leistungstransistors T2 führen! -

Wie wir bereits wissen, arbeitet die komplementäre Darlington-Schaltung im linken Bild als
Stromquelle bei der der PNP-Leistungstransistors T2 den Strom Ie in die Schaltung, d.h. in den Lastwiderstand R_Last = R1 + r_LED „drückt“.

Um den Strom Ie entstehen zu lassen, der vom Emitter E(T2) über den Lastwiderstand R_Last gegen Masse („┴“) fließt, braucht es aber einen entsprechenden Potentialunterschied zwischen Emitter E(T2) und Masse („┴“). Und zwar in Form der Spannungsdifferenz ∆U_Last:

∆U_Last = U_E(T2) – U_Masse

= Ub – U_CE(T2) – U_Masse

= 15 V – 0,83 V – 0 V = 14,17 V

Dabei wird die Spannungsdifferenz in Form des Spannungsabfalls U_Last = 14,17 V am Lastwiderstand R_Last nicht nur durch den Lastwiderstand R_Last allein bestimmt, sondern auch maßgeblich durch den Strom Ie des PNP-Leistungstransistors T2,

Ie = U_Last / R_Last

= 14,17 V / 1,14 kΩ = 12,4298 mA ≈ 12,43 mA

wiederum eine Funktion der Kollektor-Emitter-Spannung U_CE(T2) ist:

Ie = f(U_CE(T2)) = f(U_CE(T2) = 0,83 V) = f(0,83 V) = 12,43 mA

Für Ie = f(U_CE(T2)) = f(0,76 V) folgt:

Ie = U_Last / R_Last

= ( Ub – U_CE(T2) ) / R_Last

= ( 15 V – 0,76 V ) / 1,14 kΩ

= 14,24 V / 1,14 kΩ = 12,49 mA ≈ 12,5 mA

Jetzt wissen wir, dass es der PNP-Leistungstransistors T2 ist, der über den Bahnwiderstand r_CE(T2)

r_CE(T2) = U_CE(T2) / Ie

= 0,76 V / 12,5 mA = 0,0608 mΩ

das Spannungspotential U_C(T2) = Ub – U_CE(T2) = 15 V – 0,76 V = 14,24 V → U_Last

vor dem Lastwiderstand R_Last entsprechend bis auf U_Last = 14,24 V, d.h. bis nahe +Ub = +15 V anhebt, sodass sich schließlich der Strom Ie = 12,5 mA einstellt, der quasi vom PNP-Leistungstransistors T2 als Stromquelle in den Lastwiderstand R_Last „gedrückt“ wird (siehe nachfolgende Schaltung im Bild 3 links):

(Vergrößern: auf Bild klicken! | Quelle: Elektronik-Kompendium)

Wie man in der obenstehenden komplementären Darlington-Schaltung im Bild 1 rechts sieht, ist diese direkt über den Strom Ie an die Masse („┴“) angebunden, während der Lastwiderstand R1 direkt mit der Spannungsversorgung +Ub verbunden ist.

Demzufolge kann der Lastwiderstand R1 erst dann einen Strom I_C „ziehen“, wenn der nachgeschaltete PNP-Leistungstransistor T1 aufgesteuert ist und das Spannungspotential hinter dem Lastwiderstand R1 nahezu vollständig auf Masse („┴“) legt.

Bildlich gesprochen „saugt“ der PNP-Leistungstransistor T1 den Laststrom Ic ≈ Ie1 förmlich in sich hinein, um diesen dann gegen Masse („┴“) abzuleiten. Deshalb handelt es sich bei der obenstehenden komplementären Darlington-Schaltung im Bild 1 rechts um eine Stromsenke!

Wenn man sich in der obenstehenden komplementären Darlington-Schaltung im Bild 1 rechts die rot markierte Spannungsgegenkopplung wegdenkt, dann erinnert die Schaltung an die leicht zu verstehende Emitterschaltung, jedenfalls was den PNP-Steuertransistor T2 anbetrifft, der ja für die Ansteuerung des PNP-Leistungstransistor T1 zuständig ist.

Und in der Tat bietet die Vorstufe des PNP-Steuertransistors T2 in Emitterschaltung den entscheidenden Vorteil, dass der Basis-Spannungsteiler bzw. der Basiswiderstand R3 mit dem vollen Spannungspotential der Versorgungsspannung +Ub verbunden ist:

U_R3 = Ub – U_BE(T2)

= 15 V – 0,65 V = 14,35 V

Nachfolgend wird davon ausgegangen, dass beide Schaltungen mit der Stromquelle (Bild 3 links) und der Stromsenke (Bild 1 rechts) über die gleichen Stromverstärkungen verfügen!

R3 = U_R3 / Ib2 → Ib2 = Ib = 1,8 mA aus der Tabelle der Schaltung von Bild 3 links mit Rb = 1 Ω

= 14,35 V / 1,8 mA = 7,972 kΩ ≈ 7,97 kΩ

Mit der insgesamt 7-fachen Stromverstärkung des PNP-Ersatztransistors folgt für den Kollektorstrom Ic:

Ic = Ib2 * B_Ersatz

= 1,8 mA * 7 = 12,6 mA 

Spannungsgegenkopplung mit Widerstand R2

Als Erstes stellt sich die Frage, wozu man überhaupt eine Spannungsgegenkopplung braucht (siehe rot markierte „Umleitung“ um die EB-Diode(T1) herum im obenstehenden Bild 1 rechts).

Beispiel:

Es ist Hochsommer bei 30 Grad im Schatten und zwecks Abkühlung gehen wir ins Freibad. Und zwecks Unterhaltung nehmen wir das kleine Transistorradio mit, um uns nach dem Schwimmen bei leiser Berieselung mit Musik unterhalten zu lassen. Wir stellen auf FM (= engl. „frequency modulation“, d.h. Frequenzmodulation auf dem UKW-Empfangsbereich) unseren Lieblingssender ein, der aber wegen der größeren Entfernung von ca. 100 km etwas schwach und demzufolge schmalbandig hereinkommt, sodass man den UKW-Sender schon sehr exakt einstellen, d.h. feinabstimmen muss. Dann aber gibt es mit dem Lieblingssender sofort gute Laune, die aber nicht lange währt, weil es nach etwa 10 Minuten in der Sonne aus dem Lautsprecher nur noch erbärmlich krächzt.

„Was hat denn das Transistorradio gekostet und wie viele Transistoren hat es überhaupt?“ fragt mein Freund, seines Zeichens Radio- und Fernsehgerätemechaniker. „Das war ein Schnäppchen aus dem 1-Euro-Markt um die Ecke“ sage ich. „Ja, das ist ja auch nicht zu überhören!“ sagt der Radiofuzzi grinsend, „Dem Transistor fehlt die … in der NF-Stufe mit der Gegentakt-Endstufe für etwas mehr Lautstärke im Lautsprecher!“ „Was fehlt dem Transistorradio in der Endstufe“ frage ich noch mal, weil ich wegen des Gekrächzes aus dem Lautsprecher nicht alles akustisch mitbekommen habe. …

Was aber fehlt dem Billigheimer aus China wirklich? Und was hat das mit dem Gekrächze aus dem Lautsprecher zu tun?

Ganz einfach! Was dem billigen Transistorradio fehlt, ist die Spannungsgegenkopplung in der Niederfrequenz-Stufe (NF) bzw. der Gegentakt-Endstufe des NF-Verstärkers.

Dazu muss man wissen, dass wenn man das Transistorradio oberhalb der zulässigen Umgebungstemperatur von z.B. 30 Grad Celsius betreibt, die Elektronen und Defektelektronen (= Elektronenmangel, pos. geladene Elektronen-Löcher) in den Halbleitern wie z.B. Dioden und Transistoren anfangen, auf den äußeren Elektronenschalen umherzutanzen, sodass sich die Leitfähigkeit bzw. der Ladungsträgertransport im Halbleiter verstärkt. Als Folge dessen nimmt die Verstärkung im Transistor zu, sodass sich der Kollektorstrom Ic vergrößert und sich der Arbeitspunkt auf der Arbeitsgeraden verschiebt (siehe Bild 12 und Bild 14). Und im Falle des Transistorradios macht sich das Verschieben des Arbeitspunktes so gar im Lautsprecher als Krächzen bemerkbar.

Um das Krächzen beim Transistorradio zu beseitigen bzw. um es loszuwerden, muss man das Transistorradio im Freibad nur aus der prallen Sonne in den Schatten legen und warten bis sich die Temperatur im Inneren des Gerätes unter die 30 Grad Marke abgesenkt hat. Das kann dann schon mal eine halbe Stunde dauern.

Der Elektroniker, der sich mit Radiogeräten auskennt, besorgt sich vom Hersteller den Schalt- und Plantinen-Layout-Plan, schaut welche Transistoren oder Chips für das Hochfrequenz-Empfangsteil (HF), den Zwischenfrequenz-Verstärker (ZF)

und den Niederfrequenz-Verstärker (NF) verbaut sind und welche Frequenz- oder Arbeitspunkt verstellende Bauteile z.B. in Form von RC-Gliedern (Reihen- oder Parallelschaltungen von Widerständen R und Kondensatoren C) um den einen oder anderen Chip herum verbaut sind.

Um z.B. den Arbeitspunkt beim Vorverstärker in der NF-Stufe zu stabilisieren, kann man dann den Teilwiderstand R2 im Basis-Spannungsteiler des NF-Vorverstärker-Transistors durch einen temperaturabhängigen Widerstand ersetzen oder nachträglich eine Spannungsgegenkopplung zwischen Emitter und Basis oder Kollektor und Basis in Form eines entsprechenden, parallel geschalteten Widerstandes vornehmen.

Da das Krächzen bei 30 Grad Celsius aber auch von der Gegentakt-Endstufe des NF-Verstärkers herrühren kann, weil sich der Arbeitspunkt wegen der Hitze und der eventuell schwachen Batterien verschoben hat, sollte man als Erstes den Ladezustand der Batterien überprüfen und diese vorsorglich gegen neue, unverbrauchte Batterien austauschen. Neue, fabrikfrische Batterien verfügen nämlich über eine etwas höhere Klemmenspannung bei gleichzeitig größeren Entnahmeströmen, sodass der Gegentakt-Endstufe des NF-Verstärkers bei 30 Grad Celsius im Freibad nicht gleich die Puste ausgeht, wenn man den Lautstärkeregler aufdreht. -

Im nachfolgenden Bild 1 der komplementären Darlington-Schaltung gib es so gar eine Faustformel zur Berechnung des Parallelwiderstandes R2 der Spannungsgegenkopplung:

R2 = 0,65 V / (≤ 0,1 * Ib1 )

= U_EB(T1) / ( 1/10 * Ib1 )

Wenn wir 10 % ( = 10 / 100 = 10 * 1 / 100 = 1/10 = 0,1 ) vom Basisstrom Ib1 wegnehmen sollen und die Gesamtstromverstärkung B = 7 bei der Ersatzschaltung mit nur einem Transistor beträgt, dann berechnet sich der (Gesamt-) Basisstrom I_B mit dem (Gesamt-) Kollektorstrom I_C ≈ I_E = 12,5 mA wie folgt:

I_B = I_C / B

= 12,5 mA / 7 = 1,7857 mA ≈ 1,8 mA

R2 = U_EB(T1) / ( 1/10 * Ib1 )

= 0,65 V / ( 0,1 * 1,8 mA ) = 0,65 V / 0,18 mA = 65 V / 18 kΩ = 3,61 kΩ ≈ 3,6 kΩ

Da der Widerstand R2 der Spannungsgegenkopplung parallel zum Bahnwiderstand r_EB(T1) geschaltet ist und beide wiederum mit dem Lastwiderstand R1 in Reihe geschaltet sind, haben wir es bei allen drei Widerständen mit einem belasteten Spannungsteiler mit dem Gesamtwiderstand R_Sp.Teiler = R1 + ( R2 // r_EB(T1) ) zu tun:

r_EB(T1) = U_EB(T1) / Ib1

= 0,65 V / 1,8 mA = 65 V / 180 kΩ = 0,361 kΩ ≈ 360 Ω

Jetzt sieht man bereits, dass der Widerstand R2 der Spannungsgegenkopplung tatsächlich 10x größer ist als der Bahnwiderstand r_EB(T1) der EB-Diode EB(T1) des PNP-Leistungstransistors T1. -

(Vergrößern: auf Bild klicken! | Quelle: Elektronik-Kompendium)

[ easy electronic 200 ] [ Seitenanfang ] [ Versuch 95 ]